Abstract
We address the expressions for the rates of the Keplerian orbital elements within a two-body problem perturbed by the tides in both partners. Formulae for these rates appeared in the literature in various forms, at times with errors. We reconsider, from scratch, the derivation of these rates and arrive at the Lagrange-type equations which, in some details, differ from the corresponding equations obtained previously by Kaula (Rev Geophys 2:661–684, 1964). We also write down detailed expressions for \({\mathrm{d}}a{/}{\mathrm{d}}t\), \({\mathrm{d}}e{/}{\mathrm{d}}t\) and \({\mathrm{d}}i{/}{\mathrm{d}}t\), to order \(e^4\). They differ from Kaula’s expressions which contain a redundant factor of \(M{/}(M+M^{\,\prime })\), with M and \(M^{\,\prime }\) being the masses of the primary and the secondary. As Kaula was interested in the Earth–Moon system, this redundant factor was close to unity and was unimportant in his developments. This factor, however, must be removed when Kaula’s theory is applied to a binary composed of partners of comparable masses. We have found that while it is legitimate to simply sum the primary’s and secondary’s inputs in \({\mathrm{d}}a{/}{\mathrm{d}}t\) or \({\mathrm{d}}e{/}{\mathrm{d}}t\), this is not the case for \({\mathrm{d}}i{/}{\mathrm{d}}t\). So our expression for \({\mathrm{d}}i{/}{\mathrm{d}}t\) differs from that of Kaula in two regards. First, the contribution due to the dissipation in the secondary averages out when the apsidal precession is uniform. Second, we have obtained an additional term which emerges owing to the conservation of the angular momentum: a change in the inclination of the orbit causes a change of the primary’s plane of equator.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Motivation
The Darwin–Kaula theory of bodily tides is a fundamental development with many ramifications. It provides the means for calculating spin-orbit evolution of planets and moons, including their entrapment in spin-orbit resonances (e.g. Correia et al. 2003; Correia and Laskar 2003; Makarov et al. 2012; Noyelles et al. 2013) and the final obliquities (Cunha et al. 2015; Ferraz-Mello et al. 2008). In the situations where tidal heating is intensive, an approach based on this theory gives the key to the thermal histories of celestial bodies (e.g. Peale and Cassen 1978; Efroimsky and Makarov 2014; Efroimsky 2018; Makarov et al. 2018). This theory also enables one to calculate the influence of the lunisolar tides on the orbital motion of an artificial spacecraft (Pucacco and Lucchesi 2018).
In the current paper, we address the orbit evolution within a two-body problem perturbed by the tides in both partners. Specifically, we are interested in the tidal rates \({\mathrm{d}}a{/}{\mathrm{d}}t\), \({\mathrm{d}}e{/}{\mathrm{d}}t\) and \({\mathrm{d}}i{/}{\mathrm{d}}t\) to order \(e^4\) (the symbols being used as defined in Table 1). Formulae for these rates appeared in the literature in various forms, usually to a lower precision and sometimes with mistakes. So we compare our expressions with those suggested in some other publications, including the cornerstone work by Kaula (1964).
For the additional tidal potential of a disturbed body, Kaula (1964) developed an expansion valid for an arbitrary rheology (i.e. for an arbitrary frequency dependence of the quality function \(k_l{/}Q_l\)). Kaula’s derivation was terse and omitted several steps as self-evident. We accurately fill in these gaps and point out a step at which Kaula made a tacit approximation \(M\gg M^{\,\prime }\), where M and \(M^{\,\prime }\) are the masses of the primary and the secondary. Owing to that assumption, Kaula’s expressions for the orbital elements’ rates contain a redundant factor of \(M{/}(M+M^{\,\prime })\). Since Kaula was concerned with the Earth–Moon system, this approximation made little difference as the factor was close to unity. However, in the case of a binary composed of bodies of comparable masses, this redundant factor must be removed from these expressions.
We also reexamine from scratch Kaula’s derivation of the rates \({\mathrm{d}}a{/}{\mathrm{d}}t\), \({\mathrm{d}}e{/}{\mathrm{d}}t\), and \({\mathrm{d}}i{/}{\mathrm{d}}t\). We find that while it is legitimate to simply sum the primary’s and secondary’s inputs in da / dt or de / dt, this is not the case for di / dt. It turns out that in the expression for the primary’s di / dt the contribution due to the dissipation in the secondary averages out when the apsidal precession is uniform. Also, in that expression we obtain an additional term emerging from the conservation of the angular momentum: a change in the inclination of the orbit causes a change of the primary’s plane of equator. For these two reasons, our formula for di / dt differs considerably from that of Kaula.
2 Basics
2.1 The two-body problem perturbed by tides
Consider two near-spherical bodies. One, called “planet” or “primary”, has a mass M and an inertial position \({\varvec{\rho }}\). Another, named “secondary”, has a mass \(M^{\,\prime }\) and is residing in \({\varvec{\rho }}^{\,\prime }\). We are interested in the orbital evolution of this system, with tides in both partners taken into account. Within this setting, Kaula (1964) expressed the perturbing gravitational potential through the Keplerian elements of the mutual orbit, which allowed him to describe the evolution of the system by Lagrange’s planetary equations. Three caveats are in order regarding Kaula’s development.
First of all, by definition of a mutual orbit, the position of the secondary is measured with respect to the primary’s centre of mass. Let \({{\varvec{F}}}\) be the force exerted by the primary on the secondary. By virtue of Newton’s third law of motion, the secondary simultaneously exerts a force \(-\,{{\varvec{F}}}\) on the primary. Hence, the mutual acceleration reads as
In the limit of the secondary being a test particle (\(M\,\gg \,M^{\,\prime }\)), the above relation becomes simply \(\varvec{a}\,=\,{{\varvec{F}}}{/} M^{\,\prime }\), which was the tacit approximation accepted by Kaula. We in our study shall rely on the general expression (1) and therefore shall employ the reduced mass \(\beta \) defined as
Secondly, it should be noted that within Kaula’s formalism the elements \((a,\,e,\,i,\,{{\mathcal {M}}},\,\omega ,\,\Omega )\) of the mutual orbit are defined in an inertially fixed frame coinciding with the primary’s equator at the instant when the equations of motion are computed. To simplify the interpretation of the Keplerian elements, we here assume that they are defined in a frame coprecessing with the primary’s equator. Footnote 1 The perturbing forces showing up in this setting include the inertial forces associated with the non-Galilean nature of the coprecessing frame. An important feature of these forces is that they depend not only on the positions but also on velocities. As was pointed out in Efroimsky (2005a, b), for such kind of disturbances the Lagrange- and Delaunay-type planetary equations in their standard form render orbital elements which are not osculating. To be more precise, if we wish the orbital element to osculate the orbit defined in a non-inertial frame, not only must we amend the disturbing function, but we should also insert in the Lagrange- and Delaunay-type equations additional terms that are not part of the disturbing function. If, however, we choose only to amend the disturbing function, the orbital equations will give us Keplerian orbital elements which will not osculate with the orbit defined in the non-inertial frame, but will instead osculate with the orbit as seen in the inertial frame. Footnote 2
While the treatment in the coprecessing frame has its advantages, there exists alternatives to it: both the orbital motion and the primary’s spin can be described in the Laplace plane (e.g. Boué et al. 2016; Rubincam 2016), or the primary’s spin can be reckoned from the orbital plane whose Keplerian elements are given in the Laplace plane (e.g. Néron de Surgy and Laskar 1997; Correia et al. 2003; Correia and Laskar 2003, 2010).
Lastly, a complete description of motion requires not only the aforementioned set of the Keplerian elements relative to the primary’s equator, but also a set of the elements \((a^{\,\prime },\,e^{\,\prime },\,i^{\,\prime },\,{{\mathcal {M}}}^{\,\prime },\, \omega ^{\,\prime },\,\Omega ^{\,\prime })\) relative to the secondary’s equator. Footnote 3 Therefore, the equations of motion must satisfy the relations existing between these two sets.
With all these details taken into account, we now derive the Lagrange-type planetary equations compatible with Kaula’s (1964) formalism.
2.2 Lagrangian formalism
2.2.1 Lagrangian function
Let \({{\varvec{\mathbb {I}}}}_\mathrm {n}\) be the primary’s inertia matrix and \({{\varvec{\mathbb {R}}}}\) the rotation matrix, function of the Euler (\(3, -\,1,\,3\)) angles \( \Theta = (\psi , \varepsilon , \theta )\), describing orientation in an inertial frame. More explicitly,
where \({{\varvec{\mathbb {R}}}}_1\) and \({{\varvec{\mathbb {R}}}}_3\) represent the rotation matrices around the first and third axes, respectively:
The angle \(\psi \) is thus the longitude of the descending node of the equator with respect to the inertial frame, \(\varepsilon \) the inclination of the spin axis in the same inertial frame, and \(\theta \) the rotation angle around the body’s figure axis (see Fig. 1). This convention is chosen for \(\theta \) to be reckoned from the descending node of the equator, as in Kaula (1964). We similarly denote by \({{\varvec{\mathbb {I}}}}_\mathrm {n}^{\,\prime }\) and \({{\varvec{\mathbb {R}}}}^{\,\prime }(\,{\varvec{\Theta }}^{\,\prime }=(\psi ^{\,\prime },\varepsilon ^{\,\prime },\theta ^{\,\prime })\,)\) the inertia and rotation matrices of the secondary, respectively. The planetocentric position of the secondary will be denoted with \({\varvec{r}}\), when expressed in the body-fixed frame of the primary, or with \({\varvec{r}}^{\,\prime }\), when expressed in the body-fixed frame of the secondary:
where \({}^\mathrm {T}{(\cdot )}\) denotes the transposition operator. Notice that we do not strictly follow Kaula’s convention because, to represent the orbit, we are employing the corotating frames instead of the coprecessing ones. At the end of the derivation, we explain how to switch between these two classes of frames.
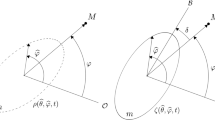
Definition of the Euler (\(3,-1,3\)) angles \((\psi , \varepsilon , \theta )\). The inertial frame is denoted with \(({\varvec{i}}_\mathcal {R}, {\varvec{j}}_\mathcal {R}, {\varvec{k}}_\mathcal {R})\), and the reference plane \(({\varvec{i}}_\mathcal {R}, {\varvec{j}}_\mathcal {R})\) is represented by the horizontal great circle. The origin of longitude, labelled \(A_\mathcal {R}\), is the intersection of \(\varvec{i}_\mathcal {R}\) with the unit sphere. The projection of the primary’s equatorial plane on the unit sphere is the great circle whose descending node on the reference plane is V. The point N is the orbit’s ascending node on the equator, while A defines a reference meridian. The intersection of the orbital plane with the unit sphere is represented by the thick great circle passing through N. The orientation of the primary on the reference plane is parameterised by three angles: the precession angle \(\psi \) measured between \(A_\mathcal {R}\) and V, the tilt \(\varepsilon \) of the figure axis, and the rotation angle \(\theta \) defining the angular separation of A from V. Analogous quantities \((\psi ', \varepsilon ', \theta ')\) are defined for the secondary (not shown in the figure). When the orbit is described in the corotating frame of the primary, its longitude of ascending node, \({\bar{\Omega }}\), is the angular separation of N from A, while its inclination on the primary’s equator is i
For the state of the system to be entirely defined, we also introduce the primary’s and secondary’s angular velocities \({\varvec{\Omega }}\) and \({\varvec{\Omega }}^{\,\prime }\), respectively. These vectors are expressed in their respective body-fixed frame.
The Lagrangian \({{\mathcal {L}}} = T-V\) of the system is a function of \(({\varvec{\Omega }},\,{\varvec{\Omega }}^{\,\prime },\,\dot{{\varvec{r}}\,},\,{\varvec{r}},\,{\varvec{r}}^{\,\prime })\). Specifically, the kinetic energy \(T({\varvec{\Omega }},\,{\varvec{\Omega }}^{\,\prime },\,\dot{{\varvec{r}}},\,{\varvec{r}})\) is given by
where \(\beta = MM^{\,\prime }{/}(M+M^{\,\prime })\) is the reduced mass of the system. As for the potential energy \(V({\varvec{r}}, {\varvec{r}}^{\,\prime })\), we decompose it into the point mass potential energy \(V_0({\varvec{r}}) = - {{\mathcal {G}}}MM^{\,\prime }{/}r\) and a perturbation \(V_1({\varvec{r}}, {\varvec{r}}^{\,\prime })\), whose expression will be specified later on:
To this Lagrangian function, we have to add the constraint \({{\varvec{\mathbb {R}}}} {\varvec{r}} = {{\varvec{\mathbb {R}}}}^{\,\prime } {\varvec{r}}^{\,\prime }\) which links two expressions of the same quantity \({\varvec{\rho }}^{\,\prime }-{\varvec{\rho }}\). This constraint will enter the Lagrangian, accompanied with Lagrange multipliers \({\varvec{\Lambda }}\in \mathbb {R}^3\), thus leading to a new Lagrangian
Note that this Lagrangian also depends on the additional variables \(({\varvec{\Theta }},\,{\varvec{\Theta }}^{\,\prime })\).
2.2.2 Spin operator
To derive the Euler–Poincaré–Lagrange equations of motion for this Lagrangian, let us first introduce the spin operator \({\varvec{\hat{J}}}\,\equiv \,{{\varvec{\mathbb {J}}}}\,\partial {/}\partial {\varvec{\Theta }}\), where \({{\varvec{\mathbb {J}}}}\) is a matrix yet to be defined (e.g. Boué 2017; Boué et al. 2017). On the one hand, by definition of the spin operator, Footnote 4 the time derivative of an arbitrary function \(f({\varvec{\Theta }})\) can be written as
with \({\varvec{\Omega }}\) the angular velocity expressed in the same frame as \({\varvec{\hat{J}}}\), which here is the body-fixed frame. On the other, applying the chain rule for the time derivative of \(f({\varvec{\Theta }})\), we get
By identification of (9) and (10), we deduce that \({{\varvec{\mathbb {J}}}}\) is the matrix such that \(\dot{{\varvec{\Theta }}} = {}^\mathrm {T}{{{\varvec{\mathbb {J}}}}}\,{\varvec{\Omega }}\), or equivalently, \({\varvec{\Omega }} = {}^\mathrm {T}{{{\varvec{\mathbb {J}}}}}^{-1}\dot{{\varvec{\Theta }}}\).
Knowing that the components of \({\varvec{\Omega }}\) in the body-fixed frame (rotated with respect to an inertial frame according to 3) are
we get
The matrix \({{\varvec{\mathbb {J}}}}^{\,\prime }\) is equivalently defined for the secondary.
In the following, we also have to determine the image of the function \({{\varvec{\mathbb {R}}}} \mapsto {\varvec{\Lambda }} \cdot {{\varvec{\mathbb {R}}}} \varvec{r}\) by the spin operator \({\varvec{\hat{J}}}\) which, by definition, evaluates the variation of a function under infinitesimal rotation of the primary (therefore the rotation matrix \({{\varvec{\mathbb {R}}}}\) alone is affected by the operator \({\varvec{\hat{J}}}\) and \({\varvec{r}}\) shall be taken constant in this calculation). Using \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}\dot{{{\varvec{\mathbb {R}}}}}\,{\varvec{v}} = {\varvec{\Omega }} \times {\varvec{v}}\) for any vector \(\varvec{v}\in \mathbb {R}^3\), we get
Identifying (9) with (15), we obtain
2.2.3 Equations of motion
Using the matrices \({{\varvec{\mathbb {J}}}}\) and \({{\varvec{\mathbb {J}}}}^{\,\prime }\) defined hereinabove, the Euler–Poincaré–Lagrange equations of motion read (e.g. Boué 2017; Boué et al. 2017)
Notice that the Euler–Lagrange equation (20) is equal to zero. This is due to the fact that the Lagrangian does not depend on \(\dot{{\varvec{r}}}^{\,\prime }\). Let us now rewrite the equations of motion (17–20) in terms of the original Lagrangian \({\mathcal {L}}\) :
with, for the problem studied in this paper, \(\partial {{\mathcal {L}}}{/}\partial {\varvec{\Theta }} = \partial {{\mathcal {L}}}{/}\partial {\varvec{\Theta }}^{\,\prime } = {\varvec{0}}\). To derive the first two equations, we made use of relation (16).
From the equation of motion (24), we determine the expression of the Lagrange multiplier, namely
Substituting this expression in the other equations of motion (21–23), we get
In the first equation of motion, we made use of the relations \({\varvec{r}} = {}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime } \varvec{r}^{\,\prime }\) and \(({{\varvec{\mathbb {R}}}}{\varvec{u}} \times {{\varvec{\mathbb {R}}}}{\varvec{v}}) = {{\varvec{\mathbb {R}}}}({\varvec{u}}\times {\varvec{v}})\). In the last equation of motion, we recognise the force \({\varvec{F}}^{\,\prime } \equiv \partial {{\mathcal {L}}}{/}\partial {\varvec{r}}^{\,\prime }\) written in the body-fixed frame of the primary thanks to the rotation matrix \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\). Moreover, in the first two equations of motion, we observe the presence of the torque \({\varvec{r}}^{\,\prime }\times {\varvec{F}}^{\,\prime }\) expressed in the body-fixed frame of the primary in Eq. (26) and in the body-fixed frame of the secondary in Eq. (27).
Inserting the expressions for the kinetic energy (6) and the potential energy (7) in Eq. (28), we get
Were the right-hand side equal to zero, we would have obtained the equation of motion of the classical two-body problem. But here this is not the case. The first three terms of the right-hand side account for the inertial forces of the non-Galilean frame in which \({\varvec{r}}\) is expressed, while the last two terms represent the perturbation induced by tides. It is common to name the quantity \(-\,V_1{/}\beta \) as the perturbing function and to denote it with \({\mathcal {R}}\). In this notation, Eq. (29) reads:
2.3 Hamiltonian formalism
To get the Hamiltonian form of the equations of motion, we apply a Legendre transformation on the Lagrangian. Let \({\varvec{\Sigma }}\), \({\varvec{\Pi }}^{\,\prime }\) and \({\varvec{p}}\) be the generalised momenta given by
\({\varvec{\Sigma }}={\varvec{\Pi }} + {\varvec{\Gamma }}\) is the sum of the angular momenta of the primary (\({\varvec{\Pi }}\)) and of the orbit (\({\varvec{\Gamma }} = {\varvec{r}}\times {\varvec{p}}\)), \({\varvec{\Pi }}^{\,\prime }\) is the angular momentum of the secondary and \({\varvec{p}}\) is the linear orbital momentum with respect to the inertial frame but expressed in the body-fixed frame of the primary.
The Hamiltonian \({{\mathcal {H}}} \equiv {\varvec{\Sigma }} \cdot {\varvec{\Omega }} + {\varvec{\Pi }}^{\,\prime }\cdot {\varvec{\Omega }}^{\,\prime } + {\varvec{p}} \cdot \dot{{\varvec{r}}} - {{\mathcal {L}}}\) can be written as \({{\mathcal {H}}} = T + V\) with
The equations of motion deduced from the Legendre transformation are
The kinematic equations of motion are
Recall that these expressions are general. In our case, the two-body problem perturbed by tides, \({{\mathcal {H}}}\) is independent of \({\varvec{\Theta }}\) and \({\varvec{\Theta }}^{\,\prime }\). So the partial derivatives of the Hamiltonian over these two quantities in equations (35) and (36) become zero.
2.4 Elliptical elements
Orientation of the orbit as seen from both partners. The projection of the primary’s equatorial plane on the unit sphere is the great circle passing through A—the reference meridian—and N—the orbit ascending node. Equivalent points are defined on the projection of the secondary’s equator on the unit sphere and are denoted \(A^{\,\prime }\) and \(N^{\,\prime }\), respectively. The intersection of the orbital plane with the unit sphere is represented by the thick great circle passing through N, \(N^{\,\prime }\) and P—the direction of the pericentre. When the orbit is described in the corotating frame of the primary, its longitude of ascending node, denoted \({\bar{\Omega }}\), is the angular separation of N from A. Otherwise, in the corotating frame of the secondary, the longitude of ascending node, denoted \({\bar{\Omega }}^{\,\prime }\), is measured between \(A^{\,\prime }\) and \(N^{\,\prime }\). The angle between N and \(N^{\,\prime }\) is equal to the difference \(\omega -\omega ^{\,\prime }\) between the two arguments of the orbit pericentre reckoned from N and \(N^{\,\prime }\), respectively. i and \(i^{\,\prime }\) are the orbital inclinations with respect to the primary’s and secondary’s equator, respectively
In Kaula’s work, the equations of motion are written in terms of elliptical elements (a, e, i, \({\mathcal {M}}\), \(\omega \), \(\Omega \)) reckoned from an inertial frame instantaneously comoving with the primary’s precessing equator. Footnote 5 This set of variables becomes singular at zero inclination or zero eccentricity. We will nevertheless provide the equations of motion in this set of variables for an easier comparison with previous works. Here, we define elliptical elements \((a,e,i,{{\mathcal {M}}},\omega ,{\bar{\Omega }})\) (represented in Fig. 2) as a change of variable from the conjugated variables \(({\varvec{p}}, {\varvec{r}})\). Therefore, they describe the instantaneous ellipse \({\mathcal {E}}\) constructed from the position vector \({\varvec{r}}\) and its inertial velocity \(\dot{{\varvec{r}}} + {\varvec{\Omega }}\times {\varvec{r}}\), both defined in the primary body-fixed frame. Our set of Keplerian elements differs from Kaula’s by the frame in which it is defined. This choice only impacts the longitude of the ascending node, hence the introduction of a new symbol \({\bar{\Omega }}\). The two longitudes of ascending node are related to each other by
As for the couple \(({\varvec{p}}, {\varvec{r}})\), to the position vector \({\varvec{r}}^{\,\prime }\) we associate the elliptical elements \((a^{\,\prime }, e^{\,\prime }, i^{\,\prime }, {{\mathcal {M}}}^{\,\prime }, \omega ^{\,\prime },\) \({\bar{\Omega }}^{\,\prime })\) of the ellipse \({\mathcal {E}}^{\,\prime }\) defined by \({\varvec{r}}^{\,\prime }\) and its inertial velocity, both expressed in the secondary body-fixed frame. Thus, both ellipses \({\mathcal {E}}\) and \({\mathcal {E}}^{\,\prime }\) are same up to a rotation, i.e. \(a=a^{\,\prime }\), \(e=e^{\,\prime }\) and \({{\mathcal {M}}}={{\mathcal {M}}}^{\,\prime }\). To get the relation between \(({\bar{\Omega }}^{\,\prime }, i^{\,\prime }, \omega ^{\,\prime })\) and \(({\bar{\Omega }}, i, \omega )\), we consider the following function with values in \(\mathrm {SO}(3)\) :
We have \({\varvec{\mathbb {F}}} = {}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\). Hence, for fixed orientation of the bodies (as in Eqs. 37 and 40), we get \(d{\varvec{\mathbb {F}}} = {\varvec{0}}\) and therefore \(d{\varvec{\mathbb {F}}}\,{}^\mathrm {T}{{\varvec{\mathbb {F}}}} = {\varvec{0}}\). Let us denote by \({\varvec{K}}\), \({\varvec{i}}\), \({\varvec{k}}\), \({\varvec{i}}^{\,\prime }\), \({\varvec{K}}^{\,\prime }\) the unit vectors of the rotations of angle \({\bar{\Omega }}\), i, \(\omega -\omega ^{\,\prime }\), \(-i^{\,\prime }\), and \(-{\bar{\Omega }}^{\,\prime }\), respectively. \({\varvec{K}}\) and \({\varvec{K}}^{\,\prime }\) are the primary’s and secondary’s figure axes, respectively, \({\varvec{i}}\) and \({\varvec{i}}^{\,\prime }\) are the directions of the orbit ascending node relative to the primary’s and the secondary’s equatorial plane, respectively, and \({\varvec{k}}\) is the orbit normal (see Fig. 2). In the orbital reference frame, we have in particular
The product \(d{\varvec{\mathbb {F}}}\,{}^\mathrm {T}{{\varvec{\mathbb {F}}}}\) belongs to the Lie algebra \(\mathrm {so}(3)\). Let \(d{\varvec{\mathbb {X}}} \equiv {{\varvec{\mathbb {R}}}}_1(-i){{\varvec{\mathbb {R}}}}_3(-{\bar{\Omega }})\,d{\varvec{\mathbb {F}}} \,{}^\mathrm {T}{{\varvec{\mathbb {F}}}} {{\varvec{\mathbb {R}}}}_3({\bar{\Omega }}) {{\varvec{\mathbb {R}}}}_1(i)\) be its expression in the orbit frame. We have (see Appendix “A”)
where the hat over any vector \({\varvec{v}} = (v_x, v_y, v_z)\) denotes the skew-symmetric matrixFootnote 6
Applying to \(d{\varvec{\mathbb {X}}} = {\varvec{0}}\) the canonical bijection from \(\mathrm {so}(3)\) to \(\mathbb {R}^3\) (i.e. the inverse of the hat application), we get
We now replace the vectors \({\varvec{K}}\), \({\varvec{i}}\), \({\varvec{k}}\), \({\varvec{i}}^{\,\prime }\), \({\varvec{K}}^{\,\prime }\) by their coordinates and get
We finally deduce the Jacobian \({\varvec{\mathbb {A}}}_1\) of the transformation \(({\bar{\Omega }}^{\,\prime }, i^{\,\prime }, \omega ^{\,\prime }) \rightarrow ({\bar{\Omega }}, i, \omega )\), which reads
and thus,
2.5 Equations of motion of the Keplerian elements
Planetary equations of motion for \((a, e, i, {{\mathcal {M}}}, \omega , {\bar{\Omega }})\) are deduced from the canonical equations of motion satisfied by Delaunay variables (rescaled by the reduced mass)
Let \({\varvec{X}} = {}^\mathrm {T}{(L, G, H)}\), \({\varvec{x}} = {}^\mathrm {T}{(l, g, h)}\), \({\varvec{Y}} = {}^\mathrm {T}{(a, e, i)}\) and \({\varvec{y}} = {}^\mathrm {T}{({{\mathcal {M}}}, \omega , {\bar{\Omega }})}\). We have
thus
where \({{\varvec{\mathbb {M}}}}\) is the Jacobian defined as
The result, written in a matrix form, reads
These are the classical planetary equations in the form of Lagrange. Let us denote by \({\varvec{\mathbb {B}}}\) the Poisson matrix, i.e. the matrix standing before the gradient of the Hamiltonian in Eq. (55). In the problem under consideration, an adjustment to this equation has to be made. Owing to the constraint between \({\varvec{r}}\) and \({\varvec{r}}^{\,\prime }\), we have to add the contribution from \(({\bar{\Omega }}^{\,\prime }, i^{\,\prime }, \omega ^{\,\prime })\) to the time derivative of the state vector, see Eq. (37). This is done through the medium of the Jacobian \({\varvec{\mathbb {A}}}\) as follows (see Appendix “B”):
where \({\varvec{\mathbb {B}}}^{\,\prime }\) is the equivalent of the matrix \({\varvec{\mathbb {B}}}\) but written as a function of \((a,\,e,\,i^{\,\prime })\) instead of \((a,\,e,\,i)\). After some algebra, we arrive at
2.6 Perturbed two-body problem
Here, we split the Hamiltonian as \({{\mathcal {H}}} = {{\mathcal {H}}}_0 + V_1\) with \({{\mathcal {H}}}_0 = T+V_0\), i.e.
We shall now write this Hamiltonian in terms of the elliptical elements \((a,e,i,{{\mathcal {M}}},\omega ,{\bar{\Omega }})\). First, we recognise the Keplerian energy of the two-body problem
Then, \({\varvec{r}}\times {\varvec{p}}\) is the orbital angular momentum, thus
Moreover, we recall that \({{\varvec{\mathbb {I}}}}_\mathrm {n}^{-1}({\varvec{\Sigma }} - {\varvec{r}}\times {\varvec{p}})\) is equal to the primary’s angular velocity \({\varvec{\Omega }} = {}^\mathrm {T}{(\Omega _X, \Omega _Y, \Omega _Z)}\). The gradient of the Hamiltonian \({{\mathcal {H}}}_0\) is then
Let \(n = ({{\mathcal {G}}}(M+M^{\,\prime })/a^3)^{1/2}\) be the Keplerian mean motion. The equations of motion become
Using the expressions \(L=\beta n a^2\) and \(G = L(1-e^2)^{1/2}\) and substituting \(V_1\) by \(-\beta {\mathcal {R}}\), these equations of motion read
Had we defined the Keplerian elements in the coprecessing frame of the primary rather than in its corotating frame, the longitude of the ascending node would have been \(\Omega = {\bar{\Omega }} + \theta \). Then, in all the equations of motion, \({\bar{\Omega }}\) would have been replaced by \(\Omega - \theta \), and in particular the last equation of motion would have become
Let us now compare Eqs. (78–83) with the well-known Lagrange planetary equations. As the Keplerian elements are here defined with respect to a moving frame, the resulting equations of motion for i, \(\omega \) and \({\bar{\Omega }}\) contain driving terms which are functions of the components \((\Omega _X, \Omega _Y, \Omega _Z)\) of the angular velocity \({\varvec{\Omega }}\) of this frame. Furthermore, we observe that the equations of motion are not symmetric in \((i,\omega ,{\bar{\Omega }})\) and in \((i^{\,\prime },\omega ^{\,\prime },{\bar{\Omega }}^{\,\prime })\). This is due to the rotation matrix \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\) between the frames in which the two sets of Keplerian elements are defined. We nevertheless recover the lost symmetry in the equations of motion when this matrix \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\) becomes a single rotation around the third axis (i.e. when \(i=i^{\,\prime }\) and \(\omega =\omega ^{\,\prime }\)).
2.7 Rotation equations of motion
Equations (78–83) are the equivalent of the Lagrange planetary equations. For completeness, we now provide the explicit equations of motion for the rotation of the two bodies, given by Eqs. (35–36) and (38–39). While these equations should involve the spin operators represented by the matrices \({{\varvec{\mathbb {J}}}}\) and \({{\varvec{\mathbb {J}}}}^{\,\prime }\), we discard those terms as the perturbing potential energy is independent of \({\varvec{\Theta }}\) and \({\varvec{\Theta }}^{\,\prime }\). The equations also involve the orbital angular momentum operator \({\varvec{\hat{L}}}^{\,\prime } = {\varvec{r}}^{\,\prime } \times \partial _{{\varvec{r}}^{\,\prime }}\) expressed by a matrix \({\varvec{\mathbb {L}}}^{\,\prime }\) such that
for all functions \(f(a^{\,\prime },\,e^{\,\prime },\,i^{\,\prime },\,{{\mathcal {M}}}^{\,\prime },\, \omega ^{\,\prime },\,{\bar{\Omega }}^{\,\prime })\). Applying the same approach as in Sect. 2.2, we arrive at
Developing the matrix products, we obtain the following dynamical equations of motion:
and the associated kinematic equations of motion:
Recall that in these equations, \({\varvec{\Omega }} = {{\varvec{\mathbb {I}}}}_\mathrm {n}^{-1}({\varvec{\Sigma }}- {\varvec{r}} \times {\varvec{p}})\) and \({\varvec{\Omega }}^{\,\prime } = {{{\varvec{\mathbb {I}}}}_\mathrm {n}^{\,\prime }}^{\,-1} {\varvec{\Pi }}^{\,\prime }\).
2.8 The gyroscopic approximation and the approximation of constant inertia matrices
In the equations of motion derived above, the inertial forces are expressed in terms of the components of the rotation vectors \({\varvec{\Omega }}\) and \({\varvec{\Omega }}^{\,\prime }\). To simplify these dependencies, we carry out two steps.
-
(a)
We employ the gyroscopic approximation, i.e. assume that the rotation about the axis of maximal inertia is much faster than any change in this axis’ orientation. Mathematically, this implies:
$$\begin{aligned} |\,\dot{\theta }\,|\,\gg \,|\dot{\psi }|,\;\,|\,\dot{\varepsilon }|\qquad \text{ and }\qquad |\,\dot{\theta }^{\,\prime }\,|\,\gg \,|\,\dot{\psi }^{\,\prime }\,|,\;\,|\,\dot{\varepsilon }^{\,\prime }\,|\,\;. \end{aligned}$$(99) -
(b)
We neglect the variation of the inertia matrices in the expressions for the angular momenta \({\varvec{\Pi }}\) and \({\varvec{\Pi }}^{\,\prime }\). This approximation is nontrivial because, after all, the tidal theory is about deformation. So one always needs to justify accurately why on one occasion the deformations must be taken into account and neglected on other. This justification is provided in Frouard & Efroimsky (2017b, Section 3.1 and Footnote 6).
Let us denote the partners’ principal moments of inertia with \((A,\,B,\,C)\) and \((A^{\,\prime }, \,B^{\,\prime },\,C^{\,\prime })\). Then, the angular momentum of the primary can be written as
In the afore-explained approximation, its rate becomes
Similar formulae will be valid for the secondary.
The rate of the angular momentum,
will, owing to Eqs. (65), (72–77), and (87–88), be equal to
Naturally, the evolution rate of \({\varvec{\Pi }}\) has a form analogous to that of \({\varvec{\Pi }}^{\,\prime }\), Eqs. (90–92). Inserting the exact expressions (100–102) and the approximate expressions (103–105) in Eqs. (107–109), we exclude the components of the angular momentum, to be left with the components of the angular velocity only:
with \(\Omega _Z \approx \dot{\theta }\). Similarly, for the secondary we have
We can now rewrite the equations of motion (78–83) where \(\Omega _X\) and \(\Omega _Z\) are substituted by their expressions (110,111). Furthermore, we make the approximations \(C \gg (B-A)\) and \(\Omega _Z \approx \dot{\theta }\) and we replace \({\bar{\Omega }}\) with \((\Omega - \theta )\). We get
To close the system, we have to add the equations
Be mindful that in Eq. (121) we employed the relation \(\Omega _Z - \dot{\theta } = \dot{\psi }\cos \varepsilon = -\,(\Omega _X\sin \theta + \Omega _Y\cos \theta ) \cot \varepsilon \), while in Eq. (122) the relation \(\dot{\varepsilon } = -\,\Omega _X\cos \theta +\Omega _y\sin \theta \) was used. Besides, we would emphasise that Eqs. (116–123) have been obtained under the gyroscopic approximation; for that reason, it would be illegitimate to consider the limit of \(\dot{\theta }\,\longrightarrow \,0\). Therefore, the presence of \(\dot{\theta }\) in the denominator in Eqs. (118) and (120–121) produces no singularity. In the cases where the gyroscopic approximation is invalid, one has to rely on the equations of motion (78–83) instead.
2.9 Comparison with Kaula (1964)
In his 1964 paper, Kaula was mainly interested in the evolution of the semimajor axis, the eccentricity and the inclination. The derivation of the equations (38) in Kaula (1964) should thus only be compared with our formulae (116), (117) and (118). Although the evolution rates of a and e are identical in both approaches up to the definition of the disturbing function (see Sect. 3.2), the two expressions of the time derivative of the inclination i display important dissimilarities. This difference of behaviour between (a, e), on the one hand, and i, on the other, is due to the fact that only i is affected by a rotation of the reference frame. Let us recall that in Kaula (1964) elliptical elements are defined with respect to a fixed reference frame coinciding with the primary’s equator at the time when the equations of motion are evaluated, whereas our set of Eqs. (116–121) is written in the coprecessing frame of the primary. Therefore, Eq. (118) contains an inertial force leading to a term in \(1/(C\dot{\theta })\) which is absent in Kaula (1964, eqn 38). But these two equations have also distinct dependencies with respect to the primed Keplerian elements. In fact, Kaula erroneously assumed that the planetary and satellite contributions in \({\mathrm{d}}i/{\mathrm{d}}t\) could simply be summed up. Within our formalism, this naive (and wrong) assumption is equivalent to omission of the rotation \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\) in Eqs. (29) and (30). Under this omission, the components of both forces (\(-\partial V_1/\partial {\varvec{r}}\) and \(-\partial V_1/\partial {\varvec{r}}^{\,\prime }\)) would have been illegitimately summed up, ignoring the fact that they were written in different coordinate systems: by construction, \(\partial V_1/\partial {\varvec{r}}\) is expressed in the primary’s frame, while \(\partial V_1/\partial {\varvec{r}}^{\,\prime }\) is expressed in the secondary’s.
3 Tidal potential energy
3.1 General expression
Within the Darwin–Kaula theory (Kaula 1964; Efroimsky 2012; Efroimsky and Makarov 2013), it is taken into account that in the general case the secondary body “feels” the tides which may be generated in the primary not only by the secondary itself but also by some other perturber located in \({\varvec{r}}^{\,*}\). Then, in an arbitrary exterior point \({\varvec{r}}\) (which is implied to be the position of the secondary), the tidally deformed planet generates an additional tidal potential \(U({\varvec{r}},\,{\varvec{r}}^{\,*})\), both vectors \({\varvec{r}}\) and \({\varvec{r}}^{\,*}\) being planetocentric and parametrised by their Keplerian elements \((a, e, i, {{\mathcal {M}}}, \omega , \Omega )\) and \((a^*, e^*, i^*, {{\mathcal {M}}}^*, \omega ^*, \Omega ^*)\), respectively. In a situation where the secondary coincides with the perturber (and, thereby, is “feeling” the tides it itself is causing in the primary), the potential of the secondary in this field is equal to the value of \(U({\varvec{r}},\,{\varvec{r}}^{\,*})\) taken for \({\varvec{r}}^{\,*}=\,{\varvec{r}}\). We, however, shall also need the gradient of the potential. To calculate it, we start out from a general expression with \({\varvec{r}}^{\,*}\ne {\varvec{r}}\), then differentiate with respect to \({\varvec{r}}\), and only thereafter set \({\varvec{r}}^{\,*}\) and \({\varvec{r}}\) equal. Hence, the tidal force (expressed in the inertial frame) acting on the perturber due to the distortion of the primary is
Likewise, the tidally deformed secondary generates the additional tidal potential \(U^{\,\prime }(\,-\,{\varvec{r}}^{\,\prime },\,{\varvec{r}}^{\,\star })\), where \(\;-\,{\varvec{r}}^{\,\prime }\) is pointing from the centre of mass of the secondary to that of the primary, while \({\varvec{r}}^{\,\star }\) is pointing from the centre of mass of the secondary to that of the fictitious perturber to be identified with the primary body, both vectors being expressed in the body-fixed frame of the secondary. Accordingly, the tidal force (expressed in the inertial frame) acting on the primary due to the tidal distortion of the secondary isFootnote 7
We endow this force with a prime, because it emerges owing to the distortion of the secondary.
\({{\varvec{F}}}_0\) being the Newtonian force (written in the inertial frame), the equations of the orbital motion in the inertial frame are: Footnote 8
Together, they render:
or, equivalently:
where we employed expressions (124) and (125). Recall that the vectors \({\varvec{r}}\) and \({\varvec{r}}^{\;\prime }\) are defined in corotating frames and are related to the inertial vector \({\varvec{\rho }}^{\,\prime }-{{\varvec{\rho }}}\) via formulae (5).
The contributions from the two partners enter our expression (129) in a symmetric manner, despite the negative signs of the arguments in the second term on the right-hand side. The easiest way to understand the origin of these negative signs is to imagine a situation where both partners are non-rotating (i.e. maintain a constant orientation with respect to an inertial frame). In this case, both rotation matrices in the definition (5) of \({\varvec{r}}\) and \({\varvec{r}}^{\;\prime }\) can be chosen equal to the unity matrix, and we simply have \({\varvec{r}}\,=\,{\varvec{r}}^{\;\prime }\,=\,{\varvec{\rho }}^{\;\prime }-\,{{\varvec{\rho }}}\). The fact that both these vectors point from the primary to the secondary explains the difference between the arguments’ signs in the two gradients in (129).
Let us now write Eq. (129) in the corotating frame of the primary, i.e. with \({\varvec{\rho }}-{\varvec{\rho }}^{\,\prime }\) replaced by \({{\varvec{\mathbb {R}}}}\,{\varvec{r}}\). Successive differentiations of the rotation matrix \({{\varvec{\mathbb {R}}}}\) with respect to time produce the classical inertial forces:
A direct comparison with Eq. (29) shows that the total tidal potential energy of the system is
and that the disturbing function, which should be inserted in the Lagrange- or Delaunay-type planetary equations, is related to the physical potential energy via \({\mathcal {R}}\,=\,-\,{V_1}/{\beta }\). This gives us:
where it is implied that in the planetary equations the differentiation of \({\mathcal {R}}\) should be carried out before \({\varvec{r}}^{\,*}\) (resp. \({\varvec{r}}^{\,\star }\)) is set equal to \({\varvec{r}}\) (resp. \({\varvec{r}}^{\,\prime }\)).
3.2 Comparison with Kaula (1964)
In his developments, however, Kaula (1964) used the approximation
Thence, Kaula’s expressions for the orbital elements’ tidal rates acquired a redundant factor of \(M/(M+M^{\,\prime })\). Tolerable for the Earth–Moon system (which Kaula was having in mind), this approximation is unacceptable for a binary comprising partners of comparable masses. So, Kaula’s expressions for the rates must be multiplied by \((M+M^{\,\prime })/M\), to compensate for that oversight. Footnote 9
This redundant factor of \(M/(M+M^{\,\prime })\) has become a source of inaccuracy in many publications. At the same time, the overall factor is given correctly in some works, such as Ferraz-Mello et al. (2003) or Ferraz-Mello et al. (2008).
3.3 Expansion of the additional tidal potential
Let the perturber reside in the point \({\varvec{r}}^{\,*}\) relative to the centre of a deformable near-spherical primary. In an exterior point \({\varvec{r}}\), the tidally deformed body generates the additional tidal potential calculated by Kaula (1964)Footnote 10
where \(G\,=\,6.674\,\times \,10^{-11}\) m\(^3\) kg\(^{-1}\) s\(^{-2}\) is Newton’s gravity constant. As ever, the orbital elements with and without asterisk pertain to \({\varvec{r}}^*\) and \({\varvec{r}}\), correspondingly, while
In the expressions (134–135), we assume that, generally, the perturber located at \({\varvec{r}}^{\,*}\) does not coincide with the secondary residing in \({\varvec{r}}\). In the special case, when they are the same body, we must first carry out the differentiation over \({\varvec{r}}\) and only then set \({\varvec{r}}^{\,*}\,=\,{\varvec{r}}\).
Both the dynamical Love numbers \(k_l\) and the phase lags \(\epsilon _l\) are functions of the tidal Fourier modes \(\omega _{lmpq}\,=\,(l-2p)\,\dot{\omega }^{\,*}\,+\,(l-2p+q)\,n^{\,*}\,+\,m\,(\dot{\Omega }^{\,*}-\,\dot{\theta }^{\,*}\,)\). After the secondary and the fictitious perturber are set to be the same body, and \({\varvec{r}}^{\,*}\) is set equal to \({\varvec{r}}\), the modes becomeFootnote 11
Interestingly, Kaula himself never addressed the Fourier modes in his works, probably (mis-)assuming that both the dynamical Love numbers \(k_l\) and the phase lags \(\epsilon _{l}\) are frequency independent. The later development of geophysics demonstrated that the forms of the frequency dependencies of \(k_l\) and \(\epsilon _{lmpq}\) play an important role in many situations. Hence, there is the necessity to introduce the Fourier modes \(\omega _{lmpq}\) (Efroimsky 2012).
For a reader-friendly introduction to the Kaula theory, see Efroimsky and Makarov (2013). It can be understood from equation (15) in that paper that the tidal modes’ absolute values,
are the physical forcing frequencies excited in the tidally deformed body.
4 Tidal evolution of the semimajor axis
4.1 The general formula
In the Lagrange-type planetary equation for the semimajor axis rate (116), we should insert formula (132) and should perform differentiation over the mean motion. We further average the result over the mean anomaly and over the argument of pericentre as in Kaula (1964). This work, carried out in Appendix “C”, leads to:
where we employed a shortened notation for the quality functions of the primary:
the Fourier tidal modes excited in the primary being
Likewise, for the quality functions of the secondary we introduced the notation
the Fourier tidal modes excited in the secondary being
Here \(\Omega \), i, \(\omega \) are the Euler angles of the orbit on the primary’s equator, while \(\Omega ^{\,\prime }\), \(i^{\,\prime }\), \(\omega ^{\,\prime }\) are those on the secondary’s. The rotation rates of the primary and secondary are \(\dot{\theta }\) and \(\dot{\theta }^{\,\prime }\).
Our expression (138) differs from its counterpart in Kaula (1964) by the factor of \((M+M^{\,\prime })/M\). The reason for this is explained above, in Sect. 3.2.
Finally, we would mention that our expression (138) behaves well when \(M^{\,\prime }\rightarrow 0\) or \(M\rightarrow 0\), because \(K_l\,=\,O(M^{\,2})\). This can be proven via formulae (31), (40b) and (42) from Efroimsky (2015).
4.2 The leading inputs
By the formulae derived in “Appendix G”, the quadrupole part of the major semiaxis’ rate is
This long formula can obviously be split into two parts:
where the first part is due to the tides in the primary and comprises the terms with \(K_2(\omega _{lmpq})\). The second part is due to the tides in the secondary and comprises the terms with \(K^{\,\prime }_2(\omega ^{\,\prime }_{lmpq})\).
4.3 The case when the spin of neither partner is synchronised
If none of the partners is synchronised and both i and \(i^{\,\prime }\) are small, the leading terms are semidiurnal, i.e. those with \(\{lmpq\}\,=\,\{2200\}\). Approximated with these terms, the major semiaxis’ rate is:
To compare the inputs, write the above as
\(\rho \) and \(\rho ^{\,\prime }\) being the mean densities of the primary and the secondary, correspondingly.
When the role of the secondary is negligible, we are left with
In the case when the spin is faster than orbiting, the Fourier mode \(\omega _{2200}\,=\,2\,(n-\dot{\theta })\) is negative, and so is the phase lagFootnote 12 \(\epsilon _{2200}\,\equiv \,\epsilon _2(\omega _{2200})\). Then, the above expression becomes:
where \(Q_2\) is the quadrupole tidal quality factor defined through
We reiterate that in expression (148) the quality function \(k_2/Q_2\), mass M and radius R are those of the partner tides wherein are dominant (the primary). The mass \(M^{\,\prime }\) is that of the secondary (the tides wherein we neglected in Eqs. 147–148).
Approximations (146–147) contain only one tidal mode, the semidiurnal one. So this approximation looks the same, no matter what the frequency dependence \(K_2(\omega _{2mpq})\). For this reason, our Eq. (147) agrees with the corresponding formulae by both Hut (1981, eqn 9) and Emelyanov (2018, eqn 18) who used the CTL (constant time lag) model. It also coincides with equation (A1) from Lainey et al. (2012) who relied on the CPL (constant phase lag) tidal model.
4.4 The case when the primary is not synchronised, while the secondary is
If the primary is not synchronised (\(\dot{\theta }\ne n\)), the part \(\;\left( {{\mathrm{d}}a}/{{\mathrm{d}}t}\right) _{l=2}^{({\mathrm{prim}})}\;\) is approximated with formulae (147–148). If the secondary is synchronised (\(\dot{\theta }^{\,\prime }=n\)), the terms with \(K^{\,\prime }_2(2n-2\dot{\theta }^{\,\prime })\) and \(K^{\,\prime }_2(n-\dot{\theta }^{\,\prime })\) in Eq. (143) get nullified. In their absence, we are left with
where we took into account that \(K^{\,\prime }_2\) is an odd function.
As expression (150) contains only one tidal mode, n, the form of this expression is independent of the shape of the frequency dependence \(K_2^{\,\prime }(\omega _{2mpq})\). So our answer coincides with equation (28) from Emelyanov (2018) and also with equation (9) from Hut (1981) if we set \(\Omega =n\) in Hut’s equation. Our answer, however, differs from the first equation (A2) in the paper by Lainey et al. (2012), which contains an erroneous factor of \(\;-\,21\) instead of \(\;-\;57\). The same oversight is contained in equation (1) in Barnes et al. (2008) and in the first equation (40) in Shoji and Kurita (2014).
Together, the tides in both the primary and the secondary generate the rate \({\mathrm{d}}a/{\mathrm{d}}t\) obtained by summing up the rates (147) and (150):
The dissipation rate in a synchronised satellite (and the corresponding input in the elements’ rates) may be considerably amplified by longitudinal librations, when the satellite has a pronounced dynamical triaxiality (Frouard and Efroimsky 2017a; Efroimsky 2018).
4.5 Beyond quadrupole
Bills et al. (2005) argued that to attain a high precision in the modelling of Phobos’ tidal dynamics the knowledge of \(k_3\) and perhaps even \(k_4\) may be needed. Later, Taylor and Margot (2010) suggested that for very close asteroidal binaries the degrees l up to 6 may matter.
In the quadrupole (\(l=2\)) approximation (143), the smallest terms taken into account are of order \((R/a)^5\,e^4\). Now, if we choose to go beyond the quadrupole approximation and take into account the \(l = 3\) terms, the largest of those will be of order \(\;(R/a)^7\,e^0\,i^0\,=\,(R/a)^7\). Such are the terms with \(\{lmpq\}\,=\,\{3300\}\) and \(\{3110\}\). We may neglect them insofar as
a somewhat stringent condition not necessarily obeyed by all close-in binaries.
At the same time, had we kept in expression (143) only the terms up to \((R/a)^5 e^2\), the neglect of the \(l = 3\) would be justified under a more relaxed condition
4.6 Final caveat
In both Sects. 4.3 and 4.4, we passingly dropped the terms containing \(e^4\,K_2(2n)\) and \(e^4\,K^{\,\prime }_2(2n)\), see the last line in Eq. (143). At first glance, this is legitimate when the eccentricity is not too high. In reality, the issue is subtle owing to the extremely sharp shapes of the frequency dependencies of both \(K_2(2n)\) and \(K^{\,\prime }_2(2n)\). When the peak frequency happens to be equal or very close to 2n, these terms may become prominent, even for modest values of e.
5 Tidal evolution of the eccentricity
The planetary equation for the eccentricity evolution is given in Eq. (117). The insertion of expressions (132), (185a) and (187b) in this equation and the removal of the short- and long-period oscillating terms give us
where we used the shortened notation (139) and (141).
As expected (see Sect. 3.2 above), our expression (154) differs from the corresponding formula in Kaula (1964, eqn 38) by a factor of \((M+M^{\,\prime })/M\).
The quadrupole part of expression (154) reads (see “Appendix H”):
where the contribution \(\;({\mathrm{d}}e/{\mathrm{d}}t)^{({\mathrm{prim}})}\;\) comprises all the primary-generated terms (those with \(K_2\)), while \(\;({\mathrm{d}}e/{\mathrm{d}}t)^{({\mathrm{sec}})}\;\) comprises the secondary-generated terms (those with \(K_2^{\,\prime }\)).
5.1 The case when neither partner is synchronised
When the spin of neither body is synchronised, while both inclinations are small, the leading terms in the above equation are those linear in \(e\;\):
Specifically, when both partners satisfy the constant time lag (CTL) model (i.e. when both \(K_2\) and \(K_2^{\,\prime }\) are linear in the tidal mode), the above expression becomes
This agrees with equations (10) from Hut (1981) and (19) from Emelyanov (2018). Apart from the aforementioned factor of \((M+M^{\,\prime })/M\), this also agrees with the first line of equation (46) from Kaula (1964). (On the second line, Kaula lost the factor of 4 in the denominator.)
When both partners satisfy the constant phase lag (CPL) model (so both \(K_2\) and \(K_2^{\,\prime }\) are constants) and both \(\dot{\theta }\) and \(\dot{\theta }^{\,\prime }\) exceed 3n / 2, we have:
and
wherefrom
This is in agreement with the second expression in equation (A1) from Lainey et al. (2012), but differs from the corresponding formulae in some other works.
5.2 The case when the primary is not synchronised, while the secondary is
If the primary is not synchronised (\(\dot{\theta }\ne n\)), the part \(\left( {{\mathrm{d}}e}/{{\mathrm{d}}t}\right) _{l=2}^{({\mathrm{prim}})}\) is still approximated by the no-asterisk terms from the expressions above. If at the same time the secondary is synchronised (\(\dot{\theta }^{\,\prime }=n\)), then in formula (156) the term with \(K^{\,\prime }_2(2n-2\dot{\theta }^{\,\prime })\) must be set zero. Thence,
where we took into consideration that \(K^{\,\prime }_2\) is an odd function.
Containing only one frequency, expression (159) bears no dependence on the shape of the frequency dependence of \(K_2^{\,\prime }\). So it coincides with the corresponding expressions from Emelyanov (2018, eqn 29) and Hut (1981, eqn 10) both of whom employed the CTL model. It also is in agreement with equation (A2) by Lainey et al. (2012) who used the CPL model.
5.3 Beyond quadrupole
Under what condition may the degree-3 terms be ignored in the expression for \({\mathrm{d}}e/{\mathrm{d}}t\)?
In the quadrupole (\(l=2\)) approximation (155), the smallest terms taken into account are of order \((R/a)^5\,e^3\). Had it been our intention to include there also the \(l = 3\) terms, the largest of those would be the ones with \(\{lmpq\}\,=\,3300\) and 3110. Being of order \(\;(R/a)^7\,e^1\,i^0\,=\,(R/a)^7\,e\), they may be ignored if
Had we kept in expression (155) only the terms up to \((R/a)^5 e\), the neglect of the \(l = 3\) would be justified in all realistic situations:
6 Tidal evolution of the inclination
In the Lagrange-type equation for the inclination rate (118), we should insert expression (132), perform the differentiation over \(\omega \), \(\omega ^{\,\prime }\), \(\Omega \), \(\Omega ^{\,\prime }\) and \(i^{\,\prime }\) and then extract the secular terms by averaging over \({{\mathcal {M}}}\), \(\omega \) and \(\omega ^{\,\prime }\) to be consistent with Kaula (1964) who also removed the oscillating part. This work is carried out in Appendices “D”, “E”, and “J”, the result being
Apart from the multiplier of \((M+M^{\,\prime })/M\) discussed previously (see Sect. 3.2), the first term of the above expression coincides with the first term of the expression (38) in Kaula (1964), while the second term in our formula differs from that in Kaula (1964, eqn 38) considerably. The second term in Kaula (1964, eqn 38) is the equivalent of the first with primed Keplerian elements. However, as explained in Sect. 3.2, the rotation matrix \({}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}^{\,\prime }\) from the secondary’s frame to the primary’s frame breaks the symmetry between primed and unprimed Keplerian elements in \({\mathrm{d}}i/{\mathrm{d}}t\). According to Eq. (118), the primed equivalent of the first line of Eq. (162) is multiplied by the slow oscillating \(\cos (\omega -\omega ^{\,\prime })\) and vanishes once averaged over the argument of pericentres \(\omega \) and \(\omega ^{\,\prime }\) (see the non-averaged expression in “Appendix J”). Moreover, in our derivation of the inclination rate, the second line of Eq. (162) is an inertial force due to the non-Galilean nature of the coprecessing frame of the primary. More explicitly, this term expresses the variation of the orbital inclination with respect to the primary’s equator induced by the motion of the primary’s spin axis.
We would emphasise that the apparent lack of symmetry between the two components in the expression of \({\mathrm{d}}i/{\mathrm{d}}t\) is due to the fact that the inclination i is reckoned from the primary’s equatorial plane. Unlike a and e which have the same definition in both body frames and whose rates are symmetric in primed and unprimed variables, here the symmetry is recovered by writing the time derivatives of the orbital inclination with respect to the secondary’s equatorial plane, namely
In addition, it shall be reminded that neither the expression (162) for \({\mathrm{d}}i/{\mathrm{d}}t\) nor the expression (163) for \({\mathrm{d}}i^{\,\prime }/{\mathrm{d}}t\) allows, by itself, to deduce the motion of the orbital plane with respect to the inertial frame. For example, if the inclination rate \({\mathrm{d}}i/{\mathrm{d}}t\) happens to be zero, the orbit is fastened to the primary’s equator, and its orientation in the inertial frame is then governed by its longitude of the ascending node \(\Omega \) and the primary’s Euler angles \((\psi , \varepsilon )\). Reciprocally, when \({\mathrm{d}}i/{\mathrm{d}}t\) is nonzero, the orbit can still remain at rest in the inertial frame, in which case the apparent inclination evolution is only due to the motion of the primary’s spin axis. This would have precisely been the situation if most of the total angular momentum of the system were associated with the orbital motion. Nevertheless, as in Kaula (1964), we are not interested in the motion of the orbit plane relative to the inertial frame. This is why the orientation of the orbit is measured either in the primary’s or in the secondary’s frame. The presence of two inclinations to represent the orientation of a single orbit plane might seem odd at first sight; however, the angles i and \(i^{\,\prime }\) can also be interpreted as the obliquities of the bodies relative to the orbit.
In a situation where the orbital angular momentum is much lower than the angular momentum of the primary’s spin, and where the dissipation in the perturber can be neglected, our result coincides with that of Kaula (1964, eqn 38), up to the aforementioned factor of \((M+M^{\,\prime })/M\).
The quadrupole inputs of expression (162) read:
with \(\varrho \,=\,\beta \,n\,a^2 / (C\,\dot{\theta })\). For a very small eccentricity, a cruder approximation is acceptable
Without loss of precision, \(\;\sin i\;\) may be changed to \(\;i\;\) in both Eqs. (164) and (165).
In many realistic situations, the inclination is stabilised in the sense that \({\mathrm{d}}i/{\mathrm{d}}t \propto -i\). Specifically, it can be seen from Eq. (165) that at small eccentricities stabilisation is taking place for a synchronous orbit (\(\dot{\theta } = n\)), for the 2:1 spin-orbit resonance (\(\dot{\theta } = 2n\)), and for fast prograde rotation (\(\dot{\theta } \gg n\)). For other values of the angular velocity, however, it is not possible to determine the sign of \({\mathrm{d}}i/{\mathrm{d}}t\) which, generally, depends on the rheology and on the value of the parameter \(\varrho \).
7 Tidal evolution of \(\omega \), \(\Omega \) and \({\mathcal {M}}_0\)
Tidal evolution of \(\omega \), \(\Omega \) and \({\mathcal {M}}_0\) can be described by the same tools.
Be mindful, though, that the rate of these angles contains an input due to the oblateness of the primary (see, for example, Efroimsky 2005a). Therefore, even if a total rate is measured, it will not be easy to single out the tidal input in it. Also, for \({\mathrm{d}}\omega /{\mathrm{d}}t\) of a very close-in planet, the relativistic correction may supersede the tidal effect, like in the case of Mercury.
8 Conclusions
In this paper, we have revisited the theory of Kaula (1964) basing our calculation on a non-canonical Hamiltonian formalism with constraint. We have written down the rates \({\mathrm{d}}a/{\mathrm{d}}t\), \({\mathrm{d}}e/{\mathrm{d}}t\) and \({\mathrm{d}}i/{\mathrm{d}}t\) to order \(e^4\), inclusively. They differ from Kaula’s expressions which contain a redundant factor of \(M/(M+M^{\,\prime })\), with M and \(M^{\,\prime }\) being the masses of the primary and the secondary. Since Kaula was interested in the Earth–Moon system, this redundant factor was close to unity and was unimportant. This omission, however, must be corrected when Kaula’s theory is applied to a binary composed of partners of comparable masses.
We have pointed out that while it is legitimate to simply sum the primary’s and secondary’s inputs in \({\mathrm{d}}a/{\mathrm{d}}t\) or \({\mathrm{d}}e/{\mathrm{d}}t\), this is not the case for \({\mathrm{d}}i/{\mathrm{d}}t\), so our expression for the inclination rate \({\mathrm{d}}i/{\mathrm{d}}t\) differs from that of Kaula in two regards. First, in the expression for the primary’s di / dt the contribution due to the dissipation in the secondary averages out completely, provided the apsidal precession is uniform. Second, we have an additional term which emerges owing to the conservation of the angular momentum: a change in the inclination of the orbit causes a change of the primary’s plane of equator.
We have carried out our developments in the gyroscopic approximation (which implies that the spin of a body is much faster than the evolution of the spin axis’ orientation). As a by-product, our work also provides a full set of equations of motion, as it reads before the said approximation is applied.
Notes
In this frame, the role of the origin of longitude is played by the descending node of the primary’s equator on an inertial plane.
Such orbital elements are sometimes called contact elements, in order to distinguish them from their osculating counterparts. For example, the semimajor axis \(a_{\mathrm{osc}}\) and eccentricity \(e_{\mathrm{osc}}\) osculating in the non-inertial frame wherein the orbit is defined are linked via \(\beta \,({\varvec{r}}\times \dot{{\varvec{{r}}}})\,=\,\beta \,\sqrt{{{\mathcal {G}}}(M+M^{\,\prime })\,a_{\mathrm{osc}}\,(1-e_{\mathrm{osc}}^2)}\,\hat{\mathbf{w}}_{\mathrm{osc}}\) to the relative position \({\varvec{r}}\) and the velocity \(\dot{{\varvec{{r}}}}\) in that same non-inertial frame. At the same time, the contact elements a and e (those rendered by the Lagrange- or Delaunay-type equations with only the disturbing function amended) are connected through \({\varvec{r}}\times {\varvec{p}}\,=\,\beta \,\sqrt{{{\mathcal {G}}}(M+M^{\,\prime })\,a\,(1-e^2)}\,\hat{\mathbf{w}}\) with the relative position \({\varvec{r}}\) and the momentum \({\varvec{p}}\) which is equal to the reduced mass multiplied by the velocity in the inertial frame: \({\varvec{p}}\,=\,\beta \,(\dot{{\varvec{{r}}}}\,+\,{\varvec{\varvec{\mu }}}\times {\varvec{r}})\;\).
In these formulae, \({\varvec{\varvec{\mu }}}\) is the precession rate of the non-inertial frame relative the inertial one, while \(\hat{\mathbf{w}}_{\mathrm{osc}}\) and \(\hat{\mathbf{w}}\) denote the unit vector in the direction of the orbital angular momentum, as seen in the non-inertial and inertial frames, correspondingly.
For comprehensive treatment, see Efroimsky (2005a, b) and references therein.
As we shall see below, in the paragraph after Eq. (42), the instantaneous ellipses, as seen from the primary’s and secondary’s equator, will have the same shape, with \(a=a^{\,\prime }\) and \(e=e^{\,\prime }\) (and also with \({\mathcal {M}}={\mathcal {M^{\,\prime }}}\)). Generally, though, these equalities are not obligatory—see an example in Footnote 2 above.
For a detailed introduction in the theory of the spin operator, see Varshalovich et al. (1988).
The frame employed by Kaula (1964) should be termed “instantaneously comoving”, not coprecessing, because in his equations of motion the inertial forces were omitted.
The skew-symmetric matrix is so defined that for any two vectors \({\varvec{a}}, \varvec{b}\in \mathbb {R}^3\), their vector product \({\varvec{a}}\times {\varvec{b}}\) is equal to \({\varvec{\hat{a}}} {\varvec{b}}\).
Deriving the right-hand side expression of Eq. (125), we substituted \({\varvec{r}}^{\,\star }\) with \(-{\varvec{r}}^{\,\star }\). This change is acceptable because \({\varvec{r}}^{\,\star }\) does not show up in the final answer anyway—after the differentiation, \({\varvec{r}}^{\,\star }\) must be set equal to \({\varvec{r}}^{\,\prime }\).
Aside from that, in the general case it is necessary to take into account the tidally-generated change in the orientation of the equator. As we shall see below, this will yield an additional term in the expression for \({\mathrm{d}}i/{\mathrm{d}}t\), see Eq. (162).
A partial sum of this series, with \(l,\,|q|,\,|j|\,\le \,2\) and \(p=h=0\), was developed by Darwin (1879). In modern notation, his derivation is discussed by Ferraz-Mello et al. (2008). Mind that in Ibid. The convention on the meaning of the notations \({\varvec{r}}\) and \({\varvec{r}}^{\,*}\) is opposite to ours.
While in Sect. 2.6 we were using the osculating mean motion (defined in a standard way on the line between equations 71 and 72), here and hereafter we are using the anomalistic mean motion defined as in Table 1. We assume that the two are close, and therefore we interchangeably use the same notation n for both. The legitimacy of this is discussed in Efroimsky and Makarov (2014, Appendix B).
Recall that the lag \(\epsilon _l\) is an odd function of the Fourier mode \(\omega _{lmpq}\).
References
Barnes, R., Raymond, S.N., Jackson, B., Greenberg, R.: Tides and the evolution of planetary habitability. Astrobiology 8, 557–568 (2008)
Bills, B.G., Neumann, G.A., Smith, D.E., Zuber, M.T.: Improved estimate of tidal dissipation within Mars from MOLA observations of the shadow of Phobos. J. Geophys. Res. Planets 110, Article id. E07004 (2005)
Boué, G.: The two rigid body interaction using angular momentum theory formulae. Celest. Mech. Dyn. Astron. 128, 261–273 (2017)
Boué, G., Correia, A.C.M., Laskar, J.: Complete spin and orbital evolution of close-in bodies using a Maxwell viscoelastic rheology. Celest. Mech. Dyn. Astron. 126, 31–60 (2016)
Boué, G., Rambaux, N., Richard, A.: Rotation of a rigid satellite with a fluid component: a new light onto Titan’s obliquity. Celest. Mech. Dyn. Astron. 129, 449–485 (2017)
Correia, A.C.M., Laskar, J.: Long term evolution of the spin of Venus-II. Numerical simulations. Icarus 163, 24–45 (2003)
Correia, A.C.M., Laskar, J.: Tidal evolution of exoplanets. In: Seager S. (ed.) Exoplanets, pp. 239–266 . University of Arizona Press, Tuson. ISBN 978-0-8165-2945-2 (2010)
Correia, A.C.M., Laskar, J., Nèron de Surgy, O.: Long term evolution of the spin of Venus-I. Theory. Icarus 163, 1–23 (2003)
Cunha, D., Correia, A.C.M., Laskar, J.: Spin evolution of Earth-sized exoplanets, including atmospheric tides and core-mantle friction. Int. J. Astrobiol. 14, 233–254 (2015)
Darwin, G.H.: On the precession of a viscous spheroid and on the remote history of the Earth. Philos. Trans. R. Soc. Lond. 170, 447–530 (1879)
Efroimsky, M.: Long-term evolution of orbits about a precessing oblate planet. 1. The case of uniform precession. Celest. Mech. Dyn. Astron. 91, 75–108 (2005a)
Efroimsky, M.: Gauge freedom in orbital mechanics. Ann. N. Y. Acad. Sci. 1065, 346–374 (2005b)
Efroimsky, M.: Bodily tides near spin-orbit resonances. Celest. Mech. Dyn. Astron. 112, 283–330 (2012)
Efroimsky, M.: Tidal evolution of asteroidal binaries. Ruled by viscosity. Ignorant of rigidity. Astron. J. 150, id. 98 (2015). ERRATA: AJ, Vol. 151, article id. 130 (2016)
Efroimsky, M.: Dissipation in a tidally perturbed body librating in longitude. Icarus 306, 328–354 (2018)
Efroimsky, M., Makarov, V.V.: Tidal friction and tidal lagging. Applicability limitations of a popular formula for the tidal torque. Astrophys. J. 764, Article id. 26 (2013)
Efroimsky, M., Makarov, V.V.: Tidal dissipation in a homogeneous spherical body. I. Methods. Astrophys. J. 795, 6 (2014)
Emelyanov, N.: Influence of tides in viscoelastic bodies of planet and satellite on the satellite’s orbital motion. Mon. Not. R. Astron. Soc. 479, 1278–1286 (2018)
Ferraz-Mello, S., Beaugé, C., Michtchenko, T.A.: Evolution of migrating planet pairs in resonance. Celest. Mech. Dyn. Astron. 87, 99–112 (2003)
Ferraz-Mello, S., Rodríguez, A., Hussmann, H.: Tidal friction in close-in satellites and exoplanets. The Darwin theory re-visited. Celest. Mech. Dyn. Astron. 101, 171–201 (2008)
Frouard, J., Efroimsky, M.: Tides in a body librating about a spin-orbit resonance: generalisation of the Darwin–Kaula theory. Celest. Mech. Dyn. Astron. 129, 177–214 (2017a)
Frouard, J., Efroimsky, M.: Precession relaxation of viscoelastic oblate rotators. Mon. Not. R. Astron. Soc. 473, 728–746 (2017b)
Hut, P.: Tidal Evolution in close binary systems. Astron. Astrophys. 99, 126–140 (1981)
Kaula, W.M.: Tidal dissipation by solid friction and the resulting orbital evolution. Rev. Geophys. 2, 661–684 (1964)
Lainey, V., Karatekin, Ö., Desmars, J., Charnoz, S., Arlot, J.-E., Emelyanov, N., et al.: Strong tidal dissipation in Saturn and constraints on Enceladus’ thermal state from astrometry. Astrophys. J. 752, Article id. 14 (2012)
Makarov, V.V., Berghea, C., Efroimsky, M.: Dynamical evolution and spin-orbit resonances of potentially habitable exoplanets: the case of GJ 581d. Astrophys. J. 761, Article id. 83 (2012) ERRATA: ApJ, 763: 68 (2013)
Makarov, V.V., Berghea, C., Efroimsky, M.: Spin-orbital tidal dynamics and tidal heating in the TRAPPIST-1 multi-planet system. Astrophys. J. 857, 142 (2018)
Néron de Surgy, O., Laskar, J.: On the long term evolution of the spin of the Earth. Astron. Astrophys. 318, 975–989 (1997)
Noyelles, B., Frouard, J., Makarov, V.V., Efroimsky, M.: Spin-orbit evolution of Mercury revisited. Icarus 241, 26–44 (2013)
Peale, S.J., Cassen, P.: Contribution of tidal dissipation to lunar thermal history. Icarus 36, 245–269 (1978)
Pucacco, G., Lucchesi, D.M.: Tidal effects on the LAGEOS-LARES satellites and the LARASE program. Celest. Mecha. Dyn. Astron. 130, Article id. 66 (2018)
Rubincam, D.P.: Tidal friction in the Earth–Moon system and Laplace planes: Darwin redux. Icarus 266, 24–43 (2016)
Shoji, D., Kurita, K.: Thermal-orbital coupled tidal heating and habitability of Martian-sized extrasolar planets around M stars. Astrophys. J. 789, Article id. 3 (2014)
Taylor, P.A., Margot, J.-L.: Tidal evolution of close binary asteroid systems. Celest. Mech. Dyn. Astron. 108, 315–338 (2010)
Varshalovich, D.A., Moskalev, A.N., Khersonskii, V.K.: Quantum Theory of Angular Momentum. World Scientific, Singapore (1988)
Acknowledgements
One of the authors (ME) would like to thank Valeri V. Makarov and Dimitri Veras for numerous stimulating discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors hereby state that they have no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection on 50 years of Celestial Mechanics and Dynamical Astronomy.
Guest Editors: Editorial Committee.
Appendices
Appendix
Differential of the rotation matrix \({\varvec{\mathbb {F}}} = {}^\mathrm {T}{{{\varvec{\mathbb {R}}}}}{{\varvec{\mathbb {R}}}}'\)
Let \({{\varvec{\mathbb {R}}}}_1(\varphi )\) and \({{\varvec{\mathbb {R}}}}_3(\varphi )\) be the rotation matrices of angle \(\varphi \) around the first axis \({\varvec{i}} = {}^\mathrm {T}{(1, 0, 0)}\) and around the third one \({\varvec{k}} = {}^\mathrm {T}{(0, 0, 1)}\), respectively:
The derivatives of these matrices read
A direct calculation gives
We introduce the hat operator which associates with any vector \({\varvec{v}} = {}^\mathrm {T}{(x, y, z)} \in \mathbb {R}^3\) the skew-symmetric matrix \({\varvec{\hat{v}}}\) defined as
This skew-symmetric matrix is such that for any two vectors \({\varvec{a}}, {\varvec{b}} \in \mathbb {R}^3\), their vector product \({\varvec{a}} \times {\varvec{b}}\) reads \({\varvec{\hat{a}}} {\varvec{b}}\). From Eq (168), one notices that
Let us recall the definition of the rotation matrix \({\varvec{\mathbb {F}}}\):
Applying the rule (170), we get
To simplify the result, we introduce the vectors \({\varvec{i}}'\), \({\varvec{K}}\), \({\varvec{K}}'\) defined as
The associated skew-symmetric matrices \({\varvec{\hat{i}}}'\), \({\varvec{\hat{K}}}\) and \({\varvec{\hat{K}}}'\) are given by
A direct calculation shows that \(d{\varvec{\mathbb {X}}}\), defined as \({{\varvec{\mathbb {R}}}}_1(-i) {{\varvec{\mathbb {R}}}}_3(-{\bar{\Omega }})\;(d{\varvec{\mathbb {F}}}\,{}^\mathrm {T}{{\varvec{\mathbb {F}}}})\;{{\varvec{\mathbb {R}}}}_3({\bar{\Omega }}) {{\varvec{\mathbb {R}}}}_1(i)\), is equal to
Equations of motion in terms of the Keplerian elements
Let \({{\varvec{\mathbb {M}}}}_{\mathrm {C}/\mathrm {C^{\,\prime }}}\) be the Jacobian \(\partial ({\varvec{p}},\,{\varvec{r}})/\partial (\varvec{p}^{\,\prime },\,{\varvec{r}}^{\,\prime })\) describing the transition between the two Cartesian coordinate systems and given by
As shown by Eqs. (37) and (40) in the main text, the Hamiltonian equations for \(({\varvec{p}},\,{\varvec{r}})\) are
We shall precise that in our problem \({{\mathcal {H}}}\) bears not dependence on \({\varvec{p}}^{\,\prime }\), wherefore \(\partial {{\mathcal {H}}}/\partial {\varvec{p}}^{\,\prime } = {\varvec{0}}\). Now, let \({{\varvec{\mathbb {M}}}}_{\mathrm {K}/\mathrm {C}}\) and \({{\varvec{\mathbb {M}}}}_{\mathrm {K}^{\,\prime }/\mathrm {C}^{\,\prime }}\) be the Jacobian matrices \(\partial ({\varvec{Y}}, {\varvec{y}})/\partial ({\varvec{p}}, {\varvec{r}})\) and \(\partial ({\varvec{Y}}^{\,\prime }, {\varvec{y}}^{\,\prime })/\partial ({\varvec{p}}^{\,\prime }, {\varvec{r}}^{\,\prime })\), respectively, where \({\varvec{Y}} = (a, e, i)\) and \({\varvec{y}} = ({{\mathcal {M}}}, \omega , {\bar{\Omega }})\). These matrices describe transitions to Keplerian (K) variables from the Cartesian (C) ones, hence the notation. Applying the chain rule, we have
Then, we define the Poisson matrices \({\varvec{\mathbb {B}}}\) and \({\varvec{\mathbb {B}}}^{\,\prime }\) as
and introduce the total Jacobian matrix
Combined, Eqs. (178–180) render us
Differentiation of \({\mathcal {R}}\) with respect to the mean motion
First, we differentiate U with respect to the mean motion \({\mathcal {M}}\):
After we set \({\varvec{r}}\) and \({\varvec{r}}^*\) equal to one another (and drop the now-redundant asterisks), the secular part of the above derivative will become
Similarly, the secular part of the derivative of the potential created by the tidally deformed secondary, at the place where the primary resides, will read:
While in Eq. (183) i stands for the secondary’s inclination on the planetary equator, in Eq. (184) \(i^{\,\prime }\) denotes the inclination of the primary’s apparent orbit on the secondary’s equator. Likewise, while \(k_l\,\sin \epsilon _{lmpq}\) is the quality function of the primary, \(k_l^{\,\prime }\,\sin \epsilon ^{\,\prime }_{lmpq}\) is that of the secondary.
According to formula (132), the sum of the primary’s and secondary’s inputs in the derivative of the disturbing function over \({\mathcal {M}}\) will be
Differentiation of \({\mathcal {R}}\) with respect to the argument of the pericentre
Differentiation of U over \(\omega \) renders us
For \({\varvec{r}}\,=\,{\varvec{r}}^*\), the secular part of the derivative reduces to
Equivalently, the secular part of the derivative of the potential created by the tidally deformed secondary and acting on the primary is:
where \(i^{\,\prime }\), \(\omega ^{\,\prime }\) and \(\Omega ^{\,\prime }\) denote the inclination, the argument of the pericentre, and the longitude of the node of the planet’s apparent orbit as seen from the perturber.
Combining the last two equations with expression (132) for \({\mathcal {R}}\) as a function of U and \(U^{\,\prime }\), we obtain:
Differentiation of \({\mathcal {R}}\) with respect to the longitude of the node
Differentiation of U over \(\Omega \) gives us
For \({\varvec{r}}\,=\,{\varvec{r}}^*\), the secular part of the above expression becomes
Combined with Eq. (132), the above formula yields:
In this situation,
Similarly, differentiation over the longitude of the node \(\Omega ^{\,\prime }\) reckoned from the secondary’s equator gives
Differentiation of \({\mathcal {R}}\) with respect to the inclination
The derivative of U with respect to i is
For \({\varvec{r}}\,=\,{\varvec{r}}^*\), the secular part of this expression takes the form of
It should be noted that in the differentiation of U with respect to i, the effect of the primary’s oblateness \(J_2\) does not average out as it was the case in the differentiation over \({\mathcal {M}}\), \(\omega \) or \(\Omega \). Combining this with formula (132), we obtain:
which gives
Similarly, the secular part of the derivative of the potential created by the tidally deformed secondary and acting on the primary is:
Details of the calculation of \({\mathrm{d}}a/{\mathrm{d}}t\)
Writing \({\mathrm{d}}a/{\mathrm{d}}t\) in the leading order over the inclination requires the knowledge of the squares of the inclination functions \(\;F_{201}^2\,=\,\frac{\textstyle 1}{\textstyle 4}\,+\,O(i^2)\;\) and \(\;F_{220}^2\,=\,9\,+\,O(i^2)\;\), the other \(F^2_{lmp}(i)\) being of order \(O(i^2)\) or higher. So we shall work with the sets of integers \(\;(lmpq)\,=\,(201q)\;\) and \(\;(lmpq)\,=\,(220q)\;\). The corresponding eccentricity functions are:
Also mind that for \(\;(lmpq)\,=\,(2010)\;\) the expression \(\;(2-2p+q)\;\) is zero—and so is the input \(({\mathrm{d}}a/{\mathrm{d}}t)_{2010}\). Below is an inventory of the relevant inputs:
where we made use of notation (139) and (141).
Details of the calculation of \({\mathrm{d}}e/{\mathrm{d}}t\)
In notation (139–142), our expression (154) becomes
its quadrupole part being
To write expression (207) in the leading order over the inclination, we shall need the squares of the two relevant \(F_{lmp}(i)\) functions: \(\;F_{201}^2\,=\,\frac{\textstyle 1}{\textstyle 4}\,+\,O(i^2)\;\) and \(\;F_{220}^2\,=\,9\,+\,O(i^2)\;\), all the other \(F^2_{lmp}(i)\) being of order \(O(i^2)\) or higher. This way, we shall be interested in the following sets of integers: \(\;(lmpq)\,=\,(201q)\;\) and \(\;(lmpq)\,=\,(220q)\;\). The relevant eccentricity functions are given by Eq. (196) above.
For \(\;(lmpq)\,=\,(2010)\;\), both the expressions \(\;(2-2p+q)\;\) and \(\;(2-2p)\;\) vanish—and so does the \(({\mathrm{d}}e/{\mathrm{d}}t)_{2010}\;\) input, up to higher-order terms in the inclinations:
Thence, of the sets \(\;(lmpq)\,=\,(201q)\;\), only those with \(q\,=\,-2,\,-1,\,1,\,2\) are important:
Of the sets \((lmpq)\,=\,(220q)\), we shall be interested in the ones with \(q\,=\,-1,\,0,\,1,\,2\;:\)
where notation (139–142) was employed.
Details of the calculation of \({\mathrm{d}}i/{\mathrm{d}}t\)
According to Eq. (118), the evolution rate of the inclination involves derivatives of the perturbing function with respect to \(\omega \), \(\omega ^{\,\prime }\), \(\Omega \), \(\Omega ^{\,\prime }\) and \(i^{\,\prime }\). Nevertheless, in the secular expression (162), only differentiations over \(\omega \) and \(\Omega \) remain. These are given in Appendices “D” and “E”.
To write expression (162) in the leading order over the inclination, we should keep in mind that in this expression the squared inclination functions \(F^{\,2}_{lmp}(i)\) are accompanied by a factor of either \(\alpha _{lmp}\,=\,\left[ (l-2p)\,\cos i-m\right] /\sin i\;\) or \(\;\beta _{lmp}\,=\,\left[ m\,\cos i-(l-2p)\right] /\sin i\). The functions \(F^{\,2}_{201}(i)\) and \(F^{\,2}_{220}(i)\) are both of order \(O(i^{\,0})\), but for \((lmp)=(201)\), the two factors \(\alpha _{201}\) and \(\beta _{201}\) vanish. In the case \((lmp)=(220)\), we have
Here, we also have to consider the functions \(F^{\,2}_{lmp}(i)\) of order \(O(i^{\,2})\), namely \(\displaystyle F^{\,2}_{210}\,= \,\frac{9}{4}\,\sin i^{\,2}\,+\,O(i^{\,4})\) and \(\displaystyle F^{\,2}_{211}\,=\,\frac{9}{4}\,\sin i^{\,2}\,+\,O(i^{\,4})\), all the other \(F^2_{lmp}(i)\) being of order \(O(i^{\,4})\). The corresponding factors are \(\alpha _{210}\,=\,1/\sin i\,+\,O(i)\), \(\;\alpha _{211}\,=\,-\,1/\sin i\,+\,O(i)\), \(\;\beta _{210}\,=\,-1/\sin i\,+\,O(i)\), \(\;\beta _{211}\,=\,1/\sin i\,+\,O(i)\).
Therefore, we shall be interested in the following sets of integers: \((lmpq)\,=\,(220q)\), \((lmpq)\,=\,(210q)\) and \((lmpq)\,=\,(211q)\), the corresponding eccentricity functions being given by Eq. (196) above. Below we provide the resulting contributions. Deriving these, we used \(1/\sqrt{1-e^2}\,=\,1\,+\,e^2/2\,+\,3e^4/8\,+\,O(e^6)\) and then, in each contribution, truncated this expansion as necessary to keep the overall answer precise up to \(e^4\), inclusively.
Without loss of precision, in all these formulae \(\;\sin i\;\) may be changed to \(\;i\;\).
Long-period oscillating terms in the inclination rate
To derive the inclination rate \({\mathrm{d}}i/{\mathrm{d}}t\) non-averaged over the long-period oscillating terms, it is necessary to include the contribution due to the \(J_2\) in the potential energy:Footnote 13
To calculate \({\mathrm{d}}i/{\mathrm{d}}t\), we insert the above in the formula (132) for \(\mathcal {R}\), then plug the result in the orbital equation (118) and finally perform averaging over the mean anomaly \(\mathcal {M}\). This entails:
with \(j=2h-2\) and \(r=2(h-p)+q\).
The subsequent averaging over the apsidal precession will nullify all the sine and cosine terms involving any linear combination of \(\omega \) and \(\omega ^{\,\prime }\), while the surviving terms will come out proportional to \(\sin \epsilon _l(\omega _{lmpq})\). Thus, Eq. (162) will emerge.
Rights and permissions
About this article
Cite this article
Boué, G., Efroimsky, M. Tidal evolution of the Keplerian elements. Celest Mech Dyn Astr 131, 30 (2019). https://doi.org/10.1007/s10569-019-9908-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-019-9908-2