Viscoelastic tides: models for use in Celestial Mechanics

Abstract

This paper contains equations for the motion of linear viscoelastic bodies interacting under gravity. The equations are fully three dimensional and allow for the integration of the spin, the orbit, and the deformation of each body. The goal is to present good models for the tidal forces that take into account the possibly different rheology of each body. The equations are obtained within a finite dimension Lagrangian framework with dissipation function. The main contribution is a procedure to associate to each spring–dashpot model, which defines the rheology of a body, a potential and a dissipation function for the body deformation variables. The theory is applied to the Earth (solid part plus oceans) and a comparison between model and observation of the following quantities is made: norm of the Love numbers, rate of tidal energy dissipation, Chandler period, and Earth–Moon distance increase.

1 Introduction

The modeling of tidal forces has challenged scientists since ancient times. The current theories owe a lot to the seminal works of Newton, Laplace, Kelvin and Darwin, among others. In a simplified way the present research is divided into two groups: one that uses first-principle physics and sophisticated scientific apparatus to obtain detailed information particularly about the Earth and the Moon tides, for instance Lambeck (1980), Wahr (1981), Yoder et al. (1981), Egbert and Ray (2001), and another that looks for simplified phenomenological models adapted for the use in Celestial Mechanics, Mignard (1979), Ferraz-Mello (2013), Correia et al. (2014), Efroimsky and Williams (2009), Zlenko (2014), Celletti (1990), Antognini et al. (2014), Bambusi and Haus (2015), Boué et al. (2016) and Wisdom and Meyer (2016). Mathematical models within the first group have infinitely many degrees of freedom while those within the second group have finitely many. The class of models presented here falls under the second group. The goal is to present a procedure based on physical principles and within the framework of finite dimensional mechanics for modeling the tidal response of almost spherical celestial bodies of different rheological behaviors.

This paper builds on our previous paper (Ragazzo and Ruiz 2015), on the dynamics of a single isolated body. In that paper, the Lagrangian formalism with dissipation function was used to obtain equations for the dynamics of a deformable body with a simple viscoelastic response. Our main contribution in this paper is a procedure to include any linear viscoelastic rheology of the bodies into the equations of the previous paper. The equations for the motion of systems of deformable bodies interacting under gravity are easily obtained from the Lagrangian and the dissipation functions of the isolated bodies.

As in Ragazzo and Ruiz (2015), our construction relies upon the following hypotheses.

• (a) When the body is at rest (no rotational motion) its distribution of mass is spherically symmetric.

• (b) When the body has a rotational motion then its distribution of mass is almost spherically symmetric in the sense that the level sets of the density function are approximately ellipsoidal shells of small eccentricities.

• (c) The body material has an incompressible behavior under small deformations.

• (d) The body internal forces are such that the motion preserves the total angular momentum. For systems of deformable bodies we must include the hypothesis:

• (e) The minimum distance between two bodies is sufficiently large such that the almost sphericity hypothesis (b) still holds.

The paper is organized as follows. In Sect. 2, starting from the Lagrangian function of the rigid body, we explain how to derive the kinetic energy of our models of deformable body. If the deformable body is incompressible or satisfies hypothesis (c) then the trace of its moment of inertia tensor does not change with time [as shown by Darwin, see Rochester and Smylie (1974)]. So, the key idea is to write the moment of inertia as $\mathbf {I}= {\mathrm{I}_\circ }(\mathbb {I} -\mathbf {B})$, where $\mathbb {I}$ is the identity matrix and ${\mathrm{I}_\circ }$ is the trace of the moment of inertia over 3, and take $\mathbf {B}$, the nondimensional traceless part of the moment of inertia tensor, as the configuration variables of the deformation part.¹ The rest of the modeling consists in finding the kinetic, the potential, and the dissipation functions associated to $\mathbf {B}$. We remark that $\mathbf {B}$ is proportional to the moment of quadrupole tensor that is the quantity of primary interest in the gravitational coupling between different bodies.

Section 3 contains our main contribution: a procedure that to each spring–dashpot model that defines a rheology of a body associates a potential and a dissipation function for the variable $\mathbf {B}$. This principle, which we call “the Association Principle”, essentially says that we can exchange the one dimensional displacement x of the spring–dashpot model by the deformation matrix $\mathbf {B}$.

In Sect. 4 we present equations of motion for one isolated body and for a system of two bodies. In order to present explicit equations we suppose that each body has a Wiechert rheology that is represented by the spring–dashpot system in Fig. 1a. The modifications for other rheologies are straightforward.

Section 5 contains a full analysis of the tide response equations. These are the equations for the deformations $\mathbf {B}$ of a body (planet) that rotates with constant angular velocity under the tidal forcing of point masses (satellites) with prescribed orbits around it.

In Sect. 6 we apply the results of the previous section to the Earth. After several attempts, we propose a model for the variations of $\mathbf {B}$ that is equivalent to the oscillator in Fig. 1b. In this figure: the rheology of the Earth is described by the Wiechert model in Fig. 1a; the spring $\gamma$ sets the static flattening of the Earth (in the particular case of the Earth $\gamma =1.621\times 10^{-6}\ \hbox {s}^{-2}$ is due to the self-gravitational force);² $\mu$ is an inertia coefficient (for a null damping it allows for the free oscillations of the system); and the tidal and the centrifugal forces are represented by F(t). According to the association principle each component of the matrix $\mathbf {B}$ moves according to the one dimensional equation associated to this oscillator.

Fig. 1

a Wiechert model with the notation used in the text. b Wiechert oscillator that is used in this paper to model the mechanical behavior of the Earth

The parameters of the rheology are determined by means of a fit procedure that uses the Love numbers of the Earth as given in Petit and Luzum (2010) (for the diurnal and semi-diurnal tides) and Ray and Erofeeva (2014) (for the longer period tides). The result is:

$$\begin{aligned} \begin{aligned} \mu =19.79 \ \text {(dimensionless)}, \quad&\alpha _1=3.679\times 10^{-6}\, \hbox {s}^{-2},\quad \alpha _2=8.879\times 10^{-7}\, \hbox {s}^{-2}\\&\eta _1=3.796\times 10^{+2}\, \hbox {s}^{-1}, \quad \eta _2=6.663\times 10^{-3}\, \hbox {s}^{-1}. \end{aligned} \end{aligned}$$

(1)

Notice that the first Maxwell element in the Wiechert model, represented by $(\alpha _1,\eta _1)$, has a dashpot much harder than that of the second Maxwell element, represented by $(\alpha _2,\eta _2)$. As a result, under harmonic forcing the spring of the first Maxwell element work almost in parallel with the spring $\gamma$, they give the elastic rigidity of the system, while the dashpot of the second Maxwell element dissipates most of the energy. Intuitively the first Maxwell element acts as the solid part of the Earth that in combination with gravity sets the elastic behavior of the Earth (the real part of the Love number) and the second element acts as the ocean that dissipates most of the energy (the imaginary part of the Love number). Section 6 ends with a comparison between model and observation of the following quantities: norm of the Love numbers, rate of tidal energy dissipation, Chandler period, and Earth–Moon distance increase.

In Sect. 7 we turn our attention to the equations for the motion of one extended body (planet) and a point mass (satellite). It can be shown that the asymptotic state of any bounded (in phase space) orbit of this system is synchronous, that is the orbit of the satellite is circular and lies on the equatorial plane of the planet and the planet spin rate coincides with the satellite orbital velocity (Hut 1980). In Sect. 7 we show that close to a synchronous state we can apply a dimensional reduction to our equations of motion such that the resulting equations become approximately those of Mignard (1979) (after a redefinition of parameters). In a previous version of this paper, we applied the same reduction procedure to a system with a different rheology (associated to a Voigt oscillator with the kinetic energy as in the “Appendix 1”) and obtained the same result. It seems that, independently of the rheology, near a synchronous state a dimensional reduction approach always lead to the equations of Mignard after a redefinition of parameters.

In Sect. 8 we present the main result in this paper: a set of equations for the motion of N deformable bodies interacting under gravity. The equations are presented in a self-contained way. Equations similar to ours recently appeared in the paper (Boué et al. 2016). The methods they used to derive the equations are very different from ours. In Sect. 8 we make a comparison of our results to those in Boué et al. (2016).

In the “Appendix 1” we propose a new form for the kinetic energy of the system. It contains an additional term to the kinetic energy given in Sect. 2. This new form must be used when the angular momentum of tidal waves is relevant in comparison to the angular momentum due to the rotation of matter. For the Earth it seems that this additional term is negligible.

In the “Appendix 2” we show that the time average dissipation of energy in our model is consistent with a formula of Zschau and Platzman (1984) obtained from a continuum mechanics argument. In the same appendix we also show that the Lagrangian function associated to our model corresponds to the time-average of the work done by the primary tidal force in deforming the planet.

Finally, we remark that several quantities of geometric character, like the planet radius, gravity acceleration at the “equator”, etc, will appear in this text. This happens because these quantities are used in the definition of several astronomical numbers as, for instance, the Love numbers. We stress that all this geometric quantities are meaningless within our theory. For a body of mass m and mean moment of inertia ${\mathrm{I}_\circ }=(\ \mathrm{Tr}\ \mathbf {I})/3$, the only “radius” that is meaningful is the mean moment of inertia radius

$$\begin{aligned} R_I=\sqrt{5{\mathrm{I}_\circ }/(2m)} \end{aligned}$$

(2)

that coincides with the radius of a homogeneous ball of mass m and moment of inertia tensor ${\mathrm{I}_\circ }\mathbb {I}$. For an incompressible deformable body this quantity does not change with time. No geometric constant appear in our equations of motion.

Remarks about the notation:

• In this paper all matrices are written in boldface except for the identity matrix that is represented as $\mathbb {I}$.

• We always denote both a skew-symmetric matrix and its associated vector by the same letter distinguishing the matrix by the boldface. For instance, angular velocity matrix ${\varvec{\varOmega }}$ and angular velocity vector $\varOmega$.

• The norm of a matrix ${{\mathbf {A}}}$ is given by $|{{\mathbf {A}}}|^2=\ \mathrm{Tr}\ ({{\mathbf {A}}}^T {{\mathbf {A}}})=\sum _{ij} {{\mathbf {A}}}_{ij}^2$. The square of the norm of a skew-symmetric matrix is twice the square of the norm of its associated vector: $|{\varvec{\varOmega }}|^2=2|\varOmega |^2$.

2 A kinetic energy for the dynamics of an isolated deformable body

One of the greatest achievements in Newtonian mechanics is the Euler’s description of the motion of a rigid body. A main step in Euler’s reasoning is the use of a frame of reference “fixed to the body” in which the geometrical and the inertial properties of the body do not change with time. In this paper we are interested in the motion of a deformable body for which the choice of a special reference frame, in some sense related to that of Euler, is crucial. Because of this and also to set a notation we recall Euler’s treatment of the rigid body problem.

Let $\mathrm {K}$ be an orthonormal reference frame (the “body frame”) with its origin at the center of mass of a rigid body that does not move with respect to $\mathrm {K}$. Let $\kappa$ be an inertial reference frame in $\mathbb {R}^3$. A trajectory of any point P in the body is given by

$$\begin{aligned} t\longrightarrow x(t)+\mathbf {Y}(t)P\in \kappa , \end{aligned}$$

(3)

where x(t) represents the position of the center of mass of the body at time t and $\mathbf {Y}(t):\mathrm {K}\rightarrow \kappa$ is an orthogonal transformation (a rotation matrix) that determines the orientation of the body at time t. For each t, the image of the orthonormal frame $\mathrm {K}$ by the map (3) is an orthonormal frame $\kappa \,_t$. The family of “moving frames” $t\rightarrow \kappa \,_t$ determines the motion of the body.

The velocity of a point P in the body is

$$\begin{aligned} v(t)={\dot{x}}(t)+{\dot{\mathbf {Y}}}(t)P={\dot{x}}(t)+ \mathbf {Y}(t){\varvec{\varOmega }}(t)P= {\dot{x}}(t)+ \mathbf {Y}(t)[\varOmega (t)\times P], \end{aligned}$$

where ${\varvec{\varOmega }}(t)=\mathbf {Y}^{-1}(t){\dot{\mathbf {Y}}}(t)=\mathbf {Y}^{T}(t){\dot{\mathbf {Y}}}(t):\mathrm {K}\rightarrow \mathrm {K}$ is the angular velocity operator (matrix) given by

$$\begin{aligned} {\varvec{\varOmega }}=\left( \begin{matrix} 0 &{} -\varOmega _3 &{} \varOmega _2 \\ \varOmega _3 &{}\quad 0 &{}\quad -\varOmega _1 \\ -\varOmega _2 &{}\quad \varOmega _1 &{}\quad 0 \end{matrix}\right) , \qquad \mathrm{and} \qquad \varOmega =\left( \begin{matrix}\varOmega _1 \\ \varOmega _2\\ \varOmega _3 \end{matrix}\right) \end{aligned}$$

is the angular velocity vector in the frame $\mathrm {K}$.

The kinetic energy of the rigid body is

$$\begin{aligned} m\frac{|{\dot{x}}|^2}{2}+\frac{\varOmega \cdot \mathbf {I}\varOmega }{2}, \end{aligned}$$

(4)

where m is the mass and $\mathbf {I}:\mathrm {K}\rightarrow \mathrm {K}$ is the inertia operator of the body.

There is an important relation between the moment of inertia matrix $\mathbf {I}$ and the moment of quadrupole matrix $\mathbf {Q}$. In the body frame $\mathrm {K}$ these matrices are given by:

$$\begin{aligned} I_{ij}=\int (|P|^2\delta _{ij}-P_iP_j)\rho (P)d^3P,\qquad Q_{ij}=\int (3P_iP_j-|P|^2\delta _{ij})\rho (P)d^3P, \end{aligned}$$

(5)

from which follows

$$\begin{aligned} I_{ij}=\frac{1}{3}\left( (\ \mathrm{Tr}\ \mathbf {I})\delta _{ij}-Q_{ij}\right) . \end{aligned}$$

This equation shows that the moment of quadrupole tensor is proportional to the traceless part of the moment of inertia tensor. Using the definitions

$$\begin{aligned} {\mathrm{I}_\circ }=\frac{1}{3}\ \mathrm{Tr}\ \mathbf {I}\qquad \text {and}\qquad \mathbf {B}=\frac{1}{3}\frac{\mathbf {Q}}{{\mathrm{I}_\circ }}, \end{aligned}$$

we write the above relation as

$$\begin{aligned} \mathbf {I}= {\mathrm{I}_\circ }(\mathbb {I} -\mathbf {B}). \end{aligned}$$

(6)

If the body is spherically symmetric then ${\mathrm{I}_\circ }$ is its moment of inertia with respect to an arbitrary axis through its center of mass. The matrix $\mathbf {B}$ is just a nondimensional form of the moment of quadrupole matrix. Now, for a body with the center of mass at rest, the kinetic energy (4) can be written as

$$\begin{aligned} \mathscr {L}={\mathrm{I}_\circ }\frac{\varOmega \cdot (\mathbb {I} -\mathbf {B})\varOmega }{2}= \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}^T\mathbf {B}{\varvec{\varOmega }})\right) , \end{aligned}$$

(7)

where we used that the norm of a matrix ${{\mathbf {A}}}$ is given by $|{{\mathbf {A}}}|^2=\ \mathrm{Tr}\ ({{\mathbf {A}}}^T {{\mathbf {A}}})=\sum _{ij} {{\mathbf {A}}}_{ij}^2$.

The equations of motion for the rigid body can be obtained from the Lagrangian function (7) in the following way. The set of orthogonal matrices $\mathbf {Y}$ can be considered as the subset of all $3\times 3$ matrices that satisfy the constraints $\mathbf {Y}^T \mathbf {Y}=\mathbb {I}$ or, equivalently,

$$\begin{aligned} f_{km}(\mathbf {Y})=\sum _l Y_{lk} Y_{lm}=\delta _{km}. \end{aligned}$$

Let $\chi _{km}$ denote the Lagrange multiplier associated to $f_{km}$. The equations of motion are obtained from the extended Lagrangian function

$$\begin{aligned} {\widehat{\mathscr {L}}}= \mathscr {L}-\sum _{k,m}\chi _{km}f_{km} \end{aligned}$$

in the usual way:

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial {\widehat{\mathscr {L}}}}{\partial {\dot{Y}}_{ij}}\right) -\frac{\partial {\widehat{\mathscr {L}}}}{\partial Y_{ij}}= \left( \frac{d}{dt}\left( \frac{\partial {\widehat{\mathscr {L}}}}{\partial {\dot{\mathbf {Y}}}}\right) \right) _{ij}-\left( \frac{\partial {\widehat{\mathscr {L}}}}{\partial \mathbf {Y}}\right) _{ij}=0. \end{aligned}$$

Using that $f_{km}=f_{mk}$, which implies $\chi _{km}=\chi _{mk}$, and

$$\begin{aligned} \sum _{k,m} \chi _{km} \frac{\partial f_{km}}{\partial Y_{ij}}= 2 (\mathbf {Y}\varvec{\chi })_{ij}, \end{aligned}$$

we get that the constrained Euler–Lagrange equations associated to $\mathbf {Y}$ are

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}}\right) -\frac{\partial \mathscr {L}}{\partial \mathbf {Y}}+2\mathbf {Y}\varvec{\chi }=0. \end{aligned}$$

Since $\varvec{\chi }$ is symmetric, in order to eliminate the Lagrangian multipliers of this equation it is enough to multiply it by $\mathbf {Y}^T$ and to take its skew-symmetric part to obtain

$$\begin{aligned} \left( \mathbf {Y}^T\left( \frac{d}{dt}\left( \frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}}\right) -\frac{\partial \mathscr {L}}{\partial \mathbf {Y}}\right) \right) - \left( \mathbf {Y}^T\left( \frac{d}{dt}\left( \frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}}\right) -\frac{\partial \mathscr {L}}{\partial \mathbf {Y}}\right) \right) ^T=0. \end{aligned}$$

(8)

Substituting into this equation the expression for $\mathscr {L}$ given in Eq. (7) we obtain

$$\begin{aligned} {\dot{{\varvec{\varOmega }}}}+{\dot{{\varvec{\varOmega }}}}\mathbf {B}+\mathbf {B}{\dot{{\varvec{\varOmega }}}} +{\varvec{\varOmega }}{\dot{\mathbf {B}}}+{\dot{\mathbf {B}}} {\varvec{\varOmega }}+[{\varvec{\varOmega }}^2,\mathbf {B}]=0, \end{aligned}$$

(9)

where $[{\mathbf {A}},{\mathbf {B}}]={\mathbf {A}} {\mathbf {B}}-{\mathbf {B}} {\mathbf {A}}$ is the usual matrix commutator.

Equation (9) can be written in a more familiar form if we use the conservation of angular momentum. Consider the action $\text {SO(3)}\times \text {SO(3)}\rightarrow \text {SO(3)}$ given by $({\mathbf {U}},\mathbf {Y})\rightarrow {\mathbf {U}}\mathbf {Y}$. The Lagrangian function ${\widehat{\mathscr {L}}}$ is invariant under this action. So, ${\widehat{\mathscr {L}}}$ is invariant under the action of any one dimensional subgroup of symmetries $(s,\mathbf {Y})\rightarrow \exp (s \varvec{\xi })\mathbf {Y}$, where $\varvec{\xi }$ is a skew-symmetric matrix and $s\in \mathbb {R}$. Noether’s theorem [see, for instance, Theorem 2 and Lemma 5 in Ragazzo and Ruiz (2015)] implies that

$$\begin{aligned} \sum _{i,j,k}\frac{\partial \mathscr {L}}{\partial {\dot{Y}}_{ij}}\xi _{ik}Y_{kj} \end{aligned}$$

is a conserved quantity. Since this holds for any skew-symmetric matrix $\varvec{\xi }$ we obtain that the skew-symmetric part of $(\frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}})\mathbf {Y}^T$, namely

$$\begin{aligned} {\varvec{\ell }}=\left( \frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}}\right) \mathbf {Y}^T-\mathbf {Y}\left( \frac{\partial \mathscr {L}}{\partial {\dot{\mathbf {Y}}}}\right) ^T \end{aligned}$$

(10)

is a conserved quantity. A simple computation shows that

$$\begin{aligned} {\varvec{\ell }}=\mathbf {Y}\,\mathbf {L}\,\mathbf {Y}^T\quad \text {where:} \ \mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B}), \end{aligned}$$

${\varvec{\ell }}$ is the angular momentum matrix in the inertial frame $\kappa$, and $\mathbf {L}$ is the angular momentum matrix in the body frame $\mathrm {K}$. Therefore, Eq. (9) can be written in the usual way as

$$\begin{aligned} {\dot{\mathbf {L}}}+[{\varvec{\varOmega }},\mathbf {L}]=0 \end{aligned}$$

that is equivalent to ${\dot{{\varvec{\ell }}}}=0$.

While the motion of a rigid body has six degrees of freedom, that of a deformable body has infinitely many. As a consequence, the motion of a deformable body is modeled by partial differential equations, which are difficult to solve. Simplifications of these equations were proposed by several authors including ourselves (Ragazzo and Ruiz 2015). The results obtained in that article can be rephrased in the following way.

The equations for the motion of a deformable body could be derived from the Lagrangian function (7) if the functions $t\rightarrow {\mathrm{I}_\circ }(t)$ and $t\rightarrow \mathbf {B}(t)$ were known. The supposed incompressibility of the body under small deformations implies that ${\mathrm{I}_\circ }$ is constant in time [as shown by Darwin, see Rochester and Smylie (1974)]. So, the remaining time dependent unknown is $\mathbf {B}$, which is symmetric and traceless and therefore has five degrees of freedom. The central idea in Ragazzo and Ruiz (2015) and in this paper is to use physical principles to write a Lagrangian function depending on the variables $(\mathbf {B}, {\dot{\mathbf {B}}})$, the deformation Lagrangian function $\mathscr {L}_D$. Then the differential equations for $(\mathbf {Y},\mathbf {B})$ can be derived from a Lagrangian function that is the sum of $\mathscr {L}_D$ and the function in Eq. (7). Dissipation of energy is being neglected.

In Ragazzo and Ruiz (2015) we simply chose $\mathscr {L}_D=\frac{{\mathrm{I}_\circ }}{4} \left( \mu |\dot{\mathbf {B}}|^2-\gamma |\mathbf {B}|^2\right)$ (with $\mu =1$). The constants ${\mathrm{I}_\circ }\mu >0$ and ${\mathrm{I}_\circ }\gamma >0$ represent an effective inertia and an effective rigidity, respectively, for the motion of $\mathbf {B}$ ($\mu$ is dimensionless while $\gamma$ has dimension $\hbox {s}^{-2}$). The Lagrangian function obtained with this choice is

$$\begin{aligned} (\mathbf {B}, \dot{\mathbf {B}}, {\varvec{\varOmega }})\rightarrow \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}{\varvec{\varOmega }}^T\mathbf {B})\right) + \frac{{\mathrm{I}_\circ }}{4} \left( \mu |\dot{\mathbf {B}}|^2-\gamma |\mathbf {B}|^2\right) , \end{aligned}$$

(11)

which is the Lagrangian function of a rigid body plus the Lagrangian function of a harmonic oscillator for $\mathbf {B}$. The differential equations obtained from this Lagrangian function are

$$\begin{aligned}&{\dot{\mathbf {L}}}+[{\varvec{\varOmega }},\mathbf {L}]=0 \quad \text {where:} \ \mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})\nonumber \\&\mu {\ddot{\mathbf {B}}}+\gamma \mathbf {B}=- {\varvec{\varOmega }}^2+\frac{1}{3}(\ \mathrm{Tr}\ {\varvec{\varOmega }}^2)\mathbb {I} . \end{aligned}$$

(12)

Integrating these equations we obtain $\mathbf {B}$ and ${\varvec{\varOmega }}$ and further integrating ${\dot{\mathbf {Y}}}=\mathbf {Y}{\varvec{\varOmega }}$ we obtain the orientation matrix $\mathbf {Y}(t):\mathrm {K}\rightarrow \kappa$. Notice that the expression for the angular momentum can be written as $L=\mathbf {I}\varOmega$. A “body-frame” $\mathrm {K}$ with the property that the angular momentum is given by $L=\mathbf {Y}^T\,\ell =\mathbf {I}\varOmega$ is called a Tisserand’s frame (see Munk and MacDonald 1961). So, $\mathrm {K}$ is a Tisserand’s frame.

In Eq. (12), the constant $\gamma /\mu$ is the square of the angular frequency of free oscillations of the inertia tensor. The constant $\gamma$ ($\hbox {s}^{-2}$) is inversely proportional to the secular Love number. Indeed, the equilibrium deformation of a body due its own rotation is set by the dimensionless secular Love number $k_\circ$ (Lambeck 1980, p. 29). The corresponding change in the inertia coefficients are [see, for instance, Williams et al. (2001), Eqs. (11)]

$$\begin{aligned} \varDelta I_{ij}({ spin})=-{\mathrm{I}_\circ }B_{ij}({ spin})= \mathrm {k}_\circ \frac{a^5}{3G}\left\{ \varOmega _i\varOmega _j-\frac{1}{3}|\varOmega |^2\delta _{ij}\right\} , \end{aligned}$$

(13)

where: a is the volumetric radius of the body and $\varDelta I_{ij}(spin)$ means the change of the inertia tensor due to the planet spin $\varOmega$. From Eq. (12), the equilibrium matrix $\mathbf {B}$ for a body rotating steadily with angular velocity $\varOmega$ is given by

$$\begin{aligned} \mathbf {B}=-\frac{1}{\gamma }\left\{ {\varvec{\varOmega }}^2-\frac{1}{3}(\ \mathrm{Tr}\ {\varvec{\varOmega }}^2)\mathbb {I} \right\} . \end{aligned}$$

This equation compared with Eq. (13) leads to

$$\begin{aligned} \gamma =\frac{3{\mathrm{I}_\circ }G}{a^5}\frac{1}{k_\circ }. \end{aligned}$$

(14)

As an example consider a mass m of homogeneous inviscid liquid under self-gravity. At rest the liquid has a spherical shape and moment of inertia ${\mathrm{I}_\circ }=0.4\,ma^2$, where a is the radius of equilibrium. Notice that in this case the geometric radius a coincides with the mean moment of inertia radius $R_I$ defined in Eq. (2). For a homogeneous fluid body in hydrostatic equilibrium it has been shown by Kelvin that $k_\circ =3/2$ (Munk and MacDonald 1961, p. 26). From Eq. (14)

$$\begin{aligned} \gamma =\gamma _f=2{\mathrm{I}_\circ }G\left( \frac{5}{2}\frac{{\mathrm{I}_\circ }}{m}\right) ^{-5/2}= \frac{2{\mathrm{I}_\circ }G}{R_I^5}. \end{aligned}$$

(15)

The square of the angular frequency of free oscillations of the spherical mass of fluid is $\frac{4}{5}Gm/a^3=2{\mathrm{I}_\circ }G/a^5$ [Lamb 1932, paragraph 262 Eq. (10)]. So, $\gamma /\mu =\gamma _f$ which implies that for a homogeneous body made of a perfect fluid the nondimensional inertia constant $\mu$ is

$$\begin{aligned} \mu _f=1. \end{aligned}$$

(16)

This is the same value obtained for the pseudo-rigid body in Ragazzo and Ruiz (2015).

The Lagrangian function (11) is composed by the potential energy term ${\mathrm{I}_\circ }\gamma \Vert \mathbf {B}\Vert ^2/4$ and the remainder kinetic energy. The potential energy term is clearly not enough to describe the complex mechanical behavior of realistic bodies. In the next section we will fix this problem by adding new terms to this potential energy and introducing dissipation of energy by means of a Rayleigh dissipation function. The kinetic energy in the Lagrangian function (11) seems to be suitable for the majority of the celestial bodies since most of their rotational kinetic energy is dominated by the rotation of matter. Nevertheless, there may occur situations where “tidal waves” (a motion not associated to mass displacement) may give a non-negligible contribution to the rotational kinetic energy of the body. In this case a new term must be added to the kinetic energy in the Lagrangian function (11). This exceptional additional term is presented in the “Appendix”.

3 Rheology: potential energy and dissipation function

This section is divided into two parts. In the first we present some basic elements of linear viscoelasticity. In the second we present our “association principle” that allows for the transition from one dimensional rheological models to potential and dissipation functions for $\mathbf {B}$. We remark that an “association principle” is also presented in equation (10) in Correia et al. (2014) and in Eq. (3) in Boué et al. (2016) using a physical integral that relates the linear deformation with the potential. It is not clear that both “association principles” are fully equivalent (see footnote 3).

3.1 Linear viscoelastic spring–dashpot models

The viscoelastic response of a linear material is analogous to the mechanical response of a one dimensional spring–dashpot system (Bland 1960). The two simplest mechanical systems for viscoelastic behavior are the Maxwell element and the Voigt element shown in Fig. 2. From these elements complex models are constructed as those shown in Fig. 3. Each model is associated to a force-extension relation. The force is represented by $\lambda$ and the extension by x. For instance, for the Wiechert model in Fig. 1a the force-extension relation is (Bland 1960)

Fig. 2

The Maxwell (left) and the Voigt (right) elements

Fig. 3

Four different models that are equivalent. The first, from left to right, is the Burgers model. The second is the Wiechert model

$$\begin{aligned} {\ddot{\lambda }}+c_1{\dot{\lambda }}+c_2\lambda =c_3{\ddot{x}}+c_4{\dot{x}} \end{aligned}$$

(17)

where

$$\begin{aligned} c_1=\frac{\alpha _1}{\eta _1}+\frac{\alpha _2}{\eta _2},\quad c_2=\frac{\alpha _1\alpha _2}{\eta _1\eta _2},\quad c_3=\alpha _1+\alpha _2,\quad c_4=(\eta _1+\eta _2)\frac{\alpha _1\alpha _2}{\eta _1\eta _2}. \end{aligned}$$

(18)

All the four models in Fig. 3 lead to the same force-extension relation in Eq. (17) and therefore they are all equivalent from the dynamical point of view (Bland 1960).

To each spring–dashpot model is associated a one dimensional oscillator. The differential equation for the motion of the oscillator can always be obtained from a Lagrangian function plus a Rayleigh dissipation function. Our goal is to determine these two functions. In the following we explain how to obtain the Lagrangian and the dissipation functions for the oscillator in Fig. 1b, which we call the Wiechert oscillator. Notice that an additional spring with elastic constant $\gamma$ was added to the Wiechert model in Fig. 1a. In the next section this extra spring will be associated to the self-gravity of the body, it sets an equilibrium position for the system under a constant force. The same procedure can be applied to any other spring–dashpot model. We remark that some models, as for instance the Voigt model in Fig. 2, have an equilibrium spring due to the rheology. In this case the final equilibrium is set by the addition of the rheological and the gravitational springs working in parallel. The resulting stiffness coefficient can still be denoted by $\gamma$.³

For the Wiechert oscillator in Fig. 1b we first write the Lagrangian function with five configuration variables $x,x_1,{\tilde{x}}_1,x_2,{\tilde{x}}_2$. The variable x represents the overall extension of the system. The spring $\gamma$ and each Maxwell arm must undergo the same extension x since they are placed in parallel. The extension of the first Maxwell arm must be split into the extension $x_1$ of the spring $\alpha _1$ and the extension ${\tilde{x}}_1$ of the dashpot $\eta _1$, so $x=x_1+{\tilde{x}}_1$. The same analysis holds for the second Maxwell arm. The two constraints $x=x_1+{\tilde{x}}_1$ and $x=x_2+{\tilde{x}}_2$ can be handled using two Lagrangian multipliers $\lambda _1$ and $\lambda _2$ that represent the force acting on each Maxwell arm. This procedure also works in the presence of a dissipation function [see, for instance, Sect. 2.1 in Ragazzo and Ruiz (2015)]. The result is the following

$$\begin{aligned} \mathscr {L}= & {} \mu \frac{{\dot{x}}^2}{2}-\gamma \frac{x^2}{2}-\alpha _1\frac{x_1^2}{2} -\alpha _2\frac{x_2^2}{2}-\lambda _1(x-x_1-{\tilde{x}}_1) -\lambda _2(x-x_2-{\tilde{x}}_2)\nonumber \\ \mathscr {D}= & {} \eta _1\frac{\dot{{\tilde{x}}}_1^2}{2}+ \eta _2\frac{\dot{{\tilde{x}}}_2^2}{2}\nonumber \\ x= & {} x_1+{\tilde{x}}_1\nonumber \\ x= & {} x_2+{\tilde{x}}_2. \end{aligned}$$

(19)

A time-dependent external force F(t) can be added to the system adding the term xF(t) to $\mathscr {L}$. The Euler–Lagrange equations with dissipation function, which for the x variable is $\frac{d}{dt}\frac{\partial \mathscr {L}}{\partial {\dot{x}}}- \frac{\partial \mathscr {L}}{\partial x}+ \frac{\partial \mathscr {D}}{\partial {\dot{x}}}=0$, are

$$\begin{aligned} \mu {\ddot{x}}+\gamma x+\lambda _1+\lambda _2=F(t),\quad \alpha _1 x_1=\lambda _1,\quad \alpha _2 x_2 = \lambda _2,\quad \eta _1{\dot{{\tilde{x}}}}_1=\lambda _1,\quad \eta _2{\dot{{\tilde{x}}}}_2=\lambda _2. \end{aligned}$$

(20)

Using the constraints these equations can be written as

$$\begin{aligned} \mu {\ddot{x}}= & {} -\gamma x-\lambda _1-\lambda _2+F(t)\nonumber \\ {\dot{\lambda }}_1= & {} -\frac{1}{\tau _1}\lambda _1+\alpha _1 {\dot{x}},\quad \text {where}\quad \tau _1=\frac{\eta _1}{\alpha _1}\nonumber \\ {\dot{\lambda }}_2= & {} -\frac{1}{\tau _2}\lambda _2+\alpha _2 {\dot{x}} ,\quad \text {where}\quad \tau _2=\frac{\eta _2}{\alpha _2}. \end{aligned}$$

(21)

The constants $\tau _1$ and $\tau _2$ are the “relaxation times” of the material. The variables $\lambda _1$ and $\lambda _2$ have units of force. They represent the force acting upon each Maxwell element. At a given time the external force F(t) splits into the inertial force $\mu {\ddot{x}}$ and the elastic force $\gamma x$, which do not dissipate energy, and $\lambda _1$ and $\lambda _2$, which do dissipate energy. Equation (21) can also be written as

$$\begin{aligned} \begin{aligned} \mu {\ddot{x}}+\gamma x+\lambda&=F(t)\\ {\ddot{\lambda }}+c_1{\dot{\lambda }}+c_2\lambda&=c_3{\ddot{x}}+c_4{\dot{x}}, \end{aligned} \end{aligned}$$

(22)

where $\lambda =\lambda _1+\lambda _2$.

3.2 The association principle for the potential and the dissipation functions

The theory of linear viscoelasticity aims at the description of rheological behavior of several materials, from crystalline solids to complex polymers. The material elastic constants and relaxation times can be measured by means of laboratory experiments. In principle, it is not clear that the same spring–dashpot models used in laboratory rheology can give good results when applied to some very complex celestial bodies like, for instance, the Earth. The fact is that these simple models have been used extensively to describe the rheology of planets and satellites [see, for instance, Henning et al. (2009)]. In this case the model constants are estimated using either astronomical data or molecular constants of some materials like ice, granite, etc. The following association principle establishes a way of relating a rheology related to a spring–dashpot model to a rheology for the nondimensional “deformation” tensor $\mathbf {B}$. We state the principle using the spring–dashpot system in Fig. 1b as a model. The generalization to other spring–dashpot systems is immediate.

Rheology Association Principle: the Lagrangian and dissipation functions for $\mathbf {B}$ that are associated to those functions for the one-dimensional spring–dashpot model in Fig. 1b are obtained after replacing: x for $\mathbf {B}$, $x_k$ for $\mathbf {B}_k$, ${\tilde{x}}_k$ for ${\tilde{\mathbf {B}}}_k$, and $\lambda _k$ for ${\varvec{\varLambda }}_k$; where $\mathbf {B}_k$, ${\tilde{\mathbf {B}}}_k$, and ${\varvec{\varLambda }}_k$, $k=1,2$, are symmetric traceless matrices. Both the Lagrangian and the dissipation functions for $\mathbf {B}$ must be subsequently multiplied by ${\mathrm{I}_\circ }/2$. The result is (compare to equation Eq. (19)):

$$\begin{aligned} \mathscr {L}_{\mathbf {B}}= & {} \frac{{\mathrm{I}_\circ }}{4}\Bigl \{\mu |{\dot{\mathbf {B}}}|^2-\gamma |\mathbf {B}|^2 -\alpha _1|\mathbf {B}_1|^2-\alpha _2 |\mathbf {B}_2|^2\Bigr \}\nonumber \\&-\frac{{\mathrm{I}_\circ }}{2}\Bigl \{\ \mathrm{Tr}\ \{{\varvec{\varLambda }}_1(\mathbf {B}-\mathbf {B}_1-{\tilde{\mathbf {B}}}_1)\}+ \ \mathrm{Tr}\ \{{\varvec{\varLambda }}_2(\mathbf {B}-\mathbf {B}_2-{\tilde{\mathbf {B}}}_2)\}\Bigr \}\nonumber \\ \mathscr {D}= & {} \frac{{\mathrm{I}_\circ }}{4}\left\{ \eta _1|\dot{{\tilde{\mathbf {B}}}}_1|^2+ \eta _2|{\dot{{\tilde{\mathbf {B}}}}}_2|^2\right\} \nonumber \\ \mathbf {B}= & {} \mathbf {B}_1+{\tilde{\mathbf {B}}}_1\nonumber \\ \mathbf {B}= & {} \mathbf {B}_2+{\tilde{\mathbf {B}}}_2 . \end{aligned}$$

(23)

Again a time-dependent external force matrix ${\mathbf {F}}(t)$ can be added to the system adding the term $\frac{{\mathrm{I}_\circ }}{2}\ \mathrm{Tr}\ ({\mathbf {F}}(t)\mathbf {B})$ to $\mathscr {L}$.⁴ The equations of motion can be computed as in the “Appendix 1”, the result is analogous to that in Eq. (21):

$$\begin{aligned} \mu {{\ddot{\mathbf {B}}}}= & {} -\gamma \mathbf {B}-{\varvec{\varLambda }}_1-{\varvec{\varLambda }}_2+{\mathbf {F}}(t)\nonumber \\ {\dot{{\varvec{\varLambda }}}}_1= & {} -\frac{1}{\tau _1}{\varvec{\varLambda }}_1+\alpha _1 {\dot{\mathbf {B}}},\quad \text {where}\quad \tau _1=\frac{\eta _1}{\alpha _1}\nonumber \\ {\dot{{\varvec{\varLambda }}}}_2= & {} -\frac{1}{\tau _2}{\varvec{\varLambda }}_2+\alpha _2 {\dot{\mathbf {B}}} ,\quad \text {where}\quad \tau _2=\frac{\eta _2}{\alpha _2}. \end{aligned}$$

(24)

Again the constants $\tau _1$ and $\tau _2$ are the “relaxation times” of the system and, at a given time, the external force ${\mathbf {F}}(t)$ splits into the inertial term $\mu {{\ddot{\mathbf {B}}}}$ and the elastic force $\gamma \mathbf {B}$, which do not dissipate energy, and ${\varvec{\varLambda }}_1$ and ${\varvec{\varLambda }}_2$, which do dissipate energy. Equation (24) can also be written as

$$\begin{aligned} \mu {{\ddot{\mathbf {B}}}}+\gamma \mathbf {B}+{\varvec{\varLambda }}= & {} {\mathbf {F}}(t)\nonumber \\ {\ddot{{\varvec{\varLambda }}}}+c_1{\dot{{\varvec{\varLambda }}}}+c_2{\varvec{\varLambda }}= & {} c_3{{\ddot{\mathbf {B}}}}+c_4{\dot{\mathbf {B}}}, \end{aligned}$$

(25)

where $c_1,c_2,c_3,c_4$ are the constants in Eq. (18) and ${\varvec{\varLambda }}={\varvec{\varLambda }}_1+{\varvec{\varLambda }}_2$.

We remark that our association principle relies upon the isotropy of space and upon the incompressibility hypothesis (c) given in the Introduction. Indeed, consider the quadratic function $\mathbf {B}\rightarrow \sum _{ijkl}\varGamma _{ijkl}B_{ij}B_{kl}$, where $\varGamma _{ijkl}$ is constant. The isotropy of space implies that $\varGamma _{ijkl}$ is a linear combination of the three tensors $\delta _{ij}\delta _{kl}$, $\delta _{ik}\delta _{jl}$, and $\delta _{il}\delta _{jk}$ [see, for instance, Kearsley and Fong (1975)]. Since $\mathbf {B}$ is symmetric and traceless, $\varGamma _{ijkl}$ can be taken as a multiple of $\delta _{ik}\delta _{jl}$. Therefore, the space of quadratic isotropic functions over the matrices $\mathbf {B}$ is one dimensional exactly as the space of quadratic functions over $\mathbb {R}$. This allows for the replacement of the scalar variable x by the matrix variable $\mathbf {B}$ in the Lagrangian function (19). The same thing holds for the variables ${\dot{\mathbf {B}}}$, $\mathbf {B}_1$, etc. The incompressibility hypothesis (c) implies that the trace of the inertia tensor $\mathbf {I}$ is constant or, equivalently, ${\mathrm{I}_\circ }$ is constant. If the body material were compressible then ${\mathrm{I}_\circ }$ would be variable and the association principle would have to be modified.

4 One and two-body systems

Equations of motion for systems of deformable bodies interacting under gravity can be easily obtained from the Lagrangian and dissipation functions given in the previous sections.

At first, consider an isolated body and an inertial reference frame where the center of mass of the body is at rest. In the body frame $\mathrm {K}$ the kinetic energy has a term due to its rotation and another due to its deformation. In this paper two expressions for the rotational part are proposed: one given in Sect. 2 and another given in the “Appendix 1”. Here we only consider that given in Sect. 2 that is

$$\begin{aligned} \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}{\varvec{\varOmega }}^T\mathbf {B}) \right) . \end{aligned}$$

(26)

The kinetic energy of deformation is just $\frac{\mu {\mathrm{I}_\circ }}{4}|\dot{\mathbf {B}}|^2$ and is contained in the Lagrangian function $\mathscr {L}_{\mathbf {B}}$ that depends on the rheology of the body. For the rheology associated to the Wiechert oscillator in Fig. 1b the expression for the Lagrangian function $\mathscr {L}_{\mathbf {B}}$ and the dissipation function $\mathscr {D}$ are given in Eq. (23). In this case, the Lagrangian function of the isolated body is given by

$$\begin{aligned} \mathscr {L}=\frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}{\varvec{\varOmega }}^T\mathbf {B})\right) +\mathscr {L}_{\mathbf {B}}. \end{aligned}$$

(27)

The equations of motion are obtained from the Euler–Lagrange equations with dissipation function by means of the same procedure as in the “Appendix 1” and in Sect. 2. The result is:

$$\begin{aligned} \mu {{\ddot{\mathbf {B}}}} +\gamma \mathbf {B}= & {} -{\varvec{\varOmega }}^2+\frac{1}{3}\ \mathrm{Tr}\ ({\varvec{\varOmega }}^2)\mathbb {I} -{\varvec{\varLambda }}\nonumber \\ {\ddot{{\varvec{\varLambda }}}}+c_1{\dot{{\varvec{\varLambda }}}}+c_2{\varvec{\varLambda }}= & {} c_3{{\ddot{\mathbf {B}}}}+c_4{\dot{\mathbf {B}}} \nonumber \\ {\dot{{\varvec{\varOmega }}}}+(\mathbf {B}{\dot{{\varvec{\varOmega }}}}+{\dot{{\varvec{\varOmega }}}} \mathbf {B})= & {} -({\dot{\mathbf {B}}}{\varvec{\varOmega }}+{\varvec{\varOmega }}{\dot{\mathbf {B}}}) +[\mathbf {B},{\varvec{\varOmega }}^2]. \end{aligned}$$

(28)

The Lagrangian function for a system of two bodies under gravitational interaction is easily obtained from the Lagrangian function (27) for an isolated body. Let $m_i$ (mass), ${\mathrm{I}_\circ }_i$, $\gamma _i$, $\mu _i$, etc, $i=1,2$, be the physical parameters of body one ($i=1$) and body two ($i=2$). Let $\kappa$ be an inertial frame of reference and $x^1$ and $x^2$ be the positions of bodies one and two, respectively, with respect to $\kappa$. The configurational degrees of freedom of the body i are $x^i$, $\mathbf {Y}^i$ (or $\mathrm {K}_i$) and $\mathbf {B}^i$ and their associated velocities are ${\dot{x}}^i$, ${\varvec{\varOmega }}^i$ and ${\dot{\mathbf {B}}}^i$, respectively. Suppose that hypothesis (e) in the Sect. 1 is verified, namely, the two bodies never get too close. Then the gravitational energy of interaction is approximately given by

$$\begin{aligned} - \frac{G m_1 m_2}{|x|}-\frac{3G}{2 |x|^5} \left\{ m_2{\mathrm{I}_\circ }_1 [(\mathbf {Y}^{1T}x)\cdot \mathbf {B}^1(\mathbf {Y}^{1T}x)] +m_1 {\mathrm{I}_\circ }_2[(\mathbf {Y}^{2T}x)\cdot \mathbf {B}^2(\mathbf {Y}^{2T}x)]\right\} , \end{aligned}$$

where we used $x=x^1-x^2$. Therefore, adding the Lagrangian functions $\mathscr {L}_1$ and $\mathscr {L}_2$ of each isolated body, given in Eq. (27), to the point mass kinetic energy and subtracting the potential energy of interaction we obtain the Lagrangian function of the system:

$$\begin{aligned} \mathscr {L}= & {} m_1\frac{|{\dot{x}}^{1}|^2}{2}+ m_2\frac{|{\dot{x}}^{2}|^2}{2} +\mathscr {L}_1+\mathscr {L}_2+\frac{G m_1 m_2}{|x|}\nonumber \\&+\frac{3G}{2 |x|^5} \Big \{m_2{\mathrm{I}_\circ }_1 [(\mathbf {Y}^{1T}x)\cdot \mathbf {B}^1(\mathbf {Y}^{1T}x)] +m_1{\mathrm{I}_\circ }_2[(\mathbf {Y}^{2T}x)\cdot \mathbf {B}^2(\mathbf {Y}^{2T}x)]\Big \}. \end{aligned}$$

(29)

The dissipation function of the system is just the sum of the dissipation function of each body:

$$\begin{aligned} \mathscr {D}=\mathscr {D}_1+\mathscr {D}_2 \end{aligned}$$

(30)

where $\mathscr {D}_i$ is the dissipation function of body i.

There are two types of two-body problems: two extended deformable bodies (${\mathrm{I}_\circ }_1>0$ and ${\mathrm{I}_\circ }_2>0$) and one extended deformable body plus one point mass (${\mathrm{I}_\circ }_1>0$ and ${\mathrm{I}_\circ }_2=0$). We focus in the second problem, for which the Lagrangian function can be simplified in the following way. Since there are no more variables $\mathbf {B}^2$, $\mathbf {Y}^2$ (or $\mathrm {K}_2$), we can omit the index 1 from ${\mathrm{I}_\circ }_1$, $\gamma _1$, $\eta _1$, $Y^1$ (or $\mathrm {K}_1$), $\varOmega ^1$, and $B^1$. We keep the indices in $x^1$, $x^2$, $m_1$, and $m_2$. Let $x_{cm}$ denote the position of the center of mass of the bodies and let $\kappa$ be an inertial reference frame where $x_{cm}=0$ is at rest. Let $q=\mathbf {Y}^Tx$ be the relative position in the rotating reference frame $\mathrm {K}$. Then, in terms of the configuration variables $(q,\mathbf {Y})$ the Lagrangian function becomes

$$\begin{aligned} \mathscr {L}= & {} m\frac{|{\dot{q}}+{\varvec{\varOmega }}q|^2}{2}+ \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}{\varvec{\varOmega }}^{T}B)\right) +\mathscr {L}_{\mathbf {B}} \nonumber \\&+ \frac{G m_1 m_2}{|q|}+\frac{3Gm_2{\mathrm{I}_\circ }}{2 |q|^5}q \cdot \mathbf {B}q, \end{aligned}$$

(31)

where $m=m_1m_2/(m_1+m_2)$ is the reduced mass and $\mathscr {L}_{\mathbf {B}}$ is the Lagrangian function associated to $\mathbf {B}$ for the extended body. Notice that $\mathbf {Y}$ does not appear in $\mathscr {L}$. The equations of motion obtained from the Lagrangian function in Eq. (31) and from the dissipation function in Eq. (30) are

$$\begin{aligned} {\dot{\mathbf {B}}}= & {} {\mathbf {U}}\nonumber \\ \mu {\dot{{\mathbf {U}}}}= & {} - \gamma \mathbf {B}-{\varvec{\varLambda }}_1-{\varvec{\varLambda }}_2 -{\varvec{\varOmega }}^2+\frac{1}{3}\ \mathrm{Tr}\ ({\varvec{\varOmega }}^2)\mathbb {I} + \frac{3G m_2}{|q|^5}\left( q\otimes q-\frac{|q|^2}{3} \mathbb {I} \right) \nonumber \\ \alpha _1^{-1}{\dot{{\varvec{\varLambda }}}}_1= & {} -\eta _1^{-1}{\varvec{\varLambda }}_1+ {\mathbf {U}}\nonumber \\ \alpha _2^{-1}{\dot{{\varvec{\varLambda }}}}_2= & {} -\eta _2^{-1}{\varvec{\varLambda }}_2+ {\mathbf {U}}\nonumber \\ {\dot{{\varvec{\varOmega }}}}= & {} -(\mathbf {B}{\dot{{\varvec{\varOmega }}}}+{\dot{{\varvec{\varOmega }}}} \mathbf {B})-({\mathbf {U}}{\varvec{\varOmega }}+{\varvec{\varOmega }}{\mathbf {U}}) +[\mathbf {B},{\varvec{\varOmega }}^2] +\frac{3G m_2}{|q|^5}\left[ q\otimes q,\mathbf {B}\right] \nonumber \\ {\dot{q}}= & {} -{\varvec{\varOmega }}q+u \nonumber \\ {\dot{u}}= & {} -{\varvec{\varOmega }}u+ GM\left\{ -\frac{1}{|q|^3}q -\frac{15}{2}\frac{{\mathrm{I}_\circ }}{m_1}\frac{1}{|q|^7}(q\cdot \mathbf {B}q)q +3\frac{{\mathrm{I}_\circ }}{m_1}\frac{1}{|q|^5} \mathbf {B}q\right\} . \end{aligned}$$

(32)

The total angular momentum is given by

$$\begin{aligned} \mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B}) +m(u\otimes q-q\otimes u). \end{aligned}$$

(33)

The Lagrangian function for a system of $N>2$ bodies under gravitational interaction is easily obtained from the Lagrangian functions (27) of each isolated body as in the case of two bodies. The dissipation function is again the sum of the dissipation functions of each isolated body. The equations of motion are presented in the Sect. 8.

5 Frequency response to tidal forcing

In this section we study the tides on a planet induced by a moving point mass, which represents, for instance, a satellite. The goal is to obtain equations that relate the parameters of the rheology to the planet Love numbers. We suppose that the planet rotates with steady angular velocity. Let $\mathrm {K}=(\mathrm{e}_1,\mathrm{e}_2,\mathrm{e}_3)$ be a frame that corotates with the planet in which the angular velocity of the planet is $\varOmega _3\mathrm{e}_3$. In this reference frame the trajectory of the satellite is given by $t\rightarrow q(t)$. Let the mass of the planet and the satellite be $m_1$ and $m_2$, respectively. Suppose that the rheology of the planet is that of the Wiechert oscillator in Fig. 1b. Then from the Lagrangian and the dissipation functions in Eq. (23) and the Lagrangian function (31) we obtain that $\mathbf {B}$ satisfies Eq. (25) with ${\mathbf {F}}(t)= {\mathbf {C}}+{\mathbf {A}}(t)$, where

$$\begin{aligned} {\mathbf {C}}=-{\varvec{\varOmega }}^2+\frac{1}{3}(\mathrm{Tr}{\varvec{\varOmega }}^2)\mathbb {I} \end{aligned}$$

(34)

is a time independent matrix due to the planet rotation and

$$\begin{aligned} {\mathbf {A}}(t)=\frac{3G m_2}{|q|^5}\left( q\otimes q- \frac{|q|^2}{3} \mathbb {I} \right) \end{aligned}$$

(35)

is a time dependent matrix that corresponds to the primary tidal force due to the point mass. Since Eq. (25) is linear the effect of the forces ${\mathbf {C}}$ and ${\mathbf {A}}$ can be studied independently. So, neglecting the steady force ${\mathbf {C}}$, the tide response equations become

$$\begin{aligned} \mu {{\ddot{\mathbf {B}}}}= & {} -\gamma \mathbf {B}-{\varvec{\varLambda }}+{\mathbf {A}}(t)\nonumber \\ \alpha _1^{-1}{\dot{{\varvec{\varLambda }}}}_1= & {} -\eta _1^{-1}{\varvec{\varLambda }}_1+ {\dot{\mathbf {B}}},\quad \nonumber \\ \alpha _2^{-1}{\dot{{\varvec{\varLambda }}}}_2= & {} -\eta _2^{-1}{\varvec{\varLambda }}_2+ {\dot{\mathbf {B}}}, \end{aligned}$$

(36)

where ${\varvec{\varLambda }}={\varvec{\varLambda }}_1+{\varvec{\varLambda }}_2$ or, equivalently,

$$\begin{aligned} \begin{aligned} \mu {{\ddot{\mathbf {B}}}}+\gamma \mathbf {B}+{\varvec{\varLambda }}&={\mathbf {A}}(t)\\ {\ddot{{\varvec{\varLambda }}}}+c_1{\dot{{\varvec{\varLambda }}}}+c_2{\varvec{\varLambda }}&=c_3{{\ddot{\mathbf {B}}}}+c_4{\dot{\mathbf {B}}}, \end{aligned} \end{aligned}$$

(37)

where $c_1,c_2,c_3,c_4$ are the constants in Eq. (18).

5.1 Frequency domain analysis of Eq. (36) and Love numbers

Any quadratic function $x\in \mathbb {R}^3\rightarrow (x\cdot {\mathbf {M}}x)$, where ${\mathbf {M}}$ is a traceless symmetric matrix, is a harmonic function and therefore can be written as:

$$\begin{aligned} (x\cdot {\mathbf {M}}x)=|x|^2 \text { Real}\left\{ \sum _{j=0}^2 m_j N_j P_{2}^j(\cos \theta )\mathrm{e}^{ij\phi }\right\} , \end{aligned}$$

where $P_{2}^j$ are the associated Legendre functions

$$\begin{aligned} P_{2}^0(\cos \theta )=\frac{3}{2}\cos ^2\theta -\frac{1}{2},\quad P_{2}^1(\cos \theta )=3\sin \theta \cos \theta ,\quad P_{2}^2(\cos \theta )=3\sin ^2\theta , \end{aligned}$$

$N_j$ are normalizing coefficients

$$\begin{aligned} N_j=(-1)^j\sqrt{\frac{5}{4\pi }\frac{(2-j)!}{(2+j)!}},\quad j=0,1,2 \end{aligned}$$

(38)

and

$$\begin{aligned} x=|x|(\sin \theta \cos \phi , \sin \theta \sin \phi ,\cos \theta ). \end{aligned}$$

The functions

$$\begin{aligned} Y_2^j(\theta ,\phi )=N_jP_2^j(\cos \theta )\mathrm{e}^{ij\phi }, \quad j=0,1,2, \end{aligned}$$

are fully normalized complex spherical harmonics of degree 2 [see, for instance, Wahr (1995)]. So, in the same way to every skew-symmetric matrix is associated a 3-dimensional real vector, to every symmetric traceless matrix is associated a 3-dimensional vector

$$\begin{aligned} {\mathbf {M}}\longrightarrow (m_0,m_1,m_2)\in \mathbb {R}\times \mathbb {C}^2, \end{aligned}$$

(39)

where the numbers $m_0,m_1,m_2$ are related to the elements $M_{ij}$ of the matrix ${\mathbf {M}}$ as:

$$\begin{aligned} N_0\, m_0=M_{33}, \quad N_1\,m_1=\frac{2}{3}(M_{13}-M_{23}i),\quad N_2\, m_2= \frac{1}{3}(\zeta -M_{12}i), \end{aligned}$$

(40)

where $\zeta =M_{11}+M_{33}/2=-(M_{22}+M_{33}/2)$. This decomposition implies that ${\mathbf {M}}$ can be written as the sum of three matrices

$$\begin{aligned} {\mathbf {M}}= \left( \begin{matrix} -\frac{M_{33}}{2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\frac{M_{33}}{2} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad M_{33} \end{matrix} \right) + \left( \begin{matrix} 0 &{}\quad 0 &{}\quad M_{13} \\ 0 &{}\quad 0 &{}\quad M_{23}\\ M_{13} &{}\quad M_{23} &{}\quad 0 \end{matrix} \right) + \left( \begin{matrix} \zeta &{}\quad M_{12} &{}\quad 0 \\ M_{12} &{}\quad -\zeta &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{matrix} \right) \end{aligned}$$

(41)

that are orthogonal with respect to the inner product $({\mathbf {M}}\cdot \mathbf {N})=\ \mathrm{Tr}\ ({\mathbf {M}}^T\mathbf {N})$ and such that their associated quadratic functions are proportional to the spherical harmonics $P_{2}^0(\cos \theta )$, $\text {Real}\{ P_{2}^1(\cos \theta )\mathrm{e}^{i\phi }\}$, and $\text {Real}\{ P_{2}^2(\cos \theta )\mathrm{e}^{i2\phi }\}$, respectively.

If we apply the decomposition (39) to

$$\begin{aligned} {\mathbf {A}}\rightarrow (a_0,a_1,a_2) \quad \text {and}\quad \mathbf {B}\rightarrow (b_0,b_1,b_2) \end{aligned}$$

then we can write the primary and the secondary potentials as

$$\begin{aligned} \overline{\varPsi }(x)=-\frac{1}{2}(x\cdot {\mathbf {A}}x)=-\frac{|x|^2}{2} \text { Real}\left\{ \sum _{j=0}^2 a_j Y^j_2(\cos \theta ,\phi )\right\} \end{aligned}$$

(42)

and

$$\begin{aligned} \varPsi ^\prime (x)=-\frac{3}{2}\frac{G{\mathrm{I}_\circ }}{|x|^5}(x\cdot \mathbf {B}x) =-\frac{3}{2}\frac{G{\mathrm{I}_\circ }}{|x|^3} \text { Real}\left\{ \sum _{j=0}^2 b_j Y^j_2(\cos \theta ,\phi )\right\} , \end{aligned}$$

(43)

respectively. We remark that the parameters $b_j$ in the secondary potential (43) are related to the normalized complex Stokes coefficients $\overline{C}_{2j}-i\overline{S}_{2j}$ [see, for instance, Petit and Luzum (2010), Eq. (6.1)] and to the unnormalized Stokes coefficients $C_{2j}-i S_{2j}$ as

$$\begin{aligned} b_j=\frac{2}{3}\frac{m_1 R_e^2}{{\mathrm{I}_\circ }}(-1)^j\sqrt{4\pi (2-\delta _{j0})} (\overline{C}_{2j}-i\overline{S}_{2j}) =\frac{2}{3}\frac{m_1 R_e^2}{{\mathrm{I}_\circ }} \frac{1}{N_j}(C_{2j}-i S_{2j}),\quad j=0,1,2 \end{aligned}$$

(44)

where $N_j$ are those in Eq. (38) and $\delta _{j0}=1$ if $j=0$ and $\delta _{j0}=0$ if $j\ne 0$.

The complex coefficients $a_j(t)$ can be Fourier expanded as

$$\begin{aligned} a_j(t)=\sum _p {\hat{a}}_p\mathrm{e}^{i(\omega _p t+\varphi _p)}, \end{aligned}$$

where $\omega _p$ and $\varphi _p$ are the frequency and phase of the $p^{th}$ frequency component and ${\hat{a}}_p> 0$ is the amplitude. If the satellite orbital frequencies are much smaller than the planet spin rate $\varOmega _3$ then $\omega _p\approx j\varOmega _3$. So, $j=0$ corresponds to long period tides, $j=1$ to diurnal tides, and $j=2$ to semi-diurnal tides. The difference $j\varOmega _3-\omega _p$ is a multiple of one of the orbital frequencies of the satellite.

The linear tide response of the planet implies that for each term of the primary complex potential of the form

$$\begin{aligned} -\frac{|x|^2}{2} \text { Real}\left\{ {\hat{a}}\mathrm{e}^{i(\omega t+\varphi )} N_jP_{2j}(\cos \theta )\mathrm{e}^{ij\phi }\right\} = \text { Real}\{\overline{\varPsi }^c(|x|,\theta ,\phi ,t)\} , \end{aligned}$$

(45)

there corresponds a term of the secondary potential of the form

$$\begin{aligned} \varPsi ^\prime (|x|,\theta ,\phi ,t) =-\frac{3}{2}\frac{G{\mathrm{I}_\circ }}{|x|^3} \text { Real}\left\{ {\hat{b}}\mathrm{e}^{i(\omega t+\varphi )} N_jP_{2j}(\cos \theta )\mathrm{e}^{ij\phi }\right\} . \end{aligned}$$

Let a be the radius of the planet. Then the complex Love number $k(\omega ,j)$ is defined as

$$\begin{aligned} \varPsi ^\prime (|x|=a,\theta ,\phi ,t)=\text { Real}\left\{ k \, \overline{\varPsi }^c(|x|=a,\theta ,\phi ,t)\right\} , \end{aligned}$$

that implies

$$\begin{aligned} k(\omega ,j)=\frac{3{\mathrm{I}_\circ }G}{a^5}\frac{{\hat{b}}}{{\hat{a}}}\ . \end{aligned}$$

(46)

The Love numbers can be estimated from observations of the primary and secondary tidal potentials.

Let W be the time-average dissipation of tidal energy and J be the time-average tidal balance of energy, as defined in “Appendix 2”. From Eqs. (46), (99), and (102), we obtain that, for a term of the primary complex potential of the form (45),

$$\begin{aligned} J=\frac{5}{32\pi }\frac{a^5}{G}{\hat{a}}^2\, \text { Real}\, k\, , \quad W=-\frac{5}{32\pi }\frac{a^5}{G}{\hat{a}}^2\,\omega \,\text {Imag}\, k. \end{aligned}$$

(47)

From this relations it is possible to obtain a new expression for the body’s specific dissipation function (or quality factor) $Q^{-1}=-\text {Imag }(k)/\text {Real}( k)$,⁵

$$\begin{aligned} Q^{-1}(\omega ,j)=-\frac{\text {Imag }(k)}{\text {Real}( k)}= \frac{W}{\omega J}. \end{aligned}$$

(48)

If we apply the decomposition (39) also to ${\varvec{\varLambda }}\rightarrow (\lambda _0,\lambda _1,\lambda _2)$, then we can rewrite Eq. (37) as

$$\begin{aligned} \begin{aligned} \mu {\ddot{b}}_j+\gamma b_j+\lambda _j&=a_j(t)\\ {\ddot{\lambda }}_j+c_1{\dot{\lambda }}_j+c_2\lambda&=c_3{\ddot{b}}_j+c_4{\dot{b}}_j\qquad j=0,1,2. \end{aligned} \end{aligned}$$

(49)

As before $a_j(t)$ can be Fourier expanded. For a term of the form $a_j(t)={\hat{a}}\mathrm{e}^{i(\omega t+\varphi )}$, there corresponds a solution of the form $b_j(t)={\hat{b}}\mathrm{e}^{i(\omega t+\varphi )}$, $\lambda _j(t)={\hat{\lambda }}\mathrm{e}^{i(\omega t+\varphi )}$, such that ${\hat{a}}$ and ${\hat{b}}$ are related as

$$\begin{aligned} \left( -\omega ^2\mu +\gamma +\frac{c_3\omega ^2-c_4\omega i}{\omega ^2-c_1\omega i-c_2}\right) {\hat{b}}={\hat{a}}. \end{aligned}$$

(50)

This equation and Eq. (46) imply that for the rheology of the Wiechert oscillator in Fig. 1b the Love number depends on the frequency as

$$\begin{aligned} k(\omega )=\frac{3{\mathrm{I}_\circ }G}{a^5} \left( -\omega ^2\mu +\gamma + \frac{c_3\omega ^2-c_4\omega i}{\omega ^2-c_1\omega i-c_2}\right) ^{-1}. \end{aligned}$$

(51)

This equation can also be written as

$$\begin{aligned} \left( \frac{3{\mathrm{I}_\circ }G}{a^5k(\omega )}+ \omega ^2\mu -\gamma \right) (-\omega ^2+c_1i\omega +c_2) +c_3\omega ^2-c_4i\omega =0, \end{aligned}$$

(52)

which is a convenient form for the fit of the parameters $c_1,c_2,c_3,c_4$.

5.2 The case of a circular orbit on the equatorial plane of the planet: dissipation of energy and phase lag

In this section we obtain the tide response of a planet under the tidal forcing of a satellite on the equatorial plane with circular orbit of radius r. In the inertial frame the orbital angular velocity of the satellite is $n\mathrm{e}_3$. So,

$$\begin{aligned} q(t)=r\cos ((n-\varOmega _3) t)\mathrm{e}_1+r\sin ((n-\varOmega _3)t)\mathrm{e}_2= r\cos (\sigma t)\mathrm{e}_1-r\sin (\sigma t)\mathrm{e}_2, \end{aligned}$$

(53)

where $\sigma =\varOmega _3-n$ (in general $\sigma >0$). Using the expression for ${{\mathbf {A}}}$ in Eq. (35) and Eqs. (41) and (40) we obtain:

$$\begin{aligned} a_0=-\frac{1}{N_0}\frac{Gm_2}{r^3},\quad a_1=0,\quad a_2=\frac{1}{N_2} \frac{Gm_2}{2r^3}\mathrm{e}^{i2\sigma t}={\hat{a}}\mathrm{e}^{i2\sigma t}. \end{aligned}$$

(54)

The time independent term $a_0$ is responsible for an additional flattening of the planet (the permanent tide). The time-varying tide is due to the semi-diurnal mode $a_2$. It implies a tidal response of the form

$$\begin{aligned} b_2(t)={\hat{b}}\mathrm{e}^{i2\sigma t}=|{\hat{b}}|\mathrm{e}^{i2(\sigma t-\psi )},\quad \text {where} \quad \psi =-\frac{1}{2}\,\text {arg}\, {\hat{b}}. \end{aligned}$$

The angle $\psi$ is the so called phase lag of the tide illustrated in Fig. 4.

Fig. 4

Tidal phase-lag $\psi$ with respect to the phase of the tidal force. The figure represents the motion of the satellite (Moon) from the point of view of an observer fixed to the planet (Earth). At $t=0$ the observer is aligned with the satellite. The horizontal axis is fixed with respect to the Earth at a certain longitude

From Eq. (46), ${\hat{b}}=k{\hat{a}}\,(a^5/3{\mathrm{I}_\circ }G)$, where k is the Love number associated to $j=2$ and to the angular frequency $\omega =2\sigma$, that implies arg$\,{\hat{b}}=$arg$\,k$.

For the Wiechert rheology, from Eqs. (47), (48), (38), (51), and (18):

$$\begin{aligned} W=9{\mathrm{I}_\circ }\left( \frac{Gm_2}{2r^3}\right) ^2\omega ^2 \frac{\left( \frac{\alpha _1\alpha _2}{\eta _1\eta _2}\right) ^2(\eta _1+\eta _2) +\omega ^2\left( \frac{\alpha ^2_1}{\eta _1}+\frac{\alpha ^2_2}{\eta _2}\right) }{[(-\mu \omega ^2+\gamma )(\omega ^2-c_2)+c_3\omega ^2]^2+ \omega ^2[c_4+c_1(-\mu \omega ^2+\gamma )]^2}, \end{aligned}$$

(55)

and

$$\begin{aligned} Q^{-1}=\tan (2\psi )= \frac{\omega \left( \frac{\alpha _1\alpha _2}{\eta _1\eta _2}\right) ^2(\eta _1+\eta _2) +\omega ^3\left( \frac{\alpha ^2_1}{\eta _1}+\frac{\alpha ^2_2}{\eta _2}\right) }{(-\mu \omega ^2+\gamma )[(\omega ^2-c_2)^2+c_1^2\omega ^2]+ \omega ^2[c_3(\omega ^2-c_2)+c_1c_4]}, \end{aligned}$$

(56)

where in both equations

$$\begin{aligned} \omega =2\sigma . \end{aligned}$$

6 The Earth as a prototype

The rheology of the Earth is quite complex. The oceans are responsible for approximately 95% of the tidal energy dissipation (Munk 1997; Egbert and Ray 2001). The Love numbers of the diurnal tides have a strong dependence on the frequency [see, for instance, Agnew (2007), paragraph 3.06.3.2.1]. By the other hand the Earth is the most studied celestial body and there are plenty of geophysical and astronomical data available. For these reasons we chose the Earth as a prototype. This section is divided into the following. At first we present some Love numbers which were estimated using experimental and observational data. Then we give a procedure to fit the parameters of the Wiechert model to the data. This procedure is also convenient when working with the kinetic energy given in the “Appendix 1”. Finally, we compare some quantities obtained from our model with those for the real Earth. We use the following values for various geophysical constants (most of them are taken from Yoder (1995)):

• $G=6.673\times 10^{-11}\, \ \mathrm{m}^3\, \mathrm{kg}^{-1}\, \hbox {s}^{-2}$,

• $m_1=5.9736\times 10^{24}$  kg (mass of the Earth),

• ${\mathrm{I}_\circ }=8.01875022\times 10^{+37}\, \ \mathrm{kg\, m}^2$ (mean moment of inertia of the Earth),

• $R_I=\sqrt{5{\mathrm{I}_\circ }/(2m_1)}=5793\times 10^3$  m [mean moment of inertia radius, Eq. (2)],

• $a=6371.01 \times 10^3$  m (volumetric mean radius of the Earth),

• $R_e=6378.14\times 10^3$  m(equatorial radius of the Earth),

• $\varOmega _3=7.292115\times 10^{-5}$  rad   $\hbox {s}^{-1}$ (mean rotation rate of the Earth),

• $J_2=-C_{20}=0.0010826265$ (dynamic flattening of the Earth),

• $g=Gm_1/a^2=9.82022\, \ \mathrm{m}\, \hbox {s}^{-2}$ (nominal acceleration of gravity on Earth),

• $g_e=9.780\, \ \mathrm{m}\, \hbox {s}^{-2}$ (acceleration of gravity on Earth at the equator),

6.1 The Love numbers for the principal tidal constituents and nominal Love numbers

Our main reference for the Love numbers of the Earth is Petit and Luzum (2010). In this reference, algorithms are presented for the computation of the Love numbers $k_s$ for the solid part of the Earth and $k_o$ for the oceans. The Love numbers k for the Earth are obtained adding both, $k=k_s+k_o$. The Love numbers for the diurnal and semi-diurnal tides in Table 1 were obtained from Petit and Luzum (2010).⁶ The Love numbers k for the longer-period tides in Table 2 were taken from Table 3 of Ray and Erofeeva (2014). Our choice of tidal constituents is based on Table 1 of Wahr (1995), from where we took the amplitudes and periods. The amplitude H in Tables 1 and 2 is related to our amplitude ${\hat{a}}$ as

$$\begin{aligned} {\hat{a}}=\frac{2}{a^2}H, \end{aligned}$$

which follows from the comparison of Eq. (1) in Wahr (1995) with our Eq. (42).

Table 1 These amplitudes are due to Cartwright and Edden (see Wahr 1995)

Table 2 The amplitudes and notation are as in Table 1

The way we will fit the parameters of the Wiechert model in the next section requires at first the definition of nominal diurnal and semi-diurnal Love numbers. Nominal Love numbers for the solid Earth tides are given in Petit and Luzum (2010), where they were described as: “The choice of these nominal values has been made so as to minimize the number of terms for which corrections will have to be applied”. Notice that the Love numbers of the solid Earth of some tidal diurnal constituents vary considerably from their nominal values while for the semi-diurnal constituents this variation is very small. In order to define nominal Love numbers for the Earth we still need to define nominal Love numbers for the ocean tides. We do it by means of a weighted average that preserves the overall time-average dissipation of tidal energy W and the time-average tidal balance of energy J. The basic formulas used in this weighted average are in Eq. (47). The result is

$$\begin{aligned} k_o(j)=\frac{\sum _p H_p^2\,\text {Real}\,[k_{o}(\omega _p)]}{\sum _pH_p^2}+ i\frac{\sum _p \omega _p H_p^2\,\text {Imag}\,[k_{o}(\omega _p)]}{j\varOmega _3\sum _pH_p^2}, \end{aligned}$$

(57)

where the sums are over the diurnal or the semi-diurnal values depending on whether $j=1$ or $j=2$, respectively. The nominal Love numbers are presented in Table 3.

Table 3 Nominal Love numbers

6.2 The fit of the parameters

The construction of the differential equations for the tidal response had two steps: at first, in Sect. 2, we introduced an inertial term, with inertia coefficient ${\mathrm{I}_\circ }\mu$, and an elastic restoring force, with elastic coefficient ${\mathrm{I}_\circ }\gamma$ ; and then, in Sect. 3, we added forces due to the rheology of the body. The number of parameters introduced in the second step depends on the complexity of the rheological model. If the body is made of a perfect fluid, there is no rheology, then $\gamma >0$ due to the self-gravitational force. It can be that the body has a rheology that resists to static forces. In this case $\gamma$ has also a contribution from the rheology. For large bodies gravity always dominate. In any case, the constant $\gamma$ is associated to the equilibrium value of $\mathbf {B}$ under steady forces. For bodies with an almost constant spin, like the Earth, the centrifugal force causes a polar flattening that allows for the computation of $\gamma$ independently from the other parameters. We remark that time independent tidal forces as, for instance, that related to the coefficient $a_0$ in Eq. (54) also contribute to the flattening. This last effect is called the “permanent tide”. For the Earth, the permanent tide contribution is $10^{-6}$ smaller than that due to the spin (Petit and Luzum 2010, section 6.2.2). So, it can be neglected. Using Eq. (14) or, equivalently, Eq. (11) in Ragazzo and Ruiz (2015) we obtain

$$\begin{aligned} \gamma =\frac{{\mathrm{I}_\circ }}{m_1R_e^2}\frac{\varOmega _3^2}{(-C_{20})}= 1.621\times 10^{-6}\ \hbox {s}^{-2}. \end{aligned}$$

(58)

If the Earth were made of a perfect fluid and had the radius equal to the mean moment of inertia radius $R_I$, then the value of $\gamma$ would be $\gamma _f$ given in Eq. (15) that is $1.640\times 10^{-6} \hbox {s}^{-2}$. So, gravity dominates the static response of the Earth.

As said before, the Earth has a complex rheological behavior. In this paper, it is not our goal to find a model that reproduces all this complexity but to find one that at least gives the correct rate of dissipation of energy and how the dissipation splits into the diurnal and the semi-diurnal tides. Using the association principle in Sect. 3 we tested six different spring–dashpot models to fit the Love numbers given in Tables 1 and 2. In some of them we used the kinetic energy given in the “Appendix 1” in order to avoid negative values of $\mu$. Among all the models we tested the most successful was the Wiechert model in Fig. 1a and its associated Wiechert oscillator in Fig. 1b. In the following the Love number associated to the Wiechert oscillator, which is given in Eq. (51), will be denoted by $k_w(\omega ,j)$ to differentiate it from the Love numbers given in Tables 1 and 2 that remain being denoted as $k(\omega ,j)$. Since the parameter $\gamma$ was already determined, for given values of $\mu$, $\omega$, and j, Eq. (52) is linear on the parameters $c_1,c_2,c_3,c_4$. So, consider the values $(\omega ,j)=(\varOmega _3,1)$ and $(\omega ,j)=(2\varOmega _3,2)$ and their respective nominal Love numbers $k(j\varOmega _3,j)$, $j=1,2$, given in Table 3. The pair of complex equations obtained after substituting $\omega =j\varOmega _3$ and $k_w(j\varOmega _3,j)$, $j=1,2$, into Eq. (52) has the solution $c_1(\mu ),c_2(\mu ),c_3(\mu ),c_4(\mu )$. The requirement that $c_n\ge 0$ implies that $\mu$ must be restricted to a certain interval $(\mu _0,\mu _1)$. In order to determine $\mu$ we minimize the function

$$\begin{aligned} \sum _{j=0}^2\sum _p H_p^2 \bigl |\text { Real}\,|k(\omega _p,j)-k_w(\mu ,\omega _p,j)]\bigr |+ H_p^2\,\omega _p\bigl |\text {Imag}\,[k(\omega _p,j)-k_w(\mu ,\omega _p,j)]\bigr |, \end{aligned}$$

where the sum is over all frequencies in Tables 1 and 2. Notice that the weights of the differences in this sum are the factors of k in Eq. (47) for J and W. The result of this computation is:

(59)

and using the relations in Eq. (18) we obtain the numbers in Eq. (1).

In Table 4 we present a comparison between the rates of dissipation of tidal energy as given by the imaginary parts of the Love numbers in Tables 1 and 2 with those given by our model.

Table 4 Rates of dissipation of tidal energy (Watts) by the longer period, diurnal, and semi-diurnal tides for the constituents in Tables 1 and 2

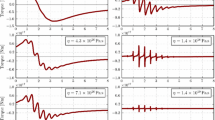
In Fig. 5 (left) we show the graph of $\omega \rightarrow -\omega \,\text {Imag} \, k_w$ and $\omega \rightarrow \text {Real} \, k_w$ and the points that correspond to the values in Tables 1 and 2. In the same figure (right) we restrict the frequency range to the diurnal and semi-diurnal frequencies and show that our $\text {Real} \, k_w$ overestimate all the corresponding values in Table 1 for the diurnal modes (the diurnal nominal Love number in Table 3 used in the fit and taken from Petit and Luzum (2010) does the same). In Fig. 6 we show the real and imaginary parts of the Love number $k_w$ in an extended frequency scale. The real part of the Love number changes sign at a frequency that corresponds to the period of 3.15 h. This is the only frequency of free-oscillations of the Earth according to our model.⁷ So, the period 3.15 h corresponds to a resonance and any forcing with a period below it is super-resonant (inertia dominates). At the end of Sect. 6.4 we show that the Earth–Moon system has an unstable synchronous state that corresponds to a period of 4.8 h and to an Earth–Moon distance of $1.46\times \, 10^7$ m. This period and distance rely solely upon conservation of angular momentum, they do not depend on the model for the rheology. Below the radius $1.46\times \, 10^7$ m, circular Kepler orbits lead to collision due to dissipation of energy. Therefore, $2\pi /4.8$ rad/h can be taken as the upper limit of high frequencies for the Earth periodic tidal forcing.

Fig. 5

Left the graph in log–log scale of $\omega \rightarrow -\omega \,\text {Imag} \, k_w$ and $\omega \rightarrow \,\text {Real} \, k_w$, where $k_w$ is the Love number as given in Eq. (51), and the points that correspond $\omega \,\text {Imag} \, k$ and $\text {Real} \, k$ in Tables 1 and 2. Right The graph of $\omega \rightarrow \text {Real} \, k_w$ on the diurnal to semi-diurnal frequency range (linear scale). The points correspond to the values of $\text {Real}\, k(\omega )$ as given in Table 1

Fig. 6

Left the sign change of the real part of $k_w(\omega )$. Right the imaginary part of $-k_w(\omega )$

6.3 Chandler wobble

The equations for the motion of an isolated body are given in Eq. (28). This equation admits a steady solution $\overline{\varOmega }=\overline{\varOmega }_3\mathrm{e}_3$, ${\varvec{\varLambda }}=0$, and $\overline{B}_{33}=-\overline{\varOmega }_3^22/(3\gamma )$, the remaining entries of $\mathbf {B}$ being null. The linearization of Eq. (28) at this solution are

$$\begin{aligned} \mu {{\ddot{\mathbf {B}}}} +\gamma \mathbf {B}+{\varvec{\varLambda }}= & {} -(\overline{{\varvec{\varOmega }}}{\varvec{\varOmega }}+{\varvec{\varOmega }}\overline{{\varvec{\varOmega }}})+\frac{2}{3}\ \mathrm{Tr}\ ({\varvec{\varOmega }}\overline{{\varvec{\varOmega }}})\mathbb {I} \nonumber \\ {\ddot{{\varvec{\varLambda }}}}+c_1{\dot{{\varvec{\varLambda }}}}+c_2{\varvec{\varLambda }}= & {} c_3{{\ddot{\mathbf {B}}}}+c_4{\dot{\mathbf {B}}} \nonumber \\ {\dot{{\varvec{\varOmega }}}}+(\overline{\mathbf {B}}{\dot{{\varvec{\varOmega }}}}+{\dot{{\varvec{\varOmega }}}} \overline{\mathbf {B}})= & {} -({\dot{\mathbf {B}}}\overline{{\varvec{\varOmega }}}+\overline{{\varvec{\varOmega }}}{\dot{\mathbf {B}}}) +[\mathbf {B},\overline{{\varvec{\varOmega }}}^2]+[\overline{\mathbf {B}},\overline{{\varvec{\varOmega }}}{\varvec{\varOmega }}+{\varvec{\varOmega }}\overline{{\varvec{\varOmega }}}]. \end{aligned}$$

(60)

These equation can be written in terms of $(b_0,b_1,b_2)$, $(\lambda _0,\lambda _1,\lambda _2)$, obtained by means of the decomposition (39) and (40), and $(\varOmega _1,\varOmega _2,\varOmega _3)$. This decomposition splits Eq. (60) into three uncoupled equations for the normal modes of oscillation. The first contains only the three real variables $(b_0,\lambda _0,\varOmega _3)$ and describes oscillations around the equilibrium that keeps the spin direction fixed and the rotational symmetry of the ellipsoid of inertia. Only the spin rate and the ellipsoid flattening change. The second contains only the complex variables $b_2,\lambda _2$ and describes oscillations that only change the two principal axis of inertia of the ellipsoid that are perpendicular to $\mathrm{e}_3$. The third equation contains the variables $b_1,\lambda _1,\varOmega _1,\varOmega _2$ and describes the precessions of the angular velocity around $\mathrm{e}_3$. This is the equation for the Chandler wobble. If we write

$$\begin{aligned} z=B_{13}-iB_{23}, \quad \lambda ={\varvec{\varLambda }}_{13}-i{\varvec{\varLambda }}_{23},\quad w=\varOmega _2+i\varOmega _1, \end{aligned}$$

then the equations for the Chandler wobble becomes

$$\begin{aligned} \begin{aligned} \mu {\ddot{z}}&=-\gamma z-\lambda +\overline{\varOmega }_3 \,w i\\ {\ddot{\lambda }}+c_1{\dot{\lambda }}+c_2\lambda&=c_3{\ddot{z}}+c_4{\dot{z}}\\ \left( 1-\frac{\overline{\varOmega }_3^2}{3\gamma }\right) {\dot{w}}&=\overline{\varOmega }_3{\dot{z}} i +\overline{\varOmega }_3^2z-\frac{\overline{\varOmega }_3^3}{\gamma }wi. \end{aligned} \end{aligned}$$

(61)

The characteristic equation associated to this equation has five roots. One of them is zero, it corresponds to the family of steady solutions $\lambda =0$ and $\gamma z=\overline{\varOmega }_3 \,w i$. There are two roots that are real and negative. Finally, there is a pair of complex conjugate roots: the real part is negative and the imaginary part is associated to the period of 438 days. The observed Chandler period is 434 days.

6.4 An estimate of the variation of the Earth–Moon distance

The distance between the Earth and the Moon has been increasing at a rate of $3.82\times 10^{-2}\,\hbox {m}/\hbox {year}$ (Dickey et al. 1994) due to the loss of energy by tidal heating. If the present values of energy dissipation rate are extrapolated to the past then some computations put the Moon extremely close to the Earth as recently as $1.5\times 10^9$ years [see, for instance, Bills and Ray (1999)]. In this paragraph we use the dissipation of energy function in Eq. (55) and a simplified orbital model to estimate the variation of the Earth–Moon distance. We alert that this is a crude estimate: the Moon orbit is supposed circular and on the equatorial plane of the Earth (only the $M_2$ tidal mode is being considered) and the influence of the Sun is completely neglected.

As already said, we assume that the orbit of the Moon is circular and that it satisfies Kepler’s third law

$$\begin{aligned} n(r)=\sqrt{\frac{GM}{r^3}}, \end{aligned}$$

where r is the Earth–Moon distance, and $M=m_1+m_2$. The system angular momentum $L={\mathrm{I}_\circ }\varOmega +mn r^2$ is supposed to be constant, where $\varOmega =\varOmega _3$ and m is the reduced mass. So,

$$\begin{aligned} \varOmega (r)=\frac{L- mn r^2}{{\mathrm{I}_\circ }}= \frac{L- m\sqrt{GMr}}{{\mathrm{I}_\circ }}. \end{aligned}$$

The energy of the system is

$$\begin{aligned} E(r)=\frac{1}{2}(mn^2 r^2+{\mathrm{I}_\circ }\varOmega ^2)-\frac{Gm_1m_2}{r}, \end{aligned}$$

that implies

$$\begin{aligned} {\dot{E}}=\left( mnn^\prime r^2+mn^2 r+{\mathrm{I}_\circ }\varOmega \varOmega ^\prime + \frac{Gm_1m_2}{r^2}\right) {\dot{r}}=h(r){\dot{r}}, \end{aligned}$$

where

$$\begin{aligned} n^\prime =\frac{dn}{dr}=-\frac{3}{2}\sqrt{\frac{GM}{r^5}} \quad \text {and}\quad \varOmega ^\prime =\frac{d\varOmega }{dr}=-\frac{m}{2{\mathrm{I}_\circ }}\sqrt{\frac{GM}{r}}. \end{aligned}$$

Using that ${\dot{E}}=-W$, where $W(\omega ,r)$ is given in Eq. (55), and that $\omega (r)=2(\varOmega (r)-n(r))$ we obtain

$$\begin{aligned} {\dot{r}}=-\frac{W(\omega (r),r)}{h(r)}=f(r). \end{aligned}$$

(62)

The time t it takes for the distance r to change from $r_i$ to $r_f$ is

$$\begin{aligned} t(r_i,r_f)=\int _{r_i}^{r_f}\frac{dr}{f(r)}. \end{aligned}$$

This equation was numerically integrated for $r_i=2.5\times 10^8\,\hbox {m}$ and $r_f=(GM/n^2)^{1/3}=3.84754 \times 10^8\,\hbox {m}$, where $n_{f}= 2.6616995\times 10^{-6}\,\hbox {rad}\,\hbox {s}^{-1}$ is the present value of the Lunar mean motion. The angular momentum we used was $L={\mathrm{I}_\circ }\varOmega _f+mn(r_f)r_f^2=3.44524\times 10^{34}\,\hbox {kg}\,\hbox {m}^2\,\hbox {s}^{-1}$, where $\varOmega _f=7.292115\times 10^{-5}\,\hbox {rad} \ \hbox {s}^{-1}$ is the present value of the Earth mean rotation rate. The values we got are: $t(r_i,r_f)=1.58\times 10^{9}\,\hbox {years}$, $f(r_i)= 41\,\hbox {cm}/\hbox {year}$ and $f(r_f)= 3.5\,\hbox {cm}/\hbox {year}$ for the Moon recession rate from the Earth, which is close to the value in Dickey et al. (1994), $W(r_i)= 8.2\times 10^{13}\,\hbox {W}$ and $W(r_f)= 2.86\times 10^{12}\,\hbox {W}$ for the Earth energy dissipation rate, and $2\pi /\varOmega (r_i)=12.28\,\hbox {h}$ and $2\pi /\varOmega (r_f)=23.93\,\hbox {h}$ for the length of the sidereal day of the Earth.

We remark that the power dissipation at $r_f$ is considerably larger than the actual power dissipation of the mode $M_2$, $W=2.536\times 10^{12}\,\hbox {W}$, given in Egbert and Ray (2001). This happens because the value of $r_f$ is different from the effective radius $3.9638\times 10^8\,\hbox {m}$ that is the radius for which the hypothetical circular orbit of the Moon induces a primary average tidal forcing that is equal to the actual $M_2$ average tidal forcing. The amount of energy dissipated by all constituents of the lunar tide is approximately 3.0 TW (Munk 1997).

The asymptotic behavior of any bounded orbit in phase space of a system composed by a deformable body and a point mass is a synchronous state (Hut 1980). At a synchronous state $n=\varOmega$ that implies $L(r)=({\mathrm{I}_\circ }+m r^2)n=\sqrt{GM}({\mathrm{I}_\circ }r^{-3/2}+mr^{1/2})$. The function L(r) has a unique minimum at $r_{min}=\sqrt{3{\mathrm{I}_\circ }/m}$ where $L(r_{min})=L_{min}=4{\mathrm{I}_\circ }n_{min}$ and $n_{min}=\sqrt{GM/r_{min}^3}$. For a given value of L, the equation $L=\sqrt{GM}({\mathrm{I}_\circ }r^{-3/2}+mr^{1/2})$ has no solution if $L<L_{min}$ (there is no bounded solution in phase space), has one solution at $r=r_{min}$ if $L=L_{min}$, and two solutions $r_u<r_s$ if $L>L_{min}$ (if $r(0)<r_u$ then $r(t)\rightarrow 0$, where r(t) is the solution of Eq. (62), if $r(0)>r_u$ then $r(t)\rightarrow r_s$). For the Earth $L>L_{min}$ and: $r_u=1.46\times \, 10^7$ m, $2\pi /\varOmega (r_u)=4.8$ h, $r_s=5.5\times \, 10^8$ m, and $2\pi /\varOmega (r_s)=1121$ h.

7 Tidal degree of freedom elimination and the Mignard’s model

Consider the motion of an extended body (planet) and a point mass (satellite). This system has a relative equilibrium where the satellite remains at rest in the planet reference frame $\mathrm {K}$, the synchronous state (Hut 1980). If the system is close to this equilibrium then the tidal degrees of freedom represented by $\mathbf {B}$ can be eliminated using a perturbative analysis. From a physical perspective the elimination of $\mathbf {B}$ is possible because the transient dynamics of $\mathbf {B}$ is faster than the orbital transient motion. From a mathematical perspective the elimination is possible because the system has a hyperbolic attracting invariant manifold in phase-space. The analysis becomes easier in the synodic coordinate system, where the Lagrangian function is given by (31) and the equations of motion are given in (32). The physical and the mathematical analysis of the system becomes easier when these equations are appropriately written in nondimensional form.

7.1 Nondimensionalization of the variables

Our almost spherical hypothesis (b) implies that the planet deformation due to steady rotation must be small. So, we define a small parameter $\varepsilon$ that measures the initial gravitational flatness of the planet

$$\begin{aligned} \varepsilon =\frac{|\varOmega (0)|}{\sqrt{\gamma }}\ll 1, \end{aligned}$$

(63)

such that $|\mathbf {B}|\approx |{\varvec{\varOmega }}|^2/\gamma$ is of order $\varepsilon ^2$. Then we define a nondimensional angular velocity matrix ${\tilde{{\varvec{\varOmega }}}}$,

$$\begin{aligned} {\varvec{\varOmega }}=\varepsilon \sqrt{\gamma }{\tilde{{\varvec{\varOmega }}}} , \end{aligned}$$

(64)

such that $|{\tilde{{\varvec{\varOmega }}}}|$ is of order one, and a rescaled ${\tilde{\mathbf {B}}}$,

$$\begin{aligned} \mathbf {B}=\varepsilon ^2{\tilde{\mathbf {B}}}, \end{aligned}$$

(65)

such that $|{\tilde{\mathbf {B}}}|$ is also of order one. The Lagrangian multipliers ${\varvec{\varLambda }}_1$ and ${\varvec{\varLambda }}_ 2$ are rescaled as $\mathbf {B}$: ${\varvec{\varLambda }}_1=\varepsilon ^2{\tilde{{\varvec{\varLambda }}}}_1$ and ${\varvec{\varLambda }}_2=\varepsilon ^2{\tilde{{\varvec{\varLambda }}}}_2$.

At the synchronous state the third Kepler law implies $|\varOmega |^2r^3=GM$ that suggests the length scale $(GM/\varepsilon ^2 \gamma )^{1/3}$ and the nondimensional distance ${\tilde{q}}$,

$$\begin{aligned} q= \left( \frac{GM}{\varepsilon ^2\gamma }\right) ^{1/3}{\tilde{q}}, \end{aligned}$$

(66)

such that ${\tilde{q}}$ is of order one. The equation ${\dot{q}}=-{\varvec{\varOmega }}q+u$ suggests the nondimensional velocity ${\tilde{u}}$,

$$\begin{aligned} u= (GM\varepsilon \sqrt{\gamma })^{1/3} {\tilde{u}} \end{aligned}$$

(67)

such that ${\tilde{u}}$ is also of order one.

A natural time scale for the dynamics of $\mathbf {B}$ is the undamped natural frequency $\sqrt{\gamma /\mu }$. So, we define a nondimensional ${\tilde{{\mathbf {U}}}}$,

$$\begin{aligned} {\mathbf {U}}=\varepsilon ^2\sqrt{\frac{\gamma }{\mu }}{\tilde{{\mathbf {U}}}}, \end{aligned}$$

(68)

such that $\vert {\tilde{{\mathbf {U}}}}\vert$ is of order not greater than one. Finally we define a nondimensional time ${\tilde{t}}$

$$\begin{aligned} t= \sqrt{\frac{\mu }{\gamma }} {\tilde{t}} \end{aligned}$$

(69)

and use the notation

$$\begin{aligned} \frac{d}{d{\tilde{t}}}f({\tilde{t}})=f' ({\tilde{t}}). \end{aligned}$$

In terms of the nondimensional variables Eq. (32) become

$$\begin{aligned} {{\tilde{\mathbf {B}}}}^\prime= & {} \tilde{{\mathbf {U}}}\nonumber \\ {{\tilde{{\mathbf {U}}}}}^\prime= & {} - {\tilde{\mathbf {B}}} -\frac{1}{\gamma }({\tilde{{\varvec{\varLambda }}}}_1+{\tilde{{\varvec{\varLambda }}}}_2) -{\tilde{{\varvec{\varOmega }}}}^2+ \frac{1}{3}\ \mathrm{Tr}\ ({\tilde{{\varvec{\varOmega }}}}^2)\mathbb {I} + \frac{ m_2}{M}\frac{1}{|{\tilde{q}}|^5}\left( 3{\tilde{q}}\otimes {\tilde{q}}-|{\tilde{q}}|^2 \mathbb {I} \right) \nonumber \\ \alpha _1^{-1} {\tilde{{\varvec{\varLambda }}}}_1^\prime= & {} -\frac{1}{\gamma } {\tilde{\eta }}_1^{-1}{\tilde{{\varvec{\varLambda }}}}_1+ {\tilde{{\mathbf {U}}}}\nonumber \\ \alpha _2^{-1} {\tilde{{\varvec{\varLambda }}}}_2^\prime= & {} -\frac{1}{\gamma } {\tilde{\eta }}_2^{-1}{\tilde{{\varvec{\varLambda }}}}_2+ {\tilde{{\mathbf {U}}}}\nonumber \\ {{\tilde{{\varvec{\varOmega }}}}}^\prime= & {} \varepsilon ^2\left\{ -({\tilde{\mathbf {B}}}{{\tilde{{\varvec{\varOmega }}}}}^\prime +{{\tilde{{\varvec{\varOmega }}}}}^\prime {\tilde{\mathbf {B}}})- ({\tilde{{\mathbf {U}}}}y{\tilde{{\varvec{\varOmega }}}}+{\tilde{{\varvec{\varOmega }}}} {\tilde{{\mathbf {U}}}}) + \varepsilon \sqrt{\mu }[{\tilde{\mathbf {B}}},{\tilde{{\varvec{\varOmega }}}}^2] +\frac{m_2}{M}\frac{3\varepsilon \sqrt{\mu }}{|{\tilde{q}}|^5} \left[ {\tilde{q}}\otimes {\tilde{q}},{\tilde{\mathbf {B}}}\right] \right\} \nonumber \\ {{\tilde{q}}}^\prime= & {} \varepsilon \sqrt{\mu }\left\{ -{\tilde{{\varvec{\varOmega }}}} {\tilde{q}}+ {\tilde{u}}\right\} \nonumber \\ {{\tilde{u}}}^\prime= & {} \varepsilon \sqrt{\mu }\left\{ -{\tilde{{\varvec{\varOmega }}}} {\tilde{u}} -\frac{1}{|{\tilde{q}}|^3}{\tilde{q}}\right. \nonumber \\&+\left. \varepsilon ^2\frac{{\mathrm{I}_\circ }}{m_1}\left( \frac{\gamma \varepsilon ^2}{GM}\right) ^{2/3} \left( -\frac{15}{2}\frac{1}{|{\tilde{q}}|^7}({\tilde{q}}\cdot {\tilde{\mathbf {B}}} {\tilde{q}}){\tilde{q}} +3\frac{1}{|{\tilde{q}}|^5} {\tilde{\mathbf {B}}} {\tilde{q}}\right) \right\} , \end{aligned}$$

(70)

where

$$\begin{aligned} {\tilde{\eta }}_1=\frac{\eta _1}{\sqrt{\mu \gamma }},\quad {\tilde{\eta }}_ 2=\frac{\eta _ 2}{\sqrt{\mu \gamma }} \end{aligned}$$

(71)

are nondimensional damping coefficients. The total angular momentum becomes

$$\begin{aligned} \frac{{\varvec{\ell }}}{{\mathrm{I}_\circ }\sqrt{\gamma }}= \mathbf {Y}\left\{ \varepsilon {\tilde{{\varvec{\varOmega }}}}+\varepsilon ^3({\tilde{\mathbf {B}}}{\tilde{{\varvec{\varOmega }}}}+{\tilde{{\varvec{\varOmega }}}} {\tilde{B}} +\varepsilon \sqrt{\mu }[{\tilde{{\mathbf {U}}}},{\tilde{\mathbf {B}}}]) +\frac{m}{{\mathrm{I}_\circ }\sqrt{\gamma }} \frac{(GM)^{2/3}}{\gamma ^{1/6}\varepsilon ^{1/3}} ({\tilde{u}}\otimes {\tilde{q}}-{\tilde{q}}\otimes {\tilde{u}})\right\} \mathbf {Y}^T, \end{aligned}$$

where $\mathbf {Y}$ is determined from

$$\begin{aligned} \mathbf {Y}^\prime =\varepsilon \sqrt{\mu } \mathbf {Y}{\tilde{{\varvec{\varOmega }}}}. \end{aligned}$$

7.2 The Mignard equation

For $\varepsilon =0$, Eq. (70) have a nine-dimensional invariant manifold of equilibria that can be described as the graph of the function

$$\begin{aligned} {\tilde{\mathbf {B}}}= & {} {\tilde{\mathbf {B}}}_0({\tilde{{\varvec{\varOmega }}}}, {\tilde{q}}, {\tilde{u}})= - {\tilde{{\varvec{\varOmega }}}}^2+\frac{1}{3}\ \mathrm{Tr}\ ( {\tilde{{\varvec{\varOmega }}}}^2)\mathbb {I} + \frac{m_2}{M}\frac{1}{| {\tilde{q}}|^5} \left( 3 {\tilde{q}}\otimes {\tilde{q}}- | {\tilde{q}}|^2 \mathbb {I} \right) \nonumber \\ {\tilde{{\mathbf {U}}}}= & {} {\tilde{{\mathbf {U}}}}_0 ( {\tilde{{\varvec{\varOmega }}}} ,{\tilde{q}} ,{\tilde{u}})=0 \nonumber \\ {\tilde{{\varvec{\varLambda }}}}_1= & {} {\tilde{{\varvec{\varLambda }}}}_{10} ( {\tilde{{\varvec{\varOmega }}}} ,{\tilde{q}} ,{\tilde{u}})=0 \nonumber \\ {\tilde{{\varvec{\varLambda }}}}_2= & {} {\tilde{{\varvec{\varLambda }}}}_{20} ( {\tilde{{\varvec{\varOmega }}}} ,{\tilde{q}} ,{\tilde{u}})=0. \end{aligned}$$

(72)

Using the Routh–Hurwitz theorem and an algebraic manipulator we can show that this invariant manifold is hyperbolic and attractive and therefore, for $\varepsilon >0$ sufficiently small, it can be continued to a smooth $\varepsilon$-family of invariant manifolds, which are hyperbolic and attractive [see Theorem 2 in Carr (1981)]. This continuation can be written as

$$\begin{aligned} \begin{aligned}&{\tilde{\mathbf {B}}}={\tilde{\mathbf {B}}}_0({\tilde{{\varvec{\varOmega }}}},q,u)+ \varepsilon {\tilde{\mathbf {B}}}_1({\tilde{\varOmega }},q,u)+ \mathscr {O}(\varepsilon ^2),\qquad {\tilde{{\mathbf {U}}}}=\varepsilon {\tilde{{\mathbf {U}}}}_1({\tilde{{\varvec{\varOmega }}}},q,u)+\mathscr {O}(\varepsilon ^2)\\&{\tilde{{\varvec{\varLambda }}}}_1=\varepsilon {\tilde{{\varvec{\varLambda }}}}_{11}({\tilde{{\varvec{\varOmega }}}},q,u)+\mathscr {O}(\varepsilon ^2),\qquad {\tilde{{\varvec{\varLambda }}}}_2=\varepsilon {\tilde{{\varvec{\varLambda }}}}_{21}({\tilde{{\varvec{\varOmega }}}},q,u)+\mathscr {O}(\varepsilon ^2). \end{aligned} \end{aligned}$$

These relations and equation ${{\tilde{\mathbf {B}}}}^\prime ={\tilde{{\mathbf {U}}}}$ imply

$$\begin{aligned} {{\tilde{\mathbf {B}}}}^\prime =(\partial _{{\tilde{{\varvec{\varOmega }}}}} {\tilde{\mathbf {B}}}_0) \underbrace{{{\tilde{{\varvec{\varOmega }}}}}^\prime }_{=\mathscr {O}(\varepsilon ^2)}+ (\partial _{{\tilde{q}}} {\tilde{\mathbf {B}}}_0) \underbrace{{{\tilde{q}}}^\prime }_{=\mathscr {O}(\varepsilon )}+\mathscr {O}(\varepsilon ^2)= \varepsilon {\tilde{{\mathbf {U}}}}_1+ \mathscr {O}(\varepsilon ^2) \end{aligned}$$

and so

$$\begin{aligned} \varepsilon {\tilde{{\mathbf {U}}}}_1=(\partial _{{\tilde{q}}} {\tilde{\mathbf {B}}}_0) {{\tilde{q}}}^\prime \Longrightarrow {\tilde{U}}_{1ij}= \sqrt{\mu }\sum _k (\partial _{{\tilde{q}}_k} {\tilde{B}}_{0ij}) (-{\tilde{{\varvec{\varOmega }}}} {\tilde{q}}+{\tilde{u}})_k . \end{aligned}$$

After some computations we obtain

$$\begin{aligned} {\tilde{{\mathbf {U}}}}_1=3\sqrt{\mu }\frac{m_2}{M} \frac{1}{|{\tilde{q}}|^5}\left\{ \left( -5\frac{{\tilde{q}}\otimes {\tilde{q}}}{|{\tilde{q}}|^2}+ \mathbb {I} \right) ({\tilde{q}}\cdot {\tilde{u}})+{\tilde{q}}\otimes (-{\tilde{{\varvec{\varOmega }}}} {\tilde{q}}+{\tilde{u}})+ (-{\tilde{{\varvec{\varOmega }}}} {\tilde{q}}+{\tilde{u}})\otimes {\tilde{q}} \right\} . \end{aligned}$$

(73)

The equation for ${{\tilde{{\mathbf {U}}}}}^\prime$ in Eq. (70) imply that

$$\begin{aligned} {{\tilde{{\mathbf {U}}}}}^\prime =\varepsilon \left\{ (\partial _{{\tilde{{\varvec{\varOmega }}}}} {\tilde{{\mathbf {U}}}}_1) \underbrace{{{\tilde{{\varvec{\varOmega }}}}}^\prime }_{=\mathscr {O}(\varepsilon ^2)}+ (\partial _{{\tilde{q}}} {\tilde{{\mathbf {U}}}}_1)\underbrace{ {{\tilde{q}}}^\prime }_{=\mathscr {O}(\varepsilon )}+ (\partial _{{\tilde{u}}} {\tilde{{\mathbf {U}}}}_1) \underbrace{{{\tilde{u}}}^\prime }_{=\mathscr {O}(\varepsilon )}\right\} =-\varepsilon {\tilde{\mathbf {B}}}_1-\frac{\varepsilon }{\gamma }({\varvec{\varLambda }}_{11}+{\varvec{\varLambda }}_{21}) +\mathscr {O}(\varepsilon ^2) \end{aligned}$$

and therefore

$$\begin{aligned} {\tilde{\mathbf {B}}}_1=-\frac{1}{\gamma }({\varvec{\varLambda }}_{11}+{\varvec{\varLambda }}_{21}). \end{aligned}$$

(74)

Finally, the equations for $\tilde{{\varvec{\varLambda }}}'_i$ imply that

$$\begin{aligned} \tilde{{\varvec{\varLambda }}}'_i=\mathscr {O}(\varepsilon ^2)= -\varepsilon \frac{{\tilde{\eta }}_i^{-1}}{\gamma }{\tilde{{\varvec{\varLambda }}}}_{i1}+\varepsilon \tilde{{\mathbf {U}}}_1+\mathscr {O}(\varepsilon ^2), \end{aligned}$$

so, $\frac{1}{\gamma }{\tilde{{\varvec{\varLambda }}}}_{i1}={\tilde{\eta }}_i{\tilde{{\mathbf {U}}}}_1$ and

$$\begin{aligned} \frac{1}{\gamma }({\tilde{{\varvec{\varLambda }}}}_{11}+{\tilde{{\varvec{\varLambda }}}}_{12})={\tilde{\eta }}{\tilde{{\mathbf {U}}}}_1, \end{aligned}$$

where

$$\begin{aligned} {\tilde{\eta }}= {\tilde{\eta }}_1+{\tilde{\eta }}_2= \frac{\eta }{\sqrt{\mu \gamma }} \end{aligned}$$

(75)

is a nondimensional damping coefficient and $\eta =\eta _1+\eta _2$. This perturbative procedure can be continued to compute the invariant manifold up to higher orders of $\varepsilon$. Here we stop at the first order and just write

$$\begin{aligned} \begin{aligned} {\tilde{\mathbf {B}}}&={\tilde{\mathbf {B}}}_0-\varepsilon {\tilde{\eta }} {\tilde{{\mathbf {U}}}}_1+\mathscr {O}(\varepsilon ^2), \qquad {\tilde{{\mathbf {U}}}}= \varepsilon {\tilde{{\mathbf {U}}}}_1+\mathscr {O}(\varepsilon ^2), \qquad {{\tilde{\mathbf {B}}}}^\prime =\varepsilon {\tilde{{\mathbf {U}}}}_1+\mathscr {O}(\varepsilon ^2)\\ {\tilde{{\varvec{\varLambda }}}}_1&=\varepsilon \gamma {\tilde{\eta }}_1{\tilde{{\mathbf {U}}}}_1+\mathscr {O}(\varepsilon ^2),\qquad {\tilde{{\varvec{\varLambda }}}}_2=\varepsilon \gamma {\tilde{\eta }}_2{\tilde{{\mathbf {U}}}}_1+\mathscr {O}(\varepsilon ^2). \end{aligned} \end{aligned}$$

(76)

For $\varepsilon >0$, the dynamics on the invariant manifold is obtained from the equations for ${{\tilde{{\varvec{\varOmega }}}}}^\prime$, ${{\tilde{q}}}^\prime$, and ${{\tilde{u}}}^\prime$ in Eq. (70) after the substitution of ${\tilde{\mathbf {B}}}$ and ${\tilde{{\mathbf {U}}}}$ by the expressions in Eq. (76).

At this point it is convenient to return to the dimensional variables t, ${\varvec{\varOmega }}$, q , and u and to the inertial reference frame

$$\begin{aligned} x=\mathbf {Y}q,\qquad v=\mathbf {Y}u,\qquad {\varvec{\omega }}=\mathbf {Y}{\varvec{\varOmega }}\mathbf {Y}^T. \end{aligned}$$

After all the substitutions the reduced equations for x and v can be written as

$$\begin{aligned} {\dot{x}}= & {} v\\ {\dot{v}}= & {} GM\left\{ -\frac{1}{|x|^3}x -\frac{15}{2}\frac{{\mathrm{I}_\circ }}{m_1}\frac{1}{|x|^7}(x\cdot \mathbf {b}x)x +3\frac{{\mathrm{I}_\circ }}{m_1}\frac{1}{|x|^5} \mathbf {b}x\right\} , \end{aligned}$$

where

$$\begin{aligned} \mathbf {b}= & {} \frac{1}{\gamma }\left\{ -{\varvec{\omega }}^2+\frac{1}{3}\ \mathrm{Tr}\ ({\varvec{\omega }}^2)\mathbb {I} + \frac{Gm_2}{|x|^5}\left( 3 x\otimes x- |x|^2 \mathbb {I} \right) \right\} \\&-\frac{\eta }{\gamma }\frac{3Gm_2}{|x|^5} \left\{ \left( -5\frac{x\otimes x}{|x|^2}+ \mathbb {I} \right) (x\cdot v)+x\otimes (v- {\varvec{\omega }}x)+(v- {\varvec{\omega }}x)\otimes x \right\} . \end{aligned}$$

This equation can also be written in vectorial form as

$$\begin{aligned} {\ddot{x}}= & {} - GM\frac{x}{|x|^3}- \frac{{\mathrm{I}_\circ }}{m_1\gamma }\frac{3GM}{|x|^5} \left\{ \frac{1}{2}|\omega |^2x-\frac{5}{2}\frac{(\omega \cdot x)^2}{|x|^2}x +(\omega \cdot x)\omega \right\} \nonumber \\&-\frac{{\mathrm{I}_\circ }}{\gamma m_1}\frac{9G^2Mm_2}{|x|^8}x -\frac{\eta }{\gamma ^2} \frac{{\mathrm{I}_\circ }}{m_1}\frac{9G^2Mm_2}{|x|^8} \left\{ {\dot{x}}+x\times \omega +2\frac{({\dot{x}}\cdot x)}{|x|^2}x\right\} . \end{aligned}$$

(77)

The term proportional to $\eta$ is the “Mignard Force” [Mignard 1979, Eq. (5)] after we make the identification

$$\begin{aligned} \varDelta t= \frac{3{\mathrm{I}_\circ }G}{a^5}\frac{1}{k_2}\frac{\eta }{\gamma ^2}, \end{aligned}$$

where we use that the equatorial radius of the planet, used by Mignard, is approximately the volumetric radius a and $M/m_1\approx 1$.

8 Summary and conclusion

The main result in this paper is a set of equations for the dynamics of N extended bodies interacting under gravity. As an example we suppose that the rheology of each body is that of the Wiechert model in Fig. 1.

The $i^{th}$ body is characterized by the following physical parameters:

• $m_i$ (kg), mass;

• ${\mathrm{I}_\circ }_i$ ($kg\, m^2$), mean moment of inertia (the trace of the moment of inertia tensor divided by three);

• $\gamma _i$ ($\hbox {s}^{-2})$, static stiffness coefficient of the moment of inertia;

• $\mu _i$ (nondimensional), inertia coefficient for the moment of inertia variations ($\mu _i=1$ for a homogeneous body made of a perfect fluid);

• $\alpha _{1i}$ and $\alpha _{2i}$ ($\hbox {s}^{-2}$), dynamic stiffness coefficients associated to the Wiechert rheology [see Fig. 1];

• $\eta _{1i}$ and $\eta _{2i}$ ($\hbox {s}^{-2}$), damping coefficients associated to the Wiechert rheology [see Fig. 1].

Let $\kappa$ be an inertial reference frame. The configuration variables of each body of the system are: $x^i$ the position with respect to $\kappa$, $\mathbf {Y}^i$ the orientation (rotation matrix) that defines the body reference frame $\mathrm {K}_i$ by means of $\mathbf {Y}^i:\mathrm {K}_i\rightarrow \kappa$, and $\mathbf {B}^i$ the nondimensional quadrupole matrix [$\mathbf {Q}^i=3{\mathrm{I}_\circ }\mathbf {B}^i$, where $\mathbf {Q}^i$ is the quadrupole matrix, see Eq. (5)] with respect to the body frame $\mathrm {K}_i$. The traceless symmetric matrices ${\varvec{\varLambda }}^i_1$ and ${\varvec{\varLambda }}_2^i$ represent internal stresses (dimension $\hbox {s}^{-2}$) that act upon the Maxwell arms of the Wiechert model, see Fig. 1 (at $t=0$ they can be taken as the null matrices). The velocities associated to the configuration variables are ${\dot{x}}^i$, ${\varvec{\varOmega }}^i$ (angular velocity matrix), and ${\dot{\mathbf {B}}}^i={\mathbf {U}}^i$. The angular momentum matrix of the body with respect to the frame $\mathrm {K}_i$ is

$$\begin{aligned} \mathbf {L}^i={\mathrm{I}_\circ }_i({\varvec{\varOmega }}^i+\mathbf {B}^i{\varvec{\varOmega }}^i+{\varvec{\varOmega }}^i\mathbf {B}^i). \end{aligned}$$

(78)

The relative position $x^i-x^j$ is denoted as $x^{ij}=x^i-x^j$ and the identity matrix as $\mathbb {I}$. The equations for the motion of the system with respect to these variables are:

$$\begin{aligned} {\dot{\mathbf {B}}}^i= & {} {\mathbf {U}}^i\nonumber \\ \mu _i {\dot{{\mathbf {U}}}}^i= & {} - \gamma _i \mathbf {B}^i-{\varvec{\varLambda }}^i_1-{\varvec{\varLambda }}^i_2 -({\varvec{\varOmega }}^{i})^2\nonumber \\&+\frac{1}{3}\ \mathrm{Tr}\ (({\varvec{\varOmega }}^i)^2)\mathbb {I} + \sum _{j \ne i} \frac{3G m_j}{|x^{ij}|^5}\left( \mathbf {Y}^{iT} x^{ij}\otimes x^{ij} \mathbf {Y}^i -\frac{|x^{ij}|^2}{3} \mathbb {I} \right) \nonumber \\ \alpha _{1i}^{-1}{\dot{{\varvec{\varLambda }}}}^i_1= & {} -\eta _{1i}^{-1}{\varvec{\varLambda }}^i_1+ {\mathbf {U}}^i\nonumber \\ \alpha _{2i}^{-1}{\dot{{\varvec{\varLambda }}}}^i_2= & {} -\eta _{2i}^{-1}{\varvec{\varLambda }}^i_2+ {\mathbf {U}}^i\nonumber \\ {\dot{\mathbf {L}}}^i= & {} -[{\varvec{\varOmega }}^i,\mathbf {L}^i]+\sum _{j \ne i}\frac{3G m_j {\mathrm{I}_\circ }}{|x^{ij}|^5} \left[ \mathbf {Y}^{iT} x^{ij}\otimes x^{ij} \mathbf {Y}^i,\mathbf {B}^i\right] \nonumber \\ {\dot{\mathbf {Y}}}^{\, i}= & {} \mathbf {Y}^{\, i}{\varvec{\varOmega }}^i \nonumber \\ {\ddot{x}}^{\,i}= & {} \sum _{j\ne i} G \left\{ -\frac{m_j}{|x^{ij}|^3}x^{ij} -\frac{15}{2 m_i}\frac{1}{|x^{ij}|^7}\left( \left( m_j {\mathrm{I}_\circ }_i \mathbf {Y}^i \mathbf {B}^i \mathbf {Y}^{i T} +m_i {\mathrm{I}_\circ }_j \mathbf {Y}^j \mathbf {B}^j \mathbf {Y}^{jT} \right) x^{ij} \cdot x^{ij}\right) x^{ij} \right. \nonumber \\&\left. +\frac{3}{m_i}\frac{1}{|x^{ij}|^5}\left( m_j {\mathrm{I}_\circ }_i \mathbf {Y}^i \mathbf {B}^i \mathbf {Y}^{i T} +m_i {\mathrm{I}_\circ }_j \mathbf {Y}^j \mathbf {B}^j \mathbf {Y}^{jT} \right) x^{ij} \right\} ,\qquad i=1,\ldots N, \end{aligned}$$

(79)

where $x \otimes y$ denotes the tensor product of the vectors x and y, i.e., the symmetric matrix whose coordinates are given by $(x \otimes y)_{k m}=x_k y_m$ and $[{\mathbf {A}},{\mathbf {B}}]= {\mathbf {A}} {\mathbf {B}}-{\mathbf {B}} {\mathbf {A}}$ is the usual matrix commutator.

In the inertial reference frame $\kappa$ the body variables become: $\mathbf {b}^i=\mathbf {Y}^i\mathbf {B}^i\mathbf {Y}^{iT}$, ${\mathbf {u}}^i=\mathbf {Y}^i{\mathbf {U}}^i\mathbf {Y}^{iT}$, ${\varvec{\ell }}^i=\mathbf {Y}^i\mathbf {L}^i\mathbf {Y}^{iT}$, and ${\varvec{\lambda }}^i_j=\mathbf {Y}^i{\varvec{\varLambda }}^i_j\mathbf {Y}^{iT}$. So, using the following relation, valid for any matrix $\mathbf {m}=\mathbf {Y}^i{\mathbf {M}}\mathbf {Y}^{iT}$,

$$\begin{aligned} \dot{\mathbf {m}}=\frac{d}{dt} (\mathbf {Y}^i{\mathbf {M}}\mathbf {Y}^{iT})= [{\varvec{\omega }}^i,\mathbf {m}]+\mathbf {Y}^i{\dot{{\mathbf {M}}}}\mathbf {Y}^{iT}, \end{aligned}$$

we obtain the equations of motion with respect to the inertial reference frame:

$$\begin{aligned} {\dot{\mathbf {b}}}^i= & {} [{\varvec{\omega }}^i,\mathbf {b}^i]+{\mathbf {u}}^i\nonumber \\ \mu _i {\dot{{\mathbf {u}}}}^i= & {} \mu _i [{\varvec{\omega }}^i,{\mathbf {u}}^i] - \gamma _i \mathbf {b}^i-{\varvec{\lambda }}^i_1-{\varvec{\lambda }}^i_2 -({\varvec{\omega }}^{i})^2+ \frac{1}{3}\ \mathrm{Tr}\ (({\varvec{\omega }}^i)^2)\mathbb {I} \nonumber \\&+ \sum _{j \ne i} \frac{3G m_j}{|x^{ij}|^5} \left( x^{ij}\otimes x^{ij} -\frac{|x^{ij}|^2}{3} \mathbb {I} \right) \nonumber \\ \alpha _{1i}^{-1}{\dot{{\varvec{\lambda }}}}^i_1= & {} \alpha _{1i}^{-1}[{\varvec{\omega }}^i, {\varvec{\lambda }}^i_1]-\eta _{1i}^{-1}{\varvec{\lambda }}^i_1+ {\mathbf {u}}^i\nonumber \\ \alpha _{2i}^{-1}{\dot{{\varvec{\lambda }}}}^i_2= & {} \alpha _{2i}^{-1}[{\varvec{\omega }}^i, {\varvec{\lambda }}^i_2]-\eta _{2i}^{-1}{\varvec{\lambda }}^i_2+ {\mathbf {u}}^i\nonumber \\ {\dot{{\varvec{\ell }}}}^i= & {} \sum _{j \ne i}\frac{3G m_j {\mathrm{I}_\circ }}{|x^{ij}|^5} \left[ x^{ij}\otimes x^{ij},\mathbf {b}^i\right] \nonumber \\ {\ddot{x}}^{\,i}= & {} \sum _{j\ne i} G \left\{ -\frac{m_j}{|x^{ij}|^3}x^{ij} -\frac{15}{2 m_i}\frac{1}{|x^{ij}|^7}\left( \left( m_j {\mathrm{I}_\circ }_i \mathbf {b}^i +m_i {\mathrm{I}_\circ }_j \mathbf {b}^j \right) x^{ij} \cdot x^{ij}\right) x^{ij} \right. \nonumber \\&\left. +\frac{3}{m_i}\frac{1}{|x^{ij}|^5}\left( m_j {\mathrm{I}_\circ }_i\mathbf {b}^i +m_i {\mathrm{I}_\circ }_j \mathbf {b}^j \right) x^{ij} \right\} \nonumber \\ {\varvec{\ell }}^{i}= & {} {\mathrm{I}_\circ }_i({\varvec{\omega }^{i}}+{\mathbf {b^{i}}}{\varvec{\omega }^{i}}+{\varvec{\omega }^{i}}{\mathbf {b}^{i}}). \end{aligned}$$

(80)

The advantage of the equations in the inertial frame is the absence of the orientation variables $\mathbf {Y}^i$. The drawback is that the equations for $\mathbf {B}^i,{\mathbf {U}}^i,{\varvec{\varLambda }}^i_j$ are linear with constant coefficients in the body frame $\mathrm {K}_i$ but not in the inertial frame.

Remarks

• The total angular momentum

  $$\begin{aligned} {\varvec{\ell }}=\sum _{i=1}^N{\varvec{\ell }}^i+m_i({\dot{x}}^i\otimes x^i-x^i\otimes {\dot{x}}^i) \end{aligned}$$

  is conserved.

• The total energy of the system is

  $$\begin{aligned} E= & {} \sum _{i=1}^N \Bigl \{ m_i\frac{|{\dot{x}}^{i}|^2}{2}+ \frac{\varOmega ^i\cdot \mathbf {I}^i\varOmega ^i}{2}+ \frac{{\mathrm{I}_\circ }_i}{4}\left( \mu _i|{\dot{\mathbf {B}}}^i|^2+\gamma _i |\mathbf {B}^i|^2 +\alpha _{1i}|\mathbf {B}_1^i|^2+\alpha _{2i} |\mathbf {B}^i_2|^2\right) \Bigr \}\nonumber \\&-\sum _{i\ne j}\Bigl \{ \frac{G m_i m_j}{|x^{ij}|} +\frac{3G}{2 |x^{ij}|^5} \bigl \{m_j{\mathrm{I}_\circ }_i (x^{ij}\cdot \mathbf {b}^i x^{ij}) +m_i{\mathrm{I}_\circ }_j( x^{ij}\cdot \mathbf {b}^jx^{ij})\bigr \}\Bigr \}, \end{aligned}$$

  (81)

  where the rotational kinetic energy $\frac{\varOmega ^i\cdot \mathbf {I}^i\varOmega ^i}{2}= ={\mathrm{I}_\circ }\frac{\varOmega \cdot (\mathbb {I} -\mathbf {B})\varOmega }{2}= \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}^T\mathbf {B}{\varvec{\varOmega }})\right)$ is written in terms of the angular velocity vector $\varOmega ^i$ and the inertia tensor $\mathbf {I}^i={\mathrm{I}_\circ }_i(\mathbb {I} -\mathbf {B}^i)$. The energy is decreasing along the motion:

  $$\begin{aligned} {\dot{E}}=-2\mathscr {D}\le 0,\quad \text {where}\quad \mathscr {D}= \sum _{i=1}^N{\mathrm{I}_\circ }_i\Bigl \{\frac{|{\varvec{\varLambda }}^i_1|^2}{2\eta _{1i}}+ \frac{|{\varvec{\varLambda }}^i_2|^2}{2\eta _{2i}}\Bigr \}. \end{aligned}$$

  Therefore, any bounded solution (in phase space) is asymptotic to a solution that does not dissipate energy, for which ${\dot{\mathbf {B}}}_i=0$, $i=1,2,\ldots ,N$.

• For a given body of mass m and mean moment of inertia ${\mathrm{I}_\circ }$ we can define the mean moment of inertia radius $R_I=\sqrt{5{\mathrm{I}_\circ }/(2m)}$ and the gravitational fluid frequency

  $$\begin{aligned} \omega _f=\sqrt{\frac{2{\mathrm{I}_\circ }G}{R_I^5}}=\sqrt{\frac{4m G}{5R_I^3}}=\sqrt{\gamma _f}, \end{aligned}$$

  (82)

  that is the lowest frequency of gravitational oscillations of a homogeneous mass m of incompressible fluid about the spherical shape of radius $R_I$ see Eq. (15) and the text below. The three numbers m(kg), $R_I (m)$, and $\omega _f (\hbox {s}^{-2})$ can be used to nondimensionalize all mechanical quantities, in particular:

  $$\begin{aligned} {\tilde{\gamma }}=\frac{\gamma }{\gamma _f}, \quad {\tilde{\alpha }}_j= \frac{\alpha _j}{\gamma _f}, \quad {\tilde{\eta }}_j=\frac{\eta _j}{\omega _f},\quad j=1,2. \end{aligned}$$

  Bodies for which the rheology follows the same model (for instance, the Wiechert model) and all nondimensional rheological parameters $(\mu ,{\tilde{\gamma }},{\tilde{\alpha }}_j,{\tilde{\eta }}_j)$ are the same are said to be physically similar. Bodies with very different sizes and with the same composition cannot be similar, because the self-gravitational forces (volume forces) increases with the cube of the dimension of the body, while elastic forces (surface forces) increase with the square of the dimension. For physically similar bodies this nondimensionalization gives an idea on how the rheological parameters depend on m and ${\mathrm{I}_\circ }$. For instance, ${\tilde{\gamma }}$ is almost one for the Earth and close to one for several planets in the solar system [see Table 1 in Ragazzo and Ruiz (2015)].

• The parameters ${\mathrm{I}_\circ }_i$, $\gamma _i$, $\mu _i$, $\alpha _{ji}$, and $\eta _{ji}$, may undergo secular variations, particularly due to cooling (planets) or internal evolution (stars).

• A particular extended body i can be replaced by a point mass simply by making ${\mathrm{I}_\circ }_i=0$ in the above equations. If a body has a rheology simpler than that of the Wiechert model, then some of the parameters and variables in the above equation are null. For instance, if a Maxwell rheology is assumed (as in Boué et al. 2016), then it is enough to make ${\varvec{\varLambda }}^i_2=0, \alpha _{2i}=\eta _{2i}=0$ in the equations above.

In a recent paper (Boué et al. 2016), Boué, Correia, and Laskar proposed equations for the motion of deformable bodies that are similar to our Eq. (79). Two of the main ideas in our paper, the characterization of the deformations by the quadrupole moment tensor and an “association principle” for the rheology, are also present in their paper, however the derivation of the equations of motion is completely different. This difference may be an indication that the equations are physically sound.

In Boué et al. (2016) explicit equations are only presented for the motion of an extended body (planet) with Maxwell rheology and a point mass (star). As the authors argue, equations for systems of bodies with Maxwell rheology can be easily obtained using the same ideas. Their tidal response equations are the same as ours, Eq. (36), after a special choice of parameters.⁸ In the following we discuss three main differences between the results in Boué et al. (2016) and ours.

The first is that in Boué et al. (2016) no inertia is associated to the deformations, namely $\mu =0$. Therefore the deformable body cannot sustain damped free oscillations. There is no doubt that body deformations have inertia, which is considered for instance in Wisdom and Meyer (2016), but is arguable that this inertia plays any role in the dynamics of tides. It is our feeling that in many situations this inertia is important (see footnote 6) and moreover it must always be in the physical model. The irrelevance of the inertial term, if any, must be noticed a posteriori as a consequence of the integration of the equations of motion. We recall that the coefficient of inertia of a body made of a perfect fluid is $\mu =1$, see Eq. (16). We also remark that $\mu =0$ prevents the existence of tidal waves as those discussed in the “Appendix 1”.

The second difference is that our equations of motion are obtained within a Lagrangian framework while a vectorial approach is adopted in Boué et al. (2016). From the Lagrangian function the expression (81) for the energy is easily obtained and from the dissipation function follows the relation ${\dot{E}}=-2\mathscr {D}\le 0$. The dissipation of energy for planar motions is analysed in Correia et al. (2014) section 4.3 [the model in Boué et al. (2016) is a nonplanar generalization of of the planar model in Correia et al. (2014)], where only the time derivative of the rotational ${\dot{E}}_{rot}$ and orbital ${\dot{E}}_{orb}$ energies are considered. The energy due to the body deformation $E_{def}$, which is much smaller than $E_{rot}$ and $E_{orb}$, is neglected in that reference. However, the time variation of $E_{def}$ may be relevant, especially for systems with more than two bodies. The analysis of the deformation energy although possible in the approach in Boué et al. (2016) is not as easy as it is in ours.

A third difference is that in Boué et al. (2016) the deformations can be parameterized by spherical harmonics of all degrees and not only by those of second degree as in our paper. This extra degrees of freedom can also be included in our model within the linear viscoelastic assumption. Our association principle has to be modified and extra rheological parameters may have to be added (by the same reason that compressibility implies in the addition of a bulk viscosity and a modulus of compressibility).

Appendices

Appendix 1: The kinetic energy when the angular momentum of tidal waves is relevant

The following analysis of a particular set of solutions to Eq. (12) shows that the Lagrangian function (11) sometimes misses important physical features of the dynamics.

Equation (12) have an interesting set of “tidal wave” (or “quadrupole wave”) solutions:

$$\begin{aligned} {\varvec{\varOmega }}=0,\qquad \mathbf {B}={\hat{a}}\mathbf {R}(\omega _\circ t){\mathbf {S}}\mathbf {R}^T(\omega _\circ t), \end{aligned}$$

(83)

where ${\hat{a}}>0$ is the wave amplitude,

$$\begin{aligned} \omega _\circ =\frac{1}{2}\sqrt{\frac{\gamma }{\mu }} \end{aligned}$$

(84)

is the wave angular velocity,

$$\begin{aligned} \mathbf {R}(\omega _\circ t)= \left( \begin{matrix} \cos (\omega _\circ t) &{}\quad -\sin (\omega _\circ t) &{}\quad 0\\ \sin (\omega _\circ t) &{}\quad \cos (\omega _\circ t) &{}\quad 0\\ 0 &{} 0 &{} 1 \end{matrix} \right) \qquad \text {and}\qquad {\mathbf {S}}=\left( \begin{matrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{matrix} \right) . \end{aligned}$$

(85)

Since ${\varvec{\varOmega }}=0$, the body frame $\mathrm {K}$ is an inertial frame (if $\mathbf {Y}(0)=\mathbb {I}$ then $\mathrm {K}=\kappa$ for all t) and the angular momentum ${\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})\in \mathrm {K}$ is null in both $\mathrm {K}$ and $\kappa$. This seems to be not physically correct since waves do usually have an associated momentum, as explained by the following interesting remarks taking from Peskin (2010). “The phenomenon of wave momentum is remarkable in several respects. First, it is not clear a priori that waves ought to have associated momentum. Waves are commonly divided into two types: transverse and longitudinal waves. In the transverse case, since nothing is moving in the direction of propagation, how can there be associated momentum in that direction? Even in the longitudinal case, since the wave motion is typically oscillatory, one would think that the average momentum density would be zero. How can there be net momentum in the direction of the wave?”. The same type of question applies to the tidal wave above, which is transverse to the radial direction. The answer is essentially the same as that given in Peskin (2010) for water waves, which are also transverse waves: “The motion of fluid particles in water waves is circular, and one might think that the net momentum in the direction of propagation would be zero. This reasoning is incorrect, however, because of the correlation between the height of the water and the direction of horizontal motion. As any swimmer knows, the water is moving forward (i.e., in the direction of the wave) at the crest of the wave, and backward in the trough. This asymmetry is the fundamental source of net momentum in the direction of wave propagation$\ldots$”

The arguments in the previous paragraph shows that a term must be added to the Lagrangian function (12) in order to a tidal wave solution to have an associated angular momentum even when $\varOmega =0$ (or even when there is no mass net rotation). The term we add is motivated by an “$\varepsilon$-expansion” of the pseudo-rigid body Lagrangian function in Ragazzo and Ruiz (2015) (it is the only term of order $\varepsilon ^{5/2}$ in that expansion). The new Lagrangian function is

$$\begin{aligned} \mathscr {L}= \frac{{\mathrm{I}_\circ }}{4}\left( |{\varvec{\varOmega }}|^2+2\ \mathrm{Tr}\ ({\varvec{\varOmega }}{\varvec{\varOmega }}^T\mathbf {B})\right) + \frac{{\mathrm{I}_\circ }}{4} \left( \mu |\dot{\mathbf {B}}|^2-\gamma |\mathbf {B}|^2\right) +{\mathrm{I}_\circ }\beta \mu \ \mathrm{Tr}\ (\mathbf {B}{\dot{\mathbf {B}}}{\varvec{\varOmega }}), \end{aligned}$$

(86)

where $\beta$ is a dimensionless constant. The Lagrangian function (86) is invariant under the action $\text {SO(3)}\times \text {SO(3)}\rightarrow \text {SO(3)}$ given by $(U,Y)\rightarrow UY$. As in the case of the rigid body the angular momentum ${\varvec{\ell }}$ defined in Eq. (10) is a conserved quantity. Again a computation gives that ${\varvec{\ell }}=\mathbf {Y}\,\mathbf {L}\,\mathbf {Y}^T$ but in this case the angular momentum $\mathbf {L}$ in the body frame $\mathrm {K}$ is given by $\mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})+{\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}].$ In this expression, the first term ${\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B}):\mathrm {K}\rightarrow \mathrm {K}$ represents the angular momentum of the body relative to the inertial frame $\kappa$ as if it had no motion relative to $\mathrm {K}$. The second term ${\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]$ represents the angular momentum of the body relative to the frame $\mathrm {K}$. The value of $\beta$ is directly connected to the choice of the body frame $\mathrm {K}$. In particular, unless $\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]=0$, the frame $\mathrm {K}$ is not a Tisserand frame (see Munk and MacDonald 1961).

As before, the equation for ${\varvec{\varOmega }}$ derived from the Lagrangian function (86) is

$$\begin{aligned} {\dot{\mathbf {L}}}+[{\varvec{\varOmega }},\mathbf {L}]=0 \qquad \text {where:}\qquad \mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})+{\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]. \end{aligned}$$

(87)

The equations of motion for $\mathbf {B}$ can be obtained in the following way. The set of matrices $\mathbf {B}$ can be considered as the subset of all $3\times 3$ matrices that satisfy the constraints $f_{km}(\mathbf {B})=B_{km}-B_{mk}=0$ and $f_0(\mathbf {B})=\ \mathrm{Tr}\ \mathbf {B}=0$. Let $\chi _{mk}$ and $\chi _0$ denote the Lagrange multipliers associated to these constraints. The equations of motion are obtained from the extended Lagrangian function

$$\begin{aligned} {\widehat{\mathscr {L}}}= \mathscr {L}-\chi _0 f_0-\sum _{m,k}\chi _{mk}f_{mk} \end{aligned}$$

in the usual way:

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial {\widehat{\mathscr {L}}}}{\partial \dot{\mathbf {B}}} \right) -\frac{\partial {\widehat{\mathscr {L}}}}{\partial \mathbf {B}}=0. \end{aligned}$$

Using the expressions for ${\widehat{\mathscr {L}}}$ we obtain

$$\begin{aligned} \frac{{\mathrm{I}_\circ }}{2}\left( \mu {\ddot{\mathbf {B}}}-2\beta \mu (\mathbf {B}\dot{{\varvec{\varOmega }}}+[\dot{\mathbf {B}},{\varvec{\varOmega }}]) +\gamma \mathbf {B}{\varvec{\varOmega }}^2 \right) +\chi _0\mathbb {I} +\varvec{\chi }-\varvec{\chi }^T =0. \end{aligned}$$

In order to eliminate the Lagrange multipliers $\chi _{ij}$ we add this equation to its transpose and divide by two to obtain

$$\begin{aligned} \frac{{\mathrm{I}_\circ }}{2}\left( \mu {\ddot{\mathbf {B}}}-\mu \beta ([\mathbf {B},\dot{{\varvec{\varOmega }}}]+2[\dot{\mathbf {B}},{\varvec{\varOmega }}]) +\gamma \mathbf {B}+ {\varvec{\varOmega }}^2 \right) +\chi _0\mathbb {I} =0. \end{aligned}$$

In order to determine $\chi _0$ we take the trace of this expression to get

$$\begin{aligned} \chi _0=-\frac{{\mathrm{I}_\circ }}{2}\frac{1}{3}\ \mathrm{Tr}\ {\varvec{\varOmega }}^2 . \end{aligned}$$

So, the differential equation for $\mathbf {B}$ is

$$\begin{aligned} \mu {\ddot{\mathbf {B}}}-\beta \mu [\mathbf {B},\dot{{\varvec{\varOmega }}}]-2\beta \mu [\dot{\mathbf {B}},{\varvec{\varOmega }}] +\gamma \mathbf {B}=- {\varvec{\varOmega }}^2+\frac{1}{3}(\ \mathrm{Tr}\ {\varvec{\varOmega }}^2)\mathbb {I} . \end{aligned}$$

(88)

Equations (87) and (88) have the same tidal wave solution as that in Eq. (83). The angular momentum associated to this wave is

$$\begin{aligned} {\varvec{\ell }}={\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]={\mathrm{I}_\circ }\beta \mu 4\omega _\circ {\hat{a}}^2 \left( \begin{matrix} 0 &{} -1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{matrix} \right) , \end{aligned}$$

which implies that the angular momentum vector have components $\ell _1=0$, $\ell _2=0$, and $\ell _3={\mathrm{I}_\circ }\beta \mu 4\omega _\circ {\hat{a}}^2$. The energy associated to this wave is

$$\begin{aligned} E=\frac{{\mathrm{I}_\circ }}{4} \left( \mu \ \mathrm{Tr}\ {\dot{\mathbf {B}}}^2+\gamma \ \mathrm{Tr}\ \mathbf {B}^2\right) = \frac{{\mathrm{I}_\circ }}{4} \left( \mu {\hat{a}}^28\omega _\circ ^2+\gamma {\hat{a}}^2 2\right) ={\hat{a}}^2\gamma {\mathrm{I}_\circ }. \end{aligned}$$

As in Sect. 2, consider a mass m of homogeneous inviscid liquid under self-gravity. At rest the liquid has a spherical shape and moment of inertia ${\mathrm{I}_\circ }=0.4\,ma^2$, where a is the radius of equilibrium. In this case $\mu =\mu _f=1$ and $\gamma =\gamma _f=2{\mathrm{I}_\circ }G\left( \frac{5}{2}\frac{{\mathrm{I}_\circ }}{m}\right) ^{-5/2}$ as given in Eqs. (16) and (15), respectively. Suppose that the liquid is rotating uniformly with constant angular velocity $\varOmega =\varOmega _3\mathrm{e}_3$. The equation for the small free oscillations of $\mathbf {B}$ about the equilibrium shape is

$$\begin{aligned} {\ddot{\mathbf {B}}}-2\beta [\dot{\mathbf {B}},{\varvec{\varOmega }}] +\gamma _f \mathbf {B}=0. \end{aligned}$$

The decomposition of matrix $\mathbf {B}\rightarrow (b_0,b_1,b_2)$ given in Eqs. (39) and (40) can be used to rewrite this equation as:

$$\begin{aligned} {\ddot{b}}_j-2j\beta \varOmega _3i{\dot{b}}_j+\gamma _f b_j=0,\quad j=0,1,2. \end{aligned}$$

(89)

The frequency of small oscillations $\sigma$ obtained from this equation is

$$\begin{aligned} \sigma =\pm \sqrt{\gamma _f}+\beta j\varOmega _3+\mathscr {O}(\varOmega _3^2). \end{aligned}$$

Comparing this expression to that in Eq. (87) in Bryan (1889) we obtain that for a mass of perfect liquid

$$\begin{aligned} \beta =\beta _f=\frac{1}{2}. \end{aligned}$$

(90)

For several types of waves (electromagnetic waves, sound waves, water waves, and certain kinds of traveling waves on strings under tension) the following simple relation holds (Peskin 2010)

$$\begin{aligned} \text {wave momentum}\cdot \text {wave phase velocity}=\text {wave energy}. \end{aligned}$$

For a wave moving along a circular path, like the tidal wave above, this relation could be changed as

$$\begin{aligned} \underbrace{\text {momentum}\cdot R}_{angular\ momentum} \cdot \overbrace{\frac{1}{R}\cdot \text {phase velocity}}^{angular\ velocity}=\text {energy} \end{aligned}$$

where $R>0$ is some reference radius. If we assumed that the previous relation would hold for the tidal wave solution then, using the expressions for $\ell _3$ and E above, we would obtain $\beta =1$. Therefore, it seems that $\beta \ge 0$ can vary depending on the rheological nature of the body.

To finish, consider the tide response equations [compare to Eq. (37)]:

$$\begin{aligned} \begin{aligned} \mu {\ddot{\mathbf {B}}}-2\beta \mu [\dot{\mathbf {B}},{\varvec{\varOmega }}] +\gamma \mathbf {B}+{\varvec{\varLambda }}&={\mathbf {A}}(t)\\ {\ddot{{\varvec{\varLambda }}}}+c_1{\dot{{\varvec{\varLambda }}}}+c_2{\varvec{\varLambda }}&=c_3{{\ddot{\mathbf {B}}}}+c_4{\dot{\mathbf {B}}}, \end{aligned} \end{aligned}$$

(91)

where ${\dot{{\varvec{\varOmega }}}}=0$ and $\varOmega =\varOmega _3\mathrm{e}_3$. If we apply the decomposition $\mathbf {B}\rightarrow (b_0,b_1,b_2)$, ${\mathbf {A}}\rightarrow (a_1,a_2,a_3)$, and ${\varvec{\varLambda }}\rightarrow (\lambda _0,\lambda _1,\lambda _2)$ given in Eqs. (39) and (40) we rewrite Eq. (91) as [compare to Eq. (49)]:

$$\begin{aligned} \begin{aligned} \mu {\ddot{b}}_j-2j\beta \mu \varOmega _3i{\dot{b}}_j+\gamma b_j+\lambda _j&=a_j(t)\\ {\ddot{\lambda }}_j+c_1{\dot{\lambda }}_j+c_2\lambda&=c_3{\ddot{b}}_j+c_4{\dot{b}}_j\qquad j=0,1,2. \end{aligned} \end{aligned}$$

(92)

As before $a_j(t)$ can be Fourier expanded. For a term of the form $a_j(t)={\hat{a}}\mathrm{e}^{i(\omega t+\varphi )}$, there corresponds a solution of the form $b_j(t)={\hat{b}}\mathrm{e}^{i(\omega t+\varphi )}$, $\lambda _j(t)={\hat{\lambda }}\mathrm{e}^{i(\omega t+\varphi )}$, such that ${\hat{a}}$, ${\hat{b}}$, and ${\hat{\lambda }}$ are related as

$$\begin{aligned} \begin{aligned} \{\mu \omega (-\omega +2j\beta \varOmega _3)+\gamma \} {\hat{b}}+{\hat{\lambda }}&={\hat{a}}\\ (-\omega ^2 +c_1\omega i+c_2)\hat{\lambda }&=(-c_3\omega ^2 +c_4\omega i) {\hat{b}}\qquad j=0,1,2. \end{aligned} \end{aligned}$$

For the diurnal and the semi-diurnal frequencies $\omega =j\varOmega _3$, $j=1,2$, the first of these equations becomes

$$\begin{aligned} \{\mu (2\beta -1)(j\varOmega _3)^2+\gamma \} {\hat{b}}+{\hat{\lambda }} ={\hat{a}}, \end{aligned}$$

that is an equation equal to that obtained in Sect. 5.1 for the same frequencies except for the change $\mu \rightarrow \mu (1-2\beta )$. This is very convenient in the fit of the parameters $c_1,c_2,c_3,c_4$ as we did in Sect. 6.2. Essentially, the same procedure used in that section can be used in this case and since $\mu (1-2\beta )$ can be either positive or negative this relaxes the positivity condition we had on the parameter $\mu$.

Appendix 2: The planetary dissipation of tidal energy and the average work done by the tidal force: relations to the dissipation function and to the Lagrangian function, respectively

In this appendix we present a classical formula of Zschau and Platzman for the time-average planetary dissipation rate of tide energy W. We apply this formula to our model and show that it gives the time average of the dissipation function of the model, which shows that our choice of dissipation function is consistent with results obtained from continuum mechanics. The clear and elegant deduction of the formula of Zschau and Platzman in Platzman (1984) lead us to an analogous, apparently new, formula for the time-average of the work done by the primary tidal force in deforming the planet. This new formula, deduced in Appendix “The average work done by the tidal force and the Lagrangian function” section, gives the “time-average planetary tidal balance of potential and kinetic energy”⁹ J. This new formula is related to the Lagrangian function of our model in the same way as the Zschau and Platzman formula is related to the dissipation function.

1.1 Appendix 2.1: A formula of Zschau and Platzman for the planetary dissipation function and the Rayleigh dissipation function

Following Platzman (1984), let $\overline{\varPsi }$ be the primary astronomical potential (due to the satellite), $\varPsi ^\prime$ be the secondary potential due to the tidal redistribution of the mass of the planet, and $\varPsi =\overline{\varPsi }+\varPsi ^\prime$ be the complete tide potential. Let

$$\begin{aligned} \varPsi =\sum _n\left[ \overline{\varPsi }_n\left( \frac{r}{a}\right) ^n+ \varPsi _n^\prime \left( \frac{a}{r}\right) ^{n+1}\right] \end{aligned}$$

(93)

be the solid harmonic decomposition of $\varPsi$, where: $\overline{\varPsi }_n$ and $\varPsi _n^\prime$ are spherical surface harmonics of degree n, $(r,\theta ,\phi )$ are spherical coordinates in the rotating reference frame $\mathrm {K}$, and a is the radius of a spherical surface $S_a$ that contains the planet inside and does not contain the satellite. In Platzman (1984, Eq. (6)), it is shown that the time-average of the planetary dissipation of tidal energy is given by

$$\begin{aligned} W=\frac{1}{4\pi G a}\sum _n(2n+1)\int _{S_{a}}\langle \overline{\varPsi }_n \partial \varPsi _n^\prime /\partial t\rangle dS, \end{aligned}$$

(94)

where dS is the surface element and $\langle \cdot \rangle$ denotes the average over a period tide. Since $\overline{\varPsi }$ is dominated by $\overline{\varPsi }_2$, all terms in this formula but those of second-degree can be neglected

$$\begin{aligned} W=\frac{5}{4\pi G a}\int _{S_{a}}\langle \overline{\varPsi }_2 \partial \varPsi _2^\prime /\partial t\rangle dS. \end{aligned}$$

(95)

The energy dissipation rate W is related to the Rayleigh dissipation function $\mathscr {D}$ in Eq. (23) as follows.

In our model, the primary potential has only the the second-degree harmonic

$$\begin{aligned} \overline{\varPsi }(x)=-\frac{1}{2}(x\cdot {\mathbf {A}}x)= \frac{|x|^2}{a^2}\overline{\varPsi }_2({\hat{x}}), \end{aligned}$$

(96)

where $x=|x|{\hat{x}}$. The secondary potential is

$$\begin{aligned} \varPsi ^\prime (x)=-\frac{3}{2}\frac{G{\mathrm{I}_\circ }}{|x|^5}(x\cdot \mathbf {B}x) =\frac{a^3}{|x|^3}\varPsi _2^\prime ({\hat{x}}). \end{aligned}$$

(97)

Using that $dS=a^2\sin \theta d\theta d\phi =a^2d{\hat{x}}$ on $S_a$, where $(\theta , \phi )$ are polar coordinates on the unit sphere, Eq. (95) can be written as

$$\begin{aligned} W= & {} \frac{5}{4\pi G a}\int _{S_{a}}\langle \overline{\varPsi }_2 \partial \varPsi _2^\prime /\partial t\rangle dS\\= & {} \frac{15}{16\pi }{\mathrm{I}_\circ }\left\langle \int _{S_1}({\hat{x}}\cdot {\mathbf {A}}{\hat{x}}) ({\hat{x}}\cdot {\dot{\mathbf {B}}}{\hat{x}}) d{\hat{x}} \right\rangle \\= & {} \frac{15}{16\pi }{\mathrm{I}_\circ }\left\langle \sum _{ijkl}A_{ij}{\dot{B}}_{kl}\underbrace{ \int _{S_1}{\hat{x}}_i{\hat{x}}_j{\hat{x}}_k{\hat{x}}_l d{\hat{x}}}_{=\varGamma _{ijkl}} \right\rangle . \end{aligned}$$

Now, the same argument as that given at the end of Sect. 3 implies that $\varGamma _{ijkl}$ is a linear combination of the three tensors $\delta _{ij}\delta _{kl}$, $\delta _{ik}\delta _{jl}$, and $\delta _{il}\delta _{jk}$. An easy computation using polar coordinates shows that

$$\begin{aligned} \varGamma _{ijkl}=\frac{4\pi }{15}(\delta _{ij}\delta _{kl}+ \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}) \end{aligned}$$

and

$$\begin{aligned} W=\frac{15}{16\pi }{\mathrm{I}_\circ }\left\langle \sum _{ijkl}A_{ij}{\dot{B}}_{kl}\varGamma _{ijkl} \right\rangle =\frac{{\mathrm{I}_\circ }}{2}\langle \ \mathrm{Tr}\ {\mathbf {A}}{\dot{\mathbf {B}}}\rangle = \frac{{\mathrm{I}_\circ }}{2}\frac{1}{T}\int _0^T\ \mathrm{Tr}\ {\mathbf {A}}{\dot{\mathbf {B}}} dt. \end{aligned}$$

(98)

In principle the time average must be taken over a period tide. It happens that the tide is not exactly periodic but only almost periodic usually with a dominance of the semi-diurnal mode, so the average is still well defined as $T\rightarrow \infty$. For the computations, T must be taken as a large multiple of the semi-diurnal period.

Finally, multiplying both sides of the first equation in (36) by ${\dot{\mathbf {B}}}$, taking the trace and the averaging of both sides, and using that the average of a time derivative is zero $\langle \frac{df}{dt}\rangle =0$, we obtain

$$\begin{aligned} \langle \ \mathrm{Tr}\ {\varvec{\varLambda }}{\dot{\mathbf {B}}}\rangle =\langle \ \mathrm{Tr}\ {\varvec{\varLambda }}_1{\dot{\mathbf {B}}}\rangle + \langle \ \mathrm{Tr}\ {\varvec{\varLambda }}_2 {\dot{\mathbf {B}}}\rangle = \langle \ \mathrm{Tr}\ {\mathbf {A}}{\dot{\mathbf {B}}}\rangle . \end{aligned}$$

Multiplying both sides of the second and third equations in (36) by ${\varvec{\varLambda }}_1$ and ${\varvec{\varLambda }}_2$, respectively, taking the trace and the averaging of both sides, we obtain

$$\begin{aligned} \langle \ \mathrm{Tr}\ {\mathbf {A}}{\dot{\mathbf {B}}}\rangle = \langle \ \mathrm{Tr}\ {\dot{\mathbf {B}}}{\varvec{\varLambda }}_1\rangle + \langle \ \mathrm{Tr}\ {\dot{\mathbf {B}}}{\varvec{\varLambda }}_2\rangle = \eta _1^{-1}\langle |{\varvec{\varLambda }}_1|^2\rangle + \eta _2^{-1}\langle |{\varvec{\varLambda }}_2|^2\rangle = \eta _1\langle |\dot{{\tilde{\mathbf {B}}}}_1|^2\rangle + \eta _2\langle |{\dot{{\tilde{\mathbf {B}}}}}_2|^2\rangle , \end{aligned}$$

where we used that ${\varvec{\varLambda }}_1=\eta _1\dot{{\tilde{\mathbf {B}}}}_1$ and ${\varvec{\varLambda }}_2=\eta _2\dot{{\tilde{\mathbf {B}}}}_2$, similarly to $\eta _1{\dot{{\tilde{x}}}}_1=\lambda _1$ and $\eta _2{\dot{{\tilde{x}}}}_2=\lambda _2$ in Eq. (20). This last equation and Eqs. (98) and (23) imply that

$$\begin{aligned} W= \frac{{\mathrm{I}_\circ }}{2}\langle \ \mathrm{Tr}\ {\mathbf {A}}{\dot{\mathbf {B}}}\rangle = \frac{1}{T}\int _0^T(2\mathscr {D}) dt. \end{aligned}$$

(99)

This equation shows that the planetary dissipation of tidal energy as given in Eq. (95) coincides with the average power dissipated by the planet in our model.

1.2 Appendix 2.2: The average work done by the tidal force and the Lagrangian function

There are two fundamental functions in our theory of tide response: the Lagrangian $\mathscr {L}_{\mathbf {B}}$ and the dissipation $\mathscr {D}$ functions both given in Eq. (23). After we showed the relation between the formula of Zschau and Platzman in Eq. (95) and the dissipation function $\mathscr {D}$, we wandered whether there would exist a similar relation for $\mathscr {L}_{\mathbf {B}}$. Indeed there is, $\mathscr {L}_{\mathbf {B}}$ is equal to the time-average of the work done by the tidal force to deform the planet or equivalently to the “time-average planetary tidal balance of energy”(see footnote at the first page).

Let ${\tilde{J}}$ be the work done by the primary tidal force to deform the planet

$$\begin{aligned} {\tilde{J}}=-\int _{B_a}\rho (d\cdot \nabla \overline{\varPsi })dV \ , \end{aligned}$$

where: $B_a$ is a solid ball that contains the planet and does not contain the satellite, d is the displacement vector, $\rho$ is the density of the deformed state, and $-\rho \nabla \overline{\varPsi }$ is the primary tidal force [see Lambeck (1980), p. 7 for details]. It is convenient to suppose that the density is a smooth function that vanishes outside the planet, so the nontrivial part of the integral is restricted to the planet interior. The result we obtain below is the same as that obtained supposing that $\rho$ varies discontinuously at some interfaces [see Platzman (1984) for the treatment of discontinuities]. Partial integration, the use of $\nabla ^2\varPsi ^\prime =-4\pi G\nabla (\rho d)$ [see Lambeck (1980), p. 7], and that $\rho =0$ over the spherical surface $S_a$ leads to

$$\begin{aligned} {\tilde{J}}=-\frac{1}{4\pi G}\int _{B_a}\overline{\varPsi }\nabla ^2\varPsi ^\prime dV. \end{aligned}$$

Partial integration twice and the use of $\nabla ^2\overline{\varPsi }=0$ in $B_a$ implies that

$$\begin{aligned} {\tilde{J}}=-\frac{1}{4\pi G}\left\{ \int _{S_a}\overline{\varPsi }(\nabla \varPsi ^\prime \cdot \mathrm{e}_r)dS -\int _{S_a}\varPsi ^\prime (\nabla \overline{\varPsi }\cdot \mathrm{e}_r)dS\right\} {.} \end{aligned}$$

Then, by using the solid harmonic decomposition of $\varPsi ^\prime$ and $\overline{\varPsi }$ in Eq. (93) the integral becomes

$$\begin{aligned} {\tilde{J}} =\frac{1}{4\pi G a}\sum _n(2n+1)\int _{S_{a}}\overline{\varPsi }_n \varPsi _n^\prime dS. \end{aligned}$$

Finally, taking the time average of this equation we obtain

$$\begin{aligned} J=\langle {\tilde{J}}\rangle =\frac{1}{4\pi G a}\sum _n(2n+1)\int _{S_{a}}\langle \overline{\varPsi }_n \varPsi _n^\prime \rangle dS, \end{aligned}$$

(100)

that is similar to Eq. (94) of Zschau and Platzman. Since $\overline{\varPsi }$ is dominated by $\overline{\varPsi }_2$, all terms but those of second-degree can be neglected in the above formula, so

$$\begin{aligned} J=\frac{5}{4\pi G a}\int _{S_{a}}\langle \overline{\varPsi }_2 \varPsi _2^\prime \rangle dS, \end{aligned}$$

(101)

that is similar to Eq. (95).

The same reasoning that lead to Eq. (98) shows that the average planetary tidal balance of energy can be written as

$$\begin{aligned} J =\frac{{\mathrm{I}_\circ }}{2}\langle \ \mathrm{Tr}\ {\mathbf {A}}\mathbf {B}\rangle = \frac{{\mathrm{I}_\circ }}{2}\frac{1}{T}\int _0^T\ \mathrm{Tr}\ {\mathbf {A}} \mathbf {B}dt. \end{aligned}$$

(102)

Finally, multiplying both sides of the equation of motion (36) by $\frac{{\mathrm{I}_\circ }}{2} \mathbf {B}$, using the constraints $\mathbf {B}=\mathbf {B}_1+{\tilde{\mathbf {B}}}_1$ and $\mathbf {B}=\mathbf {B}_2+{\tilde{\mathbf {B}}}_2$, using the relations ${\varvec{\varLambda }}_1=\alpha _1\mathbf {B}=\eta _1\dot{{\tilde{\mathbf {B}}}}_1$ and ${\varvec{\varLambda }}_2=\alpha _2\mathbf {B}=\eta _2\dot{{\tilde{\mathbf {B}}}}_2$, which are similar to those in Eq. (20), and using Eq. (102) we obtain

$$\begin{aligned} J=\frac{1}{T}\int _0^T \frac{{\mathrm{I}_\circ }}{2}\Bigl \{-\mu |{\dot{\mathbf {B}}}|^2+\gamma |\mathbf {B}|^2 +\alpha _1|\mathbf {B}_1|^2+\alpha _2 |\mathbf {B}_2|^2\Bigr \} dt= \frac{1}{T}\int _0^T(-2\mathscr {L}_{\mathbf {B}})dt, \end{aligned}$$

(103)

that is similar to Eq. (99). Therefore, J is related to the Lagrangian function $\mathscr {L}_{\mathbf {B}}$ given in Eq. (23) in the same way as the rate of dissipation of tidal energy W is related to the dissipation function $\mathscr {D}$ given in Eq. (23).