Periodic orbits for space-based reflectors in the circular restricted three-body problem

Abstract

The use of space-based orbital reflectors to increase the total insolation of the Earth has been considered with potential applications in night-side illumination, electric power generation and climate engineering. Previous studies have demonstrated that families of displaced Earth-centered and artificial halo orbits may be generated using continuous propulsion, e.g. solar sails. In this work, a three-body analysis is performed by using the circular restricted three body problem, such that, the space mirror attitude reflects sunlight in the direction of Earth’s center, increasing the total insolation. Using the Lindstedt–Poincaré and differential corrector methods, a family of halo orbits at artificial Sun–Earth $\hbox {L}_2$ points are found. It is shown that the third order approximation does not yield real solutions after the reflector acceleration exceeds 0.245 mm $\hbox {s}^{-2}$, i.e. the analytical expressions for the in- and out-of-plane amplitudes yield imaginary values. Thus, a larger solar reflector acceleration is required to obtain periodic orbits closer to the Earth. Derived using a two-body approach and applying the differential corrector method, a family of displaced periodic orbits close to the Earth are therefore found, with a solar reflector acceleration of 2.686 mm $\hbox {s}^{-2}$.

1 Introduction

The global mean Earth’s surface temperature depends mainly on the net amount of radiation arriving on the Earth’s surface (McGuffie and Henderson-Sellers 2005). Space-based geo-engineering schemes propose to alter the amount of incoming sunlight at the Earth’s surface, changing the average global temperature with minimal consequences for the ecosystem and expected favorable results (McInnes 2010a). Supposing that a period of cooling similar to the ‘little ice ace’ occurred from the sixteenth and nineteenth centuries (Le Roy Ladurie 1971; Free and Robock 1999) was coming, or future supervolcanic eruption took place, e.g. Toba mega-eruption (Zielinski et al. 1996), which would alter the reflectivity of the Earth and cool the climate. Then, in the twenty-first century, a colder weather would greatly impact agriculture, economics, and energy demand. Therefore, it is interesting to speculate on future engineering plans to avoid such climate cooling.

The use of orbiting mirrors to reflect sunlight to the Earth has been the field of study for different applications, e.g. increasing the length of daylights for electric power generation or lighting up the darks days in the winter (Glaser 1968; Oberth 1972; Ehricke 1979; Canady and Allen 1982; Leary 1993; Frass et al. 2013), or the so-called Mars climate engineering (Oberg 1981; McKay et al. 1991; Fogg 1995; Zubrin and McKay 1997; McInnes 2002, 2010b), due to the great quantity of energy leverage delivered rapidly by the mirrors (Maunter and Parks 1990). Thus, large-scale solar reflectors seem to be a fascinating instrument to prevent the occurrence of cooling events that have taken place in the past.

In this work, in order to redirect solar radiation to increase the amount of sunlight on Earth’s surface, two suitable locations have been considered in the circular restricted three body problem (CRTBP) to deploy a solar reflector. The first location is at an artificial Sun–Earth $\hbox {L}_2$ point, which can be generated from a continuous acceleration, e.g. solar sail or electric low thrust propulsion system (McInnes et al. 1994; McInnes 1999; Baig and McInnes 2009; Morimoto et al. 2007). By considering the solar radiation pressure on a perfectly flat reflecting space mirror, it is shown that the required equilibrium condition, so that sunlight is reflected in the direction of the Earth’s center, generates artificial $\hbox {L}_2$ points everywhere on the x-axis from the natural $\hbox {L}_2$ point towards the Earth’s center. The first goal of this work is to find periodic orbits about an artificial $\hbox {L}_2$ point, such that the mirror attitude is oriented to guarantee that the sunlight is reflected in the direction of Earth’s center. Analytical and numerical $\hbox {L}_2$ halo orbits for a solar reflector are obtained using the Lindstedt–Poincaré and differential corrector methods (Thurman and Worfolk 1996), respectively. Analytical solutions are derived from a third order Taylor series expansion about artificial $\hbox {L}_2$ point, while the differential corrector method uses as first guess the third order solution (Szebehely 1967; McInnes 1999; Baoyin and McInnes 2006; Baig and McInnes 2009; Salazar and Winter 2016). The analytical results yield imaginary solutions after the reflector acceleration exceeds 0.245 mm s$^{-2}$, i.e. close to the natural $\hbox {L}_2$ equilibrium point. Thus, a larger solar reflector acceleration is required to obtain periodic orbits closer to the Earth.

Displaced Earth-centered orbits are an attractive option to deploy space reflectors and increase the reflector acceleration. Since solar radiation force greatly affects the reflector orbits about Earth (Salazar et al. 2016), a family of non-Keplerian polar orbits for solar reflectors can be generated managing the reflector orientation, so that the solar radiation pressure applies a force on the mirror surface, dislocating the polar orbit from the Earth’s center to behind it along the Sun–Earth line (McInnes and Simmons 1992). A two-body analysis, i.e. Earth-reflector approximation, generates periodic orbits relative to an inertial frame, which can be introduced as initial guesses in the differential corrector method, so that displaced Earth-centered orbits can then be obtained for the Sun–Earth-reflector three-body problem.

2 Equations of motion

The motion of a solar space reflector in the Sun–Earth system can be approximated by the equations of the CRTBP (Szebehely 1967). In this approach, there exist five natural equilibrium points, known as Lagrangian points. However, for the Sun–Earth-reflector three-body problem, the solar reflector attitude may be oriented so that new artificial equilibrium solutions may be generated (McInnes et al. 1994).

Fig. 1

Earth–Sun-reflector circular restricted three-body problem, in order that sunlight is reflected in the direction of the Earth’s center. $\hbox {L}_1$ and $\hbox {L}_2$ represent the natural collinear equilibrium solutions and the reflector attitude angle is denoted by $\alpha$ (not to scale)

Assuming the distance between the Sun and Earth, the sum of the masses of them and gravitational constant equal to unity, the vector equation of motion for an idealised, perfectly reflecting solar reflector can then be written with respect to a synodic rotating frame of reference $\left( x,y,z\right)$ with unit angular velocity vector $\varvec{\omega }$ and origin at their common center-of-mass, as (McInnes et al. 1994)

$$\begin{aligned} \ddot{\mathbf {r}} + 2{\varvec{\omega }}\times \dot{\mathbf {r}}= & {} \nabla V + \mathbf {a}, \end{aligned}$$

(1)

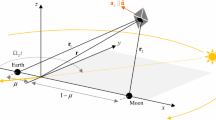
where $\mathbf {r} = \left[ x\,\,y\,\,z\right] ^T$ denotes the position vector of the solar reflector with respect to the center of mass, as shown in Fig. 1, and the solar radiation acceleration $\mathbf {a}$ and the effective potential function V are defined by

$$\begin{aligned} \mathbf {a}= & {} \beta \frac{1-\mu }{r^2_1}\left( \hat{\mathbf {r}}_{\mathrm {1}}\varvec{\cdot }\mathbf {n}\right) ^2\mathbf {n}, \end{aligned}$$

(2)

$$\begin{aligned} V= & {} \left( \frac{1-\mu }{r_1}+\frac{\mu }{r_2}\right) + \frac{1}{2}\left( \varvec{\omega }\times \mathbf {r}\right) \varvec{\cdot } \left( \varvec{\omega }\times \mathbf {r}\right) , \end{aligned}$$

(3)

where the mass ratio $\mu = 3.04036\times 10^{-6}$ (Richardson 1980), $\mathbf {r}_\mathrm {1} = \left[ x+\mu \,\,y\,\,z\right] ^T$ and $\mathbf {r}_\mathrm {2} = \left[ x-\left( 1-\mu \right) \,\,y\,\,z\right] ^T$ denote the position vectors of the space reflector with respect to the Sun and Earth, respectively. In addition, $\hat{\mathbf {r}}_{\mathrm {1}}$ is directed along the Sun-line, $\mathbf {n}$ is the reflector attitude unit normal vector, and $\beta$ is the reflector lightness number.

Equilibrium solutions require that $\ddot{\mathbf {r}} = \dot{\mathbf {r}} = 0$. It then can be shown that the equilibrium condition implies that the required reflector attitude in the synodic rotating frame for new artificial equilibrium points is given by (McInnes et al. 1994)

$$\begin{aligned} \mathbf {n}= & {} -\frac{\nabla V}{\left| \nabla V\right| }. \end{aligned}$$

(4)

Denoting by $\alpha$ the angle between the incident sunlight vector $\hat{\mathbf {r}}_{\mathrm {1}}$ and the normal vector $\mathbf {n}$, we know that, according to the law of reflection, the angle of incidence must be equal to the angle of reflection. Therefore, if the mirror is reflecting sunlight towards the Earth’s center, then the law of reflection requires

$$\begin{aligned} \mathbf {n}= & {} \frac{\hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}}{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }, \end{aligned}$$

(5)

where $\hat{\mathbf {r}}_{\mathrm {2}}$ is directed along the Earth-line, as shown in Fig. 1. Since we need to guarantee that the sunlight is reflected in the direction of Earth’s center, we will only focus on equilibrium solutions that satisfy simultaneously Eqs. (4) and (5). These regions can be easily found by taking the scalar product $\mathbf {n}_\mathrm {1}\cdot \mathbf {n}_\mathrm {2} = \frac{\nabla V \cdot \left( \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right) }{\left| \nabla V\right| \left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }$, where $\mathbf {n}_\mathrm {1} = -\frac{\nabla V}{\left| \nabla V\right| }$ and $\mathbf {n}_\mathrm {2} = \frac{\left( \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right) }{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }$. From the scalar product, we can define the angle $\theta =\cos ^{-1}\left( \mathbf {n}_\mathrm {1}\varvec{\cdot }\mathbf {n}_\mathrm {2}\right)$. Thus, the surfaces defined by $\theta =0^{\circ }$ where $\mathbf {n}_\mathrm {1} = \mathbf {n}_\mathrm {2}$, correspond to equilibrium solutions where the required reflector attitude is satisfied.

Evaluating this constraint, it is found that the family of equilibrium points, that redirect sunlight in the direction of the Earth’s center, lies on x-axis from the Lagrangian point $\hbox {L}_2$ to the Earth’s center as shown in Fig. 2. Additionally, the definition of solar radiation acceleration, Eq. (2), and the orientation of artificial equilibrium points, Eq. (4), imply that the x-coordinate of the artificial $\hbox {L}_2$ points depends explicitly on the lightness number $\beta$. In the next sections, analytical and numerical periodic orbits (i.e. halo orbits) about these new $\hbox {L}_2$ points will be obtained.

Fig. 2

Space reflector in a periodic halo orbit about an artificial equilibrium point beyond $\hbox {L}_2$, so that sunlight is redirected towards the Earth. The artificial point is denoted by $\hbox {L}^*_2$ (not to scale)

3 Reflector Sun–Earth $\hbox {L}_2$ point halo orbits

3.1 Third-order expansion

To find periodic orbits about the new collinear equilibrium points, the equations of motion near an equilibrium position $\mathbf {r}_0 = \left[ x\,\,0\,\,0\right] ^T$, with $1-\mu <x<$ 1.0101 (natural $\hbox {L}_2$ point location), will be approximated as shown in Fig. 2. Although shadows effects are important considerations (McInnes 1999; Pavlak 2011), the eclipses will not be included in this investigation. The scope of this analysis is restricted to understanding the existence of periodic orbits about new collinear points for solar reflectors in the Sun–Earth system. Thus, defining the vector force $\mathbf {F} = \nabla V + \mathbf {a}$, such that, the reflector normal vector $\mathbf {n}$ obeys the constraint Eq. (5), the definition of solar radiation pressure yields an expression of the form

$$\begin{aligned} \mathbf {a}= & {} \beta \frac{1-\mu }{r^2_1}\left( \hat{\mathbf {r}}_{\mathrm {1}} \cdot \left( \frac{\hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}}{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }\right) \right) ^2\frac{\hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}}{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| },\\= & {} \beta \frac{1-\mu }{r^2_1}\left( \frac{1+\hat{\mathbf {r}}_{\mathrm {1}}\cdot \hat{\mathbf {r}}_{\mathrm {2}}}{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }\right) ^2\frac{\hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}}{\left| \hat{\mathbf {r}}_{\mathrm {1}} + \hat{\mathbf {r}}_{\mathrm {2}}\right| }.\nonumber \end{aligned}$$

(6)

A Taylor series expansion of $\mathbf {F}$ to third-order about $\mathbf {r}_\mathrm {0}$ is then found by substituting the vector position $\mathbf {r} = \mathbf {r}_\mathrm {0} + \delta \mathbf {r}$ into Eq. (1) (Edwards 1973):

$$\begin{aligned} \delta \ddot{\mathbf {r}} + 2{\varvec{\omega }}\times \delta \dot{\mathbf {r}}= & {} \left[ \frac{\mathrm {d}\mathbf {F}}{\mathrm {d}\mathbf {r}}\right] _{\mathbf {r}_\mathrm {0}}\delta \mathbf {r} + \frac{1}{2!}\left[ \frac{\mathrm {d}^2\mathbf {F}}{\mathrm {d}\mathbf {r}^2}\right] _{\mathbf {r}_\mathrm {0}}\delta \mathbf {r}^2 + \frac{1}{3!} \left[ \frac{\mathrm {d}^3\mathbf {F}}{\mathrm {d}\mathbf {r}^3}\right] _{\mathbf {r}_\mathrm {0}}\delta \mathbf {r}^3 + O\left( {\delta }\mathbf {r}^4\right) , \end{aligned}$$

(7)

where $\delta \mathbf {r} = \left[ \delta x\,\,\delta y\,\,\delta z\right] ^T$, and $\left[ \frac{\mathrm {d}\mathbf {F}}{\mathrm {d}\mathbf {r}}\right] _{\mathbf {r}_\mathrm {0}}$, $\left[ \frac{\mathrm {d}^2\mathbf {F}}{\mathrm {d}\mathbf {r}^2}\right] _{\mathbf {r}_\mathrm {0}}$, $\left[ \frac{\mathrm {d}^3\mathbf {F}}{\mathrm {d}\mathbf {r}^3}\right] _{\mathbf {r}_\mathrm {0}}$ are the first, second and third derivative matrices of vector force $\mathbf {F} = \left[ F^x\,\,F^y\,\,F^z\right] ^T$ about $\mathbf {r}_\mathrm {0}$, respectively. Additionally, the second and third order terms for $\delta x,\delta y, \delta z$ are included in $\delta \mathbf {r}^2$ and $\delta \mathbf {r}^3$, respectively.

The scalar form of Eq. (7) is given by

$$\begin{aligned} \delta \ddot{x} -2\delta \dot{y}= & {} A \delta x + C \delta x^2 + D\left( \delta y^2 + \delta z^2\right) + F \delta x^3 + G\delta x\left( \delta y^2 + \delta z^2\right) ,\nonumber \\ \delta \ddot{y} + 2\delta \dot{x}= & {} (1+B)\delta y + E\delta x \delta y + H \delta y^3 + I\delta y\left( \delta x^2 + \delta z^2\right) ,\\ \delta \ddot{z}= & {} B \delta z + E \delta x \delta z + H \delta z^3 + \delta z \left( I \delta x^2 + J \delta y^2\right) ,\nonumber \end{aligned}$$

(8)

where $A= \left. F^x_x\right| _{\mathbf {r}_\mathrm {0}},B=\left. F^z_z\right| _{\mathbf {r}_\mathrm {0}}$, $C = \frac{\left. F^x_{xx}\right| _{\mathbf {r}_\mathrm {0}}}{2}$, $D=\frac{\left. F^x_{yy}\right| _{\mathbf {r}_\mathrm {0}}}{2}$, $E=\left. F^y_{xy}\right| _{\mathbf {r}_\mathrm {0}}$, $F=\frac{\left. F^x_{xxx}\right| _{\mathbf {r}_\mathrm {0}}}{6}$, $G=\frac{\left. F^x_{xyz}\right| _{\mathbf {r}_\mathrm {0}}}{2}$, $H=\frac{\left. F^y_{yyy}\right| _{\mathbf {r}_\mathrm {0}}}{6}$, $I =\frac{\left. F^y_{xxy}\right| _{\mathbf {r}_\mathrm {0}}}{2}$, and $J=\frac{\left. F^y_{xzz}\right| _{\mathbf {r}_\mathrm {0}}}{2}$. Thus, the constant terms in Eq. (8) depends explicitly on the $x-$coordinate of artificial $\hbox {L}_2$ point.

3.2 Third-order solution

In this section, in order to to obtain periodic solutions to the equations of motion, Eq. (8), the Lindstedt–Poincaré method will be used. Firstly, we will remove the nonlinear terms in Eq. (8), so that the problem is reduced to a linear analysis about $\mathbf {r}_\mathrm {0}$. It is then found that the linear equations of motion can be written as $\delta \dot{\mathbf {X}} = \mathbf {M}\delta \mathbf {X}$, where $\delta \mathbf {X} = \left[ \delta \mathbf {r}\,\,\delta \dot{\mathbf {r}}\right] ^T$ and the matrix $\mathbf {M}$ is given by

$$\begin{aligned} \mathbf {M}= & {} \left[ \begin{array}{cc} \mathbf {0} &{}\quad \mathbf {I}\\ \varvec{\mathcal {U}} &{}\quad \varvec{\Omega } \end{array}\right] , \end{aligned}$$

(9)

where $\mathbf {I}$ is the identity matrix, and the components of the matrices $\varvec{\mathcal {U}}$ and $\varvec{\Omega }$ are given by

$$\begin{aligned} \varvec{\mathcal {U}} = \left[ \begin{array}{ccc} A &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1+B &{}\quad 0\\ 0 &{}\quad 0 &{}\quad B \end{array}\right] ,\,\, \varvec{\Omega } = \left[ \begin{array}{ccc} 0 &{}\quad 2 &{}\quad 0\\ -2 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right] . \end{aligned}$$

(10)

Note that the z-component is decoupled from x, y, and that the out-of-plane motion corresponds to a periodic oscillation with angular frequency $\sqrt{-B}$. On the other hand, it can be shown that the characteristic polynomial for the x, y linearized dynamics has two pairs of purely imaginary eigenvalues $\pm i \lambda$ and one pair of real eigenvalues $\pm s$, corresponding to a center and saddle points, respectively (Farquhar et al. 1977; Richardson 1980; Morimoto et al. 2007; Baig and McInnes 2009). Since we are only interested in bounded solutions for $\delta x$ and $\delta y$, it is easy to show that the linear problem defined by Eq. (9) possesses a bounded solution

$$\begin{aligned} \delta x= & {} X\cos {\lambda t},\nonumber \\ \delta y= & {} \kappa X\sin {\lambda t},\\ \delta z= & {} \eta X \cos {\sqrt{-B} t},\nonumber \end{aligned}$$

(11)

where the in-plane frequency and the ratio of y- and x-axis amplitude are given by

$$\begin{aligned} \lambda= & {} \sqrt{-\frac{A+B-3}{2}+\sqrt{\left( \frac{A+B-3}{2}\right) ^2-A\left( 1+B\right) }}, \end{aligned}$$

(12)

$$\begin{aligned} \kappa= & {} -\frac{\lambda ^2+A}{2\lambda }, \end{aligned}$$

(13)

and $\eta = \frac{Z}{X}$ is an free parameter.

Since the linear solution is not, in general, periodic, then nonlinearities should be included to find periodic solutions about $\mathbf {r}_\mathrm {0}$ (Farquhar et al. 1977; Richardson 1980; Farquhar et al. 1980).

The Lindstedt–Poincaré method assumes that if the nonlinear terms are small, then a periodic solution of the nonlinear system Eq. (8) is essentially a perturbation of a periodic solution of the linear system Eq. (9) (Drazin 1992), which can be determined introducing a frequency correction, i.e. a new parameter $\tau = w t$, where $w = 1 + \varepsilon w_1 + \varepsilon ^2 w_2$. Then the original problem becomes

$$\begin{aligned} w^2\delta x'' -2w\delta y'= & {} A \delta x + C \delta x^2 + D\left( \delta y^2 + \delta z^2\right) + F \delta x^3 + G\delta x\left( \delta y^2 + \delta z^2\right) ,\nonumber \\ w^2\delta y'' + 2w\delta x'= & {} (1+B)\delta y + E\delta x \delta y + H \delta y^3 + I\delta y\left( \delta x^2 + \delta z^2\right) ,\\ w^2 \delta z'' + \lambda ^2 \delta z= & {} E \delta x \delta z + H \delta z^3 + \delta z \left( I \delta x^2 + J \delta y^2\right) + \varDelta \delta z,\nonumber \end{aligned}$$

(14)

where $\varDelta = \lambda ^2 + B$, and $\delta x'$, $\delta x''$ denote the first and second derivatives with respect to $\tau$ (similarly for $\delta y$ and $\delta z$ coordinates).

To solve the nonlinear system Eq. (14), it will be supposed solutions of the form

$$\begin{aligned} \delta x= & {} \varepsilon \delta x_1 + \varepsilon ^2\delta x_2 + \varepsilon ^3\delta x_3,\nonumber \\ \delta y= & {} \varepsilon \delta y_1 + \varepsilon ^2\delta y_2 + \varepsilon ^3\delta y_3,\\ \delta z= & {} \varepsilon \delta z_1 + \varepsilon ^2\delta z_2 + \varepsilon ^3\delta z_3,\nonumber \end{aligned}$$

(15)

and that $\varDelta = O\left( \varepsilon ^2\right)$ (Thurman and Worfolk 1996). Substituting these expressions into the equations of motion Eq. (14), and grouping components of the same order in $\varepsilon$, then system of equations of first, second and third order, as well as their periodic solutions, can be obtained as shown in Eqs. (28) through (33) (see “Appendix 1” section). The secular terms of the systems of equations of second and third order, are cancelled through the following constraints

$$\begin{aligned} w_1= & {} 0, \end{aligned}$$

(16)

$$\begin{aligned} w_2= & {} s_1X^2 + s_2Z^2, \end{aligned}$$

(17)

$$\begin{aligned} l_1 X^2 + l_2 Z^2 + \varDelta= & {} 0. \end{aligned}$$

(18)

The expressions for $s_i$, $l_i$ are listed in “Appendix 3” section. The $\varepsilon$ term is removed from all the equations changing the scale of variables by the function $X\rightarrow \frac{X}{\varepsilon }$ and $Z\rightarrow \frac{Z}{\varepsilon }$.

Combining the periodic solutions of the first, second and third order equations, the complete periodic solution for the third-order approximation Eq. (7) is given by

$$\begin{aligned} \delta x\left( t\right)= & {} X\cos {\tau _1} + P_{20} + P_2\cos {2\tau _1} + P_3\cos {3\tau _1},\nonumber \\ \delta y\left( t\right)= & {} \kappa X\sin {\tau _1} + Q_2\sin {2\tau _1} + Q_3\sin {3\tau _1},\\ \delta z\left( t\right)= & {} \eta X\sin {\tau _1} + M_2\left( 3-\cos {2\tau _1}\right) + M_3\cos {3\tau _1},\nonumber \end{aligned}$$

(19)

where $\tau _1 = \lambda w t$, and $\lambda$, $\kappa$, $\eta$ come from the linear approximation, Eq. (11). The expression for the coefficients $P_i$, $Q_i$, $M_i$ are given in “Appendix 2” section. This solution corresponds to a halo orbit about the new artificial $\hbox {L}_2$ point, whose period T is equal to $\frac{2\pi }{\lambda w}$, where $w = 1 + s_1X^2 + s_2Z^2$, and the minimum in-plane amplitude X can be computed from Eq. (18) by setting $Z = 0$, i.e. $X \ge \sqrt{-\frac{\varDelta }{l_1}}$. Counterclockwise motion corresponds to positive values of $\eta$.

Figure 3 shows the x-coordinate of the artificial $\hbox {L}_2$ point, as well as the in-plane and out-of-plane frequencies of the linearized system Eq. (9), as a function of the lightness number $\beta$. The location of the natural $\hbox {L}_2$ point corresponds to $\beta = 0$, and the difference between the in-plane and out-of-plane frequencies is quite small, or approximately, a relative difference of 3.7 %. For $\beta \ne 0$, the relative difference decreases as the lightness number increases, and it approaches zero when $\beta = 0.042$. This fact implies that the second order frequency correction $w_2$ is small when $\beta = 0$ and it approaches zero at $\beta = 0.042$, as shown below.

Fig. 3

In-plane and out-of-plane frequencies for the linear approximation and x-coordinate of artificial $\hbox {L}_2$ point versus lightness number

Figures 4 and 5 show the x-direction amplitude X and the period for the artificial halo orbits, respectively, with the z-direction amplitude set as $\eta = 0$, 1, 2, 3. For $\beta = 0$ and $\eta \approx 1$, an amplitude X of approximately 200,000 km and an orbit period of 180 days correspond to a classical halo orbit about $\hbox {L}_2$ point. As can be seen in Figs. 4 and 5, the amplitude X and orbit period are decreasing functions when $0\le \beta \le 0.042$, obtaining an amplitude of approximately 1400 km (about one-quarter the Earth’s radius) and an orbit period of 140 days at $\beta = 0.042$. Note the amplitude X decreases much faster than orbit period does. Therefore, the third order approximation and the reflectivity constraint, Eq. (5), produce periodic solutions that converge quickly to the equilibrium points when $\beta$ increases. For $\beta > 0.042$ the expression $\frac{\varDelta }{l_1 + l_2\eta ^2}$ in Eq. (18) is strictly positive for $\eta = 0$, 1, 2, 3. Therefore, imaginary solutions are found for the third-order approximation given by Eq. (19) when $\beta > 0.042$ and $\left| \eta \right| \le 3$.

Finally, Fig. 6 shows the second order frequency correction $w_2$ and $\lambda$ as functions of the lightness number. As noted above, $w_2$ is very small at $\beta = 0$ and it approaches zero quickly. Thus, the z-frequency approaches $\lambda$ as $\beta$ increases. Figures 4, 5 and 6 also show that the z-direction amplitude practically does not affect the x-direction amplitude, orbit period T and $w_2$ when $X < 2Z$.

Fig. 4

x-direction amplitude X for halo orbits at artificial $\hbox {L}_2$ near to the natural $\hbox {L}_2$ point versus lightness number, with various Z

Fig. 5

Orbit period of halo orbits at artificial $\hbox {L}_2$ near to natural $\hbox {L}_2$ point versus lightness number, with various Z

Fig. 6

Second order frequency correction $w_2$ and $\lambda$ versus lightness number, with various Z

4 Numerical computation of artificial Halo orbits

As explained in Sect. 3.2, the pair of real eigenvalues $\pm s$ for the in-plane linear approximation implies that the new $\hbox {L}_2$ points are unstable. Therefore, the initial conditions given by the Lindstedt–Poincaré analysis are not enough to generate periodic solutions for the CRTBP with solar perturbation. For the purpose of computing periodic orbits, the differential corrector method can be used, which is an iterative method that starts with the third order approximation as an initial guess, and after successively better approximations, new initial conditions converge to a desired final state (Koon et al. 2011).

Since halo orbits are symmetric about the xz-plane ($y = 0$) and that they intersect this plane perpendicularly ($\dot{x} = \dot{z} = 0$), then let $\mathbf {X}_0 = \left[ x_0\,\,0\,\,z_0\,\,0\,\,\dot{y}_0\,\,0\right] ^T$ be an initial state given by the Lindstedt–Poincaré approximation, Eq. (19), which intersects perpendicularly the xz-plane. On the first return to the xy-plane at $t= t_f$, its state is $\mathbf {X}_f = \left[ x_f\,\,0\,\,z_f\,\,\dot{x}_f\,\,\dot{y}_f\,\,\dot{z}_f\right] ^T$. Thus, a periodic solution exists if $\dot{x}_f = \dot{z}_f = 0$. Since $\dot{x}_f,\dot{z}_f$ may not be zero, the three non-zero initial conditions ($x_0$, $z_0$, and $\dot{y}_0$) can be altered slightly with the purpose of driving these velocities to zero.

Let $\varDelta \mathbf {X}\left( t\right)$ denote a slight variation relative to the reference solution $\overline{\mathbf {X}}\left( t\right)$ (known) corresponding to $\mathbf {X}_0$. Supposing that the initial and final displacements are small enough, they are linearly related by the following expression (Thurman and Worfolk 1996)

$$\begin{aligned} \varDelta \mathbf {X}\left( t_f+\varDelta t\right)= & {} \varvec{\Phi }\left( t_f,t_0\right) \varDelta \mathbf {X}\left( t_0\right) + \dot{\overline{\mathbf {X}}}\left( t_f\right) \varDelta t, \end{aligned}$$

(20)

where $\varvec{\Phi }\left( t_f,t_0\right)$ is the state transition matrix from time $t_0$ to $t_f$, evaluated along the reference solution $\overline{\mathbf {X}}\left( t\right)$ (Koon et al. 2011). If $\mathbf {X}_0 + \varDelta \mathbf {X}\left( t_0\right)$ belongs to a halo orbit, then the variation $\varDelta \mathbf {X}\left( t\right)$ when the trajectory crosses the xz-plane is given by

$$\begin{aligned} \varDelta \mathbf {X}\left( t_f+\varDelta t\right)= & {} \left[ x^*_f-x_f\,\,0\,\,z^*_f-z_f\,\,-\dot{x}_f\,\,\dot{y}^*_f-\dot{y}_f\,\,-\dot{z}_f\right] ^T, \end{aligned}$$

(21)

where $\mathbf {X}_f^{*} = [x^*_f\,\,0\,\,z^*_f\,\,0\,\,\dot{y}^*_f\,\,0]^T$ denotes the halo orbit intersection with the xz-plane at $t=t_f+\varDelta t$, as the desired final state (unknown). Thus, the correction terms ($\varDelta x_0$, $\varDelta z_0$, $\varDelta \dot{y}_0$, and $\varDelta t$) can be determined from Eq. (20). For simplicity, it will be assumed $\varDelta z_0 = 0$, so that the variations $\varDelta x_0$, $\varDelta \dot{y}_0$ and $\varDelta t$ can be easily computed inverting a $3\times 3$ matrix as follows

$$\begin{aligned} \left[ \begin{array}{c} \varDelta x_0\\ \varDelta \dot{y}_0\\ \varDelta t \end{array}\right]= & {} \left[ \begin{array}{ccc} \phi _{21} &{}\quad \phi _{25} &{}\quad \dot{y}_f\\ \phi _{41} &{}\quad \phi _{45} &{}\quad \ddot{x}_f\\ \phi _{61} &{}\quad \phi _{65} &{}\quad \ddot{z}_f \end{array}\right] ^{-1} \left[ \begin{array}{c} 0\\ -\dot{x}_f\\ -\dot{z}_f \end{array}\right] , \end{aligned}$$

(22)

where $\phi _{ij}$ are elements of the matrix $\varvec{\Phi }\left( t_t,t_0\right)$. The new initial conditions $\mathbf {X}_0 + \varDelta \mathbf {X}_0$ are then used to begin a second iteration, until $\dot{x}_f = \dot{z}_f = 0$ (or within some acceptable tolerance).

Figures 7, 8 and 9 show a family of halo orbits obtained by the differential corrector method for $\beta = 0$, 0.02, 0.042 and z-direction amplitude setting $\eta = 0,1,2$. Figure 7 shows halo orbits around the natural $\hbox {L}_2$ point. In Figs. 8 and 9, the solar reflector, placed on the artificial halo orbit, redirects sunlight towards the Earth’s center.

Fig. 7

Natural halo orbits around $\hbox {L}_2$ point with $\beta = 0$ and $\eta = 0$, 1, 2

Fig. 8

Artificial halo orbits around new $\hbox {L}_2$ point with $\beta = 0.02$ and $\eta = 0$, 1, 2

Fig. 9

Artificial halo orbits around new $\hbox {L}_2$ point with $\beta = 0.042$ and $\eta = 0$, 1, 2

The reflector areal density with $\beta = 0.042$ is given by $\sigma = \frac{1.53}{\beta } = 36.42$ g m$^{-2}$ (McInnes 1999). This value corresponds to a space reflector acceleration of 0.245 mm s$^{-2}$. Therefore, the reflector acceleration cannot exceed 0.245 mm s$^{-2}$ for the artificial halo orbits found in this work. Similar results are obtained by Baoyin and McInnes (2006) and Baig and McInnes (2009) for halo orbits about artificial $\hbox {L}_1$ and $\hbox {L}_2$ points in the Sun–Earth-spacecraft CRTBP using solar sail and low-thrust propulsion, respectively, such that, the reflector normal vector is directed along the Sun-spacecraft line (reflector attitude angle $\alpha = 0^{\circ }$) or along the Sun–Earth line (reflector attitude vector $\mathbf {n} = \left[ 1\,\,0\,\,0\right] ^T$). However, in this paper, both the angle $\alpha$ and vector $\mathbf {n}$ are changing about the orbit to satisfy the reflectivity constraint, Eq. (5).

Large scale space-based geo-engineering proposals require minimizing the mass per unit area $\sigma$ (McInnes 2010a), so that a larger reflector acceleration is required. The third order approximation, used in this work, produces imaginary values for the x-direction amplitude X when $\beta > 0.042$. It is therefore necessary to use another scheme that permits increasing the lightness number (i.e. reflector acceleration).

5 Displaced Earth-centered orbits

Displaced polar orbits have been studied for different applications, e.g. solar sails, orbiting reflectors to increase the amount of sunlight (McInnes and Simmons 1992; Dankowicz 1994; McInnes 1999, 2010b; Bewick et al. 2011; Salazar et al. 2016). These are basically polar circular orbits, displaced behind Earth along the Sun–Earth line due to the solar radiation force exerted on the space mirror surface, as shown in Fig. 10 (McInnes and Simmons 1992).

Fig. 10

Space mirror on an Earth-centered displaced orbit

Although the existence of this kind of orbits has been demonstrated in the two-body problem, and more accurate models like Hill’s approximation have been studied (Bookless and McInnes 2006), it is possible to consider them as an initial guess in the differential corrector method described previously, such that bounded solutions can be obtained in the Sun–Earth-reflector CRTBP.

In order to obtain an initial state, a perfect reflector placed at $\mathbf {r}_p$ will be assumed. The rotation of the reflector will be about the X-axis of an inertial coordinate system XYZ, with the origin of the frame at the Earth’s center, as shown in Fig. 10. Similarly, the angle between the reflector normal unit vector $\mathbf {n}$ and the Sun-line will be defined by $\alpha$, and the characteristic reflector acceleration will be denoted by a. In this two-body approximation, it is assumed that the Sun-line is given by the unit vector $\mathbf {s} = \left[ 1\,\,0\,\,0\right] ^T$, i.e. the motion of the Sun around the Earth is not accounted for.

In cylindrical polar coordinates ($\rho _p$, $\theta _p$, $z_p$) the equations of motion for a perfect space mirror are (McInnes 2010b)

$$\begin{aligned} \ddot{\rho }_p - \rho _p\dot{\theta }_p^2 + \frac{\rho _p}{r_p}\left( \frac{\mu _E}{r_p^2}\right) -a\cos ^2{\alpha }\sin {\alpha }= & {} 0,\nonumber \\ \rho _p\ddot{\theta }_p + 2\dot{\rho }_p\dot{\theta }_p= & {} 0, \\ \ddot{z}_p + \frac{z_p}{r_p}\left( \frac{\mu _E}{r_p^2}\right) -a\cos {\alpha }^3= & {} 0,\nonumber \end{aligned}$$

(23)

where $\mu _E = 398600.440$ km$^3$ s$^{-2}$ is the Earth gravitational constant and $r_p = \sqrt{\rho _p^2+z_p^2}$.

A circular displaced orbit must satisfy $\ddot{\rho }_p = \ddot{\theta }_p=\ddot{z}_p = 0$ and $\dot{\rho }_p = \dot{z}_p = 0$. On the other hand, in order to guarantee that the space mirror reflects sunlight towards the Earth’s center, the geometry of the incident ray (see Figs. 1 and 10) yields an expression for the attitude angle $\alpha$

$$\begin{aligned} \tan {\alpha }= & {} \tan \left( \frac{1}{2}\tan ^{-1}{\left( \frac{\rho _p}{z_p}\right) }\right) . \end{aligned}$$

(24)

Therefore, if this orientation is fixed previously, the required orbital angular velocity and characteristic acceleration for an Earth-centered displaced orbit can be found from Eq. (23) to be

$$\begin{aligned} w_p= & {} \tilde{w}_p\left( 1-\left( \frac{z}{p}\right) \tan {\alpha }\right) ^{1/2}, \end{aligned}$$

(25)

$$\begin{aligned} a= & {} z_p\tilde{w}_p^2\left( 1+\tan {\alpha }^2\right) ^{3/2}, \end{aligned}$$

(26)

where $w_p = \dot{\theta }_p$ and $\tilde{w}_p^2 = \frac{\mu _E}{r^3_p}$.

From Eq. (26), fixed values for a can be chosen, so that contour lines of constant acceleration are produced in the $\rho _p-z_p$ plane, as shown in Fig. 11, where it can be seen that a larger reflector acceleration is possible for orbits close to the Earth. Additionally, a linear stability analysis has shown that the boundary $\rho _p=4z_p$ (dashed line in Fig. 11) separates the $\rho _p-z_p$ plane into stable ($\rho _p > 4z_p$) and unstable regions (McInnes 2010b). Therefore, circular polar orbits inside the stable region, will be defined as an initial state in the differential corrector method.

Fig. 11

Contour lines of constant reflector acceleration a (mm $\hbox {s}^{-2}$), the dashed line ($\rho _p = 4z_p$) separates the $\rho _p-z_p$ plane into stable ($\rho _p > 4z_p$) and unstable regions

Fixing a radius $\rho _p$ and a displacement $z_p$, so that the space reflector intersects perpendicularly the xz-plane (see Fig. 10), the corresponding coordinates with respect to the inertial frame XYZ are given by $\left( z_p,0,-\rho _p,0,-\rho _p w_p,0 \right)$. Thus, the coordinates with respect to the synodic rotating frame, corresponding to the initial state $\mathbf {X}_\mathrm {0} = \left[ x_0\,\,0\,\,z_0\,\,0\,\,\dot{y}_0\,\,0 \right] ^T$, are obtained as

$$\begin{aligned} x_0= & {} z_p + 1-\mu ,\nonumber \\ z_0= & {} -\rho _p,\\ \dot{y}_0= & {} -\left( z_p + \rho _p w_p\right) ,\nonumber \end{aligned}$$

(27)

where $\rho _p,z_p$, and $w_p$ have been made nondimensional. Thus, the differential corrector is applied by iterating from the initial guess $\mathbf {X}_\mathrm {0}$.

Fig. 12

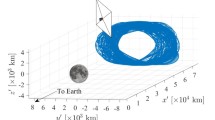
Displaced orbits with $\rho _0 = \left( 4z_p + 1\right)$ Earth radii, where the displacement $z_p = 2.5,5, 7.5, 10$ Earth radii, and the reflector acceleration $a = 35.83$, 10.1, 4.68, 2.69 mm s$^{-2}$, respectively. Earth is illustrated by an Earth-centered blue circle that has the same radius of the Earth in normalized units

Fig. 13

Unbounded Earth-centered orbit with $\rho _0 = 41$ Earth radii, $z_0 = 40$ Earth radii, and $a = 2.671$ mm $\hbox {s}^{-2}$. Earth is illustrated by an Earth-centered blue circle that has the same radius of the Earth in normalized units

Figure 12 shows a family of 1-year displaced orbits in the CRTBP, obtained by a numerical integration of Eq. (1), and using as initial states circular polar orbits that belong to the linear stable region shown in Fig. 11. The Earth is illustrated by an Earth-centered blue circle that has the same radius of the Earth in normalized units. Figure 12 shows four displaced orbits with initial radius $\rho _p = \left( 4z_p + 1\right)$ Earth radii, where the displacement $z_p = 2.5,5$, 7.5, 10 Earth radii, and the reflector acceleration $a = 35.83$, 10.1, 4.68, 2.69 mm s$^{-2}$, respectively. Thus, the differential corrector method permits to find a new set of displaced orbits in the Sun–Earth-reflector CRTBP. Previous works have only obtained this kind of orbits in the two-body problem, assuming fixed solar acceleration vector directed along the Sun-line, as was described previously (Dankowicz 1994; McInnes 1999, 2010b; Bewick et al. 2011; Salazar et al. 2016).

Although linear stable circular polar orbits could be generated with any displacement $z_p$ in the two-body scenario, as shown in Fig. 11, in three-body scenario, orbits with large displacements are found to be strongly perturbed by solar gravitational force. Additionally, the characteristic acceleration a decreases as displacement $z_p$ increases for $\rho _p > 4z_p$, as shown in Fig. 11. Despite that the solar gravitational perturbations will affect the dynamics of the solar reflector, it is possible to increase the acceleration, even for large displacements. The cost for that is the loss of stability. For example, Fig. 13 shows a classical unbounded orbit for $\rho _p < 4z_p$ in the CRTBP, with initial radius $\rho _p = 41$ Earth radii, initial displacement $z_p = 40$ Earth radii, and reflector acceleration $a = 2.671$ mm s$^{-2}$. Note that the value obtained for the acceleration is similar to the value computed for the displaced orbit presented in Fig. 12. In this way, previous studies using the two-body problem and Hill’s equations as an approximation to the CRTBP, have designed control techniques to avoid escape from the nominal displaced orbit (McInnes 1999; Bookless and McInnes 2006).

A periodic behavior for space-based reflector orbits in the CRTBP exists then near the Earth and near the natural $\hbox {L}_2$ point. However, the linear analysis in the two-body problem and the third order approximation are not enough to determine the existence of periodic orbits between these two locations. Only unbounded displaced orbits far from the Earth are found in this paper, as shown in Fig. 13.

6 Conclusions

Space-based solar reflectors have been considered to increase the amount of sunlight on the Earth’s surface. New $\hbox {L}_2$ equilibrium points were found in the Sun–Earth-reflector CRTBP, so that the reflector attitude redirected the sunlight towards the Earth. In this manner, a family of artificial halo orbits about new $\hbox {L}_2$ points were obtained through a third order approximation, such that the sunlight was reflected onto the Earth’s center by the reflectors deployed at these locations. Due to the instability of the new equilibrium points, the third order analytical solutions were used as an initial guess in the differential corrector method, which was implemented to find numerical halo orbits. Artificial halo orbits were obtained near the natural Sun–Earth $\hbox {L}_2$ point, where the reflector acceleration did not exceed 0.245 mm s$^{-2}$.

In order to increase the reflector acceleration, i.e. to reduce the areal density, a family of displaced Earth-centered orbits has been obtained. Considering the Earth-reflector two-body problem as an initial approximation, the required initial states have been derived as a function of the radius and displacement of the orbit, and used in the differential corrector method to obtain bounded solutions in the Sun–Earth CRTBP. Thus, displaced orbits relatively close to the Earth were found. As a result, the reflector acceleration was greatly increased with respect to the space mirrors placed on the artificial halo orbit. Additionally, unbounded displaced orbits with larger displacements from the Earth were also found.

Appendices

Appendix 1: Lindstedt–Poincaré method

1.1 First order equations and their periodic solutions

$$\begin{aligned} \delta x_1'' - 2\delta y_1' - A\delta x_1= & {} 0\nonumber \\ \delta y_1'' + 2\delta x_1' - \left( 1+B\right) \delta y_1= & {} 0\\ \delta z_1'' + \lambda ^2 \delta z_1= & {} 0\nonumber \end{aligned}$$

(28)

$$\begin{aligned} \delta x_1\left( \tau \right)= & {} X\cos {\lambda \tau }\nonumber \\ \delta y_1\left( \tau \right)= & {} \kappa X \sin {\lambda \tau }\\ \delta z_1\left( \tau \right)= & {} \eta X \cos {\lambda \tau }\nonumber \end{aligned}$$

(29)

1.2 Second order equations and their periodic solutions

$$\begin{aligned} \delta x_2'' - 2\delta y_2' - A\delta x_2= & {} -2w_1\delta x_1'' + 2w_1\delta y_1' + C\delta x_1^2 + D\left( \delta y_1^2 + \delta z_1^2\right) \nonumber \\ \delta y_2'' + 2\delta x_2' - \left( 1+B\right) \delta y_2= & {} -2w_1\delta y_1'' -2w_1\delta x_1' + E\delta x_1 \delta y_1\\ \delta z_2'' + \lambda ^2 \delta z_2= & {} -2w_1\delta z_1'' + E\delta x_1 \delta z_1\nonumber \end{aligned}$$

(30)

$$\begin{aligned} \delta x_2\left( \tau \right)= & {} P_{20} + P_2 \cos {2\lambda \tau }\nonumber \\ \delta y_2\left( \tau \right)= & {} Q_2 \sin {2\lambda \tau }\\ \delta z_2\left( \tau \right)= & {} M_2 \left( 3-\cos {2\lambda \tau }\right) \nonumber \end{aligned}$$

(31)

1.3 Third order equations and their periodic solutions

$$\begin{aligned} \delta x_3'' - 2\delta y_3' - A\delta x_3= & {} -w_1^2\delta x_1'' - 2w_2\delta x_1'' -2w_1\delta x_2'' + 2w_2\delta y_1' + 2w_1\delta y_2' \nonumber \\&+\, 2C\delta x_1\delta x_2 + 2D\left( \delta y_1 \delta y_2 + \delta z_1 \delta z_2\right) + F \delta x_1^3\nonumber \\&+\, G\delta x_1\left( \delta y_1^2 + \delta z_1^2\right) \nonumber \\ \delta y_3'' + 2\delta x_3' - \left( 1+B\right) \delta y_3= & {} -w_1^2\delta y_1'' -2w_2\delta y_1'' - 2w_1\delta y_2'' -2w_2 \delta x_1' - 2w_1\delta x_2' \\&+\, E\left( \delta x_1 \delta y_2 + \delta x_2 \delta y_1 \right) + \delta y_1 \left( I \delta x_1^2 + H\delta y_1^2 + J \delta z_1^2\right) \nonumber \\ \delta z_3'' + \lambda ^2 \delta z_3= & {} -w_1^2\delta z_1'' -2w_2\delta z_1'' - 2w_1 \delta z_2'' + \frac{\varDelta }{\varepsilon ^2}\delta z_1 \nonumber \\&+\, E\left( \delta x_1 \delta z_2 + \delta x_2 \delta z_1\right) + \delta z_1\left( I \delta x_1^2 + J\delta y_1^2 + H \delta z_1^2\right) \nonumber \end{aligned}$$

(32)

$$\begin{aligned} \delta x_3\left( \tau \right)= & {} P_3 \cos {3\lambda \tau }\nonumber \\ \delta y_3\left( \tau \right)= & {} Q_3 \sin {3\lambda \tau }\\ \delta z_3\left( \tau \right)= & {} M_3 \cos {3\lambda \tau }\nonumber \end{aligned}$$

(33)

Appendix 2: Coefficients

1.1 First order coefficients

$$\begin{aligned} \lambda= & {} \sqrt{-\frac{A+B-3}{2}+\sqrt{\left( \frac{A+B-3}{2}\right) ^2-A\left( 1+B\right) }} \end{aligned}$$

(34)

$$\begin{aligned} \kappa= & {} -\frac{\lambda ^2+A}{2\lambda } \end{aligned}$$

(35)

1.2 Second order coefficients

$$\begin{aligned} P_{20}= & {} p_{20}X^2 \end{aligned}$$

(36)

$$\begin{aligned} P_{2}= & {} p_{2}X^2 \end{aligned}$$

(37)

$$\begin{aligned} Q_{2}= & {} q_{2}X^2 \end{aligned}$$

(38)

$$\begin{aligned} M_{2}= & {} \eta m_{2}X^2 \end{aligned}$$

(39)

$$\begin{aligned} p_{20}= & {} -\frac{\left( C + D\left( \eta ^2+\kappa ^2\right) \right) }{2A} \end{aligned}$$

(40)

$$\begin{aligned} p_{2}= & {} \frac{\left( 4\lambda ^2 + B + 1\right) \left( C + D\left( \eta ^2-\kappa ^2\right) \right) -4\lambda \kappa E}{2r_2} \end{aligned}$$

(41)

$$\begin{aligned} q_{2}= & {} \frac{\kappa E\left( 4\lambda ^2 + A\right) -4\lambda \left( C + D\left( \eta ^2-\kappa ^2\right) \right) }{2r_2} \end{aligned}$$

(42)

$$\begin{aligned} r_{2}= & {} 16\lambda ^2 - \left( 4\lambda ^2+A\right) \left( 4\lambda ^2 + B + 1\right) \end{aligned}$$

(43)

$$\begin{aligned} m_{2}= & {} \frac{E}{6\lambda ^2} \end{aligned}$$

(44)

1.3 Third order coefficients

$$\begin{aligned} P_{3}= & {} \frac{6\lambda q_{33} - \left( 9 \lambda ^2 + B + 1\right) p_{33}}{r_3} \end{aligned}$$

(45)

$$\begin{aligned} Q_{3}= & {} \frac{6\lambda p_{33} - \left( 9 \lambda ^2 + A\right) q_{33}}{r_3} \end{aligned}$$

(46)

$$\begin{aligned} M_{3}= & {} \frac{m_{33}}{8\lambda ^2} \end{aligned}$$

(47)

$$\begin{aligned} p_{33}= & {} \left( CP_2 - \eta DM_2 - \kappa D Q_2\right) X + \frac{1}{4}\left( F + G\left( \eta ^2 - \kappa ^2\right) \right) X^3 \end{aligned}$$

(48)

$$\begin{aligned} q_{33}= & {} \frac{E}{2}\left( \kappa P_2 + Q_2\right) X + \frac{\kappa }{4}\left( I + \eta ^2 J - \kappa ^2 H\right) X^3 \end{aligned}$$

(49)

$$\begin{aligned} r_{3}= & {} \left( 9\lambda ^2 + A\right) \left( 9 \lambda ^2 + B + 1\right) -36\lambda ^2 \end{aligned}$$

(50)

$$\begin{aligned} m_{33}= & {} \frac{E}{2}\left( \eta P_2 - M_2\right) X + \frac{\kappa }{4}\left( I + \eta ^2 H - \kappa ^2 J\right) X^3 \end{aligned}$$

(51)

Appendix 3: Coefficients for the nonsecular terms constraint

$$\begin{aligned} s_1= & {} \frac{1}{s}\left[ \left( \lambda ^2 + 1 + B\right) \left( C\left( 2p_{20}-p_2\right) +\kappa q_2 D + \frac{1}{4}\left( 3F + \kappa ^2G\right) \right) \right. \\&\left. -\,2\lambda \left( E\left( \kappa \left( p_{20}-\frac{1}{2}p_2\right) +\frac{1}{2}q_2\right) +\frac{\kappa }{4}\left( I + 3\kappa ^2 H\right) \right) \right] \nonumber \end{aligned}$$

(52)

$$\begin{aligned} s_2= & {} \frac{1}{s}\left[ \left( \lambda ^2 + 1 + B\right) \left( 7m_2D + \frac{3}{4}G\right) -\frac{1}{2}\lambda \kappa J\right] \end{aligned}$$

(53)

$$\begin{aligned} s= & {} 4\lambda ^2\left( 1+\kappa \lambda \right) -2\lambda \left( \lambda + \kappa \right) \left( \lambda ^2 + 1 + B\right) \end{aligned}$$

(54)

$$\begin{aligned} l_1= & {} \frac{E}{2}\left( 5m_2 + 2p_{20} + p_2\right) + \frac{1}{4}\left( 3I + \kappa ^2 J\right) +2s_1\lambda ^2 \end{aligned}$$

(55)

$$\begin{aligned} l_2= & {} \frac{3}{4}H + 2s_2\lambda ^2 \end{aligned}$$

(56)