The flattenings of the layers of rotating planets and satellites deformed by a tidal potential

Abstract

We consider the Clairaut theory of the equilibrium ellipsoidal figures for differentiated nonhomogeneous bodies in nonsynchronous rotation (Tisserand, Mécanique Céleste, t.II, Chaps. 13 and 14) adding to it a tidal deformation due to the presence of an external gravitational force. We assume that the body is a fluid formed by $n$ homogeneous layers of ellipsoidal shape and we calculate the external polar flattenings $\epsilon _k,\, \mu _k$ and the mean radius $R_k$ of each layer or, equivalently, their semiaxes $a_k$, $b_k$, and $c_k$. To first order in the flattenings, the general solution can be written as $\epsilon _k=\mathcal {H}_k\epsilon _{h}$ and $\mu _k=\mathcal {H}_k\mu _{h}$, where $\mathcal {H}_k$ is a characteristic coefficient for each layer that depends only on the internal structure of the body and $\epsilon _{h}$ and $\mu _{h}$ are the flattenings of the equivalent homogeneous problem. For the continuous case, we study the Clairaut differential equation for the flattening profile using the Radau transformation to find the boundary conditions when the tidal potential is added. Finally, the theory is applied to several examples: (i) a body composed of two homogeneous layers, (ii) bodies with simple polynomial density distribution laws, and (iii) bodies following a polytropic pressure-density law.

1 Introduction

Several theories of tidal evolution, since the theory developed by Darwin appeared in the nineteenth century (Darwin 1880), are based on the figure of equilibrium of an inviscid tidally deformed body (e.g., Ferraz-Mello et al. 2008; Ferraz-Mello 2013). The addition of viscosity to the model is made at a later stage, but the way it is introduced is not unique and can vary when different tidal theories are considered. Frequently, the adopted figure is a Jeans prolate spheroid or, if the rotation is important, a Roche triaxial ellipsoid (Chandrasekhar 1969). It is worth recalling that ellipsoidal figures are excellent first approximations but not exact figures of equilibrium (Poincaré 1902; Lyapounov 1925, 1927). In addition, Maclaurin, Jacobi, Roche, and Jeans ellipsoids are valid only for homogeneous bodies. Real celestial objects, however, are quite far from being homogeneous. This causes significant deviations which need to be taken into account in astronomical applications.

The nonhomogeneous problem, when one considers only deformation by rotation, has been extensively studied. The problem of one body formed by $n$ rotating homogeneous spheroidal layers as well as its extension to the continuous case was studied by Clairaut (1743) [revisited by Tisserand (1891) and Wavre (1932)]. Their works were based on the hypotheses of small deformations (linear theory for the polar flattenings) and constant angular velocity inside a body. The general case of homogeneous layers rotating at different angular velocities (nonlinear theory) was studied by Montalvo et al. (1983) and Esteban and Vazquez (2001) [see Borisov et al. (2009) for a detailed review] and was generalized to the continuous inviscid case by Bizyaev et al. (2015).

The case of uniformly rotating layers has been studied by several authors. Kong et al. (2010) discussed the particular case of a body formed by two homogeneous layers with the same angular velocity. Hubbard (2013), with a recursive numerical form of the potential of an N-layer rotating planet in hydrostatic equilibrium, showed a solution for the spheroidal shapes of the interfaces of the layers.

Regarding cases where the tidal forces acting on a body are taken into account along with the rotation, the literature is much less extensive. Usually a spin-orbit synchronism is assumed, so that a rotating-body solution can be used (e.g., Van Hoolst et al. 2008). Tricarico (2014), assuming synchronism, found a recursive analytic solution for the shape of a body formed by an arbitrary number of layers. For this, he developed the potentials of homogeneous ellipsoids in terms of the polar and equatorial shape eccentricities. However, the results do not include tidally deformed bodies whose rotation is nonsynchronous, such as, for instance, the Earth, solar-type stars hosting close-in planets, and hot Jupiters in highly eccentric orbits.

In this work, we generalize the linear Clairaut theory, adding a tidal potential due to the presence of an external body, without the synchronism hypothesis. The paper is organized as follows. In Sect. 2, we present the $2n$ classical equations of equilibrium. The resolution of the system of equilibrium equations is shown in Sect. 3. In Sect. 4, we study Clairaut’s equation for the continuous problem and its solution. In Sect. 5, we calculate the potential at a point in space due to the deformed body and calculate a generalized Love number for differentiated nonhomogeneous bodies. In Sect. 6, we apply the theory to a body composed of two homogeneous layers, while bodies with continuous density laws are studied in Sect. 7. Finally, in the Sect. 8, we present our conclusions.

2 Equilibrium equation of a fluid in rotation

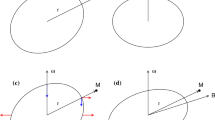
We consider a rotating inviscid fluid of mass $m_T$ and a mass point $M$ orbiting at a distance $r$ from the center of the primary in a plane perpendicular to the rotation axis. We assume that the fluid is composed of $n$ homogeneous layers of density $\rho _k$ ($k=1,\ldots ,n$) and that each layer has an ellipsoidal shape with external semiaxes $a_k$, $b_k$, and $c_k$ along the coordinate axes, and angular velocity $\varvec{\Omega }$. We define the mean radius of each layer as $R_k=\root 3 \of {a_kb_kc_k}$. We choose a reference system such that $\mathbf {r}=r\hat{x}$ and $\varvec{\Omega }={\varOmega }\hat{z}$, where $\hat{x}$ and $\hat{z}$ are unit vectors along the $x$ and $z$ axes (Fig. 1).

Fig. 1

Body of mass $m_T$ composed of $n$ homogeneous layers of density $\rho _k$ and mean radius $R_k$ rotating at angular velocity $\varvec{\Omega }={\varOmega }\hat{z}$ and a point mass $M$ orbiting at a distance $r$ from its center in a plane perpendicular to the rotation axis

Now, if we consider one point on the surface of the $\ell$th layer, with position vector $\mathbf {x}_\ell =\xi _\ell \hat{x}+\eta _\ell \hat{y}+\zeta _\ell \hat{z}$ and the velocity $\mathbf {v}_\ell =\varvec{\Omega }\times \mathbf {x}_\ell$, we can use the same equation used in the study of equilibrium ellipsoids (see Tisserand 1891, Chaps. 8 and 13; Jeans 1929, Sect. 215–216; Jardetzky 1958; Chandrasekhar 1969), which expresses the fact that the total force acting on a point of its surface must be perpendicular to the surface,

$$\begin{aligned} \nabla _\ell {\varPhi }_\ell \propto \nabla _\ell V_G + \varvec{\Omega }\times (\varvec{\Omega }\times \mathbf {x}_\ell ), \end{aligned}$$

(1)

where

$$\begin{aligned} {\varPhi }_\ell (\xi _\ell ,\eta _\ell ,\zeta _\ell ) = \frac{\xi _\ell ^2}{a_\ell ^2}+\frac{\eta _\ell ^2}{b_\ell ^2}+\frac{\zeta _\ell ^2}{c_\ell ^2}-1=0 \end{aligned}$$

(2)

is the equation of the surface of the ellipsoid, $V_G$ is the potential of the gravitational forces at $\mathbf {x}_\ell$, and the last term corresponds to the centripetal acceleration. The use of the preceding equilibrium equation in a case where the tidal force field is changing because of the external body needs a justification. Equation (1) means that no change in the shape of the body occurs because of internal forces; the shape will change, but only because of the relative change in the position of the external body.

Hence, we obtain the equilibrium equations

$$\begin{aligned} {\varOmega }^2= & {} \displaystyle \frac{1}{\xi _\ell }\displaystyle \frac{\partial V_G}{\partial \xi _\ell } - \displaystyle \frac{\alpha _\ell }{\zeta _\ell }\displaystyle \frac{\partial V_G}{\partial \zeta _\ell },\nonumber \\ {\varOmega }^2= & {} \displaystyle \frac{1}{\eta _\ell }\displaystyle \frac{\partial V_G}{\partial \eta _\ell } - \displaystyle \frac{\beta _\ell }{\zeta _\ell }\displaystyle \frac{\partial V_G}{\partial \zeta _\ell }, \end{aligned}$$

(3)

where

$$\begin{aligned} \alpha _\ell =\displaystyle \frac{c_\ell ^2}{a_\ell ^2}<1,\quad \beta _\ell =\displaystyle \frac{c_\ell ^2}{b_\ell ^2}<1. \end{aligned}$$

(4)

The problem of finding the equilibrium figure (i.e., the values of the semiaxes $a_k$, $b_k$, and $c_k$) is equivalent to finding the $2n$ external polar flattenings

$$\begin{aligned} \epsilon _k= & {} \frac{a_k-c_k}{a_k} \approx \frac{1-\alpha _k}{2},\nonumber \\ \mu _k= & {} \frac{b_k-c_k}{b_k} \approx \frac{1-\beta _k}{2} \end{aligned}$$

(5)

for each layer. For this, we will use the $2n$ equilibrium equations (3).

The gravitational potential can be written as the sum of the potential due to the mass $M$ and the sum of the potentials of each layer. It can also be written as the sum of the potentials of $n$ superposed homogeneous ellipsoids, with semiaxes $a_k$, $b_k$, and $c_k$ and densities

$$\begin{aligned} \sigma _k = \rho _k-\rho _{k+1}, \end{aligned}$$

(6)

with $\rho _{n+1}=0$. The mass of each partial ellipsoid is

$$\begin{aligned} m_k = \frac{4\pi }{3}\sigma _k R^3_k. \end{aligned}$$

(7)

If we call $V_k$ the potential of each ellipsoid, the total potential is

$$\begin{aligned} V_G = V_{tid} + \sum _{k=1}^{n} V_k. \end{aligned}$$

(8)

As the equilibrium equations (3) are linear in $V$, we can write

$$\begin{aligned} {\varOmega }^2=\chi _\ell ^{(i)}(V_{tid}) + \sum _{k=1}^{n} \chi _\ell ^{(i)}(V_k), \end{aligned}$$

(9)

where $\chi _\ell ^{(1)}$ and $\chi _\ell ^{(2)}$ are the operators

$$\begin{aligned} \chi _\ell ^{(1)}= & {} \displaystyle \frac{1}{\xi _\ell } \frac{\partial }{\partial \xi _\ell } - \displaystyle \frac{\alpha _\ell }{\zeta _\ell }\displaystyle \frac{\partial }{\partial \zeta _\ell },\nonumber \\ \chi _\ell ^{(2)}= & {} \displaystyle \frac{1}{\eta _\ell }\frac{\partial }{\partial \eta _\ell } - \displaystyle \frac{\beta _\ell }{\zeta _\ell }\displaystyle \frac{\partial }{\partial \zeta _\ell }. \end{aligned}$$

(10)

3 Flattenings of the layers

The next step is to calculate the contribution of each potential to the equilibrium equations (9). If we consider the contributions to the potentials due to the inner and outer layers on the $\ell$th layer, we obtain the equations

$$\begin{aligned} {\varOmega }^2= & {} -\frac{3GM}{r^3} + \sum _{k=1}^{\ell -1} \frac{Gm_k}{R_\ell ^3} \left[ 2\epsilon _\ell - \frac{6\epsilon _k}{5}\left( \frac{R_k}{R_\ell }\right) ^2\right] + \frac{Gm_\ell }{R_\ell ^3} \frac{4\epsilon _\ell }{5} + \sum _{k=\ell +1}^{n} \frac{Gm_k}{R_k^3} \left[ 2\epsilon _\ell -\frac{6\epsilon _k}{5}\right] ,\nonumber \\ {\varOmega }^2= & {} \sum _{k=1}^{\ell -1} \frac{Gm_k}{R_\ell ^3} \left[ 2\mu _\ell - \frac{6\mu _k}{5}\left( \frac{R_k}{R_\ell }\right) ^2\right] + \frac{Gm_\ell }{R_\ell ^3} \frac{4\mu _\ell }{5} + \sum _{k=\ell +1}^{n} \frac{Gm_k}{R_k^3} \left[ 2\mu _\ell -\frac{6\mu _k}{5}\right] \end{aligned}$$

(11)

(see Appendix A in the online supplement), which can be solved with respect to the $\ell$th-layer flattenings, giving

$$\begin{aligned} \gamma _\ell \epsilon _\ell= & {} (\epsilon _J+\epsilon _M) \left( \frac{R_\ell }{R_n}\right) ^3 + \displaystyle \sum _{k=1}^{\ell -1} \alpha _{\ell k}\epsilon _k + \displaystyle \sum _{k=\ell +1}^{n} \beta _{\ell k}\epsilon _k,\nonumber \\ \gamma _\ell \mu _\ell= & {} \epsilon _M \left( \frac{R_\ell }{R_n}\right) ^3 + \displaystyle \sum _{k=1}^{\ell -1} \alpha _{\ell k}\mu _k + \displaystyle \sum _{k=\ell +1}^{n} \beta _{\ell k}\mu _k, \end{aligned}$$

(12)

where $\epsilon _M$ and $\epsilon _J$ are the flattenings of the equivalent Maclaurin and Jeans homogeneous spheroids:

$$\begin{aligned} \epsilon _M = \frac{5R_n^3{\varOmega }^2}{4m_TG}, \qquad \qquad \epsilon _J = \frac{15MR_n^3}{4m_Tr^3}, \end{aligned}$$

(13)

where $m_T$ is the mass of the body.

These flattenings are obtained as solutions of the rotational and tidal problem, respectively, when the deformed body is a homogeneous spheroid with the same mass $m_T$ and mean radius $R_n$ as the considered body (see online Appendix B). The coefficients $\alpha _{\ell k}$, $\beta _{\ell k}$, and $\gamma _{\ell }$ are

(14)

If we divide the equations for $\epsilon _\ell$ by $\epsilon _J+\epsilon _M$ and divide the equations for $\mu _\ell$ by $\epsilon _M$, we obtain the same equation for the two polar flattenings:

$$\begin{aligned} \gamma _\ell \mathcal {H}_\ell = \left( \frac{R_\ell }{R_n}\right) ^3 + \displaystyle \sum _{k=1}^{\ell -1} \alpha _{\ell k}\mathcal {H}_k + \displaystyle \sum _{k=\ell +1}^{n} \beta _{\ell k}\mathcal {H}_k, \end{aligned}$$

(15)

where

$$\begin{aligned} \mathcal {H}_j \;\buildrel \small {\hbox {def}}\over {\,=\;}\frac{\epsilon _j}{\epsilon _J+\epsilon _M} = \frac{\mu _j}{\epsilon _M} \qquad (j=1,\ldots ,n). \end{aligned}$$

(16)

It is worth emphasizing that these equations naturally associate the flattening of the homogeneous Maclaurin spheroid with the polar flattenings $\mu _k$ calculated using the minor semiaxis of the tidally deformed equator. This is so because the tide also acts to shorten the polar axis. While the $\epsilon _k$ flattenings increase because of the tide, the $\mu _k$ flattenings remain the same as in the absence of the tide. Therefore, the tide increases the mean polar flattening of the layers. The three axes of the layer are $a_j=R_j[1+\mathcal {H}_j(\epsilon _M+2\epsilon _J)/3]$, $b_j=R_j[1+\mathcal {H}_j(\epsilon _M-\epsilon _J)/3]$, and $c_j=R_j[1+\mathcal {H}_j(-2\epsilon _M-\epsilon _J)/3]$.

It is important to note that in the case of a synchronous satellite, when the approximation $\epsilon _J \simeq 3\epsilon _M$ is adopted¹, the system (12) is equivalent to that found by Tricarico (2014), where the square of the polar and equatorial “eccentricities” used there are related to the polar flattenings through $e_{pi}^2\approx 2\epsilon _i$ and $e_{qi}^2\approx 2\epsilon _i-2\mu _i$.

The calculations done are valid only for small flattenings, i.e., they assume that the perturbation due to the tide and the rotation are small enough so as not to deform the body too much (in the second order, the figure ceases to be an ellipsoid).

4 Extension to the continuous case

To extend this approach to the continuous case (following Tisserand 1891, Chap. 14²), we assume that the number of layers tends to infinity, so that the increments $\Delta R_k=R_k-R_{k-1}$ are infinitesimal quantities. When $\Delta R_k\rightarrow 0$, Eq. (15) becomes

$$\begin{aligned} \frac{5x^2}{3}f(x) \mathcal {H}(x) = \frac{2f_n}{3} x^5 + \int _{z=0}^{z=x} \widehat{\rho }(z) \hbox {d}(z^5\mathcal {H}(z)) + x^5 \int _{z=x}^{z=1} \widehat{\rho }(z) \hbox {d}\mathcal {H}(z), \end{aligned}$$

(17)

where $x=R/R_n$ is the normalized mean radius [$x(0)=0$ in the center and $x(R_n)=1$ on the surface], $\widehat{\rho }(x)=\rho (R)/\rho _0$ is the normalized density [$\rho _0$ is the density in the center; therefore, $\widehat{\rho }(0)=1$], and the function $f(x)$ is

$$\begin{aligned} f(x)=\displaystyle 3\int _0^{x}\widehat{\rho }(z)z^2\hbox {d}z, \end{aligned}$$

(18)

with $f(0)=0$ and $f(1)=f_n$.

Deriving (17) with respect to $x$, we have

$$\begin{aligned} \frac{2f(x)}{3x^3}\mathcal {H}(x)+\frac{f(x)}{3x^2}\mathcal {H}'(x) = \frac{2f_n}{3} + \int _{z=x}^{z=1} \widehat{\rho }(z)\hbox {d}\mathcal {H}(z), \end{aligned}$$

(19)

and deriving once more we obtain the differential equation for the flattening profile

$$\begin{aligned} \mathcal {H}''(x)+ \frac{6\widehat{\rho }(x) x^2}{f(x)} \mathcal {H}'(x) + \left( \frac{6\widehat{\rho }(x) x}{f(x)}-\frac{6}{x^2}\right) \mathcal {H}(x) = 0. \end{aligned}$$

(20)

This is a homogeneous linear differential equation of second order with nonconstant coefficients, and it turns out to be the same for both flattenings. It is the same expression found by Clairaut (Jeffreys 1953).

Equation (17) allows us to calculate easily the limits $\mathcal {H}_n$ that the proportionality parameter $\mathcal {H}$ can take at the surface. In the homogeneous case $\widehat{\rho }(x)=1$, the integrals can be calculated trivially. At the surface $x=1$, we obtain $\mathcal {H}_n=1$. In the nonhomogeneous case, if the density is a nonincreasing function ($\frac{\hbox {d}\widehat{\rho }}{\hbox {d}x}\leqslant 0$), then we have, at the surface,

$$\begin{aligned} \mathcal {H}_n= & {} \frac{2}{5} + \frac{3}{5f_n}\int _{z=0}^{z=1} \widehat{\rho }(z) \hbox {d}(z^5\mathcal {H}(z))\nonumber \\= & {} \frac{2}{5} + \frac{3}{5f_n}\left[ \widehat{\rho }_n\mathcal {H}_n-\int _{z=0}^{z=1}z^5\mathcal {H}(z)\hbox {d}\widehat{\rho }(z)\right] \geqslant \frac{2}{5}. \end{aligned}$$

(21)

Then, under the assumption of equilibrium, a nonhomogeneous body will have flattenings on the surface with values between 0.4 and 1 times the values they would have if the body was homogeneous.

4.1 Boundary conditions. Radau transformation

The differential equation (20) requires two boundary conditions to be solved. However, before attempting to find these boundary conditions, we will show two relationships that will prove useful later. The first relationship is obtained from Eq. (19), where at $x=1$ we have

$$\begin{aligned} \mathcal {H}'_n = 2(1-\mathcal {H}_n). \end{aligned}$$

(22)

The second relationship is obtained from the differential equation (20) by simply multiplying it by $f(x)/x^2$ and evaluating the resulting equation in the neighborhood of $x=0$ [note that $f(x)\sim x^3 + 3(\hbox {d}\widehat{\rho }/\hbox {d}x)_0x^4/4$ and $\widehat{\rho }(x)\sim 1 + (\hbox {d}\widehat{\rho }/\hbox {d}x)_0x$]. We get

$$\begin{aligned} \mathcal {H}'_0 = -\frac{\hbox {d}\widehat{\rho _0}}{\hbox {d}x}\frac{ \mathcal {H}_0}{4}, \end{aligned}$$

(23)

where $\frac{\hbox {d}\widehat{\rho _0}}{\hbox {d}x}$ is the derivative of the density at $x=0$.

In practical applications (Sect. 6), it is convenient to introduce the Radau transformation

$$\begin{aligned} \eta (x) = \frac{x\mathcal {H}'(x)}{\mathcal {H}(x)} \end{aligned}$$

(24)

and to rewrite Clairaut equation as the Ricatti differential equation

$$\begin{aligned} \eta ' + \frac{\eta ^2}{x}+\left[ q(x)+\frac{5}{x}\right] \eta + q(x) = 0, \end{aligned}$$

(25)

where

$$\begin{aligned} q(x) \;\buildrel \small {\hbox {def}}\over {\,=\;}\frac{6}{x}\left( \frac{\widehat{\rho }(x)x^3}{f(x)}-1\right) . \end{aligned}$$

(26)

In the new variables, the boundary condition is

$$\begin{aligned} \eta (x=0) = 0. \end{aligned}$$

(27)

The variable $\eta$ is sometimes referred to as Radau’s parameter (Bullen 1975). Defining $\eta (x=1)=\eta _n$ and using relationship (22) and transformation (24), the boundary conditions of (20) are

$$\begin{aligned} \displaystyle \mathcal {H}_n = \frac{2}{2+\eta _n} \qquad \mathcal {H}'_n = \frac{2\eta _n}{2+\eta _n}. \end{aligned}$$

(28)

As a result of this relationship, if we consider that $0.4 <\mathcal {H}_n<1$, we recover the classical result $0<\eta _n<3$ (Tisserand 1891).

Finally, it should be noted that once $\eta (x)$ is found, we may find the profile flattening from Eq. (24), whose solution is

$$\begin{aligned} \mathcal {H}(x) = \mathcal {H}_n \hbox {e}^{\int _1^x \eta (z)/z\ \hbox {d}z}. \end{aligned}$$

(29)

5 Potential of the tidally deformed body

The contribution of the $k$th ellipsoid to the potential at an external point $\mathbf {x}=x\hat{x}+y\hat{y}+z\hat{z}$ is given by

$$\begin{aligned} \delta V_2^{(k)} = - \frac{Gm_kR_k^2\epsilon _k}{5r^{*3}}\left( 3\cos ^2{\varPsi }_1-1\right) - \frac{Gm_kR_k^2\mu _k}{5r^{*3}}\left( 3\cos ^2{\varPsi }_2-1\right) , \end{aligned}$$

(30)

where $r^{*}=|\mathbf {x}|$, and ${\varPsi }_1$ and ${\varPsi }_2$ are the angles between the direction of the point where the potential is taken and the coordinate axes $x$ and $y$, respectively.³ The total potential is the sum of the potentials of all ellipsoids:

$$\begin{aligned} V = -\displaystyle \frac{Gm_T}{r^*} - \frac{2k_{f}Gm_TR_n^2\epsilon _h}{15r^{*3}}\left( 3\cos ^2{\varPsi }_1-1\right) - \frac{2k_{f}Gm_TR_n^2\mu _h}{15r^{*3}}\left( 3\cos ^2{\varPsi }_2-1\right) , \nonumber \\ \end{aligned}$$

(31)

where $\epsilon _h$ and $\mu _h$ are the flattenings of the equivalent homogeneous ellipsoid, and the constant $k_f$ is often called the fluid Love number (Munk and MacDonald 1960; Correia and Rodríguez 2013). For a nonhomogeneous body, we find

$$\begin{aligned} k_{f} \;\buildrel \small {\hbox {def}}\over {\,=\;}\, \frac{3}{2}\frac{\sum _{k=1}^nm_kR_k^2\mathcal {H}_k}{m_TR_n^2} \end{aligned}$$

(32)

or, using the continuous model,

$$\begin{aligned} k_{f} = \frac{3}{2f_n}\int _{z=0}^{z=1}\widehat{\rho }(z)\hbox {d}(z^5\mathcal {H}(z)). \end{aligned}$$

(33)

Using the integral form of Clairaut’s equation (19) to evaluate the integral, we have

$$\begin{aligned} k_{f} =\frac{5}{2}\mathcal {H}_n-1, \end{aligned}$$

(34)

which shows the link of the fluid Love number to the coefficient $\mathcal {H}_n$. This relationship is based on the fact that both constants depend solely on the internal structure characterizing the inhomogeneity of the body. In the homogeneous case, $\mathcal {H}_n=1$, thereby recovering the classical result $k_f=1.5$.

6 Two-layer core–shell model

In this section we consider the simple case of a body composed of two homogeneous layers: a core with density $\rho _1$ and mean outer radius $R_1$, and a shell with density $\rho _2=\lambda \rho _1$ (with $\lambda <1$) and mean outer radius $R_2$ (Fig. 2). The densities of the superposed ellipsoids are

$$\begin{aligned} \sigma _1= & {} \rho _1(1-\lambda ), \nonumber \\ \sigma _2= & {} \rho _1\lambda , \end{aligned}$$

(35)

and their masses are

$$\begin{aligned} m_1= & {} \frac{4\pi }{3}\rho _1R_2^3(1-\lambda )\xi ^3, \nonumber \\ m_2= & {} \frac{4\pi }{3}\rho _1R_2^3\lambda , \end{aligned}$$

(36)

where $\xi =R_1/R_2$. The total mass is

$$\begin{aligned} m_T = \frac{4\pi }{3}\rho _1R_2^3\Big [\lambda +(1-\lambda )\xi ^3\Big ]. \end{aligned}$$

(37)

The polar flattenings are such that

$$\begin{aligned} \gamma _1\mathcal {H}_1= & {} \displaystyle \frac{R_1^3}{R_2^3}+\beta _{12}\mathcal {H}_2, \nonumber \\ \gamma _2\mathcal {H}_2= & {} 1 +\alpha _{21}\mathcal {H}_1 \end{aligned}$$

(38)

[see Eq. (15)], where the coefficients are given by Eq. (14):

$$\begin{aligned}&\displaystyle \alpha _{21} = \frac{3m_1}{2m_T}\left( \frac{R_1}{R_2}\right) ^2 = \frac{3(1-\lambda )\xi ^5}{2\lambda +2(1-\lambda ) \xi ^3}, \nonumber \\&\displaystyle \beta _{12} = \frac{3m_2}{2m_T}\left( \frac{R_1}{R_2}\right) ^3 = \frac{3\lambda \xi ^3}{2\lambda +2(1-\lambda ) \xi ^3}, \nonumber \\&\displaystyle \gamma _1 = 1 + \frac{3(m_T-m_1)}{2m_T} - \frac{5m_2}{2m_T} \frac{R_2^3-R_1^3}{R_2^3} =&\displaystyle \frac{(2+3\lambda )\xi ^3}{2\lambda +2(1-\lambda ) \xi ^3}, \nonumber \\&\displaystyle \gamma _2 = 1 + \frac{3(m_T-m_2)}{2m_T} = \frac{2\lambda +5(1-\lambda )\xi ^3}{2\lambda +2(1-\lambda ) \xi ^3}. \end{aligned}$$

(39)

Hence,

$$\begin{aligned} \mathcal {H}_1= & {} \frac{10\Big (\lambda +(1-\lambda )\xi ^3\Big )^2}{\Big (2+3\lambda \Big )\Big (2\lambda +5(1-\lambda )\xi ^3\Big )-9\lambda (1-\lambda )\xi ^5},\nonumber \\ \mathcal {H}_2= & {} \frac{2\Big (\lambda +(1-\lambda )\xi ^3\Big )\Big (2+3\lambda +3(1-\lambda )\xi ^5\Big )}{\Big (2+3\lambda \Big )\Big (2\lambda +5(1-\lambda )\xi ^3\Big )-9\lambda (1-\lambda )\xi ^5}. \end{aligned}$$

(40)

Fig. 2

Density profile of a body formed by two homogeneous layers. $\xi$ is the mean outer radius of the core relative to the mean outer radius of the shell $R_2$. $\lambda$ is the shell density relative to the core density $\rho _1$

Fig. 3

Possible values of $\mathcal {H}_1$ (core) and $\mathcal {H}_2$ (shell) as functions of the core size $\xi$ and of the relative density of the shell $\lambda$

Figure 3 shows the results obtained for the constants $\mathcal {H}_1$ and $\mathcal {H}_2$. We see that:

• If $\lambda =1$ or $\xi =1$, then the constants are $\mathcal {H}_1=\mathcal {H}_2$ solutions for a homogeneous body.

• When the core is denser than the mantle, $\mathcal {H}_2\geqslant \mathcal {H}_1$, and the flattenings of the nucleus are smaller than the flattenings of the surface (where $\epsilon _1=\mathcal {H}_1(\epsilon _J+\epsilon _M) \leqslant \epsilon _2=\mathcal {H}_2(\epsilon _J+\epsilon _M)$ and $\mu _1=\mathcal {H}_1\epsilon _M\leqslant \mu _2=\mathcal {H}_2\epsilon _M$).

• Since $\mathcal {H}_2\leqslant 1$, the maximum surface flattening is given by the homogeneous solution. In the presence of a core, the surface is always less flattened than it is in the homogeneous case.

• While $\mathcal {H}_1$ may take all possible values between 0 and 1, $\mathcal {H}_2$ is always larger than the critical limit 0.4, corresponding to the degenerate limit case in which the whole mass would tend to concentrate in the center and be surrounded by a zero-density shell (case of Huygens–Roche). Therefore, the flattenings of the outer surface can never be less than 40 % of the homogeneous reference values. This is the same result given by Eq. (21) for the continuous case.

6.1 Fluid Love number

Using Eq. (34), together with the expression for $\mathcal {H}_2$ (Eq. 40), the expression of the fluid Love number $k_f$ is

$$\begin{aligned} k_f = \frac{5\Big (\lambda +(1-\lambda )\xi ^3\Big )\Big (2+3\lambda +3(1-\lambda )\xi ^5\Big )}{\Big (2+3\lambda \Big )\Big (2\lambda +5(1-\lambda )\xi ^3\Big )-9\lambda (1-\lambda )\xi ^5}-1. \end{aligned}$$

(41)

Fig. 4

Possible values of $k_f$ as functions of the core size $\xi$ and of the relative density of the shell $\lambda$

Figure 4 shows the possible value of $k_f$ as a function of the core size $\xi$ and of the relative density of the shell $\lambda$. If we obtain $k_f$, for example by determining $\mathcal {H}_n$ by direct observation of the surface flattenings, then Eq. (41) defines a continuous curve of possible values for the size of the nucleus $\xi$ and the relative density of the shell $\lambda$ under the hypothesis of two homogeneous layers. Moreover, as can be seen in this figure, a maximum value for these physical parameters can be predicted.

7 Application to different density distribution laws

In this section, we present some applications of the theory developed in this paper to bodies with continuous density distributions. For this we use two examples of density distributions: polynomial and polytropic density laws.

In both cases, Clairaut’s equation is solved numerically after introduction of the variable defined by Eq. (24). The flattening profile $\mathcal {H}(x)$ and the Love number are then obtained through the inverse transformation.

7.1 Polynomial density functions

We consider initially a simple polynomial density law:

$$\begin{aligned} \widehat{\rho }(x)=1-x^\alpha , \end{aligned}$$

(42)

where $\alpha >0$. Figure 5a shows the density functions for $\alpha =0.1,1,2,10$, and $100$ as functions of the normalized mean radius $x$.

Fig. 5

a Density profiles for polynomial density distributions with different values of $\alpha$. b Flattening profile $\mathcal {H}(x)$ for the same density laws. $\alpha =0.1$ (black), $\alpha =1$ (red), $\alpha =2$ (green), $\alpha =10$ (blue), and $\alpha =100$ (magenta)

The resulting flattening profiles $\mathcal {H}(x)$ are shown in Fig. 5b. In all cases, the flattening profile $\mathcal {H}(x)$ is an increasing monotonic function, and for all $x$ the values of $\mathcal {H}(x)$ increase when the power $\alpha$ increases.

Note that, as discussed in Sect. 3, the value of $\mathcal {H}_n$ is always greater than the limit value 0.4 and less than 1. In particular, $\mathcal {H}_n$ tends to 0.570 when $\alpha$ tends to 0 and $\mathcal {H}_n$ tends to 1 when $\alpha$ tends to $\infty$ (homogeneous case). The fluid Love number increases from 0.424 (when $\alpha$ tends to 0) to 1.5 (when $\alpha$ tends to $\infty$). These results can be seen in Fig. 6, where we also show the values of the flattening factor $\mathcal {H}_n$ at the surface and the dimensionless moment of inertia $C/m_TR_n^2$. This last parameter increases from 0.24 (when $\alpha$ tends to 0) to 0.4 (when $\alpha$ tends to $\infty$).⁴

Fig. 6

Values of $\mathcal {H}_n$ (black), $k_f$ (red), and $C/m_TR_n^2$ (blue) for different values of the exponent of the polynomial density law

7.2 Polytropic pressure–density laws

We may consider a self-gravitating body in hydrostatic equilibrium with a more general polytropic pressure–density law:

$$\begin{aligned} P=K\rho ^{1+\frac{1}{n}}, \end{aligned}$$

(43)

where $P$ is the pressure, $n$ is the polytropic index, and $K$ is constant. The differential equation for the density is then given by the Lane–Emden equation (Chandrasekhar 1939)

$$\begin{aligned} \displaystyle \frac{1}{\xi ^2}\frac{\hbox {d}}{\hbox {d}\xi }\left( x^2\frac{\hbox {d}\theta }{\hbox {d}\xi }\right) +\theta ^n=0, \end{aligned}$$

(44)

where $\widehat{\rho }=\theta ^{n}$ and $R=\alpha \xi$, with $\alpha ^2=(n+1)K\rho _0^{\frac{1}{n}-1}/4\pi G$. The standard boundary conditions are $\theta (0)=1$ and $\theta '(0)=0$. If $0\le n<5$, then the solution $\theta (\xi )$ decreases monotonically and has a zero at a finite value $\xi =\xi _1$. This radius corresponds to the surface of the body where $P=\rho =0$.

It is worth mentioning that several real cases exist that correspond to polytropes. For example, when convection is established in the interior of a star, the resulting configuration is a polytrope; when the gas is degenerate, the corresponding equations of state have the same form as the polytropic equation of state, and so forth (Collins 1989). We also mention recent results by Leconte et al. (2011) showing that the density profile of hot Jupiters is well approximated by a polytrope.

Figure 7a shows the density functions for $n=0.5,1.0,1.5,3.0$, and $4.5$ as functions of the normalized mean radius $x=R/\alpha \xi _1$ obtained from the integration of the Lane–Emden equation.

Fig. 7

a Density profiles for different values of the polytropic index. b Flattening profile $\mathcal {H}(x)$ for these density laws. $n=0.5$ (black), $n=1$ (red), $n=1.5$ (green), $n=3$ (blue), and $n=4.5$ (magenta)

The resulting flattening profiles $\mathcal {H}(x)$ are shown in Fig. 7b. In all cases, the flattening profile $\mathcal {H}(x)$ is an increasing monotonic function, and for all $x$ the values of $\mathcal {H}(x)$ decrease when the polytropic index $n$ increases.

As mentioned previously, the value of $\mathcal {H}_n$ is always greater than the limit value 0.4. In particular, $\mathcal {H}_n\rightarrow 0.4$ when $n\rightarrow 5$. The fluid Love number decreases from 1.5 for $n=0$ (constant density) to 0 when $n$ tends to the limit $n=5$. These results can be seen in Fig. 8, where we also show the values of the flattening factor $\mathcal {H}_n$ and the dimensionless moment of inertia $C/m_TR_n^2$ for values of $n$ below the limit $n=5$. The adimensional moment of inertia decreases from 0.4 (when $n=0$) and tends to 0 when $n \rightarrow 5$.

Fig. 8

Values of $\mathcal {H}_n$ (black), $k_f$ (red), and $C/m_TR_n^2$ (blue) for different polytropic indices $n<5$

8 Conclusions

In this paper, we extended the classical results on nonhomogeneous rotating figures of equilibrium to the case in which a body is also under the action of a tidal potential owing to the presence of an external body, without the restrictive hypothesis of spin-orbit synchronization. The only assumptions in this paper are that the body is formed by $n$ homogeneous ellipsoidal layers in equilibrium and that there are small enough tidal and rotational deformations with symmetry axes perpendicular to each other (remember that, in the second order, the figure ceases to be an ellipsoid). We calculated the $2n$ equilibrium equations for small flattenings and found that the two polar flattenings $\epsilon _k$ and $\mu _k$ were linearly related, both being proportional to the homogeneous reference values with a factor of proportionality $\mathcal {H}_k$ that is the same in both cases. The deformations propagate toward the interior of the body in the same way, depending, in the first approximation, only on the density profile, not on the origin of the two considered deformations. Then the problem of finding the $2n$ flattenings corresponds to finding the $n$ coefficients $\mathcal {H}_k$ with $n$ equilibrium equations. An important consequence of this approach is that the flattening profile $\mathcal {H}_k$ is the same regardless of whether the rotation of the body is synchronous or nonsynchronous, and the results for $\mathcal {H}_k$ are equivalent to those found by Tricarico (2014).

We also studied the continuous case as the limit for a very large number of layers of infinitesimal thickness, which leads to Clairaut’s differential equation for the function $\mathcal {H}(x)$ (i.e., the same equation for both flattenings). This result was expected because the coefficients of the Clairaut equation only depend on the internal distribution of matter $\rho (x)$. Therefore, the differential equation that generates the functional form of the profile flattening $\mathcal {H}(x)$ does not change when we change the nature of the deformation, provided that it is small. For densities decreasing monotonically with the radius, we found that, at the surface, $\mathcal {H}_n$ takes values larger than 0.4 [see Eq. (21)] and takes the limit value 1 in the homogeneous case. This means that the surface flattenings of a differentiated body are always smaller than the flattenings of the corresponding homogeneous ellipsoids but always larger than 40 % of them.

The results were applied to several examples. In the case of a body composed of two homogeneous layers, the following results were obtained:

• In a realistic case where the core is denser than the shell, the flattening of the nucleus is smaller than the flattening of the surface. This is a result classically known to Tisserand (1891) and discussed in recent papers by Zharkov and Trubitsyn (1978), Hubbard (2013), and Tricarico (2014).

• In the presence of a core, the surface is always less flattened than the homogeneous reference flattening but larger than 40 % of the latter value.

• The fluid Love number $k_f<1.5$ defines a continuous curve of possible values for the size of the nucleus $\xi$ and the relative density of the shell $\lambda$ and predicts their maximum value.

Finally, we studied bodies with different continuous density laws, first for some simple polynomial functions and then for polytropic profiles. The following results were obtained:

• In all cases, the function $\mathcal {H}(x)$ is an increasing monotonic function.

• For all $x$, the values of $\mathcal {H}(x)$ increase from 0.530 to 1 when the power $\alpha$ increases from 0 to $\infty$, in contrast to the polytropic densities, where the values of $\mathcal {H}(x)$ decrease from 1 to 0.4 when the polytropic index $n$ increases from 0 to the limit case $n=5$.

• The fluid Love number $k_f$ varies between 0.326 and 1.5 in the same range of the power $\alpha$ for polynomial densities. For the polytropic laws, the fluid Love number $k_f$ varies between 1.5 and 0 when the polytropic index $n$ increases.

• For polynomial laws, the values of $C/m_TR^2$ increase from 0.24 to 0.4 when the power $\alpha$ increases, and for the polytropic laws, the values of $C/m_TR^2$ decreases from 0.4 to 0 when the polytropic index $n$ increases.