Coupling between corotation and Lindblad resonances in the presence of secular precession rates

Abstract

We investigate the dynamics of two satellites with masses $\mu _s$ and $\mu '_s$ orbiting a massive central planet in a common plane, near a first order mean motion resonance $m+1{:}m$ (m integer). We consider only the resonant terms of first order in eccentricity in the disturbing potential of the satellites, plus the secular terms causing the orbital apsidal precessions. We obtain a two-degrees-of-freedom system, associated with the two critical resonant angles $\phi = (m+1)\lambda ' -m\lambda - \varpi$ and $\phi '= (m+1)\lambda ' -m\lambda - \varpi '$, where $\lambda$ and $\varpi$ are the mean longitude and longitude of periapsis of $\mu _s$, respectively, and where the primed quantities apply to $\mu '_s$. We consider the special case where $\mu _s \rightarrow 0$ (restricted problem). The symmetry between the two angles $\phi$ and $\phi '$ is then broken, leading to two different kinds of resonances, classically referred to as corotation eccentric resonance (CER) and Lindblad eccentric Resonance (LER), respectively. We write the four reduced equations of motion near the CER and LER, that form what we call the CoraLin model. This model depends upon only two dimensionless parameters that control the dynamics of the system: the distance $D$ between the CER and LER, and a forcing parameter $\epsilon _L$ that includes both the mass and the orbital eccentricity of the disturbing satellite. Three regimes are found: for $D=0$ the system is integrable, for $D$ of order unity, it exhibits prominent chaotic regions, while for $D$ large compared to 2, the behavior of the system is regular and can be qualitatively described using simple adiabatic invariant arguments. We apply this model to three recently discovered small Saturnian satellites dynamically linked to Mimas through first order mean motion resonances: Aegaeon, Methone and Anthe. Poincaré surfaces of section reveal the dynamical structure of each orbit, and their proximity to chaotic regions. This work may be useful to explore various scenarii of resonant capture for those satellites.

1 Introduction

We consider the problem of two small bodies of masses $\mu _s$ and $\mu '_s$ orbiting in a common plane around a central massive body of mass $M_{p}\,(\mu _s, \mu '_s \ll M_{p})$. In this paper, the central massive body will be called the planet, while the two orbiting objects will be called the satellites.¹ We consider a configuration that is close to a first-order $m+1{:}m$ mean-motion resonance:

$$\begin{aligned} (m+1)n' \approx mn, \end{aligned}$$

where $m$ is an integer (positive or negative depending on whether $\mu _s$ orbit inside or outside $\mu '_s$), and $n$ and $n'$ are the mean motions of $\mu _s$ and $\mu '_s$, respectively. Near the resonance, the dynamics of the satellites is described by a two-degree of freedom system with two critical resonant angles $\phi$ and $\phi '$:

$$\begin{aligned} \begin{array}{ll} \phi = (m+1)\lambda ' - m\lambda - \varpi \\ \phi ' = (m+1)\lambda ' - m\lambda - \varpi ', \end{array} \end{aligned}$$

(1)

where $\lambda$ and $\varpi$ and their primed counterparts are the classical notations for the mean longitude and longitude of periapsis of the satellites, respectively.

Having two degrees of freedom, the Hamiltonian describing the motion of $\mu _s$ and $\mu '_s$ is in general not integrable, and leads to chaotic behaviors in certain regions of phase space, as shown herein.

The aims of this paper are:

• (1) To describe the problem by a generic way, also to rescale the restricted problem ($\mu _s=0$) so that it depends upon two dimensionless parameters only: the distance $D$ between the two resonances and a parameter $\epsilon _L$ that depends upon the mass and orbital eccentricity of $\mu '_s$, thus allowing a generic approach of the problem. While the problem is integrable when the $D=0$, we show numerically that large chaotic regions appear for small distances. For large $D$’s, the system tends again toward an integrable system that can be solved using adiabatic invariance arguments.

• (2) A second goal of this paper is to clearly distinguish the effects of the two kinds of resonances associated with $\phi$ and $\phi '$. When $\mu _s \ne 0$ and $\mu '_s \ne 0$, the two resonances have indeed symmetric behaviors, but this symmetry is broken when for instance $\mu _s=0$, that is, the planar restricted three-body problem. The angle $\phi$ then describes the so-called Lindblad eccentric resonance (LER), while $\phi '$ describes the corotation eccentric resonance (CER). This terminology was originated from galactic dynamics, see e.g. Lindblad (1961, 1962), Lin and Shu (1964), Goldreich and Tremaine (1979), and it is used in the case of planetary rings, however, it is not frequently used in Celestial Mechanics. As recalled later, LER’s mainly excite orbital eccentricities (leaving semi-major axes largely unaffected), while CER’s mainly change semi-major axes (leaving eccentricities largely unaffected).

• (3) The final goal of this paper is to discuss the integrability of the two-degrees-of-freedom system in the presence of the two critical angles $\phi$ and $\phi '$. There is a considerable amount of literature for the case $\mu _s=0$ and $e'=0$ (the planar, restricted and circular three-body problem), in which only the critical angle $\phi$ appears, reducing the problem to a one-degree of freedom integrable system described by the classical Andoyer Hamiltonian given in Eq. (24); see Henrard and Lemaitre (1983), Ferraz-Mello (1985, 2007). The problem where both $\phi$ and $\phi '$ are present has been treated by Sessin and Ferraz-Mello (1984) in the Keplerian case (i.e. with a central potential $\propto -\mathcal{G}M_{p}/r$, where $\mathcal{G}$ is the gravitation constant and $r$ is the distance to $M_{p}$) and for $\mu _s \ne 0$ and $\mu '_s \ne 0$. These authors show that the two-degrees-of-freedom system is then integrable. More precisely, they show that the problem can be reduced to a one-degree-of-freedom system described again by an Andoyer Hamiltonian. More discussion about this result and its developments is provided in Sect. 2.2.

Our work can be applied in a general way to various problems involving ring and satellite dynamics. This extends for instance the approach of Goldreich et al. (1986) and Porco (1991), who proposed a model to explain the stability of Neptune’s incomplete rings (arcs) under the combined effects of Lindblad and corotation resonances. More recently, Cooper et al. (2008) and Hedman et al. (2009, 2010) have studied the motion of the small Saturnian satellites Anthe, Aegaeon and Methone that are trapped in corotation resonances with Mimas, while being perturbed by nearby Lindblad resonances (Sicardy 1991; Sicardy et al. 1999).

2 General case

2.1 Derivation of the Hamiltonian

We use here standard notations: $a,\,e,\,n,\,\lambda$ and $\varpi$ denote the semi-major axis, orbital eccentricity, mean motion, mean longitude and longitude of periapsis of $\mu _s$, respectively, with similar primed quantities for $\mu '_s$. For an oblate planet, this elements denote the geometric elements (and not the osculating elements). See Borderies-Rappaport and Longaretti (1994), Renner and Sicardy (2006) for details. In that case, the quantities $\dot{\varpi }_s$ and $\dot{\varpi }'_s$ will denote the secular time variations of $\varpi _s$ and $\varpi '_s$ (precession rates) arising from the planet oblateness, i.e. the variations that are not due to the resonances themselves.

We assume that the semi-major axes of $\mu _s$ and $\mu '_s$ remain close to reference values $a_0$ and $a'_0$, respectively, where the mean motions are $n_0$ and $n'_0$, with $n_0=\sqrt{GM_{p}/a^{3}_{0}}$ and $n'_0=\sqrt{GM_{p}/a'^{3}_{0}}$. Those reference values are chosen in a uniquely defined way so that $(m+1)n'_0 - mn_0 - \dot{\varpi }'_s=0$, and so that the total orbital energy of $\mu _{s}$ and $\mu _{s}'$ is $-\mathcal{G}M_p\mu _s/2a_0 - \mathcal{G}M_p\mu '_s/2a'_0$. Then $(m+1)n'_0 -mn_0 - \dot{\varpi }_s= \dot{\varpi }'_s - \dot{\varpi }_s$, which defines the distance (in term of frequency) between the two resonances. This is more clearly evident by noting that $\dot{\varpi }'_s - \dot{\varpi }_s = \dot{\phi } - \dot{\phi '}$. This choice for the reference values $a_0$ and $a'_0$ is arbitrary, and is motivated by the fact that we will study later the behavior of a test particle near the corotation resonance, where $(m+1)n' - mn - \dot{\varpi }'_s=0$. We define:

$$\begin{aligned} \xi = \frac{a-a_0}{a_0},~~~ \xi '= \frac{a'-a'_0}{a'_0}, \end{aligned}$$

as the relative differences of the semi-major axes with respect to the reference radii. We finally assume that $\mu _s$ and $\mu '_s$ stay far apart, in the sense that their orbital eccentricities and excursions in semi-major axes are small compared to their relative orbital separation: $\xi , \xi ', e,e' \ll |a-a'|/a' \sim 1/m$.

The expansion of the disturbing function acting on $\mu _s$ and $\mu '_s$ to first order in eccentricities yields two terms slowly varying with time: $\mathcal{G}\mu _s \mu _{s}' e A \cdot \cos (\phi )$ and $\mathcal{G}\mu _s \mu _{s}' e' A' \cdot \cos (\phi ')$, where $\phi$ and $\phi '$ are given in Eq. (1). Those terms include both direct and indirect parts from the perturbing function. The quantities $A$ and $A'$ are combinations of Laplace coefficients $b_{1/2}^{(m)}$; see Shu (1984) and Ellis and Murray (2000) for details. For numerical purposes, it is useful to note that $A$ and $A'$ have opposite signs, and that

$$\begin{aligned} \begin{array}{ll} \displaystyle A = A^{m}(\alpha ) = \frac{1}{2a'} \left[ 2(m+1) + \alpha \mathcal{D}\right] b_{1/2}^{(m+1)} (\alpha ) \approx +\frac{0.802m}{a'} \\ \displaystyle A' = A'^{m}(\alpha ) = -\frac{1}{2a'} \left[ (2m+1) + \alpha \mathcal{D}\right] b_{1/2}^{(m)} (\alpha ) \approx -\frac{0.802m}{a'}, \end{array} \end{aligned}$$

(2)

where $\alpha = a/a',\,\mathcal{D}= d/d\alpha$, and where the approximations hold in the case of large $m$’s. Note that $A$ and $A'$ have the dimension of the inverse of a distance.

The derivation of the Hamiltonian of the system is classical and is described in many works, see e.g. Laskar and Robutel (1995) for a general approach. Averaging the rapidly varying terms to zero, and keeping only the terms containing $\phi$ and $\phi '$, we obtain the averaged Hamiltonian:

$$\begin{aligned} \mathcal{H}_1&= -\frac{\mu ^3(\mathcal{G}M)^2}{2\varLambda ^2} -\frac{\mu '^3(\mathcal{G}M')^2}{2\varLambda '^2} + \mathcal{G}\mu \mu ' A \sqrt{\frac{2\varGamma }{\varLambda }} \cdot \cos (\phi )\nonumber \\&\quad + \mathcal{G}\mu \mu ' A' \sqrt{\frac{2\varGamma '}{\varLambda '}} \cdot \cos (\phi ') - \dot{\varpi }_s\varGamma - \dot{\varpi }'_s\varGamma '. \end{aligned}$$

(3)

If $\mu '_s$ orbits inside $\mu _s$, then $M= M_p(M_p+\mu _s+\mu '_s)/(M_p+\mu '_s),\,M'= M_p^3/(M_p+\mu '_s)^2,\,\mu = \mu _s (\mu '_s+M_p)/(\mu _s+\mu '_s+M_p)$ and $\mu '= \mu '_s (\mu '_s+M_p)/M_p$, see Sessin and Ferraz-Mello (1984). Equivalent expressions may be derived if $\mu _s$ orbits inside $\mu '_s$. In all cases, the orbital elements refer to the center of mass of $M_p$ and the innermost satellite. Note that since $\mu _s, \mu '_s \ll M_{p}$, we have $M \approx M' \approx M_p, \mu \approx \mu _s$ and $\mu ' \approx \mu '_s$.

Moreover, since the functional dependence of the state vectors of $\mu$ and $\mu '$ upon the geometric elements is the same as for Keplerian case, to first order in eccentricities, the values of $A$ and $A'$ can be directly derived from the formulae (2), provided geometric elements are used instead of osculating elements.

The actions $\varLambda ,\,\varGamma ,\,\varLambda '$ and $\varGamma '$ are the Poincaré variables, which are respectively conjugates to the angle variables $\lambda ,\,-\varpi ,\,\lambda '$ and $-\varpi '$ as shown below:

$$\begin{aligned} \begin{array}{ll} \lambda \longleftrightarrow &{} \varLambda = \mu \sqrt{\mathcal{G}Ma} \\ -\varpi \longleftrightarrow &{} \varGamma = \mu \sqrt{\mathcal{G}Ma}(1 -\sqrt{1-e^2}) \approx \mu e^2\sqrt{\mathcal{G}Ma}/2 \\ \lambda ' \longleftrightarrow &{} \varLambda ' = \mu '\sqrt{\mathcal{G}M'a'} \\ -\varpi ' \longleftrightarrow &{} \varGamma '= \mu '\sqrt{\mathcal{G}M'a'}(1 -\sqrt{1-e'^2}) \approx \mu ' e'^2\sqrt{\mathcal{G}M'a'}/2. \end{array} \end{aligned}$$

(4)

Because $\mathcal{H}_1$ depends only on $\phi$ and $\phi '$, it is convenient to use the new pairs of conjugate variables:

$$\begin{aligned} \begin{array}{rl} \lambda \longleftrightarrow &{} J = \varLambda + m (\varGamma + \varGamma ') \\ \lambda ' \longleftrightarrow &{} J'= \varLambda ' - (m+1) (\varGamma + \varGamma ') \\ \phi \longleftrightarrow &{} \varTheta = \varGamma \\ \phi ' \longleftrightarrow &{} \varTheta ' = \varGamma ', \end{array} \end{aligned}$$

(5)

and introduce the new actions $\varLambda ,\,\varGamma ,\,\varLambda '$ and $\varGamma '$ into $\mathcal{H}_1$.

2.2 Physical interpretation of the actions

In order to better understand globally the motions of $\mu$ and $\mu '$, it is instructive to consider the various actions entering in the system. Because $\mathcal{H}_1$ does not depends on $\lambda$ and $\lambda ',\,J$ and $J'$ are constants of motion. Consequently, the initial four-degree of freedom system (two satellites moving in a common plane) reduces to a two-degree of freedom system. It is generally not integrable (see e.g. Fig. 5), unless $\dot{\varpi }_s - \dot{\varpi }'_s=0$, as discussed later.

Turning back to $J$ and $J'$, we have:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle J+J' = \mu \sqrt{\mathcal{G}Ma(1-e^2)} + \mu '\sqrt{\mathcal{G}M'a'(1-e'^2)} = \mathrm{constant} \\ \\ \displaystyle \frac{J}{m} + \frac{J'}{m+1} \approx \frac{2}{mn_0} \cdot \left[ -\frac{\mathcal{G}M\mu }{2a} - \frac{\mathcal{G}M'\mu '}{2a'} \right] = \mathrm{constant.} \end{array} \right. \end{aligned}$$

(6)

We remind that this approximation is valid only when $\xi ,\,\xi '\,\ll 1/m$. Consequently, the conservations of $J$ and $J'$ merely express the conservation of the total angular momentum and energy of the system. More precisely, the Hamiltonian $\mathcal{H}_1$ describes the motion of two satellites that would orbit a motionless central massive planet. Thus, the exchange of energy and angular momentum occurs only between the satellites, and not between the satellites and the planet. In terms of $\xi ,\,e,\,\xi '$ and $e'$, the two equations (6), under the assumption that $M \sim M'$, read:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mu (\xi -e^2)}{ a^2_0 n_0} + \frac{\mu '(\xi ' -e'^2)}{ a'^2_0 n'_0} = \mathrm{constant} \\ \\ \frac{\mu \xi }{a_0} + \frac{\mu ' \xi '}{a'_0} = \mathrm{constant} \end{array} \right. \end{aligned}$$

(7)

We now define $J_c = \varLambda + m\varGamma = J - m\varTheta '$ and $J'_c = \varLambda ' - (m+1)\varGamma ' = J' + (m+1)\varTheta$, which are averaged versions of the Jacobi quantity, or Tisserand parameter; see e.g. Murray and Dermott (2000). It can be shown that, to within additive constants:²

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle J_c = &{} \displaystyle \frac{\mu a^2_0 n_0}{2} \left[ \xi + m e^2\right] \\ \\ \displaystyle J'_c = &{} \displaystyle \frac{\mu ' a'^2_0 n'_0}{2} \left[ \xi ' - (m+1) e'^2\right] . \end{array} \right. \end{aligned}$$

(8)

The conservations of $J$ and $J'$ thus impose $\dot{J}_c = m \partial \mathcal{H}_1/\partial \phi '$ and $\dot{J}'_c = -(m+1) \partial \mathcal{H}_1/\partial \phi$, or:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d}{dt}\left( \xi + m e^2\right) = -\frac{2m \mathcal{G}\mu '}{a^2_0 n_0} A' e' \cdot \sin (\phi ') \\ \frac{d}{dt}\left[ \xi ' - (m+1) e'^2\right] = \frac{2(m+1) \mathcal{G}\mu }{a'^2_0 n'_0} A e \cdot \sin (\phi ). \end{array} \right. \end{aligned}$$

(9)

As expected, the Jacobi quantity $J_c$ (resp. $J'_c$) is constant if $e'=0$ (resp. $e=0$).

On the other hand, we have $\dot{\varGamma } = \partial \mathcal{H}_1/\partial \varpi$ and $\dot{\varGamma }' = \partial \mathcal{H}_1/\partial \varpi '$, so that:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d(e^2\sqrt{\mathcal{G}Ma})}{dt}&{}= 2 \mathcal{G} \mu ' A e \cdot \sin (\phi ) \\ \frac{d(e'^2\sqrt{\mathcal{G}M'a'})}{dt}&{}= 2 \mathcal{G} \mu A' e' \cdot \sin (\phi '), \end{array} \right. \end{aligned}$$

(10)

The quantity $e^2\sqrt{\mathcal{G}Ma}$ (resp. $e'^2\sqrt{\mathcal{G}M'a'}$) is the action associated with the fast, radial motions of $\mu$ (resp. $\mu '$). In effect, the particle radial motion has an amplitude $\varDelta r \approx ae$, while its radial velocity has an amplitude $\varDelta p_r \approx aen \propto a^{-1/2}e$, from Kepler’s third law. Thus, $\oint p_r dr \propto e^2a^{1/2}$.

In the case of a Keplerian central potential $-\mathcal{G}M_{p}/r$, we have $\dot{\varpi }_s= \dot{\varpi }'_s=0$. The two-degrees-of-freedom system described by $\mathcal{H}_1$ then admits a second integral of motion (besides the Hamiltonian itself), and is thus integrable. This second integral was found by Sessin and Ferraz-Mello (1984) for the general case $\mu \ne 0,\,\mu ' \ne 0$ and extended to the restricted case by Wisdom (1986), while being further analyzed by Henrard and Lemaitre (1986). The existence of this second constant can be demonstrated by using canonical transformations in which the sum $\mu \mu ' A e \cdot \cos (\phi ) + \mu \mu ' A' e' \cdot \cos (\phi ')$ in Eq. (3) is replaced by a unique term $\sqrt{2\varPhi } \cdot \cos (\varphi )$, and by showing that the new Hamiltonian only depends on the conjugate variables $\varPhi ,\,\varphi$, reducing the system to a one-degree-of-freedom integrable problem.

A more geometrical demonstration of the existence of a second constant of motion for $\mathcal{H}_1$ is provided here by posing $\sigma = (m+1)\lambda ' - m\lambda$ and by defining the vectors $\mathbf u = [\cos (\sigma ),\sin (\sigma )]$ and $\mathbf v = [-\sin (\sigma ),\cos (\sigma )]$. Note that $\partial \mathbf u /\partial \sigma = -\mathbf v$. We also define the eccentricity vectors of $\mu$ and $\mu '$ as

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf e = &{} (p,q)= [e \cos (\varpi ), e \sin (\varpi )] \\ \\ \mathbf e '= &{} (p',q')= [e' \cos (\varpi '), e' \sin (\varpi ')]. \end{array} \right. \end{aligned}$$

(11)

For the Keplerian case, $\dot{\varpi }_s= \dot{\varpi }'_s=0$, the Hamiltonian $\mathcal{H}_1$ now reads:

$$\begin{aligned} \mathcal{H}_{1K}= -\frac{\mu ^3(\mathcal{G}M)^2}{2\varLambda ^2} -\frac{\mu '^3(\mathcal{G}M')^2}{2\varLambda '^2} + \mathcal{G} \mu \mu ' A (\mathbf e \cdot \mathbf u ) + \mathcal{G} \mu \mu ' A' (\mathbf e ' \cdot \mathbf u ). \end{aligned}$$

(12)

Using the approximations $e \ll 1$ and $\varLambda \approx \varLambda _0 = \mu \sqrt{\mathcal{G}Ma_0}$, we obtain $\dot{p}= (\partial \mathcal{H}_{1K}/\partial q)/ \varLambda _0$ and $\dot{q}= -(\partial \mathcal{H}_{1K}/\partial p)/\varLambda _0$, so that ${\dot{\mathbf{e}}}= -(\mathcal{G} \mu \mu ' A/\varLambda _0) \mathbf v$. Likewise, ${\dot{\mathbf{e}'}}= -(\mathcal{G} \mu \mu ' A'/\varLambda '_0) \mathbf v$. Using Kepler’s third law and noting that $A$ and $A'$ have opposite signs, the two latter equations provide the following vectorial constant of motion:

$$\begin{aligned} \frac{\varLambda _0}{A} \mathbf e - \frac{\varLambda '_0}{A'} \mathbf e ' \propto \frac{\mu }{a_0 |A| n_0}\mathbf e + \frac{\mu '}{a'_0 |A'| n'_0}\mathbf e ' = \mathbf e _\mathrm{tot} = \mathrm{constant}, \end{aligned}$$

(13)

where the vector $\mathbf e _\mathrm{tot}$ defined here is called the “total eccentricity” of the system. Moreover, $\dot{\varLambda }= -\partial \mathcal{H}_{1K}/\partial \lambda = m \partial \mathcal{H}_{1K}/\partial \sigma = - m(\varLambda _0 \mathbf e \cdot \dot{\mathbf{e }} + \varLambda '_0 \mathbf e ' \cdot \dot{\mathbf{e }}')$. Using the conservation of $\mathbf e _\mathrm{tot}$, and performing the same calculation for $\dot{\varLambda }'$, we obtain:

$$\begin{aligned} \begin{array}{ll} \frac{A^2 \dot{\varLambda }}{m \varLambda _0}= -\left[ A \mathbf{e} + A' \mathbf{e}'\right] \cdot A {\dot{\mathbf{e}}} \\ \frac{A'^2 \dot{\varLambda }'}{(m+1) \varLambda '_0}= +\left[ A \mathbf e + A' \mathbf e '\right] \cdot A' {\dot{\mathbf{e}'}}. \end{array} \end{aligned}$$

Subtracting these two equations and noting that $\dot{\varLambda }/\varLambda _0 \approx \dot{\xi }/2$ and $\dot{\varLambda }'/\varLambda '_0 \approx \dot{\xi }'/2$, we finally arrive at:

$$\begin{aligned} J_{c,\mathrm relat}= \frac{A^2 \xi }{m} - \frac{A'^2 \xi '}{m+1} + \left( |A| \mathbf e - |A'| \mathbf e '\right) ^2 = \mathrm{constant}. \end{aligned}$$

(14)

Comparison with Eq. (8) shows that the second constant of motion can be interpreted as a “relative Jacobi constant”, which extends the notion of Jacobi constant to the non-circular 3-body problem. Equation (14) tells us that the exchange of energy between the satellites only depends on the relative eccentricity vector $\mathbf e _\mathrm{relat}= |A| \mathbf e - |A'| \mathbf e '$. Moreover, Eq. (7) tells us how this energy is distributed between $\mu$ and $\mu '$. Finally, Eq. (13) shows that the interaction between $\mu$ and $\mu '$ conserves the total eccentricity of the system $\mathbf e _\mathrm{tot}$. For large $m$’s, $|a_0 A n_0| \approx |a'_0 A' n'_0|$, and the total eccentricity is just proportional to $\mu \mathbf e + \mu ' \mathbf e '$. This is a classical result already obtained by Hénon and Petit (1986) for the Hill’s Keplerian limiting case and by Foryta and Sicardy (1996) for the generalization to an oblate planet.

3 Restricted case

When $\mu = 0$, the actions describing the motion of $\mu$ must be expressed in terms of unit mass, we remind that $\mu '$ is a dimensionless parameter. Thus, the Hamiltonian $\mathcal{H}_1$ must be divided by $\mu$. This new Hamiltonian is not autonomous anymore, since $\lambda '$ and $\varpi '$ are now linear functions of time: $\lambda '= n' t$ and $\varpi '= \dot{\varpi }'_s t$. This yields the Hamiltonian:

$$\begin{aligned} \mathcal{H}_2&= -\frac{(\mathcal{G}M)^2}{2\varLambda ^2} -\frac{\mu '(\mathcal{G}M')^2}{2\mu \varLambda '^2} + \mathcal{G} \mu ' A \sqrt{\frac{2\varGamma }{\varLambda }} \cdot \cos (\phi )\nonumber \\&\quad + \mathcal{G} \mu ' A' e' \cdot \cos (\phi ') - \dot{\varpi }_s\varGamma + \frac{n' \varLambda '}{\mu } - \dot{\varpi }'_s\varGamma ', \end{aligned}$$

(15)

where the angle-action variables are now:

$$\begin{aligned} \begin{array}{ll} \lambda \longleftrightarrow \varLambda = \sqrt{\mathcal{G}Ma} \\ -\varpi \longleftrightarrow \varGamma = \sqrt{\mathcal{G}Ma}(1 -\sqrt{1-e^2}) \approx e^2\sqrt{\mathcal{G}Ma}/2 \\ \lambda '= n't \longleftrightarrow \varLambda ' = \sqrt{\mathcal{G}M'a'}\\ -\varpi ' = -\dot{\varpi }'_s t \longleftrightarrow \varGamma ' = \sqrt{\mathcal{G}M'a'}(1 -\sqrt{1-e'^2}) \approx e'^2\sqrt{\mathcal{G}M'a'}/2 \end{array} \end{aligned}$$

(16)

Note that for $\mu = 0,\,\varLambda '$ and $\varGamma '$ being constants, the corresponding terms above can be dropped from the Hamiltonian. Then, the treatment of $\mathcal{H}_2$ proceeds in the same way as for the general case previously considered, i.e. by defining the same transformations as in Eq. (5). Again the Hamiltonian is reduced to that of a two-degrees-of-freedom system which is in general not integrable, except for the special case of a central Keplerian potential $-\mathcal{G}M_{p}/r$. In this case, $\xi '$ and $\mathbf e '$ are constant, so that Eq. (14) can be re-written:

$$\begin{aligned} J_{c,\mathrm relat}= \xi + m \left( \mathbf e - \left| \frac{A'}{A}\right| \mathbf e '\right) ^2 = \mathrm{constant}, \end{aligned}$$

(17)

which generalizes the expression of the Jacobi constant $\xi + me^2$ associated with $\mu$, where the eccentricity vector $\mathbf e$ has been replaced by the relative eccentricity vector

$$\begin{aligned} \mathbf e _\mathrm{relat} = \mathbf e - \left| \frac{A'}{A}\right| \mathbf e '. \end{aligned}$$

(18)

Physically, this means that, at the first order approximation in eccentricities used here, the exchange of energy between the satellite and the particle (described by $\dot{\xi }$) only depends on the relative eccentricity vector $\mathbf e _\mathrm{rel}$.

Finally, both Eqs. (14) and (17) show why the relative Jacobi constant is destroyed when the central potential departs from the Keplerian form $-\mathcal{G}M_{p}/r$. In fact, a general potential induces a differential secular precession rate $\dot{\varpi }_s - \dot{\varpi }'_s$ between the vectors $\mathbf e$ and $\mathbf e '$, which causes a drift of the angle between $\mathbf e$ and $\mathbf e '$ which is imposed “from outside”, i.e. independent of the interactions between $\mu$ and $\mu '$.

We conjecture that as soon as $\dot{\varpi }_s \ne \dot{\varpi }'_s$, the Hamiltonians $\mathcal{H}_1$ and $\mathcal{H}_2$ (Eqs. 3 and 15) are not integrable, as shown for instance in Fig. 5. The demonstration of such a result is beyond the scope of this paper, however, and will be accepted on numerical grounds.

4 Lindblad versus corotation resonances

Equations (9) and (10) show that the term $A' \cdot \sin {(\phi '})$ modifies the Jacobi quantity of $\mu$ and the radial action of $\mu '$. Conversely, the term $A \cdot \sin {(\phi })$ modifies the Jacobi quantity of $\mu '$ and the radial action of $\mu$. Consequently, the resonances associated with $\phi$ and $\phi '$ play symmetrical roles, and cannot be distinguished, as it is clearly apparent from the form of $\mathcal{H}_1$ (Eq. 3).

This symmetry is broken, however, when the mass of one of the satellites tends to zero (restricted case), and the different roles played by the two resonances clearly appear. Taking for instance $\mu =0$, the resonance associated with $\phi$ is then called the LER, while the resonance associated with $\phi$ is called the CER.³ This nomenclature comes from galactic and ring dynamics, where those resonances were studied; see Goldreich and Tremaine (1979) and the references already quoted in the introduction.

If we consider the LER alone (i.e. taking $A'=0$), then $\xi + me^2$ is constant. Using $\xi = (a-a_0)/a_0$, this yields

$$\begin{aligned} \frac{\delta a}{a} = -2m e^2 \cdot \frac{\delta e}{e}. \end{aligned}$$

(19)

Thus, the LER mainly excites the orbital eccentricity of $\mu$, and much less its semi-major axis. This is physically understandable by noting that the LER corresponds to $(m+1)n' -mn - \dot{\varpi }_s = 0$, i.e. $\kappa = (m+1)(n-n')$, where $\kappa = n - \dot{\varpi }_s$ is the epicyclic, radial oscillation of the particle. The quantity $n-n'$ is the synodic frequency, i.e. the frequency at which the satellite and the particle are in conjunction. Thus, $n-n'$ is the frequency at which $\mu '$ perturbs $\mu$ through periodic kicks in the radial direction. For $\kappa = (m+1)(n-n')$, those kicks resonantly excite the radial action of $\mu$ (Eq. 10). On the other hand, because they are radial, the kicks essentially conserve the energy of the particle, and thus, its semi-major axis, as shown in Eq. (19).

Conversely, let us consider the case where the LER is far away from the CER. Then $\phi$ varies rapidly in $\mathcal{H}_2$, and the corresponding term can be zeroed, which is equivalent to taking $A=0$, so that the radial action $\varGamma \propto e^2 a^{1/2}$ is constant. This imposes

$$\begin{aligned} \frac{\delta e}{e} = -\frac{\delta a}{4a}. \end{aligned}$$

(20)

The comparison of Eqs. (19) and (20) shows that the corotation resonance affects much less the orbital eccentricity of the particle than the Lindblad resonance.

This is physically understandable by noting that the CER corresponds to $(m+1)n' -mn - \dot{\varpi }'_s = 0$, i.e. $n= n' + \kappa '/m$, where $\kappa '= n' - \dot{\varpi }'_s$ is the epicyclic, radial oscillation of the satellite $\mu '$. Then, the mean motion of $\mu$ matches the pattern speed $n_\mathrm{pattern} = n' + \kappa '/m$ of one of the harmonics of the disturbing potential of $\mu '$, hence the denomination corotation. Those resonances are in fact identical in essence to the classical 1:1 co-orbital resonance, but they occur at radii that are different from $a'$.

Note in particular that the CER slowly modulates the azimuthal potential acting on the particle since $\mathcal{G}\mu \mu ' e' A' \cdot \cos (\phi ') \approx \mathcal{G}\mu \mu ' e' A' \cdot \cos [m(\theta - n_\mathrm{pattern} t)]$, where $\theta$ is the true longitude of $\mu$. This periodic potential creates a small, slowly varying azimuthal acceleration on the particle that slowly modifies its semi-major axis $a$. As $a$ slowly varies, the radial action of $\mu ,\,\varGamma \propto e^2 a^{1/2}$ is conserved, as expressed in Eq. (20). More exactly, this conservation is actually the adiabatic conservation of the fast radial action $e^2 a^{1/2}$, as the azimuthal action $\sqrt{\mathcal{G}M_{p}a}$ slowly varies. More discussions about the conservation of $e^2a^{1/2}$ in various contexts can be found in Fleming and Hamilton (2000) and Sicardy and Dubois (2003).

While the separate effects of LER and CER are easy to describe in term of 1-degree-of-freedom systems, the problem is complex when they are coupled. The following section provides the simplest equations that permit to explore this complexity.

5 The CoraLin model

The restricted case $\mu = 0$ can be studied through the Hamiltonian $\mathcal{H}_2$ (Eq. 15). The derivation of the equations of motion stemming from $\mathcal{H}_2$ is standard, see for instance Murray and Dermott (2000). Near $a_0$, the actions $\varLambda$ and $J$ can be written $\varLambda = \varLambda _0 + \varDelta \varLambda$ and $J= J_0 + \varDelta J$, respectively, where $\varDelta J= \varDelta \varLambda + m(\varTheta + \varTheta ')$ is a constant of motion. The Hamiltonian $\mathcal{H}_2$ is then expanded to second order in $\varDelta \varLambda$, providing an approximation of the Hamiltonian valid near $a_0$.

At this point, it is useful to consider the Jacobi quantity $J_c= \varDelta \varLambda + m\varGamma$ that appears in the first line of Eq. (5), from which we obtain $J_c= \varDelta J - m\varTheta '$. Consequently, $\dot{J_c}= -m\dot{\varTheta }'= m \partial \mathcal{H}_2/\partial \phi '$ and $\dot{\phi }' = -m\partial \mathcal{H}_2/\partial J_c$. These are almost the canonical Hamiltonian equations, but not quite, because of the appearance of the factor $-m$. This suggests to take $\phi '$ and $J_c$ as conjugate variables, after redefining the action $J_c$ and the Hamiltonian $\mathcal{H}_2$ to within multiplicative and additive factors. The choice of those factors is rather arbitrary. We choose them so that to simplify as much as possible the expression of $\mathcal{H}_2$, so that to obtain the form in Eq. (22). Moreover, as the particle remains close to the corotation resonance radius $a_0$, it is convenient to use the new time scale $\tau = n_c t$, where $n_c$ is the libration frequency of $\phi _c$ near the corotation fixed point in the absence of the Lindblad resonance, see Table 1.

Table 1 Quantities entering in the Hamiltonian $\mathcal{H}$ (Eq. 22), where $A$ and $A'$ are a combination of Laplace coefficients given by (2) and $a_{0}$ is the reference value of the corotation

As discussed in Sect. 4, the resonances associated with $\phi$ and $\phi '$ can be separated into LER and CER types, respectively. To enhance this distinction, we will use from now on the conjugate variables ($\phi _c,\phi _L,J_c,J_L$) instead of ($\phi ^{'},\phi ,\varTheta ^{'},\varTheta$). The actions $J_c$ (proportional to $\varDelta \varLambda + m\varGamma )$ and $J_L$ (proportional to $\varTheta$) are defined in Table 1. Moreover, the angles $\phi _c$ and $\phi _L$ are defined by:

$$\begin{aligned} \left\{ \begin{array}{llll} \phi _c= +\phi ' + \pi = +(m+1)\lambda ' - m\lambda - \varpi '+\pi &{} \mathrm{if}\; m>0\, (\mu \, \mathrm{inside}\, \mu ') \\ \phi _c=+\phi ' = +(m+1)\lambda ' - m\lambda - \varpi ' &{} \mathrm{if}\; m<0\, (\mu \, \mathrm{outside}\, \mu ') \\ \phi _L= -\phi = -(m+1)\lambda ' + m\lambda + \varpi &{} \end{array} \right. \end{aligned}$$

(21)

The particular choice for $\phi _c$ is motivated by the fact that it allows a unique form of $\mathcal{H}$, avoiding a $\pm 1$ factor in front of the term $\cos (\phi _c)$ in Eq. (22). With this convention, the stable corotation point is always at $\phi _c=0$. Moreover, the minus sign used to define $\phi _L$ from $\phi$ stems from the requirement that we retrieve the canonical equations $\dot{h} = -\partial \mathcal{H}/\partial k$ and $\dot{k} = +\partial \mathcal{H}/\partial h$ with the correct signs in the system (23).

Using the equations $(m+1)n'_0 -mn_0 - \dot{\varpi }'_s=0$ and $(m+1)n'_0 -mn_0 - \dot{\varpi }_s= \dot{\varpi }'_s - \dot{\varpi }_s$ (see Sect. 2.1), and the quantities $D,\,\epsilon _L,\,J_c$ and $J_L$ defined in Table 1, we finally obtain the following Hamiltonian with the two pairs of conjugate variables $(J_c,\phi _{c})$ and $[h=\sqrt{2 J_L} \cdot \cos (\phi _L),k=\sqrt{2 J_L} \cdot \sin (\phi _L)]$:

$$\begin{aligned} \mathcal{H}= \frac{(J_c - J_L)^2}{2} - D J_L - \cos (\phi _{c}) - \epsilon _L h. \end{aligned}$$

(22)

The associated equations of motion are:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{dJ_c}{d\tau }&{}= -\frac{\partial \mathcal{H}}{\partial \phi _c}= -\sin (\phi _c) \\ \frac{d\phi _{c}}{d\tau }&{}= +\frac{\partial \mathcal{H}}{\partial J_c}= J_c - [J_L] \\ \frac{dh}{d\tau } &{} = -\frac{\partial \mathcal{H}}{\partial k}= +([J_c] - J_L + D) k \\ \frac{dk}{d\tau } &{}= +\frac{\partial \mathcal{H}}{\partial h}= -([J_c] - J_L + D) h - \epsilon _L, \end{array} \right. \end{aligned}$$

(23)

where $\tau = n_c t$ and $J_L= (h^2 + k^2)/2$. Note from Eq. (2) and Table 1 that $\mathrm{sgn}(\epsilon _L) = \mathrm{sgn}(m)$. Note that $D$ (defined in Table 1) depends on both $e'$ and $\mu '$. Our choice of $D$ is such that the width of corotation resonance is fixed to $\pm 2$, (see Fig. 1).

Fig. 1

Scheme of the CoraLin model. In the absence of the Lindblad resonance (LER), the pendular motion forced by the corotation resonance (CER) is confined into the red separatrix curve, whose full width is given by $\varDelta \chi = \pm 2$. In the absence of the CER, the LER radius is at $\chi = -D$ (dotted blue line). The coupling between the two resonance strongly depends on $D$, see Fig. 5

We call this system of equations the “CoraLin” model, as it describes the motion of a particle near a corotation and a Lindblad resonances, for which, the centers occur respectively at $J_{c} = J_{L}$ and $J_{c}-J_{L} = -D$. It is completely non-dimensional and can be used in a generic way to analyze the coupling between the two resonances. In fact, this system is parametrized by only two quantities: $D$, which measures the distance between the two resonances, and $\epsilon _L$, which measures the forcing of the particle orbital eccentricity by the satellite, while absorbing the satellite’s orbital eccentricity. Finally, the time scale $\tau$ is parametrized by the quantity $n_c$, see Table 1.

The coupling between the two resonances comes from the bracketed terms in Eq. (23), namely $(i)$ the term $J_L$ in the second equation, which tells us how the particle orbital eccentricity (mainly driven by the Lindblad resonance) perturbs the simple pendulum motion and $(ii)$ the term $J_c$ in the third and fourth equations, which tells us how the corotation resonance affects the motion of $(h,k)$ driven by the Lindblad resonance.

If we suppress the term $\cos (\phi _c)$ in $\mathcal{H}$ in order to keep only the LER, then the Hamiltonian takes the form

$$\begin{aligned} \mathcal{H}_\mathrm{And}= J_L^2/2 - (J_c + D)J_L - \epsilon _L h, \end{aligned}$$

(24)

where $J_c$ is now a constant parameter. This is the classical Andoyer Hamiltonian that has been extensively studied and reviewed in many publications in the last few decades, see e.g. Henrard and Lemaitre (1983), Ferraz-Mello (1985) and Ferraz-Mello (2007).

On the other hand, if we make $\epsilon _L=0$, then $J_L$ is constant, $\mathcal{H}$ reduces to the Hamiltonian of the simple pendulum:

$$\begin{aligned} \mathcal{H}_\mathrm{pen}= \chi ^2/2 - \cos (\phi _{c}), \end{aligned}$$

(25)

where we define $\chi = J_c- J_L$. Then we obtain $\ddot{\phi }_c= - \sin (\phi _c)$, which describes the stable oscillatory motion of the particle guiding center around the corotation fixed point at $\phi _c=0$. Note that in this case, $J_L=$ constant, meaning that the particle orbital eccentricity is conserved, as announced by Eq. (20).

An alternative form of the system (23), although not using conjugate variables, is:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\chi }&{}= -\sin (\phi _{c}) - \dot{J}_L\\ \dot{\phi }_{c}&{}= \chi \\ \dot{h} &{}= -(\chi + D) k \\ \dot{k} &{}= +(\chi + D) h + \epsilon _L. \end{array} \right. \end{aligned}$$

(26)

If the corotation motion of the particle is not perturbed by the LER, then the librating zone for $\phi _c$ has a width of $\varDelta \chi = \pm 2$, see Fig. 1. The exact LER occurs at $\chi = -D$. Consequently, the two resonances collapse into a single one for $D=0$, and are well separated for $|D|$ significantly larger than 2. We now explore the dynamics of the system for intermediate values of $D$, showing that significant chaotic zones appear in the phase space for those intermediate cases.

6 Asymptotic behaviors

6.1 Superimposed resonances

If $D=0$, the CER and LER are superimposed, and the problem is integrable (Sect. 2.2). Poincaré surfaces of section taken at $k=0$ are then regular, and they can be obtained analytically by noting that the second constant of motion in Eq. (17) can be re-written:

$$\begin{aligned} S = J_{c} + \frac{\sqrt{2J_{L}}}{\epsilon _{L}}\cos (\phi _{c}-\phi _{L}), \end{aligned}$$

(27)

which is another expression of the relative Jacobi constant defined in Eq. (17).

Using Eqs. (22) and (27) and making $k=0$, we obtain:

$$\begin{aligned} \chi ^4 - 4H\chi ^2 + 8\epsilon _{L}^2\chi - 4\cos ^2(\phi _{c}) + 4H^2 = 8\epsilon _{L}^2 S, \end{aligned}$$

(28)

where $H$ is the value of the Hamiltonian $\mathcal{H}$. For $H$ fixed, the surface of sections are the level contours of the surface defined by Eq. (28) for various values of $S$. Note that these contours are $\pi$-periodic, not $2\pi$-periodic. The fixed points are given by the singular points of that surface:

$$\begin{aligned} \left\{ \begin{array}{ll} \chi ^3 - 2H\chi +2\epsilon _{L}^2 = 0 \\ &{} \\ \phi _{c} = k\frac{\pi }{2}, ~~~~~~ k \in \mathbb {Z} \end{array} \right. \end{aligned}$$

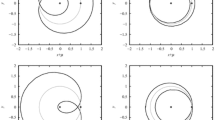
The number of solutions in $\chi$ depends of the sign of the discriminant $\varDelta = 32H^3 - 108\epsilon _{L}^4$. Therefore, there exists a critical value $H_{0}=(27\epsilon _{L}^4/8)^{1/3}$: for $H<H_{0}$ the system has only one solution in $\chi$:

$$\begin{aligned} \chi _{0} = \left( \frac{2\epsilon _{L}^2 + \sqrt{-\varDelta /27}}{2}\right) ^{1/3} + \left( \frac{2\epsilon _{L}^2 - \sqrt{-\varDelta /27}}{2}\right) ^{1/3} \end{aligned}$$

For $H>H_{0}$ a pitchfork bifurcation occurs and provides three solutions:

$$\begin{aligned} \chi _{p} = 2\sqrt{\frac{-2H}{3}} \cos \left[ \frac{1}{3} \arccos \left( -\epsilon _{L}^2\sqrt{27/8H^3}\right) + \frac{2p\pi }{3} \right] \end{aligned}$$

with $p \in \{0,1,2\}$.

Examples of surfaces of section with $H<H_{0}$ and $H>H_{0}$ are given in Fig. 2. Note that orbits near the fixed elliptical points do not correspond to librations of $\phi _c$ (i.e. to particles trapped in a CER). For instance the fixed point near $\phi _c=0,\,\chi =0$ in the left panel corresponds to the trajectory shown in blue, for which $\phi _c$ is circulating.

Fig. 2

Phase portraits of the system (23) when the corotation and Lindblad resonances (CER and LER, respectively) are superimposed, i.e. $D=0$. We show Poincaré surfaces of section corresponding to $k=0$, with prescribed values $H$ of the Hamiltonian $\mathcal{H}$, and various values of the second constant of motion $S$ (Eq. 27). For both panels, $\epsilon _{L} = -0.123$, which provides a critical value $H_{0}=(27\epsilon _{L}^4/8)^{1/3}= 0.091$. Left panel $H = -1 < H_0$, there is only one solution in $\chi$ for the fixed points. Right panel $H=1 > H_0$, there are three solutions in $\chi$ for the fixed points. See text for details

6.2 Well separated resonances

We consider the situation in which the CER and LER are well separated, $|D| \gg 2$. Two cases are discussed.

• (a) The particle is trapped in the corotation region: In this case, the variations of $(h,k)$ in the systems (23) and (26) are much faster than the variations of $(J_c,\phi _{c})$. Consequently, the action $\oint hdk$ is adiabatically conserved. Since the vector $(h,k)$ essentially describes a circle centered on the forced value $(-\epsilon _L/(\chi +D),0)$, it means that $(h,k)$ rapidly moves on a circle of constant radius, whose center slowly moves along the $Oh$ axis, see Fig. 3. In particular, if $(h,k)$ starts at the forced value $(-\epsilon _L/(\chi +D),0)$, then it will stay at that value as $\chi$ slowly changes. In other words, the orbital eccentricity of the particle will permanently adjust itself so that $e= |\epsilon _L/(\chi +D|$ as $\chi$ varies.

• (b) The particle is trapped in the Lindblad resonance: The situation is now reversed: $(h,k)$ slowly varies as $J_c$ as $\phi _{c}$ oscillates rapidly. Thus $\int J_c d\phi _{c}$ is adiabatically conserved. In fact, the system:

  $$\begin{aligned} \left\{ \begin{array}{ll} \dot{J}_{c} =-\sin (\phi _{c}) \\ \dot{\phi }_{c} = J_{c} - J_{L} \end{array} \right. \end{aligned}$$

  (29)

  correspond to a simple pendulum with a slowly varying parameter, $J_L$. Thus, the particle will librate around the slowly varying point $(J_c= J_L, \phi _{c}=0)$, while adiabatically conserving $\int J_c d\phi _{c}$, see Fig. 4.

Fig. 3

Left: Poincaré surfaces of section $k=0$ of the system (23) with $D = 10$ (the Lindblad resonance is far away from the corotation radius at $\chi =-D=-10$) and $\epsilon _{L} = -0.1$. The phase portrait of the CER is very close to that of a simple pendulum. Right: the vector $(h,k)$ rapidly describes a circle centered on the forced value ($h= e_f= |\epsilon _L/(\chi +D|,k=0$) that moves slowly as $\chi$ varies (red circles). When $\chi = 1.4$ (green point at left), then $e_{f} = e_{A} = (0.008,0)$, corresponding to the green orbit at right. When $\chi = -1.4$ (blue point at left), then $e_{f} = e_{B} = (0.016,0)$ (blue orbit at right)

Fig. 4

Poincaré surfaces of section $k=0$ of the system (23) with $D = 10$ and $\epsilon _{L} = -0.1$. The particle is now close to the Lindblad resonance, $\phi _c$ and $\chi$ vary rapidly compared to $h$ and $k$, while keeping $\int J_c d\phi _{c}$ adiabatically constant

7 Intermediate cases

7.1 Chaoticity

We have explored numerically the transition from the integrable case $D=0$ to the chaotic regime for $D$ of order unity. We consider here an illustrative case where $\epsilon _{L} = -0.1$ and $H = -0.5$. The value of $H$ using the orbital elements is:

$$\begin{aligned} \displaystyle H = \frac{(3m\varDelta a/a_{0})^{2} }{8\sqrt{\epsilon _{c}}} - \frac{3Dm^{2}e^{2}}{2\sqrt{\epsilon _{c}}} - \cos {\phi _{c}} - \epsilon _{L}\frac{\sqrt{3m^{2}e^{2}}}{{\epsilon _{c}}^{1/4}}\cos {\phi _{L}}, \end{aligned}$$

with $\epsilon _{c} = 3m^{2}a_{0}|A'| e' \mu '/M$. This choice is motivated by the fact that they are typical values relevant to the small Saturnian satellites Anthe, Methone and Aegaeon, see Table 2.

Table 2 Critical angles and values of $D,\,\epsilon _L$ and $H$ appropriates to Anthe, Methone and Aegaeon given by CoraLin model. These parameters depend of the configurations of the small satellites in the Saturnian system

Figure 5 shows that the phase portrait of system (23) is rapidly invaded by a chaotic region for values of $D$ as small as $\sim 0.01$. As $D$ increases, a central regular region appears, corresponding to the trapping of the particle in the corotation site, i.e. to a libration of the critical angle $\phi _c$. Only for value of $|D|$ significantly larger than 2 does the system retrieve its regularity, and can the orbits be described using adiabatic invariant arguments, see Sect. 6. In fact, Fig. 5 shows that for $0< |D| < 2$ the motion of the particle near the CER is dominated by chaos. This is true for the actual Saturnian satellites that we examine now.

Fig. 5

Poincaré surfaces of section of system (23) using $\epsilon _{L} = -0.1$ and $H=-0.5$ for 11 different values of $D$. Each phase portrait is obtained when $k=0$ for sixteen different trajectories with the same value of $H$. When $D = 0$ and $D=10$, the trajectories are regular. For intermediate cases, chaos is prevalent. In the CoraLin system (23), we can see that for $D=J_{c}-J_{L}$, the vector $(h,k)$ moves slowly, so that $k$ passes more rarely through zero, explaining the rarefaction of points along the line $D=J_{c}-J_{L}$

7.2 Numerical exploration of the chaoticity

In order to give a better and a global view of the dynamics in the intermediate cases, we perform a more systematic analysis of the dynamics for all of the regimes: the two limit cases (CER and LER) and the intermediate regime by measuring the Fast Lyapunov Indicator (FLI) detailed in (Froeschlé et al. 1997; Morbidelli 2002). In practice, we have studied the FLI near the separatrix (see Fig. 5) and corresponding to these initial conditions: $\chi = 0,\,\phi _{c} = \pi ,\,h= 0$ and $k=0$.

The values of FLI represent the irregularity degree for each orbit. We show in Fig. 6 a FLI map for several values of $D$ and $\epsilon _{L}$. Here we are interested by the global dynamics of the test particle, we note that for values of $D$ between $\sim$ 0 and 2, the chaoticity area grows gradually (clear colors). Beyond $D=6$, the orbits become regular (dark colors) what is in agreement with the previous discussion. For $\epsilon _{L} =0$, the trajectories becomes regulars as expected, because the system is not perturbed as the mass of the perturber satellite is equal to zero.

Fig. 6

Maps of FLI, for 90000 trajectories, the initial conditions used are: $\chi = 0,\,\phi _{c} = \pi ,\,h= 0$ and $k=0$. We integrated numerically several orbits ($90000$ orbits) during $2000$ years, with these initial conditions: $\chi = 0,\,\phi _{c} = \pi ,\,h= 0$ and $k=0$, for 100 values of $\epsilon _{L}$ between $[-0.3,0]$ and 900 values of $D$ between $[0,7.5]$. A FLI of 400 corresponds to 5 years in terms of divergence of two close orbits, smaller values of the FLI correspond to longer divergence times that scale like 5 years/FLI.

7.3 Real applications

In this section, we show that in some cases, a strong coupling between corotation and Lindbald resonances may lead to chaotic behavior. We apply the CoraLin model to several recently discovered small satellites dynamically linked to Mimas through first-order mean-motion resonances: Anthe, Methone and Aegaeon (Cooper et al. 2008; Hedman et al. 2009, 2010), all associated with arc of material. The presence of these structures are consistent with their confinement by CER with Mimas : Aegaeon is trapped in an inner 7:6 CER with Mimas, while Anthe and Methone are respectively near the outer 10:11 and a 14:15 CER resonances. All satellites are trapped in CER with Mimas and perturbed enough ($D < 2$) by the associated LER. Indeed, the phase space topology depends of two parameters (Table 2) which are given by the configurations between the particle (one of these small moons) and Mimas (the disturbing satellite) orbiting a central planet (Saturn). Poincaré surfaces of section reveal the dynamical structure of each orbit, and for some of them, their proximity to chaotic regions (Fig. 7).

Fig. 7

Green curve Position of Lindblad resonance at $J_c - J_L = -D$. Blue curve Trajectory of the small satellite. Red curve Surfaces of section of a particle having the same parameters of each satellites with different initials conditions in terms of $\chi = J_c - J_L$. Note that the corotation site is very affected by chaotocity due to the interaction with LER

Indeed the system (23) is numerically integrated for twenty separated trajectories and ($J_{c} - J_{L}$) was plotted versus $\phi _{c}$. From (Fig. 7), we see that this dynamical system displays both regular and irregular orbits as most of the Hamiltonian systems. A surface of section is obtained by getting back ($J_{c}, \phi _{c}$) with period $2\pi$ or only when $k=0$ and $\dot{k} > 0$. This approach gives an idea on the structure of phase space for each of the moons, we see also that the chaos results from a strong coupling between CER and LER, and that the chaotic sea is very large occupying totally the corotation site. We notice that Anthe is close to a chaotic region. The amplitude of libration is $\pm$26 km, i.e. about half of the corotation width (50.7 km). The orbit of Methone is farther away from the chaotic zone than Anthe, with an amplitude of libration of $\pm$20 km and a corotation width of 55.36 km. The case of Aegaeon (inside the orbit of Mimas) is slightly different, its orbit seems to be more stable than those of Anthe and Methone, as it is far enough from the chaotic region, the width of the corotation site is 31.62 km, and the magnitude of libration in terms of semi-major axis is $\pm$4 km (Hedman et al. 2009, 2010).

We notice that the chaotic region is surrounding by many regular trajectories, this behavior means that the corotation stability is not affected. This result will be investigated in future works by analysis of capture probability of this structures inside CER site.

8 Conclusion

We have studied the behavior of two satellites of masses $\mu _s$ and $\mu '_s$, revolving along coplanar, small-eccentricity orbits around a planet of mass $M_p \gg \mu _s, \mu '_s$. We have averaged the equations of motion close to a first-order mean-motion commensurability $m+1{:}m$, keeping only perturbing terms of first order in eccentricity and accounting for the secular apsidal precessions rates $\dot{\varpi }_s$ and $\dot{\varpi }'_s$ of the satellites. This allows to derive the classical Hamiltonian of the system, with the two critical resonant arguments $\phi = (m+1)\lambda ' - m\lambda - \varpi$ and $\phi ' = (m+1)\lambda ' - m\lambda - \varpi '$. Using the constants of motion (total energy and angular momentum), the initial four-degree of freedom system reduces to a two-degree of freedom problem that is not in general integrable.

For $\dot{\varpi }_s- \dot{\varpi }'_s=0$ (as it is the case for the Keplerian problem), the Hamiltonian is integrable, a result initially derived by Sessin and Ferraz-Mello (1984). The integrability of the system stems from the existence of a second constant of motion, besides the Hamiltonian. Here we show that this constant is actually a generalized version of the Jacobi constant (Eq. 14), where the orbital eccentricities of $\mu _s$ or $\mu '_s$ are replaced by a quantity that we call the relative eccentricity of the two orbits (Eq. 18). Secular terms forces a differential precession between the two orbits (i.e. $\dot{\varpi }_s- \dot{\varpi }'_s \ne 0$), and destroys the generalized Jacobi constant.

In the general case ($\mu _s \ne 0, \mu '_s \ne 0$), the two satellites play symmetrical roles. This symmetry is broken, however, in the restricted problem (e.g. $\mu _s =0$). The two critical resonant angles $\phi$ and $\phi '$, or their counterparts $\phi _L$ and $\phi _c$, are then associated with two resonances (Lindblad and corotation, or LER and CER, respectively) that plays very different roles. While the LER mainly excites the orbital eccentricity of the test particle, leaving its semi-major axis relatively unaltered (Eq. 19), the CER mainly changes its semi-major axis, leaving its eccentricity almost constant (Eq. 20).

The two resonances may be simultaneously described by a reduced Hamiltonian (Eq. 22), that depends upon only two dimensionless parameters that control the dynamics of the system: $(i)$ the distance $D \propto \dot{\varpi }_s - \dot{\varpi }'_s$ between the CER and LER, and $(ii)$ the forcing parameter $\epsilon _{L}$ that includes both the mass and the orbital eccentricity of the disturbing satellite, see Table 1.

The resulting equations of motion are summarized by four simple differential equations that constitute the “CoraLin model” (see the system (23)). This system describes the coupling between the motion of a simple pendulum (Eq. 25) that has a separatrix of width $\pm 2$, and an Andoyer-type oscillator (Eq. 24) centered at $\chi =-D$, see Fig. 1. It has the advantage to permit a generic exploration of the dynamics of the system through simple numerical integrations, Poincaré surfaces of section, etc...Furthermore, it uses dimensionless parameters that encapsulate all the parameters of the systems (mass and orbital eccentricity of the perturber, secular precessions of the orbits, etc...).

As an example, we have examined the phase portraits relevant to small Saturnian satellites trapped in CER’s with Mimas: Aegaeon, Methone and Anthe. While the system is integrable for $D=0$, chaos is rapidly prevalent for values of $D$ as small as about 0.01, see Fig. 5. Only for large values of $D \gg 2$ is the system almost integrable again, with a behavior that can be qualitatively described using simple adiabatic invariant arguments.

More specific integrations (Fig. 7) show that Aegaeon, Methone and especially Anthe are close to prominent chaotic regions. Future works are now in order to explain how those satellites may have been captured inside their respective corotation sites. The numerical implementation of orbital migrations of Mimas and/or the small satellites in the CoraLin system is in fact very simple, and we will use that model to explore various scenarii of resonant capture.