On the Feasibility of Using Large-Eddy Simulations for Real-Time Turbulent-Flow Forecasting in the Atmospheric Boundary Layer

Abstract

We investigate the feasibility of using large-eddy simulation (LES) for real-time forecasting of instantaneous turbulent velocity fluctuations in the atmospheric boundary layer. Although LES is generally considered computationally too expensive for real-time use, wall-clock time can be significantly reduced by using very coarse meshes. Here, we focus on forecasting errors arising on such coarse grids, and investigate the trade-off between computational speed and accuracy. We omit any aspects related to state estimation or model bias, but rather look at the size and evolution of restriction errors, subgrid-scale errors, and chaotic divergence, to obtain a first idea of the feasibility of LES as a forecasting tool. To this end, we set-up an idealized test scenario in which the forecasting error in a neutral atmospheric boundary layer is investigated based on a fine reference simulation, and a series of coarser LES grids. We find that errors only slowly increase with grid coarsening, related to restriction errors that increase. Unexpectedly, modelling errors slightly decrease with grid coarsening, as both chaotic divergence and subgrid-scale error sources decrease. A practical example, inspired by wind-energy applications, reveals that there is a range of forecasting horizons for which the variance of the forecasting error is significantly reduced compared to the turbulent background variance, while at the same time, associated LES wall times are up to 300 times smaller than simulated time.

1 Introduction

Turbulence in the atmospheric boundary layer (ABL) plays an important role in many natural processes and engineering applications. Depending on atmospheric stability, turbulent flow structures attain longitudinal scales up to several times the boundary-layer height, (Jiménez 1998; Kim and Adrian 1999; Abe et al. 2004; Hutchins and Marusic 2007; Shah and Bou-Zeid 2014; VerHulst and Meneveau 2014; Fang and Porté-Agel 2015) leading, for example, to coherent wind gusts or unsteady loading of built structures. In recent years, lidar has emerged as a new technology that observes turbulent wind fields over areas of several square kilometres (see, e.g., Sathe and Mann 2013; Mikkelsen 2014; Hirth et al. 2016). This provides many new opportunities, including the use of observed wind fields for real-time turbulent flow forecasting in the ABL, with possible prediction horizons ranging from several minutes up to one hour. The latter can be relevant for monitoring of atmospheric dispersion (Holmes and Morawska 2006), hazard response at chemical or nuclear plants (Katata et al. 2015), power forecasting of wind turbines and farms for short-term trading or grid services (Jung and Broadwater 2014), and may also include the use of such forecasting models as a control model to reduce loads (e.g., of wind turbines), or to increase overall energy capture in wind farms (Knudsen et al. 2015). In the present study, we investigate whether it is feasible to use large-eddy simulation (LES) for real-time turbulent flow forecasting in the ABL, focusing on the neutrally-stratified ABL over flat terrain. As an application example, we use power forecasting in wind energy, but many of our results and conclusions are relevant to other application areas as well.

An important aspect of real-time forecasting models is computational speed. These models are typically integrated in state estimation and possibly optimization algorithms, so that their wall time must be multiple times shorter than the simulation time if the overarching algorithm is to be evaluated more rapidly than for real time. Therefore, models that are used today are all based on simplified semi-heuristic formulations, and differ depending on application area. For instance, in atmospheric dispersion modelling, examples include Gaussian plume models and Gaussian puff models (Leelssy et al. 2014), street-canyon models (Belcher et al. 2015), or Reynolds-averaged Navier–Stokes based reduced-order models (Vervecken et al. 2015). For wind-energy applications, examples include mainly turbine-wake models, e.g. static models such as the Jensen model (Katic et al. 1986), the Ainslie model (Ainslie 1988), or Gaussian wake models (Niayifar and Porté-Agel 2015), as well as dynamic models, such as the dynamic wake-meandering model (Larsen et al. 2008), the FLORIS model (Gebraad et al. 2016), or a dynamic Jensen model (Shapiro et al. 2017). In fact, most of these models do not even include atmospheric turbulence in their predictions, but rather focus on the prediction of mean statistics given known background meteorological conditions. To the authors’ knowledge, the use of LES for short-term forecasting of turbulence has not been considered to date.

Recently, LES was used in the context of wind-farm optimal control (Goit and Meyers 2015; Goit et al. 2016; Munters and Meyers 2017a, 2018). However, these studies did not envisage the use of LES for real-time control, since LES is computationally too slow, but instead, used the optimal control study as a means to explore improved ways for a wind farm to interact with the ABL. However, thanks to efficient parallelization, the use of large-eddy simulation in these studies almost achieved parity between simulation time and wall-clock time (Munters and Meyers 2017a, b). We emphasize that much depends on the physical length and velocity scales at which the large-scale motions that are simulated in the LES occur. For instance, with the ABL height on the order of ${1}\,\hbox {km}$ and a friction velocity $\approx \,{1}\,\hbox {m}\,\mathrm{s}^{-1}$, large time scales are in the order of ${100}\,\hbox {s}$. Scaling the same system down to a comparable high-Reynolds-number boundary layer with a boundary-layer height of, say ${0.1}\,\hbox {m}$, and the same friction velocity, leads to time scales of ${10}\,{\upmu }\hbox {s}$. Although the computational cost of LES of both systems would be roughly the same, the ratio of simulation time to wall time is quite different. Nevertheless, for turbulent flow forecasting in the ABL, it may suffice to speed-up current LES by one to two orders of magnitude. A simple solution is to coarsen the simulations, i.e. coarsening an LES by a factor of n, reduces the computational cost by $n^4$. Thus coarsening by a factor of four may already suffice to obtain a speed-up of a factor of 100 compared to a high-fidelity baseline resolution. This highlights the trade-off between computational cost and model accuracy.

A further challenge to the accuracy of turbulent-flow forecasting is the chaotic nature of turbulence. It is well understood that small perturbations lead to an exponential divergence of trajectories in state space, at a rate of the most unstable Lyapunov exponent of the system [see Mukherjee et al. (2016) for an extensive LES study]. However, when considering finite size perturbations, the predictability horizon is mainly dependent on the scale of interest (Lorenz 1969). This was later formalized by Aurell et al. (1997) for systems with finite size Lyapunov exponents, which were later experimentally determined for the ABL by Basu et al. (2002). Consequently, computational accuracy depends not only on the LES grid size, but also on the envisaged prediction horizon. We remark that, in contrast to the above forecasting of turbulence in the ABL, long term statistical averages in LES are well studied, including the effects of grid resolution (see, e.g., Sullivan and Patton 2011).

1.1 Scope of the Study

In practice, LES models used for turbulent-flow forecasting may be initialized by online measurements (e.g. by lidar) and integrated in a longer algorithmic chain that includes state estimation [e.g. based on variants of Kalman filtering (Kalman 1960), three-dimensional variational assimilation (3D-Var) (Lorenc 1981), or four-dimensional variational assimilation (4D-Var) (Le Dimet and Talagrand 1986)]. Moreover, when used for control, it could also include, e.g., control optimization using a receding horizon approach. In the present work, we do not consider this full algorithmic chain. Rather, in a first step we focus on the forecasting-error dependence of coarse-grid LES on resolution and estimation time horizon only, next to the trade-off between computational speed and accuracy. We omit all aspects of measurement errors, state estimation, errors introduced by model bias as well as the effects of atmospheric stability. Although these are all important for the practical use of LES as a real-time turbulent-flow forecasting model, the present study precedes these issues, by investigating whether the use of LES is feasible at all, given modelling errors on coarse grids, and given the chaotic divergence of turbulence.

To this end, we envisage a series of simulations on different grids, on a domain of $40 \times 5 \times {1}\,\hbox {km}^3$, using periodic boundary conditions in horizontal directions. The domain and computational set-up is chosen such that the throughflow time is roughly ${4000}\,\hbox {s}$, which is the longest prediction horizon that we consider. The finest LES grid, which has approximately ${0.125}\times 10^{9}$ grid points, is used as a baseline reference (details of the computational set-up are further provided in Sect. 2.2). We then consider a series of coarser grids, with the coarsest containing only ${0.25}\times 10^{6}$ grid points, and study the evolution of the error between the coarse and the baseline grids as a function of the prediction horizon. We simply initialize the coarse-grid LES by filtering the fine-grid LES at the start of the prediction horizon. Thus (as mentioned above), we presume perfect knowledge of the coarse-grid LES initial conditions, and all difficulties related to state estimation based on real observations, and model bias are omitted.

The paper is organised as follows: in Sect. 2, the LES methodology is introduced, and the case set-up is discussed, and in Sect. 3 the main framework is constructed for analyzing the errors. Finally, in Sect. 4 results are discussed.

2 Large-Eddy Simulation Equations, Case Set-Up and Methodology

2.1 Governing LES Equations and Discretization

All simulations use SP-Wind, which is a pseudo-spectral LES code developed at KU Leuven over the last decade (Calaf et al. 2010). The governing equations are the filtered incompressible Navier–Stokes equations,

$$\begin{aligned}&\frac{ \partial {{\varvec{u}}}}{\partial t} = -{{\varvec{u}}}\cdot \nabla {{\varvec{u}}} -\frac{1}{\rho } \nabla (p + p_{\infty }) - \nabla \cdot {\varvec{\tau }}_{{\mathrm {SGS}}}, \end{aligned}$$

(1)

$$\begin{aligned}&\nabla \cdot {{\varvec{u}}} = 0, \end{aligned}$$

(2)

where ${\varvec{u}}=(u_1,u_2,u_3)$ represents the filtered velocity field, and p is the pressure. Furthermore, in boundary-layer simulations, $\nabla p_{\infty } = [f_{\infty },0,0]$ represents the background pressure gradient that we presume in the x-direction. We neglect contributions of the viscous stresses on the resolved scales, and model the subgrid-scale (SGS) stresses $\varvec{\tau }_{\mathrm {SGS}}$ using a Smagorinsky model (Smagorinsky 1963)

$$\begin{aligned} {\varvec{\tau }}_{\text {SGS}}= 2l^2(2\varvec{S}:\varvec{S})^{1/2}\varvec{S}, \end{aligned}$$

(3)

where $\varvec{S}= \left( \nabla {\varvec{u}} + (\nabla {\varvec{u}})^T\right) /2$ is the rate-of-strain tensor. For the Smagorinsky length scale l, we employ Mason and Thomson’s (1992) damping function, such that $l^{-n}=\left( C_s\varDelta \right) ^{-n}+\left( \kappa (z+z_0)\right) ^{-n}$, where $\varDelta = (\varDelta _x\varDelta _y\varDelta _z)^{1/3}$ is the local grid spacing, and $C_s$ is the Smagorinsky constant, and $\kappa =0.4$ is the von Kármán constant. We take $C_s=0.14$, $n=1$, see Meyers (2011) for a discussion.

Periodic boundary conditions are used in all horizontal directions, and at the top of the domain we use a symmetry condition. At the wall, impermeability is used in combination with a wall-stress model, which is applied to the first grid point (see Moeng 1984; Bou-Zeid et al. 2005),

$$\begin{aligned} \tau _{w,1}&= - \left( \frac{\kappa }{ln(z_1/z_0)}\right) ^2\left( {\widetilde{u}}_1^2 + {\widetilde{u}}_2^2\right) {\widetilde{u}}_1, \end{aligned}$$

(4a)

$$\begin{aligned} \tau _{w,2}&= - \left( \frac{\kappa }{ln(z_1/z_0)}\right) ^2\left( {\widetilde{u}}_1^2 + {\widetilde{u}}_2^2\right) {\widetilde{u}}_2, \end{aligned}$$

(4b)

where the parallel velocity components ${\widetilde{u}}_1$ and ${\widetilde{u}}_2$ are obtained from filtering the horizontal velocity components $u_1$, $u_2$ with a 2D Gaussian filter, using filter widths $4\varDelta _x$ and $4\varDelta _y$ in the x- and y-directions. Further $z_1$ is the vertical coordinate of the first grid point, while $z_0$ is the roughness length.

SP-Wind uses a pseudo-spectral discretization for the horizontal directions, in which the non-linear terms are evaluated in real space and de-aliased using the 3/2 rule (Canuto et al. 1988). Fourier transforms are performed using the FFTW library (Frigo and Johnson 2005), and parallelization is performed using a 2D pencil decomposition of the Fourier transforms (Li and Laizet 2010). For the vertical direction, a fourth-order energy conservative scheme is used (Verstappen and Veldman 2003), and for the time integration, a fourth-order explicit Runge–Kutta scheme is employed. The timestep is, in general, chosen by applying a Courant–Friedrichs–Lewy number of 0.4. If however a sample point is approached, the Courant–Friedrichs–Lewy timestep is adapted (reduced), so that output data are generated at the desired time instance.

2.2 Case Set-Up

All simulations are performed on a cuboid, with specifications as summarized in Table 1. The domain is chosen to be sufficiently long for the effects of periodicity on turbulent structures in the streamwise direction to be minimal (Munters et al. 2016). The roughness length $z_0$ is taken to be ${0.1}\,\hbox {m}$, which is a typical overland value (Wiernga 1993). The selected horizontal pressure gradient leads to a friction velocity $u_{*}={0.5}\,\hbox {m}\,\mathrm{s}^{-1}$, which gives a common wind speed of around ${10}\,\hbox {m}\,\mathrm{s}^{-1}$ between the 100 to ${1000}\,\hbox {m}$ heights. Given these parameters, the total throughflow time of the domain is approximately ${4000}\,\hbox {s}$, which is also the longest prediction horizon that is considered. We remark here that all our results can be non-dimensionalized with friction velocity and boundary-layer height, so that results can be scaled to different conditions. Nevertheless, we present results in real units, as this will keep the discussion more concrete. Moreover, rescaling is not always meaningful. For instance, changing the reference length will effectively change the physical height of reference structures of interest such as wind turbines, while changing the velocity scale will change the Coriolis parameter and thus the latitude of the simulation (though the latter is only relevant in LES models that include the effects of Coriolis forces—in the present study, Coriolis forces are neglected). It is interesting to note that rescaling a simulation to higher wind speed, effectively decreases the time scales and thus also the prediction time horizon. In that case, length scales are conserved, and therefore also the ‘prediction distance’, simply defined as the distance the flow will convect downstream during the time horizon, remains invariant.

Table 1 Summary of the domain specifications and ABL parameters

As discussed above (Sect. 1.1), we are interested in the forecast-error evolution on a series of simulation grids. To this end, four different uniform rectangular grids are defined, with cell sides that are coarsened each time by a factor of two. Henceforth, we denote results and sizes of the different grids using a superscript $i\,(i=0,1,2,3)$, with $i=0$ referring to the finest grid level. Thus, the velocity field on grid i is denoted by ${\varvec{u}}^i$, and given the coarsening factor of two, $\varvec{\varDelta }^i=2^i\varvec{\varDelta }^0$, where $\varvec{\varDelta }^0 = \left[ \varDelta ^0_x, \varDelta ^0_y, \varDelta ^0_z\right]$ is the finest/reference grid resolution. A detailed summary of the grid specifications is given in Table 2. Note that the grid resolutions in the Table represent the true degrees of freedom in our simulations. De-aliasing of the non-linear terms using Orzag’s 3 / 2 rule is performed on grids that are refined by a factor of 3 / 2 in both horizontal directions.

Table 2 Summary of the different grid specifications

For the initialization of all simulations, a spin-up is first performed on the finest grid resolution, until the turbulence is fully developed, and the flow fields are statistically stationary. In a second step that initializes the coarse grid simulations, the fine grid initial condition, shown in Fig. 1a, is filtered and restricted to the coarser grids (see Sect. 3.1 for details).

The initial streamwise component of the flow fields for the different grids is shown on the left side of Fig. 1a–d. On the right side of the figure a zoom of a rectangular box of ${700}\,\hbox {m}\times {500}\,\hbox {m}\times {100}\,\hbox {m}$ is shown, which is a representative size for the spacing between turbines in a wind farm. The black lines represent the grid-cell boundaries of the different grid levels.

Simulations are performed over a time horizon of ${4000}\,\hbox {s}$, and flow fields are sampled every ${4}\,\hbox {s}$. To ensure that the fields are sampled at the exact same times, the integration timestep is chosen as $\varDelta _t^i = \mathrm {min}\big (\varDelta _t^{i,\mathrm {CFL}},\varDelta _t^{i,\mathrm {s}}\big )$, where $\varDelta _t^{i,\mathrm {CFL}}$ is the Courant–Friedrichs–Lewy timestep, and $\varDelta _t^{i,\mathrm {s}}$ is the timestep to the next sample. A detailed discussion of errors and comparisons of results is presented below.

Fig. 1

Initial streamwise velocity fluctuations $u^i_1(\varvec{x},0)-U_1^i(z)$ for the different grids at $z={100}\,\hbox { m}$, with increased grid coarsening from a to d. (Left): visualization on the full domain; (right) zoom on a ${700}\,\hbox {m}\times {500}\,\hbox {m}\times {100}\,\hbox {m}$ rectangular box. The top figure each time represents a vertical x–z cross-section, while the bottom figures represent a horizontal x–y plane at a height of ${100}\,\hbox {m}$

Finally, we note that the size of the reference grid 0 is limited by current computational feasibility, and not all physical scales up to the Kolmogorov scale of turbulence are resolved. Thus, for a meaningful error analysis, only flow properties that are sufficiently larger than the simulation grid should be considered. Here, we mainly focus on the prediction of turbulent velocities averaged over areas (and heights) that correspond to the size of modern large turbines (see properties of interest defined in Sect. 3.3 below). As shown in earlier LES studies, the fine resolution is sufficient to properly resolve these scales (Meyers and Meneveau 2013), so that any residual errors between the fine reference and at a theoretical continuous solution are small. However, if one were to consider physical properties at much smaller scales, or much closer to the wall, a different approach or a finer reference mesh would be required for proper error analysis.

2.3 Benchmarking

All simulations are performed on the ThinKing supercomputer of KU Leuven. Simulations are repeated with two, four, eight and 16 nodes, except for the reference grid, which is not simulated on two nodes due to a shortage of random-access memory for this mesh size.¹ The ratio of wall-clock time to simulated time ($t_{\mathrm {wall}}/t_{\mathrm {sim}}$) is shown in Fig. 2. To compare the parallel efficiency of the different computational set-ups, Table 3 shows the billing time ($t_{\mathrm {bill}}$) per grid point per timestep, where the billing time is defined as $t_{\mathrm {bill}}=N_{\mathrm {nodes}}t_{\mathrm {wall}}$.

Fig. 2

Ratio of wall-clock time ($t_{\mathrm {wall}}$) and simulated time ($t_{\mathrm {sim}}$) for the different grids. Simulations are repeated with 1 ( ), 2 ( ), 4 ( ), 8 ( ) and 16 nodes ( ). The vertical black dashed line corresponds to $t_{\mathrm {wall}}=t_{\mathrm {sim}}$

Results in Fig. 2 show the rapid decrease of wall time with grid coarsening. The finest grid is more than a factor 10 slower than wall time, while the coarsest grid is almost 100 times faster. Moreover, good strong scaling is observed, except for the coarsest grid, where a saturation in speed-up is seen with increasing amount of nodes due to communication overhead becoming the bottle neck. Overall, simulations on the coarsest two grid levels may be sufficiently fast for real-time use, but much will depend on their overall accuracy. This is further discussed in next sections.

It is emphasized that despite these simulations being performed on a state-of-the-art computing system and simulation platform, additional speed-up may further be possible, by e.g., graphic processor unit based computation (see, e.g. Fuhrer et al. 2018; Lapillonne et al. 2017), or single precision computation (Váňa et al. 2017). This is, however, not the focus here but, if successful, would only benefit the methodology and strengthen conclusions.

Table 3 Summary of the billing time per grid point and timestep in microseconds

3 Error Definitions and Decomposition

3.1 Restriction and Interpolation Operations

Since we are using and comparing LES at different resolutions, it is important to define proper intergrid transfer operations, so that errors between different simulations can be properly defined.

We consider a sequence of grids with spacing $\varvec{\varDelta }^i= \left[ \varDelta ^i_x, \varDelta ^i_y, \varDelta ^i_z\right]$, with the finest grid having index $i=0$, and where $\varvec{\varDelta }^i=f\left( i,\varvec{\varDelta }^0\right)$, where f is a monotonically increasing function of i. Herein, we simply use $\varvec{\varDelta }^i=\varvec{\varDelta }^02^i$. Solutions on grid i are denoted using $\varvec{u}^{i} = [u_1^i,u_2^i,u_3^i]$. In practice, SP-Wind uses a pseudo-spectral method in horizontal directions, with collocation points that are uniformly distributed in real space on a Cartesian mesh. Thus, $x^i_{k}=k\varDelta _x^i \quad \forall k \in 0\dots N^i_x-1$, $y^i_{l}=l\varDelta _1^i \quad \forall l \in 0\dots N^i_y-1$. In the z-direction a fourth-order finite-volume discretization is used on a staggered mesh. Velocity components $u_1^i,u_2^i$, and pressure p are defined at locations $z^i_{m+1/2}=(m+1/2)\varDelta _z^i\quad \forall m \in 0\dots N^i_z-1$, while $u_3^i$ is defined at $z^i_{m}=m\varDelta _z^i\quad \forall m \in 1\dots N^i_z-1$.

Given a coarse grid j and a fine grid i ($i<j$), we now introduce interpolation and restriction operations such that

$$\begin{aligned} \varvec{u}^{i}&= {\mathcal {I}}_{j}^{i} \varvec{u}^{j}, \end{aligned}$$

(5)

$$\begin{aligned} \varvec{u}^{j}&= {\mathcal {R}}_{i}^{j} \varvec{u}^{i}. \end{aligned}$$

(6)

Both ${\mathcal {I}}_{j}^{i}$, and ${\mathcal {R}}_{i}^{j}$ are linear operators (matrices). In practice, we implement them using subsequent interpolations and restrictions in the x, y, and z directions, so that ${\mathcal {I}}_{j}^{i} = I_{j,z}^iI_{j,y}^iI_{j,x}^i$, and ${\mathcal {R}}_{i}^{j}=R_{i,z}^jR_{i,y}^jR_{i,x}^j$. In horizontal directions (x and y), we employ spectral interpolation and spectral projection respectively for interpolation and restriction. In the z direction we employ fourth-order interpolation and box filtering; see Appendix A for details.

Finally, we note that for the error analysis, we use grid 0 as a reference, so that in practice, we only need the operators ${\mathcal {I}}_{j}^{0}$ and ${\mathcal {R}}_{0}^{j}$. We further note that the current selection of grid levels yields straightforward and convenient interpolation and restriction operators. However, also if the reference grid is not so well structured (e.g. with data coming from experiments) or if the reference is given by a continuous function, similar operators can be defined.

3.2 Full-Field Error Definition and Decomposition

In order to define errors, we always interpolate properties back to the reference grid 0. Thus, the field error $\varvec{\epsilon }^i_{\text {tot}}$ of a grid i with respect to the reference is introduced as

$$\begin{aligned} \varvec{\epsilon }^i_{\text {tot}}&\triangleq {\mathcal {I}}_{i}^{0}\varvec{u}^{i} - \varvec{u}^{0}\nonumber \\&=\underbrace{{\mathcal {I}}_{i}^{0}\left( \varvec{u}^{i} - {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) }_{\varvec{\epsilon }^i_{\text {model}}} + \underbrace{{\mathcal {I}}_{i}^{0}{\mathcal {R}}_{0}^{i}\varvec{u}^{0} - \varvec{u}^{0}}_{\varvec{\epsilon }^i_{\text {restr}}}, \end{aligned}$$

(7)

where we further split the error into a part due to model mismatch $\varvec{\epsilon }^i_{model}$, and a part due to the restriction on a coarse grid $\varvec{\epsilon }^i_{restr}$. As observed in Eq. 7, the restriction error is not related to the simulation error on the coarse grid, but only relates to the potential inability to represent the fine details of the reference solution on the coarse grid.

The evolution of the modelling error can be further derived from the Navier–Stokes equations, and we find

$$\begin{aligned} \frac{\partial \varvec{\epsilon }^i_{model}}{\partial t}&= {\mathcal {I}}_{i}^{0}\left( \frac{\partial \varvec{u}^{i}}{\partial t} - {\mathcal {R}}_{0}^{i}\frac{\partial \varvec{u}^{0}}{\partial t}\right) \nonumber \\&={\mathcal {I}}_{i}^{0}\left( \varvec{f}^{i}\left( \varvec{u}^{i}\right) - {\mathcal {R}}_{0}^{i} \varvec{f}^{0}\left( \varvec{u}^{0}\right) \right) \nonumber \\&=\underbrace{{\mathcal {I}}_{i}^{0}\left( \varvec{f}^{i}\left( \varvec{u}^{i}\right) - \varvec{f}^{i}\left( {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) \right) }_{S^i_{\mathrm {div}}} + \underbrace{{\mathcal {I}}_{i}^{0}\left( \varvec{f}^{i}\left( {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) - {\mathcal {R}}_{0}^{i} \varvec{f}^{0}\left( \varvec{u}^{0}\right) \right) }_{S^i_{\mathrm {sgs}}}, \end{aligned}$$

(8)

where $\varvec{f}^{i}\left( \varvec{u}^{i}\right)$ represents the spatial terms in Eqs. 1 and 2, discretized on grid i, and evaluated using $\varvec{u}^{i}$. We find that the evolution of the modelling error is forced by two source terms, which are further discussed below.

The second source term $S^i_\mathrm {sgs}$ can be elaborated by using Eq. 1, leading to

$$\begin{aligned} S^i_{\mathrm {sgs}}&={\mathcal {I}}_{i}^{0}\nabla \cdot \left( \underbrace{\left( {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) \left( {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) -{\mathcal {R}}_{0}^{i}\left( \varvec{u}^{0}\varvec{u}^{0}\right) }_{\varvec{L}} + \underbrace{{\mathcal {R}}_{0}^{i}\varvec{\tau }^0\left( \varvec{u}^{0}\right) }_{\varvec{\tau }}-\underbrace{\varvec{\tau }^i\left( {\mathcal {R}}_{0}^{i}\varvec{u}^{0}\right) }_{\varvec{T}}\right) , \end{aligned}$$

(9)

which corresponds to a discrete variant of Germano’s identity (Germano 1992), where $\varvec{L}$ are the Leonard stresses, and $\varvec{\tau }$, $\varvec{T}$ the SGS stresses on respectively the reference and the coarser grids. Thus, this source term corresponds to the SGS-modelling error. Note that this source term does not depend on $\varvec{u}^{i}$, but only on the inability of the coarse grid to correctly represent the dynamics when evaluated using the reference solution.

The first source term $S^i_{\mathrm {div}}$ represents the divergence of the solutions $\varvec{u}^{i}$ and ${\mathcal {R}}_{0}^{i}\varvec{u}^{0}$. It is well known that nearby solutions diverge due to the chaotic behaviour of turbulence (even if the SGS-modelling error were zero). Initially, at time $t=0$, the source $S^i_{\mathrm {div}}(\varvec{x},0)=0$ as a result of the particular ‘exact’ coarse-grid initialization that we use ($\varvec{u}^{i}(\varvec{x},0)={\mathcal {R}}_{0}^{i}\varvec{u}^{0}(\varvec{x},0)$), so that $S^i_\mathrm {sgs}$ is dominant. However, as we will further show below, $S^i_{\mathrm {div}}$ becomes dominant very fast.

To get additional insight in the different terms, they are also discussed for a standard identical-twin simulation with a perturbation [see e.g. Mukherjee et al. (2016)], as often used to study divergence of trajectories in chaotic systems. Since, identical twin simulations are performed on an identical grid, the restriction error $\epsilon ^0_{\text {restr}}=0$, because ${\mathcal {R}}_0^0$, and ${\mathcal {I}}_0^0$ are both identity matrices, such that the only term contributing will be the modelling error $\epsilon ^0_{\text {model}}$. Further analyzing the source terms of the modelling error ${\mathcal {S}}^0_{\text {div}}$ and ${\mathcal {S}}^0_{\text {SGS}}$, it is trivially found that the latter is zero, such that only the term ${\mathcal {S}}^0_{\text {div}}$ determines the error growth. This term is very close to zero initially due to the small initial perturbation, but then, as is well known, causes an exponential growth of errors, characterized by the leading Lyapunov exponent of the system. Simulation experiments in the present work differ from a classical identical-twin set-up, as they include non-zero SGS error-source terms, as well as non-zero restriction errors.

3.3 Wind-Turbine Error Definitions

We look at the field errors $\varvec{\epsilon }^i_{\text {tot}}$, and in particular into the evolution of their norm $\Vert \varvec{\epsilon }^i_{\text {tot}}\Vert$ as a function of time. However, from a practical perspective, these errors are usually not very relevant, and errors on derived properties (that depend on the application) are more useful. Therefore, we also investigate errors that are relevant in a wind-energy context.

To this end, we consider virtual wind turbines in the lower part of our simulation domain, and investigate prediction errors on the turbine wind speed. The turbine wind speed on grid i is determined using

$$\begin{aligned} u^{i}_{\mathrm {wt}}(t) = {\mathcal {G}}({\varvec{x}}_{\mathrm {wt}}) \circ {\mathcal {I}}_{i}^{0}u^i_1({\varvec{x}},t), \end{aligned}$$

(10)

where ${\mathcal {G}}$ is a spatial filter centered around the turbine-hub location ${\varvec{x}}_{\mathrm {wt}}$ and $u^i_1({\varvec{x}},t)$ is the streamwise velocity component. We use a simple box filter of size D, so that $u^{i}_{wt}$ represents an appropriate spatially averaged velocity in the mean flow direction (values of $D={100}\,\hbox {m}$, as well as a hub height of ${100}\,\hbox {m}$ are employed).

We also define a time-filtered turbine wind speed over a time interval $\tau$ as

$$\begin{aligned} {\overline{u}}^{i}_{\mathrm {wt},\tau }(t) = \frac{1}{\tau } \int _{t-\tau }^{t} u^{i}_{\mathrm {wt}}\left( t'\right) \ \mathrm {d}t'. \end{aligned}$$

(11)

Such a time-averaged turbine wind speed is relevant for many application areas, e.g., for the power-grid, energy and ancillary service markets typically operate among others using 1-$\hbox {min}$, 5-$\hbox {min}$ or 15-$\hbox {min}$ averages (see e.g., Rebours et al. 2007; Wang et al. 2015; Brijs 2017).

In order to speed-up the convergence of error statistics, we sample turbine wind speeds at every horizontal grid collocation point, for a total of $N_x^iN_y^i$ different positions. We assemble these different measurements in the vector ${{\overline{{\varvec{u}}}}}^{i}_{\mathrm {wt},\tau }(t)$, and define the prediction error

$$\begin{aligned} \epsilon ^i_{\mathrm {wt},\tau }(t) = \left( \mathrm {E}\left[ \left( {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }(t) - {\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }(t) \right) ^2\right] \right) ^{1/2}, \end{aligned}$$

(12)

with $\mathrm {E}[\cdot ]$ the expected value or sample mean.

A useful reference for LES predictions is the use of the time-averaged turbine wind speed. This type of prediction does not take into account short-term turbulent fluctuations, but simply uses the expected mean (given constant meteorological conditions). Denoting the mean turbine wind speed obtained from the finest grid with $U^0_{\mathrm {wt}}$ (formally, $U^0_{\mathrm {wt}}={\overline{u}}^0_{\mathrm {wt},\infty }$), we can define the error that results from using the mean flow as a prediction, as

$$\begin{aligned} \epsilon ^0_{U,\tau }(t) = \left( \mathrm {E}\left[ \left( {\overline{{\varvec{u}}}}^0_{\mathrm {wt},\infty }(t) - {\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }(t)\right) ^2 \right] \right) ^{1/2}. \end{aligned}$$

(13)

Using this, we further introduce a scaled norm $\varepsilon ^i_{\mathrm {wt},\tau } = \epsilon ^i_{\mathrm {wt},\tau } / \epsilon ^0_{U,\tau }$. Thus, if $\varepsilon ^i_{\mathrm {wt},\tau } > 1$, it is more appropriate to use a simple prediction of the mean flow instead of trying to predict turbulent-flow effects with a more complex LES model.

The error $\epsilon ^i_{\mathrm {wt},\tau }$ can be further decomposed, viz.

$$\begin{aligned} \left( \epsilon ^i_{\mathrm {wt},\tau }\right) ^2&=\mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }-{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] + \mathrm {Bias}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] ^2\nonumber \\&=\mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }\right] + \mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] -2 \mathrm {Cov}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] \nonumber \\&\quad + \mathrm {Bias}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] ^2, \end{aligned}$$

(14)

and where $\mathrm {Bias}[{\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }]= \mathrm {E}[{\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }] - \mathrm {E}[{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }]$. For the error of a prediction based on the mean flow, we simply have $(\epsilon ^0_{U,\tau })^2 = \mathrm {Var}[{\overline{u}}_{\mathrm {wt},\tau }^{0}]$, leading to an expression for the scaled norm $\varepsilon ^i_{\mathrm {wt},\tau }$

$$\begin{aligned} \left( \varepsilon ^i_{\mathrm {wt},\tau }\right) ^2&= \frac{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }-{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] }{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}\right] } + \frac{\mathrm {Bias}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] ^2}{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}\right] }. \end{aligned}$$

(15)

For our idealized set-up, the bias is close to zero (see also Appendix B), such that the expression simplifies to $\left( \varepsilon ^i_{\mathrm {wt},\tau }\right) ^2\approx \mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }-{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] /\mathrm {Var}\left[ {\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}\right]$, the ratio of the prediction error variance to the background variance.

For long prediction time horizons, the LES prediction becomes totally decorrelated from the reference solution because of chaotic divergence of trajectories and accumulation of modelling errors, simplifying to

$$\begin{aligned} \lim _{t\rightarrow \infty } \left( \varepsilon ^i_{\mathrm {wt},\tau }\right) ^2&= 1 + \frac{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }\right] }{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}\right] } + \frac{\mathrm {Bias}\left[ {\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau },{\overline{{\varvec{u}}}}^{0}_{\mathrm {wt},\tau }\right] ^2}{\mathrm {Var}\left[ {\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}\right] }. \end{aligned}$$

The variance of the turbine wind speed is approximately equal for the different grids $\mathrm {Var}[{\overline{{\varvec{u}}}}^{i}_{\mathrm {wt},\tau }]= \mathrm {Var}[{\overline{{\varvec{u}}}}_{\mathrm {wt},\tau }^{0}]$, so that for long prediction time horizons $\varepsilon ^i_{\mathrm {wt},\tau }\approx \sqrt{2}$. Thus overall, LES predictions are expected to improve on a simple mean-flow estimate only when time horizons are not too long for the covariance between the LES prediction and the real turbulent-flow realization to have disappeared. This is further discussed in Sect. 3.3.

4 Results

As discussed in Sect. 1.1, we only evaluate part of the modelling chain, i.e. we omit all errors related to state estimation based on measurements, and presume that our coarse-grid simulations start with an exact initial condition. We further note that the type of error analysis that is performed here is quite different from classical validation or verification of LES, in which the focus is on comparing time-averaged mean fields such as velocity and Reynolds stresses in a statistical sense. This type of error analysis is performed by averaging simulation results over much longer time horizons than considered here, during which instantaneous velocity fields are usually fully decorrelated. For completeness, we have added a comparison of time-averaged results for the different grid levels in Appendix B.

4.1 Evolution of Full-Field Errors

We first look at full field errors, and in particular focus on the evolution of the error $\epsilon _1^i$ of the streamwise velocity field. To this end, we introduce a scaled norm of $\epsilon _1^i$ as follows

$$\begin{aligned} \varepsilon ^i(t) = \frac{\Vert \epsilon _1^i(\varvec{x},t) \Vert }{\Vert u_1^0(\varvec{x},t) \Vert }, \end{aligned}$$

(16)

representing the classical two-norm of the error (over the full field) normalized by the two-norm of the velocity field, yielding a measure for the overall relative error. The evolution of relative error $\varepsilon ^i(t)$ is shown in Fig. 3 for the different grids (1 to 3). From top to bottom, the figure shows the restriction $\varepsilon _{\mathrm {restr}}$, modelling $\varepsilon _{\mathrm {model}}$, and total error $\varepsilon _{\mathrm {tot}}$; left and right, results are plotted in logarithmic and linear scaling respectively.

Fig. 3

Evolution of model, restriction, and total error as a function of time on different simulation grids. (Left) logarithmic scaling; (right) linear scaling. The symbols ( ), ( ), ( ) respectively represent grid levels 1 to 3. The horizontal black lines represent the error of a prediction using the time-averaged flow profile

We first look at the restriction error in Fig. 3a, b, while appreciating that this error is nearly constant in time, and is largest for the coarsest grid. The former is related to the fact that the fine-grid solution is in statistical equilibrium, so that the distribution of energy over different scales does not change over time. In terms of size, we observe that the full-field restriction error remains below 6%. This is an acceptable level that will, however, much depend on the selected quantity of interest. As long as it is related to large scales in the flow (such as the velocity field or derived properties such as wind-turbine power extraction), we expect that restriction will not remove a lot of the essential information. Other properties, such as vorticity or velocity fluctuations very close to the ground, are not well predicted by LES, and typically have large restriction errors (since these are essentially small-scale properties with dominant length scale around the Kolmogorov scale or the roughness length respectively).

Looking at the model error in Fig. 3c, d, we observe features that are quite different, and it is unexpected to see that the model error is lowest for the coarsest grid. This is related to two aspects: first of all, on the coarser grid less scales are represented, so that the initial SGS error is smaller (see also Fig. 4, and further discussion below). Second, chaotic divergence of turbulence is a process that starts at the small scales with an inverse cascade, increasing rapidly into the large scales over time (Lorenz 1969). Thus effects of chaos are felt earlier on finer grids, in which smaller scales are present. Further looking at the modelling error in Fig. 3, three zones are observed, in which the error grows proportional to t, $t^{1/2}$, and saturates to a constant value, respectively. The last zone is best understood, and is simply related to the fact that the LES prediction is fully decorrelated from the reference, so that the square of the error roughly saturates at twice the variance of the signal (cf. discussion in Sect. 3.3).

The first zone ($\sim t$) is explained by looking at the source terms $S^i_{\mathrm {sgs}}$ and $S^i_{\mathrm {div}}$ in Fig. 4. By definition, at $t=0$, $S^i_{\mathrm {div}}(\varvec{x},0)=0$, so that the evolution of $\varvec{\epsilon }_{\mathrm {model}}$ is dominated by $S^i_{\mathrm {sgs}}$. We further observe that $\Vert S^i_{\mathrm {sgs}}\Vert$ is roughly constant, which is explained by the fact that the turbulent boundary layer is in statistical equilibrium. Thus, for t small, we find

$$\begin{aligned} \frac{\partial \varvec{\epsilon }^i_{\mathrm {model}}}{\partial t}&\approx S^i_{\mathrm {sgs}}, \end{aligned}$$

(17)

$$\begin{aligned} \frac{1}{2}\frac{\partial \Vert \varvec{\epsilon }^i_{\mathrm {model}}\Vert ^2}{\partial t}&\approx \left( \varvec{\epsilon }^i_{\mathrm {model}},S^i_{\mathrm {sgs}}\right) ,\nonumber \\&= \int _0^t \left( S^i_{\mathrm {sgs}}\left( \varvec{x},t'\right) ,S^i_{\mathrm {sgs}}(\varvec{x},t)\right) \ \mathrm{d}t', \end{aligned}$$

(18)

with $(\cdot ,\cdot )$ the classical Euclidean inner product between vector fields. As long as the time t remains small, $S^i_{\mathrm {sgs}}(\varvec{x},t')$ and $S^i_{\mathrm {sgs}}(\varvec{x},t)$ remain correlated, so that $\left( S^i_{\mathrm {sgs}}(\varvec{x},t'),S^i_{\mathrm {sgs}}(\varvec{x},t)\right) \approx \Vert S^i_{\mathrm {sgs}}\Vert ^2 \approx \text{ C }$, where C is a constant. Combining all this into Eq. 18 leads to $\Vert \varvec{\epsilon }^i_{\mathrm {model}}\Vert \sim t$, a behaviour that is different from the standard chaotic exponentional growth. This is attributed to the source term $S^i_{\mathrm {sgs}}$, which initially dominates the error growth in contrast to a standard perturbation experiment (Mukherjee et al. 2016) where this term is absent, and the growth is determined by $S^i_{\mathrm {div}}$.

Fig. 4

The evolution of the source terms ${\mathcal {S}}^i_{\mathrm {sgs}}$ ( ) and ${\mathcal {S}}^i_{\mathrm {div}}$ ( ) and $\partial \varepsilon ^i_{\mathrm {model}}/\partial t$ ( ) as a function of time. The lines ( ), ( ), ( ) respectively represent the grid levels 1 to 3

A similar scaled norm is introduced for the source terms as for the errors in Eq. 16, i.e.,

$$\begin{aligned} {\mathcal {S}}^i(t) = \frac{\Vert S_1^i(\varvec{x},t) \Vert }{\Vert f_1^0(\varvec{x},t) \Vert }. \end{aligned}$$

(19)

Further looking at the evolution of the source terms in Fig. 4, it is observed that after an initial transient, the total source is dominated by $S^i_{\mathrm {div}}$. At this point the second zone in the error growth in Fig. 3 starts ($\sim t^{1/2}$). This zone is well understood, and relates to the rate of chaotic divergence of turbulent flows. Although chaotic trajectories initially diverge exponentially in the linear regime, this changes when non-linear effects play a role. In the non-linear regime, the 1 / 2 scaling simply results from the inverse cascade, given a classical Kolmogorov inertial range [see Aurell et al. (1997) for details].

Fig. 5

The evolution of the SGS error source ${\mathcal {S}}^i_{\mathrm {sgs}}$ as a function of grid level i, where $\varDelta ^i/\varDelta ^0=2^i$. Symbols ( ), ( ) and ( ) respectively represent the case with no restriction in vertical direction, restriction based on a Gaussian filter, and based on a box filter

As mentioned above, the SGS-error source ${\mathcal {S}}_{\mathrm {sgs}}$ in Fig. 4 is roughly constant in time. However, it is unexpected to see that the SGS-error source is larger for finer grids than for coarser grids. This error-source level initially forces the LES and reference trajectories apart, and this may be a second explanation for faster chaotic divergence of predictions on finer meshes. However, from a grid-refinement perspective, fine grids are expected to yield lower SGS errors. To further investigate this, we evaluated the SGS-error source for a series of grids that are much more gradually refined between level 3 and level 0 (instead of just using factors of two). Results are presented in Fig. 5. In horizontal directions, for which we use a restriction operator in spectral space, it is straightforward to gradually coarsen the grid with non-integer ratios. However, in the vertical direction, the box-filter formulation that we use only works for coarsening with a factor of two. Therefore, we present two results in Fig. 5, one without any restriction in the vertical direction, and one where we restrict in the vertical direction with the use of a Gaussian filter. The results in Fig. 5 indicate that the SGS-error source does approach zero when the grid approaches the reference grid. However, the source increases very rapidly when the grid is coarsened, and reaches a maximum around a grid coarsening with a factor $n\approx 1.5$ for the current case. At higher coarsening factors, the source starts to decrease again, explaining the unexpected trends observed above in Fig. 4.

Finally, looking at the total error in Fig. 3e, f, it is observed that overall, coarser grids lead to larger errors than finer grids. This is a result of the restriction errors, that are largest for the coarsest grids. However, this is partly offset by the unexpected behaviour of modelling errors discussed above, and the effect of SGS errors and chaotic divergence of trajectories. As a result, error levels remain remarkably close overall, indicating that coarse-grid LES may be very well suited for forecasting of turbulent boundary layers. In Fig. 3e, f, we also added the error that would result from a prediction that simply uses the time-averaged velocity profile (i.e. a logarithmic wind speed profile). Obviously, a LES prediction only makes sense if it outperforms this prediction. For longer time horizons, this is no longer the case. At this point, the LES error saturates and the coarse-grid prediction is fully decorrelated from the reference. In fact over long times, turbulence behaves as a random process, such that the best possible prediction simply corresponds to the expected value, i.e. the time-averaged profile.

Fig. 6

Comparison of turbine wind speed on grid level 2, ${\overline{u}}^{2}_{\mathrm {wt},\tau }$ ( ), and reference grid, ${\overline{u}}^{0}_{\mathrm {wt},\tau }$ ( ), normalized with the mean turbine wind speed on the reference grid ${\overline{u}}^{0}_{\mathrm {wt},\infty }$ for different time filters. Top to bottom the unfiltered signal, time-averaging windows $\tau$ of 1 min, 5 min, 15 min and 30 min respectively. The grey coloured lines are the results using a Taylor frozen turbulence model, which almost collapse for the different grids

Fig. 7

Comparison of the turbine wind-speed error $\varepsilon ^i_{\mathrm {wt},\tau }$ as a function of time for different time filter widths and grid levels. The unfiltered, 5 min and 30 min averaged signals are respectively represented by ( ), ( ) and ( ). The line styles ( ), ( ), ( ) respectively represent the grid levels 1 to 3. The grey coloured lines are the results from a Taylor frozen-turbulence model, which almost collapse for the different grids

4.2 Turbine Hub-Height Wind-Speed Predictions

We now turn towards the error prediction of more practically oriented quantities of interest, and focus on wind-energy applications. We consider predictions of average incoming turbine wind speed using definitions introduced in Sect. 3.3. Moreover, since energy markets usually use local time-averaged signals (e.g., using 1-min, 5-min, 15-min, or 1-h averages, depending on the market), we also consider the prediction of time-filtered signals with different averaging windows.

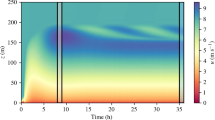
In order to give an impression of the effect of time filtering, Fig. 6 shows a comparison of the time-filtered turbine wind speed on the reference grid and grid number 2 for the unfiltered signal, and for filter windows of respectively ${1}\,\hbox {min}$, ${5}\,\hbox {min}$, ${15}\,\hbox {min}$ and ${30}\,\hbox {min}$. It is appreciated that the variance of the signal reduces significantly for longer time filters, thus also reducing the errors on the predictions. However, at the same time, also a prediction with the mean value of the turbine wind speed (i.e. the expected value) will improve, and thus it is important to properly scale errors. Therefore, the scaling introduced in Sect. 3.3 is used.

In Fig. 7 the evolution of the turbine wind-speed error as a function of time is shown for the different grid levels, for the unfiltered signal, and for 5-min and 5-min filtered signals. It is clearly seen that the longer time filters give better results, and is explained by the fact that small scales have shorter turnover times and therefore tend to chaotically diverge more rapidly. Further, the total error increases with increased grid coarsening. The dependency, however, is not very strong, similar to observations above.

Further looking at Fig. 7, we see that 5-min and 30-min averaged LES predictions significantly outperform the mean-flow estimate for time horizons up to 2000 and ${4000}\,\hbox {s}$ respectively. For the instantaneous field prediction, only time horizons below ${1000}\,\hbox {s}$ appear to work. Thus depending on the case and the application requirements (e.g. short-term control versus market predictions), quite different results can be found with respect to what prediction horizons are feasible.

Additionally the results are compared to a simple Taylor frozen-turbulence model, where the flow field is advected downstream with the mean hub-height velocity $U^i(z_h)$ (see e.g. Schlipf et al. 2010, 2013). It is found that the Taylor frozen-turbulence model results are almost completely independent of the grid, except for some small differences in the unfiltered signals. Overall, it is observed that coarse-grid LES significantly outperforms the Taylor frozen-turbulence model.

Finally, we emphasize that the numerical values discussed here very much depend on the selected simulation case. As discussed in Sect. 2.2, results can be rescaled based on friction velocity and boundary-layer height. For instance, rescaling the friction velocity to ${0.25}\,\hbox {m}\,\mathrm{s}^{-1}$, would double all time scales. In general, the time scales are inversely proportional to the velocity scale, and overall, conclusions will depend on atmospheric conditions. Nevertheless, the current case set-up corresponds to realistic atmospheric conditions, and clearly shows that course-grid LES can be sufficiently accurate to be considered for real-time forecasting.

Fig. 8

The error $\varepsilon ^i_{\mathrm {wt},\tau }$ as a function of the ratio of wall time and simulated time $t_{\mathrm {wall}}/t_{\mathrm {sim}}$, for the different computational grids. Figures a–d respectively represent the unfiltered signal and filter lengths 1 min, 5 min and 30 min. The different colours represent different prediction horizons [0 min ( ), 5 min ( ), 15 min ( ), 30 min ( ) and 60 min ( )]. The horizontal and vertical line respectively represent the normalized mean flow prediction error and $t_{\mathrm {wall}}=t_{\mathrm {sim}}$

4.3 Accuracy Versus Speed-Up

In Fig. 8 accuracy versus speed-up is assessed for the current simulation set-up based on the prediction of turbine wind speeds. All speed-ups are calculated using the 16-node benchmark, which is shown in Fig. 2. Figure 8 contains four parts a–d that respectively represent results for the prediction of instantaneous turbine wind speed, and 5-min, 15-min, and 30-min averaged wind speeds. Moreover, in the different subplots, results are presented for different prediction horizons. Overall, we see that errors do not increase rapidly with grid coarsening (as discussed above), so that meaningful predictions may be possible with simulation times that are more than 200 times faster than real time. The level of the errors is highly dependent on the specific prediction horizon and the time-average window width, but as seen in the figure, various combinations exist for which the coarse-grid LES is more than twice as accurate than an estimation based on the mean flow (thus effectively reducing the variance of the prediction error by a factor of four compared to simply considering turbulence as a random process and using the expected value as predictor).

Finally, we recall that the current results are obtained for an idealized set-up that excludes additional errors arising from experiments, state estimation, and possible model bias if LES were to be integrated in a real prediction chain. We note that different stability regimes have also to be tested; the convective and neutral regimes are expected to perform in line with our case study, the stable regime is known to have turbulent structures that are much finer grained (see, e.g., van Stratum and Stevens 2015; de Roode et al. 2017), such that with coarse resolutions the resolved part of the turbulent fluctuations is significantly smaller compared to the other regimes. This is known to give rise to problems sustaining resolved turbulence (Beare et al. 2006). In this case predictions with a simple logarithmic profile may be better suited, or, for sufficiently small time horizons, the Taylor frozen-turbulence model could be considered. These are topics for further research. Nevertheless, the current results give a first clear indication that coarse-grid LES may be sufficiently rapid and reliable to consider its integration for short-term forecasting of turbulence in the ABL in future studies.

5 Conclusions

We performed a first feasibility study on the use of LES as a real-time prediction tool for atmospheric boundary-layer turbulence. The focus was on the growth of prediction errors for a coarse-grid LES due to SGS modelling errors and chaotic divergence of trajectories, and the resulting trade-off between accuracy and computational cost. To this end, we set up an idealized testing environment consisting of a fine reference LES, and a series of coarsened simulations, in which we omit errors caused by state estimation based on observations or simulation bias. The reference grid contains $128\,\times 10^6$ grid points, with a wall time that is approximately ten times shorter than the simulated time when executed on 16 nodes of our supercomputing system. A series of coarser grids is constructed by repeatedly coarsening with a factor of 2 in each direction. The coarsest grid contains only $2.5\,\times 10^5$ grid cells, and results in a simulation wall time that is approximately 250 times smaller than the simulated time.

Errors are split into restriction and modelling errors. Moreover, with respect to the modelling errors, two different source terms are identified, related to the subgrid model error and the chaotic divergence of trajectories. Restriction errors are largest on the coarsest meshes, but this is partly compensated by modelling errors that are decreasing with mesh coarsening. This is quite unexpected, and explained by the fact that instantaneous SGS errors behave strongly non-linearly as a function of resolution, initially increasing with grid coarsening, but later again decreasing. A second reason is the chaotic divergence of solution trajectories, which is stronger when smaller scales are present in the solution. Overall errors increase relatively slowly when coarsening the mesh. While wall time decreases by a factor of 2000 for the coarsest mesh (compared to the finest), errors increase only slowly with factors that remain mostly below 2. This picture is very interesting when considering coarse-grid LES for short-term turbulent-flow prediction in the atmospheric boundary layer.

We further elaborated a case that relates to the prediction of turbine hub-height wind speeds for wind-energy applications, and looked into the prediction of instantaneous, 5-min, 15-min and 30-min averages for different prediction horizons (up to ${4000}\,\hbox {s}$). Overall we find that errors are lowest for long time averages and low prediction horizons, but there is a significant number of combinations for which the variance of the prediction error is more than four times smaller than the variance of the turbine wind speed. This suggests that the use of coarse-grid LES for short-term turbulent-flow predictions in real time may well be feasible. Future work will focus on further investigating aspects of state estimation, observation errors, and modelling bias, as well as the effect of different stability regimes. Next to this, the choice of the specific aspect ratio of the grid cells $\varDelta ^i_y/\varDelta ^i_x$, $\varDelta ^i_z/\varDelta ^i_x$ is currently chosen following typical ABL simulation studies. Optimizing these ratios might significantly improve results.

Appendices

A Restriction and Interpolation

We provide further details on the interpolation and restriction operators introduced in Sect. 3.1. First of all, formally, we define $\varvec{u}^{i} = [u_1^i,u_2^i,u_3^i] \in {\mathbb {R}}^{N^i}$, with $N^i = 3N_x^iN_y^iN_z^i-N_x^iN_y^i$ (cf. staggered arrangement of variables discussed in Sect. 3.1). Similarly, $\varvec{u}^{j}\in {\mathbb {R}}^{N^j}$, further using the convention that $i<j$ (so that j is the coarser grid). Consequently, for the interpolation and restriction operators in Eqs. 5 and 6, we have ${\mathcal {I}}_{j}^{i} \in {\mathbb {R}}^{N^i\times N^j}$, and ${\mathcal {R}}_{i}^{j} \in {\mathbb {R}}^{N^j\times N^i}$.

Since we use a Cartesian mesh, we split the interpolation and restriction operators in three consecutive one-dimensional operators, so that ${\mathcal {I}}_{j}^{i} = I_{j,z}^i I_{j,y}^i I_{j,x}^i$, and ${\mathcal {R}}_{i}^{j}=R_{i,z}^j R_{i,y}^j R_{i,x}^j$. The matrix $I_{j,z}^i$ has dimensions $N^i \times N^{iij}$ with $N^{iij}= 3N_x^i N_y^i N_z^j - N_x^i N_y^i$. The dimensions of $I_{j,y}^i$ are $N^{iij} \times N^{ijj}$, with $N^{ijj}= 3N_x^i N_y^j N_z^j - N_x^i N_y^j$, and the dimensions of $I_{j,x}^i$ correspond to $N^{ijj} \times N^j$. Similar dimensions follow straightforwardly for $R_{i,x}^j$, $R_{i,y}^j$, and $R_{i,z}^j$.

The rows of $I_{j,x}^i$, $I_{j,y}^i$, $I_{j,z}^i$ contain one-dimensional interpolation stencils (and similar for the restriction matrices). Therefore, below, we provide the stencils that we use based on a simple scalar function $\phi ^i$ and $\phi ^j$ along one-dimensional grids ${\varvec{r}}^i$ and ${\varvec{r}}^j$. The allocation of the different coefficients in these stencils to elements in the different rows of $I_{j,x}^i$, $I_{j,y}^i$, etc., is straightforward, and not further detailed for sake of brevity.

For the interpolation in the x- and y-directions, spectral interpolation is used, simply leading to

$$\begin{aligned} \phi ^i_k = \frac{1}{N^j}\sum _{m=0}^{N^j-1}\sum _{l=0}^{N^j-1}\mathrm {exp}\left( {-2\uppi {\mathrm{i}} m\frac{r^i_l-r^j_k}{L}}\right) \phi _l^j. \end{aligned}$$

(20)

where $\phi ^i_k$ and $\phi _l^j$ correspond to fine- and coarse-grid values on locations $r^i_k$ and $r^j_l$ respectively. In practice, we do not implement the interpolation in real space, but instead perform the operation in Fourier space.

For the interpolation in the z-direction, we use a polynomial interpolation of order p, where we take $p=4$, in analogy with our vertical discretization scheme. First to simplify notation, we define the operator $min_c(a,{\varvec{b}})$, which returns a set of the $c\in {\mathbb {N}}$ closest points in set ${\varvec{b}}\in {\mathbb {R}}^N$ to a scalar $a\in {\mathbb {R}}$. This simply gives for the interpolation operator

$$\begin{aligned} \phi ^i_k = \sum _{l\in {\mathcal {P}}}\left( \prod _{\begin{array}{c} m\in {\mathcal {P}}\\ m\ne l \end{array}}\frac{r_k^i -r_m^j}{r_l^j-r_m^j}\right) \phi ^j_l, \text { with } {\mathcal {P}} = min_p\left( r_k^i,{\varvec{r}}^j \right) , \end{aligned}$$

(21)

In analogy, the rows of $R_{i,x}^j$, $R_{i,y}^j$, $R_{i,z}^j$, contain the one-dimensional restriction stencils. For the restriction in x- and y-directions, a spectral cut-off filter is used in combination with simple injection to the coarse grid, leading to

$$\begin{aligned} \phi _l^j = \frac{1}{N^j}\sum _{m=0}^{N^j-1}\sum _{k=0}^{N^i-1}\mathrm {exp}\left( {-2\uppi {\mathrm{i}} m\frac{r^j_k-r^i_l}{L}}\right) \phi ^i_k. \end{aligned}$$

(22)

For the restriction in the z-direction, we use a combination of a box filter and an injection. For the box filter we use a width of $\varDelta _z^j$, which comes down to $s=\varDelta _z^j/\varDelta _z^i$ cells on the fine grid. It is easily shown that the following relation holds to filter a field $\phi ^i$, which is assumed to have been filtered with a width $\varDelta _z^i$, to a field $\phi ^j$ with a width $\varDelta _z^j$

$$\begin{aligned} {\widetilde{\phi }}^i_l = \frac{1}{s}\sum _{k=-s/2}^{s/2-1}\phi ^i_{l+k+1/2}, \end{aligned}$$

(23)

where the interpolation of $\phi ^i_{l+k+1/2}$ happens with the same fourth-order interpolation as is described above.

For the refinement experiment we use a Gaussian filter where the standard deviation is chosen as $\sigma ^2=(s^2-1)/12$, and where the factor 1 / 12 is determined such that the second moments of the Gaussian and box filter are equal [see Leonard (1975) for a derivation], and the factor $-1$ appears due to the successive filtering [see e.g. Pope (2000)], such that choosing $s=1$ leaves the field unaltered. This leads to the following relation

$$\begin{aligned} {\widetilde{\phi }}^i_l = \frac{\sum _{k=-\infty }^{\infty }\mathrm {exp}\left( {-\frac{1}{2}\left( \frac{k}{\sigma }\right) ^2}\right) \phi ^i_{l+k}}{\sum _{k=-\infty }^{\infty }\mathrm {exp}\left( -\frac{1}{2}\left( \frac{k}{\sigma }\right) ^2\right) }. \end{aligned}$$

(24)

In a further step the field is restricted to the coarser grid. Due to mismatching cell locations for the u and v velocity components an additional interpolation is needed. For this we again use the fourth-order polynomial interpolation, which leads to the following expression

$$\begin{aligned} \phi ^j_l = \sum _{k\in {\mathcal {P}}}\left( \prod _{\begin{array}{c} m\in {\mathcal {P}}\\ m\ne k \end{array}}\frac{r_l^j -r_m^i}{r_k^i-r_m^i}\right) {\widetilde{\phi }}^i_k, \text { with } {\mathcal {P}} = \mathrm {min}_p\left( r_l^j,{\varvec{r}}^i \right) . \end{aligned}$$

(25)

B Comparison of Time-Averaged Mean Fields

For the sake of completeness, we provide a comparison of time-averaged velocity and turbulent kinetic energy fields obtained on the different grids, which is the standard basis for comparing LES results (using different grids, models, or codes). In contrast to the error analysis in the main text, we present long time averages that omit the initial transient that occurs when initializing with a turbulent field that is not in statistical equilibrium on the simulation grid. To this end the simulations on the different grids are spun up until a statistical steady state is reached. Afterwards, averaging is performed over a period of ${8000}\,\hbox {s}$, ensuring sufficient statistical convergence.

Results are shown in Fig. 9, and overall, it is appreciated that profiles of the mean flow match closely. Profiles of turbulent kinetic energy show a more pronounced grid dependency close to the wall. This is quite standard, as the integral length scale decreases proportional with the distance to the wall, so that less large-scale motions are resolved in this region on coarser grids.

Fig. 9

Time-averaged equilibrium streamwise velocity component, $U_1^i$ (left) and turbulent kinetic energy, $E^{i}$ (right) for the different grids. Grid numbers: 0 ( ), 1 ( ), 2 ( ) and 3 ( )