On Displacement Height, from Classical to Practical Formulation: Stress, Turbulent Transport and Vorticity Considerations

Abstract

Displacement height (d) is an important parameter in the simple modelling of wind speed and vertical fluxes above vegetative canopies, such as forests. Here we show that, aside from implicit definition through a (displaced) logarithmic profile, accepted formulations for d do not consistently predict flow properties above a forest. Turbulent transport can affect the displacement height, and is an integral part of what is called the roughness sublayer. We develop a more general approach for estimation of d, through production of turbulent kinetic energy and turbulent transport, and show how previous stress-based formulations for displacement height can be seen as simplified cases of a more general definition including turbulent transport. Further, we also give a simplified and practical form for d that is in agreement with the general approach, exploiting the concept of vortex thickness scale from mixing-layer theory. We assess the new and previous displacement height formulations by using flow statistics derived from the atmospheric boundary-layer Reynolds-averaged Navier–Stokes model SCADIS as well as from wind-tunnel observations, for different vegetation types and flow regimes in neutral conditions. The new formulations tend to produce smaller d than stress-based forms, falling closer to the classic logarithmically-defined displacement height. The new, more generally defined, displacement height appears to be more compatible with profiles of components of the turbulent kinetic energy budget, accounting for the combined effects of turbulent transport and shear production. The Coriolis force also plays a role, introducing wind-speed dependence into the behaviour of the roughness sublayer; this affects the turbulent transport, shear production, stress, and wind speed, as well as the displacement height, depending on the character of the forest. We further show how our practical (‘mixing-layer’) form for d matches the new turbulence-based relation, as well as correspondence to previous (stress-based) formulations.

1 Introduction

In order to simply describe the mean wind above a surface covered by vegetative canopy, using similarity theory, a displacement height (d) is needed in addition to the effective aerodynamic roughness length $(z_{0})$ characterizing the vegetation. Applying surface-layer theory to canopy flow implies that the flow should be “deflected” upward in such way that the mean flow properties above a vegetative canopy (hereafter also referred to as forest), beginning roughly from a height d within the forest, are similar to those above open flat ground. The displacement height can first be defined ideally in neutral conditions (i.e. without stability effects) over a flat surface through the logarithmic wind profile,

$$\begin{aligned} U(z)=\frac{u_{*h}}{\kappa }\ln \left[ {\frac{(z-d)}{z_{0}}} \right] , \end{aligned}$$

(1)

where z is height above the ground, $u_{*h}$ is the friction velocity at the ‘virtual’ surface (generally the mean tree top height h), and $\kappa$ is the von Kármán constant (usually accepted to be 0.4). Thus the mixing length and eddy diffusivity for momentum (and also for most scalars) are proportional to the distance above d. Eddy diffusivities are typically also applied for the prediction of vertical turbulent fluxes from vertical gradients of corresponding mean profiles, via dimensionless stability profile functions (derived empirically from measurements over uniform open terrain), i.e. Monin–Obukhov theory (Monin and Obukhov 1954; c.f. Foken 2004).

As stated by Simpson et al. (1998), “flux-gradient relationships based upon similarity theory have been reported to severely underestimate scalar fluxes in the roughness sublayer above forests, as compared to independent flux estimates (e.g. eddy-covariance or energy balance measurements).” Raupach (1979) labelled this phenomenon ‘aerodynamic discrepancy,’ and it has been noted more generally to occur in the atmospheric surface layer (ASL) when terms such as turbulent transport become significant in the rate equations for momentum fluxes (e.g. Zeman 1981; Wyngaard 2004).

Though uncertainty in the estimation of d was postulated to be one reason for such a ‘discrepancy’ (Thom et al. 1975; Hicks et al. 1979; Raupach 1979), this reasoning was rejected after a short debate (Hicks et al. 1979; Raupach 1979; Garratt 1979). With eddy-covariance measurements of stresses becoming common and the work of Thom (1971) connecting these measurements with definitions of displacement height, such arguments disappeared from the scientific literature. However, some studies found that d calculated from micrometeorological data was best fit via an assumption of a logarithmic wind profile (e.g. Bache 1986; Simpson et al. 1998), suggesting that similarity theory can be used within the roughness sublayer (RSL) with greater confidence than previously believed. Because micrometeorologists are generally constrained to work within the roughness sublayer above forests for practical reasons, the issue of displacement height definition is still relevant; in the present study we try to reconsider it and re-open discussion about d.

Different interpretations of displacement-height formulations have been made (Hicks et al. 1979; Raupach 1979; Garratt 1979; Poggi et al. 2004), following the concept of Thom (1971). However, they all aim to satisfy the ‘displaced logarithmic law’ (1) for the neutral mean wind profile (or a surface-layer/similarity expression for non-neutral conditions),¹ at least over some range of heights. But they can miss other (higher-order) effects on the mean flow (they admit as much), which can also be approximated within the framework of surface-layer theory, in part through d. The leading source of turbulent kinetic energy (TKE), shear production (P), varies negligibly with height in the surface layer above open ground when normalized by surface-layer scales (Wyngaard 2010). Above a forest, P (which is $-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle {\mathrm{d}U}/{\mathrm{d}z}=u_*^{2}{\mathrm{d}U}/{\mathrm{d}z}$ for horizontally homogeneous conditions²) should be roughly equal to the dissipation rate of TKE, $\varepsilon ={u_*^{3}}/{\left[ {\kappa (z-d)} \right] }$, when surface-layer theory applies. That is, the ratio of these $(\phi _{m}=P/\varepsilon )$ should be constant and close to 1 in neutral conditions over relatively homogeneous forest, as in the ASL; we remind the reader that the dimensionless wind shear is also described by $\phi _{m}={\kappa z(\mathrm{d}U / \mathrm{d}z)}/{u_*}$ for a given height z above a uniform flat surface.

In the present work we show that none of the extant stress-based expressions for d consistently provides such a result—the mean flow is much more dependent upon the vegetation structure and inflow conditions than the stress-based expressions allow. The surface-layer framework (using such formulations of d) was extended for use above forests through RSL theory, whereby the dimensionless wind-speed gradient (and thus the ratio of shear production to dissipation of TKE), and consequently the form for the wind profile, are modified to account for the mean effect of the forest, via introduction of an additional length scale (Garratt 1978; Raupach et al. 1979; Harman and Finnigan 2007).

Without looking into RSL theory, we extend a formulation for d to improve its application over forests, for both mean wind and dimensionless profiles of sources/sinks of TKE. We derive a formulation for d congruent with second-order flow statistics, starting with a form that is independent of atmospheric stratification and that satisfies surface-layer theory for both wind speed and normalized TKE in neutral conditions. We show that previous stress-based formulations can be seen as simplified cases of this new definition. Perhaps more importantly, we further offer a practical alternative that is readily obtained from typical measurements; it is also related to the vorticity penetration depth exploited in RSL theory (e.g. Raupach et al. 1996; Harman and Finnigan 2007).

Examination and comparison of the extant and new displacement height formulations are done using flow data from the wind-tunnel experiments of Brunet et al. (1994) and from simulations of the atmospheric boundary-layer model SCADIS (Sogachev et al. 2002; Sogachev and Panferov 2006), for various sets of canopy structure and inflow conditions. In this study only neutrally stratified flow is considered.

2 Previous Formulations for Displacement Height

There are a number of formulations for displacement height and approaches for its estimation. Beginning with the implicit functional definition of d through assumption of a logarithmic profile of wind speed U above the canopy (1), using wind-speed measurements at two levels $z_{1}$ and $z_{2}$, we may eliminate $z_{0}$ and estimate the displacement height as

$$\begin{aligned} d=\frac{z_{2}-z_{1}\exp \left[ {\kappa \left( {U_{2}-U_{1}} \right) /u_*} \right] }{1-\exp \left[ {\kappa \left( {U_{2}-U_{1}} \right) /u_*} \right] }, \end{aligned}$$

(2)

where $u_{*}$ is typically taken to be $u_{*h}$. Alternately, the friction velocity can be eliminated to give

$$\begin{aligned} d=\bar{{z}}+\Delta z\frac{\bar{{U}}}{\Delta U}W\left\{ {\frac{{\bar{{U}}}/{z_{0}}}{{\Delta U}/{\Delta z}}} \right\} =\bar{{z}}\left( {1+\frac{1}{\alpha }W\left\{ {\frac{{\bar{{z}}}/{z_{0}}}{\alpha }} \right\} } \right) , \end{aligned}$$

(3)

with $\bar{{U}}\equiv (U_{1}+U_{2})/2$, $\Delta U\equiv (U_{2}-U_{1})$, $\bar{{z}}\equiv (z_{1}+z_{2})/2$, $\Delta z\equiv (z_{2}-z_{1})$, expressible via the shear exponent $\alpha \simeq (\bar{{z}}/\bar{{U}})\Delta U/\Delta z$, and W is the Lambert–W function.³ However, since the effective roughness over forest depends on the displacement height itself (e.g. $z_{0}=(z_{2}-d)\exp (\kappa U_{2}/u_{*h})$ following Eq. 1), and because the friction velocity $u_{*h}$ is typically measured, then (2) is used instead of (3); we hereafter refer to (2) as the ‘classical’ formulation for d. In cases where profile measurements are not available, simplified empirical expressions are often applied in practice, such as $d =0.67h$; many empirical forms can be found in the literature (e.g. Raupach and Thom 1981; Shaw and Pereira 1982).

With the ability to measure fluxes via eddy covariance, stress-based prescriptions for displacement height became popular in the 1970s. Based on flow measurements made above and within a simply-structured artificial crop in a wind tunnel, Thom (1971) identified d as the mean level of momentum absorption. Though Thom’s (most quoted) expression for d depends on the momentum flux being expressed in terms of drag, it derives from the more general form

$$\begin{aligned} d=\frac{\int \nolimits _{0}^{h}z\left( \hbox {d}\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \big /\hbox {d}z\right) \hbox {d}z}{\int \nolimits _{0}^{h} \left( \hbox {d}\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \big /\hbox {d}z\right) \hbox {d}z}, \end{aligned}$$

(4)

where again the (canopy-affected) mean momentum flux is $\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle$; here we denote turbulent fluctuations about the mean by primes, and note that the friction velocity $u_{*}$ is equal to $\sqrt{-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle }$. The form (4) gained support from experimentalists (e.g. Landsberg and Jarvis 1973) and became popular with researchers using eddy-covariance measurements. Analysis of Thom’s (1971) concept by Jackson (1981) placed d on a more secure theoretical foundation, but, as noted Raupach and Thom (1981), the concept “does not ease the problem of measuring it unless an accurate drag profile within the canopy can be deduced.”

Thom’s relation (4) can in turn be considered as a relative of the Poggi et al. (2004) expression

$$\begin{aligned} d=\frac{\int \nolimits _{0}^{h}zF_{d}(z)\hbox {d}z}{ \int \nolimits _{0}^{h}F_{d}(z)\hbox {d}z}, \end{aligned}$$

(5)

which gives the mean level of drag force $F_{d}(z)$—generally prescribed in terms of the drag coefficient $C_{d}$ and leaf-area density A (as $F_{d}=C_{d}AU|U|)$, where $C_{d}$ and A can be functions of height z. When the stress divergence ${d\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle }/{dz}$ is balanced solely by $F_{d}(z)$ in the mean momentum conservation equation, then (4) follows from (5). If one further assumes that the drag coefficient and leaf-area density are independent of height (in addition to form drag dictating the stress, so that (4) and (5) are equivalent), then d can be reduced to the yet simpler form (e.g. Raupach et al. 1986)

$$\begin{aligned} d=\frac{\int \nolimits _{0}^{h}z\left[ U(z)\right] ^{2}\hbox {d}z}{\int \nolimits _{0}^{h}\left[ U(z)\right] ^{2}\hbox {d}z} \end{aligned}$$

(6)

Alternately, multiplying (4) by a factor of $\left[ {1-{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{0}}/{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{h}}} \right]$ (where subscripts 0 and h refer to near-ground and canopy-top values respectively) to correct for the surface-induced drag (Jackson 1981; Shaw and Pereira 1982), or using the less restrictive assumption $z_\mathrm{0,sfc} \left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{0}\ll h\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _\mathrm{h}$, yields⁴

$$\begin{aligned} d=h-\frac{\int \nolimits _{0}^{h}{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \hbox {d}z}}{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{h}}. \end{aligned}$$

(7)

Thus the commonly-accepted ‘surface-corrected’ form (7) implies that the effective zero-plane or virtual surface is located a distance (h – d) below mean tree height h, with this distance being a fraction of h that is equal to the ratio of canopy-averaged stress to canopy-top stress.

Equations 4 and 6–7 allow d to be estimated from direct field measurements and are widely used by experimentalists, while (5) requires knowledge of the drag force via parameters related to both the vegetation and flow; the latter may be available from specially designed observations or model simulations.

3 New Formulations for Displacement Height

3.1 Formulation Considering Turbulent Transport

Sogachev et al. (2005) found that integral methods based on the momentum flux (i.e. Eqs. 4, 6–7) provide similar results for d over a spatially homogeneous forest, with approach (7) also providing reasonable results in the vicinity of forest edges and behaviour closer to that of (2). Equation 7, which is the only method attempting to account for the ground-induced drag (Shaw and Pereira 1982), can, particularly considering its ad hoc correction factor, also be interpreted as a slightly different conceptual definition of displacement height: d is simply the mean canopy depth, reduced by a factor equal to the ratio of the canopy-averaged stress and (mean) canopy-top stress, $d=h\left( {1-{h^{-1}\int \nolimits _{0}^{h}{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \hbox {d}z}}/{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{h}}} \right)$. Here we build upon this definition, which gives in effect the level of canopy-mean momentum flux $\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle _{0...h} \equiv h^{-1}\int \nolimits _{0}^{h}{\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \mathrm{d}z}$.

In Eqs. 4–7, the displacement height is based on the momentum flux, which had been assumed to follow from the balance between shear production and dissipation of TKE. In contrast to this assumption and the forms (4–7), we argue that a useful definition of d can include the impact of other significant contributions to the TKE balance in the canopy (e.g. turbulent transport), information that might not be uniquely reflected in the profile of $\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle$, and which is not included in such forms. Shaw and Pereira (1982) concluded that d is the level at which the above-canopy mixing length (for momentum) would be zero, extrapolating downward into the canopy. For flux-gradient relations, then d, as well as the mixing length $\ell$ (or diffusivity) in the RSL, should depend upon contributions to the TKE budget; basic turbulence theory (Kolmogorov 1941) gives $\ell \propto E^{3/2}/\varepsilon$, and e.g. two-equation turbulence closures are driven by TKE and dissipation budgets $(\hbox {d}E/\hbox {d}t,~\hbox {d}\varepsilon /\hbox {d}t)$, from which mixing length is derived (again as $E^{3/2}/\varepsilon )$. In order to properly characterize the similarity (RSL) behaviour of the various components that contribute to TKE, we suggest a displacement height amenable to the TKE budget. We thus advance the definition of d, using the level of canopy-mean production of TKE instead of canopy-mean stress.

Beginning with the simplest TKE-based form analogous to (7), one may write

$$\begin{aligned} d= h-\frac{\int \nolimits _{0}^{h}{P(z)\hbox {d}z}}{P_{h}}= h-\frac{\int \nolimits _{0}^{h}{-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \left( {{\hbox {d}U}/{\hbox {d}z}} \right) \hbox {d}z}}{\left. {\left[ {-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle \left( {{\hbox {d}U}/{\hbox {d}z}} \right) } \right] } \right| _{h}}, \end{aligned}$$

(8)

i.e. for an implied equilibrium between shear production and dissipation $(P=\varepsilon )$. This can be re-written as

$$\begin{aligned} d=h-\frac{\int \nolimits _{0}^{h}u_{*}^{2}(z)\frac{\hbox {d}U}{\hbox {d}z}\Big |_{h}\left[ 1+s^{\prime }(z)\right] \hbox {d}z}{P_{h}}=h- \int \nolimits _{0}^{h}u_{*}^{2}(z)\left[ 1+s^{\prime }(z)\right] \hbox {d}z\big /u_{*h}^{2}, \end{aligned}$$

(9)

where ${s}^{\prime }(z)\equiv \left( {{\left. {\frac{\mathrm{d}U}{\mathrm{d}z}} \right| _{z}}/{\left. {\frac{\mathrm{d}U}{\mathrm{d}z}} \right| _{h}}-1} \right)$ is the local normalized shear exceedance relative to canopy top, and $u_*^{2}(z)=-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle$ for height z. Thus one can see that when $\int \nolimits _{0}^{h}u_{*}^{2}(z)s^{\prime }(z)\mathrm{d}z$ is much smaller than $\int \nolimits _{0}^{h}u_{*}^{2}(z)\mathrm{d}z$, or more simply in the limit that $s^{\prime }{\ll } 1$, i.e. the mean shear in the canopy does not differ substantially from the (mean) shear at canopy top, then the energy-based expression (9) simplifies to (7). That is, Eq. 7 can be seen as a particular case of (9). However, this correction is not quite enough to provide consistency between d and the TKE budget in neutral conditions, when the TKE is affected significantly by turbulent transport.

Including turbulent transport in the TKE budget, then (8) can be extended to

$$\begin{aligned} d =h-\frac{\int \nolimits _{0}^{h}{\left[ {P(z)+T(z)} \right] \hbox {d}z}}{\left. {\left[ {P+T} \right] } \right| _{h}}, \end{aligned}$$

(10)

where for modelling convenience we include both pressure-transport and turbulent transport in the total transport (T) of TKE (see e.g. Pope 2000; Wilcox 2002). Then (9) becomes

$$\begin{aligned} d=h-\frac{\int \nolimits _{0}^{h}\left\{ \frac{\hbox {d}U}{\hbox {d}z}\Big |_{h} u_{*}^{2}(z)\left[ 1+s^{\prime }(z)\right] +T(z)\right\} \hbox {d}z}{\left[ P+T\right] \big |_{h}}, \end{aligned}$$

(11)

which for T / P at canopy top significantly smaller than 1, can be cast again as a perturbation of the stress-based forms, or vice versa,

$$\begin{aligned} d\,\approx \;\;h-\frac{(1-T_{h}/P_{h})}{u_{*h}^{2}} \int \nolimits _{0}^{h} {\left\{ {u_{*}^{2} (z)\left[ {1 + s^{\prime }(z)} \right] + \frac{{T(z)}}{{\left. {\left( {{\text {d}}U{\text {/d}}z} \right) } \right| _{h} }}} \right\} {\text {d}}z} \end{aligned}$$

(12)

For negligible canopy-top transport $(T_{h}/P_{h}\rightarrow 0)$, in neutral conditions the expressions (10–12) are seen to simply revert to (9). For near-uniform shear through the canopy $({s}^{\prime }\ll 1)$ then

$$\begin{aligned} d\approx h-\frac{u_{*h}^{3}/\kappa }{P_{h}}, \end{aligned}$$

(13)

consistent with similarity forms for dissipation in the equilibrium limit $\left( P_{h}=\varepsilon _{h}=\right. \left. {u_{*h}^{3}}/{\left[ {\kappa (h-d)} \right] }\right)$; this is expected to be the case for higher wind speeds, as shown below.

3.2 Practical Formulation Considering Vortex Penetration Depth

From mixing-layer theory, the concept of vortex penetration depth (Raupach et al. 1996; Harman and Finnigan 2007) can be exploited to estimate d, roughly along the lines of (8–13); we take the distance that motions penetrate below into the canopy to be the mean penetration depth,⁵ $\delta _{\omega }$. In the flow around the mean canopy ‘top’, the magnitude of mean vorticity is dominated by the vertical gradient: $\left| {\varvec{\omega }} \right| _{h}\approx \left( {{\mathrm{d}U}/{\mathrm{d}z}} \right) _{h}$. This leads to a displacement height approximation of

$$\begin{aligned} d{\,\approx \,}(h-\delta _{\omega })= h-\frac{c_{\omega } U_{h}}{\left| {\left\langle {\varvec{\omega }} \right\rangle _{h}} \right| }\, \approx \, h-\;\frac{c_{\omega } U_{h}}{\left( {{\mathrm{d}U}/{\mathrm{d}z}} \right) _{h}}. \end{aligned}$$

(14)

The coefficient $c_{\omega }$ can be estimated by comparing (13) and (14); for $P_{h}=u_{*h}^{2}\left( {{\mathrm{d}U}/{\mathrm{d}z}} \right) _{h}$ one obtains

$$\begin{aligned} c_{\omega } \approx \frac{u_{*h}}{\kappa U_{h}}, \end{aligned}$$

(15)

exhibiting a clear dependence upon the ratio ${U_{h}}/{u_{*h}}$, and as such, upon the structure of vegetation and surrounding flow conditions. For engineering use, the constant $c_{\omega }$ can also be re-written simply in terms of the shear exponent; e.g. $c_{\omega } ={u_{*h}}/{(\kappa U_{h})=1/{\ln \left[ {(h-d)/z_{0}} \right] \approx \alpha _{h}}}$ (c.f. Kelly et al. 2014). The ratio ${U_{h}}/{u_{*h}}$ typically varies from 3–5 (e.g. Bache 1986; Finnigan and Brunet 1995), which is consistent with shear exponents measured above forests, i.e. $c_{\omega } \approx \alpha _{h}$ is roughly 0.5–0.8. Note that $c_{\omega }$ found from measurements using (15) can satisfy ${u_{*h}^{3}}/{ \left[ {\kappa (z-d)} \right] }=1$; however, estimating it (and thus $\delta _{\omega }$) without consideration of transport can be problematic, especially at low wind speeds. Further consideration of $c_{\omega }$, its evaluation, and equivalent values to match other d formulations are given below.

4 Data: Flow Modelling and Wind-Tunnel Observations

4.1 SCADIS Model

All flow statistics used to test the suggested method were calculated using the one-dimensional version of the (SCAlar DIStribution) SCADIS model (Sogachev et al. 2002). This RANS model of the atmospheric boundary layer (ABL) with two-equation turbulence closure is well-documented, and verified against many datasets pertaining to canopy flow (including vertical profiles of $\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle$ and U) over the last decade (Sogachev and Panferov 2006; Panferov and Sogachev 2008; Boy et al. 2011). Several numerical experiments are presented below for illustrative purposes, to demonstrate the theories given here as well as subsequent implications. Using flow statistics from ABL simulations, d was estimated using the four previously established, commonly-used forms (Eqs. 2, 4, 6 and 7), along with the new formulations (10) and (14).

4.2 Reynolds Number-Independent and ABL Flows

We used the one-dimensional version of the SCADIS model, with a vertical ‘grid’ consisting of 250 levels of variable spacing; this ranged from about 0.04 m near the ground, growing to 130 m near the top of the domain at $z = 4~\hbox {km}$. The flow statistics were calculated for canopies having different structures, and also for two sets of model cases. First, in an idealized ‘engineering’ flow, without the Coriolis force nor a length-scale limiter in the turbulence closure, and thus independent of Reynolds number (Re), the model reproduces the “classical” constant-flux layer through the whole model domain (insets of Fig. 1a, c), just as in other RANS schemes lacking these two model parts (c.f. Apsley and Castro 1997). Then, including the Coriolis force and turbulence length scale limiter (as in typical ABL simulations, c.f. Sogachev and Panferov 2006), the model approximates the vertical structure of a neutrally-stratified ABL (insets of Fig. 5a, c). The driving force in the model was a geostrophic wind of varying magnitude $U_{g}$, and calculations including Coriolis force were done at a latitude of $50^{\circ }$. Two different leaf area density (LAD) profiles, having pre-defined constant aerodynamic drag coefficients $(C_{d} = 0.2)$, were used for canopy-flow calculations: the first approximates forest-like vegetation ($h=20\hbox { m}$, leaf area index LAI = 3, LAD distribution shown in Fig. 1b) and the second represents bush-like vegetation ($h=15~\hbox {m}$, LAI = 1, LAD distribution in Fig. 1d). The vertical foliage distribution uses beta distribution (e.g. Meyers and Paw-U 1986; Sogachev et al. 2008). Two parameters, $\alpha$ and $\beta$, determine the shape of the distribution. When $\alpha ~>~\beta$, the maximum value occurs at $z/h > 0.5$, thus representing a region of maximum foliage concentrated in the upper part of the canopy. The parameters $\{\alpha , \beta \}$ were specified as {7, 3} for forest-like vegetation and as {1, 3} for bush-like vegetation. For both cases $U_{g}$ was set to $10\hbox { m s}^{-1}$, and the aerodynamic (surface) roughness length in all experiments was set to 0.03 m.

Fig. 1

(a, c): logarithmic ‘displaced’ wind profiles and ‘observed’ (fully modelled by SCADIS) U(z) for two different forest types in idealized flow, using Eq. 1 with d calculated using the logarithmic law  Eq. (2), from stress-based forms (4, 6–7) and the new form (10); note Eq. 5 is identical to Eq. 4 in this flow case. Dotted line shows ‘observed’ stress. All values are normalized by respective SCADIS value at the canopy top. Inset shows U(z) and the stress profile through/beyond the ASL. Right panels (b, d): normalized profiles of ${u_{*h}^{3}}/{\left[ {\kappa (z-d)} \right] }$ using different formulations for d (solid, colour), as well as simulated P, dissipation $\varepsilon$, and transport T; shaded areas indicate normalized leaf area density (LAD). Data for (14) are not shown, because for specific values of $c_{\omega }$, they match the plotted formulations (see text for detail)

4.3 Wind-Tunnel Flow Simulations

The SCADIS model was also used to reproduce data from the experiment carried out in the CSIRO Pye Laboratory wind tunnel (Wooding 1968) by Brunet et al. (1994) to study flow over a modelled aeroelastic canopy with $h = 0.047~\hbox {m}$ (LAI = 0.47, $C_{d} = 0.68$). Sogachev and Panferov (2006) demonstrated how the SCADIS model can reproduce the flow for such conditions, using two different approaches to drive the flow:

• (i) based on a driving pressure gradient that simulates a vertical gradient in Reynolds stress above the canopy (Wilson et al. 1998); and

• (ii) based on surface-layer assumptions without such a gradient.

In both approaches the vertical dimension of the model domain $(H_{t} = 0.65\hbox { m})$ was divided into a grid of 550 nodes, with constant grid spacing of h / 40. Additionally, for the tunnel simulations the Coriolis force is neglected, the aerodynamic roughness length of the tunnel walls is 0.0007 m, the turbulence length scale limiter was fitted as $0.08H_{t}$, and a no-slip condition was taken at the bottom. For approach (i) the wind speed at tunnel top was taken to be zero, with a driving kinematic pressure gradient set by $\rho ^{-1}{\partial \left\langle p \right\rangle }/{\partial x}=-2u_{*h}^{2}/h$. For approach (ii), the forcing of the airflow was provided by setting the wind speed to $16\hbox { m s}^{-1}$ at the upper boundary. The boundary conditions for other parameters were also adapted for different cases according to Sogachev and Panferov (2006). Both approaches were used, because experimental data show that directly above the vegetation canopy the shear stress is almost constant with height up to roughly 2h.

5 Comparison and Behaviour of Displacement Height Formulations

5.1 Re-Independent Flow

Figure 1 shows normalized profiles of wind speed, momentum flux, shear production, transport, and dissipation of TKE, for the first (ideal) set of cases, i.e. flow independent of Reynolds number (Re). These results are generated for two different leaf-area density profiles, with the flow above the canopy experiencing the constant-flux layer conditions under which the theory and definition (1–2) of d was created (i.e. surface-layer theory). For finding d in practice, wind speeds from all existing (or arbitrary) measurement levels are typically used. For a purely logarithmic profile, ideally the number of observational heights does not matter: two is sufficient (as in Eq. 2), and under such ideal conditions it is irrelevant which levels are chosen for estimation of d. This is in contrast to most real-world situations, as will be shown below.

Figure 1 also demostrates an advantage of the new d formulation (10): the mean wind profile practically coincides with both the analytical solution (1) and the model result above the canopy. Equations 4–7 give d values that are close to each other, but fail to reproduce the wind profile and dimensionless wind shear (shear production) $\phi _{m}$. In the absence of the Coriolis force, and in the case of small surface stress, the stress- and drag-based approaches are essentially identical and overpredict d. This is consistent with Garratt’s (1978) suggestion that overpredicted d is a possible cause for the underestimation of $\phi _{m}$. Equation 14 is a simplified approach for estimation of d, and it can be matched to old or new formulations, depending on the choice of $c_{\omega }$. Setting $c_{\omega }$ to 0.41 and 0.32 in the case of forest and bush-like vegetation, respectively, results in values of d estimated by (14) that are the same as those defined by the stress-based Eq. 7. Values for $c_{\omega }$ of 0.63 and 0.56 (respectively) provide a match to the new formulation (10). Note that the bush-like canopy probably represents a worst-case scenario for both measurements and modelling of vegetation, and the values of $c_{\omega }$ for this case define some limit. Thus for practical application, as a first estimate of $c_{\omega }$ a constant value for a more typical forest type should be used: 0.41 to match (7) and 0.63 to match (10). Analogous to the geometric interpretation of the von Kármán constant $\kappa$ (Monin and Yaglom 1971), we postulate $c_{\omega }$ to be a ratio of dominant vertical and streamwise length scales for the mean flux-containing eddies interacting with the canopy (e.g. Raupach et al. 1996). Interesting to note is that to force (14) to match (7) one must set $c_{\omega } \approx \kappa$, while (14) gives the same results as (10) for $c_{\omega } =0.632 \approx \sqrt{\kappa }$. The latter might be interpreted dimensionally, regarding turbulent transport versus stress; showing this, however, follows from (more) formal connection between (10) and (14), which is beyond the scope of the present work. At any rate, $c_{\omega } =0.632$ is our first estimate for use in (14–15).

Figure 2 shows how the profile of shear production and the subsequent profile of $(P + T)$ differ from that of the shear stress, demonstrating how their vertically integrated values give smaller d in the new formulation. One can see in the figure that the (orange) ‘area’ implied by the normalized integration of $P + T$ as in (10) has a relatively greater contribution from farther below the canopy top than the analogous (blue) area of normalized stress corresponding to (7), leading to a smaller displacement height. Because contemporary flux-based approaches for d follow from the original suggestion of Thom (1971), it is worth noting that Thom only proposed some “identity of the levels $z = d$ and $z = c$”, where in his case the level c (the level of action of the drag force) was estimated using an expression similar to Eq. 4 but with integration only up to an “adjusted crop height” that was set as 0.825h. Because such an “adjusted height” can be varied (reduced) depending on flow conditions and canopy structure, it seems this point was ignored in further use; in the following paragraphs we continue to demonstrate why such a reduction in stress-based height is needed.

Fig. 2

Vertical profiles of $-\left\langle {{u}^{\prime }{w}^{\prime }} \right\rangle$, P and $P+T$, normalized by their respective values at canopy top, for forest-like and bush-like canopies. Shaded areas indicate the integral values arising from common stress-based expressions (blue, cf. Eq. 7) and new TKE-based form including transport (orange, Eq. 10)

5.2 Wind-Tunnel Flow

The experimental data of Brunet et al. (1994) allows some scrutiny on how observations can be used for d estimation, and we consider the consequences of such. Data presented in Fig. 3 indicate that the SCADIS model simulates well the wind-tunnel flow of Brunet et al. (1994). Two approaches are used in the simulation (see Sect. 4.3): (i) driving the flow with an effective pressure gradient, and (ii) one based on a constant-flux layer assumption. The first is more natural because it allows a no-slip condition at the walls (Figs. 3b, e), though this approach is not able to model the constant shear-stress layer above the canopy (Fig. 3a, d), which, together with the shift of observed maximum dissipations to the height of 1.5h (c.f. Fig. 7 in Brunet et al. 1994), can be attributed to wind-tunnel issues unrelated to the canopy (Seginer et al. 1976). The approach based on a constant-flux layer assumption reproduces the constant-flux layer not only at heights close to the canopy, but over most of the domain (Fig. 3a, d); as such, it provides unrealistic and unphysical wind-speed profiles for a wind tunnel (Fig. 3b). Though each approach has its own weaknesses, together they allow us to reproduce very well the experimental data, and also extend these data in a way that allows reliable calculation of $P, T, \hbox {d}U/\hbox {d}z$, and turbulent diffusivities with some degree of accuracy.

Fig. 3

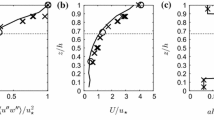
Comparison between measured and modelled flow statistics for the wind-tunnel experiment of Brunet et al. (1994). Points denote observations (bars denote standard deviations); red lines model driven with an effective pressure gradient; blue lines model driven with assumption of constant-flux layer above canopy. The black lines in f represent the surface-layer (inertial sublayer) diffusivity $K_{0}=\kappa u_{*}(z-d)$, with differently defined d: solid with d by (7), as in Brunet et al. (1994); dotted via (14) with $c_{\omega } = 0.632$; and dashed via (14) with $c_{\omega } = 0.716$

According to the approaches used, the SCADIS model calculated two different profiles of eddy diffusivity (Fig. 3c). Approach (i) provides physically representative turbulent diffusivity K over the whole domain, but (due to the lack of constant-flux layer discussed above) provides a worse result for K near the canopy than demonstrated by approach (ii). In general, both profiles are close to each other, and match experimental data up to heights of 2h. Inertial sublayer diffusivities calculated by using different formulations for d, plotted in Fig. 3f, clearly give support to our new formulation (14).

Data presented in Fig. 4 support our formulation further: it is clear that different modelling approaches provide different production profiles inside the domain, and Fig. 4a reminds us that the constant-flux assumption (ii) provides better agreement with measured production above the canopy, but approach (i) does so higher up. But what is more remarkable from Fig. 4 is that the old formulations provide neither a value near 1 for ${u_*^{3}}/{\left[ {\kappa (z-d)} \right] }$, nor more realistic wind profiles at greater heights. Brunet et al. (1994) discussed the presence of a thin inertial layer between dimensionless heights z / h of roughly 1.7 and 2.4, and the displaced logarithmic wind profile with the ‘old’ d values (which they defined using Eq. 7) matches measurements in this layer (Fig. 4b). The new formulation (14) matches measurements in a layer from $z \approx d$ to $z \approx 2h$, where ${u_*^{3}}/{\left[ {\kappa (z-d)} \right] }\approx P$ as well. Moreover we can see that a small adjustment of $c_{\omega }$ provides a better agreement with both normalized $P_{h}$ and wind speed. The adjustment is made using data from Brunet et al. (1994) via the single-point Eulerian (integral) length scales $L_{u}/h = 1.35$ and $L_{w}/h =0.38$ at $z = h$; thus $c_{\omega } =\sqrt{1.35\times 0.38}= 0.716$ instead of 0.632. We postulate that $c_{\omega }$ depends on the sizes of the large (mean) turbulent structures in the streamwise and vertical directions, but without knowledge or specific information, we suggest a ratio of 2.5:1 for such structures (resulting in $c_{\omega } =\sqrt{\kappa }$, as postulated in Sect. 5.1).

Fig. 4

Comparison between measured and modelled shear production P and wind speed U, for the wind-tunnel experiment of Brunet et al. (1994). Points denote observations (bars denote standard deviations); red lines model driven with an effective pressure gradient; blue lines model driven with assumption of constant flux layer above canopy. Black lines represent profile of (a) ${u_{*h}^{3}}/{ \left[ {\kappa (z-d)} \right] }$ and (b) logarithmic ‘displaced’ wind profiles (Eq. 1), using different formulations for d, as in Fig. 3

5.3 ABL Flow Cases

Figure 5 shows the mean wind and TKE component profiles as in Fig. 1, except for calculation conditions intrinsic to the ABL: the Coriolis force is included, along with a finite ABL depth and subsequent length-scale limitation (c.f. Apsley and Castro 1997; Sogachev et al. 2012). Comparing Figs. 1a, c and 5a, c we can see that momentum flux is not constant above the canopy layer (though its divergence is), and that a wind-speed maximum occurs in the trunk space of the crown-dominated forest (Fig. 5a), which results in additional production of TKE in this area (Fig. 5b). Significant changes in turbulence statistics affect the new d defined as in (10), but differently than the stress-based forms (4, 6 and 7). We can see that the old formulations still result in higher d values than implied by the model output or from both the classical definition (2) and new formulation (10); however, when implemented in Eq. 1 they provide a better match with ‘observed’ SCADIS model wind profiles far above the forest. The d values defined by the classical (2) and new formulation (10) provide a better match to U(z) in the RSL near the mean vegetation top. Note that d defined through the logarithmic law as in (2) now strongly depends on the particular height levels chosen for its estimation. In the plots here we used $z_{1}=h$ and $z_{2}=1.5h$, and the estimated wind profile coincides with the ‘observed’ one at these levels. Nevertheless, only the new d formulations (10, 14) and logarithmically defined d (2) predict the normalized total TKE production profiles, i.e. ${u_{*h}^{3}}/{\left[ {\kappa (z - d)} \right] }\approx P\approx (\varepsilon - T)$. The fact that formulations (4, 6 and 7), i.e. those stemming from the Thom (1971) idea of d based on momentum flux, provide a good match to wind speed above the RSL (supported by observation), can explain their wide use and consequent neglect of the existing inconsistency between TKE components and the flux formulation.

Fig. 5

The same as in Fig. 1, but for finite ABL conditions including Coriolis force (see text for details)

Due to the effect of the Coriolis force, we expect a wind-speed dependence in the TKE, stresses, and possibly displacement height; in the mean, the Coriolis force still leads to modified stresses and vertical transport [e.g. Grønnegaard et al. (2014)]. To show this effect, and to further demonstrate the role of turbulent transport in (reduction of) the displacement height, Fig. 6a displays the ratio of the vertically-integrated transport $\int \nolimits _{0}^{h} {T\mathrm{d}z}$ and shear production $\int \nolimits _{0}^{h} {P\mathrm{d}z}$ as a function of wind speed for the two types of vegetation considered, showing that the contribution of transport increases to an asymptotic value for strong winds. Figure 6b shows normalized canopy-top shear production ${P_{h}}/{\left[ {{u_{*h}^{3}}/{\left( {\kappa (h-d)} \right) }} \right] }$ (equivalently $\phi _{m}(h;d))$ versus geostrophic wind speed and canopy-top friction velocity. It implies the logarithmic law formulation (2) gives d similar to the simplified stress formulations (4–7) at low wind speeds, though the wind-speed dependence of the results from (2) are different than when using the other forms for d. We do note that all formulations give constant $\phi _{m}(h;d)$ at higher wind speeds. The stress-based models produce $\phi _{m}(h;d)$ of $\approx 0.6-0.7$ in high winds, while the log-based form converges to a value slightly greater than 1. The new formulation (10) gives larger canopy-top $\phi _{m}(h;d)$ with decreasing wind speeds, due to the diminishing effect of transport on d, also converging in high winds to a value just above 1. This is as it should be in horizontally homogeneous conditions: the negative transport at canopy top causes $\phi _{m}+\phi _{T}\rightarrow 1$ (see Fig. 5b, d), with the dimensionless transport defined by $\phi _{T}\equiv T/{\left\{ {{u_{*h}^{3}}/{\left[ {\kappa (h-d)} \right] }} \right\} }$; the corresponding model (8–9) without transport gives $\phi _{m}\rightarrow 1$ (not shown). The formulation (14) with $c_{\omega } = 0.632$ provides practically the same results as formulation (10), with only a small deviation for forest-like vegetation.

Fig. 6

a ratio of canopy-integrated transport to canopy-integrated shear-production, as seen in (10–12), as a function of geostrophic wind speed (and approximate canopy-top friction velocity $u_{*h})$. b wind speed dependence of canopy-top TKE production rate normalized by displacement–height adjusted surface-layer power scale ${u_{*h}^{3}}/{ \left[ {\kappa (z-d)} \right] }$. Solid lines for forest-like and dotted for bush-like vegetation types; LAD profiles for these types shown in Fig. 1b, d

As for the actual displacement height d, its behaviour as a function of wind speed is shown in Fig. 7, along with the subsequent roughness implied by its functional definition (e.g. $z_{0}=(z_{2}-d) \exp \left( {\kappa U_{2}/u_{*h}} \right)$ from Eq. 1). The new forms (10) and (14) give lower d values than the other formulations; the logarithmically defined-model (2) gives larger values of d for low winds, similar to the simplified stress/drag-based formulations (4–7), though it gives d values comparable to the new models at high wind speeds for the top-crown forest case. The smaller d from the new models is consistent with the shift of spectral peaks of vertical velocity to larger scales observed by Mammarella et al. (2008), i.e. lower values of d imply a greater distance from above-canopy measurement heights to the virtual ‘surface’. The new formulations remain relatively insensitive to wind speed for the ‘top-heavy’ forest-crown case—with more speed dependence for the sparser low-vegetation case—due to the relatively more severe decrease in transport at small wind speeds (see Fig. 6a). However, the effective roughness increases with wind speed for all models and all cases, consistent with measurements (Raupach et al. 1996; Dellwik and Jensen 2005).

Fig. 7

Displacement height (a) and roughness length (b) for two vegetation types (solid for forest-like and dotted for bush-like; LAD profiles shown in Fig. 1b, d), as a function of geostrophic wind speed. Range of friction velocity values at canopy tops is also given, as in Fig. 6

Figure 8 demonstrates the limit of the use of displacement height for the case of very low wind speeds, here $U_{g}= 2\hbox { m s}^{-1}~(u_{*h} \approx 0.1\hbox {m s}^{-1})$. Results presented in Fig. 8 reveal that for low $U_{g}$, the log-law layer (if it exists) is very shallow, because the real boundary layer has a limited depth. This will dictate the behaviour of the mixing length, with its vertical derivative corresponding to the classical value of $\kappa$ (accepted as 0.4) over only a limited range of heights; for low speed conditions, this is one reason the choice of $z_{1}$ and $z_{2}$ is important when using (2). Choosing $z_{2} = 1.1h$ causes $\phi _{m}$ resulting from (2) to become closer to 1 (as shown in Fig. 6b). A shallower ABL, i.e. not much deeper than the mean canopy depth, tends to ‘shrink’ the logarithmic layer, and demand measurements closer to the canopy, which increases the uncertainty in estimating d.

Fig. 8

Normalized “observed” (fully modelled by SCADIS) and logarithmic ‘displaced’ wind profiles for forest-like canopy using (1), with d from the older expressions (2, 4, 6 and 7) and from the new form (10), for two different geostrophic wind speeds $U_{g}$ (solid, dashed). Inset shows $U(z)/U_{g}$ through/beyond the ABL

6 Discussion and Conclusions

Over the last half-century, the validity of similarity theory and applicability of flux-gradient measurements above forests was shown to be limited (e.g. Raupach 1979; Högström 1996; Simpson et al. 1998; Nakamura and Mahrt 2001). The difference between measured flow properties and those estimated using surface-layer formulations led to the development of the RSL concept (Thom et al. 1975; Garratt 1978; Raupach et al. 1979; Harman and Finnigan 2007). We note that differences in estimation of the displacement height d can significantly alter observation-based predictions of vertical profiles for both fluxes and (mean) wind speed. Along those lines, we argue that d estimated from its ‘classical’ logarithmic definition can better capture the mean wind profile within the RSL, down to the mean canopy top, and thus demanding measurements there; our ABL simulations support this (e.g. Fig. 5). The choice of observational heights can affect estimates of d, with increased impact for a shallower ABL and lower wind speeds; there is a compromise between measuring at ‘low enough’ heights above the canopy, versus taking measurements with sufficient vertical separation to minimize uncertainty. This classic “logarithmic law” d is in contrast to the oft-used stress-based formulations (Thom 1971; Shaw and Pereira 1982; Raupach et al. 1986) that improve mean wind profiles above the RSL. But for these accepted stress-based forms for d (Eqs. 4, 6–7), another, paradoxical compromise arises: useful measurements for stress-based d need to be taken above the RSL, but the constant-flux assumption and similarity theory both become less valid with increasing height above the canopy.

To address these paradoxical aspects, we developed a TKE-influenced displacement height concept, which had yet to be considered within the context of consistency with the turbulent kinetic energy (TKE) budget. We are reminded that above forests, any TKE ‘imbalance’ (i.e. $\hbox {d}E/\hbox {d}t$ involving terms other than shear production P and viscous dissipation $\varepsilon$), or deviations from similarity theory (e.g. Monin–Obukhov theory, where only buoyant production/destruction balances P and $\varepsilon$), have come to be accepted as properties of the RSL. While RSL theory (Harman and Finnigan 2007) extends surface-layer theory to account for the forest’s effect upon the dimensionless wind-speed profile $\phi _{m}$, i.e. allowing for varying ratios of P to $\varepsilon$ (and thus non-constant $\phi _{m}$), RSL theory does not include such effects on the displacement height (though it can include stability). Our original motivation also included a desire for consistency between the displacement height and Monin-Obukhov similarity theory, so that the components of the dimensionless TKE budget (e.g. shear production $\phi _{m}$, buoyant production $\phi _{B}$, and dissipation $\phi _\varepsilon$) above a canopy behave predictably with atmospheric stability, i.e. as a function of ${\left( {z-d} \right) }/L$ where L is the Obukhov length (Monin and Obukhov 1954).

Here we have adopted a more general definition of d, in analogy with the flexible Shaw and Pereira (1982) formulation. Whereas the latter prescribes d as the level of mean stress relative to that at canopy top, we estimate d defined through the relative canopy-mean production of TKE, not only to account for a logarithmic mean wind-speed profile (approximately, in neutral conditions), but to also treat the (integrated) height-dependent contributions to TKE that affect the flow above vegetative canopies. We show that the stress- and drag-based formulations (4–7) can be seen as simplified cases of a more general definition via our new TKE-based form (8–9), and we extend the latter to include turbulent transport (Eq. 10), which is an integral part of the RSL.

The new theory indeed shows improvements in prediction of simple flow properties in neutral conditions (also with preliminarily success including buoyancy effects, not shown); in the present article we focus on the neutral case and the generalized definition of d,  reserving stability-dependent results for a later study. Though the expressions considered here are not limited to neutrally-stratified flow, it is relevant to have validated their performance first in neutral conditions, before further application to stable or unstable regimes. Applying the generalized expressions here in other stability regimes can have serious consequences on interpretation of measurements above the forest under real flow conditions, where surface-layer theory is often applied for analysis.

Using observations from multiple heights, the new approach tends to give smaller (generally more realistic) d than previous stress-based formulations, and slightly larger than d from the classic logarithmic definition (2). The new ‘extended’ definitions of d give better estimates of the combined effect of turbulent transport and shear production than the classic and stress-based formulations (Fig. 5b, d), leading to better predictions of the mean wind speed within the RSL (Fig. 5a, c). The improved behaviour of the new approach over stress-based forms is yet more pronounced in ‘real-world’ conditions, which include the Coriolis force and a finite atmospheric boundary-layer depth, and also depends on the character of the forest. The Coriolis force affects the balance between (canopy-affected) production, transport, and dissipation, and this introduces a wind-speed (Reynolds number) dependence into flow statistics in the RSL. It also mitigates the integrated effect of transport relative to shear production, which acts to reduce the overall Reynolds-number dependence of the displacement height (Fig. 7a).

Again one might argue that in reality, the wind profile is not often observed to be logarithmic near the canopy top (as in Fig. 1a); however, for horizontally homogeneous conditions, as in our simulations, one can expect an approximately logarithmic profile above the canopy, with some caution (the results in Fig. 8 are a good example of this). We recognize that the flow statistics involved in estimation of P and T (particularly higher moments of wind fluctuations such as turbulent transport) are difficult to measure, especially in stratified cases. But in an ideally defined framework (just as with previous definitions of d), using a well-validated model (e.g. SCADIS) in the consistency-testing process is not presently an issue, because there are few measured statistics available. Further, we note that although the representation of third-order moments in SCADIS is limited (turbulent transport and pressure transport are parametrized together in a diffusive manner), the results we present were insensitive to use of an enhanced turbulent transport model including the parametrization of pressure transport.

Along with the TKE-related form for d, we also applied the mixing-layer concept of vortex penetration depth to displacement height (14), using a mean vorticity magnitude with canopy-top wind speed. This includes a constant $(c_{\omega })$ approximately equal to the local shear exponent $(\alpha )$, but that also appears to have a geometrical interpretation (Sect. 5.2); further exploration of this, through theoretical connection of turbulent transport to penetration depth, is also the subject of ongoing investigation. The practical form (14) facilitates estimation of d from measurements of shear and wind speed in the RSL, and we show how it can approximate the turbulent transport form (10) for d that we had derived earlier.

Though it does not appear to affect the wind profile dramatically in all cases, more precise estimation of d also helps to improve not only predictions of energy fluxes, but can also improve scalar flux predictions above forests. Further, though improved estimates of d may still involve an uncertainty that is comparable to that inherent in characterizing the mean canopy height, we note that our improvements appear to rectify a bias in estimation of d that was present in the popular stress-based formulations. Along these lines, the vortex-penetration form (14) is convenient and practical, allowing estimation of d via mean wind speed observed at two heights, as is commonly measured.

While we have not (yet) used the new formulations for displacement height in combination with RSL theory, we do note that d cannot alone give proper improvement of dimensionless wind speed or scalar profiles. However, via the present study we re-open a discussion about such: the use of these together, along with refinement of RSL theory for consistency with turbulent transport, is perhaps worthy of further consideration. Without reconsidering RSL theory, since the new formulation works optimally around the canopy top and in the RSL, some existing flux datasets can be reconsidered using the newly derived forms for displacement height. Overall, the new forms for the displacement height d, based on TKE and mixing-layer (vortex penetration) considerations, give generally improved results compared to stress-based forms.