Timestep Buffering to Preserve the Well-Mixed Condition in Lagrangian Stochastic Simulations

Abstract

Using one or more physical time scales as a basis for timestep ($\Delta t$) selection is common in Lagrangian stochastic simulations of particle dispersion. This approach generally works well when the velocity statistics (and thus $\Delta t$) vary slowly but problems such as the $\Delta t$ bias and imbalanced particle fluxes at interfaces can occur when the velocity statistics vary rapidly. These problems can result in violations of the well-mixed condition (WMC) and inaccurate predictions. An additional problem is that unrealistically high (or rogue) particle velocities can occur if $\Delta t$ is too large. A small constant timestep can be used to reduce or eliminate these problems but incurs the penalty of considerable computational cost. A timestep-buffering technique that eliminates abrupt changes in a variable timestep through linear interpolation is demonstrated to be effective at satisfying the WMC and minimizing rogue velocities for particle dispersion in an idealized one-dimensional turbulence regime with a steep gradient. The technique is also shown to be effective when applied to a more realistic three-dimensional system.

1 Introduction

The timestep ($\Delta t$) used to integrate particle paths with Lagrangian stochastic (LS) models of turbulent dispersion (Rodean 1996; Wilson and Sawford 1996; Thomson and Wilson 2013) is commonly selected as a fraction of one or more physical time scales of the process under consideration. The Lagrangian integral time scale ($T_\mathrm{L}$) is arguably the most frequently selected as a basis for timestep selection (e.g., Flesch and Wilson 1992; Flesch et al. 1995; Nasstrom and Ermak 1999; Luhar et al. 2000; Sawford 2004; Shadwick et al. 2007; Postma et al. 2012b), with the restriction that $\Delta t$ is “small” relative to $T_\mathrm{L}$. By comparing analytical and modelled plume widths in homogeneous turbulence, Wilson and Zhuang (1989) demonstrated that $\Delta t = 0.1T_\mathrm{L}$ resulted in a discretization error of about two percent. Sawford (2004) used $\Delta t = 0.02T_\mathrm{L}$ for a micromixing model in homogeneous turbulence and noted that the model predictions changed very little with a smaller timestep. A constant of proportionality, or timestep constant ($\mu _\mathrm{t}$), with a value of 0.02 has been used for simulations of dispersion in inhomogeneous flows as well (e.g., Luhar and Sawford 2005; Postma et al. 2011b).

As LS models began to be used to address more realistic physical processes (for some recent examples, see Lin et al. 2013) with steep gradients and strong inhomogeneities in the turbulence, additional time scales have been added to the selection pool for timestep determination (e.g., Thomson 1987; Stohl and Thomson 1999; Wilson et al. 2010; Lin and Gerbig 2013). Some of these inhomogeneity time scales ($T_\mathrm{I}$) involve gradients of the standard deviation of velocity or the coefficients of the LS model and consequently can be very small. Applying such small timesteps globally would needlessly increase the computational burden in regions with slowly-varying velocity statistics. This issue can be circumvented by selecting the timestep to be a fraction of the minimum time scale at a given position: $\Delta t = \mu _\mathrm{t}\min (T_\mathrm{L},T_\mathrm{I})$, for example.

Simulating real-world processes requires a physically realistic LS model. Thomson and Wilson (2013) review the evolution toward increased physical realism of LS models, the principal criterion being the well-mixed condition (WMC; Thomson 1987). If the particles are well mixed, then they retain their initial distribution after any number of timesteps. For example, if the turbulence is assumed to be Gaussian then the velocities of the particles are initialized in accordance with the Gaussian probability density function (PDF). If the model satisfies the WMC, then at any time during the simulation the velocities of the particles will have retained their initial Gaussian distribution. Violation of the WMC results in the accumulation of particles in regions of low velocity variance.

While the derivation of a well-mixed LS model does not require quantification of the timestep, practical applications have shown that $\Delta t$ must be sufficiently small or violations will occur. Violations of the WMC can also occur when $\Delta t$ varies with position, which results in a “$\Delta t$ bias error” (Wilson and Flesch 1993). Yet another mechanism leading to violation the of WMC is a large discontinuity in the flow (Thomson et al. 1997). In this situation, the particle fluxes on each side of the interface are imbalanced. A reflection/transmission algorithm was proposed to eliminate this imbalance. Lin et al. (2003) and Lin and Gerbig (2013) utilized a similar approach for the highly inhomogeneous planetary boundary layer.

Along with difficulties enforcing the WMC, another complication arising from the use of inhomogeneous flows to drive LS models is the generation of unrealistically high particle velocities. These are commonly referred to as rogue trajectories, rogue velocities or simply rogues (Luhar and Britter 1989; Wilson and Yee 2000; Yee and Wilson 2007; Postma et al. 2012a; Wilson 2013). The qualifier “unrealistic” is subjective, thus it is common for there to be a predefined velocity threshold, usually in terms of the local standard deviation of velocity $\sigma _u$, that defines a rogue. For example, a particle with velocity $|u| > r\sigma _u$ where $r$ is a positive real number is considered a rogue. Once flagged as such, the particle velocity is usually reinitialized based on the local velocity statistics.

A shortcoming of this definition is that it does not capture all particles with velocities that are inconsistent with the Eulerian velocity statistics used to drive the particle dispersion. Postma et al. (2012a) found that many particles require two or three timesteps to reach the rogue velocity threshold. During these timesteps, the velocities of these particles are inconsistent with the Eulerian velocity statistics but below the rogue velocity threshold. They go undetected, violate the WMC and contribute to inaccurate predictions. It may therefore be more accurate to define rogue velocities as those that are inconsistent with the Eulerian velocity statistics. Since it would be difficult to determine whether or not at any given timestep a particle velocity is inconsistent with the Eulerian velocity statistics, avoidance of rogue velocities is the best approach.

Yee and Wilson (2007) explain that rogue velocities arise from the inability of the forward Euler scheme to maintain control of numerical round-off errors, which exacerbates dynamical instabilities in the stiff generalized Langevin equations. They proposed a semi-analytical fractional timestep integration scheme that eliminates rogue velocities in certain situations but the model no longer satisfies the WMC. Another approach to prevent rogue velocities is simply to reduce $\Delta t$. Wilson (2013) put forth the suggestion that rogue velocities may occur as a result of $\Delta t$ failing to satisfy some limitation implicit to the velocity statistics and demonstrated such a failure for an idealized one-dimensional flow consisting of two zones of homogenous turbulence connected by a region of inhomogeneous turbulence.

In the following, we use the same one-dimensional flow to evaluate a timestep-buffering technique that permits the integration of particle paths over steep gradients while satisfying the WMC and eliminating excessive rogue velocities. Due to the varying velocity statistics in different regions of flow, the time scales used as the basis of timestep selection can vary considerably in space. These variable timesteps combined with changing velocity statistics can, under certain conditions, lead to violations of the WMC and the generation of rogue velocities. The timestep buffers proposed herein linearly join regions with different timesteps so that at any given step there is only a small change in $\Delta t$.

Motivation can be found in Postma et al. (2012a), where it is demonstrated that rogue velocities break the first-order consistency requirement of a particular implementation of the Interaction by Exchange with the Conditional Mean micromixing model (hereafter, the micromixing model). That is, the mean concentration field predicted by the micromixing model is not equal to the mean concentration field predicted by a traditional LS marked-particle model. No solution for this problem is presented. The objective is to develop a simple solution that can easily be implemented into existing computer programs of varying complexity.

The reflection/transmission algorithm used by Thomson et al. (1997), Lin et al. (2003) and Lin and Gerbig (2013) requires a particle to stop at each interface to determine if it should be reflected or transmitted. This has been applied to boundary-layer scales of hundred of metres to kilometres with resolutions in the range of 30–100 m. Each level within the boundary layer was treated as homogenous with no gradients in velocity variance, and the approach has been shown to satisfy the WMC for these boundary-layer scales.

The motivating problem in Postma et al. (2012a) is micrometeorological with length scales of few metres and resolutions of fractions of metres. The one-dimensional turbulence regime that is used to evaluate the timestep-buffering technique has a narrow velocity variance transition zone with a non-zero gradient. This will be resolved at a scale of few millimetres. Using the reflection/transmission algorithm, a particle would be stopped approximately twenty-five times while traversing the transition zone to determine if it should be reflected or transmitted. This would be highly inefficient. Further, setting the gradients to zero may not be appropriate at micrometeorological scales. For these reasons, along with the fact that the reflection/transmission algorithm has elsewhere been evaluated, it is not included in the evaluation of the timestep-buffering technique.

Section 2 outlines a one-dimensional well-mixed LS model and the timestep-buffering technique and application of the technique to a three-dimensional system is also described. Section 3 evaluates the performance of the timestep-buffering technique for one and three-dimensional systems, and Sect. 4 summarizes the findings.

2 Model Equations and Numerical Implementation

A one-dimensional LS model formulated in accordance with the WMC is outlined in Sect. 2.1. Section 2.2 presents the timestep-buffering technique and details the numerical set-up for the one-dimensional simulations, while Sect. 2.3 demonstrates application of the technique to a three-dimensional system.

2.1 One-Dimensional Well-Mixed LS Model

The evolution of the position ($x$) and velocity ($u$) of a fluid element can be modelled in one-dimensional stationary turbulence using a first-order Langevin approach (e.g. Wilson and Sawford 1996; Rodean 1996; Thomson and Wilson 2013),

$$\begin{aligned} \mathrm{d}x&= u\mathrm{d}t, \end{aligned}$$

(1)

$$\begin{aligned} \mathrm{d}u&= a(u,x)\mathrm{d}t+\sqrt{C_0\epsilon }\mathrm{d}\xi . \end{aligned}$$

(2)

The first term on the right-hand side of Eq. 2 represents drift and the coefficient $a$ is the deterministic acceleration. The second term on the right-hand side represents stochastic diffusion where $\mathrm{d}\xi$ is a Wiener process with mean zero and variance equal to the infinitesimal timestep $\mathrm{d}t$. The coefficient $b = \sqrt{C_0\epsilon }$ ensures consistency between the LS model and Kolmogorov’s theory of local isotropy. The dimensionless constant $C_0$ arises from Kolmogorov’s similarity law for the second-order Lagrangian structure function, and $\epsilon$ is the turbulent kinetic energy dissipation rate.

By specifying the form of the PDF for the Eulerian velocity fluctuations to be Gaussian with variance $\sigma _u^2 = \sigma _u^2(x)$,

$$\begin{aligned} g_\mathrm{a}(u,x) = \frac{1}{\sqrt{2\pi }\sigma _u}\exp \left( {-\frac{u^2}{2\sigma _u^2}}\right) , \end{aligned}$$

(3)

the unique, well-mixed (Thomson 1987) expression for the deterministic acceleration is

$$\begin{aligned} a(u,x) = -\frac{C_0\epsilon }{2\sigma _u^2}u +\frac{1}{2}\frac{\partial \sigma _u^2}{\partial x} \left( 1+\frac{u^2}{\sigma _u^2} \right) . \end{aligned}$$

(4)

While a small number of stochastic differential equations can be solved analytically, the solutions to the remainder must be approximated numerically. A common, and perhaps the simplest, technique for integrating stochastic differential equations is the forward Euler-Maruyama (or simply Euler) scheme, which is detailed in several sources (e.g., Kloeden and Platen 1992; Higham 2001). Space and time are discretized and the derivatives replaced by forward approximations. Under this scheme, the position and velocity of a fluid element at step $n+1$ can be explicitly calculated as

$$\begin{aligned} x_{n+1}&= x_n + u_n \Delta t_n, \end{aligned}$$

(5)

$$\begin{aligned} u_{n+1}&= u_n + a(u_n,x_n)\Delta t_n+\sqrt{C_0\epsilon }\Delta \xi _n , \end{aligned}$$

(6)

where $\Delta \xi$ is an incremental Wiener process with mean zero and variance equal to the discretized timestep $\Delta t$.

2.2 Numerical Set-Up and Timestep Buffering

A ramp function described by Wilson (2013) with zero mean velocity and variance profile

$$\begin{aligned} \sigma _u^2 = \left\{ \begin{array}{lll} \sigma _1^2 &{}\quad x < x_{\mathrm{tr1}} &{}\quad \text {(zone 1)},\\ \sigma _1^2+m(x+D/2) &{}\quad x_{\mathrm{tr1}} \le x \le {x_{\mathrm{tr2}}} &{}\quad \text {(transition zone)},\\ \sigma _2^2 &{}\quad x > x_\mathrm{{tr2}} &{}\quad \text {(zone 2)},\\ \end{array} \right. \end{aligned}$$

(7)

where $x_{\mathrm{tr1}} = -D/2, x_\mathrm{{tr2}} = D/2$ and $m = \Delta \sigma ^2_u/\Delta x = (\sigma _2^2-\sigma _1^2)/D$ is used to drive the particle dispersion along the $x$-axis. It consists of two broad zones of homogeneous turbulence joined by a transition zone of width $D$ centred on $x = 0$. This simple one-dimensional flow characterizes the discontinuities prevalent in the gridded flow fields commonly used to drive more complex, three-dimensional LS models. It is ideal for studying the effects of timestep selection on the satisfaction of the WMC and generation of rogue velocities.

Two time scales, and combinations thereof, are used to select the timesteps for the integration of Eqs. 5 and 6: $T_\mathrm{L} = 2\sigma ^2_u/C_0\epsilon$ and $T_\mathrm{d} = \sigma _u/\max (|u\partial \sigma _u/\partial x|)$, which for convenience is referred to as the derivative time scale.

Unless otherwise specified, one-dimensional simulations use $\sigma ^2_1 = 1$ m$^2$ s$^{-2}$, $\sigma ^2_2 = 2$ m$^2$ s$^{-2}$ and $D = 0.1$ m. Any particle with a speed greater than six times the local standard deviation ($|u| > 6\sigma _u$) is considered to be rogue. Since the maximum speed of a particle is $\pm 6\sigma _u$ and $\partial \sigma ^2_\mathrm{w}/\partial x$ is constant, the derivative time scale simplifies to $T_\mathrm{d} = (1/6)\partial \sigma _u/\partial x$. The timestep constant is $\mu _t = 0.02$. All simulations use $C_0\epsilon = 1~\text {m}^2\,\text {s}^{-3}$, which, although not representative of what is observed near a boundary (e.g., the ground), is suitable for the idealized one-dimensional analysis below. The three-dimensional application of the timestep-buffering technique in Sect. 2.3 incorporates realistic treatment of $\epsilon$.

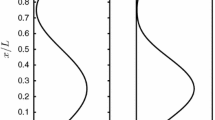
Figure 1 shows profiles of the $\Delta t$ for $T_\mathrm{L}$- and $T_\mathrm{d}$-based timestep selection and some frequently used terms and locations. In zones 1 and 2, $T_\mathrm{L}$ is constant and $T_\mathrm{d}$ is zero. In the transition zone, $T_\mathrm{L}$ varies with $\sigma ^2_u$ (since $C_0\epsilon$ is constant) and $T_\mathrm{d}$ is non-zero (see inset of Fig. 1) and considerably smaller than $T_\mathrm{L}$. As discussed in Sect. 1, these discontinuities in the flow and timestep can give rise to violations of the WMC.  The abrupt changes in the timestep can be eliminated through the use of timestep buffers, which linearly interpolate between the edges of the transition zone ($x_{\mathrm{tr1}}$ and $x_{\mathrm{{tr2}}}$) and the edges of the buffers ($x_{\mathrm{b1}}$ and $x_{\mathrm{b2}}$; to be defined presently).¹

The width of the timestep buffers are sufficient that particles, in one timestep, cannot traverse them. Since $\max (|u|) = 6\sigma _u$, we have $x_{\mathrm{b1}} = x_{\mathrm{tr1}}-6\sigma _1\mu _tT_{\mathrm{L}_1}$ and $x_{\mathrm{b2}} = x_{\mathrm{{tr2}}}+6\sigma _2\mu _tT_{\mathrm{L}_2}$. With the extents defined, the buffered timesteps are calculated as,

$$\begin{aligned} \Delta t(\text {buffer 1})&= \frac{\Delta t(x_{\mathrm{b1}})-\Delta t(x_{\mathrm{tr1}})}{x_{\mathrm{b1}}-x_{\mathrm{tr1}}} (x-x_{\mathrm{tr1}})+\Delta t(x_{\mathrm{tr1}}),\end{aligned}$$

(8)

$$\begin{aligned} \Delta t(\text {buffer 2})&= \frac{\Delta t(x_{\mathrm{b2}})-\Delta t(x_{\mathrm{{tr2}}})}{x_{\mathrm{b2}}-x_{\mathrm{{tr2}}}} (x-x_{\mathrm{{tr2}}})+\Delta t(x_{\mathrm{{tr2}}}). \end{aligned}$$

(9)

where the resulting buffered timestep is shown as the solid line in Fig. 1.

The final component of the timestep-buffering technique is timestep randomization. As designed, particles moving towards the transition zone will take, on average, larger steps than particles moving away from the transition zone. This is the $\Delta t$ bias described in Wilson and Flesch (1993). Moreover, a second bias arises since a particle can jump from just outside a buffer in zones 1 or 2 to deep into the buffer (i.e., towards the transition zone). The inverse is not true. Particles cannot jump from deep into buffers out into zones 1 or 2. The $\Delta t$ bias gives rise to a small bias velocity but the second bias can, as will be shown in Sect. 3.3, lead to a significant violation of the WMC.

Timestep randomization is used to eliminate the second bias. After the timestep for a particular step has been determined, it is uniformly randomized between its current value and the smallest timestep in the domain, $\Delta t_{\mathrm{min}}$. The timestep to be used for the step is therefore given by

$$\begin{aligned} \Delta t_{\mathrm{new}} = (\Delta t_{\mathrm{old}}-\Delta t_{\mathrm{min}})\chi +\Delta t_{\mathrm{min}}, \end{aligned}$$

(10)

where $\chi$ is a random deviate drawn uniformly from [0,1]. The minimum timestep for the current set-up is found within the transition zone and is $\Delta t_{\mathrm{min}} = 0.02T_\mathrm{d} = 8.05\times 10^{-4}~\mathrm {s}$.

2.3 Timestep Buffering in Three Dimensions

A LS marked-particle model along with the LS micromixing model are used to demonstrate the timestep-buffering technique in three dimensions. Both models are identical to those used by Postma et al. (2012a) to demonstrate how rogue velocities can break the first-order consistency requirement. Both the marked particle and micromixing models utilize three-dimensional Gaussian turbulence and model the deterministic acceleration in accordance with Thomson’s simplest solution for three-dimensional turbulence (Thomson 1987). The models work as a pair with the marked-particle model pre-calculating the conditional mean concentrations to be used by the micromixing model. Thorough descriptions of the models can be found in Postma et al. (2011a).

Rogue velocities break the first-order consistency requirement through two mechanisms. First, they alter the accumulation of residence time (used to calculate the conditional mean concentration field), which is a function of position and conditioned on velocity. Second, they result in inaccurate normalization constants for the conditional mean concentrations. These constants are calculated using the analytical velocity PDF of the driving Eulerian velocity statistics. The combination of an improper accumulation of residence times and inaccurate normalization constants, both a product of the particles not propagating in accordance with the velocity PDF (i.e., rogue velocities or other violations of the WMC), results in a first-order inconsistency. See Postma et al. (2012a) for further details.

As in Postma et al. (2012a), a horizontally-homogeneous wall-shear-layer flow (Fackrell and Robins 1982) with a friction velocity $u_* = 0.188\,\mathrm{m~s^{-1}}$ and a roughness length $z_0 = 2.88 \times 10^{-4}\,\mathrm{m}$ is modified to include a rogue cell in the volume bounded by $2.85 \le x < 3.00~\mathrm {m}, 0.30 \le y < 0.375~\mathrm {m}$ and $0.60 \le z < 0.63~\mathrm {m}$. The centre of the rogue cell is $(x_\mathrm{r},y_\mathrm{r},z_\mathrm{r}) = (2.925,0.3375,0.615)~\mathrm {m}$. The bin widths of the driving velocity statistics in the $x, y$ and $z$ directions are: $\Delta B_x = 0.15~\mathrm {m}, \Delta B_y = 0.075~\mathrm {m}$ and $\Delta B_z = 0.30~\mathrm {m}$. There is no interpolation of the velocity statistics to the particle position within each grid cell.

Within the rogue cell, the variance of vertical velocity is increased to twenty times its wall-shear-layer value.² This results in sharp discontinuities in the $\sigma ^2_w$ profile and steep gradients in the $x, y$ and $z$ directions (i.e., $\partial \sigma ^2_w/\partial x, \partial \sigma ^2_w/\partial y, \partial \sigma ^2_w/\partial z$) surrounding the rogue cell. Without intervention, these discontinuities and gradients will produce rogue velocities and break the required first-order consistency of the micromixing model.

Two interventions are employed. The first is to build a $\sigma ^2_w$ transition zone around the rogue cell. Consider the grid cell one cell upstream of the rogue cell and at the same spanwise and vertical locations. In this upstream cell, $\partial \sigma ^2_w/\partial x > 0$, which will act to increase the vertical velocity of a particle travelling through that cell. However, due to the discretized nature of the driving velocity statistics, $\sigma ^2_w$ of the grid cell cannot increase as it would in a continuous system. A particle with increasing vertical velocity combined with a fixed $\sigma ^2_w$ in the grid cell is a recipe for rogue velocities. A transition zone, which can be regarded as a sub-grid process, can help to prevent this mechanism of rogue velocity formation.

The second intervention is to buffer the timestep around the rogue cell to ensure particles do not take too large a step when their deterministic accelerations are increased due to the non-zero gradients surrounding the rogue cell, helping to prevent rogue velocities that may form through the $a\Delta t$ or $b\Delta \xi = \sqrt{C_0\epsilon }\Delta \xi$ contributions to the velocity increment in Eq. 6.

Both the $\sigma ^2_w$ transition zone and $\Delta t$ buffer are constructed using truncated ellipsoids. For a particle at position $(x,y,z)$, first calculate

$$\begin{aligned} R^2_\mathrm{e} = \left( \frac{x-x_\mathrm{r}}{a_\mathrm{e}}\right) ^2 + \left( \frac{y-y_\mathrm{r}}{b_\mathrm{e}}\right) ^2 + \left( \frac{z-z_\mathrm{r}}{c_\mathrm{e}}\right) ^2, \end{aligned}$$

(11)

where $a_\mathrm{e}, b_\mathrm{e}$ and $c_\mathrm{e}$ are respectively the semi-principal axes in the $x, y$ and $z$ directions. Any particle with $R^2_\mathrm{e} \le 1$ is within the ellipsoid. We desire $\sigma ^2_w$ and $\Delta t$ to reach the values of rogue cell at the boundaries of the rogue cell, not at the centre of it, and this requires the ellipsoid to be truncated. We define a cut-off point $C^2$ so that the rate of change of $\sigma ^2_w$ within the truncated transition ellipsoid is

$$\begin{aligned} m_{\mathrm{tr}} = \frac{\sigma ^2_w(x_\mathrm{r},y_\mathrm{r},z_\mathrm{r})-\sigma ^2_w(x,y,z)}{1-C^2}. \end{aligned}$$

(12)

The variance of vertical velocity within the truncated transition ellipsoid is then given by

$$\begin{aligned} \sigma ^2_w\left( C^2 \le R^2_\mathrm{e} \le 1\right) = \sigma ^2_w(x,y,z)+m_{\mathrm{tr}}\left( 1-R^2_\mathrm{e}\right) . \end{aligned}$$

(13)

The timestep buffer is constructed in a similar manner. First, the minimum buffer timestep is selected as $\Delta t_\mathrm{b} = \mu _t\min (T_{\mathrm{d}_i})= \mu _t\min (T_{\mathrm{d}_u},T_{\mathrm{d}_v},T_{\mathrm{d}_w})$. A unified buffer timestep must be chosen otherwise buffering would depend on the direction a particle is moving since $T_{\mathrm{d}_u},T_{\mathrm{d}_v}$ and $T_{\mathrm{d}_w}$ are in general not equal. Then the buffer slope is calculated as

$$\begin{aligned} m_\mathrm{b} = \frac{\Delta t_\mathrm{b}-\Delta t(x,y,z)}{1-C^2}, \end{aligned}$$

(14)

and the buffered timestep is calculated as

$$\begin{aligned} \Delta t\left( C^2 \le R^2_\mathrm{e} \le 1\right) = \Delta t(x,y,z) +m_\mathrm{b}\left( 1-R^2_\mathrm{e}\right) . \end{aligned}$$

(15)

The derivative time scale in the rogue cell is zero due to the central-difference approximations used to calculate the derivatives. In addition to the buffering, the timestep in the rogue cell is set to $\Delta t_\mathrm{b}$ to produce a smooth timestep profile across the entire buffered region,

$$\begin{aligned} \Delta t\left( R^2_\mathrm{e} < C^2\right) = \Delta t_\mathrm{b}. \end{aligned}$$

(16)

Finally, timestep randomization in accordance with Eq. 10 is performed. The semi-principal axes are selected to be $a_{\mathrm{e}} = 1.5\Delta B_x, b_{\mathrm{e}} = 1.5\Delta B_y$ and $c_{\mathrm{e}} = 1.5\Delta B_z$ to allow the transition zone and buffer to begin at the boundaries of the neighbouring cells farthest from the rogue cell. Using the $x$-coordinate as an example, we have $x_\mathrm{r}-a_\mathrm{e} = 2.70~\mathrm {m}$, which is the upstream edge of the cell directly upstream of the rogue cell.

Recall that in the one-dimensional case in Sect. 2.2, the width of the $\Delta t$ buffers is determined by considering the maximum distance a particle can travel in one timestep (see paragraph above Eqs. 8 and 9). Such consideration is not necessary in this three-dimensional example since the resolution of the driving velocity statistics determines the semi-principal axes of the truncated ellipsoid and the bin widths are significantly larger than the maximum travel distance of a particle. For the grid cell directly upstream of the rogue cell, we have $(\overline{u}+6\sigma _u)\mu _tT_\mathrm{L}/\Delta B_x\approx 0.25$. Similarly for $y$ and $z$. It is not possible for the particles to jump in one timestep over the timestep buffer.

The value of the cut-off point is related to the resolution of the driving velocity statistics and to the semi-principal axes. When measured along the $x, y$ or $z$ axes, the centre of the rogue cell is half a bin width away from the boundaries of the rogue cell. Setting $y = y_\mathrm{r}, z = z_\mathrm{r}$ and on the upstream face of the rogue cell, $x = 2.85~\mathrm {m}$, Eq. 11 gives $R^2_\mathrm{e} = ((2.85-2.925)/a_{\mathrm{e}})^2 = (0.5\Delta B_x/1.5\Delta B_x)^2\approx 0.111$; identically for the $y$ and $z$ directions. The required cut-off is therefore $C^2 = (0.5/1.5)^2 \approx 0.111$.

The results of the truncated ellipsoid transition and buffering processes are shown in Fig. 2, which displays streamwise transects of $\sigma ^2_w$ and $\Delta t$ for three different scenarios along $(y,z) = (y_\mathrm{r},z_\mathrm{r})$ and in the vicinity of the rogue cell.

Fig. 2

Streamwise transects for $(y,z) = (y_r,z_r)$ in the vicinity of the rogue cell. a The vertical velocity variance and b the timestep used for the three-dimensional micromixing model simulations. Note the A and B transects overlap in (a). The transects are identified by their Sect. 3.4 run letters, timestep selection criteria and other interventions: tran. transition zone; buf. timestep buffering and ran. timestep randomization

3 Results and Discussion

This section presents results from one-dimensional and three-dimensional simulations. In Sect. 3.1, the timestep-buffering technique in one-dimension is compared with other timestep selection criteria and its effectiveness at maintaining the WMC evaluated. Section 3.2 investigates the velocity bias produced by the constant-slope buffers while Sect. 3.3 investigates the sensitivity to the spatial resolution of timestep buffering and timestep randomization. Section 3.4 examines for a three-dimensional micromixing model the effectiveness of timestep buffering, and a $\sigma ^2_w$ transition zone at eliminating rogue velocities and achieving first-order consistency with a traditional LS marked-particle model. Lastly, Sect. 3.5 suggests further improvements that could be made to the technique.

3.1 Dispersion in One-Dimensional Inhomogeneous Turbulence

We now consider particle dispersion in the one-dimensional inhomogeneous turbulence regime given by Eq. 7. A total of $N = 10^9$ particles are initialized uniformly in the domain $x \in [-5,5]~\text {m}$ and their initial velocities assigned in accordance with Eqs. 3 and 7. Perfect reflection is used to keep the particles within the domain. Equations 5 and 6 are numerically integrated to $t_{\mathrm{max}} = 0.20~\text {s}$, a time sufficient for particles to cross the transition zone (if they are in the vicinity).

The sub-domain $x\in [-1,2]~\text {m}$ (asymmetry is to accommodate differing buffer widths in zones 1 and 2) is discretized into $N_x = 750$ bins with $\Delta x = 0.004~\text {m}$. The velocity space $u\in [-6\sigma _u,6\sigma _u]$ was divided into $N_u = 120$ bins with $\Delta u = 0.1\sigma _u$. When $t \ge t_{\mathrm{max}}$, the particle is binned accordingly in position-velocity space. After all $N$ particles have propagated, numerical velocity PDFs $f_u$ are calculated, and a mean absolute error ($\textit{MAE}$)

$$\begin{aligned} \textit{MAE} =\frac{1}{N_\mathrm{d}}\sum _{j=1}^{N_u}\sum _{i=1}^{N_x}\left| f_u(u_j,x_i)-g_\mathrm{a}(u_j,x_i)\right| , \end{aligned}$$

(17)

where $N_\mathrm{d} = N_x N_u$, is used to quantify the results. If the numerical velocity PDF is equal to the analytical Gaussian PDF then $\textit{MAE} = 0$.

A misleadingly small $\textit{MAE}$ can be achieved if the numerical PDF closely conforms to the analytical Gaussian PDF at most comparison locations and has only a small number of significant deviations from it. This situation is countered by identifying the maximum single point error

$$\begin{aligned} E_{\mathrm{max}} = \max \left| f_u(u_j,x_i)-g_\mathrm{a}(u_j,x_i)\right| , \end{aligned}$$

(18)

for $1 \le j \le N_u$ and $1 \le i \le N_x$ along with qualitative evaluation of the numerical PDFs in regions where WMC violations are expected: near the boundaries of, and within, the transition zone and near the buffer boundaries, if applicable.

In addition to the time scales $T_\mathrm{L}$ and $T_\mathrm{d}$, the times to the transition boundaries, $\Delta t_{\mathrm{tr1}} = (x_{\mathrm{tr1}}-x)/u$ and $\Delta t_{\mathrm{{tr2}}} = (x_{\mathrm{{tr2}}}-x)/u$, which are only valid when positive (i.e., when a particle is moving towards a boundary), form the timestep selection pool for four variable timestep simulations. A fifth simulation uses a constant timestep throughout the entire domain. Table 1 summarizes the timestep selection and performance of the five runs to be examined while timestep profiles for Runs 1–4 (excluding $\Delta t_{\mathrm{tr1}}$ and $\Delta t_{\mathrm{{tr2}}}$, which vary with the velocity of the particle) are shown in Fig. 1. Note that the $\textit{MAE}$ values are significantly smaller than the $E_{\mathrm{max}}$ values since they are averaged by $N_\mathrm{d}$.

Table 1 Timestep selection criteria and performance measures for the one-dimensional runs

Figure 3 shows the numerical PDFs predicted by the five runs in Table 1 at the boundary between zone 1 and the transition zone (i.e., $x_{\mathrm{tr1}}$) and near the centre of the transition zone. Runs 1–3 fail to satisfy the WMC at $x_{\mathrm{tr1}}$ while Runs 4 and 5 show good conformance with the Gaussian PDF. Although ending a particle step at the transition zone boundaries (Run 3) improves the numerical PDF, a large violation of the WMC remains. The results are slightly different near the centre of the transition zone: Runs 1 and 2 still fail to satisfy the WMC, Run 3 shows good conformance with the Gaussian PDF, and Runs 4 and 5 once again satisfy the WMC.

There is some correlation between the number of rogue velocities and satisfaction of the WMC. Runs 1 and 2, both of which fail to satisfy the WMC, have respectively 9949 and 835 rogue velocities, but Run 3 has only five rogue velocities and also does not in all locations satisfy the WMC. Both Runs 4 and 5 have a comparable number of rogue velocities as Run 3, and at all locations satisfy the WMC.  It appears that the absence of a significant number of rogue velocities is a necessary but not sufficient requirement for WMC satisfaction.

Examining the errors in Table 1 reveals that Runs 1–4 have $\textit{MAE}$ values of the same order of magnitude and Run 5 has an $\textit{MAE}$ that is an order of magnitude smaller than the other runs. The $\textit{MAE}$ for Run 4 is approximately 2.7–3.7 times smaller than Runs 1–3 and twice as large as Run 5. The similar values for the $\textit{MAE}$ are due to the fact that the numerical PDFs may be very accurate in all but a few locations, where large violations of the WMC occur. That said, Runs 4 and 5 do satisfy the WMC and have the lowest $\textit{MAE}$ values.

The maximum one-point errors are more revealing. Runs 1–3 have $E_{\mathrm{max}}$ values that are an order of magnitude larger than Runs 4 and 5, as can be seen in the top panel of Fig. 3. Qualitatively assessing other locations reveals that the numerical PDFs for Runs 1–3 have some significant departures from the Gaussian PDF. In contrast, the numerical PDFs from Runs 4 and 5 conform well to the Gaussian PDF at all locations. The success of Runs 4 and 5 at satisfying the WMC is in part attributable to the use of significantly smaller timesteps either around the transition zone or in the entire domain. Consequently, the simulation times for these runs are larger. While Run 5 produced the most accurate results with a small constant timestep, it took 195 min to do so. Run 4 had results of similar accuracy and took approximately 15 min, roughly eight percent of the time of Run 5. The Run 4 simulation time is two to three times larger than Runs 1–3, but that is an acceptable trade off for accurate results.

Fig. 3

Analytical (solid line) and numerical (symbols) PDFs showing WMC satisfaction or violation for the runs in Table 1. a is for the boundary between zone 1 and the transition zone ($x_{\mathrm{tr1}}$). b is for near the centre of the transition zone. The legends show the run number and the timestep selection criteria and apply to both panels

Looking more closely into the causes of WMC violations in Runs 1–3 reveals a few causes: particles jumping directly between zones 1 and 2 without going through the transition zone; an imbalance in the number or particles travelling between zones 1 and 2, and a mixing of particles with significantly different timesteps.

Particles far from the transition zone experience homogeneous turbulence and tend to remain in the same zone after each timestep. In contrast, particles close to the transition zone may experience in a single timestep inhomogeneities either by changing from zone 1 to zone 2 (or vice versa) or by entering the transition zone. Since $\Delta t_1 < \Delta t_2$ and $\sigma _1 < \sigma _2$ (i.e., particles can have higher velocities in zone 2), particles are biased toward moving from zone 2 to zone 1. This is similar to the $\Delta t$ bias described in Wilson and Flesch (1993). Both Runs 1 and 2 have approximately $3.55\times 10^6$ particles jump in a single timestep over the transition zone, and of these, approximately $3.51\times 10^6$ travel from zone 2 to zone 1. Since a similar number of particles does not leave zone 1 (i.e., the particle fluxes across the transition zone are not balanced), the excess particles with negative velocities accumulate and result in the secondary maxima seen around $u/\sigma _u \approx -1.8$ in the $f_u$ profiles for these runs in the top panel of Fig. 3.

Ending a particle step at the transition boundaries reduces the WMC violation by preventing particles from jumping over the transition zone. Run 3 had no particles that jump the transition zone in a single timestep and has a lower $\textit{MAE}$ value and $E_{\mathrm{max}}$ than is the case for Runs 1 or 2. There is also no secondary maximum in the negative tail of the numerical PDF at $x_{\mathrm{tr1}}$.  However, the violation of the WMC is still unacceptably large.

Figure 4 displays two causes of WMC violations. Two simulations using $\sigma _u^2 = 1~\text {m}^2\,\text {s}^{-2}$ are used to produce the $f_u$ profiles; one simulation uses the timestep $\Delta t = 0.01T_\mathrm{L} = 0.02~\mathrm {s}$ for $x < 0$ and $\Delta t = 0.02T_\mathrm{L} = 0.04~\mathrm {s}$ for $x > 0$, both of which are sufficiently small to satisfy the WMC in homogeneous turbulence. The other simulation uses $\Delta t = 0.02T_\mathrm{L} = 0.04~\text {s}$ and is lacking the stochastic diffusion term from Eq. 6.

The WMC violation is evident in the run with the factor two change in the timestep, despite each timestep being sufficiently small on its own to satisfy the WMC. The secondary maximum at $u/\sigma _u \approx -0.5$ has similar counterparts in the $f_u$ profiles for Runs 1 and 2 in the top panel of Fig. 3. This violation is a result of imbalanced particle fluxes at $x = 0$ (Thomson et al. 1997). Since there is homogeneous turbulence across the domain, the imbalance in particles jumping across $x = 0$ is reduced relative to Runs 1 and 2. There are 390 more particles going from positive $x$ to negative $x$ than the other way around, hence the WMC violation is less severe than is shown in Fig. 3. As the change in $\Delta t$ across $x = 0$ increases, so too does the severity of the WMC violation. Adding a velocity variance change across the $x = 0$ boundary increased the particle flux imbalance and WMC violation further. This is the same process as is occurring in Runs 1 and 2.

Fig. 4

Two causes of WMC violations: an abrupt change in the timestep (triangles) and a negligible stochastic diffusion term (circles)

The WMC violation is also evident in the run that is lacking a stochastic diffusion term. In homogeneous turbulence, the deterministic term in Eq. 4 drives the velocity of the particles towards the mean velocity, which in this case is zero. The stochastic diffusion term randomizes the particle velocities; without it, the $f_u$ profile becomes longer and narrower with each step. The stochastic term of Eq. 4 ensures consistency with Kolmogorov’s theory of local isotropy; without it, the consistency is broken.

None of the runs herein lacks a stochastic diffusion term, however many have disparate timesteps between zones. The timesteps at selected locations are $\Delta t_1 = 0.04~\text {s}, \Delta t_{\mathrm{tr1}} = \Delta t_{\mathrm{{tr2}}} = 0.02, T_\mathrm{d} = 8.05\times 10^{-4}~\mathrm {s}$ and $\Delta t_2 = 0.08~\text {s}$. Consider a position in zone 1 very close to the $x_{\mathrm{tr1}}$ boundary. Particles in zone 1 approaching $x_{\mathrm{tr1}}$ from the left have $\overline{\Delta \xi ^2} = \Delta t_1$ whereas particles in the transition zone approaching $x_{\mathrm{tr1}}$ from the right have $\overline{\Delta \xi ^2} \approx \Delta t_{\mathrm{tr1}}$. Around $x_{\mathrm{tr1}}$, there is a mixing of particles with stochastic diffusion terms of vastly differing magnitudes. In zone 1, the contribution to maintaining local isotropy of particles that have just left the transition zone (and thus have $\overline{\Delta \xi ^2} \approx \Delta t_{\mathrm{tr1}}$) is negligible compared with those particles in zone 1 with $\overline{\Delta \xi ^2} = \Delta t_1$. This results in a narrowing of the numerical PDF and violation of the WMC.

This is likely the main cause of the WMC violation seen in Run 3 at $x_{\mathrm{tr1}}$. Particles are forced to terminate a step at the transition-zone boundaries so that particles cannot therefore jump across boundaries, thus eliminating this type of flux imbalance as a source of the violation. However, $x_{\mathrm{tr1}}$ in Run 3 is a location where particles with vastly different timesteps mix, which can also lead to a WMC violation. By the middle of the transition zone (bottom panel of Fig. 3), all of the particle in Run 3 will have equal and small timesteps ($\Delta t = 0.02T_\mathrm{d}$) and, as seen in the figure, there is no violation of the WMC at this location. The large violations seen in the PDFs for Runs 1 and 2 are a result of imbalanced particle fluxes and/or a mixing of particles with differing timesteps.

Similar to WMC violations, rogue velocity genesis can result from particles jumping from one zone to another as well as from too large a timestep. Both Runs 1 and 2 have a significant number of particles jumping from zone 2 to zone 1. If a particle with $u = 5\sigma _2$ in zone 2 crosses into zone 1, its velocity relative to the lower velocity variance is $u=7.07\sigma _1$. The particle is rogues in zone 1 whereas it is not in zone 2. Of the 9949 rogues in Run 1, 2362 are a result of the change in $\sigma _u$ when a particle changes zones. Of the 835 rogues in Run 2, 732 are a result of the change in $\sigma _u$ when a particle changes zones. Recall that particles in both of these runs have a significant fraction that jump directly into zone 1 from zone 2.

The forward Euler scheme uses velocity statistics from the current location to move a particle to its new location. A particle beginning in zone 2 will have $a, b, \Delta t$ and $u$ suitable for and permissible in zone 2. This may not hold true should the particle move to a new location with differing velocity statistics. In particular, $u$ may exceed the rogue threshold at the new location.

The remainder of the rogue velocities are a result of large changes to the particle velocity through the deterministic term $a\Delta t$ and/or the stochastic term $b\Delta \xi$, of Eq. 6. Since the coefficients $a$ and $b$ are products of the driving velocity statistics and turbulent kinetic energy dissipation rate, it is $\Delta t$ that is responsible for the formation of rogue velocities. Run 1 has the largest timesteps throughout the domain and has the most rogue velocities. Of those not formed through the $\Delta \sigma _u$ mechanism, 6482 are a result of the $a\Delta t$ mechanism and 179 a result of the $b\Delta \xi$ mechanism. The remainder are a result of the combination of all mechanisms. Run 2 has fewer rogues on account of using $\Delta t = 0.02T_\mathrm{d}$ in the transition zone. With this small timestep where $a$ is large, there are no rogues generated through the $a\Delta t$ mechanism. The 103 rogues not resulting from a change in $\sigma _u$ all form through the $b\Delta \xi$ mechanism. All 103 became rogue in zone 1 and have negative velocities. It is likely that they recently jumped from zone 2 directly into zone 1 and $b\Delta \xi$ was sufficient for the velocity to exceed the rogue threshold. Runs 3 – 5 have very few rogues largely due to the usage of small timesteps.

3.2 Timestep and Velocity Biases

Both Runs 4 and 5 satisfy the WMC but the performance of Run 5 is slightly better. This is a result of the $\Delta t$ bias caused by the linearly-changing timesteps in the buffers. As described in Wilson and Flesch (1993), the timestep bias gives rise to a velocity bias ($u_\mathrm{B}$) that can be calculated as the difference between the numerical mean velocity and the analytical mean velocity. Since the analytical mean is zero, the velocity bias at position $x_i$ is calculated as

$$\begin{aligned} u_\mathrm{B}(x_i) = \sum _{j = 1}^{N_u} u_j f_u(u_j,x_i) \Delta u. \end{aligned}$$

(19)

Figure 5 shows the velocity bias for Run 4 and an identical run with double-width buffers. Beginning in zone 1, the velocity bias in Run 4 is approximately zero, with statistical error due to the use of a finite number of particles resulting in noise about zero. Around $x \approx -0.35~\mathrm {m}$, slightly outside of buffer 1, the velocity bias begins to have a non-zero value. It reaches a maximum value of $u_\mathrm{B} \approx 0.052~\mathrm {m~s^{-1}}$ inside buffer 1 at $x \approx -0.15~\mathrm {m}$, after which the value remains constant until the transition zone is reached at $x = x_{\mathrm{tr1}}$. In the transition zone, the timestep is constant (since $\partial \sigma _w/\partial x$ is constant) and there is no velocity bias. After $x = x_{\mathrm{{tr2}}}$, the velocity bias is approximately constant with a value $u_\mathrm{B} \approx -0.077~\mathrm {m~s^{-1}}$ until $x \approx 0.4~\mathrm {m}$. The magnitude of the velocity bias lessens throughout the remainder of buffer 2 until reaching zero again at $x \approx 0.9~\mathrm {m}$. The profile for the double-width buffer run is similar but the regions of constant velocity bias are larger and the magnitudes smaller because the buffers are larger and the timestep slope within them smaller. The regions where the velocity bias is changing is a result of particle from within and without the buffers mixing.

Fig. 5

Velocity bias resulting from a changing timestep in the buffers. The solid line is for Run 4. The dashed line is for a run identical in every way to Run 4 except the buffers are double the width. The dotted lines demarcate the buffers for Run 4

Following Wilson and Flesch (1993), consider a particle in buffer 1 with velocity $u$. The change in timestep experienced by this particle is $\Delta t_\mathrm{B} = m_{\mathrm{B}_1}\Delta x = m_{\mathrm{B}_1}u\Delta t$, where $m_{\mathrm{B}_1}$ is the timestep slope in buffer 1. The distance the particle moves with this timestep is $\Delta x_\mathrm{B} = u\Delta t_\mathrm{B}$. Substituting the expression for $\Delta t_\mathrm{B}$ into this equation gives $\Delta x_\mathrm{B} = m_{\mathrm{B}_1}u^2\Delta t$; assuming $u_\mathrm{P} \propto \Delta x_\mathrm{B}/\Delta t$ and the result is $u_\mathrm{P} \propto m_{\mathrm{B}_1}u^2$. As stated in Wilson and Flesch (1993), the velocity bias does not act on a single particle trajectory, so we take the mean over all particles: $\overline{u_\mathrm{P}} = u_\mathrm{B} \propto \overline{m_{\mathrm{B}_1}u^2}= m_{\mathrm{B}_1}\overline{u^2}$, and note the last term is equal to the velocity variance. Therefore the velocity bias is $u_\mathrm{B} = -\alpha m_{\mathrm{B}_1}\sigma ^2_u$, where $\alpha$ is a constant of proportionality and the negative is added so that $\alpha > 0$.

The slopes of buffers 1 and 2 are calculated from Eq. 8 to respectively be $m_{\mathrm{B}_1} = -0.163~\mathrm {s~m^{-1}}$ and $m_{\mathrm{B}_2} = 0.117~\mathrm {s~m^{-1}}$. Using these and the constant $u_\mathrm{B}$ values from Fig. 5, along with corresponding values from other simulations (not shown), suggest that $\alpha \approx 1/3$, which differs from the value of $1/2$ reported by Wilson and Flesch (1993). The difference may be due to the manner in which the values are calculated. In Wilson and Flesch (1993), $\alpha$ is determined using concentration data whereas velocity data are used above.

The velocity bias is the significant source of error in Run 4, contributing approximately $6.33\times 10^{-4}$ (51 %) to the $\textit{MAE}$. If this is subtracted from the $\textit{MAE}$ values shown in Table 1, the remainder is $6.07\times 10^{-4}$, which is almost equal to the $\textit{MAE}$ value of Run 5.

3.3 Sensitivity to Spatial Resolution

Many practical applications of LS models have a lower spatial resolution than those used for the simulations in Sect. 3.1. It is therefore worthwhile to investigate the sensitivity to spatial resolution of timestep buffering and timestep randomization. Simulations in this section have parameters used in Run 4 unless otherwise noted.

The top panel of Fig. 6 shows four PDFs from low ($\Delta x = 0.12~\mathrm {m}$) and high ($\Delta x = 0.004~\mathrm {m}$) resolution simulations in which the timestep randomization was either active or not. The results show both low and high resolution simulations with timestep randomization satisfying the WMC but the results differ without timestep randomization. The violation of the WMC in the low resolution simulation without timestep randomization is relatively minor and consists of slight PDF narrowing and overprediction of the PDF maximum. This error may not be noticeable in more realistic systems with other sources of error. In contrast, the violation of the WMC in the high resolution simulation without timestep randomization is much larger, with the PDF inaccurately predicted for $1\lesssim u/\sigma _u\lesssim 2$. These WMC violations are a result of the flux imbalance arising from particles jumping towards the transition zone and being unable, on account of smaller timesteps in the buffer, to be replaced by particles jumping away from the transition zone. To clarify, consider a particle at $x = x_{\mathrm{b1}} = -0.29~\mathrm {m}$, with $u = 1~\mathrm {m~s^{-1}}$ and $\Delta t = 0.02T_\mathrm{L} = 0.04~\mathrm {s}$. A step brings the particle into buffer 1 at $x = -0.25~\mathrm {m}$; a particle at this location with $u = -1~\mathrm {m~s^{-1}}$ has $\Delta t = 0.033~\mathrm {s}$. One step will take it to $x = -0.283~\mathrm {m} \ne x_{\mathrm{b1}}$ with timestep randomization mitigating this flux imbalance. With larger bins, the effects of the flux imbalance are lessened through a smoothing out and cancellation of errors.

Fig. 6

Effects of spatial resolution on WMC satisfaction for timestep randomization (a) and timestep buffering (b). The solid line shows the analytical Gaussian PDF and the symbols show the numerical PDFs. The circles are for Run 4

Timestep buffering appears to be more sensitive to spatial resolution. The bottom panel of Fig. 6 shows four PDFs from low and high resolution simulations with and without timestep buffering. Both low and high resolution simulations with timestep buffering satisfy the WMC while both low and high resolution simulations without it do not. The PDFs for low and high resolution simulations without timestep buffering are inaccurately predicted for $-4\lesssim u/\sigma _u\lesssim 1$. In addition, the high resolution simulation has a large spike in the numerical PDF at $u/\sigma _u\approx -1.3$ (the location of this spike varies with position; not shown). As with timestep randomization, the low resolution simulation appears to average over these spikes and produces a smoother, but still inaccurate, numerical PDF.

3.4 Dispersion in Three-Dimensional Inhomogeneous Turbulence

We arrive at the motivating problem for the development of the timestep-buffering technique. Both the marked-particle and micromixing model simulations use $N = 2\times 10^7$ particles, and are initialized within a 1-mm diameter tophat source at $(x_\mathrm{s},y_\mathrm{s},z_\mathrm{s}) = (0,0,0.6)~\mathrm {m}$ for the marked-particle simulations and uniformly on the upstream face of the domain for the micromixing simulations. Position and velocity spaces are respectively divided into $N_x = 40, N_y = 40, N_z = 40$, $N_u = 20, N_v = 20$, and $N_w = 40$ bins. The model constants are immaterial to first-order consistency but for completeness we use: Kolmogorov constant, $C_0 = 6$, Richardson constant, $C_\mathrm{r} = 0.45$ and micromixing constant, $\mu = 0.75$.

Table 2 summarizes the timestep selection and performance of the simulations. Run A uses the same timestep as Postma et al. (2012a) while Run B includes the derivative time scale in the timestep selection. Run C uses the same timestep selection as Run B but incorporates the interventions described in Sect. 2.3: a $\sigma ^2_w$ transition zone, timestep buffering and randomization. Run D uses the same timestep selection as Runs B and C but uses only the $\sigma ^2_w$ transition zone intervention. The $\textit{MAE}$ and $E_{\mathrm{max}}$ values listed are for the region surrounding the rogue cell, transition zone and buffer, since elsewhere in the domain all runs had identical timesteps and very similar performance. Figure 2 shows streamwise transects of $\sigma ^2_w$ and $\Delta t$ in the vicinity of the rogue cell.

Table 2 Parameters and performance measures for the three-dimensional marked-particle and micromixing model runs

The effectiveness of the interventions is apparent in the spanwise concentration transects for $(x,z) = (2.85,0.60)~\mathrm {m}$ shown in Fig. 7. Each of the runs has a corresponding marked-particle simulation but only one is shown in the figure since the transects from the four marked-particle simulations vary only slightly near the rogue cell and the differences are unnoticeable on the scale used in Fig. 7.

Run A, with no interventions and a relatively large timestep, displays a significant first-order inconsistency. This is not surprising since there are 14,278 rogue velocities in the marked-particle simulation used to pre-calculate the conditional mean concentrations used by the micromixing model. All but twelve of these were clustered in the grid cells neighbouring the rogue cell. In these cells, gradients of $\sigma ^2_w$ are non-zero and relatively large when compared with the gentle vertical gradients in the wall-shear-layer flow. These gradients increase the vertical velocity of a particle but since $\sigma ^2_w$ in these grid cells is fixed, the vertical velocity of the particle will eventually cross the rogue threshold. Indeed, all but six of the 14,278 rogue velocities are a result of the vertical velocity exceeding the rogue threshold, as opposed to rogue velocities in the streamwise or spanwise directions. For 13,793 of them, the $a\Delta t$ contribution to $\Delta w$ was sufficient for the particle to go rogue. As discussed in Sect. 2.3 and Postma et al. (2012a), these rogue velocities are responsible for the first-order inconsistency.

Fig. 7

Spanwise transects of concentration at $(x,z) = (2.85,0.60)~\mathrm {m}$ from the three-dimensional marked-particle (solid line) and micromixing model runs (symbols with thin lines) in Table 2. The dotted lines demarcate the spanwise extent of the rogue cell. The legend shows the run letter, the timestep selection criteria and other interventions

Reducing the timestep in the cells neighbouring the rogue cell (i.e., including $T_\mathrm{d}$ in the timestep selection criteria; Run B) increases the number of rogue trajectories and the magnitude of the first-order inconsistency. Corresponding increases in $\textit{MAE}$ and $E_{\mathrm{max}}$ are observed. As with Run A, the vast majority of the 23043 rogue velocities were in the cells neighbouring the rogue cell, in the $w$ component of velocity and a result of the $a_w\Delta t$ contribution to $\Delta w$. The combination of large accelerations and large grid cells with constant $\sigma ^2_w$ promotes the generation of rogue velocities regardless of the timestep. Smaller timesteps simply result in the particle taking more steps to reach the rogue velocity threshold. A larger timestep, as in Run A, may help particles avoid or escape regions of large acceleration without going rogue, particularly in multi-dimensional simulations where particles can traverse diagonally across grid cells potentially resulting in shorter paths (e.g., cutting across the corner of a grid cell).

The results from Runs C and D are qualitatively very similar although quantitatively, Run C, which uses three interventions, is more accurate at the $N_\mathrm{d} = 539$ comparison locations. The small number of rogue velocities in both runs was spread throughout the simulation domain as opposed to clustered around the rogue cell. These results suggest that for this three-dimensional example, the $\sigma ^2_w$ transition zone is the most effective intervention. However, timestep buffering and randomization does improve the performance slightly.

The minimal performance increases resulting from timestep buffering and randomization are probably a result of the relatively low resolution used for the simulations. Any overpredictions and underpredictions within the large cells are smoothed out as described in Sect. 3.3 and shown in Fig. 6. There is some supporting evidence to be found for this assertion by examining the streamwise distribution of error.

The ratio of $\textit{MAE}$ from Runs D and C in Table 2 is $\textit{MAE}_D/\textit{MAE}_C \approx 1.09$. Examining this ratio at each of the seven streamwise data-extraction locations ($x_k = [2.425$, 2.50, 2.85, 3.00, 3.15, 3.35, $3.425]~\mathrm {m}$) reveals: $\textit{MAE}_D(x_k)/\textit{MAE}_C(x_k) = [1.26$, 1.15, 1.04, 1.05, 1.09, 1.06, $1.07]$, noting that the performance differs most significantly at $x = 2.425$ and $2.50~\mathrm {m}$.

The lower panel of Fig. 2 shows $x = 2.70~\mathrm {m}$ and $x = 3.15~\mathrm {m}$ to be locations where particles with large differences in $\Delta t$ may mix in Run D and give rise to WMC violations similar to those seen in the one-dimensional results in Fig. 3 (Run 2 in particular). Higher resolution simulations of Runs C and D ($N_x$ increased to 70 from 40) resulted in the $\textit{MAE}_D(x_k)/\textit{MAE}_C(x_k)$ ratios improving except at $x = 2.425$ and $2.50~\mathrm {m}$, where they worsened respectively to 1.35 and 1.21. This worsening performance with increasing resolution is also observed in the one-dimensional results without timestep buffering and randomization (see Fig. 6).

The performances of Runs C and D around $x = 3.15~\mathrm {m}$ were similar although this too is an area where particles with different $\Delta t$ can mix. This is suspected to be due to the alternating timestep determination in Run D upstream of this location. In the streamwise direction and on a line centred on the rogue cell, the timesteps are: $0.02T_\mathrm{L}$ for $x < 2.70~\mathrm {m}, 0.02T_\mathrm{d}$ one cell upstream of the rogue cell, $0.02T_\mathrm{L}$ in the rogue cell, $0.02T_\mathrm{d}$ downstream of the rogue cell and $0.02T_\mathrm{L}$ for $x > 3.15~\mathrm {m}$; similarly for the spanwise and vertical directions. This alternating pattern may act to pre-mix the $T_\mathrm{L}$- and $T_\mathrm{d}$-based timesteps. In contrast, the $x = 2.70~\mathrm {m}$ boundary is the first place particles with different timesteps can interact, there is no pre-mixing. This perhaps is why the $\textit{MAE}_D(x_k)/\textit{MAE}_C(x_k)$ values around here are larger than for $x = 3.15~\mathrm {m}$.

The similarity of the location of poorer relative performance in Run D to those observed in the one-dimensional simulations suggests that the increased errors in this run relative to Run C are the result of the absence of timestep buffering and randomization. However, these interventions added another 67 min of simulation time that may or may not be worth the performance increases they provide, depending on the physical system being studied, research objectives, resolution, desired accuracy, time constraints and so on.

3.5 Improving Performance

The rate limiting step of the timestep-buffering technique is timestep randomization. By uniformly mixing the timesteps, the simulation times are approximately doubled, and is unsurprising since the expectation value of a uniform deviate in [0,1] is 0.5. In both the one and three-dimensional examples, the discontinuity occupied a small portion of the overall domain. Timestep randomization must occur in the entire domain to prevent imbalanced fluxes between regions with and without timestep randomization. This domain-wide randomization is computationally wasteful but acceptable with the short-duration simulations presented above, but may not be the case for longer simulations.

It may be possible to construct additional buffers to slowly phase out timestep randomization as the distance from the discontinuity increases. Perhaps by changing the randomization rate from every step, to every two steps, to every three steps and so on until there is no more randomization. Alternatively, imposing some form of functional dependence on $t_\mathrm{min}$ may achieve the desired result. This is an area for further development.

The velocity bias is the major source of error for the timestep-buffering technique. Eliminating or correcting for it would decrease the error. Since its magnitude is deterministic to within a constant, eliminating it by adding or subtracting (depending on the sign of the velocity bias) a small velocity from each particle step was attempted. The value of the correction was a small fraction of the velocity bias since a particle takes several steps in a buffer and the correctional effects are cumulative. Although this approach did eliminate the velocity bias in certain areas, it generally produced other errors elsewhere in the domain. Difficulties arose in determining the magnitude of the correction velocity and in what spatial range it should be applied. This too is an area for further development.

4 Summary

The timestep-buffering technique has been demonstrated to satisfy the WMC for steep velocity variance gradients in an idealized one-dimensional flow. The relationships between $\Delta t$, WMC satisfaction and rogue velocities have been demonstrated, with smaller timesteps resulting in more accurate predictions and fewer rogue velocities. However, abrupt changes in $\Delta t$ (Runs 1–3) continued to produce WMC violations. Timestep reduction can be used to minimize or eliminate rogue velocities but this does not necessarily ensure satisfaction of the WMC (Run 3). A simulation that utilized the timestep-buffering technique (Run 4) prevented these abrupt changes in $\Delta t$ and produced accurate results in approximately eight percent of the computation time for an accurate simulation using a small constant timestep (Run 5). A velocity bias resulting from the $\Delta t$ bias in the timestep buffers was responsible for the majority of the error in Run 4. This error was acceptably small in light of the simulation time savings.

Run 5 demonstrates that a small constant timestep can be used to satisfy the WMC by eliminating the $\Delta t$ bias and equalizing $\Delta \xi$ throughout the domain. There was however considerable computational cost (simulation time of 195 min). Using a variable timestep greatly decreases the simulation time (5–8 min) but if not done carefully can lead to an imbalance in particle fluxes across interfaces, rogue velocities and violations of the WMC (Runs 1–3). In Run 4, particles began taking smaller and smaller steps in the timestep buffers as they approached a transition boundary. By doing so, abrupt changes in $\Delta t$ were eliminated, fluxes across interfaces maintained, and near elimination of rogue velocities realized. The result was the satisfaction of the WMC with reasonable computational cost (15 min of simulation time).

Timestep randomization, a part of the timestep-buffering technique, could be considered optional in low resolution simulations. The low resolution simulations in Sect. 3.3 have $\Delta x = 0.12~\mathrm {m}$, but in general, what constitutes low resolution will depend on the system being simulated. Not using timestep randomization would cut simulations times by approximately a factor of two but it has been demonstrated that simulations with timestep randomization are more accurate than those without. Whether or not the performances increases are worth the extra simulation time depends upon the physical system being studied, research objectives, desired accuracy and time constraints. Timestep buffering is more sensitive to the spatial resolution as there were significant violations of the WMC in both the low and high resolution simulations without it (see Fig. 6).

The first-order inconsistency seen in the micromixing model of Postma et al. (2012a) was eliminated using the timestep-buffering technique along with building a sub-grid velocity variance transition zone (Run C). The three-dimensional flow used to drive these simulations was idealized: a horizontally homogeneous wall shear layer with a single region of steep gradients and a strong inhomogeneity created by increasing $\sigma ^2_w$ to twenty times its wall-shear-layer value within the rogue cell. Application to more realistic flows to drive LS simulations (e.g., a flow with many regions of strong gradients and inhomogeneities) would be straightforward but difficulties may occur. With multiple regions requiring timestep buffering and transitions zones, it is possible that these may overlap. It would not be difficult to smoothly join the buffers themselves but doing so might produce consistently small timesteps in each grid cell and possibly result in long simulation times, which is exactly what was to be avoided. However, this potential complication depends upon the grid-cell size and the Eulerian velocity statistics. It is therefore conceivable that there exist many problems of practical importance where the timestep-buffering technique could be used to eliminate excessive rogue velocities, maintain balanced particle fluxes, satisfy the WMC and prevent the domain-wide use of small timesteps. However, if there is no other way to simulate the system without violations to the WMC, then the longer simulations resulting from overlapping buffers times must be endured.

The objective was to develop an easily-implemented solution to WMC violations. Incorporating timestep buffering into complex three-dimensional marked-particle and micromixing models is straightforward and requires only basic linear algebra, a uniform random number generator and one short subroutine. More important than the ease of implementation, the timestep-buffering technique has been demonstrated effective at preserving the WMC in one- and three-dimensional flows.