A generalization of Filon–Clenshaw–Curtis quadrature for highly oscillatory integrals

Abstract

The Filon–Clenshaw–Curtis method (FCC) for the computation of highly oscillatory integrals is known to attain surprisingly high precision. Yet, for large values of frequency $\omega$ it is not competitive with other versions of the Filon method, which use high derivatives at critical points and exhibit high asymptotic order. In this paper we propose to extend FCC to a new method, FCC$+$, which can attain an arbitrarily high asymptotic order while preserving the advantages of FCC. Numerical experiments are provided to illustrate that FCC$+$ shares the advantages of both familiar Filon methods and FCC, while avoiding their disadvantages.

1 Introduction

The highly oscillatory integral

$$\begin{aligned} I_\omega [f]=\int _{-1}^1 f(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d}x, \quad \omega \ge 0, \end{aligned}$$

(1.1)

where $f, g \in \mathbf {C}^\infty [-1,1]$, occurs in a wide range of applications, e.g. the numerical solution of oscillatory differential and integral equations, acoustic and electromagnetic scattering and fluid mechanics. It is a difficult problem when approached by classical quadrature methods. However, once the mathematics of high oscillation is properly understood, the quadrature of (1.1) becomes fairly simple and affordable. Indeed, high oscillation is actually helpful in the design of a computational method, rather than a stumbling block. A number of innovative methods have been developed in the last two decades: an asymptotic expansion and Filon-type method [9,10,11], Levin’s method [12, 13] and numerical steepest descent [8]. These methods behave very well for $\omega \gg 1$.

The emphasis in the design of the above methods has been on large $\omega$, yet there is significant merit in methods which are uniformly good for all $\omega \ge 0$. This reflects much of recent research. Complex-valued Gaussian quadrature [1, 2] is constructed (and equally efficient) for all $\omega \ge 0$. The FCC method can be traced to [15,16,17] and they are surveyed in [14]. Recently, Domínguez, Graham and Smyshlayev studied the implementation and error estimate of FCC for the highly oscillatory integrals in [3,4,5]. Their method does not require the computation of derivatives of the endpoints. FCC, applied extensively in many applications, is so popular because of its simple implementation, high precision and easy extension for different integrands f. However, when it comes to the behaviour of the FCC for $\omega \rightarrow \infty$, it has very low asymptotic order—its error for $\omega \gg 0$ (in the absence of stationary points) decays like $O(\omega ^{-2})$, while other quadrature methods for oscillatory integrals (like the asymptotic algorithm, the plain Filon method, ...) can attain any $O(\omega ^{-s})$ for $s\ge 2$.

The idea underlying all Filon-type methods is to replace the non-oscillatory function f in (1.1) by a polynomial p, subject to the assumption that the moments $\int _{-1}^1 x^k \mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x$ can be computed for all $k\ge 0$. Suppose for the time being that there are no stationary points, i.e. that $g' \ne 0$ in $[-1,1]$, and recall the asymptotic expansion

$$\begin{aligned} I_{\omega }[f] \sim- & {} \sum _{k = 0}^{s-1} \frac{1}{(-\mathrm {i}\omega )^{k + 1}} \left[ \frac{\sigma _{k}[f](1)}{g'(1)} \mathrm {e}^{\mathrm {i}\omega g(1)} - \frac{\sigma _{k}[f](-1)}{g'(-1)} \mathrm {e}^{\mathrm {i}\omega g(-1)}\right] \nonumber \\+ & {} O\left( \omega ^{-(s+1)}\right) \!, \end{aligned}$$

(1.2)

where

$$\begin{aligned} \sigma _0[f](x)= & {} f(x),\\ \sigma _{k}[f](x)= & {} \frac{\mathrm {d}}{\mathrm {d}x}\frac{\sigma _{k-1}[f](x)}{g'(x)}= \sum _{j = 0}^{k} \sigma _{k, j}(x) f^{(j)}(x), \quad \sigma _{k, k} = \frac{1}{{g'}^k(x)} \ne 0, \end{aligned}$$

[11]. The functions $\sigma _{k,j}$ are independent of f, depending just on $g'$ and its derivatives. Note that the error of Filon, $I_{\omega }[f-p]$, is still a highly oscillatory integral. Replacing f by $f-p$ in (1.2), we obtain the error of a Filon-type method. To derive the asymptotic order $O(\omega ^{-s-1})$, we let

$$\begin{aligned} p^{(j)}(1) = f^{(j)}(1), \quad p^{(j)}(-1) = f^{(j)}(-1), \quad j = 0, 1, \ldots , s-1, \end{aligned}$$

which determines a Filon method with a Hermite interpolation polynomial p of degree $2s-1$, referred here as the sth plain Filon method

$$\begin{aligned} \mathcal {Q}_{\omega }^{\mathbf {F},s}[f]=\int _{-1}^1 p(x) \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x. \end{aligned}$$

The error of a plain Filon method can be reduced (without changing its asymptotic order) by adding extra N interpolation points in the interval $(-1,1)$ and this leads to an extended Filon method [6]. The errors of the extended Filon method are analysed in [6] with general interpolation points for large $\omega$, and with Clenshaw–Curtis points and zeros of Jacobi polynomials for small $\omega$. Note that the Filon–Clenshaw–Curtis (FCC) procedure of [4, 5] is a particular case of extended Filon that does not require derivatives of the endpoints, where the interpolation points are chosen as $\cos (k\pi /N)$, $k=0,\ldots ,N$, and it enjoys a number of important advantages. Firstly, everything is explicit,

$$\begin{aligned} p_0= & {} \frac{1}{N}\left[ \frac{1}{2} f(1)+\sum _{\ell =1}^{N-1} f\left( \cos \frac{\ell \pi }{N}\right) +\frac{1}{2} f(-1)\right] ,\\ p_n= & {} \frac{2}{N}\left[ \frac{1}{2} f(1)+\sum _{\ell =1}^{N-1} f\left( \cos \frac{\ell \pi }{N}\right) \cos \frac{\ell n\pi }{N} +\frac{(-1)^n}{2} f(-1)\right] ,\quad n=1,\ldots ,N-1,\\ p_N= & {} \frac{1}{N}\left[ \frac{1}{2} f(1)+\sum _{\ell =1}^{N-1} f\!\left( \cos \frac{\ell \pi }{N}\right) (-1)^\ell +\frac{(-1)^N}{2} f(-1)\right] \end{aligned}$$

and

$$\begin{aligned} \mathcal {Q}_{\omega }^{\mathbf {FCC}, N, 1}[f]=\int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x = \sum _{n=0}^N p_n \int _{-1}^1 \mathbf {T}_n(x) \mathrm {e}^{\mathrm {i}\omega g(x)} \hbox {d} x, \end{aligned}$$

where $\mathbf {T}_n(x)$ is the Chebyshev polynomial of the first kind. Note that for large values of N we can compute the $p_n$s with Discrete Cosine Transform I (DCT-I) in $O(N\log N)$, rather than $O(N^2)$ operations.

The error of FCC (in absence of stationary points) can be computed, in a large measure because of the explicit form of the coefficients, and it is

$$\begin{aligned} \mathcal {Q}_{\omega }^{\mathbf {FCC},N, 1}[f]-I_\omega [f]=O\left( \omega ^{-2} N^{-r}\right) , \end{aligned}$$

where r is the regularity of f, which is consistent with asymptotic order 2. (Recall that $\pm 1$ are interpolation points and this is fully compliant with the reasoning underlying extended Filon methods.) The low asymptotic order notwithstanding, the error of FCC is determined by $\omega$ and N.

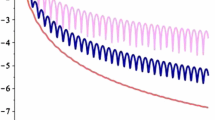
As an example, we display in Fig. 1 the errors (in logarithmic scale) committed by plain Filon with $s=1,2,3,4$ (from the top to bottom, in the right figure) and by FCC with $N=8$ for

$$\begin{aligned} f(x)=\frac{1+x}{1+x^2}, \quad g(x) = x. \end{aligned}$$

(1.3)

Note that while $\mathcal {Q}_{\omega }^{\mathbf {FCC},N,1}[f]$ has asymptotic error $O(\omega ^{-2})$, a plain Filon method $\mathcal {Q}_{\omega }^{\mathbf {F},s}[f]$ carries an asymptotic error of $O(\omega ^{-s-1})$. For $s=1$ the two asymptotic errors are the same and it can be seen from the figure on the left that FCC emerges as a decisive winner when measuring the maximal error for $\omega \ge 0$. However, the figure on the right confirms the clear fact that higher asymptotic order always wins for sufficiently large $\omega$. Recalling that $\mathcal {Q}_{\omega }^{\mathbf {FCC},N,1}[f]$ requires $N+1$ function evaluations, while $\mathcal {Q}_{\omega }^{\mathbf {F},s}[f]$ ‘costs’ 2s function and derivative evaluations, it transpires that the better performance of Filon with $s\ge 2$ for $\omega \gg 1$ need not be accompanied by greater computational cost.

Fig. 1

Logarithmic errors. On the left $\mathcal {Q}_{\omega }^{\mathbf {FCC},8,1}[f]$ (solid, blue) and $\mathcal {Q}_{\omega }^{\mathbf {F},1}[f]$ (dot, orange), while on the right $\mathcal {Q}_{\omega }^{\mathbf {F},s}[f]$, $s=1, 2, 3, 4$ (The line styles are dotted (orange), dashed (purple), dash dotted (red), space dotted (green), from the top to bottom) (colour figure online)

Figure 2 redraws Fig. 1 (left) in a different form, scaling the absolute value of the error by $\omega ^2$. Since asymptotically the error behaves like $O(\omega ^{-2})$, we expect both Filon (the top, dotted, orange) and FCC (the bottom, solid, blue) to tend to a straight line (or at least being bounded away from zero and infinity) for $\omega \gg 1$, and this is confirmed in the figure—clearly, FCC is much more accurate!

Fig. 2

The absolute value of the error, scaled by $\omega ^2$: $\mathcal {Q}_{\omega }^{\mathbf {FCC},8, 1}[f]$ at the bottom (the solid line in blue) and $\mathcal {Q}_{\omega }^{\mathbf {F},1}[f]$ on the top (the dotted line in orange) (colour figure online)

Another way of looking at our methods is by examining the interpolation error. In Fig. 3, we sketch the error function $p-f$ for FCC with $N = 8$ (the left figure) and a plain Filon method for $s=1, 2, 3, 4$ (dotted (orange), dashed (purple), dash dotted (red), space dotted (green), from the bottom to top in the right figure). As we might have expected, FCC, based on interpolation at Chebyshev points of the second kind, gives hugely better minimax approximation, while for plain Filon $p-f$ is larger in magnitude, but flat near the endpoints. It is precisely this flatness that explains superior performance for $\omega \gg 1$.

Fig. 3

The functions $p-f$ for FCC with $N=8$ (on the left, the solid line in navy blue) and for Filon with $s=1,2,3,4$ on the right. The corresponding line styles are dotted (orange), dashed (purple), dash dotted (red), space dotted (green), from the bottom to top (colour figure online)

Let us set up the competing advantages of the two methods:

• 1. Plain Filon demonstrates much better accuracy for $\omega \gg 1$ which, after all, is the entire point of highly oscillatory quadrature.

• 2. FCC behaves much better for small $\omega$ and has smaller uniform error for $\omega \ge 0$. ‘Better’, rather than ‘best’: even better behaviour can be obtained replacing Chebyshev by Jacobi points, at the price of a minor deterioration in asymptotic behaviour [6].

• 3. FCC does not require derivatives of the nodes, the quid pro quo being worse asymptotic error. The method might be more suitable when the derivatives of f are not easily available but note that in principle a Filon-type method can be implemented while replacing derivatives with suitable finite-difference approximations [10].

• 4. An issue often disregarded in papers on highly oscillatory quadrature is that FCC has a considerably simpler form: this is important once we wish to compute (1.1) for a large number of different values of $\omega$ or, for that matter, for different values of f. Specifically, we can represent any extended Filon method in the form

  $$\begin{aligned} \sum _{\ell =0}^{N} \sum _{k=0}^{m_\ell -1} b_{\ell ,k}(\omega ) f^{(k)}(c_\ell ) \end{aligned}$$

  here $c_0=-1<c_1<\cdots<c_{N-1}<c_N=1$ are the interpolation points with weights $m_\ell$: $N=1$, $m_0=m_1=s$ for plain Filon and $c_\ell =\cos (\pi \ell /N)$, $m_\ell \equiv 1$, $\ell = 1, 2, \ldots , N-1$, for FCC. Given an interpolating polynomial $p(x)=\sum _{\ell =0}^{N} \sum _{k=0}^{m_\ell -1} p_{\ell ,k}(x) f^{(k)}(c_\ell )$, we have $b_{\ell ,k}(\omega )=\int _{-1}^1 p_{\ell ,k}(x)\mathrm {e}^{\mathrm {i}\omega g(x)} \mathrm {d}x$. For plain Filon the generalised weights $b_{\ell ,k}$ are fairly complicated, e.g. for $s=2$ and $g(x)=x$ we have

  $$\begin{aligned} b_{0,0}(\omega )= & {} \frac{\mathrm {e}^{-\mathrm {i}\omega }}{-\mathrm {i}\omega }-\frac{3\cos \omega }{(-\mathrm {i}\omega )^3}-\frac{3\mathrm {i}\sin \omega }{(-\mathrm {i}\omega )^4},\\ b_{0,1}(\omega )= & {} \frac{\mathrm {e}^{-\mathrm {i}\omega }}{(-\mathrm {i}\omega )^2}-\frac{\mathrm {e}^{\mathrm {i}\omega }+2\mathrm {e}^{-\mathrm {i}\omega }}{(-\mathrm {i}\omega )^3}-\frac{3\mathrm {i}\sin \omega }{(-\mathrm {i}\omega )^4},\\ b_{1,0}(\omega )= & {} -\frac{\mathrm {e}^{\mathrm {i}\omega }}{-\mathrm {i}\omega }+\frac{3\cos \omega }{(-\mathrm {i}\omega )^3}+\frac{3\mathrm {i}\sin \omega }{(-\mathrm {i}\omega )^4},\\ b_{1,1}(\omega )= & {} -\frac{\mathrm {e}^{\mathrm {i}\omega }}{(-\mathrm {i}\omega )^2}-\frac{2\mathrm {e}^{\mathrm {i}\omega }+\mathrm {e}^{-\mathrm {i}\omega }}{(-\mathrm {i}\omega )^3}-\frac{3\mathrm {i}\sin \omega }{(-\mathrm {i}\omega )^4}. \end{aligned}$$

  Complexity grows rapidly for larger s. An alternative is to compute $\int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x$ but this must be done (having formed p, e.g. by solving a linear system) separately for every $\omega$. The formation of FCC, however, is considerably simpler! We first compute the fast cosine transform $\{\hat{p}_\ell \}_{\ell =0}^N$ of the sequence $f(c_\ell )$, $\ell =0, \ldots ,N$ using $O(N\log N)$ operations—the interpolating polynomial is then

  $$\begin{aligned} p(x)=\sum _{\ell =0}^N \hat{p}_\ell \mathbf {T}_\ell (x)\quad \text{ hence }\quad \mathcal {Q}_\omega ^{\mathbf {FCC},N,1}[f]=\sum _{\ell =0}^N \hat{p}_\ell \hat{b}_\ell (\omega ), \end{aligned}$$

  where $\hat{b}_\ell (\omega )=\int _{-1}^1 \mathbf {T}_\ell (x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x$ can be formed rapidly [4] and their form is typically much simpler.

It is obvious how to reconcile 1 and 2: choose a polynomial p of degree $N+2s-2$, where $N,s\ge 1$, which interpolates f at $\cos (k\pi /N)$, $k=1,\ldots ,N-1$, and $f^{(i)}$, $i=0,\ldots ,s-1$, at $\pm 1$, and compute $\int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x$—this is precisely the method we term “FCC$+$” and denote by $\mathcal {Q}_\omega ^{\mathbf {FCC},N,s}[f]$. While FCC$+$ has been already stated in [6] and its error, in tandem with the Filon–Jacobi method, analysed by the tools introduced there, nothing has been said in that paper about the construction of such a method. This is the main challenge in the present paper, where we demonstrate that the unique selling point of FCC, namely its computation with FCT, can be extended to FCC$+$. More specifically, the method also ticks point 4: it can be reduced to standard FCC plus solving two systems of linear equation with dimension $s-1$ and requires just $O(N\log N)+O(s^3)$ operations.

In Sect. 2 we introduce FCC$+$ in an orderly manner and describe its basic properties. In Sect. 3 we present a construction of FCC$+$ which is consistent with the above point 4 and present some numerical experiments. We conclude with a brief Sect. 4, reviewing the results of this paper.

2 Basic properties of FCC$+$

Letting $s,N\ge 1$, we seek a polynomial p of degree $N+2s-2$ such that

$$\begin{aligned}&p^{(i)}(-1)=f^{(i)}(-1),\quad p^{(i)}(1)=f^{(i)}(1),\quad i=1,\ldots ,s-1,\nonumber \\&p\!\left( \!\cos \frac{j\pi }{N}\right) =f\!\left( \!\cos \frac{j\pi }{N}\right) ,\quad j=0, \ldots ,N. \end{aligned}$$

(2.1)

(Note that the case $i=0$ is automatically covered by $j=0$ and $j=N$.) We then let

$$\begin{aligned} \mathcal {Q}_\omega ^{\mathbf {FCC},N,s}[f]=\int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x. \end{aligned}$$

This is our FCC$+$ method. In fact, FCC$+$ is a special case of Extended Filon Method in [6] whose interpolation nodes are chosen as $\cos \left( \frac{j \pi }{N}\right)$, $j = 1, 2, \ldots , N-1$. The error estimate with the infinity norm of f has been introduced in [6] as follows:

$$\begin{aligned} \left| E_\omega ^{\mathbf {FCC},N,s}[f]\right|= & {} \left| I[f] - \mathcal {Q}_\omega ^{\mathbf {FCC},N,s}[f]\right| = \left| \int _{-1}^1 \left( f(x)-p(x)\right) \mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x\right| \nonumber \\\le & {} \frac{s!2^s }{\omega ^{s+1} (N-1+2s)!} \left[ \frac{\prod _{j=1}^{N-1} \left( 1-\cos \left( \frac{j \pi }{N}\right) \right) }{{g'}^{s+1}(1)} \right. \nonumber \\&\left. +\, \frac{\prod _{j=1}^{N-1} \left( 1+\cos \left( \frac{j \pi }{N}\right) \right) }{{g'}^{s+1}(-1)}\right] \!\Vert f^{(N+2s-1)}\Vert _\infty +O(\omega ^{-s-2})\nonumber \\= & {} \frac{s!N}{(N-1+2s)!2^{N-s-1}} \left[ \frac{1}{{g'}^{s+1}(1)}+\frac{1}{{g'}^{s+1}(-1)}\right] \!\Vert f^{(N+2s-1)}\Vert _\infty \nonumber \\&+\, O(\omega ^{-s-2}) \end{aligned}$$

(2.2)

for $\omega \gg 1$. This is true since $\prod _{j=1}^{N-1} \left( 1-\cos \left( \frac{j \pi }{N}\right) \right) =\prod _{j=1}^{N-1} \left( 1+\cos \left( \frac{j \pi }{N}\right) \right) =N/2^{N-1}$.

We do not require $g'\ne 0$ in $[-1,1]$, yet note that, once this condition is satisfied, $\mathcal {Q}_\omega ^{\mathbf {FCC},N,s}[f]-I_\omega [f]\sim O\left( \omega ^{-s-1}\right)$ from (2.2), while for $\omega \rightarrow 0$ we have Birkhoff–Hermite quadrature with Clenshaw–Curtis nodes. It is convenient to represent

$$\begin{aligned} p(x)=\sum _{m=0}^{N+2s-2} p_m \mathbf {T}_m(x). \end{aligned}$$

The next conceptual step is to calculate the coefficients $p_m$ quickly using DCT-I.

We need first to compute $\mathbf {T}_m^{(k)}(\pm 1)$ for relevant values of k and m. To this end we recall from DLMF (http://dlmf.nist.gov) that

$$\begin{aligned} 18.7.3:&\mathbf {T}_m(x)=\frac{\mathbf {P}_m^{(-1/2,-1/2)}(x)}{\mathbf {P}_m^{(-1/2,-1/2)}(1)},\\ 18.6.1:&\mathbf {P}_m^{(\alpha ,\alpha )}(1)=\frac{(\alpha +1)_m}{m!}, \quad \mathbf {P}_m^{(\alpha ,\alpha )}(-1)=(-1)^m \mathbf {P}_m^{(\alpha ,\alpha )}(1),\\ 18.9.15:&\frac{\hbox {d} \mathbf {P}_m^{(\alpha ,\alpha )}(x)}{\hbox {d} x}=\frac{1}{2} (m+2\alpha +1) \mathbf {P}_{m-1}^{(\alpha +1,\alpha +1)}(x). \end{aligned}$$

Iterating the last expression, we have

$$\begin{aligned} \frac{\hbox {d}^k \mathbf {P}_m^{(\alpha ,\alpha )}(x)}{\hbox {d} x^k}=\frac{1}{2^k} (m+2\alpha +1)_k \mathbf {P}_{m-k}^{(\alpha +k,\alpha +k)}(x), \end{aligned}$$

in particular

$$\begin{aligned} \frac{\hbox {d}^k \mathbf {P}_m^{(-1/2,-1/2)}(x)}{\hbox {d} x^k}=\frac{(m)_k}{2^k} \mathbf {P}_{m-k}^{(k-\frac{1}{2},k-\frac{1}{2})}(x). \end{aligned}$$

Consequently,

$$\begin{aligned} \mathbf {T}_m^{(k)}(x)=\frac{(m)_k}{2^k} \frac{\mathbf {P}_{m-k}^{(k-\frac{1}{2},k-\frac{1}{2})}(x)}{\mathbf {P}_m^{(-1/2,-1/2)}(1)}. \end{aligned}$$

We deduce that

$$\begin{aligned} \mathbf {T}_m^{(k)}(1)=\frac{(m)_k}{2^k} \frac{\mathbf {P}_{m-k}^{(k-\frac{1}{2},k-\frac{1}{2})}(1)}{\mathbf {P}_m^{(-1/2,-1/2)}(1)}=\frac{(m)_k}{2^k} \frac{(k+\frac{1}{2})_{m-k}}{(m-k)!} \frac{m!}{(\frac{1}{2})_m}, \end{aligned}$$

where

$$\begin{aligned} (m)_k=\frac{(m+k-1)!}{(m-1)!},\quad (k+{\textstyle \frac{1}{2}})_{m-k}=\frac{(2m)!k!}{4^{m-k}m!(2k)!}. \end{aligned}$$

Therefore

$$\begin{aligned} \mathbf {T}_m^{(k)}(1)= & {} \frac{2^k k! m(m+k-1)!}{(2k)!(m-k)!},\quad m,k\ge 0,\quad m+k\ge 1,\nonumber \\ \mathbf {T}_m^{(k)}(-1)= & {} (-1)^{m - k}\mathbf {T}_m^{(k)}(1). \end{aligned}$$

(2.3)

Over to (2.1). Incorporating (2.3) and the definition of Chebyshev polynomials, we obtain the linear system

$$\begin{aligned}&\sum _{m=1}^{N+2s-2} \frac{m(m+i-1)!}{(m-i)!} p_m = \frac{(2i)!}{2^ii!} f^{(i)}(1),\nonumber \\&\sum _{m=1}^{N+2s-2} (-1)^{m-i} \frac{m(m+i-1)!}{(m-i)!} p_m = \frac{(2i)!}{2^ii!} f^{(i)}(-1),\quad i=1,\ldots ,s-1,\nonumber \\&\sum _{m=0}^{N+2s-2} \cos \!\left( \!\frac{jm\pi }{N}\right) p_m = f\!\left( \!\cos \frac{j\pi }{N}\right) \!,\quad j=0,\ldots ,N. \end{aligned}$$

(2.4)

Let

$$\begin{aligned} \hat{p}_0= & {} 2p_0,\quad \hat{p}_k=p_k,\quad k=1,\ldots ,N-1,\quad \hat{p}_N=2p_N,\nonumber \\ h_j= & {} f_j-\sum _{m=N+1}^{N+2s-2} \cos \!\left( \frac{jm\pi }{N}\right) p_m, \quad f_j = f\!\left( \!\cos \frac{j\pi }{N}\right) , \quad j=0,\ldots ,N.\nonumber \\ \end{aligned}$$

(2.5)

The bottom line in (2.4) is equivalent to

$$\begin{aligned} \frac{1}{2} \hat{p}_0 +\sum _{m=1}^{N-1} \cos \!\left( \frac{jm\pi }{N}\right) \hat{p}_m +\frac{(-1)^j}{2} \hat{p}_N=h_j,\quad j=0, \ldots ,N. \end{aligned}$$

This is DCT-I, $\mathcal {C}_N\hat{\mathbf {p}}=\mathbf {h}$, and its inverse is $\mathcal {C}_N^{-1}=(2/N)\mathcal {C}_N$. We deduce that

$$\begin{aligned} \hat{p}_m=\frac{2}{N} \left[ \frac{1}{2} h_0+\sum _{j=1}^{N-1} \cos \!\left( \frac{jm\pi }{N}\right) h_j +\frac{(-1)^m}{2} h_N\right] \!,\quad m=0,\ldots ,N. \end{aligned}$$

(2.6)

Consequently, the coefficients $p_m$, $m=0,\ldots ,N$, can be calculated in $O(N\log N)$ operations with DCT-I from the unknown coefficients $p_m$ for $m=N+1,\ldots ,N+2s-2$. Specifically, we need first to solve a linear system of $2s-2$ unknowns $p_{N+1},\ldots ,p_{N+2s-2}$, and subsequently recover $p_0,\ldots ,p_N$ as above.

3 The construction of FCC$+$

In this section, we complete the construction of FCC$+$ for a general $s\ge 2$ by identifying explicitly the linear system for $p_{N+1},\ldots ,p_{N+2s-2}$. We commence with the simplest case, $s=2$, subsequently generalising to all $s>2$.

3.1 $s = 2$

We have

$$\begin{aligned} h_j= & {} f_j-\cos \!\left( \!\frac{j(N+1)\pi }{N}\right) p_{N+1}-\cos \!\left( \frac{j(N+2)\pi }{N}\right) p_{N+2}\nonumber \\= & {} f_j-(-1)^j\cos \frac{j\pi }{N} p_{N+1}-(-1)^j \cos \frac{2j\pi }{N} p_{N+2},\quad j=0,\ldots ,N, \end{aligned}$$

and it follows from (2.6) that

$$\begin{aligned} \hat{p}_m= & {} \frac{2}{N}\left\{ \frac{1}{2} f_0-\frac{1}{2}p_{N+1}-\frac{1}{2} p_{N+2} \right. \nonumber \\&+\, \sum _{j=1}^{N-1} \cos \!\left( \frac{jm\pi }{N}\right) \left[ f_j-(-1)^j\cos \frac{j\pi }{N}p_{N+1}-(-1)^j\cos \frac{2j\pi }{N} p_{N+2}\right] \nonumber \\&\left. +\, \frac{(-1)^m}{2} f_N +\frac{(-1)^{m+N}}{2} p_{N+1} -\frac{(-1)^{m+N}}{2} p_{N+2}\right\} \nonumber \\= & {} \frac{2}{N}\left[ \frac{1}{2} f_0+\sum _{j=1}^{N-1}\cos \!\left( \frac{jm\pi }{N}\right) f_j+\frac{(-1)^m}{2}f_N\right] \nonumber \\&- \, \frac{2}{N} p_{N+1} \left[ \frac{1}{2}+\sum _{j=1}^{N-1} (-1)^j \cos \!\left( \frac{jm\pi }{N}\right) \cos \frac{j\pi }{N}-\frac{(-1)^{m+N}}{2} \right] \nonumber \\&- \, \frac{2}{N}p_{N+2} \left[ \frac{1}{2} +\sum _{j=1}^{N-1} (-1)^j \cos \!\left( \frac{jm\pi }{N}\right) \cos \frac{2j\pi }{N}+\frac{(-1)^{m+N}}{2}\right] . \end{aligned}$$

Since

$$\begin{aligned} \sum _{j=0}^{N-1} (-1)^j \cos \frac{jM\pi }{N}= \left\{ \begin{array}{lllll} \displaystyle \frac{1-(-1)^{N+M}}{2}, &{}\quad M\ne N,\\ N, &{}\quad M=N, \end{array}\right. \end{aligned}$$

for $M=0,1,\ldots ,N-2$ and $M=N$ derived from the formula (1.3.43-1) of page 37 in [7], we have

$$\begin{aligned}&\frac{1}{2}+\sum _{j=1}^{N-1} (-1)^j \cos \!\left( \frac{jm\pi }{N}\right) \cos \frac{j\pi }{N}-\frac{(-1)^{m+N}}{2} \nonumber \\&\quad =\frac{1}{2} +\frac{1}{2} \sum _{j=1}^{N-1} (-1)^j \cos \frac{j(m+1)\pi }{N} +\frac{1}{2} \sum _{j=1}^{N-1} (-1)^j \cos \frac{j(m-1)\pi }{N} -\frac{(-1)^{m+N}}{2}\nonumber \\&\quad =\frac{1}{2} \sum _{j=0}^{N-1}(-1)^j \cos \frac{j(m+1)\pi }{N}+\frac{1}{2} \sum _{j=0}^{N-1} (-1)^j \cos \frac{j(m-1)\pi }{N} \nonumber \\&\qquad -\, \frac{1+(-1)^{m+N}}{2}=0, \quad m \ne N-1, \end{aligned}$$

while for $m=N-1$ the sum is N / 2.

In exactly the same fashion

$$\begin{aligned}&\frac{1}{2} +\sum _{j=1}^{N-1} (-1)^j \cos \!\left( \frac{jm\pi }{N}\right) \cos \frac{2j\pi }{N}+\frac{(-1)^{m+N}}{2} \nonumber \\&\quad =\, \frac{1}{2}\sum _{j=0}^{N-1} (-1)^j \cos \frac{j(m+2)\pi }{N}+\frac{1}{2} \sum _{j=0}^{N-1}(-1)^j \cos \frac{j(m-2)\pi }{N} -\frac{1-(-1)^{m+N}}{2} \end{aligned}$$

and we deduce that the sum equals zero for $m\ne N-2$ and N / 2 for $m=N-2$.

Let

$$\begin{aligned} \check{p}_m=\frac{2}{N}\left[ \frac{1}{2} f_0+\sum _{j=1}^{N-1}\cos \!\left( \frac{jm\pi }{N}\right) f_j+\frac{(-1)^m}{2}f_N\right] \!,\quad m=0,\ldots ,N \end{aligned}$$

(3.1)

be the coefficients that feature in the original FCC. We thus deduce that

$$\begin{aligned}&\hat{p}_m=\check{p}_m,\quad m\ne N-2,N-1, \nonumber \\&\hat{p}_{N-2}=\check{p}_{N-2}-p_{N+2},\quad \hat{p}_{N-1}=\check{p}_{N-1}-p_{N+1}, \end{aligned}$$

except for $m=N-2$ and $m=N-1$, exactly like in standard FCC!

We have the two remaining equations from (2.4), namely

$$\begin{aligned} \sum _{m=1}^{N+2} m^2 p_m=f'(1),\quad \sum _{m=1}^{N+2} (-1)^{m-1} m^2 p_m=f'(-1). \end{aligned}$$

Therefore

$$\begin{aligned} 4Np_{N+1}+8Np_{N+2}= & {} f'(1)-\sum _{m=1}^{N-1}m^2\check{p}_m-\frac{N^2}{2}\check{p}_N, \nonumber \\ 4Np_{N+1}-8Np_{N+2}= & {} (-1)^N f'(-1)+\sum _{m=1}^{N-1}(-1)^{N-m} m^2 \check{p}_m+\frac{N^2}{2}\check{p}_N. \end{aligned}$$

All this results in two linear equations, whose solution is

$$\begin{aligned} p_{N+1}= & {} \frac{1}{8N} \left\{ f'(1)+(-1)^N f'(-1)-\sum _{m=1}^{N-1}[1-(-1)^{N-m}]m^2\check{p}_m\right\} ,\nonumber \\ p_{N+2}= & {} \frac{1}{16N} \left\{ f'(1)-(-1)^Nf'(-1)-\sum _{m=1}^{N-1} [1+(-1)^{N-m}] m^2\check{p}_m -N^2\check{p}_N\right\} \!, \end{aligned}$$

for the unknowns $p_{N+1}$ and $p_{N+2}$.

3.2 A general $s\ge 3$

Given a general $s \ge 3$, we have

$$\begin{aligned} h_j= & {} f_j-\sum _{n=N+1}^{N+2s-2} \cos \!\left( \frac{jn\pi }{N}\right) p_n\\= & {} f_j-\sum _{n=1}^{2s-2} (-1)^j \cos \!\left( \frac{jn\pi }{N}\right) p_{N+n},\quad j=0,\ldots ,N. \end{aligned}$$

Subject to the definition (3.1), for $m=0,\ldots ,N$, the formula (2.5) can be written as

$$\begin{aligned} \hat{p}_m= & {} \frac{2}{N}\left[ \frac{1}{2} h_0+\sum _{j=1}^{N-1} \cos \!\left( \frac{jm\pi }{N}\right) h_j+\frac{(-1)^m}{2}h_N\right] \nonumber \\= & {} \check{p}_m-\frac{2}{N} \sum _{n=1}^{2s-2} p_{N+n} \left[ \frac{1}{2} +\sum _{j=1}^{N-1} (-1)^j \cos \!\left( \!\frac{jm\pi }{N}\right) \cos \!\left( \!\frac{jn\pi }{N}\right) +\frac{(-1)^{m+n+N}}{2}\right] \nonumber \\= & {} \check{p}_m-\frac{1}{N}\sum _{n=1}^{2s-2} p_{N+n} \left[ \sum _{j=0}^{N-1}(-1)^j \cos \!\left( \!\frac{j(m+n)\pi }{N}\right) \right. \nonumber \\&\left. +\, \sum _{j=0}^{N-1}(-1)^j \cos \!\left( \!\frac{j(m-n)\pi }{N}\right) +(-1)^{m+n+N}-1\right] . \end{aligned}$$

Since

$$\begin{aligned}&\sum _{j=0}^{N-1}(-1)^j \cos \!\left( \!\frac{j(m-n)\pi }{N}\right) \\&\quad =\frac{1-(-1)^{m-n+N}}{2},\quad m=0,\ldots ,N,\;\; n=1,\ldots ,2s-2, \nonumber \\&\sum _{j=0}^{N-1}(-1)^j \cos \!\left( \!\frac{j(m+n)\pi }{N}\right) =\frac{1-(-1)^{m+n+N}}{2},\quad m+n\ne N, \nonumber \\&\sum _{j=0}^{N-1}(-1)^j \cos \!\left( \!\frac{j(m+n)\pi }{N}\right) =N,\quad m=N-2s+2,\ldots ,N-1,\;\; n=N-m, \end{aligned}$$

we obtain

$$\begin{aligned} \hat{p}_m= & {} \check{p}_m,\quad m=0,\ldots ,N-2s+1\;\; \text{ or }\;\; m=N, \nonumber \\ \hat{p}_m= & {} \check{p}_m-p_{2N-m},\quad m=N-2s+2,\ldots ,N-1. \end{aligned}$$

(3.2)

Over to the remaining conditions in (2.4). Substituting (3.2), we have

$$\begin{aligned}&\sum _{m=1}^{2s-2} \left[ \frac{(N+m)(N+m+i-1)!}{(N+m-i)!} - \frac{(N-m)(N-m+i-1)!}{(N-m-i)!} \right] p_{N+m} \nonumber \\&\quad = \, \frac{(2i)!}{2^ii!} f^{(i)}(1)-\sum _{m=1}^{N-1} \frac{m(m+i-1)!}{(m-i)!} \check{p}_m-\frac{N(N+i-1)!}{2(N-i)!}\check{p}_N, \nonumber \\&\sum _{m=1}^{2s-2} (-1)^m \left[ \frac{(N+m)(N+m+i-1)!}{(N+m-i)!} - \frac{(N-m)(N-m+i-1)!}{(N-m-i)!} \right] p_{N+m} \nonumber \\&\quad = \, (-1)^{N+i} \frac{(2i)!}{2^ii!} f^{(i)}(-1)-(-1)^{N} \sum _{m=1}^{N-1} (-1)^m \frac{m(m+i-1)!}{(m-i)!} \check{p}_m\\&\qquad - \frac{N(N+i-1)!}{2(N-i)!}\check{p}_N \end{aligned}$$

for $i=1,\ldots ,s-1$, which can be written into matrix form

$$\begin{aligned} \left( \begin{array}{ccccccc} b_{1,1}&{} b_{1, 2}&{}b_{1, 3}&{}\cdots &{} b_{1, 2s-2}\\ b_{2,1}&{} b_{2, 2}&{}b_{2, 3}&{}\cdots &{} b_{2, 2s-2}\\ \vdots \\ b_{s-1,1}&{} b_{s-1, 2}&{}b_{s-1, 3}&{}\cdots &{} b_{s-1, 2s-2}\\ -b_{1,1}&{} b_{1, 2}&{}-b_{1, 3}&{}\cdots &{} b_{1, 2s-2}\\ -b_{2,1}&{} b_{2, 2}&{}-b_{2, 3}&{}\cdots &{} b_{2, 2s-2}\\ \vdots \\ -b_{s-1,1}&{} b_{s-1, 2}&{}-b_{s-1, 3}&{}\cdots &{} b_{s-1, 2s-2}\\ \end{array} \right) \left( \begin{array}{ccccccc} p_{N+1}\\ p_{N+2}\\ \vdots \\ p_{N+s-1}\\ p_{N+s}\\ p_{N+s+1}\\ \vdots \\ p_{N+2s-2}\\ \end{array} \right) =\left( \begin{array}{ccccccc} a_{1,1}\\ a_{1,2}\\ \vdots \\ a_{1,s-1}\\ a_{-1,1}\\ a_{-1,2}\\ \vdots \\ a_{-1,s-1}\\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} b_{i,m}= & {} \frac{1}{(N+2s)^{2i}}\left[ \frac{(N+m)(N+m+i-1)!}{(N+m-i)!} - \frac{(N-m)(N-m+i-1)!}{(N-m-i)!}\right] \nonumber \\= & {} \frac{1}{(N+2s)^{2i}}\left[ (N+m)^2 \prod _{k=1}^{i-1} [(N+m)^2 - k^2] - (N-m)^2 \prod _{k=1}^{i-1} [(N-m)^2 - k^2]\right] , \nonumber \\ a_{1,i}= & {} \frac{1}{(N+2s)^{2i}}\left[ \frac{(2i)!}{2^ii!} f^{(i)}(1)-\sum _{m=1}^{N-1} \frac{m(m+i-1)!}{(m-i)!} \check{p}_m-\frac{N(N+i-1)!}{2(N-i)!}\check{p}_N\right] , \nonumber \\ a_{-1, i}= & {} \frac{1}{(N+2s)^{2i}}\left[ (-1)^{N+i} \frac{(2i)!}{2^ii!} f^{(i)}(-1)-(-1)^{N} \sum _{m=1}^{N-1} (-1)^m \frac{m(m+i-1)!}{(m-i)!} \check{p}_m \right. \nonumber \\&\left. -\, \frac{N(N+i-1)!}{2(N-i)!}\check{p}_N\right] , \end{aligned}$$

for $i = 1, 2, \ldots , s-1$. This also can be separated into two smaller systems adding and subtracting the equations,

$$\begin{aligned}&\left( \begin{array}{ccccccc} b_{1, 2}&{}b_{1, 4}&{}b_{1, 6} &{}\cdots &{} b_{1, 2s-2}\\ b_{2, 2}&{}b_{2, 4}&{}b_{2, 6} &{}\cdots &{} b_{2, 2s-2}\\ \vdots \\ b_{s-1, 2}&{}b_{s-1, 4}&{}b_{s-1, 6} &{}\cdots &{} b_{s-1, 2s-2}\\ \end{array} \right) _{(s-1) \times (s-1)}\left( \begin{array}{ccccccc} p_{N+2}\\ p_{N+4}\\ p_{N+6}\\ \vdots \\ p_{N+2s-2}\\ \end{array} \right) _{(s-1) \times 1}\nonumber \\&\quad =\left( \begin{array}{ccccccc} \frac{a_{1,1}+a_{-1,1}}{2}\\ \frac{a_{1,2}+a_{-1,2}}{2}\\ \vdots \\ \frac{a_{1,s-1}+a_{-1,s-1}}{2}\\ \end{array} \right) _{(s-1) \times 1} \end{aligned}$$

(3.3)

and

$$\begin{aligned}&\left( \begin{array}{ccccccc} b_{1, 1}&{}b_{1, 3}&{}b_{1, 5} &{}\cdots &{} b_{1, 2s-1}\\ b_{2, 1}&{}b_{2, 3}&{}b_{2, 5} &{}\cdots &{} b_{2, 2s-1}\\ \vdots \\ b_{s-1, 1}&{}b_{s-1, 3}&{}b_{s-1, 5} &{}\cdots &{} b_{s-1, 2s-1}\\ \end{array} \right) _{(s-1) \times (s-1)}\left( \begin{array}{ccccccc} p_{N+1}\\ p_{N+3}\\ p_{N+5}\\ \vdots \\ p_{N+2s-1}\\ \end{array} \right) _{(s-1) \times 1}\nonumber \\&\quad =\left( \begin{array}{ccccccc} \frac{a_{1,1}-a_{-1,1}}{2}\\ \frac{a_{1,2}-a_{-1,2}}{2}\\ \vdots \\ \frac{a_{1,s-1}-a_{-1,s-1}}{2}\\ \end{array} \right) _{(s-1) \times 1}. \end{aligned}$$

(3.4)

Solving the equations directly, we can compute for $s=3$

$$\begin{aligned} p_{N+1}= & {} \frac{2N^2+17}{128N} [f'(1)+(-1)^Nf'(-1)]-\frac{3}{128N} [f''(1)-(-1)^Nf''(-1)] \nonumber \\&- \, \frac{1}{128N}\sum _{m=1}^{N-1} m^2(2N^2-m^2+18)[1-(-1)^{N-m}]\check{p}_m, \nonumber \\ p_{N+2}= & {} \frac{2N^2+31}{384N} [f'(1)-(-1)^Nf'(-1)] -\frac{1}{128N} [f''(1)+(-1)^Nf''(-1)] \nonumber \\&- \, \frac{1}{384N} \sum _{m=1}^{N-1}m^2(2N^2-m^2+32)[1+(-1)^{N-m}]\check{p}_m -\frac{N(N^2+32)}{384} \check{p}_N, \nonumber \\ p_{N+3}= & {} -\frac{2N^2+1}{384N}[f'(1)+(-1)^Nf'(-1)]+\frac{1}{128N} [f''(1)-(-1)^Nf''(-1)] \nonumber \\&+ \, \frac{1}{384N} \sum _{m=1}^{N-1} m^2(2N^2-m^2+2)[1-(-1)^{N-m}]\check{p}_m, \nonumber \\ p_{N+4}= & {} -\frac{2N^2+7}{768N}[f'(1)-(-1)^Nf'(1)] +\frac{1}{256N}[f''(1)+(-1)^Nf''(-1)] \nonumber \\&+ \, \frac{1}{768N} \sum _{m=1}^{N-1} m^2(N^2-m^2+8)[1+(-1)^{N-m}]\check{p}_m+\frac{N(N^2+8)}{768} \check{p}_N. \end{aligned}$$

For $s\ge 4$ it probably makes more sense to solve the equations directly than to write down a general solution like above.

3.3 The general algorithm for FCC$+$

To construct the general algorithm for the computation of FCC$+$ coefficients,

$$\begin{aligned} I[f] \approx \mathcal {Q}_\omega ^{\mathbf {FCC},N,s}[f]= & {} \int _{-1}^1 p(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x =\sum _{m=0}^{N+2s-2} p_m \int _{-1}^1 T_m(x)\mathrm {e}^{\mathrm {i}\omega g(x)}\hbox {d} x \nonumber \\= & {} \sum _{m=0}^{N+2s-2} p_m \mu _m, \end{aligned}$$

(3.5)

where

$$\begin{aligned} \mu _m = \int _{-1}^{1} \mathbf {T}_m(x) \mathrm {e}^{\mathrm {i}\omega g(x)} \hbox {d} x, \end{aligned}$$

(3.6)

a concrete process is presented as follows:

Step 1 Calculate the coefficients $\check{p}_m$, $m = 0, 1, \ldots , N$, defined in (3.1), which can be represented in matrix form

$$\begin{aligned} \check{\mathbf {p}} = \mathcal {L}^{-1}_N \mathbf {f}, \end{aligned}$$

(3.7)

where

$$\begin{aligned}&\mathcal {L}_N = \left( c_{ij}\right) _{0 \le i, j \le N}, \nonumber \\&\mathcal {L}^{-1}_N = \frac{2}{N} \mathcal {L}_N, \nonumber \\&\check{\mathbf {p}} = (p_0, p_1, \ldots , p_N)^\top , \nonumber \\&\mathbf {f} = (f_0, f_1, \ldots , f_N)^\top , \nonumber \\ c_{ij}= & {} \left\{ \begin{array}{lllll} \frac{1}{2}, &{}\quad \text {for} \quad j=0, \quad i=0, 1, \ldots , N,\\ \cos \left( \frac{ij \pi }{N}\right) , &{} \quad \text {for} \quad j = 1, 2, \ldots , N-1, \quad \text {and} \quad i = 0, 1, \ldots , N,\\ \frac{(-1)^i}{2}, &{} \quad \text {for} \quad j=N, \quad i=0, 1, \ldots , N.\\ \end{array} \right. \end{aligned}$$

We observe that the computation of (3.7) is nothing else but the discrete cosine transform appearing in the FCC whose cost is $O\left( N \log (N)\right)$ in [5].

Step 2 Compute the coefficients $p_m$, for $m = N+1, N+2, \ldots , N+2s-2$, by solving the system comprising of (3.3) and (3.4). The computational cost for a general system of linear equations is at most $O\left( s^3\right)$.

Step 3 Based on the coefficients $p_m$, $m = N+1, N+2, \ldots , N+2s-2$, in Step 1, and $\check{p}_j$, $j = 0, 1, \ldots , N$ in Step 2, derive the coefficients $\hat{\mathbf {p}} = (\hat{p}_0, \hat{p}_1, \ldots , \hat{p}_{N})^\top$ using the relations (3.2). It is observed that only $2s-2$ subtraction operations occur which can be omitted. The matrix form for the transformation is

$$\begin{aligned} \hat{\mathbf {p}}_{(N+1) \times 1}= & {} \left[ \check{p}_0, \check{p}_1, \ldots , \check{p}_{N-2s+1}, \check{p}_{N-(2s-2)}-p_{N+(2s-2)}, \ldots , \check{p}_{N-1}\right. \\&\left. - \, p_{N+1}, \check{p}_N\right] ^\top _{(N+1) \times 1}. \end{aligned}$$

Step 4 Now, using $\hat{\mathbf {p}} = (\hat{p}_0, \hat{p}_1, \ldots , \hat{p}_{N})^\top$ from Step 3, the coefficients $p_{m}$, $m = 1, 2, \ldots , N$ can be represented by (2.5). This completes our derivation of the coefficients $p_m$, $m = 1, 2, \ldots , N+2s-2$. The corresponding matrix form for (2.5) is

$$\begin{aligned} \mathbf {p}_{(N+1) \times 1} = \left[ \frac{1}{2} \hat{p}_0, \hat{p}_1, \hat{p}_2, \ldots , \hat{p}_{N-1}, \frac{1}{2} \hat{p}_{N}\right] ^\top _{(N+1) \times 1}. \end{aligned}$$

Step 5 Calculate the coefficients $\mu _m$ from (3.6), which have been studied in Section 3 of [5], inclusive of its stability. Finally, to calculate the approximate value of (3.5), $O\left( N+2s-1\right)$ multiplications are required to form the sum.

Altogether, the computational cost is $O\left( N \log (N)\right) + O\left( s^3\right)$.

Insofar as stability of this algorithm is concerned, stability of Step 1 has been analysed in reference [5]. In the sequel we are concerned with the conditioning of the system of linear equations in Step 2. There are two linear systems with dimension $s-1$ to be solved. The condition numbers of the two coefficient matrices decide the stability of numerical solution for (3.3) and (3.4), they are displayed in Tables 1 and 2 for $s \ge 3$ and $N = 2^j$, $j = 2, 3, \ldots , 6$, respectively. It transpires from the two tables that the condition number becomes large with increasing s and N. Therefore, for large N, to improve the asymptotic order s, numerical solution of the system might lead to an unacceptable error accumulation. Thus, a suitable algorithm, e.g. singular value decomposition, should be applied to get the numerical values to approximate $p_{N+m}$, $m = 1, 2, \ldots , 2s-2$.

Table 1 The condition numbers of the coefficient matrix of (3.3)

Table 2 The condition numbers of the coefficient matrix of (3.4)

3.4 A numerical example

We have demonstrated that FCC$+$ can attain any asymptotic order $s \ge 1$ at a cost similar to standard FCC: a single DCT-I computation and a solution of an $(2s-2)\times (2s-2)$ linear system. (Since s is likely to be small, the extra expense of solving a linear system is marginal.) To illustrate the gain in accuracy, we revisit the problem (1.3). Figure 4 displays the magnitude of the error, $\log _{10}\left| \mathcal {Q}_{\omega }^{\mathbf {FCC},8, s}[f] - I[f]\right|$, for $s=1$ (i.e., plain FCC, solid line), 2 (dotted line), 3 (dashed line), 4 (dash-dotted line) and $N=8$, from the top to bottom. We observe that the curves have for $\omega \gg 1$ the same slope as plain Filon methods in Fig. 1 (right), but the curves lie much lower: the error is considerably smaller! Moreover, for small $\omega \ge 0$ the performance is starkly better than of plain Filon and marginally improves with greater $s\ge 1$.

Fig. 4

The error (in logarithmic scale) of $\mathcal {Q}_{\omega }^{\mathbf {FCC},8, 1}[f]$ (the solid line in blue), $\mathcal {Q}_{\omega }^{\mathbf {FCC},8, 2}[f]$ (the dotted line in orange), $\mathcal {Q}_{\omega }^{\mathbf {FCC},8, 3}[f]$ (the dashed line in brown) and $\mathcal {Q}_{\omega }^{\mathbf {FCC},8, 4}[f]$ (the dash-dotted line in purple). The corresponding order is from the top to bottom (colour figure online)

4 Conclusions

Several effective algorithms to compute highly oscillatory integrals have emerged in the last two decades. Among these methods, an extended Filon method enjoys the advantage of simplicity and flexibility: once we can compute the moments $\int _{-1}^1 x^k \mathrm {e}^{\mathrm {i}\omega g(x)}\mathrm {d}x$, $k\in \mathbb {Z}_+$, we can construct an extended Filon method with great ease.

Choosing an extended Filon method, we need to make three choices: how many derivatives to compute at critical points, how many extra interpolation points to add and how to choose these interpolation points. We are guided by three goals: good performance for large $\omega$, good performance for small $\omega \ge 0$ (and hence good uniform performance) and simplicity of the underlying expressions and ease of their computation. Plain Filon method exhibits excellent behaviour for $\omega \gg 1$, while FCC is superior for small $\omega \ge 0$, can be derived cheaply and has a pleasingly simple form. In this paper we have introduced an approach that shares the advantages of both.

We have focused on the case $g'(x)\ne 0$, $x\in [-1,1]$, but, like FCC in [4], our approach can be easily generalised to the presence of stationary points, where $g'$ vanishes.