Abstract
In this paper the numerical approximation of stochastic differential equations satisfying a global monotonicity condition is studied. The strong rate of convergence with respect to the mean square norm is determined to be \(\frac{1}{2}\) for the two-step BDF-Maruyama scheme and for the backward Euler–Maruyama method. In particular, this is the first paper which proves a strong convergence rate for a multi-step method applied to equations with possibly superlinearly growing drift and diffusion coefficient functions. We also present numerical experiments for the \(\tfrac{3}{2}\)-volatility model from finance and a two dimensional problem related to Galerkin approximation of SPDE, which verify our results in practice and indicate that the BDF2-Maruyama method offers advantages over Euler-type methods if the stochastic differential equation is stiff or driven by a noise with small intensity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Strong convergence rates of numerical approximations to stochastic differential equations (SDEs) are a well studied topic. Under a global Lipschitz condition on the coefficients the picture is rather complete, both for one-step methods [13, 17] and multi-step methods [2, 14]. Many important equations in application have coefficients that do not satisfy the global Lipschitz condition, and it is therefore important to study a more general setting. Many convergence results for explicit and implicit one-step methods have also been proven for equations without the global Lipschitz condition, see for instance [1, 7–10, 12, 16, 19, 21]. In the present paper we determine the strong rate \(\tfrac{1}{2}\) for the backward Euler–Maruyama method (BEM), in the mean-square norm, which improves [16] in terms of a weaker assumption on the coefficients.
For multi-step schemes, on the other hand, there are no previously known results on strong convergence for equations with coefficients not satisfying a global Lipschitz condition. In this paper we determine the strong rate \(\tfrac{1}{2}\) for the BDF2-Maruyama scheme for equations whose, possibly superlinearly growing, coefficient functions satisfy a global monotonicity condition. Backward difference formulas (BDF) are popular in applied sciences for the approximation of stiff equations, see [2] for a list of references to such works.
Let \(d,m \in {\mathbf {N}}\), \(T > 0\) and \((\varOmega ,{\mathscr {F}},({\mathscr {F}}_t)_{t \in [0,T]}, {\mathbf {P}})\) be a filtered probability space satisfying the usual conditions, on which an \({\mathbf {R}}^d\)-valued standard \(({\mathscr {F}}_t)_{t \in [0,T]}\)-Wiener process \(W :[0,T] \times \varOmega \rightarrow {\mathbf {R}}^d\) is defined. We consider the equation
with drift \(f :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^m\) and diffusion coefficient function \(g :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^{m\times d}\). The functions f and g are assumed to satisfy a global monotonicity, a coercivity and a local Lipschitz condition in Assumption 2.1 below. The initial condition fulfills \(X_0\in L^2(\varOmega ,\mathscr {F}_0,{\mathbf {P}};{\mathbf {R}}^m)\) with some additional integrability, admitting higher moments of the solution.
For a given equidistant time step size \(h \in (0,1)\) we discretize the exact solution to (1.1) along the temporal grid \(\tau _h = \{ t_n = nh \; : \; n = 0,1,\ldots ,N_h \}\). Here \(N_h \in {\mathbf {N}}\) is uniquely determined by the inequality \(t_{N_h} \le T < t_{N_{h} + 1}\). We set \(\varDelta _h W^j := W(t_j) - W(t_{j-1})\) for \(j\in \{1,\dots ,N_h\}\). We consider discretizations by means of the backward Euler–Maruyama method
with \((X_h^0)_{h\in (0,1)}\) satisfying \({\mathbf {E}}[\Vert X_h^0-X_0\Vert ^2]=\mathscr {O}(h)\), and by means of the BDF2-Maruyama scheme from [2]. The latter is given by the recursion
for \(j\in \{2,\dots ,N_h\}\), with initial values \((X_h^0,X_h^1)\) where \((X_h^0)_{h\in (0,1)}\) is the same as above and \((X_h^1)_{h\in (0,1)}\) is determined, for instance, by one step of the backward Euler scheme or some other one-step method satisfying \({\mathbf {E}}[\Vert X_h^1-X(h)\Vert ^2]=\mathscr {O}(h)\). In practice, the implementation of the methods (1.2) and (1.3) often requires to solve a nonlinear equation in each time step. In Sect. 3 we discuss that under our assumptions a solution does indeed always exists provided the step size h is small enough. The choice of the root-finding algorithm may depend on the coefficient function f and its smoothness. We refer to [18] for a collection of such methods.
We prove that for \((X_h^j)_{j\in \{0,\dots ,N_h\}, h\in (0,1)}\), determined either by (1.2) or (1.3), and X being the solution to (1.1), there exist a constant C such that the following mean-square convergence holds:
The precise statements of our convergence results are found in Theorems 4.4 and 5.4. The proofs are based on two elementary identities: for all \(u_1,u_2\in {\mathbf {R}}^m\) it holds that
and for all \(u_1,u_2,u_3\in {\mathbf {R}}^m\) it holds that
found in [3], which has been derived from results on G-stability for linear multi-step methods, see [4, 20]. Up to the best of our knowledge (1.6) has not previously been used in the study of the BDF2 scheme for stochastic differential equations.
The paper is organized as follows: Sect. 2 contains notation and our precise assumptions on the coefficients f and g in (1.1). We cite well known results on existence, uniqueness and moment bounds for the solution under these conditions. A well-posedness result for general implicit stochastic difference equations is proved in Sect. 3. Sections 4 and 5 contain the analysis of the backward Euler–Maruyama and the BDF2-Maruyama schemes, respectively. Sections 4.1 and 5.1 contain a priori estimates for the respective schemes, in Sects. 4.2 and 5.2 stability results are proved, while Sects. 4.3 and 5.3 are concerned with the consistency of the two schemes. The two main results on the strong mean-square convergence rate are stated in Sects. 4.4 and 5.4, respectively. Further, in Sect. 5.5 we have a closer look on the second initial value for the BDF2-Maruyama scheme and it is shown that using one step of the BEM method is a feasible choice. Section 6 contains numerical experiments involving the \(\frac{3}{2}\)-volatility model from finance which verify our theoretical results and indicate that the BDF2-Maruyama method performs better than Euler-type methods in case of stiff problems or equations with a small noise intensity.
2 Setting and preliminaries
2.1 Notation and function spaces
Let \((\cdot ,\cdot )\) and \(|\cdot |\) denote the scalar product and norm in \({\mathbf {R}}^m\) and let \(|\cdot |_{{\mathrm {HS}}}\) denote the Hilbert–Schmidt norm on the space \({\mathbf {R}}^{m\times d}\) of all m times d matrices, i.e., \(|S|_{{\mathrm {HS}}}=\sqrt{{\text {Tr}}(S^*S))}\) for \(S\in {\mathbf {R}}^{m\times d}\).
Let \((\varOmega ,{\mathscr {F}},({\mathscr {F}}_t)_{t \in [0,T]}, {\mathbf {P}})\) be a filtered probability space satisfying the usual conditions. For \(p \in [1,\infty )\) and a sub-\(\sigma \)-field \(\mathscr {G} \subset {\mathscr {F}}\) we denote by \(L^p(\varOmega , \mathscr {G}, {\mathbf {P}}; E)\) the Banach space of all p-fold integrable, \(\mathscr {G} / \mathscr {B}(E)\)-measurable random variables taking values in a Banach space \((E, | \cdot |_E)\) with norm
If \(\mathscr {G} = {\mathscr {F}}\) we write \(L^p(\varOmega ;E) := L^p(\varOmega , {\mathscr {F}}, {\mathbf {P}}; E)\). If \(p = 2\) and \(E = {\mathbf {R}}^m\) we obtain the Hilbert space \(L^2(\varOmega ;{\mathbf {R}}^m)\) with inner product and norm
for all \(X, Y \in L^2(\varOmega ;{\mathbf {R}}^m)\). We denote by \({\vert \vert \vert }\cdot {\vert \vert \vert }\) the norm in \(L^2(\varOmega ;{\mathbf {R}}^{m\times d})\), i.e., \({\vert \vert \vert }Z {\vert \vert \vert }= ({\mathbf {E}}[|Z|_{{\mathrm {HS}}}^2])^\frac{1}{2}\) for \(Z\in L^2(\varOmega ;{\mathbf {R}}^{m\times d})\).
We next introduce notation related to the numerical discretizations. Recall from Sect. 1 the temporal grids \(\tau _h\), \(h\in (0,1)\). For \(h\in (0,1)\) and \(j\in \{0,\dots ,N_h\}\), we denote by
the orthogonal projector onto the closed sub-space \(L^2(\varOmega ,\mathscr {F}_{t_j},{\mathbf {P}};{\mathbf {R}}^m)\), which is also known as the conditional expectation. More precisely, for \(Y\in L^2(\varOmega ;{\mathbf {R}}^m)\) we set \(P_h^j\,Y={\mathbf {E}}[Y|\mathscr {F}_{t_j}]\). We introduce the spaces \((\mathscr {G}_h^2)_{h\in (0,1)}\) of all adapted grid functions, which enjoy the following integrability properties
These will play an important role in the error analysis.
2.2 Setting
Consider the setting introduced in Sect. 1. We now formulate our assumptions on the initial condition and the coefficient functions f and g which we work with throughout this paper.
Assumption 2.1
There exists \(q \in [1, \infty )\) such that the initial condition \(X_0:\varOmega \rightarrow {\mathbf {R}}^m\) satisfies \(X_0\in L^{4q-2}(\varOmega ,{\mathscr {F}}_{0},{\mathbf {P}};{\mathbf {R}}^m)\). Moreover, the mappings \(f :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^m\) and \(g :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^{m \times d}\), are continuous and there exist \(L \in (0,\infty )\) and \(\eta \in (\tfrac{1}{2},\infty )\) such that for all \(x_1,x_2 \in {\mathbf {R}}^m\) it holds
where \(q \in [1,\infty )\) is the same as above. Further, it holds for all \(x\in {\mathbf {R}}^m\) that
Assumption 2.1 guarantees the existence of an up to modification unique adapted solution \(X:[0,T]\times \varOmega \rightarrow {\mathbf {R}}^m\) to (1.1) with continuous sample paths, satisfying
see, e.g., [15, Chap. 2]. In the proof of Theorem 5.3 on the consistency of the BDF2 scheme, the \(L^{4q-2}(\varOmega ;{\mathbf {R}}^m)\)-moment bound is of importance in order to apply the bounds (4.5), (4.6) below.
For later reference we note several consequences of Assumption 2.1. From (2.2) we deduce the following polynomial growth bound:
where \(\tilde{L} = 2L + |f(0)|\). Indeed, (2.2) implies that
Moreover, from (2.1) followed by a use of (2.2) it holds, for \(x_1,x_2\in {\mathbf {R}}^m\), that
This gives the local Lipschitz bound
and, in the same way as above, the polynomial growth bound
where \(\bar{L} = 2 \sqrt{\frac{2 L}{\eta }} + |g(0)|_{{\mathrm {HS}}}\). Finally, we note for later use that the restriction \(X|_{\tau _h}\) of the exact solution to the time grid \(\tau _h\), given by
is an element of the space \(\mathscr {G}_h^2\) for every \(h \in (0,1)\). This follows directly from (2.4) and the growth bounds (2.5) and (2.7).
2.3 Preliminaries
Here we list some basic results that we use in this paper. Frequently, we apply the Young inequality and the weighted Young inequality
which holds true for all \(a, b \in {\mathbf {R}}\) and \(\nu >0\). We make use of the following discrete version of Gronwall’s Lemma: If \(h>0\), \(a_1,\dots ,a_{N_h},b,c \in [0,\infty )\), then
Finally we cite a standard result from nonlinear analysis which we use for the well-posedness of the numerical schemes, see for instance [18, Chap. 6.4] or [20, Thm. C.2]:
Proposition 2.1
Let \(G :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^m\) be a continuous mapping satisfying for some \(c \in (0, \infty )\)
Then G is a homeomorphism with Lipschitz continuous inverse. In particular, it holds
for all \(y_1, y_2 \in {\mathbf {R}}^m\).
3 A well-posedness result for stochastic difference equations
In this section we prove existence and uniqueness of solutions to general stochastic k-step difference equations. This result applies in particular to all implicit linear multi-step schemes for SDE with coefficients satisfying Assumption 2.1 including the backward Euler–Maruyama method, the Crank–Nicolson scheme, the k-step BDF-schemes, and the k-step Adams–Moulton methods. We refer the reader to [2, 14] for a thorough treatment of these schemes for stochastic differential equations with Lipschitz continuous coefficients.
Theorem 3.1
Let the mappings f and g satisfy Assumption 2.1 with \(q \in [1,\infty )\) and \(L \in (0,\infty )\), let \(k\in {\mathbf {N}}\), \(\alpha _0,\dots ,\alpha _{k-1}, \beta _0,\dots ,\beta _{k-1}, \gamma _0,\dots , \gamma _{k-1}\in {\mathbf {R}}\), \(\alpha _k=1\), \(\beta _k \in (0,\infty )\), and \(h_1 \in (0, \tfrac{1}{\beta _kL})\) with \(k h_1<T\). Assume that initial values \(U_h^\ell \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^m)\) are given with \(f(U_h^\ell ) \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^m)\) and \(g(U_h^\ell ) \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^{m \times d})\) for all \(\ell \in \{0,\dots ,k-1\}\). Then, for every \(h\in (0,h_1]\) there exists a unique family of adapted random variables \(U_h\in \mathscr {G}_h^2\) satisfying
for \(j\in \{k,\dots ,N_h\}\). In particular, it holds true that \(U_h^j,\, f(U_h^j) \in L^2(\varOmega , {\mathscr {F}}_{t_j}, {\mathbf {P}}; {\mathbf {R}}^m)\) and \(g(U_h^j) \in L^2(\varOmega , {\mathscr {F}}_{t_j}, {\mathbf {P}}; {\mathbf {R}}^{m \times d})\) for all \(j \in \{k,\dots ,N_h\}\).
Proof
Let \(F_h :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^m\), \(h\in (0,h_1]\), be the mappings defined by
Note that for every \(h \in (0,h_1]\) it holds that \(1-\beta _k h L\ge 1-\beta _k h_1 L > 0\) and from the global monotonicity condition (2.1) we have that
Consequently, by Proposition 2.1 the inverse \(F_h^{-1}\) of \(F_h\) exists for every \(h \in (0, h_1]\) and is globally Lipschitz continuous with Lipschitz constant \((1-h_1 \beta L)^{-1}\). Using these properties and the fact that \(\alpha _k = 1\) we can rewrite (3.1) as
for all \(j\in \{k,\dots ,N_h\}\), where
for \(j\in \{k,\dots ,N_h\}\). Therefore, by (3.2) and the continuity of \(F_h^{-1}\) we have that for every \(h\in (0,h_1]\), \(U_h\) is an adapted collection of random variables, uniquely determined by the initial values \(U_h^0,\dots ,U_h^{k-1}\).
In order to prove that \(U_h\in \mathscr {G}_h^2\) for all \(h\in (0,h_1]\), by means of an induction argument, we introduce \(U_h^{j,n}:=U_h^j\mathbf {1}_{\{0,\dots ,n-1\}}(j)\). By the assumptions on the initial values \(U_h^0,\dots , U_h^{k-1}\) it holds that \((U_h^{j,k})_{j \in \{0,\ldots ,N_h\}} \in \mathscr {G}_h^2\). For the induction step, we now assume that \((U_h^{j,n})_{j \in \{0,\ldots ,N_h\}} \in \mathscr {G}_h^2\) for some \(n\in \{k,\dots ,N_h\}\). This assumption and the fact that
imply immediately that \(R_h^n\in L^2(\varOmega ,\mathscr {F}_{t_n},{\mathbf {P}};{\mathbf {R}}^m)\). Thus, from the linear growth of \(F_h^{-1}\) we get \(U_h^{n}=F_h^{-1}(R_h^n)\in L^2(\varOmega ,\mathscr {F}_{t_n},{\mathbf {P}};{\mathbf {R}}^m)\).
In addition, we recall from [1, Cor. 4.2] the fact that under Assumption 2.1 the mapping \(h^{\frac{1}{2}} g \circ F_h^{-1}\) is also globally Lipschitz continuous with a Lipschitz constant independent of h. More precisely, there exists a constant C such that for all \(h \in (0, h_1]\) and all \(x_1,x_2 \in {\mathbf {R}}^m\) it holds true that
Consequently, the mapping \(h^{\frac{1}{2}} g \circ F_h^{-1} :{\mathbf {R}}^m \rightarrow {\mathbf {R}}^m\) is also of linear growth and we conclude as above
In particular, this gives \(g( U_h^{n} ) \in L^2(\varOmega ,{\mathscr {F}}_{t_n},{\mathbf {P}};{\mathbf {R}}^{m \times d})\). Finally, from the definition of \(F_h\) and (3.2) we have that
Hence, by the linear growth of \(F_h^{-1}\) and the fact that \(R_h^n \in L^2(\varOmega ,\mathscr {F}_{t_n},{\mathbf {P}};{\mathbf {R}}^m)\) we conclude that \(f(U^n_h) \in L^2(\varOmega ,\mathscr {F}_{t_n},{\mathbf {P}};{\mathbf {R}}^m)\).
Altogether, this proves that \((U_h^{j,n+1})_{j \in \{0,\ldots ,N_h\}} \in \mathscr {G}_h^2\) and, therefore, by induction \((U_h^{j,n})_{j \in \{0,\ldots ,N_h\}} \in \mathscr {G}_h^2\) for every \(n\in \{k,\dots ,N_h+1\}\). By finally noting that \(U_h^{j}=U_h^{j,N_h+1}\), \(j\in \{0,\dots ,N_h\}\), the proof is complete. \(\square \)
4 The backward Euler–Maruyama method
In this section we prove that the backward Euler–Maruyama scheme is mean-square convergent of order \(\frac{1}{2}\) under Assumption 2.1. The proof is split over several subsections: First we familiarize ourselves with the connection between the BEM method and the identity (1.5). This is done by proving an a priori estimate in Sect. 4.1. In Sect. 4.2 we then derive a stability result which gives an estimate of the distance between an arbitrary adapted grid function and the one generated by the BEM method. As it turns out this distance is bounded by the error in the initial value and a local truncation error. The latter is estimated for the restriction of the exact solution to (1.1) to the temporal grid \(\tau _h\) in Sect. 4.3. Altogether, this will then yield the desired convergence result in Sect. 4.4.
4.1 Basic properties of the backward Euler–Maruyama scheme
Here and in Sect. 4.2 we study \(U\in \mathscr {G}_h^2\), \(h\in (0,\tfrac{1}{L})\), satisfying
with initial condition \(U^0\in L^2(\varOmega ,\mathscr {F}_0,{\mathbf {P}};{\mathbf {R}}^m)\) such that \(f(U^0)\in L^2(\varOmega ,\mathscr {F}_0,{\mathbf {P}};{\mathbf {R}}^m)\) and \(g(U^0)\in L^2(\varOmega ,\mathscr {F}_0,{\mathbf {P}};{\mathbf {R}}^{m\times d})\). Here L is the parameter in Assumption 2.1 and from Theorem 3.1 there exist for every \(h\in (0,\tfrac{1}{L})\) a unique \(U\in \mathscr {G}_h^2\) satisfying (4.1). \(U_0\) is not necessarily related to the initial value \(X_0\) of (1.1).
In order to prove the a priori bound of Theorem 4.1 and the stability in Theorem 4.2 the following lemma is used:
Lemma 4.1
For all \(h\in (0,\tfrac{1}{L})\) and \(U,V\in \mathscr {G}_h^2\) with U satisfying (4.1) it holds for all \(j \in \{1,\ldots ,N_h\}\) \({\mathbf {P}}\)-almost surely that
where \(E:=U-V\) and \((Z^j)_{j\in \{1,\dots N_h\}}\) are the centered random variables given by
Proof
From the identity (1.5), and since U satisfies (4.1) by assumption the assertion follows directly. Note that \(Z^j\) is well-defined as a centered real-valued integrable random variable due to the independence of the centered Wiener increment \(\varDelta _h W^{j}\) and the square integrable random variables \(g(U^{j-1})\) and \(E^{j-1}\). \(\square \)
The proof of the next theorem is the first and simplest demonstration of the, in principle, same technique used to prove Theorems 4.2, 5.1 and 5.2 below. This a priori estimate is in fact not needed further in the analysis and it can be deduced from the stability Theorem 4.2, but with larger constants, and for a more narrow range for the parameter h. We include it for completeness.
Theorem 4.1
Let Assumption 2.1 hold with \(L\in (0,\infty )\), \(q\in [1,\infty )\). For \(h\in (0,\tfrac{1}{2L})\) denote by \(U\in \mathscr {G}_h^2\) the unique adapted grid function satisfying (4.1). Then, for all \(n \in \{1,\ldots ,N_h\}\) it holds that
where \(C_h= \max \{1,2LT\}(1-2Lh)^{-1}\).
Proof
Lemma 4.1 applied with \(V=0\) and taking expectations yields
From the coercivity condition (2.3) and the Young inequality (2.8) we have that
Summing over j from 1 to n gives that
Since \(q \in [1, \infty )\) it holds \(1 \le 4q - 3\) and \(4 - 4q \le 0\). By elementary bounds we get
We conclude by a use of the discrete Gronwall Lemma (2.9). \(\square \)
4.2 Stability of the backward Euler–Maruyama scheme
For the formulation of the stability Theorem 4.2 we define for \(h\in (0,1)\) and \(V\in \mathscr {G}_h^2\) the local truncation error of V given by
where the local residuals \(\varrho ^j_h(V)\) of V are defined as
for \(j\in \{2,\ldots ,N_h\}\). Note that \(\varrho ^j_h(V) \in L^2(\varOmega ,{\mathscr {F}}_{t_j},{\mathbf {P}};{\mathbf {R}}^m)\) for every \(V \in \mathscr {G}_h^2\). We also introduce a maximal step size \(h_E\) for the stability, which guarantees that the stability constant in Theorem 4.2 does not depend on h. It is given by
Using the same arguments as in Theorem 4.1 the assertion of Theorem 4.2 stays true for all \(h \in (0,\frac{1}{2L})\) but with a constant C depending on \(\frac{1}{1 - 2hL}\) as in Theorem 4.1.
Theorem 4.2
Let Assumption 2.1 hold with \(L\in (0,\infty )\), \(\eta \in (\tfrac{1}{2}, \infty )\). For all \(h\in (0,h_E]\), \(U\in \mathscr {G}_h^2\) satisfying (4.1), \(V\in \mathscr {G}_h^2\), and all \(n \in \{1,\ldots ,N_h\}\) it holds that
where \(C= \max \{ 3 , 4 \eta , \frac{4 \eta }{2 \eta - 1} \}\).
Proof
Fix arbitrary \(h \in (0, h_E]\) and \(V \in \mathscr {G}^2_h\). To ease the notation we suppress the dependence of h and V and simply write, for instance, \(\varDelta W^j := \varDelta _h W^j\). We also write \(E^j := U^j - V^j\) and
From Lemma 4.1 we get after taking expectations that
In order to treat the residual term we first notice that \(P_h^{j-1} E^{j-1}=E^{j-1}\). Then, by taking the adjoint of the projector and by applying the weighted Young inequality (2.8) with \(\nu =h>0\) we obtain
Moreover, further applications of the Cauchy-Schwarz inequality, the triangle inequality, and the weighted Young inequality (2.8) with \(\nu = \mu \) yield
Therefore, together with the global monotonicity condition (2.1) this gives
Setting \(\mu = 2\eta -1 >0\) gives that \(1 + \mu = 2 \eta \). Then, summing over j from 1 to n and thereby identifying two telescoping sums yields
Since \(1 - 2 Lh \ge 1 - 2 L h_E > \frac{1}{2}\) as well as \(h\le h_E<\tfrac{1}{2}\) and \(\eta >\tfrac{1}{2}\) we obtain after some elementary transformations the inequality
The proof is completed by applying the discrete Gronwall Lemma (2.9). \(\square \)
4.3 Consistency of the backward Euler–Maruyama scheme
In this subsection we give an estimate for the local truncation error (4.2) of the BEM method. For the proof we first recall that the restriction \(X|_{\tau _h}\) of the exact solution to the temporal grid \(\tau _h\) is an element of the space \(\mathscr {G}_h^2\), see Sect. 2.2. Further, we make use of [1, Lemmas 5.5, 5.6], which provide estimates for the drift integral
for all \(\tau , \tau _1,\tau _2\in [0,T]\) with \(\tau _1 \le \tau \le \tau _2\), and for the stochastic integral
for all \(\tau _1,\tau _2\in [0,T]\) with \(\tau _1 \le \tau _2\), respectively.
Theorem 4.3
Let Assumption 2.1 hold and let \(X|_{\tau _h}\) be the restriction of the exact solution to (1.1) to the temporal grid \(\tau _h\). Then there exists \(C>0\) such that
where the local truncation is defined in (4.2).
Proof
Recall the definitions of \(\rho _h^\mathrm {BEM}(X|_{\tau _h})\) and \(\varrho _h^j(X|_{\tau _h})\) from (4.2). It suffices to show
Inserting (1.1) it holds for every \(j\in \{1,\dots ,N_h\}\) that
Note that inequalities (4.5) and (4.6) apply to (4.7) due to the moment bound (2.4). These estimates together with an application of the triangle inequality and the fact that \(\Vert {\mathbf {E}}[ V | {\mathscr {F}}_{t_{j-1}} ] \Vert \le \Vert V \Vert \) for every \(V \in L^2(\varOmega ;{\mathbf {R}}^m)\) completes the proof of (4.7). \(\square \)
4.4 Mean-square convergence of the backward Euler–Maruyama method
Here we consider the numerical approximations \((X_h^j)_{j=0}^{N_h}\), \(h\in (0,h_E]\), uniquely determined by the backward Euler–Maruyama method (1.2) with a corresponding family of initial values \((X_h^0)_{h\in (0,h_E]}\). Recall from (4.3) that \(h_E=\tfrac{1}{2(4L+1)}\). This family is assumed to satisfy the following assumption.
Assumption 4.1
The family of initial values \((X_h^0)_{h\in (0,h_E]}\) satisfies
for all \(h\in (0,h_E]\) and is consistent of order \(\tfrac{1}{2}\) in the sense that
as \(h\downarrow 0\), where X is the exact solution to (1.1).
Note that Assumption 4.1 is obviously satisfied for the choice \(X_h^0 := X_0\) for every \(h \in (0,h_E]\). This said we are now ready to state the main result of this section.
Theorem 4.4
Let Assumptions 2.1 and 4.1 hold, let X be the exact solution to (1.1) and let \((X_h^j)_{j=0}^{N_h}\), \(h \in (0,h_E]\), be the family of backward Euler–Maruyama approximations determined by (1.2) with initial values \((X_h^0)_{h\in (0,h_E]}\). Then, the backward Euler–Maruyama method is mean-square convergent of order \(\tfrac{1}{2}\), more precisely, there exists \(C>0\) such that
Proof
For \(h\in (0,h_E]\), we apply Theorem 4.2 with \(U=(X_h^j)_{j=0}^{N_h}\in \mathscr {G}_h^2\) and \(V=X|_{\tau _h}=(X(t_j))_{j=0}^{N_h}\in \mathscr {G}_h^2\) and get that there is a constant \(C>0\), not depending on h, such that
The first and second term on the right hand side are of order \(\mathscr {O}(h)\) by Assumption 4.1. Since the same holds true for the consistency term \(\rho _h^\mathrm {BEM}(X|_{\tau _h})\) by Theorem 4.3 the proof is completed. \(\square \)
5 The BDF2-Maruyama method
In this section we follow the same procedure as in Sect. 4 with identity (1.6) in place of (1.5). Every result in Sect. 4 has its counterpart here for the BDF2-Maruyama method. As the multi-step method involves more terms the proofs in this section are naturally a bit more technical, but rely in principle on the same arguments as in the previous section.
5.1 Basic properties of the BDF2-Maruyama method
Here and in Sect. 5.2 our results concern \(U\in \mathscr {G}_h^2\), \(h\in (0,\tfrac{3}{2L})\), satisfying
with initial values \(U^\ell \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^m)\) such that \(f(U^\ell ) \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^m)\) and \(g(U^\ell ) \in L^{2}(\varOmega ,\mathscr {F}_{t_\ell },{\mathbf {P}};{\mathbf {R}}^{m\times d})\) for \(\ell \in \{0,1\}\). Here L is the parameter of Assumption 2.1 and from Theorem 3.1 there exists for every \(h\in (0,\tfrac{3}{2L})\) a unique \(U\in \mathscr {G}_h^2\) satisfying (5.1). The initial values \((U^0,U^1)\) are not necessarily related to the initial value \(X_0\) of (1.1).
Next, we state an analogue of Lemma 4.1, used for the proof of the a priori estimate in Theorem 5.1 and the stability result in Theorem 5.2.
Lemma 5.1
For all \(h\in (0,\tfrac{3}{2L})\) and \(U,V\in \mathscr {G}_h^2\) with U satisfying (5.1) it holds for all \(j \in \{2,\ldots ,N_h\}\) \({\mathbf {P}}\)-almost surely that
where \(E:=U-V\) and \((Z^j)_{j\in \{2,\dots N_h\}}\), are the centered random variables given by
Proof
From the identity (1.6) and since U satisfy (5.1) by assumption it holds for \(j\in \{2,\dots ,N_h\}\) that
Adding, subtracting and rearranging terms completes the proof of the asserted identity. Further note that \(Z^j\) is centered due to the independence of the centered Wiener increment \(\varDelta _h W^{j}\) from \(g(U^{j-1})\), \(E^{j-1}\), and \(E^{j-2}\). \(\square \)
Theorem 5.1
Let Assumption 2.1 hold with \(L\in (0,\infty )\), \(\eta \in [\tfrac{1}{2}, \infty )\), \(q\in [1,\infty )\). For \(h\in (0,\tfrac{1}{4L})\) denote by \(U\in \mathscr {G}_h^2\) the unique adapted grid function satisfying (5.1). Then, for all \(n \in \{2,\ldots ,N_h\}\) it holds that
where \(C_h=4\max \{1,LT\}(1-4Lh)^{-1}\).
Proof
Applying Lemma 5.1 with \(V=0\) and taking expectations yields
From the Young inequality (2.8), the orthogonality
and the coercivity condition (2.3) we have that
Summing over j from 2 to n, identifying three telescoping sums, using the Young inequality (2.8) gives that
This yields
Since \(q \in [1, \infty )\) it holds \(8 - 8 q \le 0\) and \(8q-6\ge 2\). By elementary bounds we get
We conclude by a use of the discrete Gronwall Lemma (2.9). \(\square \)
5.2 Stability of the BDF2-Maruyama scheme
Similar to the stability of the BEM scheme, for \(h\in (0,1)\), \(V\in \mathscr {G}_h^2\) we define the local truncation error of V by
where
for \(j\in \{2,\dots ,N_h\}\). Similar to (4.3) we define the maximal step size
Note that the proof of Theorem 5.1 indicates that the assertion of the following theorem actually holds true for all \(h \in (0, \frac{1}{4L})\) but the constants on the right hand side then depend on \(\frac{1}{1 - 4 h L}\).
Theorem 5.2
Let Assumption 2.1 hold with \(L\in (0,\infty )\), \(\eta \in (\tfrac{1}{2}, \infty )\). For all \(h\in (0,h_B]\), \(U\in \mathscr {G}_h^2\) satisfying (5.1), \(V\in \mathscr {G}_h^2\), and all \(n \in \{2,\ldots ,N_h\}\) it holds that
where \(C= \max \{30, 4\eta + 2, \tfrac{16 \eta }{2\eta -1}\}\).
Proof
Fix arbitrary \(h \in (0, h_B]\) and \(V \in \mathscr {G}^2_h\). We reuse the notation from the proof of Theorem 4.2. In particular we set \(E := U - V\) and we often suppress h from the notation. The local residual of V is given by
for \(j\in \{2,\ldots ,N_h\}\). From Lemma 5.1 we get after taking expectations that
We observe that \(P_h^{j-1}(2E^{j-1}-E^{j-2})=2E^{j-1}-E^{j-2}\) and \(P_h^{j-2} E^{j-2}=E^{j-2}\). Further, we decompose the local residual of V by
where \(\rho _i^j := \rho _i^j(V)\), \(i \in \{1,2,3\}\), are defined in (5.3). Then, by taking the adjoints of the projectors and by applying the weighted Young inequality (2.8) with \(\nu =\mu >0\) and with \(\nu =h >0\), respectively, and by noting that \(-2\rho _3^j=\rho _1^{j-1}\), we obtain
Together with the global monotonicity condition (2.1) and the weighted Young inequality (2.8) with \(\nu =2\eta \) this gives that
Setting \(\mu =\tfrac{4\eta }{2\eta -1}>0\) gives that \(\tfrac{2}{\mu }+ \tfrac{1}{2\eta } - 1=0\). Then, summing over j from 2 to n and identifying four telescoping sums yields
Next, we get from the weighted Young inequality (2.8) with \(\nu = \frac{2}{h}\) that \(4\big \langle \rho _1^{n}, E^{n} \big \rangle \le \frac{4}{h} \Vert \rho _1^n \Vert ^2 + h \Vert E^{n}\Vert ^2\). A further application of the weighted Young inequality (2.8) with \(\nu =2\eta \) yields
At this point we notice that
In addition, since \(1 - h (4L+1) > 1 - h_B (4L+1) = \frac{1}{2}\) and \(h\le h_B<\tfrac{1}{2}\) and \(\eta >\tfrac{1}{2}\) as well as \(\Vert 2 E^1 + E^0 \Vert ^2 \le 5 ( \Vert E^1\Vert ^2 + \Vert E^0 \Vert ^2 )\) we obtain after some elementary transformations the inequality
The proof is completed by an application of (2.9). \(\square \)
5.3 Consistency of the BDF2 scheme
In this Subsection we bound the local truncation error of the exact solution.
Theorem 5.3
Let Assumption 2.1 hold and let X be the solution to (1.1). Then there exists \(C>0\) such that
Proof
In this proof we write \(\rho _i^j:=\rho _{h,i}^j(X|_{\tau _h})\), \(i\in \{1,2,3\}\), \(j\in \{2,\dots ,N_h\}\), \(h\in (0,1)\). From the definition of \(\rho _h\) we see that it suffices to show that
It holds for \(j\in \{2,\dots ,N_h\}\) that
As in the proof of Theorem 4.3, we note that the estimates (4.5) and (4.6) are applicable to (5.5) due to the moment bound (2.4). We further make use of the fact that \(\Vert {\mathbf {E}}[ V | {\mathscr {F}}_{t_{j-1}} ] \Vert \le \Vert V \Vert \) for every \(V \in L^2(\varOmega ;{\mathbf {R}}^m)\) and the bound
which is obtained from (2.5). By these estimates and an application of the triangle inequality we directly deduce (5.5). \(\square \)
5.4 Mean-square convergence of the BDF2 scheme
Here we consider the numerical approximations \((X_h^j)_{j=0}^{N_h}\), \(h\in (0,h_B]\), \(h_B = \frac{1}{\max \{8L,2\}}\), which are uniquely determined by the backward difference formula (1.3) and a family of initial values \((X_h^0,X_h^1)_{h\in (0,h_B]}\). This family is assumed to satisfy the following assumption.
Assumption 5.1
The family of initial values \((X_h^0,X_h^1)_{h\in (0,h_B]}\) satisfies
for all \(h\in (0,h_B]\), \(\ell \in \{0,1\}\), and is consistent of order \(\tfrac{1}{2}\) in the sense that
as \(h\downarrow 0\), where X is the solution to (1.1).
We are now ready to state the main result of this section.
Theorem 5.4
Let Assumptions 2.1 and 5.1 hold, let X be the solution to (1.1) and \((X_h^j)_{j=0}^{N_h}\), \(h \in (0,h_B]\), the solutions to (1.3) with initial values \((X_h^0,X_h^1)_{h\in (0,h_B]}\). Under these conditions the BDF2-Maruyama method is mean-square convergent of order \(\tfrac{1}{2}\), more precisely, there exists \(C>0\) such that
Proof
For \(h\in (0,h_B]\), we apply Theorem 5.2 with \(U=(X_h^j)_{j=0}^{N_h}\in \mathscr {G}_h^2\) and \(V=X|_{\tau _h}=(X(t_j))_{j=0}^{N_h}\in \mathscr {G}_h^2\) and get that there is a constant \(C>0\), independent of h, such that
The sums are of order \(\mathscr {O}(h)\) by (5.7). In addition, the consistency term \(\rho _h^\mathrm {BDF2}(X|_{\tau _h})\) is also of order \(\mathscr {O}(h)\) by Theorem 5.3. \(\square \)
5.5 Admissible initial values for the BDF2-Maruyama scheme
Assumption 5.1 provides an abstract criterion for an admissible choice of the initial values for the BDF2-Maruyama method such that the mean-square convergence of order \(\frac{1}{2}\) is ensured. Here we consider a concrete scheme for the computation of the second initial value, namely the computation of \(X_h^1\) by one step of the backward Euler–Maruyama method.
Theorem 5.5
Let Assumption 2.1 be fulfilled. Consider a family \((X_h^0)_{h\in (0,h_B]}\) of approximate initial values satisfying Assumption 4.1. If \((X_h^1)_{h\in (0,h_B]}\) is determined by one step of the backward Euler–Maruyama method, i.e, if for all \(h\in (0,h_B]\) the random variable \(X_h^1\) solves the equation
then \((X_h^0,X_h^1)_{h\in (0,h_B]}\) satisfy the conditions of Assumption 5.1.
Proof
The fact that the solution of (1.2) belongs to \(\mathscr {G}_h^2\) proves (5.6) of Assumption 5.1. By Theorem 4.2 it holds that
From Theorem 4.3 and Assumption 4.1 the right hand side is of order \(\mathscr {O}(h)\) as \(h\downarrow 0\), and this proves (5.7). \(\square \)
Remark 5.1
Consider the same assumption as in Theorem 5.5. From the Hölder continuity of the solution X of (1.1) and Assumption 4.1 it holds that
Therefore, also the choice \(X_h^1:=X_h^0\) satisfies the conditions of Assumption 5.1 and, therefore, is feasible in terms of the asymptotic rate of convergence. However, numerical simulations similar to those in Sect. 6 indicate that, although the experimental convergence rates behave as expected, this simple choice of the second initial value leads to a significantly larger error compared to \(X_h^1\) being generated by one step of the backward Euler–Maruyama method.
6 Numerical experiments
In this section we perform some numerical experiments which illustrate the theoretical results from the previous sections. In Sect. 6.1 we consider the \(\tfrac{3}{2}\)-volatility model from finance, which is a one dimensional equation. In Sect. 6.2 we do computations for a two dimensional dynamics which mimics the form and properties of the discretization of a stochastic partial differential equation, like the Allen-Cahn equation.
6.1 An example in one dimension: the \(\tfrac{3}{2}\)-volatility model
Hereby we consider the stochastic differential equation
with \(m = d = 1\), \(\lambda > 0\), \(\sigma \in {\mathbf {R}}\), and \(X_0 \in {\mathbf {R}}\). For positive initial conditions this equation is also known as the \(\frac{3}{2}\)-volatility model [5, 6]. From the quadratic growth of the drift it holds that \(q=2\) in Assumption 2.1 and, as the reader can check, the coercivity condition (2.3) is valid for \(L=1\) provided that \(\lambda \ge \tfrac{4q-3}{2} \sigma ^2 =\tfrac{5}{2} \sigma ^2\). From the calculation in [19, Appendix] it holds for all \(x_1,x_2\in {\mathbf {R}}\) that
The global monotonicity condition (2.1) is therefore satisfied with \(L=1\) and \(\eta \le \tfrac{\lambda }{2\sigma ^2}\). As we require \(\eta >\tfrac{1}{2}\) this imposes the condition \(\lambda >\sigma ^2\) and altogether we have that Assumption 2.1 is valid for \(L=1\), \(q=2\), \(\eta \in (\tfrac{1}{2},\tfrac{\lambda }{2\sigma ^2})\) provided that \(\lambda \ge \tfrac{5}{2} \sigma ^2\).
In our experiments we approximate the strong error of convergence for the explicit Euler–Maruyama method (EulM) (see [13]), the backward Euler–Maruyama method (BEM), and the BDF2-Maruyama method (BDF2), respectively. More precisely, we approximate the root mean square error by a Monte Carlo simulation based on \(M = 10^6\) samples, that is
where for every \(m \in \{1,\ldots ,M\}\) the processes \(X^{(m)}\) and \((X_h^{n,(m)})_{n = 0}^{N_h}\) denote independently generated copies of X and \(X_h\), respectively. Here we set \(h := \frac{T}{N_h}\) and for the number of steps \(N_h\) we use the values \(\{ 25 \cdot 2^{k}\; : \; k =0,\ldots ,7\}\), i.e., \(N_h\) ranges from 25 to 3200. Since there is no explicit expression of the exact solution to (6.1) available, we replace \(X^{(m)}\) in the error computation by a numerical reference solution generated by the BDF2-Maruyama method with \(N_{\mathrm {ref}} = 25 \cdot 2^{12}\) steps.
As already discussed in Sect. 3, in every time step of the implicit schemes we have to solve a nonlinear equation of the form
for \(X_h^j\). Here, we have \(f(x) = x - \lambda x|x|\) and \(g(x) = \sigma |x|^{\frac{3}{2}}\) for \(x \in {\mathbf {R}}\) and
for the backward Euler–Maruyama method, and
for the BDF2-Maruyama method. For the \(\frac{3}{2}\)-volatility model it turns out that (6.2) is a simple quadratic equation, which can be solved explicitly. Depending on the sign of the right hand side \(X_h^j\) is given by
As the first initial value we set \(X_h^0 \equiv X_0\) for both schemes. In addition, we generate the second initial value for the BDF2-Maruyama method by one step of the BEM method as proposed in Sect. 5.5. Note that the computation of one step of the BDF2-Maruyama method is, up to some additional operations needed for the evaluation of \(R_h^j\), as costly as one step of the BEM method.
In all simulations the initial condition of Eq. (6.1) is set to be \(X_0 = 1\), while the length of the time interval equals \(T= 1\). Regarding the choice of the noise intensity \(\sigma \) let us note that in the deterministic situation with \(\sigma = 0\) it is well-known that the BDF2 method converges with order 2 to the exact solution. In the stochastic case with \(\sigma > 0\), however, the order of convergence reduces asymptotically to \(\frac{1}{2}\) due to the presence of the noise. Hence, the BDF2-Maruyama method offers apparently no advantage over the backward Euler–Maruyama method. But, as it has already been observed in [2], one still benefits from the higher deterministic order of convergence if the intensity of the noise is small compared to the step size of the numerical scheme. To illustrate this effect we use three different noise levels in our simulations: the deterministic case \(\sigma =0\), a small noise intensity with \(\sigma = \frac{1}{3}\), and a higher intensity with \(\sigma = 1\).
Moreover, the Eq. (6.1) behaves stiffer in the sense of numerical analysis if the value for \(\lambda \) is increased. Since implicit numerical schemes like the backward Euler method and the BDF2 method are known to behave more stable in this situation than explicit schemes, we will perform our simulations with two different values for \(\lambda \): The non-stiff case with \(\lambda = 4\) and the stiff case with \(\lambda = 25\). Note that the condition \( \lambda \ge \tfrac{5}{2} \sigma ^2\) is satisfied for all combinations of \(\lambda \) and \(\sigma \).
Further, to better illustrate the effect of the parameter \(\lambda \) on explicit schemes explains why we also included the explicit Euler–Maruyama method in our simulations. Although this scheme is actually known to be divergent for SDEs involving superlinearly growing drift- and diffusion coefficient functions, see [11], it nonetheless often yields reliable numerical results. But let us stress that the observed experimental convergence of the explicit Euler–Maruyama scheme is purely empirical and does not indicate its convergence in the sense of (1.4).
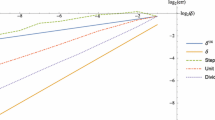
The first set of numerical results are displayed in Tables 1, 2 and 3, which are concerned with the non-stiff case \(\lambda = 4\). In Table 1 we see the errors computed in the deterministic case \(\sigma =0\). As expected the explicit Euler scheme and the backward Euler method perform equally well, while the experimental errors of the BDF2 method are much smaller. This is also indicated by the experimental order of convergence (EOC) which is defined for successive step sizes and errors by
As expected the numerical results are in line with the theoretical orders.
In Table 2 the noise intensity is increased to \(\sigma = \frac{1}{3}\). Here we see that for larger step sizes, that is \(N_h \in \{25, 50\}\), the erros are only slightly larger than in the deterministic case. In fact, for the two Euler methods the discretization error of the drift part seems to dominate the total error for almost all step sizes as the errors mostly coincide with those in Table 1. On the other hand, the BDF2-Maruyama method performs significantly better for larger and medium sized step sizes. Only on the two finest refinement levels \(N_h \in \{1600, 3200\}\) the estimated errors of all three schemes are of the same magnitude. This picture changes drastically in Table 3, which shows the result of the same experiment but with \(\sigma = 1\). Here the errors of all schemes agree for almost all step sizes and the BDF2-Maruyama method is no longer superior.
The second set of experiments shown in Tables 4, 5 and 6 are concerned with the stiff case \(\lambda = 25\) while all other parameters remain unchanged. At first glance we see that the explicit Euler–Maruyama method performs much worse than the two implicit methods for \(N_h \in \{25, 50, 100, 200\}\) in the deterministic case \(\sigma = 0\). This even stays true when noise is present. On the other hand, the BDF2 method clearly performs best in the deterministic case although the experimental order of convergence increases rather slowly to 2 compared to the non-stiff case in Table 1. Further note that the error of the BEM method and the BDF2 method agree for \(N_h = 25\). This is explained by the fact that the second initial value of the multi-step method is generated by the BEM method and, apparently, this is where the error is largest for both schemes.
Moreover, we observe that the errors in Table 5 with \(\sigma = \frac{1}{3}\) are of the same magnitude as those in Table 4. Due to the larger value of \(\lambda \) the presence of the noise only seems to have a visible impact on the error of the BDF2-Maruyama method with \(N_h = 3200\). Hence, the BEM method performs significantly worse than the BDF2-Maruyama scheme for all larger values of \(N_h\).
In contrast to the non-stiff case this behaviour does not change so drastically when the noise intensity is increased to \(\sigma = 1\). In Table 6 we still observe a better performance of the BDF2-Maruyama method, although the estimated errors are seemingly affected by the presence of a stronger noise.
To sum up, in our numerical experiments the BDF2-Maruyama method and the two Euler methods performed equally well if the equation is non-stiff and driven by a higher noise intensity. In all other tested scenarios (with stiffness and/or with small noise intensity) the BDF2-Maruyama method is often superior to the two Euler methods in terms of the experimental error. Hence, our observations confirm the results reported earlier in [2].
6.2 An example in two dimensions: a toy discretization of an SPDE
Here we consider the two dimensional equation
for \(t\in (0,T]\), \(X(0)=X_0\in {\mathbf {R}}^2\) with \(\sigma \ge 0\) and \(\lambda>>0\). We write this equation in the form
with A being the positive and symmetric \(2\times 2\)-matrix
and the non-linearities \(f:{\mathbf {R}}^2\rightarrow {\mathbf {R}}^2\), \(g:{\mathbf {R}}^2\rightarrow {\mathbf {R}}^{2\times 2}\) given by
The reason why we are interested in (6.5) is its similarity to the equation obtained when discretizing a stochastic partial differential equation with a Galerkin method. The matrix \(-A\) is a substitute for a discrete Laplacian, which is a symmetric and negative definite matrix. With a Galerkin approximation in k dimensions the eigenvalues \(\lambda _1<\lambda _2,\dots ,\lambda _{k-1}<\lambda _k\) satisfy that \(\lambda _k>>0\) is very large, causing a stiff system. Our matrix A is chosen to mimic this stiffness. Moreover, our choice of f is due to its similarity with the nonlinearity of the Allen–Cahn equation. We take the diffusion coefficient to be quadratic in order to demonstrate an example with superlinear growth.
Assumption 2.1 is valid for all \(\lambda \ge 0\) and \(\sigma \in [0,\sqrt{2}/3)\) with \(L=1\), \(q=3\) and \(\eta =\tfrac{1}{2\sigma ^2}\). The coercivity condition (2.3) is left to the reader to check and it is in fact it that determines the upper bound for \(\sigma \). To verify the global monotonicity condition (2.1), we first notice that for \(x,y\in {\mathbf {R}}^2\), it holds that
and that
Since it also holds that \( - ( A(x-y),x-y ) \le 0 \) we get for all \(x,y\in {\mathbf {R}}^2\) that
Under the assumption that \(2\eta \sigma ^2=1\) we obtain that
which proves the global monotonicity for \(L=1\).
We use the experimental setup of Sect. 6.1. As the equation (6.2) is not explicitly solvable with f and g from the present subsection we use \(K=5\) Newton iterations in each time step to obtain an approximate solution. More precisely, these iterations \(\tilde{X}_h^{j,0},\dots ,\tilde{X}_h^{j,K}=X_h^j\) are given \(\tilde{X}_h^{j,0} = X_h^{j-1}\) and for \(k\in \{1,\dots ,K\}\) by \(\tilde{X}_h^{j,k}=\tilde{X}_h^{j,k-1}-(D\varPhi _h^j(X_h^{j,k-1}))^{-1}\varPhi _h^j(X_h^{j,k-1})\), where \(\varPhi _h^j(x)=x-\beta h (f(x)-Ax)-R_h^j\) and \(D\varPhi _h^j\) is the Jacobian. With \(c=\tfrac{1-\lambda }{2}\) it holds that
This is used for the Newton iterations.
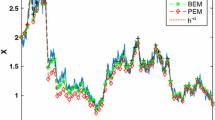
We perform three experiments, all with \(\lambda =96\), \(T=1\), \(X_0=[2,3]^t\), one without noise, i.e., \(\sigma =0\), one with small noise intensity \(\sigma =0.47\), which is just below the threshold \(\sqrt{2}/3\) for \(\sigma \), allowed for the theoretical results to be valid, and one with large noise intensity \(\sigma =1\) to see how the methods compare outside the allowed parameter regime. Comparing Tables 7 and 8 we observe that the errors differ very little. This suggests that the noise is negligible for the small noise case and therefore does not effect the dynamics much, but this suggestion is false. This is clear from Fig. 1, where a typical path is shown and in Fig. 2, where the same solution path, together with two other solution paths are projected in the directions of the eigenvectors \(v_1=\tfrac{1}{\sqrt{2}}[1,1]^t\) and \(v_2=\tfrac{1}{\sqrt{2}}[1,-1]^t\), corresponding to the eigenvalues 1 and \(\lambda \), respectively, of the matrix A. Direction \(v_2\) is the stiff direction. This expresses itself in Fig. 2 by a strong drift towards zero of \((X,v_2)\), while \((X, v_1)\) is more sensitive to the noise.
For \(N_h=25\) the CFL-condition \(|1-\lambda h|<1\) is not satisfied while for \(N_h\ge 50\) it is. Table 7 shows, in the case of no noise, explosion of the Euler–Maruyama method, for the crude refinement levels for which the CFL condition is not satisfied. The backward Euler–Maruyama and BDF2 methods work for all refinement levels and perform better than the Euler–Maruyama method, but only the BDF2 method performs significantly better. For small noise Table 8 shows essentially the same errors as for those without noise, only with slightly worse performance for the Euler–Maruyama scheme. Taking into account that the computational effort for the BEM and BDF2-Maruyama schemes are essentially the same our results show the latter to be superior for this problem. Our results confirm the conclusion from the previous subsection that the BDF2-Maruyama scheme performs better for stiff equations with small noise. For \(\sigma =1\) the Euler–Maruyama scheme explodes for all refinement-levels and BDF2 has lost most of its advantage over BEM. For the crudest step size the error is even higher than for BEM. In Table 9 the errors for the large noise simulations are shown.
References
Beyn, W.-J., Isaak, E., Kruse, R.: Stochastic C-stability and B-consistency of explicit and implicit Euler-type schemes. J. Sci. Comput. 67(3), 955–987 (2016)
Buckwar, E., Winkler, R.: Multistep methods for SDEs and their application to problems with small noise. SIAM J. Numer. Anal. 44(2), 779–803 (2006). (electronic)
Emmrich, E.: Two-step BDF time discretisation of nonlinear evolution problems governed by monotone operators with strongly continuous perturbations. Comput. Methods Appl. Math. 9(1), 37–62 (2009)
Girault, V., Raviart, P.-A.: Finite Element Approximation of the Navier–Stokes Equations. Lecture Notes in Mathematics, vol. 749. Springer, Berlin (1979)
Goard, J., Mazur, M.: Stochastic volatility models and the pricing of VIX options. Math. Financ. 23(3), 439–458 (2013)
Henry-Labordère, P.: Solvable local and stochastic volatility models: supersymmetric methods in option pricing. Quant. Financ. 7(5), 525–535 (2007)
Higham, D.J., Mao, X., Stuart, A.M.: Strong convergence of Euler-type methods for nonlinear stochastic differential equations. SIAM J. Numer. Anal. 40(3), 1041–1063 (2002)
Hu, Y.:. Semi-implicit Euler–Maruyama scheme for stiff stochastic equations. In: Koerezlioglu, H. (eds.) Stochastic Analysis and Related Topics V: The Silvri Workshop, vol. 38 of Progr. Probab., pp. 183–202. Birkhauser, Boston (1996)
Hutzenthaler, M., Jentzen, A.: On a perturbation theory and on strong convergence rates for stochastic ordinary and partial differential equations with non-globally monotone coefficients. arXiv:1401.0295v1 (2014) (Preprint)
Hutzenthaler, M., Jentzen, A.: Numerical approximations of stochastic differential equations with non-globally Lipschitz continuous coefficients. Mem. Am. Math. Soc. 236(1112), 1–112 (2015)
Hutzenthaler, M., Jentzen, A., Kloeden, P.E.: Strong and weak divergence in finite time of Euler’s method for stochastic differential equations with non-globally Lipschitz continuous coefficients. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 467(2130), 1563–1576 (2011)
Hutzenthaler, M., Jentzen, A., Kloeden, P.E.: Strong convergence of an explicit numerical method for SDEs with nonglobally Lipschitz continuous coefficients. Ann. Appl. Probab. 22(4), 1611–1641 (2012)
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differential Equations, 3rd edn. Springer, Berlin (1999)
Kruse, R.: Characterization of bistability for stochastic multistep methods. BIT Numer. Math. 52(1), 109–140 (2012)
Mao, X.: Stochastic Differential Equations and Their Applications. Horwood Publishing Series in Mathematics & Applications. Horwood Publishing Limited, Chichester (1997)
Mao, X., Szpruch, L.: Strong convergence rates for backward Euler–Maruyama method for non-linear dissipative-type stochastic differential equations with super-linear diffusion coefficients. Stochastics 85(1), 144–171 (2013)
Milstein, G.N., Tretyakov, M.V.: Stochastic Numerics for Mathematical Physics. Scientific Computation. Springer, Berlin (2004)
Ortega, J.M., Rheinboldt, W.C.: Iterative Solution of Nonlinear Equations in Several Variables, vol. 30 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2000) (Reprint of the 1970 original)
Sabanis, S.: Euler approximations with varying coefficients: the case of superlinearly growing diffusion coefficients. arXiv:1308.1796v2 (2014) (Preprint)
Stuart, A.M., Humphries, A.R.: Dynamical Systems andNumerical Analysis, vol. 2 of Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (1996)
Tretyakov, M.V., Zhang, Z.: A fundamental mean-square convergence theorem for SDEs with locally Lipschitz coefficients and its applications. SIAM J. Numer. Anal. 51(6), 3135–3162 (2013)
Acknowledgments
The authors wish to thank Etienne Emmrich for bringing the identity (1.6) to our attention and for informing us about its connection to the BDF2-scheme. Stig Larsson and Chalmers University of Technology are acknowledged for our use of the computational resource Ozzy. This research was carried out in the framework of Matheon supported by Einstein Foundation Berlin.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by David Cohen.
Rights and permissions
About this article
Cite this article
Andersson, A., Kruse, R. Mean-square convergence of the BDF2-Maruyama and backward Euler schemes for SDE satisfying a global monotonicity condition. Bit Numer Math 57, 21–53 (2017). https://doi.org/10.1007/s10543-016-0624-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-016-0624-y
Keywords
- SODE
- Backward Euler–Maruyama method
- BDF2-Maruyama method
- Strong convergence rates
- Global monotoncity condition