1 Introduction

In the case of ordinary differential equations (ODEs), stiffness arises as a consequence of widely differing eigenvalues. This necessitates either implicit methods or explicit methods (Chebyshev methods) with extended stability intervals. We will, in this paper, consider these issues in relation to the solution of Itô stochastic ordinary differential equations (SODE), given by

(1)

where \(\mathbb{E}(X_{0})^{2} < \infty\) and f(⋅),g 1(⋅),…,g d (⋅) are m-dimensional Lipschitz continuous vector valued functions that fulfil a linear growth condition. The W i(t),t≥0 represent d independent standard Wiener processes on a filtered probability space \((\Omega, \mathcal{F}, (\mathcal {F}_{t})_{t\geq0}, \mathbb{P})\). In this article, for simplicity, numerical methods on a given time interval [0,T] are fixed by schemes based on equidistant time discretisation points t n =nh, n=0,1,…N with stepsize h=T/N, N=1,2,… . We shall use the abbreviation Y n to denote the value of the numerical approximation at time nh.

In the case of SODEs, stiffness is characterised by widely differing Lyapunov exponents. Thus in (1), when f(X)=AX and g i (X)=B i X the Lyapunov exponents are given by

A number of authors have developed implicit numerical methods to solve SODEs, including [9], [4] and [8]. However these authors have introduced implicitness in the deterministic term only. Such methods are generally known as semi-implicit. For example the semi-implicit Euler method has the form

$$Y_{n+1} = Y_{n} + f(Y_{n+1})h + \sum_{j=1}^{d} g_{j}(Y_{n}) I_j,$$

where the Itô integral \(I_{j}=\int _{t_{n}}^{t_{n+1}}dW_{j}(s)=W_{j}(t_{n+1})-W_{j}(t_{n})\) is calculated using the Normally distributed random variable ΔW n ∼N(0,Δt). In this article, we follow the notational convention of [9] to denote various Itô integrals: I 0=h, I 1=ΔW(n)(1), I 11=0.5[(ΔW(n)(1))2−h] etc. We note that Abdulle & Cirilli have in [1] generalised the idea of explicit methods with extended stability regions to SODEs and these methods can be effective on mildly stiff problems.

Problems arise, however when we try to introduce implicitness in the stochastic terms, as convergence is no longer guaranteed. For example, if we examine the solution to the Itô equation

$$dX_{t} = \beta X_{t} \,dW_{t}.$$

The fully implicit Euler method, given by

$$Y_{n+1} = Y_{n} + \beta Y_{n+1} I_{1},$$

is not guaranteed to converge because \(\mathbb{E} | (1 - \beta\Delta W_{n} )^{-1} |\) is not finite.

The Balanced method [11] was presented as a method incorporating quasi-implicitness in the stochastic terms, that converges to the Itô solution and is suitable for solving stiff systems of SODEs. Alcock & Burrage have in [2] examined in detail the asymptotic and mean-square stability properties of a number of variants of the Balanced method in the case where there is just one Wiener process. However, all these variants still give rise to a method with strong order 0.5.

In this article we employ the principles developed by [11] to generate a class of numerical schemes for solving stiff SODEs with strong order 1.0. Our work is related to that of [7] who also introduce Balanced Milstein schemes and explore their stability properties. We present an extended exploration, that further explores the extension of these concepts to higher orders of convergence and considers the optimal choice of parameters for these methods. The presentation of our article is as follows. The concepts of convergence and stability are presented in Sect. 2. The Balanced method is reviewed and the new class of methods is presented in Sect. 3, along with convergence proofs. Section 4 explores an Ansatz on optimal parameter selection. Asymptotic stability properties are presented in Sect. 5. Our method is applied to Sagirow’s Satellite [12] problem in Sect. 6. We conclude in Sect. 7.

2 Convergence and stability issues

Perhaps the most well-known numerical method for solving (1) is the Euler-Maruyama method, given by

$$Y_{n+1} = Y_{n} + f(Y_{n})I_{0} + \sum_{j=1}^{d}g_{j}(Y_{n})I_{j}, $$
(2)

that converges strongly (weakly) with order 0.5 (1.0) and the explicit Milstein and semi-implicit Milstein schemes, given by

(3)
(4)

respectively, that both converge strongly (weakly) with order 1.0 (1.0). Note that here the Itô integrals are approximated by

Strong convergence refers to the expected pathwise convergence of a numerical solution, whereas weak convergence refers to the convergence of the moments of a process. The following definitions and theorems make these concepts clearer.

Definition 1

(Strong Convergence)

We say that a time discrete approximation Y converges strongly with order γ>0 at time T if there exists a positive constant C, that does not depend on h, and a finite h 0>0 such that

$$\mathbb{E} \left( | X(T) - Y_{T} | \right) \leq Ch^{\gamma},$$

for each h∈(0,h 0).

Let \(\mathcal{C}^{l}\) denote the space of l times continuously differentiable functions that, together with their partial derivatives of orders up to and including order l, have polynomial growth.

Definition 2

(Weak Convergence)

We say that a time discrete approximation Y (h) converges weakly with order β>0 to X at time T as h↓0 if for each \(v \in\mathcal{C}^{2(\beta+1)}(\mathbb{R}^{d},\mathbb{R})\), there exists a positive constant C that does not depend on h, and a finite h 0>0 such that

$$\left| \mathbb{E}( v(X(T)) ) - \mathbb{E} ( v(Y_T) )\right| \leq C h^{\beta},$$

for each h∈(0,h 0).

Theorem 1

(General Strong Order Convergence [10])

Suppose that a time discrete approximation, Y n+1, to an Itô SODE \(X_{t_{n+1}}\) has local strong order p 1 and mean local order p 2, that is

such that p 1≥0.5 and p 2≥p 1+0.5. Then the time discrete approximation will converge to the Itô solution with global strong order p=p 2−0.5,

$$\bigl[ \mathbb{E} \left( X(T) - Y_T\right)^{T}\left( X(T) - Y_T\right)\bigr]^{1/2} =O(h^{p}).$$

Stability of a numerical scheme refers to the conditions under which the numerical solution tends to zero with the true solution. The asymptotic stability of an SODE, similar to asymptotic stability of an ODE, is often determined with reference to the scalar linear test equation (for the d=1 case),

$$dX(t) = aX(t)\,dt + bX(t)\,dW(t), \quad a,b \in\mathbb{R}. $$
(5)

Solutions of (5) have the following propertiesFootnote 1 [14]:

(6)
(7)

The asymptotic stability region of a one-step numerical SODE scheme can be derived by applying the scheme to the linear test equation (5) resulting in

$$Y_{n+1} = R(h,a,b)Y_{n}. $$
(8)

The asymptotic stability region, \(\hat{R}(h,a,b)\), of the numerical scheme is defined by the parameters h,a,b that satisfy

$$\lim_{n\rightarrow\infty} |Y_{n}(h,a,b)| = 0 \quad\mbox{with probability one}. $$
(9)

On the other hand, a numerical scheme is said to be MS-stable [13] for (h,a,b) if

$$\check{R}(h,a,b) := \mathbb{E} \bigl( | R(h,a,b) | ^{2} \bigr) <1. $$
(10)

The function, \(\check{R}(h,a,b)\), is called the MS-stability function of the numerical scheme. The Milstein scheme (d=1) has a mean-square stability region \(\check {R}(h,a,b)\), defined by the parameters h,a,b that satisfy

$$|1+ah|^{2} + |b^{2}h|+\frac{1}{2}|b^{4} h^{2}| < 1. $$
(11)

Plots of the asymptotic and mean-square stability regions for the Euler-Maruyama method are given in [2] while those of the explicit Milstein method are given in Fig. 1. The figure shows that the Milstein scheme is not a particularly stable scheme. Even for very small stepsizes, the MS stability region falls quite short of the region defined by (6). The lower order Euler-Maruyama scheme has better stability properties than the Milstein scheme (see Figs. 2.2 and 2.3 in [2]). Thus the Milstein scheme offers a higher order of convergence than the EM scheme at the cost of reduced stability properties.

Fig. 1
figure 1

(a) Asymptotic and (b) Mean-square stability regions for the explicit Milstein scheme. The respective stability regions of the Milstein scheme lie within the dashed lines. The respective stability regions for the linear test equation (5) are the regions bounded above the fixed lines

Full size image

3 A stable strong order 1.0 scheme

Milstein, Platen and Schurz [11] developed a class of quasi-implicit numerical schemes of strong order 0.5 based upon the Euler-Maruyama method, collectively called the Balanced method, to solve (1), given by

$$Y_{n+1} = Y_{n} + f(Y_{n}) I_{0} + \sum_{j=1}^{d} g_{j}(Y_{n})I_{1}^{j} + D_{n}(Y_{n} - Y_{n+1}), $$
(12)

where D n is a m×m matrix, given by

$$D_{n}= d_{0}(Y_{n})I_{0} + \sum_{j=1}^{d}d_{j}(Y_{n}) |I_{1}^{j}|,$$

and the d j ,j=0,…,d are matrix functions that are often chosen as constant matrices.

It is assumed that for any non-negative sequence of numbers, α i , and x∈ℝm, the matrix

$$M(x) = I + \alpha_{0} d_{0}(x) + \sum_{j=1}^{d} \alpha_{j}d_{j}(x), $$
(13)

has an inverse with finite norm.

Recently, [2] derived the mean-square stability region for the Balanced method with d=1, given by

(14)

To understand why the Balanced method is a relatively stable method, consider the implicit Euler-Maruyama method for solving (1) with d=1, given by

$$Y_{n+1} = Y_{n} + f(Y_{n+1})I_{0}+ g(Y_{n+1})I_{1}. $$
(15)

First note that the implicit Euler-Marayama method is not guaranteed to converge, as described earlier. In addition, the evaluation of Y n+1 at each timestep involves solving a non-linear equation (using a non-linear solver such as Newton’s method). Inspecting (12) and (15) shows that the Balanced method introduces quasi-implicitness through a form of splitting, using an implementation that maintains guarantees of convergence. (12) can be rewritten

(16)

As such, the Balanced method has linearised the implicitness. Consequently there is no need for a non-linear solver at each timestep. In this way, the Balanced method can be considered a stochastic analog to the Rosenbrock methods for solving deterministic ODEs [5].

We now propose a class of numerical schemes of strong order 1.0 (SSO1), based upon both the Balanced scheme and the Milstein scheme to solve (1), given by

(17)

where D n is given by

$$D_{n} = d_{0}(Y_{n})I_{0} + \sum_{j_1,j_2=1}^{d}d_{j_1,j_2}(Y_{n})\left |I_{j_1,j_2}\right|. $$
(18)

In order to demonstrate convergence in the case of multiple Wiener processes, two lemmas must first be proven:

Lemma 1

$$\mathbb{E}\left(I_{j_1,j_2}\left|I_{k_1,k_2}\right|\right) =O(h^2)\quad\forall j_1,j_2,k_1,k_2 \in\mathbb{Z}^{+}.$$
(19)

Proof

Given j 1,j 2≠0, \(\mathbb{E}(I_{j_{1},j_{2}})=0\) and \(\mathbb{E}(|I_{j_{1},j_{2}}|^{2})=O(h^{2}) \mbox{ so } \mathbb {E}(|I_{j_{1},j_{2}}|^{2})^{1/2}=O(h)\) (Lemma 5.7.5 in [9]). Then

$$\mathbb{E}\left( \left| I_{j_1,j_2} |I_{k_1,k_2}|\right|\right) \leq \mathbb{E}\left(|I_{j_1,j_2}|^2\right)^{1/2} \mathbb{E}\left(\left|I_{k_1,k_2} \right|^2\right)^{1/2}=O(h^2).$$

By Jensens’ inequality,

$$\left| \mathbb{E}\left( I_{j_1,j_2} |I_{k_1,k_2}| \right) \right| =O(h^2),\nonumber $$

and the result follows. □

Lemma 2

$$\mathbb{E}\left[I_{p}I_{j_1j_2}\left|I_{k_1k_2}\right|\right] = 0\quad\forall p, j_1, j_2, k_1, k_2 \in\mathbb{Z}^{+}.$$

Proof

If p≠j 1≠j 2 then at least one of \((I_{p}, I_{j_{1}}, I_{j_{2}})\) is independent of \(|I_{k_{1}k_{2}}|\). Without loss of generality then,

$$\mathbb{E}[I_{p}I_{j_1j_2}|I_{k_1k_2}|] = \mathbb {E}(I_{p})\mathbb{E}(I_{j_1j_2}|I_{k_1k_2}|) = 0.$$

If either p=j 1, p=j 2, j 1=j 2 or p=j 1=j 2 then the expectation is the integral of a linear combination of odd functions, and the result follows. □

We are now in a position to prove convergence for the arbitrary Wiener case.

Theorem 2

Let g possess all necessary partial derivatives for all y∈ℝm. Then the numerical scheme to solve (1), defined by (17) with D given by (18) will converge to the Itô solution with strong order 1.0, provided that for any non-negative sequence of numbers, {α i } and x∈ℝm, the matrix

$$M(x) = \mathbf{I} + \alpha_{0}d_{0}(x) + \sum_{j_1,j_2=1}^{d}\alpha _{j_1,j_2} d_{j_1,j_2}(x), $$
(20)

has an inverse bounded by

$$|M^{-1}(x)|\leq K < \infty, \quad\mbox{\textit{for all}}\ x. $$
(21)

Proof

The error term at any time, t∈(t 0,T), can be written

$$\left| X(t) - Y_{t_{n}} \right| \leq |X(t)-Y_{t_{n}}^{(\mathit{Mil})}| +|Y_{t_{n}}^{(\mathit{Mil})}-Y_{t_{n}} |,$$

where \(Y_{n}^{(\mathit{Mil})}\) represents the approximation at step t n given by the Milstein scheme (3). Consequently the strong order of convergence of (17) will be the minimum of the strong order of convergence of the Milstein scheme and the strong order of convergence of Y n to \(Y_{n}^{(\mathit{Mil})}\). The strong order of convergence of the Milstein scheme is well known to be 1.0 [10]. Hence we need only examine the local deviation from the Milstein scheme. Now

By the symmetry of I j ,j=1,…,d and the boundedness of the components of the matrices d 0,d 1,… , then

$$\left|\mathbb{E}\left(Y^{(\mathit{Mil})}-Y\right)\right| \leq K\left|\mathbb {E}(D_nfI_0)\right| + \sum_{j_1,j_2=1}^{d}K\left|\mathbb{E}(D_ng_{j_1}'g_{j_2} I_{j_1j_2})\right|.$$

Thus, by Lemma 1, \(\mathbb {E}[Y_{n}^{(\mathit{Mil})}-Y_{n}]=O(h^{2})\) implying that the local mean order will be

$$\left| \mathbb{E}\left( Y^{(\mathit{Mil})}-Y \right)\right| = O(h^{2}).$$

Again by Lemmas 1 and 2, the local strong order will be

$$\mathbb{E}\bigl( \bigl(Y^{(\mathit{Mil})}-Y\bigr)^T\bigl(Y^{(Mil)}-Y\bigr)\bigr)^{1/2} = O(h^{3/2}).$$

So by Theorem 1, the result follows. □

The specific form of the \(d_{j_{1},j_{2}}(Y_{n})\) will depend on stability issues, but quite often we will only assume that these quantities are non-zero. A similar examination for general D gives rise to a more general convergence proof for higher order stable schemes based upon the Balanced method (12). First define \(\texttt{I}_{1^{(q)}}\) to be the Itô integral denoted by I ∗ where ∗ is q ones. That is \(\texttt{I}_{1^{(1)}}=I_{1}\) and \(\texttt{I}_{1^{(3)}}=I_{111}\). Define \(\mathbb{I}_{q}\) to be first q members of the set \(\mathbb {I}_{q}=\{\texttt{I}_{1^{(1)}}, \texttt{I}_{1^{(2)}}, \texttt {I}_{1^{(3)}}, \ldots,\texttt{I}_{1^{(q)}} \}\). Also let us define the set \(\mathbb{D}_{(p)}\) to be the set of coefficient functions of all integrals in \(\mathbb{I}_{q}\).

For notational simplicity, the proof is given with respect to the single Wiener case, (d=1), although the same proof can be simply extended to the multiple Wiener case albeit with significantly greater notational complexity.

Theorem 3

Let us define a general balanced numerical scheme to solve (1) with d=1, given by

$$Y_{n+1}^{(G)} = Y_{n} + \Phi(Y_{n},\mathbb{D}_{p},\mathbb{I}_{q}) +(Y_{n} - Y_{n+1})D_{n},$$

where \(Y_{n+1}^{(Tayl)}=Y_{n} + \Phi(\cdot)\) is the corresponding explicit Itô-Taylor scheme of strong order O(h p) and where the damping term D n is a function of required coefficient terms (d 0,d 1,d 11,d 111,…) and the Itô integral increments, \(\mathbb{I}_{q}\), in the following form:

(22)

Let us also assume that all required partial derivatives exist and are finite, and that

$$M(x) = \Biggl(\mathbf{I}+\alpha_0d_0(x) + \sum_{i=1}^{s}\alpha_id_i(x)\Biggr),$$

where s is the cardinality of \(\mathbb{I}_{q}\), has an inverse bounded by

$$\left|M^{-1}(x)\right| \leq K < \infty, \quad\mbox{\textit{for all}}\ x.$$

Then this general balanced scheme will also converge to the Itô solution with strong order p if the expectation of the damping term, \(\mathbb{E}[D_{n}]\) is O(h p).

Proof

As for Theorem 2, the expected local error between the general balanced scheme and the Itô-Taylor scheme of the same order is given by,

$$\left|\mathbb{E}\left(Y^{(G)} - Y^{(Tayl)}\right)\right| =\left|\mathbb{E}\left((\mathbf{I}+D_n)^{-1}D_n\right)\Phi(\cdot)\right |.$$

Now the Taylor scheme can be written as \(\Phi(\cdot) = \bar{\Phi}(\cdot ) +g_{1}(Y_{n})I_{1}\), where \(\mathbb{E}[g_{1}(Y_{n})I_{1}]=O(h^{1/2})\) and \(\mathbb{E}[\bar{\Phi}(\cdot)] = O(h)\), so by the symmetry of I 1 and the boundedness of the components of the matrices d 0,d 1,… , then

$$\left|\mathbb{E}\left(Y^{(G)} - Y^{(Tayl)}\right)\right| \leq K\Biggl|\sum_{i=1}^{n}\mathbb{E}\left(D_n \bar{\Phi}(\cdot)\right) \Biggr|.$$

By choosing the d j (Y n ) such that \(\mathbb{E}[D_{n}]=O(h^{p})\) then, as I 1|I 11…1| has a zero expectation, the mean local order will be O(h p+1). This means that d j (Y n )=0 for j=1…2p−1.

Again following standard arguments, then

$$\mathbb{E}\bigl[\bigl(Y_{n+1}^{G} - Y_{n+1}\bigr)^{T}\bigl(Y_{n+1}^{G}- Y_{n+1}\bigr)\bigr] = O(h^{2p+1}),$$

and so the local strong order is O(h p+1/2). By Theorem 1, the result follows. □

As a direct result of Theorem 3, we can observe the following quality of an alternate attempt at a higher order Balanced scheme:

Corollary 1

A Balanced scheme, for the d=1 case, given by

$$Y_{n+1} = Y_{n} + f(Y_{n}) I_{0} + g(Y_{n}) I_{1} +g'(Y_{n})g(Y_{n})I_{11} + D_{n}(Y_{n} - Y_{n+1}), $$
(23)

where D n is given by

$$D_{n}(Y_{n})= d_{0}(Y_{n})I_{0} + d_{1}(Y_{n})|I_{1}| + d_{2}(Y_{n})|I_{11} |,$$

cannot be guaranteed to converge with strong order 1.0 unless d 1=0.

However closer examination of the mean order and local strong order expansions will reveal that a Balanced scheme given by (23) can converge with strong order 1.0 if d 1 g(Y n )=0,∀n. Appropriately, the conditions listed in Theorem 3 are not listed as ‘if and only if’.

4 Optimal parameter selection

The SSO1 method given in Sect. 3, allows for many different implementations depending on the choice of the parameters d j . Clearly the choice of parameters will effect stability and the constant of convergence. We now examine the optimal selection of these parameters with respect to the local truncation error in the strong order convergence. More formally, what follows is an Ansatz, rather than a formal theorem, on the optimal parameters due to a subtle measurability issue. As we shall illustrate, significant information is nevertheless revealed from this examination.

In the case of one noise term (d=1) the SSO1 method can be rewritten as

$$y_{n+1}^{(\mathit{SSO}1)} = y_{n} + \left( \mathbf{I}+D_{n}\right)^{-1}\left(fI_{0} + g I_{1} + g'g I_{(1,1)} \right).$$

The following Ansatz will utilise a Taylor expansion of (I+D n )−1 that, for convergence, requires that (I+D n )≠0 and |D n |<1. The first condition is assured by the regularity assumptions underlying the SSO1 method (20). To examine the second convergence condition note that D n can be partitioned in the following manner,

where 1 X is the indicator function given by

$$1_X = \left\{\begin{array}{l@{\quad }l}1 & \mbox{if}\ X \\0 & \mbox{if}\ \neg X.\end{array}\right.$$

While the Wiener increment ΔW n is unbounded, D n behaves as \(d_{1}\sqrt{h}\epsilon_{n}\) where ϵ n ∼N(0,1). Hence

$$\lim_{h \rightarrow0} Pr(|D_{n}|<1) \rightarrow1.$$

Hence

$$\lim_{h \rightarrow0} D_n = D_n 1_{|D_n|<1}.$$

Ansatz 1

Assume the previous conditions on (1) and (17) hold. The parameters of the scheme (17) to solve (1) with one Wiener process that result in the minimum constant of strong order convergence are given by the solution to

(24)

where \(\mathcal{I}^{*}\) is the indicator function given by

$$\mathcal{I}^{*} = \left\{\begin{array}{l@{\quad }l} 0 & \mbox{\textit{if}}\ I_{(1,1)} >0 \\1 & \mbox{\textit{if}}\ I_{(1,1)}<0.\end{array}\right.$$

Proof

The scheme (17) can be rewritten

Recall that the simplified Ito-Taylor expansion is given by,

Then the local error of the scheme (17) is given by

Thus the expected first order difference is given by

$$\mathbb{E} \bigl[ \bigl| Y_{n+1}^{Tayl} - Y_{n+1}^{\mathit{SSO}1} \bigr| \bigr] = O(h^{1.5}).$$

By Theorem 1, we need to consider the expressions that ensure the second order expansions have O(h 3).

When I (1,1)<0, I 1|I (1,1)|=−(3I (1,1,1)+I (1,0)+I (0,1)), and so the local error for the scheme (17) can be rewritten

(25)

and thus a conditional strong order condition is given by

Clearly the conditional strong order condition is minimised when (d 0,d 1) are given by

A similar examination when I (1,1)>0 reveals a conditional strong order condition given by

(26)

which is to be minimised subject to the constraint (20). The value for d 1 which minimises (26) subject to (20) is d 1=0. Consequently the optimal value for d 0 is thus \(d_{0}=-\frac{1}{2} f'g + g'f + \frac{1}{2}g''(g,g)\) and the result follows. □

Corollary 2

For the numerical solution of (17), when g(X)=QX where Q is a matrix of constants, the optimal value for d 1 is \(d_{1}^{opt}=\frac{\mathcal{I}^{*}}{3}Q^{2}\). If, in addition f(X)=FX, then \(d_{0}^{opt} = -\frac{1}{2} \left(F + QFQ^{-1}\right) + \frac{\mathcal {I}^{*}}{3}Q^{2}\).

Selecting (d 0,d 1) in such a way generates a stable strong order 1.0 scheme for solving (1) with one Wiener process, that has minimal error and satisfies (20). Figure 2 shows a log plot of error generated by the optimal SSO1 method (24) when solving a geometric Brownian motion. The parameters of the geometric Brownian motion, \((\alpha, \beta)=(-4,\sqrt{8})\), are on the boundary of the mean-square stability region (10) and so provide a good test for the capabilities of the method (17). The results shown in Fig. 2 indicate that the scheme (17) does converge with strong order 1.0. Moreover it shows better stability properties compared to the explicit Milstein method, with the main improvements appearing when h>2−4, as well as convergence improvements over the Euler-based Balanced method.

Fig. 2
figure 2

A study of error behaviour for the numerical method (17) when solving dX t =αX t   dt+βX t   dW t , \((\alpha,\beta)=(-4, \sqrt{8})\). In this case \(d_{0}^{opt}g= (4 +\frac{\mathcal{I}^{*} 16\sqrt{2}}{3} ) Y_{n}\) and \(d_{1}^{opt}=\frac{\mathcal{I}^{*} 16\sqrt{2}}{3} Y_{n}\) and error is given by \(\log _{2}(\frac{1}{n}\sum_{i=1}^{n}|Y_{N}^{(i)}-X^{(i)}(T)|)\). Each of these expected values were estimated using N=10000 sample paths

Full size image

However this choice of optimal parameters is \(\mathcal {F}_{t_{n+1}}\)-measurable. The SSO1 method assumes that the parameters (d 0,d 1) are both \(\mathcal{F}_{t_{n}}\)-measurable. While this choice of parameters was motivated by the analysis of the Balanced method given in [2], clearly this parametric choice results in a numerical scheme which is not guaranteed to converge. Although numerical experiments indicate that this scheme does converge.

5 Asymptotic stability

We can examine the stability properties of the scheme (17) more formally by calculating the asymptotic stability region of (17) and comparing it to the asymptotic stability properties of the linear test equation (5). The asymptotic stability region of (17) can be calculated numerically using the following theorem [6].

Theorem 4

(Higham)

Given a sequence of real-valued, non-negative, independent and identically distributed random variables {Z n }, consider the sequence of random variables, {Y n } n≥1 defined by

$$Y_{n} = \Biggl( \prod_{i=0}^{n-1} Z_{i} \Biggr) Y_{0},$$

where Y 0≥0 and where Y 0≠0 with probability 1. Suppose that the random variables log(Z i ) are square integrable. Then

$$\lim_{n\rightarrow\infty} Y_{n} = 0, \quad\mbox{\textit{with probability 1}}\ \Leftrightarrow\ \mathbb{E}(\log(Z_{i})) < 0. $$
(27)

The asymptotic stability region of (17), using the optimal parameters (24), is given in Fig. 3(b). For comparison, the asymptotic stability regions of the semi-implicit Milstein scheme

$$Y_{n+1} = Y_{n} + f(Y_{n+1})I_{0} + g(Y_{n})I_{1} +g'(g(Y_{n}))I_{(1,1)}, $$
(28)

is given in Fig. 3(a).

Fig. 3
figure 3

Asymptotic stability regions for the semi-implicit Milstein scheme and the optimal stable strong order 1.0 scheme (17). Note that the shape of the asymptotic stability region for the Balanced method is dependent on the stepsize, h. This is in contrast to Wagner-Platen series based methods, such as the explicit Milstein method (see Fig. 1)

Full size image

The comparative advantages of using (17) to solve stiff SODEs become apparent when viewing the asymptotic stability regions of the respective numerical schemes. The explicit-Milstein scheme has strong order 0.5 greater than the Euler-Maruyama scheme but it has reduced asymptotic stability, while the semi-implicit Milstein scheme does present limited improvements. However the asymptotic stability region of (17) is significantly better than either the Milstein scheme or semi-implicit Milstein scheme. The results in Fig. 3 even suggest that an optimal stepsize with respect to asymptotic stability may exist—with h=2−2 being close to optimal.

6 Application—Sagirow’s Satellite

The effect of a rapidly fluctuating density of the atmosphere of the earth on the motion of a satellite in a circular orbit leads to the stochastic differential equation [12]

$$dU_{t} = \left(\begin{array}{c}U_t^{(2)} \\C\sin2U_t^{1} - B U_t^{(2)}-\sin U_t^{(1)}\end{array}\right)\,dt+ \left(\begin{array}{c}0 \\-A(\sin U_t^{(1)} + B U_t^{(2)})\end{array}\right)\, dW_{t}. $$
(29)

Following [3], substitution of X t =sinU t gives

$$\sin2U_t = 2\sin U_t \sqrt{1-\sin^2 U_t}=2 \sin U_t + O(U_t^2)\approx2 X_t.$$

These substitutions yield a linearised equation with constant coefficients, given by

$$dX_{t} = \left(\begin{array}{c@{\quad }c}0 & 1\\2C-1 & -B\end{array}\right) X_{t} \,dt+ \left(\begin{array}{c@{\quad }c}0 & 0\\-A & -AB\end{array}\right) X_{t} \,dW_{t}. $$
(30)

Sufficient conditions for the system (30) to be asymptotically stochastically stable are given by [3]

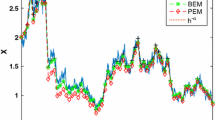
$$B>0, \qquad1-2C>0, \qquad A^{2} < \frac{2B(1-2C)}{B^2(1-2C)+1}. $$
(31)

Plots of the trajectory of the deterministic implementation of (30), with A=0.6,B=5 and C=0.2, are given in Fig. 4. Both displacement, U (1), and velocity, U (2), tend to zero as time tends to infinity, however at significantly different rates. Velocity quickly approaches zero while displacement has a rapid initial change, then slowly approaches zero. The different relative time scales make this a challenging problem to solve.

Fig. 4
figure 4

Trajectory analysis of deterministic Sagirow’s Satellite

Full size image

The stochastic system will serve as a useful test equation for the implementation of the different schemes discussed so far. While we are largely interested in the value of the displacement, \(X_{t}^{(1)}\) of (30), it is clear the accuracy of the numerical scheme will be highly dependent on the effectiveness of the numerical scheme to solve for the velocity, \(X_{t}^{(2)}\).

The Milstein Scheme to solve (30) is given by

The matrix of diffusion coefficients is not invertible and so the sub-optimal parameters \(d_{0}=-\frac{1}{2}F + d_{1}\) where \(d_{1}=\frac {\mathcal{I}^{*}}{3}Q^{2}\) are used. That is, the SSO1 scheme to solve (30) is given by

For further comparison the optimal Balanced method, as implemented in [2] is also used to solve (30). The optimal Balanced scheme to solve (30) is given by

All three numerical schemes were implemented to obtain numerical solutions of (30) with A=0.6, B=5 and C=0.2 which satisfy (31). It is worth noting that these choices of parameters are also close to the boundary of asymptotic stochastic stability for (30) and so should be a good test for our method. The stepsize h=2−2 was chosen in the hope of reflecting the asymptotic stability behaviour given in Sect. 5.

An inspection of Fig. 5 suggests that the SSO1 method is reasonably accurate when a large stepsize is used. In comparison the Milstein method and the Balanced scheme, both with stepsize h=2−2, seem unable to cope with the stability demands of larger stepsizes and consistently generated unstable solutions. The Milstein scheme is clearly exhibiting unstable behaviour, in as little as the first step. The Balanced method, which is considered to be a stable method, also generated unstable solutions after the first step. Both the Milstein and Balanced methods resulted in solutions having little relevance to the application for this particular value of the stepsize.

Fig. 5
figure 5

Comparison of numerical schemes, using stepsize h=2−2, for the solution to Sagirows Satellite problem. ‘True solutions’ are obtained using an Euler-Maruyama scheme with a stepsize of h=2−12

Full size image

7 Conclusions

The Balanced method was introduced as a class of quasi-implicit numerical schemes that converges to the exact solution with strong order 0.5 and exhibits signs of improved numerical stability over the Euler-Maruyama method. This class of methods provided insight that led us to develop a new class of stable strong-order 1.0 (SSO1) numerical schemes based upon the explicit Milstein scheme. The parameters of the SSO1 method that result in minimal global error were explored by conditionally minimising a Taylor series expansion of the linearised expression of the SSO1 scheme.

An asymptotic stability of SSO1 was given and it was shown that the SSO1 scheme is significantly more stable than either the Milstein, semi-implicit Milstein or the Balanced methods, especially for larger stepsizes. Indeed the asymptotic stability region of the SSO1 scheme when h=2−2 closely mapped the asymptotically stochastic stability region of the linear test equation. Thus the SSO1 scheme, as with the midpoint rule for deterministic integration, will generate stable solutions for stable problems and unstable solutions for unstable problems.

The stability properties were tested by solving Sagirow’s satellite problem. This problem proved to be a good test of the performance of numerical solution schemes. For a large stepsize (h=2−2), Milstein’s method and the optimal Balanced method performed very poorly indeed. Most solutions of this type were quite inadequate and generated unstable solutions to a stable problem. The SSO1 method performed significantly better than either of these two methods. While still not exceptional, the SSO1 method obtained a solution that was close to the true value and, importantly, a stable solution for larger stepsizes, h.

Clearly the SSO1 method is a more stable class of methods than the Milstein method. In addition, it offers convergence improvements over the Balanced method, along with asymptotic stability improvements. Similarly with the Balanced method, it remains to be seen if, in addition to an optimal parameter choice, certain parameter choices turn out to be better suited for different types of problems. In addition while the form of higher order methods that are inspired by the Balanced method may be known, the stability properties are unknown. The usefulness of any of these methods will only be determined once these stability properties are understood. This seems to be a valuable area for future research efforts.