Force–displacement response of in-plane loaded unreinforced brick masonry walls: the Critical Diagonal Crack model

Abstract

This article introduces an analytical model to compute the monotonic force–displacement response of in-plane loaded unreinforced brick masonry walls accounting for walls failing in shear or flexure. The masonry wall is modelled as elastic in compression with zero tensile strength using a Timoshenko beam element. Its cross-section properties (moment of inertia and area) are continuously updated to capture the non-linearity that results from flexural and shear cracking. For this purpose, diagonal cracking of shear critical walls is represented by one Critical Diagonal Crack. The ultimate drift capacity of the wall is determined based on an approach evaluating a plastic zone at the wall toe. Validation against results of cyclic full-scale tests of unreinforced masonry walls made with vertically perforated clay units shows that the presented formulation is capable of accurately predicting the effective stiffness, the maximum strength and the ultimate drift capacity of the wall. It outperforms current empirical code equations with regard to stiffness and ultimate drift capacity estimates and yields similar results concerning strength prediction.

1 Introduction

1.1 Current design practice

Many residential buildings in regions of low to moderate seismicity are constructed using unreinforced masonry (URM) walls and reinforced concrete (RC) slabs (Fig. 1a). Under earthquake loading, when considering forces that act in the plane of the wall, the masonry walls of the bottom storey are typically critical as the acting forces are largest.

Fig. 1

a Schematic drawing of a 2D system of walls and slabs, b storey-high wall element with considered degrees of freedom at its top (u—horizontal displacement, w—axial displacement, θ—rotation) and corresponding cantilever system subjected to an axial force (N), a moment (M) and a shear force (V)

URM walls show a highly non-linear force–displacement behaviour when subjected to in-plane loading. This behaviour can be classified as (1) flexure dominated if it is characterised by rocking of the wall with toe crushing as failure mode (Fig. 2a) or (2) controlled by shear if characteristic diagonal cracks form (Fig. 2b). After reaching the peak shear force, the deformations of shear-controlled walls tend to concentrate in a single diagonal crack and the force–displacement response often shows a pronounced post-peak behaviour (Petry and Beyer 2015a). Typical shear force–horizontal displacement curves for walls showing these two behaviour types are presented in Fig. 2c. In addition, hybrid modes that comprise characteristics of both types are quite common too. The walls that determine the displacement capacity of a building are in general shear-controlled walls, since they fail at a distinctively lower horizontal displacement than flexure dominated walls.

Fig. 2

a Photo of wall failing in flexure (Petry and Beyer 2014), b photo of wall failing in shear (Petry and Beyer 2014), c shear force–horizontal displacement curves qualitatively representing typical flexure and shear response of an in-plane loaded URM wall

For the seismic assessment, the non-linear force–displacement response of URM walls loaded in-plane is often approximated by a bi-linear curve. These curves are defined by the effective stiffness, the peak strength and the ultimate drift capacity of the wall; the drift is the horizontal displacement at the top of the wall divided by the wall height. The effective stiffness is typically estimated as a percentage of the gross sectional stiffness and estimates of the peak strength have long been established and included in codes. Recent codes contain also empirical drift capacity models for URM walls [e.g. Eurocode 8 (CEN 2005a), the Italian Code (NTC 2008), the New Zealand Code (NZSEE 2011) and the Swiss Code (SIA 2011)]. Typically, the drift capacity for walls is determined with empirical relations that depend on the failure mode (shear vs. flexure). Past studies have shown that such empirical drift capacity models lead to a large scatter when compared to tests (Petry and Beyer 2015a). New formulations of empirical drift capacity models that account for other parameters than the failure mode can slightly improve the fit (Lang 2002; Petry and Beyer 2014; Salmanpour et al. 2015).

To improve the prediction of the drift capacity, analytical formulations of the load–displacement behaviour of URM walls could be a remedy. So far, a number of formulations have been developed, either to be used as standalone beam element models to predict the response of single walls or to be used in equivalent frame analysis of buildings. Some of the most recently developed models are formulations by Benedetti and Steli (2008), Chen et al. (2008), Belmouden and Lestuzzi (2009), Caliò et al. (2012), Penna et al. (2014), Raka et al. (2015), Petry and Beyer (2015b). However, none of these models fully describes the load–displacement behaviour of shear critical URM walls including an estimate of the ultimate drift capacity, either since the formulation is only valid for flexure dominated walls or because only stiffness and strength but not the drift capacity are predicted.

The objective of this article is to fill this gap and to present an analytical model that describes the monotonic load–displacement behaviour of in-plane loaded URM walls developing a shear, flexure or a hybrid mode. The model which will be introduced in the following, is developed for walls constructed with modern vertically perforated clay units and normal strength cement mortar with bed joints of about 1 cm in thickness. The walls considered in this article are storey-high elements (Fig. 1a, b), which are supported at the top and bottom by RC slabs.

1.2 The force–displacement response of URM walls

The stages of the force–displacement response of URM walls that are considered as most characteristic are briefly introduced (Fig. 3a). The model presented herein is based on the Timoshenko beam theory (Sect. 2) and represents those stages by means of mechanical considerations.

Fig. 3

Horizontal force–displacement behaviour of an URM wall; a force–displacement curve with different stages of the loading process, mechanisms that cause the softening of the wall, b flexural cracking (decompression) of bed joints, c diagonal shear cracking in the wall

In the very beginning, the wall behaves linear elastically until either flexural cracks in the bed joints (Fig. 3b) or diagonal stair-stepped shear cracks start to form (Fig. 3c). Which of these two mechanisms occurs first and is more prevalent mainly depends on the geometry of the wall and the applied static and kinematic boundary conditions. The cracks lead to a softening of the wall and its non-linear response before reaching the wall’s peak strength. The presented model captures the softening by reducing the section properties (moment of inertia and cross sectional area). Flexural cracking of the wall is accounted for using the approach already employed by Benedetti and Steli (2008) and Petry and Beyer (2015b); the influence of shear cracking is simulated by a novel analytical approach, which is introduced in Sect. 3.

The peak shear resistance represents the point where the maximum flexural or shear capacity of the wall is reached (see also Fig. 3a). This paper presents innovative approaches for predicting the wall’s shear force capacity that are based on local rather than global demand and capacity parameters (Sect. 4.2). It is assumed that the wall will, subsequently, either show a pronounced post-peak load–displacement behaviour (shear controlled behaviour) or a sudden failure at peak shear force (flexure controlled). Walls experiencing a shear controlled behaviour show a concentration of the deformations in one critical diagonal crack when pushed beyond their peak shear resistance (Petry and Beyer 2014). The strength of the shear controlled wall then degrades and the wall ultimately fails at a certain residual strength. In Sect. 5, a novel concept for predicting the ultimate drift capacity of URM walls based on a plastic zone approach is presented.

The paper concludes with a validation of the model against 32 full-scale masonry walls that were tested under quasi-static cyclic loading (Sect. 6). The comparison shows that the presented model is capable of predicting well the effective stiffness, the peak strength and the ultimate drift capacity of the wall. The results are better than those obtained with the approaches included in current codes.

2 Timoshenko beam theory

The model that is presented in this paper is based on the Timoshenko beam theory, which assumes that plane sections remain plane but not orthogonal to the beam axis. The Timoshenko beam theory was already applied by Benedetti and Steli (2008) and Petry and Beyer (2015b) for the computation of the force–displacement curve of URM walls. The following sections summarise the principal equations and outline the limitations of this approach when applied to URM walls.

2.1 Formulation

The considered static system is a wall that is fixed at the base and subjected to a moment M, a shear force V and an axial force N at its top. The deformations at the top of the wall (horizontal displacement—u, rotation of a cross section—θ, vertical displacement—w, see Fig. 1c) are obtained by numerically integrating the curvatures, the normal strains and the shear strains along the wall height. Assuming that the modulus of elasticity and the shear modulus are constant along the wall height, the rotation at the top of the wall is:

$$ \theta = \int\limits_0^H {\frac{{M\left( x \right)}}{{EI\left( x \right)}}} dx \cong \sum\limits_{i = 1}^n {\frac{{{M_i}}}{{E{I_i}}}} \Delta l$$

(1)

where n is the number of discrete points used for the numerical integration (n = H/Δl). The lateral displacement u at the top of the wall is computed as the sum of the flexural displacement u _fl and the shear displacement u _sh :

$$u = u_{fl} + u_{sh}$$

(2)

$$u_{fl} = \mathop \int \limits_{0}^{H} \theta \left( x \right) dx \cong \mathop \sum \limits_{i = 1}^{n} \theta_{i} \Delta l$$

(3)

$$u_{sh} = \mathop \int \limits_{0}^{H} \kappa \frac{ V\left( x \right)}{GA\left( x \right)} dx \cong \mathop \sum \limits_{i = 1}^{n} \kappa \frac{{V_{i} }}{{GA_{i} }} \Delta l$$

(4)

where κ = 6/5 is the shear factor for a rectangular homogeneous cross sections. The axial displacement is obtained by integrating the normal strains along the centre line of the cross section over the wall height:

$$w = \mathop \int \limits_{0}^{H} \varepsilon_{xx} \left( {y = \frac{L}{2},x} \right)dx \cong \mathop \sum \limits_{i = 1}^{n} \varepsilon_{xx,i} \left( {y = \frac{L}{2}} \right) \Delta l$$

(5)

If the wall is uncracked, the moment of inertia I(x) and the cross sectional area A(x) correspond to the gross section properties of the wall. The effect of flexural cracks and shear cracks on the stiffness of the wall is accounted for by modifying the section properties I(x) and A(x) based on simple mechanical models that are described in the following sections. Flexural cracks cause a partial decompression of the section. Its influence on the flexural stiffness was already accounted for by Benedetti and Steli (2008), Penna et al. (2014) and Petry and Beyer (2015b) and its effect on the shear stiffness by Petry and Beyer (2015b). The method for capturing the impact of the formation of diagonal shear cracks on the force–displacement response is new.

2.2 Limitations of beam theory

The simulated load–displacement response of an URM wall is derived from beam theory, which is, strictly speaking, only applicable to structural elements with length to width ratios larger than approximately two. URM walls have, however, mostly smaller aspect ratios, which will limit the achievable accuracy of results with beam element models. An advantage of beam theory is its simplicity when compared to membrane theory and its suitability for engineering practice.

3 Pre-peak response

3.1 The critical diagonal crack

The crack pattern of shear critical URM walls is characterised by the appearance of diagonal cracks. The effect of these cracks is in the following modelled by a single virtual crack, which is called the Critical Diagonal Crack (CDC). It is assumed that the CDC starts to form as soon as a certain shear force V _cr is exceeded. It grows in length as the shear force V increases until it extends over the entire wall height. The crack divides the wall into two parts and therefore reduces the wall stiffness. The CDC model captures this decrease in stiffness by a reduction of the cross section values of the wall [A(x), I(x)]—in the cracked state, the wall is modelled as two parallel beams with varying cross sections representing the wall sections left and right of the CDC. This approach is combined with a further reduction of the cross sectional values as soon as flexural decompression in a wall section occurs.

For the sake of clarity, the following terminology is adopted: A cross section that is crossed by the CDC and thus divided by the shear crack in two sections is referred to as cracked. A section that undergoes flexural cracking (partial decompression of a cross section) is mentioned as decompressed.

3.1.1 Principal assumptions

One principal assumption of the CDC model concerns the positioning of the diagonal crack, which is determined from the geometry of the wall and the size of the masonry units. For the sake of simplicity, the CDC is modelled as linear and not as stair-stepped. It is assumed that with increasing lateral force V, the CDC only grows in length but does not rotate and thus the crack inclination is constant throughout the loading process. For short walls, the crack is assumed to span diagonally from corner brick to corner brick. Excluded are the top and bottom brick row, which cannot rotate due to constraints imposed by the adjacent reinforced concrete slabs (see Fig. 4b). For long walls, the CDC is assumed to have an inclination of 45° (Fig. 4b). Furthermore, the base corner (l _cor,1) is assumed to have the length of one brick. Both assumptions are based on observations from tests of long walls (Ganz and Thürlimann 1984; Bosiljkov et al. 2006). The length of the upper corner l _cor,2 and the geometry of the CDC, y _CDC (x), can be described by the following equations (applicable to short and long walls):

$$l_{cor,1} = l_{B}$$

(6)

$$l_{{cor,2}} = \left\{ {\begin{array}{ll} {l_{B} } \hfill & {{\text{for }}L - 2l_{B} \le H - 2h_{B} } \hfill \\ {L - H - l_{B} + 2h_{B} } \hfill & {{\text{for }}L - 2l_{B} > H - 2h_{B} } \hfill \\ \end{array} } \right.$$

(7)

$$y_{CDC} \left( x \right) = \frac{{L - l_{cor,1} - l_{cor,2} }}{{H - 2h_{B} }}\left( {x - h_{B} } \right) + l_{cor,1}$$

(8)

Fig. 4

CDC Model: geometry of the fully emerged CDC for loading in the positive direction (grey hatch represents decompressed part of cross sections); a short walls, b long walls, c moment profile along the wall height for a given shear span

Further assumptions concern the material behaviour of masonry. It is assumed that (1) masonry has zero tensile strength and behaves linear elastically in compression; (2) head joints are stress-free; (3) shear stresses are only transferred by bed joints that are in compression; (4) the wall can be analysed as a 2D-problem, i.e., the influence of out-of-plane bending is not considered.

3.1.2 Formation of the CDC

It is assumed that the shear force that triggers diagonal cracking can be computed by a modified Mann and Müller criterion. Mann and Müller (1982) used the criterion to estimate the peak shear strength of masonry walls; in the following their criterion is modified to capture the onset of shear cracking. This criterion formulates equilibrium of a single brick to estimate the normal stress distribution in the bed joints. It is based on the assumption that head joints do not transfer stresses and, consequently, the shear force is transmitted solely by the bed joints (Fig. 5). The resulting torque moment has to be equilibrated by additional vertical stresses in the bed joints (σ _T ), which lead to decompression over half the brick length and thus to the appearance of local cracks. The vertical stresses in the bed joints are therefore the sum of the stresses that result from the axial force (σ _N ), the bending moment (σ _M ) and the torque moment (σ _T ). It is assumed that a crack forms when the sum of these vertical stresses is equal to zero.

Fig. 5

Different distributions of the normal stresses (σ _T ) on the bricks due to the torque moment, after Elsche (2008)

The following paragraphs outline the simulation of the formation of the CDC from its onset at the shear force V _cr until it has formed completely and spans over the entire wall height (leaving out the bottom and top brick rows). An assumption of the vertical stress distribution in the bed joints due to the torque moment is required which is discussed first.

3.1.2.1 Vertical stresses due to torque moment

The vertical normal stress distribution in bed joints induced by the torque moment was presented by several researchers (Schneider et al. 1976; Atkinson et al. 1990; Lourenço 1996; Elsche 2008). They showed by means of finite element simulations that the actual stress distribution is non-linear and follows qualitatively the distribution shown in Fig. 5a. For analytical models, this stress distribution is typically approximated by simpler ones. The usual assumption of a linear stress distribution (Fig. 5b) cannot be employed because the stresses above and below a bed joint would not be in equilibrium (Elsche 2008). An alternative distribution satisfying equilibrium has been proposed by Mann and Müller (1982), who assume that the vertical stresses due to the torque moment are constant over half the brick length (Fig. 5c). In the following, distribution d, which was suggested by Elsche (2008), is used to approximate distribution a.

For the distribution shown in Fig. 5d, the relationship between the shear stress τ _xy and the resulting maximum vertical stress on a brick due to the torque moment is:

$$\sigma_{T,max} = \frac{{4 \tau_{xy} h_{B} }}{{l_{B} }}$$

(9)

Test results (Petry and Beyer 2015a) and finite element simulations (Zhang et al. 2014) showed that the shear strains in a cross section are largest at the position of the future CDC. Assuming, thus, a skew parabolic shear stress distribution with its peak at the CDC (see Fig. 6b) results in maximum shear stresses of:

$$\tau_{xy} \left( {x,y_{CDC} \left( x \right)} \right) = \tau_{xy,max} = \frac{3}{2}\frac{V}{A}$$

(10)

The maximum torque stress at the CDC is therefore (inserting Eq. (10) into (9)):

$$\sigma_{T,max} = \frac{{6 V h_{B} }}{{A l_{B} }}$$

(11)

Fig. 6

a Distributions of normal stresses due to moment, b distribution of shear stresses, c assumed stress distribution on the bricks that determine V _cr (1) and the shear force at the completion of cracking (2)

3.1.2.2 Vertical stresses due to axial force and moment

Assuming that plane sections remain plane, the vertical stresses in a wall cross section due to axial force and moment (σ _xx (x,y)) are:

$$\sigma_{xx} \left( {x,y} \right) = \sigma_{N} + \sigma_{M} \left( {x,y} \right) = \frac{N}{A} + \frac{M\left( x \right)}{I}\left( {\frac{L}{2} - y} \right)$$

(12)

The vertical stresses at the location of the CDC along the wall height are obtained by replacing the coordinate y in Eq. (12) with Eq. (8), which describes the geometry of the CDC.

3.1.2.3 Computation of V _cr

It is assumed that the CDC starts to form at the height where the vertical stresses due to axial force, moment and torque moment along the CDC are first equal to zero (x = H _crit , y = y _CDC (H _crit ), see Fig. 6). Since the shear force is constant over the wall height, the maximum vertical stresses due to the torque moment (σ _T,max ) are also constant (for fully compressed cross sections). The same applies to the axial force N and the resulting stresses σ _N .

The crack starts, therefore, to form at the height x = H _crit where the tensile stresses due to the moment alone along the CDC are largest:

$$\left. {\frac{{\partial \sigma_{M} \left( x \right)}}{\partial x}} \right|_{{x = H_{crit} }} = \frac{\partial }{\partial x}\left[ {\frac{M\left( x \right)}{I}\left( { \frac{L}{2} - y_{CDC} \left( x \right)} \right)} \right]_{{x = H_{crit} }} = 0$$

(13)

Equation (13) leads to:

$$H_{crit} = \left\{ {\begin{array}{*{20}c} {\frac{{H_{0} }}{2} + \frac{{H_{M} }}{2} \hfill {\text{for }}H_{0} \le H} \\ {\frac{H}{2} + \frac{{H_{M} }}{2} \hfill {\text{ for }}H_{0} > H} \\ \end{array} } \right.$$

(14)

where H _M is the smallest value of x for which the CDC is subjected to tensile stresses when considering stresses due to the moment M alone:

$$H_{M} = \hbox{min} \left[ {\frac{{\left( {\frac{L}{2} - l_{cor,1} } \right)\left( {H - 2h_{B} } \right)}}{{L - l_{cor,1} - l_{cor,2} }} + h_{B} , H_{0} } \right]$$

(15)

As discussed above, the torque stresses vary along the length of a brick; for the sake of simplicity the maximum value of σ _T is considered throughout [value given by Eq. (11)]. Vertical equilibrium leads to the following equation (Fig. 6c1):

$$\sigma_{xx} \left( {H_{crit} , y_{CDC} \left( {H_{crit} } \right)} \right) - \sigma_{T,max} = \sigma_{N} - \sigma_{M} \left( {H_{crit} , y_{CDC} \left( {H_{crit} } \right)} \right) - \sigma_{T,max} = 0$$

(16)

Solving Eq. (16) yields the shear force V _cr that triggers the formation of the CDC:

$$V_{cr} = \frac{N}{{\frac{{6h_{B} }}{{l_{B} }} + m}}$$

(17)

with:

$$m = \frac{12}{{L^{2} }}\left( {H_{0} - H_{crit} } \right)\left[ {l_{cor,1} + \frac{{L - l_{cor,1} - l_{cor,2} }}{{H - 2h_{B} }}\left( {H_{crit} - h_{B} } \right) - \frac{L}{2}} \right]$$

(18)

3.1.2.4 Propagation of the CDC

When the wall is loaded beyond V _cr the CDC propagates towards the two corners. The growth of the CDC is simulated by applying the approach described in the previous section to all wall cross sections along the CDC. A cross section cracks if the sum of the vertical stresses at the location of the CDC is zero:

$$\sigma_{xx} \left( {x,y_{CDC} \left( x \right)} \right) - \sigma_{T,max} = 0$$

(19)

Once the formation of the CDC in a cross section is triggered, it splits the section into two parts with lengths L ₁ (x) and L ₂ (x) (see Fig. 7a) respectively, which correspond to the wall length on either side of the CDC:

$$L_{1} \left( x \right) = L - l_{cor,1} + \frac{{l_{cor,1} + l_{cor,2} - L}}{{H - 2h_{B} }}\left( {x - h_{B} } \right)$$

(20)

$$L_{2} \left( x \right) = l_{cor,1} + \frac{{L - l_{cor,1} - l_{cor,2} }}{{H - 2h_{B} }}\left( {x - h_{B} } \right)$$

(21)

Fig. 7

a Fully cracked wall undergoing decompression (grey hatch represents decompressed parts of sections), b-(1) normal stresses in wall part 2 at M ₂ = M _e,2, b-(2) normal stresses in wall part 2 in decompression, c internal force distributions in wall

3.1.2.5 Internal forces in wall parts

In the two wall parts that are created by the formation of the CDC, it is assumed that that the normal force N is distributed proportional to the respective lengths (L ₁ (x), L ₂ (x)) on either side of the CDC (Fig. 7c):

$$N_{i} (x) = \frac{{L_{i} \left( x \right)}}{L} \quad {\text{for }}i \in \{ 1,2\}$$

(22)

At a height x, the moment M(x) is split between the two parts of the cross section in proportion to the moments of inertia of the sections with respect to their respective centre of gravity (I _eig,1 (x), I _eig,2 (x)) (neglecting the parallel axis theorem part):

$$M_{i} \left( x \right) = M\left( x \right)\frac{{I_{eig,i} \left( x \right)}}{{I_{eig,1} \left( x \right) + I_{eig,2} (x)}} = M\left( x \right)\frac{{L_{i}^{3} (x)}}{{L_{1}^{3} (x) + L_{2}^{3} (x)}} \quad {\text{for }}i \in \{ 1,2\}$$

(23)

It shall be noted that—to avoid any iterations—the internal forces M _i (x) and N _i (x) are distributed between cross section parts 1 and 2 based on their gross section properties neglecting the effect of decompression on the distribution of the internal forces.

3.2 Decompression of a wall section

A cross section becomes partially decompressed as soon as the combined normal stresses due to the axial force N and the moment M would result in tension at one edge of the cross section. Since it is assumed that mortar joints cannot transfer tension, the decompressed area no longer transfers shear or normal stresses and therefore the effective cross section and bending stiffness is reduced.

For the sake of simplicity, it is assumed that decompression can occur only in wall part 2 for 0 ≤ x ≤ H ₀ and in wall part 1 for H ₀  < x ≤ H while the other wall section is always considered with its gross section properties. The numbering of the wall parts is shown in Fig. 7a. Considering decompression in the shorter wall section would have merely a small influence on the overall wall stiffness, since it would only occur near one of the wall corners where the section is very short and, hence, the effect on the overall moment of inertia I(x) is negligible.

Assuming a linear vertical stress distribution, the moment for which decompression occurs at a height x can be calculated as follows (see Fig. 7b1):

$$M_{e,i} (x) = \frac{{N_{i} \left( x \right)L_{i} }}{6}$$

(24)

where i denotes the number of the wall part (wall part 1 and wall part 2). If the moment is increased, partial decompression takes place. The compressed length L _c,i can be determined from moment equilibrium of the reduced cross section (see Fig. 7b-2). It leads to Eq. (25) with the subscript i, again, denoting a wall part:

$$L_{c,i} \left( x \right) = 3\left( {\frac{{L_{i} (x)}}{2} - \frac{{|M_{i} \left( x \right)|}}{{N_{i} \left( x \right)}}} \right)$$

(25)

The curvature χ _i of a wall section part i undergoing partial decompression is (see Fig. 7b-2):

$$\chi_{i} (x) = \frac{{M_{i} \left( x \right)}}{{EI_{i} \left( x \right)}} = \frac{{\sigma_{xx} \left( {x,y = 0} \right)}}{{EL_{c,i} (x)}} = \frac{{2N_{i} (x)}}{{L_{c,i}^{2} \left( x \right) TE}}$$

(26)

The corresponding moment of inertia of a section part undergoing decompression is thus:

$$I_{i} \left( x \right) = \frac{{M_{i} \left( x \right) L_{c,i}^{2} \left( x \right)T}}{{2 N_{i} (x)}}$$

(27)

3.3 Cross sectional values of a wall section

The computation of the non-linear force–displacement response by means of an elastic Timoshenko beam element requires the continuous updating of the cross section properties, i.e., of the moment of inertia I(x) and the area A(x), in order to account for the effect of decompression and shear cracking with increasing shear force. The computation of these properties based on the previously introduced concepts is described in this section.

3.3.1 The moment of inertia of a wall cross section

The moment of inertia of a cross section reduces when the section is cracked (i.e., when the CDC passes through the section) and/or when the section becomes partially decompressed. The next paragraphs summarise the procedure to obtain the moment of inertia of a wall cross section dependent on its state.

3.3.1.1 Uncracked and fully compressed section

If neither shear cracking nor global decompression have yet occurred, the moment of inertia is calculated according to elastic beam theory taking into account the full gross section properties of the wall.

Criteria

$$\begin{aligned}&{\text{No decompression}}{:}\,M(x) < M_{e} \\ &{\text{No shear cracking}}{:}\,\sigma_{xx} (x,y_{CDC} (x)) - \sigma_{T,max} > 0\end{aligned}$$

Corresponding moment of inertia

$$I = \frac{{L^{3} T}}{12}$$

(28)

3.3.1.2 Uncracked and partially decompressed section

For a cross section that is not yet split in two by the CDC but that undergoes partial decompression, the moment of inertia is determined by Eq. (27) in Sect. 3.2 (without considering the subscripts since the section is not yet cracked in shear) and Eq. (29) respectively.

Criteria

$$\begin{aligned}&{\text{Decompression}}{:}\,M(x) > M_{e} \hfill \\ &{\text{No shear cracking}}{:}\,\sigma_{xx} (x,y_{CDC} (x)) - \sigma_{T,max} > 0\end{aligned}$$

Corresponding moment of inertia

$$I = \frac{{ML_{c}^{2} T}}{2N}$$

(29)

3.3.1.3 Cracked and fully compressed section

Wall cross sections that are split in two by the CDC but that are still fully compressed are assumed to have a moment of inertia corresponding to the sum of the moment of inertias of the two cross section parts with respect to their respective centres of gravity.

Criteria

$$\begin{array}{*{20}l} {\text{for}\,\,\,x < H_{0} } \hfill & {\text{for}\,\,\,x > H_{0} } \hfill \\ {M_{2} \left( x \right) < M_{e,2} } \hfill & {M_{1} \left( x \right) < M_{e,1} } \hfill \\ {\sigma_{xx} \left( {x,y_{CDC} \left( x \right)} \right) - \sigma_{T,\hbox{max} } = 0} \hfill & {\sigma_{xx} \left( {x,y_{CDC} \left( x \right)} \right) - \sigma_{T,\hbox{max} } = 0} \hfill \\ \end{array}$$

Corresponding moment of inertia

$$I = I_{eig,1} + I_{eig,2} = \frac{{L_{1}^{3} T}}{12} + \frac{{L_{2}^{3} T}}{12}$$

(30)

3.3.1.4 Cracked and partially decompressed section

The moment of inertia of shear cracked and decompressed cross sections is obtained by adding the moment of inertias of both parts. Decompression is considered using Eq. (27) but for the sake of simplicity it is only accounted for in one of the two parts, i.e., for part 2 if x < H ₀ and part 1 if x > H ₀ (as discussed in Sect. 3.2). The total moment of inertia corresponds to the sum of the moments of inertia of the two cross section parts with respect to their respective centres of gravity.

Criteria

$$\begin{array}{*{20}l} {\text{for}\,\,\,x < H_{0} } \hfill & {\text{for}\,\,\,x > H_{0} } \hfill \\ {M_{2} \left( x \right) > M_{e,2} } \hfill & {M_{1} \left( x \right) > M_{e,1} } \hfill \\ {\sigma_{xx} \left( {x,y_{CDC} \left( x \right)} \right) - \sigma_{T,max} = 0} \hfill & {\sigma_{xx} \left( {x,y_{CDC} \left( x \right)} \right) - \sigma_{T,max} = 0} \hfill \\ \end{array}$$

Corresponding moment of inertia

$$I = \frac{{L_{1}^{3} T}}{12} + \frac{{M_{2} L_{c,2}^{2} T}}{{2N_{2} }} \quad {\text{for}\,\,\,x <; H_{0} }$$

(31)

$$I = \frac{{L_{2}^{3} T}}{12} + \frac{{M_{1} L_{c,1}^{2} T}}{{2N_{1} }} \quad {\text{for}\,\,\,x >; H_{0} }$$

(32)

3.3.1.5 Introducing a deformation constraint in the CDC

It was assumed that the CDC does not restrain the relative movement of the two wall parts. This was reflected in considering only the two terms I _eig,1 and I _eig,2 and neglecting the moment of inertia that results from the parallel axis theorem. This modelling approach represents two beams that can bend freely with respect to each other (see Fig. 8b). In reality, the relative movement of the two wall parts along the CDC will not be completely unrestrained. The restraint will be stronger the larger the curvature of the cross section at a certain load level. This partial restraint will lead to additional forces to be transferred by the CDC and will increase the stiffness of the wall. The effect can be captured by considering a fraction of the moment of inertia resulting from the parallel axis theorem (in the following referred to as Steiner’s component of the moment of inertia—I _st ).

Fig. 8

Graphical representation of the concept of superposition of states; a full cross section, b two sections that can deform freely (no coupling), c system of two elastically bonded sections where shear stresses (arrows) can be used to represent the constrained deformation and hence increase in flexural stiffness

This partial restraint can be modelled by the γ-method (Möhler 1956). It was originally derived for parallel timber beams connected by discrete fasteners. As the name suggests, the method introduces a factor γ to reduce Steiner’s component of the moment of inertia in order to account for the fact that the fasteners provide only a partial restraint along the interface. Thus, the total moment of inertia can be written as:

$$I\left( x \right) = I_{eig} + \gamma I_{st}$$

(33)

with:

$$0 \le \gamma \le 1$$

(34)

If γ = 0, the stiffness corresponds to the stiffness of two parallel beams that deform without any restraint along the interface (see Fig. 8b). A factor γ = 1 represents the case where relative displacements along the interface are fully restrained, i.e., when the two beams act as one (Fig. 8a). The latter case corresponds to flexural walls where the influence of any diagonal cracking on the load–displacement behaviour of the wall is negligible.

Equation (33) is rewritten to reflect that any condition of deformation constraint between the two wall parts separated by the diagonal crack can be interpreted as a linear combination of the states no crack at all (thus full deformation compatibility, Fig. 8a) and crack without deformation constraint (hence free flexural deformation of the two parts with respect to each other, Fig. 8b):

$$I\left( x \right) = \gamma \left( {I_{eig} \left( x \right) + I_{st} \left( x \right)} \right) + \left( {1 - \gamma } \right) I_{eig} \left( x \right)$$

(35)

The first term of Eq. (35)—I _eig (x) + I _st (x)—represents the contribution of the uncracked system (Fig. 8a) to the flexural stiffness of the wall. This stiffness can be easily determined by neglecting the influence of the CDC and just considering the effect of decompression by means of Eq. (28) and (29). The stiffness obtained with this approach corresponds exactly to the model by Petry and Beyer (2015b) for URM walls controlled by flexure. The second term of Eq. (35)—I _eig (x)—describes the stiffness of a wall for which the movement along the CDC is not restrained (Fig. 8b). This stiffness corresponds to the moment of inertia employing the full set of equations given above [Eqs. (28)–(32)].

3.3.1.6 The factor γ

It can be shown by means of linear elastic analysis that the γ-factor varies slightly along the wall height and depends on the shear span and geometry of the wall. For the sake of simplicity and based on comparisons with test results (Sect. 6), it is, however, suggested to use a constant value for the γ-factor along the wall height. The choice of the γ-factor should reflect that the deformations in the CDC are less constrained for shear critical walls than for flexural dominated walls. The factor γ should, therefore, be a function of a variable that distinguishes between shear and flexure dominated walls.

Tests indicate a dependency of the type of wall behaviour (shear or flexure controlled) on the applied axial load, the shear span and the wall geometry [e.g. Bosiljkov et al. (2006); Salmanpour et al. (2015); Petry and Beyer (2015a)]. Thus, a criterion to explicitly distinguish a flexural from a shear dominated behaviour should take these influences into account.

For this purpose, it is proposed to consider the ratio between the height over which flexural decompression of the bed joints occurs (h _d ) and the half wall height (H/2). The height h _d is computed for a reference shear force V _ref  = c L T (see Fig. 9b):

$$h_{d} = \hbox{max} \left[ {H_{0} - \frac{NL}{{6V_{ref} }},0} \right]$$

(36)

Fig. 9

a Representation of suggested distribution of the factor γ dependent on the variable 2h _d /H along with depiction of tests that showed a shear dominated behaviour and tests controlled by flexure, b sketch of decompressed height in wall at a reference shear force (grey hatch represents the decompressed area in the wall)

Substituting N with σ ₀  L T and dividing Eq. (36) by H/2 leads to

$$\frac{{2h_{d} }}{H} = \frac{{2H_{0} - \frac{{\sigma_{0} L}}{3c}}}{H}$$

(37)

The formulation of the reference shear force V _ref as the local cohesion times the wall section area is chosen in order to uncouple it from the applied axial load and shear span and to only capture the influence of the geometry of the wall cross section. Applying this force on a wall and changing the boundary conditions shear span and axial load, yields the influence of the aforementioned parameters on the behaviour of the wall in terms of decompressed height to wall height.

To verify whether the ratio 2h _d /H is indeed suitable for distinguishing between walls that fail in shear and walls that fail in flexure, it is applied to 32 tests for which the behaviour types are known (see Table 2 in “Appendix 1”). Shear dominated walls are assigned γ = 0 and walls that are flexure controlled γ = 1. Figure 9a shows that the ratio 2h _d /H allows to distinguish between these two types of behaviours.

For a value of 2 h _d /H < 1, the walls tend to show a shear controlled behaviour in tests whereas for values larger than one, the walls exhibit a behaviour controlled by flexure. Based on this finding, a distribution for the factor γ is suggested as presented in Eq. (38) and Fig. 9a, accounting for a transition zone for walls showing a hybrid behaviour as well.

$$\gamma = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{for}}\frac{{2h_{d} }}{H}<0.5} \hfill \\ {2\left( { - \frac{1}{2} + \frac{{2h_{d} }}{H}} \right)} \hfill & {{\text{for }}0.5 \le \frac{{2h_{d} }}{H} \le 1} \hfill \\ 1 \hfill & {{\text{for }}\frac{{2h_{d} }}{H}>1} \hfill \\ \end{array} } \right.$$

(38)

The approach to distinguish the wall behaviour types according to EC8—part 3 (CEN2005)—along with other code approaches doing it in a similar manner [e.g. FEMA 356 (ASCE 2000); NZSEE (NZSEE 2011)]—would be to take the minimum of the two equations describing the shear force capacity of the wall (one for flexure and one for shear failure). However, both are similarly sensitive to the applied axial load—increasing axial load increases the shear force capacity of a wall in a similar order of magnitude for both equations up to a certain point [see Eqs. (48), (54)]. Moreover, both equations show a certain negative influence of the shear span on the shear load capacity. This means that the sensitivity towards the influence of the axial load and the shear span on the—to-be-predicted—type of load–displacement behaviour is reduced.

Furthermore, the mechanism of failure does not necessarily reflect the type of load–displacement behaviour of a wall—e.g. a shear wall failing due to compression at the wall toe would be graded a flexure dominated wall according to EC8. In this article, the failure mode and behaviour type of a URM wall are assumed to be closely related but not the same. A failure mechanism is in many cases a direct result of the behaviour type but a failure mode such as toe crushing can be preceded by a flexure controlled or a shear dominated behaviour. Yet, many code approaches do not make this distinction and treat failure mode and behaviour type as an equivalent. In order to avoid this, the wall load–displacement behaviour type in the CDC model is characterised using a variable (h _d /H (V _ref )) directly distinguishing flexure dominated and shear controlled walls without deriving it from a governing failure mechanism.

3.3.2 The area of a wall cross section

The cross sectional area A(x) that is required for computing the wall’s shear stiffness, is calculated by introducing a virtual compressed length L _c,v , which varies along the wall height reflecting the cracking state of the respective cross sections. It is referred to as virtual length since it does not only account for the effect of decompression but also for the effect of shear cracking on the wall stiffness. The area of the wall cross section at height x is:

$$A\left( x \right) = L_{c,v} \left( x \right) T$$

(39)

In the following, the virtual compressed length is defined and its properties discussed.

3.3.2.1 The virtual compressed length

According to Sect. 3.2 and Eq. (26), the curvature of a section that is partially decompressed but uncracked in shear (hence no subscript i) is:

$$\chi (x) = \frac{M(x)}{EI(x)} = \frac{2N}{{EL_{c,v}^{2} (x)T}}$$

(40)

Solving for L _c,v (x) yields:

$$L_{c,v} (x) = \hbox{min} \left[ { \sqrt {\frac{2NI\left( x \right)}{M\left( x \right)T}} ,L} \right]$$

(41)

The moment of inertia I(x) is computed as introduced in Sect. 3.3.1. For a cross section that just undergoes decompression without being cracked in shear, L _c,v corresponds to the real compressed length L _c as introduced in Eq. (25). A cross section that is just cracked in shear but fully compressed, however, will also experience a reduction in shear stiffness, which is captured by this approach (L _c,v (x) reduces since I(x) reduces due to diagonal cracking). This reduced shear stiffness would not be captured if the shear stiffness were computed based on the area of the compressed cross section alone. In this case, the area and therefore the shear stiffness would stay the same. To conclude, the approach of the virtual compressed length allows to capture not only a decrease in the flexural stiffness EI(x) but also in the shear stiffness GA(x) once decompression and/ or shear cracking occurs.

3.4 Stress distributions in a wall section

Computing the normal and shear stress distributions throughout the wall requires some assumptions in order to account for the effect of the CDC, which represents a point of discontinuity. The approximate solution proposed in the following makes, again, use of the virtual compressed length L _c,v that was introduced in Sect. 3.3.1.6. The stress distributions are used, in further course, to determine the axial displacement and the peak shear resistance of the wall.

3.4.1 Normal stresses

It is assumed that the normal stress distribution is linear along L _c,v and that there is no discontinuity in normal stresses at the CDC. The entire section is therefore subjected to a mean curvature. Using plane section analysis and a section length L _c,v (x), the compressive stresses can be calculated for each cross section along the wall height. Figure 10 shows the distribution of compressive stresses for wall configurations corresponding to (a) a shear-controlled wall, (b) a hybrid wall and (c) a wall dominated by flexure.

Fig. 10

Assumed distribution of compressive stresses within the wall; a shear wall, b wall exhibiting a hybrid mode, c wall controlled by flexure

As shown in Fig. 10a there is a jump in the decompressed wall area at the height of the first brick row—the decompressed length is lower in the first row of bricks than directly above. This is due to the application of the virtual compressed length L _c,v . To account for the confinement effect, the CDC is assumed not to cut through the first and last rows of bricks and in these rows the compressed length accounts, therefore, only for the effect of decompression. In between, the virtual compressed length represents both the influence of flexural decompression as well as diagonal shear cracking of sections.

3.4.2 Shear stresses

The shear stress distribution is computed assuming a skew parabolic distribution with the maximum stresses (τ _xy,max ) generally occurring at the CDC (see Fig. 11b). As proposed in Petry and Beyer (2015b), no shear stress is transferred in the decompressed parts of the cross section.

For one particular configuration the maximum peak shear stress is assumed not to occur at the CDC: this is the case when, in a cracked cross section undergoing decompression, the available length on the side of the CDC where decompression occurs (L _c,v −L ₁ (x), see Fig. 11b2) is smaller than the length on the side of the CDC that does not undergo decompression (L ₁ (x)). In this case it is assumed that the shear stress follows a symmetric parabolic distribution with its maximum (τ _xy,max ) not at the CDC but at the midpoint of L _c,v . Figure 12 shows the resulting shear stress distributions of the wall configurations for which the normal stresses were plotted in Fig. 10.

Fig. 11

Determination of shear stresses and axial strains; a system under virtual decompression (i.e. decompression and/ or cracking, grey hatch represents the virtually decompressed parts of sections) including indication of assumed shear stress distributions in selected cross sections, b more detailed view of shear stress distributions, c sketch of the corresponding axial strain distributions

Fig. 12

Assumed distribution of shear stresses within the wall; a shear-critical wall, b wall exhibiting a hybrid mode, c wall controlled by flexure

The functions employed to calculate the shear stress distribution per cross section have to satisfy the following condition:

$$V = \mathop \int \limits_{0}^{{L_{c,v} (x)}} \tau_{xy} (x,y)dy$$

(42)

The skew parabolic shear stress distribution can be described by the following function:

$$\tau_{xy,i} \left( {x,y^{*} } \right) = \tau_{xy,\hbox{max} } \left( x \right)\left( {1 - \frac{{y^{*2} }}{{L_{i,v} \left( x \right)^{2} }}} \right) \quad {\text{for}} \quad i \in \{ 1,2\}$$

(43)

where y* is the horizontal coordinate measured from the CDC. The maximum shear stress is:

$$\tau_{xy,max} (x) = 1.5\frac{V}{{L_{c,v} (x) T}}$$

(44)

3.5 Computing the axial displacement

Since the material is assumed to be linear elastic in compression, the normal strains are directly proportional to the normal stresses (see Fig. 11c). If the section is uncracked in shear and fully compressed, the normal strains at the centre line of the wall can be determined as:

$$\varepsilon_{xx} \left( {x, y = \frac{L}{2}} \right) = - \frac{N}{EA}$$

(45)

If decompression and/or shear cracking of the wall occurs, the normal strains at the centre line of the wall can be computed via the virtual compressed length using Eq. (46). The resulting axial displacement can be obtained by numerically integrating the normal strains according to Eq. (5).

$$\varepsilon_{xx} \left( {x, y = \frac{L}{2}} \right) = \frac{2N}{{EL_{c,v}^{2} (x)T}}\left( {\frac{L}{2} - L_{c,v} (x)} \right)$$

(46)

4 Peak shear resistance

Ensuing, different approaches from literature for estimating the peak shear resistance of URM walls are reviewed. Furthermore, a new method for determining the peak shear capacity of shear dominated walls based on local demand and capacity parameters is presented. Finally, different failure mechanisms for flexure dominated walls based on the development of a crushed zone at the wall toe are introduced.

4.1 Existing models

4.1.1 Shear failure of a bed joint

In EC8—part 3 (CEN 2005a), the shear force capacity of walls controlled by shear is estimated based on a Mohr–Coulomb criterion [Eq. (47)]. In EC8 design values are used for the material parameters c and μ while in this paper expected (mean) values will be used.

$$V_{P} = \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } \frac{N}{{L_{c} T}}} \right)L_{c} T = f_{V} L_{c} T$$

(47)

where f _v  ≤ 0.065 f _B,c . Failure would occur at the wall toe where the compressed length is smallest. If the expression for L _c as given in Eq. (25) (without subscripts) is inserted into Eq. (47), it reads

$$V_{P} = \frac{{1.5 \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} LT + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } N}}{{1 + \frac{3}{N}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} H_{0} T}}$$

(48)

The same criterion can also be found in EC6—part 1 (CEN 2005b) for determining at the ultimate limit state the design value of the shear load applied to the masonry wall. Originally, the Mohr–Coulomb friction criterion to assess the in-plane shear force capacity of masonry was introduced in slightly different form by Mann and Müller (1982) and was modified to the presented approach by Magenes and Calvi (1997).

The global material parameters $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}$ and $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }$ in Eqs. (47) and (48) differ from local values that are typically derived from triplet tests. By formulating equilibrium on a single brick, Mann and Müller (1982) derived the following relationship between local and global parameters:

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } = \mu \frac{1}{{1 + 2\mu \frac{{h_{B} }}{{l_{B} }}}}$$

(49)

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} = c\frac{1}{{1 + 2\mu \frac{{h_{B} }}{{l_{B} }}}}$$

(50)

As an alternative approach, this paper proposes a friction criterion that is based on local stresses and the local material values c and μ which can be directly derived from triplet shear tests (Sect. 4.2.1).

4.1.2 Tensile failure of a brick

Mann and Müller (1982) suggest a further criterion to account for the tensile failure of a brick:

$$V_{P} = \tau \frac{LT}{n} = \frac{{f_{B,t} LT}}{2.3 \, n}\sqrt {1 + \frac{{\sigma_{0} }}{{f_{B,t} }}}$$

(51)

The factor 2.3 originates from the fact that the maximum shear stress in the centre of the brick is 2.3 times the average shear stress on the brick (Mann and Müller 1982). Newer studies yield slightly different values [e.g. 2.13 for a brick with an aspect ratio of h _B /l _B  = ½ in Elsche (2008)].

When applied to entire walls rather than single bricks, σ ₀ is taken as the average axial stress on the wall although the axial stress varies significantly along the wall length and over the wall height. The smallest shear capacity would be obtained if one applies the criterion to a point in the wall where the section is decompressed (σ ₀  = 0 MPa). However, experimental results have shown that in the decompressed area the shear strains and, therefore, stresses are near zero (Petry and Beyer 2015b).

4.1.3 Crushing of the wall toe

Petry and Beyer (2015b) present failure criteria for walls failing in flexure. Such walls exhibit a toe crushing due to the exceedance of the compressive strength of the brick (f _B,c ) or the masonry as a whole (f _u ). Two different possible positions of failure due to crushing are considered.

Test observations showed that the first splitting cracks initiate from the second bed joint at a half-brick inwards from the external fibre (Petry and Beyer 2015b). This is attributed to the confining effect of the foundation slab increasing the strength of the bottom brick row. The first criterion checks therefore the compressive strength of the masonry at x = h _B and y = l _B /2. It is further assumed that at this instant the distribution of compressive stresses is still linear. Thus, the stresses at the edge of the brick have already exceeded the masonry compressive strength before failure occurs.

$$V_{P} = \frac{{N\left( {\frac{L}{2} - \frac{{N + \sqrt {N^{2} - Nf_{u} Tl_{B} } }}{{3f_{u} T}}} \right)}}{{\left( {H_{0} - h_{B} } \right)}}$$

(52)

The criterion only applies if f _u T l _B  < N. In Petry and Beyer (2015b), Eq. (52) is used to determine the onset of splitting of bricks at the wall toe and the beginning of the plastic branch of the load–displacement curve. Peak strength is assumed to be attained soon afterwards.

The second criterion assesses the strength of the bottom row of bricks. In the absence of a simple model that accounts for the confinement effect by the foundation, it is assumed that the bottom brick row can reach the full compressive strength of the brick (f _B,c ) at the extreme fibre of the section.

$$V_{P} = \frac{NL}{{2H_{0} }}\left( {1 - \frac{4N}{{3 LTf_{B,c} }}} \right)$$

(53)

In EC8—part 3 (CEN 2005a) the load carrying capacity of walls controlled by flexure is determined using a stress block model assuming that the critical section is the base joint which has a similar form as Eq. (53).

$$V_{P} = \frac{NL}{{2H_{0} }}\left( {1 - 1.15\frac{N}{{LTf_{u} }}} \right)$$

(54)

4.1.4 Further approaches

Further analytical approaches to determine the shear force capacity of URM walls loaded in-plane can be found in Ganz (1985) and Turnsek and Cacovic (1971). They are not discussed here as the failure criteria introduced in Sect. 4.2 do not build on these approaches.

4.2 Estimating the peak strength using local criteria

The failure criteria developed in the following are based on the CDC model as introduced in Sect. 3. The approaches assess local stress and strain states to retrieve the peak shear resistance of URM walls loaded in-plane. To start with, shear and flexure dominated walls are distinguished by applying different failure criteria according to their pre-peak behaviour. The reasons for this methodology are explained in the following paragraphs.

4.2.1 Walls dominated by shear

In walls showing a behaviour controlled by shear, the response before and after reaching the peak strength V _P differs significantly (Fig. 13c). In the pre-peak phase, damage to the wall is largely limited to relatively fine cracks. In the post-peak phase, however, the diagonal crack starts degrading significantly and the shear force that the wall can sustain reduces with increasing displacement. Eventually, once the shear strength has dropped to the residual shear strength V _R , the wall ultimately fails.

Fig. 13

a Wall dominated by shear at peak shear resistance with graphical representation of both considered failure modes, b1 criterion for shear failure, b2 criterion for compression failure in second bed joint, c qualitative shear force–horizontal displacement curve indicating the point of peak shear resistance (V _P )

It is assumed that the peak strength is reached as soon as one of two local failure modes occurs; shear failure at a point in the wall where the shear stresses reach the respective shear strength or compression failure of the outermost fibre in the second bed joint (Fig. 13a, b). Whichever stress limit is attained first is assumed to represent the point of transition from the pre- to the post-peak response.

In the CDC model, walls that develop a hybrid behaviour according to the criterion introduced in Sect. 3.3.1 (0.5 < γ < 1), are subjected to a significant amount of flexural decompression but also diagonal cracking. In order to account for the influence of the diagonal crack, their peak shear resistance is evaluated according to the same criteria as for shear dominated walls.

4.2.1.1 Shear failure

To assess the shear strength within the wall, a Mohr–Coulomb criterion is used, employing parameters characterising the local cohesion and local coefficient of friction [Eq. (55)]. These parameters can be obtained directly from triplet tests.

$$f_{v} \left( {x,y} \right) = c + \mu \sigma_{xx} (x,y)$$

(55)

It is not possible to determine a priori the position where failure will occur since the shear strength depends on the normal stress distribution σ _xx (x,y). Wherever the ratio of shear stresses to shear strength (with shear and normal stresses obtained as presented in Sect. 3.4) approaches unity, shear failure is triggered, implicitly yielding a prediction of the position where failure occurs (x = x _f , y = y _f – see Fig. 13a1, b1). It is assumed that the peak shear resistance of the wall (V _P ) is attained as soon as the shear stress reaches the shear strength in a single point only.

4.2.1.2 Compression failure in the second bed joint

Corresponding to the approach chosen in Petry and Beyer (2015b), the compressive strength of a brick (f _B,c ) is assigned to the first and last row of bricks respectively. This is done to account for the confinement by the adjacent concrete slabs, which locally increases the masonry strength. All other brick rows are assigned the compressive strength of masonry (f _u ).

The confinement effect needs to be revisited if a wall is modelled that spans only over parts of the storey height (i.e., a wall framed by spandrels). Furthermore, the boundary conditions that cause the confinement effect might differ between laboratory tests and actual buildings. It can be influenced by several factors such as, for example, the material of the supporting elements or slabs. Due to a lack of models that quantify these influences, the focus herein lies on a representation of laboratory tests.

Compressive failure in walls that are shear controlled or show a hybrid mode (γ < 1) is assumed to be triggered in the second row of bricks in the outermost fibre (x = h _B , y = 0) as soon as the unconfined masonry strength f _u is reached as represented graphically in Fig. 13a2, b2.

4.2.2 Walls dominated by flexure

The peak shear resistance in flexure controlled walls is assumed to directly represent the point of ultimate failure (Fig. 14c), since tests, e.g. Petry and Beyer (2015a), show that such walls usually do not exhibit a pronounced post-peak behaviour.

Fig. 14

a Wall dominated by flexure at peak shear resistance with graphical representation of crushed wall toe and flexural cracks in bed joints, b1.1 elastic stress distribution at the onset of crushing in the second brick row, b1.2 assumed stress distribution for partly crushed zone in compressed second brick row, b1.3 corresponding assumed stress distribution for fully crushed compressed zone, b2 criterion for compression failure at wall toe, c qualitative shear force–horizontal displacement curve indicating the point of peak shear resistance (V _P ) and shear force at the onset of failure (V _CP )

Due to the confinement effect of the foundation, the first and second row of bricks show different compressive strengths as already discussed above. This, however, leads to the possibility of various crushing mechanisms at the wall toe depending on geometrical and loading conditions which are discussed in the following (see Fig. 14b1.1–1.3). The estimation of the ultimate drift for walls showing a flexure dominated behaviour as presented in Sect. 5.2 will depend upon the assumed respective mechanism.

4.2.2.1 Crushing of second row of bricks

Experimental evidence shows that in flexure dominated walls splitting cracks often start to form in the second row of bricks. These cracks, however, do not instantly lead to failure but the shear force can still be increased (Petry and Beyer 2015a). The shear force at the onset of this crushing can be determined considering an elastic normal stress distribution in the second bed joint (x = h _B ), reaching the masonry compressive strength in the outermost fibre as shown in Fig. 14b1.1.

$$V\left( {\sigma_{xx} \left( {x = h_{B} ,y = 0} \right) = f_{u} } \right) = \frac{NL}{{2\left( {H_{0} - h_{B} } \right)}}\left( {1 - \frac{4}{3}\frac{{\sigma_{0} }}{{f_{u} }}} \right)$$

(56)

The tangent stiffness of the load–displacement curve at the point where crushing in the second row of bricks commences is usually already rather low, see Fig. 14c, which gives rise to the concept of considering the area where this preliminary crushing occurs as zone with a certain plastic deformation capacity [same concept as in Petry and Beyer (2015b)]. As the shear force further increases, the length L _p of a plastic part of the normal stress distribution increases as well (see Fig. 14b1.2). It is assumed that failure is reached when the length L _p comprises the whole compressed length L _c and a fully plastic stress block has formed (Fig. 14b1.3). The corresponding shear force is:

$$V\left( {L_{c} \left( {x = h_{B} } \right) = L_{p} \left( {x = h_{B} } \right)} \right) = \frac{NL}{{2\left( {H_{0} - h_{B} } \right)}}\left( {1 - \frac{{\sigma_{0} }}{{f_{u} }}} \right)$$

(57)

4.2.2.2 Compression failure at the wall toe

For walls with a rather high h _B /H ratio and/or a low level of axial loading (σ ₀ ), the compressive stresses at the wall toe (x = 0, y = 0) can exceed the compression strength of the brick f _B,c before the plastic zone in the second brick row has built up (Fig. 14b2). This is assumed to instantly cause failure of the wall. To consider this failure mode, Eq. (53), as presented in Sect. 4.1.3, is employed and is repeated here for convenience.

$$V\left( {\sigma_{xx} \left( {x = 0, y = 0} \right) = f_{B,c} } \right) = \frac{NL}{{2H_{0} }}\left( {1 - \frac{4}{3}\frac{{\sigma_{0} }}{{f_{B,c} }}} \right)$$

(58)

4.2.2.3 Determination of crushing mechanism

All aforementioned conditions to determine the state of the normal stress distributions in the crushed zone in the second row of bricks at the onset of failure are summarised in Eq. (59).

$${\text{State}} \to \left\{ {\begin{array}{*{20}l} {{\text{elastic}}} \hfill & {{\text{if }}V\left( {\sigma _{{xx}} \left( {0,0} \right) = f_{{B,c}} } \right)<V\left( {\sigma _{{xx}} \left( {h_{B} ,0} \right) = f_{u} } \right)} \hfill \\ {{\text{partly plastic}}} \hfill & {{\text{if }}V\left( {\sigma _{{xx}} \left( {h_{B} ,0} \right) = f_{u} } \right)<V\left( {\sigma _{{xx}} \left( {0,0} \right) = f_{{B,c}} } \right)<V\left( {L_{c} \left( {h_{B} } \right) = L_{p} \left( {h_{B} } \right)} \right)} \hfill \\ {{\text{fully plastic}}} \hfill & {{\text{if }}V\left( {\sigma _{{xx}} \left( {0,0} \right) = f_{{B,c}} } \right)>V\left( {L_{c} \left( {h_{B} } \right) = L_{p} \left( {h_{B} } \right)} \right)} \hfill \\ \end{array} } \right.$$

(59)

This state determines the procedure adopted for determining the ultimate drift capacity of the wall, which will be introduced in Sect. 5.2. The shear force at the onset of flexural failure, V _CP , can be estimated according to Eq. (60).

$$V_{CP} = \hbox{min} \left[ {V\left( {\sigma_{xx} \left( {0,0} \right) = f_{B,c} } \right);V\left( {L_{c} \left( {h_{B} } \right) = L_{p} \left( {h_{B} } \right)} \right)} \right]$$

(60)

Observe that V _CP —the shear force at the onset of flexural failure—will be close to the peak shear resistance (V _P ), which represents the shear force at the ultimate drift of the wall. The difference is small since the tangent stiffness at this point is already low for flexure dominated walls (see Fig. 14c). This is discussed in more detail in Sect. 5.2.

5 The ultimate drift capacity

The force–displacement relationship of many walls that were tested in a displacement-controlled manner and fail in a shear or a hybrid mode feature a marked post-peak branch. This is less common for walls failing in flexure of which the force–displacement relationship is typically characterised by a curve with a tangent stiffness near zero towards the point of failure. However, both types of walls develop a extended crushed zone at the wall toe upon reaching ultimate failure. This leads to the concept of determining the ultimate drift capacity by means of a plastic zone model, with very large curvatures in a confined zone at the wall toe. Yet, the approach of calculating these curvatures differs between shear and flexure dominated walls.

5.1 Walls dominated by shear

The post-peak behaviour of walls failing in a shear or hybrid mode is characterised by the ability of the wall to sustain a decreasing amount of horizontal force with increasing displacement demand until at a certain point a sudden drop in force and hence ultimate failure occurs. To describe this behaviour, first a model for the residual strength V _R at ultimate failure is developed (Fig. 15). Second, a plastic hinge approach is introduced to determine the displacement at ultimate failure. Finally, the load–displacement behaviour in the post-peak range is described in between the peak strength (V _P ) and the residual strength (V _R ) by means of an interpolation function.

Fig. 15

System at vertical failure with fully degraded diagonal crack; a system for short walls, b system for long walls

5.1.1 Concept of residual strength

It is assumed that the residual strength is reached when the CDC has degraded to a point where it cannot transfer any shear or axial force (Fig. 15).

$$V_{3} = N_{3} = 0$$

(61)

Thus, the internal forces have to be transmitted by the two corners as shown in Fig. 15. It is further assumed that a plastic load distribution can take place for both corners to reach their full capacity. The maximum load carrying capacity per corner can be determined using Eq. (51) which describes the tensile failure of a brick due to shear stresses in the bed joints (Mann and Müller 1982) and is repeated here with a slightly different notation for convenience:

$$V_{i} = \frac{{f_{B,t} l_{cor,i} T}}{2.3}\sqrt {1 + \frac{{N_{i} }}{{f_{B,t} l_{cor,i} T}}} \quad {\text{for }}i \in \{1,2\}$$

(62)

To satisfy horizontal and vertical equilibrium, the following equations apply:

$$V_{R} = V_{1} + V_{2}$$

(63)

$$N = N_{1} + N_{2}$$

(64)

The moment at the centre of the top section is (Fig. 15):

$$M = \left( {V_{1} + V_{2} } \right)\left( {H_{0} - H} \right)$$

(65)

Moment equilibrium around the centre of the top section leads to:

$$M = N_{1} \frac{1}{2}\left( {L - l_{cor,2} } \right) + V_{1} h_{B} + V_{2} \left( {H - h_{B} } \right) - N_{2} \frac{1}{2}\left( {L - l_{cor,1} } \right)$$

(66)

The five unknowns (N ₁ , N ₂ , V ₁ , V ₂ , V _R ) can be computed by solving the system of Eqs. (62)–(66) (note that Eq. (62) yields one equation for the bottom and one for the top corner). If the residual strength V _R is larger than the peak strength V _p , it is assumed that there is no post-peak branch and that failure occurs at a load level corresponding to peak strength.

5.1.2 Determination of ultimate displacements

To obtain an estimate of the ultimate displacement capacity of an URM wall, a plastic hinge approach is adopted. In tests it has been observed that at ultimate failure a more or less well defined zone at the wall toe always crushes as shown graphically in Fig. 16a.

Fig. 16

a Brick crushing in shear dominated wall at ultimate failure, b the considered equivalent system to determine the ultimate flexural displacements including assumed curvature profile, c shear force–horizontal displacement curve, indicating point of ultimate failure

In the following, it is assumed that this crushed corner is responsible for the majority of displacements at ultimate failure. Hence, an equivalent system is introduced, which consists of a deformable zone at the wall toe defined by its crushed height (h _cr ) and length (l _cr ). It is assumed that the curvature distribution is linear over h _cr (Fig. 16b). At failure, the base curvature (χ _cr ) is dependent on the maximum compressive strain (ε _u ) of masonry as well as a strain (ε ₂ ) taking into account the influence of the axial load. The curvature can be given as:

$$\chi_{cr} = \frac{{\varepsilon_{u} - \varepsilon_{2} }}{{l_{cr} }}$$

(67)

Furthermore, it is assumed that this curvature tends to zero for x = h _cr (Fig. 16b). Curvatures above the crushed zone are assumed to be small compared to the one at the wall toe and hence neglected. Moreover, shear displacements are assumed to be small compared to the flexural displacement components at ultimate failure and omitted as well.

For masonry with vertically perforated clay units, which is considered here, the ultimate strain capacity is estimated to correspond to the ratio of the compressive strength of a brick and the elastic modulus of the material masonry, however, limited to a maximum strain of 7 ‰, as described in Eq. (68).

$$\varepsilon_{u} \cong \hbox{min} \left[ {\frac{{f_{B,c} }}{E};0.007} \right]$$

(68)

The strain ε ₂ at y = l _cr , as shown in Fig. 16b, is determined from vertical equilibrium and linear-elastic material behaviour.

$$\varepsilon_{2} = \frac{{2\sigma_{0} L}}{{El_{cr} }} - \varepsilon_{u}$$

(69)

Based on test observations, the length of the crushed zone is chosen to be the length of a brick. Hence:

$$l_{cr} = l_{B}$$

(70)

The height of this crushed zone is assumed to be dependent on the shear span, i.e., the higher the shear span ratio, the higher the crushed zone:

$$h_{cr} \cong h_{B} \left( {\frac{1}{2} + \frac{{H_{0} }}{H}} \right)$$

(71)

Based on the abovementioned assumptions, the rotation at the wall top, which is approximately equivalent to the ultimate horizontal drift (since the shear component and elastic flexural deformations are neglected), can be given as:

$$\theta_{ult} \cong \delta_{ult} = \frac{1}{2}(\varepsilon_{u} - \varepsilon_{2} )\frac{{h_{cr} }}{{l_{cr} }}\left( {1 - \frac{{h_{cr} }}{3H}} \right)$$

(72)

The above-derived model indicates that the larger the axial stress, the smaller is the ultimate drift. This is in agreement with observations form experimental tests (Ganz and Thürlimann 1984; Bosiljkov et al. 2006; Petry and Beyer 2015a). It also shows that the ultimate drift increases with increasing shear span, which has also been confirmed by experimental tests (Petry and Beyer 2014). The mechanical model further indicates that the brick aspect ratio influences the ultimate drift. This is a point that could not yet be confirmed experimentally since it is difficult to vary the aspect ratio of bricks in tests systematically while keeping all other parameters the same.

5.1.3 Describing the post-peak branch of the load–displacement response

To connect the points of peak shear resistance (V _P , δ _P ) and ultimate failure (V _R , δ _ult ), an interpolation function (Fig. 17) is suggested.

$$\delta \left( V \right) = \delta_{P} + \left( {V_{P}^{exp} - V^{exp} } \right)\frac{{\delta_{ult} - \delta_{P} }}{{V_{P}^{exp} - V_{R}^{exp} }}$$

(73)

Fig. 17

Graphical representation of Eq. (73) with the exponent varying

The shape of the post-peak branch can be alternated by varying the exponent (exp) in Eq. (73). Based on test results, it is proposed to use exp = 6.

5.2 Walls dominated by flexure

Unlike shear dominated walls, flexure controlled walls usually do not develop significant, the load–displacement behaviour influencing, diagonal cracks. They exhibit, however,—as shear walls do—a crushed zone at the wall toe upon reaching ultimate failure. In the following, the influence of the crushing (see Sect. 4.2.2) on the curvature profile is discussed. Figure 18 shows the assumed curvature profiles along the wall height for the three different considered cases. It is, once again, assumed that the curvatures above the crushed zones are negligible and that shear displacements can be disregarded as well.

Fig. 18

a Brick crushing at wall toe and flexural cracks in bed joints in flexure dominated wall at ultimate failure, b assumed curvature profile of equivalent system if second row of bricks remains elastic, c curvature profile if second row of bricks is partly plastic, d curvature profile if second row of bricks is fully plastic stress block

Petry and Beyer (2015b) already proposed a criterion to assess the ultimate drift capacity of flexural walls based on a consideration of a plastic deformability at the wall toe. However, while Petry and Beyer (2015b) limit the plastic potential that can be exploited, the approach presented herein permits a full plastification of the normal stress distribution in the 2nd bed joint (see Sects. 4.2.2 and 5.2.3).

5.2.1 Elastic normal stress distribution in the second bed joint

If Eq. (58) (Sect. 4.2.2) < Eq. (56): The first case to be considered occurs if the brick compressive strength at the wall toe (x = 0, y = 0) is reached before the masonry compressive strength in the second bed joint is attained (x = h _B , y = 0). Thus, the second row of bricks at the point of failure is still fully elastic. This is reflected in a linear curvature profile over h _cr (Fig. 18b). The resulting ultimate drift is therefore [the crushed height h _cr can be estimated corresponding to Eq. (71)]:

$$\delta_{ult} = \chi_{1} \frac{{h_{cr} }}{2}\left( {1 - \frac{{h_{cr} }}{3H}} \right)$$

(74)

With the curvature at the wall base being [the maximum strain ε _u can be determined according to Eq. (68) and the shear force at crushing V _CP corresponding to Eq. (60)]:

$$\chi_{1} = \frac{{\varepsilon_{u} }}{{L_{c} \left( {x = 0, V = V_{CP} } \right)}}$$

(75)

5.2.2 Partly plastic normal stress distribution in the second bed joint

If Eq. (56) (Sect. 4.2.2) < Eq. (58) < Eq. (57): At the attainment of the compressive strength of a brick at the wall base (x = 0, y = 0), the masonry compressive strength in the outermost fibre in the second bed joint (x = 0, y = h _B ) has already been exceeded, but the normal stress distribution in the second bed joint does not yet correspond to a plastic stress block. Hence, the second row of bricks is only partly plastic, which results in an assumed curvature profile as shown in Fig. 18c. The resulting ultimate drift can be estimated as:

$$\delta_{ult} = \chi_{1} \frac{{h_{B} }}{2}\left( {1 - \frac{{h_{cr} }}{H} + \frac{{2h_{B} }}{3H}} \right) + \chi_{2} \frac{{h_{cr} }}{2}\left( {1 - \frac{{h_{cr} }}{H} + \frac{2}{3H}\left( {\frac{{h_{cr}^{2} - h_{B}^{2} }}{{h_{cr} - h_{B} }}} \right)} \right)$$

(76)

In this equation, the curvature at the wall base (χ ₁) is calculated according to Eq. (75) and the one at the second bed joint (χ ₂) as:

$$\chi_{2} = \hbox{min} \left[ {\frac{{f_{u} }}{{E\left( {L_{c} \left( {x = h_{B} ,V = V_{CP} } \right) - L_{p} \left( {x = h_{B} ,V = V_{CP} } \right)} \right)}};\frac{{\varepsilon_{cr} }}{{L_{c} \left( {x = h_{B} ,V = V_{CP} } \right)}}} \right]$$

(77)

The length along which a plastic stress distribution has already built up (L _p ) can be determined, based on vertical and moment equilibrium at the cross section (see also Fig. 14b1.2), as:

$$L_{p} \left( {x = h_{B} , V = V_{CP} } \right) = \frac{{N - \sqrt { - 3N^{2} + 3f_{u} LTN - 6f_{u} V_{CP} \left( {H_{0} - h_{B} } \right)T} }}{{f_{u} T}}$$

(78)

The complete compressed length can be determined as:

$$L_{c} \left( {x = h_{B} ,V = V_{CP} } \right) = \frac{2N}{{f_{u} T}} - L_{p} \left( {x = h_{B} ,V = V_{CP} } \right)$$

(79)

5.2.3 Fully plastic normal stress distribution in the second bed joint

If Eq. (58) (Sect. 4.2.2) > Eq. (57): If a full plastic stress block in the second bed joint has emerged before the compressive strength of a brick at the wall base is reached, the assumed curvature profile and the strain distribution for its determination are depicted in Fig. 18d. The ultimate drift can be obtained according to:

$$\delta_{ult} = \chi_{2} \frac{{h_{B} }}{2}\left( {1 - \frac{{h_{cr} }}{H} + \frac{{2h_{B} }}{3H}} \right) + \chi_{2} \frac{{h_{cr} }}{2}\left( {1 - \frac{{h_{cr} }}{H} + \frac{2}{3H}\left( {\frac{{h_{cr}^{2} - h_{B}^{2} }}{{h_{cr} - h_{B} }}} \right)} \right)$$

(80)

The curvature in the second bed joint can be estimated as:

$$\chi_{2} = \frac{{\varepsilon_{cr} }}{{L_{c} \left( {x = h_{B} , V = V_{P} } \right)}}$$

(81)

The length of the stress block at x = h _B is:

$$L_{P} \left( {x = h_{B} , V = V_{P} } \right) = L_{c} \left( {x = h_{B} , V = V_{P} } \right) = \frac{N}{{f_{u} T}}$$

(82)

5.2.4 Combining plastic zone and pre-peak approach

Section 5.2 presents an approach to determine the ultimate drift of flexure dominated walls based on a plastic hinge approach. The force–displacement curve, which is computed according to Sect. 3, is simply cut at the ultimate drift as predicted by the plastic hinge approach. The corresponding shear force is considered to be the peak shear capacity of the wall. Hence:

$$V_{P} = V\left( {\delta = \delta_{ult} } \right)$$

(83)

The peak shear force V _P will be very close to but slightly higher than V _CP [as introduced in Sect. 4.2.2; Eq. (60)], which is used to determine the compressed lengths (L _c , L _p ) and curvatures (χ₁, χ₂) in the previous sections. The difference is very small since, as already highlighted earlier, the tangent stiffness close to the point of ultimate failure is generally close to zero for flexure dominated walls.

The force–displacement response (Sect. 3) is determined assuming elastic material behaviour and does not take into account any material non-linearity or plasticity. The non-linearity of the response itself originates from the change in the cross-section properties A(x) and I(x). The approach of the plastic zone is used merely to estimate the point of ultimate drift.

6 Validation

6.1 Comparison to tests

The presented model is compared to 32 full-scale quasi-static cyclic URM wall tests reported in literature (see Table 2 in “Appendix 1”) and design provisions given in EC8–part 1 and 3 (CEN 2004, 2005a). The wall tests were selected based on the following criteria: (1) wall made of vertically perforated clay units and normal strength mortar with joints of normal thickness, (2) wall height ≥ 1.5 m, (3) wall length ≥ 1.0 m, (4) masonry unit aspect ratio (h _B /l _B ) from 0.5 to 1, (5) constant shear span during test, (6) constant axial load during test, (7) application of a cyclic testing protocol and (8) availability of the load–displacement history. Table 3 in “Appendix 1” lists the material parameters of the walls.

The model is validated with regard to: (1) the effective stiffness—k _ef , which is defined as the wall stiffness at 70% of the peak shear resistance (e.g. Penna et al. (2014); Frumento et al. (2009)), (2) the peak shear resistance of the wall—V _P and (3) the ultimate horizontal drift—δ _ult , defined as the drift at a 20% drop in the wall’s shear force capacity in the post-peak domain.

According to EC8–part 1 (CEN 2004), in the absence of accurate evaluation of the stiffness properties, the effective stiffness can be estimated as 50% of the gross sectional elastic stiffness (CEN 2004):

$$k_{ef,EC8} = \left( {\frac{{H_{0} H^{2} - \frac{{H^{3} }}{3}}}{EI} + \kappa \frac{2H}{GA}} \right)^{ - 1}$$

(84)

The shear force carrying capacity of shear dominated walls is estimated in EC8–part 3 (CEN 2005a) according to a modified Mohr–Coulomb criterion using global values for coefficient of friction and cohesion [Eq. (48)] while walls failing in flexure are assessed by means of a compressive stress block approach [Eq. (54)].

EC8–part 3 (CEN 2005a) gives an estimate [Eq. (85)] for the drift at the limit state of near collapse (δ _ult,EC ), which corresponds to the drift at 20% drop in strength.

$$\delta_{ult,EC8} = \left\{ {\begin{array}{ll} {\frac{4}{3}0.4 [\% ] \qquad {\text{for walls controlled by shear }}} \\ {\frac{4}{3}0.8 \frac{{H_{0} }}{L}[\% ] \quad {\text{for walls controlled by flexure}}} \\ \end{array} } \right.$$

(85)

According to EC8–part 3, the distinction between shear and flexure controlled walls is made by taking the minimum of the equations governing the wall’s shear capacity (Eqs. (48), (54) respectively).

6.1.1 Peak shear resistance

Figure 19 compares the predictions for the peak shear resistance by the CDC model and those by EC8 to the experimental results. Both approaches yield good results with the CDC model showing a slightly better agreement.

Fig. 19

a Predicted (CDC model and EC8) versus measured shear force capacity of respective wall test, b boxplot comparing performance in predicting the shear force capacity of the wall tests of CDC model and EC8

6.1.2 Effective stiffness

The performance of the CDC model and EC8 in predicting the effective stiffness is compared in Fig. 20. The CDC model is able to capture the test results in average quite well whereas the approach suggested in EC8 tends to underestimate the effective stiffness of the walls.

Fig. 20

a Predicted (CDC model and EC8) versus measured effective stiffness of respective wall test, b boxplot comparing performance in predicting the effective stiffness of the wall tests of CDC model and EC8

6.1.3 Ultimate drift capacity

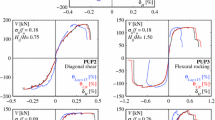
Figure 21 shows the performance of the CDC model as well as of EC8 in predicting the ultimate drift capacity of the wall tests listed in Table 2 (“Appendix 1”). The CDC model shows a good fit in predicting the ultimate drift capacities of all wall tests; the mean of predicted to observed drift capacities is close to unity and the standard deviation small. The predictions by EC8, on the other hand, lead to a large scatter and tend to be unconservative. Figure 21b also differentiates between shear and flexure dominated walls. While the CDC model shows a good fit in both cases, EC8 is especially unconservative for flexure dominated walls.

Fig. 21

a Predicted versus measured ultimate drift capacity, b boxplot comparing performance in predicting the ultimate drift capacity of the wall tests of CDC model, EC8 and SIA D0237

6.1.4 Load–displacement curves

Figures 22 and 23 compare the results of the CDC model for a shear controlled and a flexure dominated wall tested by Petry and Beyer (2015a) with regard to the shear force-horizontal displacement curves (a), the shear force-axial displacement curves (b) and the contribution of flexural and shear displacements to the total horizontal displacement (c). The bilinear approximation of the force–displacement response as predicted by EC8 [(CEN 2004, 2005a)] is included as well (only for the shear force-horizontal displacement curves). The comparison with remaining walls of the testing campaign is omitted here for brevity but is shown in “Appendix 2”.

Fig. 22

Comparison of CDC model and experimental results for a shear controlled wall: a Shear force–horizontal displacement curves for specimen PUP2, b shear force–vertical displacement curves, c contribution of flexural and shear displacements

Fig. 23

Comparison of CDC model and experimental results for a flexure dominated wall: a shear force–horizontal displacement curves for specimen PUP3, b shear force–vertical displacement curves, c contribution of flexural and shear displacements

6.2 Parametric studies

In this section, the CDC model is used to investigate the sensitivity of peak shear resistance, effective stiffness and ultimate drift capacity to the axial load ratio, the shear span and the wall size. The obtained results are compared to those from the provisions in EC8–parts 1 and 3. Table 1 lists geometrical values and material parameters that are kept constant throughout the parametric analysis.

Table 1 Values used for all parametric studies

6.2.1 Peak shear resistance

Figure 24 investigates the sensitivity of the peak shear resistance to the axial load ratio σ ₀ /f _u to the normalised shear span H ₀ /H and the size of the wall. The aspect ratio H/L is equal to 1.0 for all walls that are represented in Fig. 24. As expected, the shear capacity increases with increasing axial force (Fig. 24c). This applies both to walls with a shear span of H ₀ /H = 0.5 (shear controlled) and walls with H ₀ /H = 1.5 (flexure dominated). A larger shear span leads to significantly smaller peak shear force capacities. This is in line with the peak strength equations in EC8, which show a very similar trend and lead to just slightly lower values.

Fig. 24

CDC model: a, b influence of the wall size on peak shear resistance (aspect ratio and shear span are kept constant), c influence of the axial load ratio on the peak shear resistance (shear span and wall size are kept constant). Full markers indicate shear dominated, unfilled markers designate flexure controlled behaviour

6.2.2 Effective stiffness

Good approximations to predict the effective wall stiffness are currently missing. EC8–part 1 (CEN 2004) recommends to use 50% of the gross sectional stiffness if better estimates are not available. Figure 25 investigates by means of the CDC model the sensitivity of the ratio of effective to gross sectional stiffness to the axial load ratio. The results show that the effective stiffness tends to remain constant with increasing wall size (Fig. 25a, b) but increases slightly with increasing axial load (Fig. 25c). This applies both to walls with H ₀ /H = 0.5 and 1.5 and therefore to flexure as well as shear dominated walls. While a constant ratio of effective to gross sectional stiffness could be a reasonable estimate, the results of the CDC model and the comparison against test results (Sect. 6.1.2) suggest that this ratio should be higher than 50 %.

Fig. 25

CDC model: a, b influence of the wall size on the effective-to-gross-sectional-stiffness ratio (aspect ratio and shear span are kept constant), c influence of axial load ratio on the effective-to-gross-sectional-stiffness ratio (shear span and wall size are kept constant). Full markers indicate shear dominated, unfilled markers designate flexure controlled behaviour

6.2.3 Ultimate drift capacity

Parametric studies investigating the ultimate drift capacity as predicted by the CDC model are presented in Fig. 26. In this figure, the shear span, axial load ratios as well as the wall size are varied while keeping the wall aspect ratio the same.

Fig. 26

CDC model: a, b influence of the wall size on the ultimate drift capacity (aspect ratio and shear span are kept constant), c influence of the axial load ratio on the ultimate drift capacity (shear span and wall size are kept constant). Full markers indicate shear dominated, unfilled markers designate flexure controlled behaviour

Figure 26a depicts the ultimate drift capacity for walls with a shear span ratio of 0.5 of which the size is increased whilst keeping the ratio of wall height to length constant. It shows that the ultimate drift capacity decreases with increasing wall size, thus, agreeing with the size effect stipulated in Petry and Beyer (2014). The figure further shows that an increase in axial load leads to a reduced ultimate drift capacity.

In Fig. 26b, the shear span ratio is set to 1.5. With increasing wall size, the ultimate drift decreases agreeing with the idea of a pronounced size effect for flexural walls (characterised by higher shear span ratios and lower levels of axial load). For a higher level of axial load, the size effect is not as strong but still clearly discernible.

The influence of the axial load ratio on the ultimate drift is presented in Fig. 26c. For small shear span ratios (H ₀ /H = 0.5—usually corresponding to shear critical walls), the drift capacity decreases slightly with increasing axial load while for a high shear span ratio of 1.5 that is more characteristic of flexure controlled walls, the drift capacity reduces first rapidly and the more slowly with increasing axial load ratio.

Figure 26 also shows the drift capacities according to the empirical models in EC8. It shows that the simple equations according to EC8 do not capture any of the aforementioned trends (size effect, influence of axial load ratio) and that the provisions are generally unconservative for the investigated wall parameters when compared to results obtained with the CDC model.

Parametric studies investigating the influence of a changing wall aspect ratio on the ultimate drift capacity are presented in Fig. 27. The drifts increase with increasing H/L ratio. The plots further confirm the trend to higher drift capacities for lower axial load ratios.

Fig. 27

Development of ultimate drift with changing wall aspect ratio a shear span ratio of 0.5, b shear span ratio of 1, c shear span ratio of 1.5—full markers indicate shear dominated, unfilled markers designate flexure controlled behaviour

As for the provisions according to EC8, they are generally unconservative for the parameters used in this study. They seem to fit best for small walls tested with a shear span ratio of one and low axial loads, i.e., for the wall configurations that have been tested very frequently and were therefore probably overrepresented in the data set used for determining empirical drift capacity models (Petry and Beyer 2014). Another point that can be observed from Fig. 27a, b is that EC8 often assesses the type of wall behaviour (shear, flexure dominated) differently than the CDC model, i.e., EC8 grades walls to be of the flexural dominated type while the CDC model still assigns them to the shear/hybrid kind.

7 Conclusion

This article presents the Critical Diagonal Crack (CDC) model, which is a novel analytical model for predicting the monotonic load–displacement response of in-plane loaded unreinforced brick masonry walls. Based on the Timoshenko beam model, it simulates the effect of horizontal flexural cracking as well as diagonal shear cracking on the stiffness of the wall by means of mechanical considerations that update the cross sectional parameters to account for the extent of shear and flexural cracking. The peak shear resistance of URM walls is estimated using local strength criteria, which compare local stresses directly to local parameters of material resistance. The ultimate drift capacity is estimated by means of a plastic zone model, which reflects the large curvatures in the crushed area at the wall toe at failure.

A comparison with the envelope response of 32 cyclic full-scale wall tests shows that the CDC model constantly performs better than the current provisions in EC8 in predicting the effective stiffness and the ultimate drift capacity of the wall; the peak shear resistance is predicted with similar accuracy as EC8. Parametric studies show that the model agrees with trends observed in tests with regard to the influence of wall size, shear span and axial load ratio on stiffness, strength and drift capacity while the provisions according to EC8 do not consider many important relations.

Herein, the CDC model was solely validated against one masonry typology; modern vertically perforated clay blocks and normal strength mortar with bed joints of about 1 cm thickness. Future research should be devoted to validating the model for other masonry typologies and assessing if key parts of the model also hold in these cases (e.g. the model for ultimate drift that is based on a certain height of a crushed zone, the influence of the Critical Diagonal Crack on the force–displacement response).

The CDC model is a further step towards establishing a more complete mechanical basis for estimating the force–displacement response of unreinforced masonry walls by means of analytical models. Future work will be directed to considering the effect of cyclic loading explicitly. Furthermore, the model should be transformed to simpler closed-form equations for the effective stiffness, strength and deformation capacity that can be easily considered in the assessment of structures.

Appendices

Appendix 1: Wall tests used for the validation

The walls and their parameters used in the validation of the model are presented in Tables 2 and 3. The shear modulus G is always taken as ¼ of the elastic modulus E, the tensile strength of a brick (f _B,t ) was assumed to be 1.27 MPa for all walls corresponding to the testing campaign by Petry and Beyer (2015a) as values in other reference documents were not provided.

Table 2 Wall parameters used in the comparison of model/tests

Table 3 Material parameters taken from corresponding reference document except where indicated explicitly

Appendix 2: Comparison of CDC model to wall tests

See Figs. 28, 29 and 30.

Fig. 28

a Shear force—horizontal displacement curves for specimen PUP1, b shear force—vertical displacement curves, c contribution of flexural and shear displacements

Fig. 29

a Shear force—horizontal displacement curves for specimen PUP4, b shear force—vertical displacement curves, c contribution of flexural and shear displacements

Fig. 30

a Shear force—horizontal displacement curves for specimen PUP5, b shear force—vertical displacement curves, c contribution of flexural and shear displacements