Displacement versus pseudo-static evaluation of the seismic performance of sliding retaining walls

Abstract

Pseudo-static seismic analysis of retaining walls requires the selection of an equivalent seismic coefficient synthetically representing the effects of the transient seismic actions on the soil-wall system. In this paper, a rational criterion for the selection of the equivalent seismic coefficient is proposed with reference to sliding retaining walls. In the proposed approach earthquake-induced permanent displacements are assumed as a suitable parameter to assess the seismic performance and an alternative definition of the wall safety factor is introduced comparing expected and limit values of permanent displacements. Using a simplified displacement prediction model it is shown that, for a given design earthquake, reliable values of the equivalent seismic coefficient should depend on all the factors affecting the stability condition of the soil-wall system and on a threshold value of permanent displacement related to a given ultimate or serviceability limit state. To achieve a match between the results of the pseudo-static and of the displacement-based analysis, the proposed procedure detects the value of the equivalent seismic coefficient for which the two approaches provide the same factor of safety. Thus, without necessarily carrying out a displacement analysis, a measure of the safety condition of a soil-wall system consistent with the actual seismic performance may be achieved through an equivalent pseudo-static analysis.

1 Introduction

Current procedures for seismic design of retaining walls rely on the pseudo-static approach. In these procedures the Coulomb (1776) earth pressure theory is generally adopted to estimate the active thrust behind the wall. Generally, the earthquake effects on the active thrust are introduced through the well-known Mononobe–Okabe solution (Okabe 1926; Mononobe and Matsuo 1929) which provides the value of the seismic active earth-pressure coefficient for a dry cohesionless backfill; however, other limit equilibrium or limit analysis solutions can be used for estimating the seismic active thrust accounting for particular boundary and/or surcharge conditions and for both cohesive and frictional soil shear resistance.

In the pseudo-static approach the actual effects of the transient seismic action, characterised by abrupt changes in modulus and sign, are represented by a pair of static forces computed multiplying the weight of the wall and of the retained soil by the horizontal $k_\mathrm{h,eq}$ and vertical $k_\mathrm{v,eq}$ components of an equivalent seismic coefficient $k_\mathrm{eq}$. The seismic stability conditions of the soil-wall system are then evaluated using a force-balance approach and are quantified through pseudo-static safety factors $F_\mathrm{ps}$, against sliding, tilting and bearing capacity; correspondingly, $F_\mathrm{ps}$ is defined as the ratio between resisting and driving forces or moments. Despite the shortcomings of this conventional approach, in current practice the pseudo-static analysis is usually preferred to more sophisticated numerical finite element (FE) or finite difference (FD) methods.

However, evidence of damages caused by recent large earthquakes (e.g. Tateyama et al. 1995; Fang et al. 2003; Huang and Chen 2004; Trandafir et al. 2009) showed that performance-based design must be considered an emerging methodology able to overcome most of the limitations of the conventional pseudo-static approach (e.g. Zeng and Steedman 2000; Taylor et al. 2007).

Unlike the pseudo-static method of analysis, performance-based design procedures provide information on the response of the soil-wall system when the force-balance is exceeded and permanent deformations occur due to unbalanced forces or moments. The magnitude of the earthquake-induced permanent displacement and/or rotation can then be compared with corresponding limit values which may be suffered by the soil-wall system without reaching an ultimate or a serviceability limit state.

As an alternative to dynamic FE or FD approaches, performance-based analyses may be carried out through simplified procedures that, starting from the early study by Richards and Elms (1979), were derived following the sliding block approach introduced by Newmark (1965). In these procedures permanent displacements or rotations of the wall and, in some cases, permanent displacements of the retained soil wedge, can be assessed through double integration of the equation of motion of the soil-wall system subjected to a given acceleration time-history.

2 Purpose of the study and paper outline

Although pseudo-static and performance-based procedures may be regarded as alternative methods of analysis, the seismic coefficient to be used in a pseudo-static analysis may be related to the earthquake-induced displacements and/or rotations and, then, to the expected level of damage.

This paper presents a procedure to relate limit values of permanent displacement and the horizontal seismic coefficient $k_\mathrm{h,eq}$ to be used in the pseudo-static analysis of sliding retaining walls. The procedure involves solutions concerning: (i) the factors affecting the equation of motion and the critical acceleration coefficient of the soil-wall system; (ii) a rational criterion to link the results of the conventional pseudo-static analysis and of the displacement-based analysis.

Using a simplified model for the prediction of the expected wall displacements and a suitable definition of the seismic safety factor of the soil-wall system, an expression of the equivalent seismic coefficient $k_\mathrm{h,eq}$ is derived allowing, without necessarily carrying out a displacement analysis, a measure of the safety condition consistent with that of a more reliable performance-based analysis.

The procedure is presented accounting only for the horizontal component of the seismic acceleration time-history; this assumption is not relevant since, in most cases, the influence of the vertical component of the ground acceleration on the magnitude of earthquake-induced permanent displacements of sliding system is negligible (e.g. Yan et al. 1996; Ling et al. 1997; Ling and Leshchinsky 1998; Inglès et al. 2006; Sarma and Scorer 2009; Caltabiano et al. 2012).

A critical review of existing solutions for seismic displacement analysis of sliding retaining walls, as well as of original solutions recently proposed by the Authors, is preliminarily presented in Sects. 3 and 4 in order to: (i) clarify the reference framework for the present study; (ii) introduce the theoretical assumptions required for the development of the proposed procedure which is described in Sect. 5 together with the solution developed for the evaluation of the equivalent seismic coefficient $k_\mathrm{h,eq}$.

3 Seismic displacements of sliding retaining walls

Earthquake-induced permanent displacements of retaining walls sliding along the soil-foundation interface can be computed through several procedures.

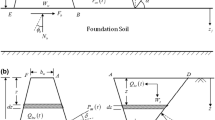
Richards and Elms (1979) applied the sliding block approach, proposed by Newmark (1965), to the evaluation of the earthquake-induced permanent displacements of sliding retaining walls. The reference soil-wall scheme considered by Richards and Elms is shown in Fig. 1a. The Authors assumed that a soil wedge in the retained backfill reaches an active stress state and used the Mononobe–Okabe ($M$–$O$) earth-pressure coefficient $K_\mathrm{ae}$ to evaluate the seismic active earth-thrust $S_\mathrm{ae}$. In the analysis only the dynamic equilibrium condition of the wall is considered; thus, the effect of the active soil wedge, which slides down when the wall moves outward, is ignored in the evaluation of both critical acceleration coefficient and permanent displacements.

Fig. 1

Soil-wall schemes

Biondi and Cascone (2014) recently showed that, using the Richards and Elms ($R$–$E$) procedure, it is not possible to derive closed-form solutions for the horizontal critical acceleration coefficient $k_\mathrm{h,c}$ and derived the equations listed in the “Appendix 1” (together with the relevant notations) for an iterative evaluation of $k_\mathrm{h,c}$. Moreover, since the $R$–$E$ procedure requires an expression of the active earth-pressure coefficient $K_\mathrm{ae}$, in current practice it can be applied to a limited number of cases. As an example, the Mononobe–Okabe ($M$–$O$) solution for computing $K_\mathrm{ae}$ can be used for the soil-wall scheme of Fig. 1a but it cannot be used for the schemes of Fig. 1b–d or in the case of both cohesive and frictional shear resistance. In these cases other limit equilibrium or limit analysis solutions can be used to estimate $K_\mathrm{ae}$ accounting for particular boundary and/or surcharge conditions (e.g Motta 1993, 1994; Caltabiano et al. 2000, 2012; Stamatopoulos and Velgaki 2001; Stamatopoulos et al. 2006; Mylonakis et al. 2007), for both cohesive and frictional shear resistance (e.g. Shukla et al. 2009), for its post-peak reduction along previously formed slip surfaces (e.g. Koseki et al. 1998) and, finally, for the influence of the length of the foundation heel (e.g. Greco 2009; Evangelista and Scotto di Santolo 2010; Kloukinas and Mylonakis 2011).

In the $R$–$E$ procedure permanent displacements of the wall $d_\mathrm{w}$ are evaluated assimilating the actual soil-wall system to an ideal rigid block sliding on a horizontal plane corresponding to the interface between the wall-base and the underlying foundation-soil. In this analogy the actual wall and the block are subjected to the same horizontal acceleration time-history, $a_\mathrm{h}= k_\mathrm{h}\cdot g$, are characterized by the same horizontal component $k_\mathrm{h,c}$ of the critical acceleration coefficient and the soil wedge is not directly accounted for in the analysis. The equation of motion of the block can be derived equating the excess of driving to resisting force to the inertia force arising in the block due to its relative acceleration with respect to the base. Neglecting the vertical component of the ground motion ($a_\mathrm{v}= k_\mathrm{v}\!\cdot \! g = 0$) it is:

$$\begin{aligned} \ddot{d}_\mathrm{o} =g\cdot \left[ {(k_\mathrm{h} -k_{\mathrm{h,c}} )} \right] \end{aligned}$$

(1)

In Eq. (1) $d_\mathrm{o}$ is the current value of the permanent displacement cumulated by the block that, in the $R$–$E$ procedure, is treated as $d_\mathrm{w}$.

Starting from the pioneer study by Richards and Elms (1979) other procedures were proposed, ranging from one-block sliding and/or tilting wall analysis (e.g. Nadim and Whitman 1983; Wu and Prakash 2001; Zeng and Steedman 2000), to two-wedge soil-wall system sliding analysis (e.g. Zarrabi-Kashani 1979; Stamatopoulos and Velgaki 2001; Stamatopoulos et al. 2006), to multi-block sliding analysis incorporating mass transfer between adjacent blocks (e.g. Chlimintzas 2002).

In fact, when the wall accumulates permanent displacements, the active soil wedge slides downward with the inclination of the least soil resistance and the soil-wall system actually consists of two bodies; in this case a two-wedge (2-$W$) approach is suitable for the analysis of the seismic stability condition and for the evaluation of earthquake-induced permanent displacements (Stamatopoulos et al. 2006), even in the case of particular boundary and surcharge conditions (e.g. Caltabiano et al. 2000, 2012).

3.1 Two-wedge approach

Two-wedge (2-$W$) approaches were recently proposed by Stamatopoulos and Velgaki (2001), Stamatopoulos et al. (2006) and by Caltabiano et al. (1999, 2005, 2012) with reference to soil-wall schemes characterized by different boundary and surcharge conditions (Figs. 1, 2).

Fig. 2

Scheme of the soil-wall system considered by Stamatopoulos et al. (2006)

Using a 2-$W$ model with kinematically compatible displacement components subjected only to horizontal seismic acceleration ($k_\mathrm{v} = 0$), Stamatopoulos and Velgaki (2001) showed that during the relative motion: (i) the earth thrust acting on the wall does not coincide with the active earth-thrust $S_\mathrm{ae}$ predicted by the $M$–$O$ formula; (ii) the angle $\upalpha _\mathrm{c}$ of the critical wedge do not coincide with that predicted by Zarrabi-Kashani (1979). The $R$–$E$ and the 2-$W$ approaches provide coincident solutions for both the inter-wedge force (i.e. the earth thrust) and the critical wedge angle when the soil-wall system is at limit equilibrium.

More recently, Stamatopoulos et al. (2006) extended the 2-$W$ solution by Stamatopoulos and Velgaki (2001) to the case of cohesive and frictional backfill and foundation soils. In the reference scheme (Fig. 2) the wall base is inclined of an angle $\upalpha _\mathrm{b}$ to the horizontal, no surcharge acts on the sloping backfill and the vertical component of the ground motion is neglected ($k_\mathrm{v}$ $=$ 0); the solution is proposed in terms of critical acceleration coefficient $k_\mathrm{hc}$, critical wedge angle $\upalpha _\mathrm{c}$ and coefficients of the equations of motion for both the wall and the retained soil wedge. The Authors performed a small and a large displacements analysis in which the effects of the change in the system geometry as displacements develop is neglected or is accounted for, respectively.

Using a 2-$W$ approach, Caltabiano et al. (2012) also proposed closed form solutions for the computation of $k_\mathrm{hc}, \upalpha _\mathrm{c}$ and of the coefficients involved in the equation of motion for several soil-wall systems characterized by different surcharge and boundary conditions. In the reference soil-wall schemes (Fig. 1a, b) a cohesionless soil is considered both in the backfill ($c^{\prime }\!=\! 0$) and in the foundation soils ($c_\mathrm{b}\! =\! 0$), no change in system geometry is assumed (small displacements assumption) and the effect of the vertical component ($k_\mathrm{v}\ne 0$) of the ground motion and of a uniformly distributed distanced surcharge ($q$) are accounted for.

In the following sub-sections, the more relevant aspects of a 2-W small displacements analysis in comparison with the sliding block approach are presented and discussed with reference to the soil-wall schemes described in Figures 1a and 2 (coinciding for $\upalpha _\mathrm{b}$ $=$ 0) together with the notations relevant for the discussion. Then, the influence of the change in system geometry (large displacements analysis) will be discussed in order to derive a simplified displacement predictive model which is required by the proposed procedure for the selection of the equivalent seismic coefficient.

3.1.1 Evaluation of the critical acceleration coefficient

As previously stated, the $R$–$E$ and the 2-$W$ procedures provide the same result at limit equilibrium; then, $k_\mathrm{h,c}$ can be computed using any of these approaches. The $R$–$E$ procedure leads to very simple expressions of $k_\mathrm{h,c}$ which must be solved iteratively and require closed form expressions of the seismic active thrust coefficient $K_\mathrm{ae}$ (e.g. “Appendix 1”); conversely, closed form solutions for $k_\mathrm{h,c}$ may be derived using the 2-$W$ approach, though characterized by some mathematical complexity. The need of closed form solutions for $k_\mathrm{h,c}$ is apparent when the effect (i) of the change in system geometry, (ii) of the cyclic reduction of soil shear strength or (iii) of the vertical component $k_\mathrm{v}$ of the seismic acceleration is included in the displacement analysis.

In all these cases $k_\mathrm{h,c}$ is time dependent and must be computed at each time step of the input accelerogram and the use of closed form solutions may drastically reduce the computational effort in the displacement evaluation.

Examples of 2-$W$ solutions giving the critical acceleration coefficient $k_\mathrm{h,c}$ may be found in the papers by Caltabiano et al. (1999, 2000, 2012), Stamatopoulos and Velgaki (2001), Stamatopoulos et al. (2006) together with, coupled or uncoupled, expressions providing the critical wedge angle $\upalpha _\mathrm{c}$ at the limit equilibrium condition and the corresponding earth pressure coefficient $K_\mathrm{ae}$. Table 1 lists the main features of some of the above mentioned 2-$W$ solutions together with the corresponding boundary and surcharge conditions and the reference soil-wall schemes.

Table 1 Closed-form solutions for $k_\mathrm{h,c}$ and $\upalpha _\mathrm{c}$

Differently from the conventional $R$–$E$ procedure, in a 2-$W$ analysis a potential sliding surface in the retained soil, inclined of an angle $\upalpha$ to the horizontal, is considered and the equations describing the limit equilibrium conditions of the wall and of the retained soil wedge are contemporarily satisfied. In these coupled equations the weight $W_\mathrm{s}$ of the retained soil wedge involved in the potential failure mechanism and the seismic active thrust $S_\mathrm{ae}$, representing the inter-wedge force, depend on $\upalpha$; the solution of the problem is obtained searching for the critical value $\upalpha _\mathrm{c}$ of the wedge angle for which, contemporarily, $S_\mathrm{ae}$ and $k_\mathrm{h,c}$ attain their maximum and minimum value, respectively.

According to Biondi and Cascone (2014) for the soil-wall schemes of Figs. 1a and 2, the equations describing the limit equilibrium conditions of the retained soil wedge and of the wall can be reduced to the following system of two equations:

$$\begin{aligned} \left\{ {\begin{array}{l} K_{\mathrm{ae}{(\upalpha )}} =\frac{\Phi _1 }{\Phi _2 } \\ \frac{k_{\mathrm{h,c}(\upalpha )} }{1-\Omega \cdot k_{\mathrm{h,c}(\upalpha )}}=\frac{\Psi _1 }{\Psi _2 } \\ \end{array}} \right. \end{aligned}$$

(2)

where:

$$\begin{aligned} \left\{ {\begin{array}{l} \Phi _1 =A_1 \cdot \left( {\tan \upalpha } \right) ^{2}+B_1 \cdot \tan \upalpha +\, C_1 \\ \Phi _2 =A_2 \cdot \left( {\tan \upalpha } \right) ^{2}+B_2 \cdot \tan \upalpha +\, C_2 \\ \Psi _1 =A_3 \cdot \left( {\tan \upalpha } \right) ^{2}+B_3 \cdot \tan \upalpha +\, C_3 \\ \Psi _2 =A_4 \cdot \left( {\tan \upalpha } \right) ^{2}+B_4 \cdot \tan \upalpha +\, C_4 \\ \end{array}} \right. \end{aligned}$$

(3)

and $K_{\mathrm{ae}(\upalpha )}$ and $k_{\mathrm{h,c}(\upalpha )}$ are the unknown variables representing the seismic active earth pressure coefficient and the critical acceleration coefficient computed for the potential sliding surface; in Eq. (3), $\Omega = k_\mathrm{v}/k_\mathrm{h}$ is the ratio between the vertical ($k_\mathrm{v}$) and the horizontal components of the seismic coefficient (positive values of $\Omega$ and of $k_\mathrm{v}$ meaning vertical inertia forces directed upward) and, finally, $A_{1}$–$A_{4}$, $B_{1}$–$B_{4}$ and $C_{1}$–$C_{4}$ are numerical constants.

$A_{1}$ and $A_{2},\,B_{1}$ and $B_{2},\,C_{1}$ and $C_{2}$ depend on the angle of shear strength $\upvarphi ^{\prime }$ of the retained soil, on the geometrical parameters ($\upbeta , i, H$—see Figs. 1a, 2) of the retained soil wedge having unit weight $\upgamma$ and initial $H = H_\mathrm{o}$ (Fig. 1a) and current $H = H(t$) (Fig. 2) height of the retained soil, on the inclination $\updelta$ of the inter-wedge force and on the critical value of the seismic coefficient $k_\mathrm{h,c}$. $A_{3}$ and $A_{4},\,B_{3}$ and $B_{4},\,C_{3}$ and $C_{4}$ depend on the mechanical ($\upgamma ,\upvarphi ^{\prime }$) and geometrical ($\upbeta ,\,i,\,H$) parameters of the retained soil, on the mechanical ($c_\mathrm{b},\,\upphi _\mathrm{b}$) and geometrical ($\upalpha _\mathrm{b} , B_\mathrm{b}$) parameters of the wall-foundation soil interface, on the inclination $\updelta$ of the inter-wedge force and, finally, on the normalized wall weight:

$$\begin{aligned} \Gamma _\mathrm{w} =\frac{2\cdot W_\mathrm{w} }{\upgamma \cdot H^{2}} \end{aligned}$$

(4)

being $W_\mathrm{W}$ the wall weight.

Setting:

$$\begin{aligned} \Phi _3&= \Phi _2 \cdot K_{\mathrm{ae}(\upalpha )} -\Phi _1 \nonumber \\ \Psi _3&= \Psi _2 \cdot \frac{k_{\mathrm{h,c}(\upalpha )}}{1-\Omega \cdot k_{\mathrm{h,c}(\upalpha )}}-\Psi _1 \end{aligned}$$

(5)

it can be shown (Biondi and Cascone 2014) that the functions $\Phi _{3}$ and $\Psi _{3}$ describe the limit equilibrium conditions of the soil wedge and of the wall, respectively, and their discriminants allow detecting the critical wedge angle $\upalpha _\mathrm{c}$ for which $K_{\mathrm{ae}(\upalpha )}$ and $k_{\mathrm{h,c}(\upalpha )}$ attain, contemporarily, the maximum $K_\mathrm{ae}= K_{\mathrm{ae}(\upalpha \mathrm{c})}$ and the minimum $k_\mathrm{h,c}$ = $k_{\mathrm{h,c}(\upalpha \mathrm{c})}$ respectively. Concerning $k_\mathrm{h,c}$ it is:

$$\begin{aligned} \tan \frac{k_{\mathrm{h,c}} }{1-\Omega \cdot k_{\mathrm{h,c}} }=\frac{b+\sqrt{b^{2}-a\cdot c}}{a} \end{aligned}$$

(6)

where:

$$\begin{aligned} a=B_4^2 -4\cdot A_4 \cdot C_4 \quad b=2\cdot A_3 \cdot C_4 -2\cdot C_3 \cdot A_4 -B_3 \cdot B_4 \quad c=B_3^2 +4\cdot A_3 \cdot C_3\qquad \end{aligned}$$

(7)

The expressions of the constants $A_{1}-A_{4}, B_{1}-B_{4}$ and $C_{1}-C_{4}$ are given in the “Appendix 2” assuming for simplicity $\upalpha _\mathrm{b}$ $=$ 0 and $c_\mathrm{b}$ $=$ 0.

Using Eqs. (6–7) Biondi and Cascone (2014) performed a parametric analysis in order to check the influence of all the mechanical and geometrical parameters involved in the estimation of $k_\mathrm{h,c}$ and found that, among all the investigated parameters, the inclination $\updelta$ of the active thrust, the normalized wall weight $\Gamma _\mathrm{w}$ and the friction angle $\upphi _\mathrm{b}$ at the soil-foundation interface are those which mostly influence $k_\mathrm{h,c}$.

In Figs. 3, 4 and 5, for the case $i = \upbeta = 0, k_\mathrm{h,c}$ is plotted versus the angle of shear strength $\upvarphi ^{\prime }$ of the retained soil, varying $\updelta$ (Fig. 3), $\upphi _\mathrm{b}$ (Figs. 4a, 5a) and $\Gamma _\mathrm{w}$ (Figs. 4b, 5b); specifically, the influence of $\upphi _\mathrm{b}$ and $\Gamma _\mathrm{w}$ is analyzed for the case $\updelta /\upvarphi ^{\prime }= 0$ (Fig. 4) and $\updelta /\upvarphi ^{\prime } = 2/3$ (Fig. 5).

Fig. 3

Influence of $\upvarphi ^{\prime }$ and $\updelta$ on the critical acceleration coefficient $k_\mathrm{h,c}$ computed for the soil-wall system of Fig. 1a with $k_\mathrm{v}$ $=$ 0 and $c_\mathrm{b}$ $=$ 0

Fig. 4

Influence of $\upvarphi ^{\prime },\,\Gamma _\mathrm{w}$ and $\upphi _\mathrm{b}$ on the critical acceleration coefficient $k_\mathrm{h,c}$ computed for the soil-wall system of Fig. 1a with $k_\mathrm{v}$ $=$ 0, $c_\mathrm{b}$ $=$ 0 and $\updelta /\upvarphi ^{\prime }$ $=$ 0

Fig. 5

Influence of $\upphi _\mathrm{b}$ (a) and $\Gamma _\mathrm{w}$ (b) on the critical acceleration coefficient $k_\mathrm{h,c}$ for the soil-wall system of Fig. 1a computed for $k_\mathrm{v}$ $=$ 0, $c_\mathrm{b}$ $=$ 0 and $\updelta /\upvarphi ^{\prime }$ $=$ 2/3

From all the plots it is evident that higher values of $\updelta , \Gamma _\mathrm{w}$ and $\upphi _\mathrm{b}$ lead to more stable soil-wall systems characterized by greater values of the critical acceleration coefficient $k_\mathrm{h,c}$.

As an example for $\Gamma _\mathrm{w}$ $=$ 0.7 and $\updelta /\upvarphi ^{\prime }$ in the range $0$–$2/3$ (Fig. 3), $k_\mathrm{h,c}$ increases from about 0.17 to about 0.28, for $\upvarphi ^{\prime } = 35^{\circ }$, and from about 0.26 to about 0.43, for $\upvarphi ^{\prime } = 40^{\circ }$.

It is evident that the influence of $\upphi _\mathrm{b}$ (Figs. 4a, 5a) and $\Gamma _\mathrm{w}$ (Figs. 4b, 5b) is remarkable regardless the values of $\updelta$. For example for $\upvarphi ^{\prime } = 35^{\circ }, \Gamma _\mathrm{w}$ $=$0.7 and $\updelta /\upvarphi ^{\prime } = 2/3$ (Fig. 5a) the critical acceleration coefficient is $k_\mathrm{h,c} \approx 0.1$ for $\upphi _\mathrm{b}/\upvarphi ^{\prime } = 2/3$ and it almost triplicates ($k_\mathrm{h,c}\approx 0.28$) for $\upphi _\mathrm{b}/\upvarphi ^{\prime } = 1$; similarly, in the case $\updelta /\upvarphi ^{\prime } = 0$ (Fig. 4a) the value of $k_\mathrm{h,c}$ computed for $\upphi _\mathrm{b}/\upvarphi ^{\prime } = 1$ is about seven times larger than that corresponding to the case $\upphi _\mathrm{b}/\upvarphi ^{\prime } = 2/3$.

3.1.2 Equation of motion of sliding walls

The enhancements of the 2-$W$ approach with respect to the sliding block procedure are mainly related to the actual equations of motion of the soil-wall system. To derive these equations the dynamic equilibrium condition in the direction of sliding must be considered:

$$\begin{aligned} \ddot{d}_\mathrm{w} \cdot \frac{W_\mathrm{w} }{g}&= D_\mathrm{w} -R_\mathrm{w} \nonumber \\ \ddot{d}_\mathrm{s} \cdot \frac{W_\mathrm{s} }{g}&= D_\mathrm{s} -R_\mathrm{s} \end{aligned}$$

(8)

In Eq. (8) $\ddot{d}_\mathrm{w}$ and $\ddot{d}_\mathrm{s}$ are the relative acceleration of the wall (suffix $w$) and of the soil wedge (suffix $s$), respectively, caused by the excess of driving ($D_\mathrm{w},\,D_\mathrm{s}$) to resisting ($R_\mathrm{w},\,R_\mathrm{s}$) forces in the time interval during which it is $k_\mathrm{h}>k_\mathrm{h,c}$.

Assuming $k_\mathrm{v}$ $=$ 0 and using the expressions of the driving and of the resisting forces derived by Biondi and Cascone (2014), Eq .8 can be rewritten in the form:

$$\begin{aligned} \ddot{d}_\mathrm{w}&= \left[ {k_\mathrm{h} -k_{\mathrm{h,c}} } \right] \cdot C_\mathrm{w} \cdot g \nonumber \\ \ddot{d}_\mathrm{s}&= \left[ {k_\mathrm{h} -k_{\mathrm{h,c}} } \right] \cdot C_\mathrm{s} \cdot g \end{aligned}$$

(9)

where $C_\mathrm{w}$ and $C_\mathrm{s}$ are the wall and the soil displacement factors, respectively, depending on all the mechanical ($\upvarphi ^{\prime }, \updelta , c_\mathrm{b}, \upphi _\mathrm{b}$) and geometrical ($i, \upbeta , \upalpha _\mathrm{w}, H, \Gamma _\mathrm{w}$) parameters of the soil-wall system (see Figs. 1, 2).

The wall displacement factor $C_\mathrm{w}$ is given by the following equation:

$$\begin{aligned} C_\mathrm{w} =\frac{\Gamma _\mathrm{w} \cdot A_5 +B_5 }{\Gamma _\mathrm{w} \cdot A_6 +B_6 } \end{aligned}$$

(10)

where the constants $A_{5},\,A_{6},\,B_{5}$ and $B_{6}$ depend on the same factors affecting $C_\mathrm{w}$; the “Appendix 3” lists the expressions giving $A_{5},\,A_{6},\,B_{5}$ and $B_{6}$ for the case $k_\mathrm{v}= 0 (\Omega = 0)$ and $c_\mathrm{b}$ $=$ 0.

According to Stamatopoulos and Velgaki (2001) and to Stamatopoulos et al. (2006) the kinematic compatibility of the displacements requires that the components of the displacement vectors $d_\mathrm{w}$ (of the wall) and $d_\mathrm{s}$ (of the soil wedge), normal to the boundary between the two wedges, have the same magnitude; this allows introducing the shape factor $S_\mathrm{F}$:

$$\begin{aligned} S_\mathrm{F} =\frac{d_\mathrm{w} }{d_\mathrm{s} }=\frac{\cos \left( {\upalpha _c -\upbeta } \right) }{\cos \left( {\upbeta +\upalpha _\mathrm{b} } \right) } \end{aligned}$$

(11)

In a small displacement analysis ($H(t)=H_\mathrm{o}$) carried out assuming $k_\mathrm{v}$ $=$ 0, the factors $C_\mathrm{w},\,C_\mathrm{s}$ and $S_\mathrm{F}$ are constant with time and Eqs. (9–11) lead to:

$$\begin{aligned} d_\mathrm{w}&= C_\mathrm{w} \cdot d_\mathrm{o}\nonumber \\ d_\mathrm{s}&= C_\mathrm{s} \cdot d_\mathrm{o} =\frac{C_\mathrm{w} }{S_\mathrm{F} }\cdot d_\mathrm{o} \end{aligned}$$

(12)

Therefore, once $C_\mathrm{w}$ (Eq. 10) and $S_\mathrm{F}$ (Eq. 11) are estimated, the displacements of the wall ($d_\mathrm{w}$) and of the soil wedge ($d_\mathrm{s}$) involved in the failure mechanism can be computed starting from the displacement $d_\mathrm{o}$ of the rigid block sliding along a horizontal plane with the same critical acceleration coefficient $k_\mathrm{h,c}$ of the actual soil-wall system.

3.2 Sliding block versus sliding retaining wall: small displacement analysis

Equation (12) state that permanent displacements cumulated by the soil-wall system ($d_\mathrm{w},\,d_\mathrm{s}$) differ for a factor ($C_\mathrm{w},\,C_\mathrm{s}$) from those computed referring to the rigid block sliding on a horizontal plane (Eq. 1), despite the same values of $k_\mathrm{h,c}$ is adopted in the two displacement analyses.

Stamatopoulos et al. (2006) and Biondi and Cascone (2014) performed an extensive parametric analysis concerning the influence of the various parameters affecting the displacement factor $C_\mathrm{w}$. These Authors showed that $C_\mathrm{w}$ can assume values larger or smaller than one depending on the combination of the geometrical and mechanical parameters describing the soil-wall system. However, in most cases it is $C_\mathrm{w} <1$ reflecting that the permanent displacements of a sliding retaining wall, computed according to a 2-$W$ analysis, are smaller than those evaluated for the corresponding rigid block. Thus, in most cases, the sliding block analogy leads to a conservative estimate of the wall displacements.

Using the expressions of $C_\mathrm{w}$ (Eq. 10) and of the numerical constants $A_{5},\,A_{6},\,B_{5}$ and $B_{6}$ (“Appendix 3”) the plots of Figs. 6, 7 and 8 were obtained for the case $\upalpha _\mathrm{b}$ $=$ 0.

Fig. 6

Influence of $\upvarphi ^{\prime }$ and $\updelta$ on the displacement ratio $C_\mathrm{w}$ computed for the soil-wall system of Fig. 1a with $k_\mathrm{v}$ $=$ 0 and $c_\mathrm{b}$ $=$ 0

Fig. 7

Influence of $\upvarphi ^{\prime },\,\Gamma _\mathrm{w}$ and $\upphi _\mathrm{b}$ on the displacement ratio $C_\mathrm{w}$ computed for the soil-wall system of Fig. 1a with $k_\mathrm{v}$ $=$ 0 and $c_\mathrm{b}$ $=$ 0

Fig. 8

Influence of $\updelta$ (a) and of $\upphi _\mathrm{b}$ (b) on the displacement ratio $C_\mathrm{w}$ computed for the soil-wall system of Fig. 1a with $k_\mathrm{v}$ $=$ 0 and $c_\mathrm{b}$ $=$ 0

In Figs. 6 and 7, for the case $i = \upbeta = 0$, the values of $C_\mathrm{w}$ are plotted versus $\upvarphi ^{\prime }$ varying $\updelta$ (Fig. 6), $\upphi _\mathrm{b}$ (Fig. 7a) and $\Gamma _\mathrm{w}$ (Fig. 7b). For each of the investigated parameters the same range of variation adopted for $k_\mathrm{h,c}$ (Figs. 3, 4) was considered; specifically, the ratios $\updelta /\upvarphi ^{\prime }$ and $\upphi _\mathrm{b}/\upvarphi ^{\prime }$ range in the intervals $0$–$2/3$ and $2/3$–$5/4$, respectively, and the normalized wall weight $\Gamma _\mathrm{w}$ ranges from 0.5 to 1.3. From the plots it is apparent that all the considered parameters remarkably affect the displacement ratio $C_\mathrm{w}$.

Concerning the inclination of the seismic active thrust (Fig. 6), the lower values of $C_\mathrm{w}$ correspond to the lower values of $\updelta$ and the differences between the values of $C_\mathrm{w}$ computed for different $\updelta$ seem to be not significantly affected by $\upvarphi ^{\prime }$.

From the plots of Fig. 7 it is also apparent that the greater are the friction angle $\upphi _\mathrm{b}$ (Fig. 7a) and the normalized wall weight $\Gamma _\mathrm{w}$ (Fig. 7b), the greater is $C_\mathrm{w}$. Assuming $\upvarphi ^{\prime } = 35^{\circ }$ and $\updelta /\upvarphi ^{\prime }$ $=$ 0 for the case of Fig. 7a ($\Gamma _\mathrm{w}$ $=$ 1.1) $C_\mathrm{w}$ increases from 0.81 to 0.96 for $\upphi _\mathrm{b}/\upvarphi ^{\prime }$ increasing from 2/3 ($k_\mathrm{h,c}$ $=$ 0.121) to 5/4 ($k_\mathrm{h,c}$ $=$ 0.414); similarly, for the case $\upphi _\mathrm{b}/\upvarphi ^{\prime }$ $=$ 1 (Fig. 7b), $C_\mathrm{w}$ ranges from 0.71 to 0.89 for $\Gamma _\mathrm{w}$ increasing from 0.5 ($k_\mathrm{h,c}$ $=$ 0.075) to 1.1 ($k_\mathrm{h,c}$ $=$ 0.281).

Among all the investigated parameters, the normalized wall weight $\Gamma _\mathrm{w}$ is, probably, the one with the largest range of variation; values of $\Gamma _\mathrm{w}$ in the range 0.5–0.85 are typical of gravity retaining walls with no or short foundation heel, $\Gamma _\mathrm{w}$ $=$ 0.85–1.15 is frequent in cantilever retaining walls and, finally, $\Gamma _\mathrm{w}$ $=$ 1–2.5 is usual for reinforced soil walls ($\upbeta >60^{\circ }$) or slopes ($\upbeta \le 60^{\circ }$). In Fig. 8 $C_\mathrm{w}$ is plotted versus $\Gamma _\mathrm{w}$ varying $\updelta$ (Fig. 8a) and $\upphi _\mathrm{b}$ (Fig. 8b). In the plots $\Gamma _\mathrm{w}$ ranges from 0.5 to 2, covering a wide typology of earth retaining structures.

From the results in Figs. 7 and 8 it is apparent that increasing the soil-wall system stability conditions (i.e. greater values of $k_\mathrm{h,c}$ or $\Gamma _\mathrm{w})$ the displacement ratio $C_\mathrm{w}$ approaches unity, meaning minor differences between the displacement of the wall $d_\mathrm{w}$ and that of the sliding block $d_\mathrm{o}$.

Consistently with the studies by Stamatopoulos and Velgaki (2001) and by Stamatopoulos et al. (2006), all the computed values of $C_\mathrm{w}$ (Figs. 6, 7, 8) are in the range 0.6–1.1. However, it is apparent that in most cases $C_\mathrm{w}$ is smaller than unity meaning $d_\mathrm{w} < d_\mathrm{o}$. The condition $C_\mathrm{w} >1$ (i.e. $d_\mathrm{w}>d_\mathrm{o})$ occurs in very few cases related to the combination of the higher values of the angle of shear strength of the retained soil $\upvarphi ^{\prime }$ together with the higher values of $\upphi _\mathrm{b}$ and $\Gamma _\mathrm{w}$ and the lower values of $\updelta$.

Therefore, it can be stressed that though the sliding-block analogy neglects the coupled soil-wall behaviour and the kinematic compatibility of their displacements, generally it leads to values of permanent displacement of the wall greater than that predicted by a more reliable 2-$W$ displacement analysis ($d_\mathrm{o}> d_\mathrm{w})$; in a very few cases it is ($d_\mathrm{o} < d_\mathrm{w})$.

3.3 Effect of change in the system geometry

Actually, if the wall slides the geometry of the soil-wall system changes during motion.

Several authors proposed large displacements analyses introducing the effect of the change in the system geometry as displacements develop (e.g. Zarrabi-Kashani 1979; Caltabiano et al. 1999; Sarma and Chlimintzas 2000; Stamatopoulos and Velgaki 2001; Stamatopoulos et al. 2006). During the motion the height of the backfill reduces from the initial value $H_\mathrm{o}$ (Fig. 2) and, as displacements increase, new failure surfaces may develop in the retained soil. The reduction of the backfill height ($H(t) \le H_\mathrm{o}$—Fig. 2) leads to more stable configurations of the soil-wall system for which, if no shear strength degradation occurs, the critical acceleration progressively increases. In this case, a large displacements analysis usually allows predicting smaller permanent displacements than a small displacements analysis.

In large displacements analyses a 2-$W$ approach can be adopted and the change in the ground surface of the retained soil can be estimated through a combined application of the mass conservation principle and of the kinematic compatibility condition of the wall and wedge displacements, (e.g. Caltabiano et al. 1999; Stamatopoulos et al. 2006). Closed-form, as well as numerical, solutions are available for the evaluation of the current height $H(t)$ of the retained soil-wedge, of the critical wedge angle $\upalpha _\mathrm{c}(t)$, of the seismic earth pressure coefficient $K_\mathrm{ae}(t)$, of the horizontal component of the soil-wall critical acceleration coefficient $k_\mathrm{h,c}(t)$ and, finally, of the displacement factors affecting the equations of motion of the wall and of the soil-wedge.

To the author’s knowledge, the most comprehensive solutions available in the literature are those proposed by Stamatopoulos et al. (2006) referring to the soil-wall system shown in Fig. 2. According to these Authors, in the case of a large displacements analysis, carried out neglecting the effect of the vertical component of the ground motion ($k_\mathrm{v}$ $=$ 0), the equations of motion of the wall and of the retained soil wedge, can be written as:

$$\begin{aligned} \ddot{d}_\mathrm{w}&= \left[ {k_\mathrm{h} -k_{\mathrm{h,c}} (t)} \right] \cdot C_\mathrm{w} (t)\cdot g \nonumber \\ \ddot{d}_\mathrm{s}&= \left[ {k_\mathrm{h} -k_{\mathrm{h,c}} (t)} \right] \cdot C_\mathrm{s} (t)\cdot g \end{aligned}$$

(13)

where $C_\mathrm{w}(t)$ and $C_\mathrm{s}(t)$ represent the current (time dependent) values of the wall and of the soil-wedge displacement factors ($C_\mathrm{w}$ and $C_\mathrm{s}$ in Eq. 9) respectively. Also the soil-wall critical acceleration coefficient $k_\mathrm{h,c}(t)$ varies with time since it is evaluated at each time step of the analysis referring to the current geometrical configuration of the soil-wall system (i.e. the current values of $H(t)$ and $\upalpha _\mathrm{c}(t)$—Fig. 2). In the following $k_\mathrm{h,co}$ denotes the initial ($t = 0$) value of the critical acceleration coefficient computed for the undeformed configuration of the soil-wall system.

The result of a 2-W large displacements analysis can be quantified through the ratio between the maximum values of the permanent displacement of the wall computed including ($d_\mathrm{w,max})$ and neglecting ($\overline{d}_{\mathrm{w,max}}$—small displacements analysis with $k_\mathrm{h,c}(t)=k_\mathrm{h,co})$ the change in the system geometry:

$$\begin{aligned} \upxi =\frac{d_{\mathrm{w,max}} }{\overline{d}_{\mathrm{w,max}} } \end{aligned}$$

(14)

Since $d_\mathrm{w,max} \le \overline{d}_{\mathrm{w,max}}$, it is always $\upxi \le 1$.

Stamatopoulos et al. (2006) carried out an extensive parametric analysis using four acceleration time-histories and a great number of combinations of the mechanical and geometrical parameters describing the reference soil-wall scheme (Fig. 2). The time-histories represent the horizontal components of the ground acceleration recorded, at epicentral distances ranging from 5 to 40 km, during four large earthquakes with magnitude in the range 5.75–7.3; the accelerograms have peak values $a_\mathrm{h,max} = k_\mathrm{h,max} \cdot g$ in the range 0.15$g$–0.7$g$ and fundamental period in the range 0.1–0.6 s and, thus, cover a very wide range of energy and frequency content. The results of the analysis were presented in terms of variation of $\upxi$ with the acceleration ratio $k_\mathrm{h,co}/k_\mathrm{h,max}$. The shaded area in Fig. 9 represents the envelope of the values of $\upxi$ presented by Stamatopoulos et al. (2006). It can be observed that $\upxi$ is close to unity for values of the ratio $k_\mathrm{h,co}/k_\mathrm{h,max}$ greater than about 0.30–0.4, while values in the range 0.15–0.9 can be obtained for $k_\mathrm{h,co}/k_\mathrm{h,max }<0.30$.

Fig. 9

Values of the ratio $\upxi$ computed by Stamatopoulos et al. (2006) and proposed upper bound

Most of the $\upxi$–$k_\mathrm{h,co}/k_\mathrm{h,max}$ plots presented by Stamatopoulos et al. (2006) seem to suggest a unique fit curve regardless the acceleration record adopted in the analysis, the wall weight ($W_\mathrm{w})$, the initial height ($H_\mathrm{o})$ of the retained soil, the slope $\upalpha _\mathrm{b}$ and the adhesion $c_\mathrm{b}$ and friction angle $\upphi _\mathrm{b}$ at the base of the wall; conversely, the results are affected by a certain dispersion (enclosed in the shaded area in Fig. 9) when the effects of $i,\,\upbeta$ and $\updelta$ are accounted for.

The results provided by Stamatopoulos et al. (2006) were used herein to derive an empirical expression of the $\upxi$–$k_\mathrm{h,co}/k_\mathrm{h,max}$ relationship. Specifically, the upper bound of the data enclosed in the shaded area of Fig. 9 with $k_\mathrm{h,co}/k_\mathrm{h,max}<0.35$ was fitted using the following functional form:

$$\begin{aligned} \upxi = \mathop {\upxi }\nolimits _\mathrm{o} +\frac{\frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}{{\upxi }_{1} + {\upxi }_{2} \cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }} \end{aligned}$$

(15)

The best estimate of the regression parameters, obtained through an ordinary least squares method, is $\upxi _\mathrm{o}$ $=$ 0.2618, $\upxi _{1}$ $=$ 0.0649 and $\upxi _{2}$ $=$ 1.1678 and the corresponding upper bound curve is plotted in Fig. 9 as a thick dashed line.

Using the computed upper bound of the $\upxi$–$k_\mathrm{h,co}/k_\mathrm{h,max}$ relationship a conservative estimate of the maximum value of the actual permanent displacement cumulated by the wall, $d_\mathrm{w,max}$, can be assessed, by-passing the large displacements analysis, and applying the reduction coefficient $\upxi$ (Eq. 15) to the value of the maximum permanent displacement, $\overline{d}_{\mathrm{w,max}}$, given by a traditional small displacements analysis:

$$\begin{aligned} d_{\mathrm{w,max}} =\left( {\mathop {\upxi }\nolimits _\mathrm{o} +\frac{\frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}{{\upxi }_{1} + {\upxi }_{2} \cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}} \right) \cdot \overline{d}_{\mathrm{w,max}} \end{aligned}$$

(16)

For $k_\mathrm{h,co}/k_\mathrm{h,max }\ge$ 0.35, $d_{\mathrm{w,max}} =\overline{d}_{\mathrm{w,max}}$ can be assumed without appreciable error (Fig. 9).

4 Simplified displacement predictive model

In the previous sections it was shown that the equation of motion to be solved for the evaluation of the earthquake-induced permanent displacements of sliding retaining walls (Eqs. 12–14) is formally similar to that of a rigid block sliding on a horizontal plane with the same critical acceleration coefficient of the actual soil-wall system (Eq. 1).

These equations differ in a displacement factor which is unity in the case of the sliding block (Eq. 1) and, for usual combinations of the relevant parameters characterizing the soil-wall system, is less than one ($C_\mathrm{w} \le$ 1) in a 2-$W$ displacement analysis.

The effect of the change in system geometry during motion can be accounted for through the reduction factor $\upxi$ (Eq. 15) by-passing a large displacements analysis.

Based on these considerations the first of Eqs. (12) and (14) together with Eqs. (10) and (15) allow introducing the following relationship for a simplified evaluation of the maximum value of the expected wall displacement:

$$\begin{aligned} d_{\mathrm{w,max}} =\upxi \cdot C_\mathrm{w} \cdot d_{\mathrm{o,max}} =\left( {\mathop {\upxi }\nolimits _\mathrm{o} +\frac{\frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}{{\upxi }_{1} +{\upxi }_{2} \cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}} \right) \cdot \frac{\Gamma _\mathrm{w} \cdot A_5 +B_5 }{\Gamma _\mathrm{w} \cdot A_6 +B_6 }\cdot d_{\mathrm{o,max}} \end{aligned}$$

(17)

In Eq. (17) $d_\mathrm{o,max}$ is the maximum permanent displacement cumulated by a rigid block sliding on a horizontal plane, characterized by the same critical acceleration coefficient $k_\mathrm{h,co}$ of the actual soil-wall system and subjected to the same acceleration time-history.

The values of $d_\mathrm{w,max}$ provided by Eq. (17) can be regarded as the result of a two-wedge large displacements analysis and requires only the evaluation of the maximum value of the sliding block displacement $d_\mathrm{o,max}$ to be corrected using the factors $C_\mathrm{w}$ and $\upxi$, depending on all the geometrical and mechanical parameters describing the soil-wall system (Eqs. 10, 15). Both these coefficients are generally smaller than unity and therefore the expected wall displacement $d_\mathrm{w,max}$ is usually smaller than the block displacement $d_\mathrm{o,max}$.

If the effect of the change in system geometry is neglected in the displacement analysis ($\upxi$ $=$ 1; $k_\mathrm{h,c}(t) = k_\mathrm{h,co})$, Eqs. (16) and (17) reduce to:

$$\begin{aligned} d_{\mathrm{w,max}} =\overline{d}_{\mathrm{w,max}} =C_\mathrm{w} \cdot d_{\mathrm{o,max}} =\frac{\Gamma _\mathrm{w} \cdot A_5 +B_5 }{\Gamma _\mathrm{w} \cdot A_6 +B_6 }\cdot d_{\mathrm{o,max}} \end{aligned}$$

(18)

For a given earthquake record $d_\mathrm{o,max}$ can be estimated through a conventional Newmark-type analysis. Alternatively, many empirical relationships are available in the literature relating $d_\mathrm{o,max}$ to one or more seismic parameters describing the characteristics of the reference ground motion in terms of peak values (e.g. Ambraseys and Menu 1988; Whitman and Liao 1984), amplitude distribution and energy content (e.g. Ausilio et al. 2007; Jibson 2007), frequency content, spectral parameters and strong motion duration (e.g. Saygili and Rathje 2008; Madiai 2009; Biondi et al. 2011). These empirical relationships represent displacement predictive equations and were derived through best-fit regression analyses of permanent displacements computed using given sets of earthquake records. The accelerogram database, the seismic parameters selected as predictor variables and the functional form of the regression model adopted in the best-fit analysis are the main factors affecting the reliability of the predictive equations.

The choice of an appropriate functional form (e.g. Ambraseys and Menu 1988; Hwang 2012) and of suitable seismic parameters as predictors (e.g. Saygili and Rathje 2008) are crucial aspects, especially when the analysis is aimed to minimize the aleatory variability in the prediction of $d_\mathrm{o,max}$. Conversely, when a conservative estimate of $d_\mathrm{o,max}$ is pursued, simple functional forms and few predictor variables can be used to derive upper-bound predictive equations of practical use. As an example Ambraseys and Menu (1988), Yegian et al. (1991) and Biondi et al. (2011) used the following functional forms to describe the logarithm of the expected maximum permanent displacement as a linear, polynomial or non-linear function of the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$:

$$\begin{aligned} \log d_{\mathrm{o,max}}&= a+b\cdot \frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} }\end{aligned}$$

(19)

$$\begin{aligned} \log d_{\mathrm{o,max}}&= a+b\cdot \frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} }+c\cdot \left( {\frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} }} \right) ^{2}+d\cdot \left( {\frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} }} \right) ^{3}\end{aligned}$$

(20)

$$\begin{aligned} \log d_{\mathrm{o,max}}&= a+b\cdot \log \left( {1-\frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} }} \right) +c\cdot \log \frac{k_{\mathrm{h,c}} }{k_{\mathrm{h,max}} } \end{aligned}$$

(21)

In Eqs. (19–21) $a,\,b, c$ and $d$ are regression parameters evaluated for a given confidence level and the ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ is the unique predictor variable included in the model.

In this paper the procedure proposed for the assessment of the equivalent seismic coefficient $k_\mathrm{h,eq}$ is illustrated with reference to the Italian seismicity using the displacement predictive model derived by Biondi et al. (2011). However, as it will be apparent in the next section any other simplified predictive model can be used to derive numerical values of $k_\mathrm{h,eq}$.

The displacement regression model by Biondi et al. (2011) was derived using a set 405, uniformly processed, free-field horizontal acceleration time-histories recorded at site-source distances $R \le$ 100 km, during 110 shallow crustal earthquakes occurred in Italy with moment magnitude in the range $4.1$–$6.9$. For the selected records the peak acceleration $a_\mathrm{h,max }= k_\mathrm{h,max}\cdot g$ and the Arias Intensity $I_\mathrm{a}$ (Arias 1970) vary in the ranges $0.05\cdot g$–$0.675 \cdot g$ and $0.4$–$2874$ cm/s, respectively, the duration of the strong motion phase $D_{5\hbox {-}95}$ (Trifunac and Brady 1975) and the mean period $T_\mathrm{m}$ (Rathje et al. 1998) range from 0.4 to 51 s and from 0.07 to 0.57 s, respectively.

In the analysis by Biondi et al. (2011) the original accelerograms and also sets of accelerograms scaled to peak values up to 0.15, 0.25 and 0.35$g$ were adopted and displacements were computed for values of the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ in the range 0.1–0.8; in the regression analysis several sets of seismic parameters, including $k_\mathrm{h,c}/k_\mathrm{h,max},\,I_\mathrm{a},\,D_{5\hbox {-}95}$ and $T_\mathrm{m}$, were used as predictive variables.

Herein, reference is made to the predictive model developed assuming the ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ as predictor (Eq. 19); Table 2 lists the values of the regression parameters $a$ and $b$ evaluated for a probability of exceedance $p$ equal to 90, 95 and 99 %. According to Eqs. (17–19) the following simplified predictive model can be derived for a conservative estimate of the maximum permanent displacement of the wall:

$$\begin{aligned} \log d_{\mathrm{w,max}} =a+b\cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }+\log C_\mathrm{w} +\log \left( {\upxi _\mathrm{o} +\frac{\frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}{\upxi _{1} +\upxi _{2} \cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }}} \right) \end{aligned}$$

(22)

or, alternatively, for $\upxi$ $=$ 1:

$$\begin{aligned} \log d_{\mathrm{w,max}} =\log \overline{d}_{\mathrm{w,max}} =a+b\cdot \frac{k_{\mathrm{h,co}} }{k_{\mathrm{h,max}} }+\log C_\mathrm{w} \end{aligned}$$

(23)

In the following, the suffix ‘o’ in the initial value of the critical acceleration coefficient $k_\mathrm{h,co}$ is omitted for simplicity and the symbol $k_\mathrm{h,c}$ denotes the value computed with reference to the undeformed geometry of the soil-wall system (small displacement analysis).

Table 2 Regression parameters of the displacement predictive model proposed by Biondi et al. (2011) $\log d_\mathrm{o,max } =a+b\cdot \frac{k_\mathrm{h,c}}{k_\mathrm{h,max}}$

5 Performance-based pseudo-static analysis

The result of a pseudo-static stability analysis critically depends on the values of the horizontal, $k_\mathrm{h,eq}$, and vertical, $k_\mathrm{v,eq}$, equivalent seismic coefficients. These allow the evaluation of the pseudo-static inertia forces that, acting on both the wall and the soil wedge involved in the failure mechanism, should represent the overall earthquake effects on the soil-wall system.

In current practice $k_\mathrm{h,eq}$ and $k_\mathrm{v,eq}$ are provided by seismic codes and, usually, are related to the expected peak ground acceleration at a given site. Specifically, in most codes and guidelines for seismic design $k_\mathrm{h,eq}$ is assumed to be a fraction $\upbeta _\mathrm{w}$ of the horizontal peak ground acceleration coefficient $k_\mathrm{h,max}$ while $k_\mathrm{v,eq}$ is assumed to be a percentage $\Omega$ of $k_\mathrm{h,eq}$:

$$\begin{aligned} k_{\mathrm{h,eq}}&= \upbeta _\mathrm{w} \cdot k_{\mathrm{h,max}} \nonumber \\ k_{\mathrm{v,eq}}&= \Omega \cdot k_{\mathrm{h,eq}} \end{aligned}$$

(24)

The coefficient $\upbeta _\mathrm{w}$ is usually denoted as acceleration reduction factor.

According to Eq. (24) $k_\mathrm{h,eq}$ and $k_\mathrm{v,eq}$ do not depend on the mechanical and geometrical properties of the considered soil-wall system (that actually represent crucial factors for its seismic response), refer only to the peak acceleration amplitude (that is not suitable to describe all the characteristics and the potential effects of the expected ground motion), and, finally, do not seem to reflect any criteria concerning the quantification of the earthquake effects on the seismic performance of the soil-wall system.

Cascone and Biondi (2014) recently showed that, introducing a suitable definition of the safety factor in terms of cumulated displacements, the equivalent seismic coefficients to be used in the pseudo-static analysis could be related to threshold values $d_\mathrm{w,lim}$ or $d_\mathrm{s,lim}$ of the permanent displacement which may be suffered by the wall ($d_\mathrm{w,lim})$ or by the soil-wedge ($d_\mathrm{s,lim})$ without reaching an ultimate or a serviceability limit state. These Authors assumed that the earthquake-induced permanent displacement, predicted by a proper modified Newmark-type analysis (e.g. the 2-$W$ approach previously described), reliably represents the earthquake effects and is a suitable index for assessing the seismic performance if compared with proper limit values ($d_\mathrm{w,lim}$ or $d_\mathrm{s,lim})$ related to the operational characteristics of the soil-wall system.

Accordingly, if the equivalent seismic coefficient $k_\mathrm{h,eq}$ has to reliably represent the overall earthquake effects on a given soil-wall system, then it must depend on the limit displacements $d_\mathrm{w,lim}$ and $d_\mathrm{s,lim}$ and on the factors affecting the wall displacement response, such as the characteristics of the design earthquake (e.g. $k_\mathrm{h,max})$, the initial stability condition of the soil-wall system and the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$.

Herein, reference is made to limit states of the soil-wall system defined through the limit value $d_\mathrm{w,lim}$ and a procedure for defining the equivalent seismic coefficient $k_\mathrm{h,eq}$ as a function of $d_\mathrm{w,lim}$ and of the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ is described assuming $k_\mathrm{v}$ $=$ 0 ($\Omega$ $=$ 0) since the effect of the vertical component of the ground motion is almost negligible in the evaluation of the permanent displacement.

In the following sub-sections an appropriate definition of the wall safety factor, alternative to the conventional pseudo-static one, is preliminarily proposed and a solution for the evaluation of $k_\mathrm{h,eq}$ is provided introducing an equivalence between the conventional pseudo-static force-balanced approach and a performance-based analysis based on permanent displacements evaluation.

5.1 An alternative definition of the wall safety factor

In a displacement analysis the seismic performance of a soil-wall system can be evaluated comparing the maximum value of the earthquake-induced permanent displacement of the wall $d_\mathrm{w,max}$ with a proper limit value $d_\mathrm{w,lim}$; the ratio $d_\mathrm{w,lim}/d_\mathrm{w,max}$ represents a displacement safety factor. However, in two cases, namely $d_\mathrm{w,lim }$ $=$ 0 or $d_\mathrm{w,max }$ $=$ 0, this definition of the safety factor fails in providing a reliable measure of the wall performance and an alternative index is needed to reliably check the results of the displacement analysis.

Using a displacement predictive model, instead of computing $d_\mathrm{w,max}$ for given values of the peak ground acceleration coefficient $k_\mathrm{h,max}$, a limit value, $k_\mathrm{h,lim}$, of the peak seismic coefficient associated to a given limit displacement $d_\mathrm{w,lim}$ of the wall can be detected. Specifically, $k_\mathrm{h,lim}$ represents the peak horizontal acceleration coefficient required to induce a permanent displacement equal to the limit value $d_\mathrm{w,lim}$.

For example, with reference to the displacement predictive model described by Eq. (22), it is:

$$\begin{aligned} \frac{k_{\mathrm{h,lim}} }{k_{\mathrm{h,c}} }=\frac{-b}{a+\log \left( {\upxi \cdot C_\mathrm{w} } \right) -\log d_{\mathrm{w,lim}} } \end{aligned}$$

(25)

Values of the peak ground acceleration coefficient $k_\mathrm{h,max}$ lower than the limit seismic coefficient $k_\mathrm{h,lim}$ given by Eq. (25) yield earthquake-induced displacements $d_\mathrm{w,max}$ smaller than the limit value $d_\mathrm{w,lim}$, the associated limit state not being achieved.

In Fig. 10, with reference to the soil-wall system described in Fig. 1a with $\upvarphi ^{\prime }=35^{\circ }, i=\upbeta =\updelta /\upvarphi ^{\prime }= c_\mathrm{b}=0, \upphi _\mathrm{b}/\upvarphi ^{\prime }$ $=$ 2/3 and $k_\mathrm{v}$ $=$ 0,$k_\mathrm{h,lim}$ is plotted versus $\Gamma _\mathrm{w}$ for values of the limit displacement $d_\mathrm{w,lim}$ ranging from 0.1 to 10 cm. In the analysis the displacement predictive model (Eq. 23) derived with reference to the original set of accelerograms, with a probability of exceedance $p$ $=$ 90 %, was used (Table 2) and $\upxi$ $=$ 1 was assumed for simplicity (Eq. 23).

Fig. 10

Tolerable acceleration coefficient

From the plots it is evident that the limit displacement significantly affects the tolerable acceleration coefficient $k_\mathrm{h,lim}$. For a given soil-wall system (i.e. a given value of $k_\mathrm{h,c}$ in Eq. 25) the greater $d_\mathrm{w,lim}$ the greater is $k_\mathrm{h,lim}$; similarly, $k_\mathrm{h,lim}$ increases as the system becomes more stable (increasing values of $\Gamma _\mathrm{w}$, that is increasing value of $k_\mathrm{h,c}$—see Fig. 4b).

As an example for $d_\mathrm{w,lim}$ equal to 1, 5 and 10 cm the tolerable acceleration $k_\mathrm{h,lim}$ varies in the range 0.12–0.26 for $\Gamma _\mathrm{w}$ $=$ 0.8 ($k_\mathrm{h,c} \approx 0.055$), 0.21–0.46 for $\Gamma _\mathrm{w}$ $=$ 1 ($k_\mathrm{h,c}\approx 0.102$) and 0.29–0.61 for $\Gamma _\mathrm{w}$ $=$ 1.2 ($k_\mathrm{h,c} \approx 0.138$). In all the cases for values of $d_\mathrm{w,lim}$ gradually reducing to zero, $k_\mathrm{h,lim}$ tends to $k_\mathrm{h,c}$ (dashed line in Fig. 10).

A factor of safety $F_\mathrm{k}$ representing a reliable measure of the seismic performance of the soil-wall system can then be defined as the ratio between the tolerable acceleration coefficient $k_\mathrm{h,lim}$, that can be sustained by the wall without attaining a given limit state (corresponding to a limit displacement $d_\mathrm{w,lim})$, and the peak value of the acceleration coefficient $k_\mathrm{h,max}$ to which the wall is subjected during the earthquake:

$$\begin{aligned} F_\mathrm{k} =\frac{k_{\mathrm{h,lim}} }{k_{\mathrm{h,max}} } \end{aligned}$$

(26)

Since $k_\mathrm{h,lim}$ and $k_\mathrm{h,max}$ are related to the limit $d_\mathrm{w,lim}$ (Eq. 25) and to the earthquake-induced $d_\mathrm{w,max}$ (Eqs. 22–23) displacements, $F_\mathrm{k}$ represents a measure of the safety against a given limit state evaluated comparing accelerations rather than displacements.

Values of $F_\mathrm{k}$ greater than one indicate wall stability with respect to the limit state related to the selected limit displacement $d_\mathrm{w,lim}$; in fact, if $k_\mathrm{h,lim} > k_\mathrm{h,max}$ (that is $F_\mathrm{k}>1$) the earthquake-induced displacement will be smaller than the limit one ($d_\mathrm{w,lim}> d_\mathrm{w,max})$.

Convenience in using $F_\mathrm{k}$ rather than the conventional pseudo-static safety factor $F_\mathrm{ps}$ will be shown with reference to the soil-wall scheme of Fig. 1a ($\upalpha _\mathrm{b}$ $=$ 0). In the case $k_\mathrm{v}$ $=$ 0 ($\Omega$ $=$ 0) the pseudo-static safety factor with respect to a sliding failure mechanism can be expressed as:

$$\begin{aligned} F_{\mathrm{ps}} =\frac{\frac{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }{\Gamma _\mathrm{w} \cdot \upgamma \cdot H^{2}}+\tan \upphi _\mathrm{b} \cdot \left[ {1+\frac{K_{\mathrm{ae}} }{\Gamma _\mathrm{w} }\cdot \sin \left( {\updelta +\upbeta } \right) } \right] }{\frac{K_{\mathrm{ae}} }{\Gamma _\mathrm{w} }\cdot \cos \left( {\updelta +\upbeta } \right) +k_{\mathrm{h,eq}} } \end{aligned}$$

(27)

where $k_\mathrm{h,eq}$ is the equivalent seismic coefficient adopted in the conventional pseudo-static analysis (i.e. $k_\mathrm{h,eq} = \upbeta _\mathrm{w} \cdot k_\mathrm{h,max}$ and $\Omega = k_{v,eq }/k_\mathrm{h,eq}),\,K_\mathrm{ae}$ represents the active earth-pressure coefficient and the other symbols are described in Fig. 1a and have been already introduced.

In Fig. 11, $F_\mathrm{k}$ and $F_\mathrm{ps}$ are plotted versus $k_\mathrm{h,max}$ with reference to the soil-wall system of Fig. 1a with $\Gamma _\mathrm{w}$ $=$ 1 and the other geometrical ($i,\,\upbeta )$ and mechanical ($\upvarphi ^{\prime },\,\updelta ,\,\upphi _\mathrm{b})$ parameters as in the case of Fig. 10.

Fig. 11

Comparison between conventional ($F_\mathrm{ps})$ and proposed ($F_\mathrm{k})$ safety factors

Specifically, for the case $c_\mathrm{b}=0, F_\mathrm{k}$ was computed through Eq. (26) evaluating $k_\mathrm{h,lim}$ (Eq. 25) for several values of $d_\mathrm{w,lim}$ assuming $\upxi$ $=$ 1 (no change in system geometry); $F_\mathrm{ps}$ was computed through Eq. (27) for $\upbeta _\mathrm{w}$ $=$ 1/2 and $\upbeta _\mathrm{w}$ $=$ 2/3 using the Mononobe–Okabe active earth-pressure coefficient given by Eq. 35 of “Appendix 1”.

For the considered soil-wall system the critical acceleration coefficient and the wall displacement factor are $k_\mathrm{h,c} \approx 0.10$ (Eqs. 6–7) and $C_\mathrm{w} \approx 0.79$ (Eq. 10), respectively.

According to the conventional pseudo-static approach, the wall is stable ($F_\mathrm{ps}>1$) if $k_\mathrm{h,eq}$ is smaller than $k_\mathrm{h,c}$; this means $k_\mathrm{h,max}<k_\mathrm{h,c}/\upbeta _\mathrm{w}$ that is $k_\mathrm{h,max}<0.104$ for $\upbeta _\mathrm{w}$ $=$ 1/2 and $k_\mathrm{h,max}<0.203$ for $\upbeta _\mathrm{w}$ $=$ 2/3. Conversely, using $F_\mathrm{k}$, the values of $k_\mathrm{h,max}$ for which the wall stability is ensured ($F_\mathrm{k}>1$) depend on the adopted value of the limit displacement $d_\mathrm{w,lim}$, that is, on the permanent displacement which may be undergone by the wall without reaching a limit state.

As an example (Fig. 11), for $d_\mathrm{w,lim}$ equal to 1, 5 and 10 cm the wall is stable for $k_\mathrm{h,max}$ smaller than about 0.22, 0.34 or 0.47, respectively, all these values being larger than the value obtained from the traditional pseudo-static approach (from Fig. 11 it is $F_\mathrm{ps}$ $=$ 1 for $k_\mathrm{h,max}$ $=$ 0.21 or 0.15 if $\upbeta _{w }$ $=$ 1/2 or 2/3).

Similarly, for a given $k_\mathrm{h,max}$, different values of $F_\mathrm{k}$ are obtained depending on the selected values of $d_\mathrm{w,lim}$. As an example if $k_\mathrm{h,max}$ $=$ 0.25 is assumed, for the considered soil-wall system it is $d_\mathrm{w,max}$ = 3.4 cm (Eq. 23) and, correspondingly, Eq. (26) or Fig. 11 give $F_\mathrm{k}$ = 0.74, 0.86, 1.21 and 1.38 for $d_\mathrm{w,lim}$ equal to 0.5, 1, 3.5 and 5 respectively, denoting that wall stability may be ($F_\mathrm{k} > 1$) or may be not ($F_\mathrm{k} <$ 1) satisfied depending on the assumed limit displacement. Correspondingly, the conventional pseudo-static approach yields $F_\mathrm{ps}$ = 0.92 for $\upbeta _\mathrm{w}$ = 1/2 and $F_\mathrm{ps}$ = 0.80 for $\upbeta _\mathrm{w}$ = 2/3 denoting a wall instability ($F_\mathrm{ps} < 1$) regardless the earthquake-induced displacement $d_\mathrm{w,max}$ and the assumed limit value $d_\mathrm{w,lim}$.

5.2 A rational criterion for the selection of the pseudo-static coefficient $k_\mathrm{h,eq}$

In order to achieve a match between the results of the pseudo-static and of the performance-based analysis, an equivalence criterion between the two approaches must be introduced.

A rational criterion to define this equivalence consists in the detection of the equivalent seismic coefficient $k_\mathrm{h,eq}$ for which the two approaches provide the same factor of safety: $F_\mathrm{k} = F_\mathrm{ps}$.

In this way, although no displacement analysis is performed, even using the pseudo-static approach a measure of the wall safety condition consistent with that of performance-based analysis can be obtained.

Using Eqs. (26) and (27) and imposing $F_\mathrm{ps} = F_\mathrm{k}$ the following expression for $k_\mathrm{h,eq}$ can be derived:

$$\begin{aligned} k_{\mathrm{h,eq}} =\frac{\frac{{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }/{\cos \upalpha _\mathrm{b} }}{\upgamma \cdot H^{2}\cdot \Gamma _\mathrm{w} }\cdot \frac{k_{\mathrm{h,max}} }{k_{\mathrm{h,lim}} }+E_{\mathrm{eq}} }{\cos \upalpha _\mathrm{b} +\sin \upalpha _\mathrm{b} \cdot \tan \upphi _\mathrm{b} \cdot \frac{k_{\mathrm{h,max}} }{k_{\mathrm{h,lim}} }+\Omega \cdot E_{\mathrm{eq}} } \end{aligned}$$

(28)

where:

$$\begin{aligned} E_{\mathrm{eq}}&= \left( {\frac{\cos \upalpha _\mathrm{b} \cdot \tan \upphi _\mathrm{b} \cdot k_{\mathrm{h,max}} }{k_{\mathrm{h,lim}} }-\sin \upalpha _\mathrm{b} } \right) \nonumber \\&\quad +\frac{K_{\mathrm{ae,eq}} }{\Gamma _\mathrm{w} }\cdot \left[ {\cos \left( {\updelta +\upbeta -\upalpha _\mathrm{b} } \right) -\frac{\tan \upphi _\mathrm{b} \cdot \sin \left( {\updelta +\upbeta -\upalpha _\mathrm{b} } \right) \cdot k_{\mathrm{h,max}} }{k_{\mathrm{h,lim}} }} \right] \end{aligned}$$

(29)

$K_\mathrm{ae,eq}$ is the active earth pressure coefficient computed at limit equilibrium (i.e. for $k_\mathrm{h}=k_\mathrm{h,eq}$ and $\Omega =k_\mathrm{v,eq}/k_\mathrm{h,eq})$ and all the other symbols have been already introduced (Figs. 1a, 2).

As expected the equivalent seismic coefficient $k_\mathrm{h,eq}$ depends on all the geometrical ($i,\,\upbeta ,\,B_\mathrm{b},\,\upalpha _\mathrm{b})$ and mechanical ($\upgamma ,\,\upvarphi ^{\prime },\,\updelta ,\,\Gamma _\mathrm{w},\,c_\mathrm{b},\,\upphi _\mathrm{b})$ parameters describing the soil-wall system, on the peak ground acceleration ($k_\mathrm{h,max},\,\Omega )$ and, through $k_\mathrm{h,lim}$ (Eq. 25), on the acceptable wall displacement $d_\mathrm{w,lim}$ and on the critical acceleration coefficient $k_\mathrm{h,c}$.

Like in the case of the critical acceleration coefficient (Eq. 32 in “Appendix 1”), Eq. (28) must be solved iteratively since the earth-pressure coefficient $K_\mathrm{ae,eq}$ depends on $k_\mathrm{h,eq}$.

It is worth noting that Eqs. (28) and (29) are formally similar to Eqs. (31) and (32) of “Appendix” giving the critical acceleration coefficient $k_\mathrm{h,c}$ and the quantity $E_\mathrm{c}$; the only difference consists in the safety factor which is unity in the equations giving $k_\mathrm{h,c}$ and $E_\mathrm{c}$ and is equal to $F_\mathrm{k}$ in the equations giving $k_\mathrm{h,eq}$ and $E_\mathrm{eq}$.

Moreover, since when $k_\mathrm{h,eq}=k_\mathrm{h,c}$ it is $F_\mathrm{k}$ = 1:

• the condition $k_\mathrm{h,eq} < k_\mathrm{h,c}$ occurs if $F_\mathrm{k} > 1$, meaning that both the expected wall displacement and the expected peak acceleration do not overcome the corresponding limit values: $d_\mathrm{w,max} < d_\mathrm{w,lim}$ and $k_\mathrm{h,max} < k_\mathrm{h,lim}$; accordingly, the proposed equivalent pseudo-static analysis provides $F_\mathrm{ps} = F_\mathrm{k}> 1$;

• the condition $k_\mathrm{h,eq} > k_{h,c }$ occurs if $F_\mathrm{k} < 1$, implying that a limit state of the wall is achieved since it is also $k_\mathrm{h,max}> k_\mathrm{h,lim}$ and $d_\mathrm{w,max} > d_\mathrm{w,lim}$; accordingly, the proposed approach leads to $F_\mathrm{ps} = F_\mathrm{k} <$ 1.

Finally, it must be pointed out that the obtained expressions for $k_\mathrm{h,eq}$ (Eq. 28) do not depend on the adopted displacement predictive model since this is only involved in the computation of the limit acceleration $k_\mathrm{h,lim}$ (Eq. 25). Expressions of $k_\mathrm{h,lim}$, alternative to Eq. (25), can be derived using any other displacement regression model providing $d_\mathrm{w,max}$ as a function of $k_\mathrm{h,c}$ and $k_\mathrm{h,max}$ through different functional forms (e.g. Eqs. 20, 21) or introducing other suitable seismic parameters.

Once the expression of $k_\mathrm{h,eq}$ is known, the acceleration reduction factor $\upbeta _\mathrm{w}$ may be computed normalizing Eq. (28) with respect to $k_\mathrm{h,max}$:

$$\begin{aligned} \upbeta _\mathrm{w} =\frac{k_{\mathrm{h,eq}} }{k_{\mathrm{h,max}} }=\frac{\frac{{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }/{\hbox {cos}\upalpha _\mathrm{b} }}{\gamma \cdot H^{2}\cdot \Gamma _\mathrm{w} \cdot k_{\mathrm{h,lim}} }+\frac{E_{\mathrm{eq}} }{k_{\mathrm{h,max}} }}{\cos \upalpha _\mathrm{b} +\sin \upalpha _\mathrm{b} \cdot \tan \upphi _\mathrm{b} \cdot \frac{k_{\mathrm{h,max}} }{k_{\mathrm{h,lim}} }+\Omega \cdot E_{\mathrm{eq}} } \end{aligned}$$

(30)

Equation (30) shows that the acceleration reduction factor $\upbeta _\mathrm{w}$ depends on the same quantities affecting $k_\mathrm{h,eq}$, including the expected peak ground accelerations ($k_\mathrm{h,max},\,\Omega )$, the geometrical and mechanical parameters of the soil-wall system, reflected also in the value of $k_\mathrm{h,c}$, and the limit displacement $d_\mathrm{w,lim}$, implicit in the limit acceleration $k_\mathrm{h,lim}$ (Eq. 25).

With reference to the soil-wall system of Fig. 1a, the values of $\upbeta _\mathrm{w}$ were computed for the case $\upvarphi ^{\prime } = 35^{\circ },\,\updelta /\upvarphi ^{\prime } = \upphi _\mathrm{b}/\upvarphi ^{\prime }=2/3, \upbeta =i=c_\mathrm{b}$ $=$ 0 and $k_\mathrm{v}$ $=$ 0 ($\Omega$ $=$ 0) assuming several values of the wall limit displacement $d_\mathrm{w,lim}$ ranging from 1 to 10 cm and neglecting the effect of the change in system geometry ($\upxi$ $=$ 1); in the analysis the Mononobe–Okabe active earth-pressure coefficient (Eq. 35) and the parameters $a$ and $b$ of the displacement predictive model (Eq. 22) obtained for $p$ $=$ 90 % with reference to the accelerograms scaled to $k_\mathrm{h,max}$ $=$ 0.25 (Table 2) were adopted.

The results are shown in Fig. 12a were $\upbeta _\mathrm{w}$ is plotted against $\Gamma _\mathrm{w}$; in the figure, also the values $\upbeta _\mathrm{w}$ $=$ 1/2 and $\upbeta _\mathrm{w}$ $=$ 2/3 suggested by the European Committee for Standardization (2003) in part 5 of Eurocode 8 (EC8), for gravity retaining walls which can undergo permanent displacements up to $d_\mathrm{w,lim}$ (mm) $=$ $300\cdot k_\mathrm{h,max}$ and $d_\mathrm{w,lim}$ (mm) $=$ $200\cdot k_\mathrm{h,max}$ are plotted with a thin and a thick dashed line, respectively.

Fig. 12

Acceleration reduction factor (a) and comparison between $k_\mathrm{h,eq}$ and $k_\mathrm{h,c}$ (b)

It can be observed that both $d_\mathrm{w,lim}$ and $\Gamma _\mathrm{w}$ significantly affect the computed values of $\upbeta _\mathrm{w}$. Generally, for a given value of $\Gamma _\mathrm{w},\,\upbeta _\mathrm{w}$ reduces as $d_\mathrm{w,lim}$ increases. As an example, assuming $\Gamma _\mathrm{w}$ $=$ 1 ($k_\mathrm{h,c}$ $=$ 0.078, $C_\mathrm{w}$ $=$ 0.84), the plots in Fig. 12a yield values of $\upbeta _\mathrm{w}$ equal to 0.865, 0.651, 0.511, 0.232 for $d_\mathrm{w,lim}$ $=$ 2, 3.5, 5 and 10 cm respectively. Then, the greater is the value of $d_\mathrm{w,lim}$ that can be suffered by the wall, the lower is the equivalent seismic coefficient $k_\mathrm{h,eq}$=$\upbeta _\mathrm{w} \cdot k_\mathrm{h,max}$ to be adopted in the pseudo-static analysis. Thus, soil-wall systems that can undergo larger permanent displacements without reaching a limit state, can be verified assuming smaller values of the equivalent seismic actions.

As a consequence a unique value of $\upbeta _\mathrm{w}$ leads unavoidably to erroneous evaluations of the equivalent seismic actions and, then, of the wall seismic performance.

For example for $d_\mathrm{w,lim}$ $=$ 10 cm the proposed procedure provides $\upbeta _\mathrm{w}$ $=$ 0.23 which is lower than the values suggested by EC8. In this case the expected wall displacement is $d_\mathrm{w,max}$ $=$ 8.2 cm and the corresponding limit acceleration (Eq. 25) is $k_\mathrm{h,lim}$ $=$ 0.27; therefore, the limit state is not achieved by the wall (since it is $d_\mathrm{w,max}$ $=$ 8.2 cm $< d_\mathrm{w,lim}$ $=$ 10 cm and $k_\mathrm{h,max}$ $=$ 0.25 $< k_\mathrm{h,lim}$ $=$ 0.27).

A reliable selection of the equivalent seismic coefficient should reflect this result leading to a pseudo-static safety factor $F_\mathrm{ps}$ greater than unity.

Assuming $\upbeta _\mathrm{w}=0.23$, as predicted by the proposed procedure, it is $F_\mathrm{k}=k_\mathrm{h,lim}/k_\mathrm{h,max}$ $=$ 1.08 and $F_\mathrm{ps}=F_\mathrm{k}>1$ consistently with the condition $d_\mathrm{w,lim} > d_\mathrm{w,max}$; conversely, using $\upbeta _\mathrm{w}$ $=$ 1/2 or $\upbeta _\mathrm{w}$ $=$ 2/3 as suggested by EC8 (regardless $d_\mathrm{w,lim})$ it is $F_\mathrm{ps}=0.92<1$ or $F_\mathrm{ps}$ $=$ 0.80 $<$ 1 which, in both cases, is not consistent with the actual seismic performance of the wall ($d_\mathrm{w,max} < d_\mathrm{w,lim})$.

As shown in Fig. 12a, for a given limit displacement $d_\mathrm{w,lim}$ the greater is $\Gamma _\mathrm{w}$ (i.e. the greater is $k_\mathrm{h,c})$, the lower is the acceleration reduction factor $\upbeta _\mathrm{w}$ and, then, $k_\mathrm{h,eq}$.

As an example for $d_\mathrm{w,lim}$ $=$ 3.5 cm it is $\upbeta _\mathrm{w}$ $=$ 0.65, 0.40 and 0.31 for $\Gamma _\mathrm{w}$ equal to 1, 1.1 and 1.2 respectively; similarly, for the same values of $\Gamma _\mathrm{w}$ and for $d_\mathrm{w,lim}$ $=$ 5 cm it is $\upbeta _\mathrm{w}$ $=$ 0.51, 0.29 and 0.22. Then, for a given limit state and design value of peak ground acceleration $k_\mathrm{h,max}$, the more stable is the considered soil-wall system, the smaller is the equivalent seismic coefficient $k_\mathrm{h,eq}$=$\upbeta _\mathrm{w} \cdot k_\mathrm{h,max}$ to be adopted in the pseudo-static analysis.

In Fig. 12b, the plot of the ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ is superimposed to the curves representing the acceleration reduction factor $\upbeta _\mathrm{w}$ depicted in Fig. 12a.

Assuming $\Gamma _\mathrm{w}$ $=$ 1 which leads to $k_\mathrm{h,c}$ $=$ 0.078 (Eqs. 5–6) and to $C_\mathrm{w}$ $=$ 0.84 (Eq. 9) for $k_\mathrm{h,max}$ $=$ 0.25 Eq. (22) leads to $d_\mathrm{w,max}$ $=$ 8.2 cm; in this case it is worth observing that:

• for $d_\mathrm{w,lim}$ $=$ 5 cm the limit displacement is exceeded ($d_\mathrm{w,lim}< d_\mathrm{w,max})$ and the proposed procedure gives $\upbeta _\mathrm{w}$ $=$ 0.51 and $F_\mathrm{k}= 0.84<1$; in the diagram of Fig. 12b the corresponding point ($\Gamma _\mathrm{w}$ $=$ 1; $\upbeta _\mathrm{w}$ $=$ 0.51) is located above the thick line representing the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$;

• assuming $d_\mathrm{w,lim}$ $=$ 10 cm ($\upbeta _\mathrm{w}$ $=$ 0.23) it is $F_\mathrm{k}=1.08>1$ consistently with the condition $d_\mathrm{w,lim}> d_\mathrm{w,max}$ and in Fig. 12b the point relevant to this case ($\Gamma _\mathrm{w}$ $=$ 1; $\upbeta _\mathrm{w}$ $=$ 0.23) is located below the thick line representing the ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$.

Similarly, in the case $\Gamma _\mathrm{w}$ $=$ 1.2 ($k_\mathrm{h,c}$ $=$ 0.11, $C_\mathrm{w}$ $=$ 0.87, $d_\mathrm{w,max}$ $=$ 3.1 cm), in the diagram of Fig. 10b, the points relevant for the cases $d_\mathrm{w,lim}$ $=$ 2 cm ($\upbeta _\mathrm{w}$ $=$ 0.08 and $F_\mathrm{k}$ $=$ 0.89 $<$ 1) and $d_\mathrm{w,lim}$ $=$ 5 cm ($\upbeta _\mathrm{w}$ $=$ 0.29 and $F_\mathrm{k}$ $=$ 1.15 $>$ 1) are located below and above of the line representing the ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ respectively.

Then, for a given value of the limit displacement $d_\mathrm{w,lim}$, the curve representing the acceleration ratio $k_\mathrm{h,c}/k_\mathrm{h,max}$ divides Fig. 10b in two zones:

• above the curve, the equivalent seismic coefficient $k_\mathrm{h,eq}$ is greater than the corresponding critical value $k_\mathrm{h,c}$ and wall stability evaluated in terms of displacement ratio is not satisfied since it is $d_\mathrm{w,lim}<d_\mathrm{w,max}$; consistently it is also $k_\mathrm{h,lim}<k_\mathrm{h,max}$ and $F_\mathrm{k}=F_\mathrm{ps}<1$;

• below the curve, $k_\mathrm{h,eq}$ is smaller than $k_\mathrm{h,c}$, and since the expected permanent displacement does not overcome the limit value ($d_\mathrm{w,lim}>d_\mathrm{w,max})$ the wall stability is ensured and the limit state associated to $d_\mathrm{w,lim}$ is not achieved; consistently, the proposed approach leads to the condition $F_\mathrm{k}=F_\mathrm{ps}>1 (k_\mathrm{h,lim}>k_\mathrm{h,max})$.

6 Discussion and conclusions

Pseudo-static and displacement analyses are usually regarded as alternative methods for the evaluation of the seismic performance of retaining walls. However, the equivalent seismic coefficients adopted in the pseudo-static representation of the transient seismic action can be related to earthquake-induced permanent displacements in the attempt to link the conventional pseudo-static approach to more reliable performance-based analyses.

This paper presents a rational procedure for a proper selection of the horizontal seismic coefficient $k_\mathrm{h,eq}$ as a function of a limit value of the earthquake-induced permanent displacement $d_\mathrm{w,lim}$ that can be suffered by the wall without reaching a serviceability or an ultimate limit states.

The proposed procedure assumes that earthquake-induced permanent displacement represents a proper index of the wall seismic performance, requires the evaluation of the critical acceleration coefficient $k_\mathrm{h,c}$ and of the factors $C_\mathrm{w}$ and $C_\mathrm{s}$ affecting the equation of motion of the soil-wall system and, finally, involves a suitable displacement predictive model, possibly accounting for the change in the system geometry during motion.

Solutions for the evaluation of $k_\mathrm{h,c},\,C_\mathrm{w}$ and $C_\mathrm{s}$ are presented and discussed in the paper showing that the Newmark sliding-block analogy, which neglects the coupled soil-wall behavior and the kinematic compatibility, generally overestimates the wall displacements. It is shown that the higher is the critical acceleration coefficient $k_\mathrm{h,c}$ of the considered soil-wall system, the less relevant are the effect of the change in system geometry due to displacement development and the difference between the actual wall displacements and those predicted by the sliding block analogy.

Using a displacement predictive model the procedure allows evaluating a limit value $k_\mathrm{h,lim}$ of the horizontal acceleration coefficient representing the maximum value of the seismic acceleration coefficient that can be sustained by the wall without reaching a limit state corresponding to a limit permanent displacement $d_\mathrm{w,lim}$.

Introducing a safety factor $F_\mathrm{k}$, defined as the ratio between the limit acceleration coefficient $k_\mathrm{h,lim}$ and the earthquake-induced peak ground acceleration $k_\mathrm{h,max}$, it has been demonstrated that, for a given design earthquake, reliable values of the equivalent seismic coefficient $k_\mathrm{h,eq}$ should depend on all the factors affecting the stability condition of the soil-wall system and on the permanent displacement that can be sustained by the wall without reaching a limit state; also, it has been shown that the use of an equivalent acceleration coefficient not related to $d_\mathrm{w,lim},\,k_\mathrm{h,max}$ and $k_\mathrm{h,c}$ may lead to a pseudo-static evaluation of the wall performance (i.e to a value of the pseudo-static safety factor $F_\mathrm{ps})$ inconsistent with that of a more reliable displacement-based analysis.

To achieve a match between the results of the two kinds of analysis the procedure proposed in this paper detects the value of the equivalent seismic coefficient $k_\mathrm{h,eq}$ for which the two approaches provide the same factor of safety: $F_\mathrm{ps} = F_\mathrm{k}$.

The proposed expression for the evaluation of $k_\mathrm{h,eq}$ involves all the geometrical and mechanical parameters describing the soil-wall system, the expected peak ground acceleration $k_\mathrm{h,max}$ and the acceptable wall displacement $d_\mathrm{w,lim}$. Through a parametric analysis it has been shown that the more stable is the considered soil-wall system, the smaller is the equivalent seismic coefficient to be used in the pseudo-static analysis; similarly, the greater is the limit displacement $d_\mathrm{w,lim}$ that can be suffered by the wall, the lower is the seismic force to be adopted in the equivalent pseudo-static analysis.

Using the proposed expression of $k_\mathrm{h,eq}$ (Eq. 28) without necessarily carrying out a displacement analysis, a measure of the safety condition of a soil-wall system consistent with its expected seismic performance may be achieved through an equivalent pseudo-static analysis.

Appendices

Appendix

For the soil-wall systems shown in Figs. 1a, 2 this Appendix lists the equations derived by Biondi and Cascone (2014) and by Cascone and Biondi (2014) for the evaluation of the critical,$k_\mathrm{h,c}$, and of the equivalent, $k_\mathrm{h,eq}$, seismic coefficients and of the displacement factor $C_\mathrm{w}$ assuming $k_\mathrm{v}$ $=$ 0 ($\Omega$ $=$ 0).

Appendix 1: Horizontal component of the critical acceleration coefficient, $k_\mathrm{h,c}$: R–E procedure

$k_\mathrm{h,c}$ can be computed solving, iteratively, the following equation (Biondi and Cascone 2014):

$$\begin{aligned} k_{\mathrm{h,c}} =\frac{\frac{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }{\gamma \cdot H^{2}\cdot \Gamma _\mathrm{w} \cdot \cos \upalpha _\mathrm{b} }+E_\mathrm{c} }{\frac{\cos \left( {\upphi _\mathrm{b} -\upalpha _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }+\Omega \cdot E_\mathrm{c} } \end{aligned}$$

(31)

where $c_\mathrm{b}$ and $\upphi _\mathrm{b}$ are the shear strength parameters at the wall-foundation soil interface, $B_\mathrm{b}$ is the wall base width, $\upalpha _\mathrm{b}$ is the inclination of the wall base to the horizontal and $H$ is the height of the retained soil having a unit weight $\upgamma$;

$$\begin{aligned} E_\mathrm{c}&= \frac{\sin \left( {\upphi _\mathrm{b} -\upalpha _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }+\frac{K_{\mathrm{ae,c}} }{\Gamma _\mathrm{w} }\cdot \frac{\sin \left( {\updelta +\upbeta +\upphi _\mathrm{b} -\upalpha _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }\end{aligned}$$

(32)

$$\begin{aligned} \Omega&= \frac{k_{\mathrm{v,c}} }{k_{\mathrm{h,c}} } \end{aligned}$$

(33)

is the ratio of the vertical to the horizontal seismic coefficient at limit equilibrium;

$$\begin{aligned} \Gamma _\mathrm{w} =\frac{2\cdot W_\mathrm{w} }{\upgamma \cdot H^{2}} \end{aligned}$$

(34)

is the normalized wall weight ($W_\mathrm{w}$ is the wall weight);

$K_\mathrm{ae,c}$ is the value at limit equilibrium of the Mononobe–Okabe active earth-pressure coefficient $K_\mathrm{ae}$:

$$\begin{aligned} K_{\mathrm{ae}} =\frac{\cos ^{2}(\upbeta +\uptheta -\upvarphi ^{\prime })}{\cos ^{2}\upbeta \cdot \cos \uptheta \cdot \cos (\updelta +\upbeta +\uptheta )\cdot \left[ {1+\sqrt{\frac{\sin (\upvarphi ^{\prime }-i-\uptheta )\cdot \sin (\updelta +\upvarphi ^{\prime })}{\cos (i-\upbeta )\cdot \cos (\upbeta +\updelta +\uptheta )}}} \right] ^{2}} \end{aligned}$$

(35)

with:

$$\begin{aligned} \tan \uptheta =\tan \mathop {\uptheta }\nolimits _\mathrm{c} =\frac{k_{\mathrm{h,c}} }{1-k_{\mathrm{v,c}} }=\frac{1}{1/{k_{\mathrm{h,c}} }-\Omega _\mathrm{c} } \end{aligned}$$

(36)

In the case of horizontal wall base ($\upalpha _\mathrm{b}$ $=$ 0; Fig. 1a) Eqs. 31 and 32 reduce to:

$$\begin{aligned} k_{\mathrm{h,c}}&= \frac{\frac{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }{\upgamma \cdot H^{2}\cdot \Gamma _\mathrm{w} }+E_\mathrm{c} }{1+\Omega \cdot E_\mathrm{c} }\end{aligned}$$

(37)

$$\begin{aligned} E_\mathrm{c}&= \tan \upphi _\mathrm{b} +\frac{K_{\mathrm{ae,c}} }{\Gamma _\mathrm{w} }\cdot \frac{\sin \left( {\updelta +\upbeta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b}} \end{aligned}$$

(38)

If the vertical component of the ground acceleration is neglected ($k_\mathrm{v}$ $=$ 0; $\Omega$ $=$ 0), it is:

$$\begin{aligned} k_{\mathrm{h,c}} =\frac{2\cdot c_\mathrm{b} \cdot B_\mathrm{b} }{\upgamma \cdot H^{2}\cdot \Gamma _\mathrm{w} }+\tan \upphi _\mathrm{b} +\frac{K_{\mathrm{ae,c}} }{\Gamma _\mathrm{w} }\cdot \frac{\sin \left( {\updelta +\upbeta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b}} \end{aligned}$$

(39)

Appendix 2: Horizontal component of the critical acceleration coefficient: 2-$W$ procedure

For the case $c_\mathrm{b}$ $=$ 0 and $\upalpha _\mathrm{b}$ $=$ 0, the horizontal component of the critical acceleration coefficient $k_\mathrm{h,c}$ can be computed through the following equation (Biondi and Cascone 2014):

$$\begin{aligned} \frac{k_{\mathrm{h,c}} }{1-\Omega \cdot k_{\mathrm{h,c}} }=\frac{b+\sqrt{b^{2}-a\cdot c}}{a} \end{aligned}$$

(40)

where:

$$\begin{aligned} a=B_4^2 -4\cdot A_4 \cdot C_4 \quad b=2\cdot A_3 \cdot C_4 -2\cdot C_3 \cdot A_4 -B_3 \cdot B_4 \quad c=B_3^2 +4\cdot A_3 \cdot C_3\nonumber \\ \end{aligned}$$

(41)

being:

$$\begin{aligned} A_3&= \frac{\hbox {cos}\left( \upbeta +\updelta +\upphi _\mathrm{b} \right) }{\cos \upphi _\mathrm{b}}\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \cdot \tan \upbeta \nonumber \\&\quad -\frac{\sin \left( {\upbeta +\updelta +\upvarphi ^{\prime }} \right) }{\cos \upvarphi ^{\prime }}\cdot \tan {\upphi }_\mathrm{b} \cdot \Gamma _\mathrm{w}\end{aligned}$$

(42)

$$\begin{aligned} A_4&= \frac{\cos \left( {\upbeta +\updelta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \cdot \tan \upbeta \cdot \tan {\upvarphi }^{\prime }\nonumber \\&\quad +\frac{\sin \left( {\upbeta +\updelta +\upvarphi ^{\prime }} \right) }{\cos \upvarphi ^{\prime }}\cdot \Gamma _\mathrm{w}\end{aligned}$$

(43)

$$\begin{aligned} B_3&= \frac{\cos \left( {\upbeta +\updelta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \cdot \left( {1-\tan \upbeta \cdot \tan {\upvarphi }^{\prime }} \right) \nonumber \\&\quad -\frac{\cos \left( {\upbeta +\updelta +\upvarphi ^{\prime }+i} \right) }{\cos \upvarphi ^{\prime }\cdot \cos i}\cdot \Gamma _\mathrm{w} \cdot \tan {\upphi }_\mathrm{b}\end{aligned}$$

(44)

$$\begin{aligned} B_4&= \frac{\cos \left( {\upbeta +\updelta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \cdot \left( \tan \upbeta +\tan {\upvarphi }^{\prime } \right) \nonumber \\&\quad +\frac{\cos \left( {\upbeta +\updelta +\upvarphi ^{\prime }+i} \right) }{\cos \upvarphi ^{\prime }\cdot \cos i}\cdot \Gamma _\mathrm{w}\end{aligned}$$

(45)

$$\begin{aligned} C_3&= \frac{\cos \left( {\upbeta +\updelta +\upphi _\mathrm{b}} \right) }{\cos \upphi _\mathrm{b} }\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \cdot \tan {\upvarphi }^{\prime }\nonumber \\&\quad -\frac{\cos \left( {\upbeta +\updelta +\upvarphi ^{\prime }} \right) }{\cos \upvarphi ^{\prime }}\cdot \Gamma _\mathrm{w} \cdot \tan i\cdot \tan {\upphi } _\mathrm{b}\end{aligned}$$

(46)

$$\begin{aligned} C_4&= \frac{\cos \left( {\upbeta +\updelta +\upphi _\mathrm{b} } \right) }{\cos \upphi _\mathrm{b} }\cdot \left( {1+\tan i\cdot \tan \upbeta } \right) \nonumber \\&\quad -\frac{\cos \left( {\upbeta +\updelta +\upvarphi ^{\prime }} \right) }{\cos \upvarphi ^{\prime }}\cdot \tan i\cdot \Gamma _\mathrm{w} \end{aligned}$$

(47)

Appendix 3: Wall displacement factor $C_\mathrm{w}$

For the case $c_\mathrm{b}$ $=$ 0 the wall displacement factor $C_\mathrm{w}$ is (Biondi and Cascone 2014):

$$\begin{aligned} C_\mathrm{w} =\frac{\Gamma _\mathrm{w} \cdot A_5 +B_5 }{\Gamma _\mathrm{w} \cdot A_6 +B_6 } \end{aligned}$$

(48)

where:

$$\begin{aligned} A_5&= \cos \left( {\upalpha _\mathrm{c} -\updelta -\upbeta -\upvarphi _{}^{\prime }} \right) \cdot \cos \left( {\upalpha _\mathrm{c} -\upbeta } \right) \cdot \cos \left( {\upphi _\mathrm{b} -\upalpha _\mathrm{b} } \right) \end{aligned}$$

(49)

$$\begin{aligned} \hbox {A}_\mathrm{6}&= \cos \left( {\upalpha _\mathrm{c} -\updelta -\upbeta -\upvarphi _{}^{\prime }} \right) \cdot \cos \left( {\upalpha _\mathrm{c} -\upbeta } \right) \cdot \cos \upphi _\mathrm{b}\end{aligned}$$

(50)

$$\begin{aligned} B_5&= \frac{\cos \left( {\upbeta -i} \right) \cdot \cos \left( {\upalpha _\mathrm{c} -\upvarphi ^{\prime }} \right) \cdot \cos \left( {\upphi _\mathrm{b} -\upalpha _\mathrm{b} +\updelta +\upbeta } \right) }{\cos \left( {\upalpha _\mathrm{c} -i} \right) }\cdot \left[ {\frac{\cos \left( {\upalpha _\mathrm{c} -\upbeta } \right) }{\cos \upbeta }} \right] ^{2}\end{aligned}$$

(51)

$$\begin{aligned} B_6&= \frac{\cos \upvarphi ^{\prime }\cdot \cos \left( {\upphi _\mathrm{b} -\upalpha _\mathrm{w} +\upbeta +\updelta } \right) \cdot \cos \left( {\upbeta -\upalpha _\mathrm{w} } \right) \cdot \left( {\cot \upalpha _\mathrm{c} +\tan \upbeta } \right) \cdot \left( {1+\tan i\cdot \tan \upbeta } \right) }{1-\tan i\cdot \cot \upalpha _\mathrm{c} }\nonumber \\ \end{aligned}$$

(52)