Fault localization using itemset mining under constraints

Abstract

We introduce in this paper an itemset mining approach to tackle the fault localization problem, which is one of the most difficult processes in software debugging. We formalize the problem of fault localization as finding the k best patterns satisfying a set of constraints modelling the most suspicious statements. We use a Constraint Programming (CP) approach to model and to solve our itemset based fault localization problem. Our approach consists of two steps: (i) mining top-k suspicious suites of statements; (ii) fault localization by processing top-k patterns. Experiments performed on standard benchmark programs show that our approach enables to propose a more precise localization than a standard approach.

1 Introduction

Developing software programs is universally acknowledged as an error-prone task. The major bottleneck in software debugging is how to identify where the bugs are (Vessey 1985), this is known as fault localization problem. Nonetheless, locating a fault is still an extremely time-consuming and tedious task. Over the last decade, several automated techniques have been proposed to tackle this problem.

Most of automated techniques for fault localization compare two kinds of execution traces, namely the passed and failed executions (Jones et al. 2002), such as Tarantula  (Jones and Harrold 2005) which is one of the most popular fault localization technique. These methods are based on a scoring function to evaluate the suspiciousness of each statement in the program by exploiting the occurrences of the considered statements in passing and failing test cases. Since, the statements with high scores correlate highly with faults and that brings us to a total order on statements from highly suspicious to guiltless statements. It is important to stress that this technique does not differentiate between two failing (resp. passing) test cases, and consequently it ignores the dependencies between statements that can help us to locate the fault.

Other techniques take in account the cause effect chains with a dependence analysis by using, for instance, program slicing (Agrawal et al. 1993). The disadvantage here is that fault can be located in a quite large slice (static slicing) and/or can be time/space consuming (dynamic slicing).

Recently, the problem of fault localization was abstracted as a data mining problem. Cellier et al. (2009, 2011) propose a combination of association rules and Formal Concept Analysis (FCA) to assist in fault localization. The proposed methodology tries to identify rules between statement execution and corresponding test case failure. The extracted rules are then ordered as a lattice and explored bottom up to detect the fault.

In the data mining community, many approaches have promoted the use of constraints to focus on the most promising knowledge according to a potential interest given by the final user. As the process usually produces a large number of patterns, a large effort is made to a better understanding of the fragmented information conveyed by the patterns and to produce pattern sets i.e. sets of patterns satisfying properties on the whole set of patterns (De Raedt and Zimmermann 2007; Rojas et al. 2014). Discovering top-$k$  patterns (i.e. the k best patterns according to a score function) is a recent trend in constraint-based data mining to produce useful pattern sets (Crémilleux and Soulet 2008).

In this spirit of this promising avenue, we propose in this paper an itemset mining approach to tackle the fault localization problem. We formalize the problem of fault localization as finding the k best patterns satisfying a set of constraints modeling the most suspicious statements. We use the test cases coverage of a program collected during the testing phase for finding the location of program fault. Our approach, which benefits from the recent progress on cross-fertilization between data mining and Constraint Programming (Guns et al. 2011; Khiari et al. 2010), is achieved in two steps:

• (1) Mining top-$k$  suspicious patterns (i.e., set of statements) according to dominance relations and using constraints dynamically posted,

• (2) Ranking the statements by processing the top-$k$  patterns in an ad-hoc ranking algorithm to locate the fault.

Our localization approach is based on two working hypothesis. The first hypothesis is usually called the competent developer hypothesis (DeMillo et al. 1978) . It states that, even some faults are introduced, the resulting program would certainly fulfill almost all of its specifications. In other words, the resulting program may contain faults, but it will certainly tackle the problem it has been designed for. The second requirement on which our approach is based is the single fault hypothesis, i.e., there is only one faulty statement in the program. This requirement might appear as being restrictive but it has been shown that complex faults usually result from the coupling of single faults [a.k.a. the coupling effect (Jones et al. 2002)].

Experiments performed on several benchmark of single fault programs (Siemens suite) show that our approach enables to propose a more precise localization as compared to the most popular fault-localization technique Tarantula  (Jones and Harrold 2005). To the best of our knowledge, our proposal is the first data mining approach that exploits pattern sets to fault localization.

This paper is organized as follows. Section 2 sketches definitions and presents the context. Section 3 gives a background on pattern discovery and describes the CP modeling for itemset mining. Section 4 presents the detail of our approach for fault localization. Section 5 presents an illustrative example of fault localization using our approach. Section 6 reports experimental results and a complete comparison with Tarantula. Section 7 presents the related fault-localization methods in the area of data mining and using failing/passing executions. Section 8 concludes the paper and gives some directions for the future works.

2 Background and motivation

This section presents background knowledge about the problem of fault localization and constraint satisfaction problems.

2.1 Fault localization problem

In software engineering, a failure is a deviation between expected and actual result. An error is the part of the program that is liable to lead to a subsequent failure. Finally, a fault in the general sense is the adjudged or hypothesized cause of an error (Laprie et al. 1992). The purpose of fault localization is to pinpoint the root cause of observed symptoms under test cases.

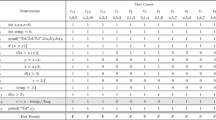
Given a faulty program P having n lines, labeled $L = \{e_{1}, e_{2},\ldots , e_{n}\}$. For instance, for the program “Character counter” given in Fig. 1, we have $L=\{e_1, e_2,\ldots ,e_{10}\}$.

Definition 1

(Test case) A test case $tc_{i}$ is a tuple $\langle D_{i},O_{i} \rangle$, where $D_{i}$ is a collection of input settings for determining whether a program P works as expected or not, and $O_{i}$ is the expected output.

Definition 2

(Passing and failing test case) Let $\langle D_{i},O_{i} \rangle$ a test case and $A_{i}$ be the current output returned by a program P after the execution of its input $D_{i}$. If $A_{i} = O_{i}$, $tc_{i}$ is considered as a passing (i.e. positive), failing (i.e. negative) otherwise.

Definition 3

(Test suite) A test suite $T = \{tc_{1}, tc_{2},\ldots , tc_{m}\}$ is a set of m test cases that are intended to test whether the program P follows the specified set of requirements.

Definition 4

(Test case coverage) Given a test case $tc_i$ and a program P, the set of executed (at least once) statements of P with $tc_i$ is a test case coverage $I_i = (I_{i,1},\ldots , I_{i,n})$ where $I_{i,j} = 1$ if the j th statement is executed, 0 otherwise.

A test case coverage indicates which parts of the program are active during a specific execution. For instance, the test case $tc_{4}$ in Fig. 1 covers the statements $\langle e_1, e_2, e_3, e_4, e_6, e_7,$ $e_{10} \rangle$. The according test case coverage is then $I_4 = (1,1,1,1,0,1,1,0,0,1)$.

Fig. 1

Example of program and its associated transactional dataset

2.2 Constraint satisfaction problem

A CSP consists of a finite set of variables $X = \{x_1, \ldots , x_n\}$ with finite domains ${\mathcal {D}} = \{D_1, \ldots , D_n\}$ such that each $D_i$ is the set of values that can be assigned to $x_i$, and a finite set of constraints ${\mathcal {C}}$. Each constraint $C(Y) \in {\mathcal {C}}$ express a relation over a subset Y of variables X. The objective is to find an assignment ($x_i = d_i$) with $d_i \in D_i$ for $i = 1, \ldots , n$, such that all constraints are satisfied.

Example 1

Let be the following CSP:

$$\begin{aligned} X= & {} \{x_1, x_2, x_3\} \\ {\mathcal {D}}= & {} \{D_1, D_2, D_3\} \text{ where }, D_1 = \{1,2\}, D_2 = \{0,1,2,3\}, D_3 =\{2,3\}\\ {\mathcal {C}}= & {} \{C_1(x_1, x_2), C_2(x_1, x_2,x_3), C_3(x_1)\} \text{ where },\\&C_1(x_1, x_2): x_1 > x_2\\&C_2(x_1, x_2, x_3): x_1 + x_2 = x_3\\&C_3(x_1) : x_1 \ne 0 \end{aligned}$$

Here, the current CSP admits two solutions : $(x_1 = 2, x_2 = 0, x_3 = 2)$ and $(x_1 = 2, x_2 = 1, x_3 = 3)$.

In Constraint Programming [see Rossi et al. (2006)], the resolution process consists of iteratively interleaving search phases and propagation phases. The search phase essentially consists of enumerating all possible variable–value combinations, until we find a solution or prove that none exists. It is generally performed on a tree-like structure. In order to avoid the systematic generation of all the combinations and reduce the search space, the propagation phase shrinks the search space: each constraint propagation algorithm (also called propagator) removes values that a priori cannot be part of a solution w.r.t. the partial assignment built so far. The removal of inconsistent domain values is called filtering. If all inconsistent values are removed from the domains with respect to a constraint C, we say that C is domain consistent.

Consider for example the constraint $C_1(x_1, x_2): x_1 > x_2$. The propagator for this constraint will remove values 2 and 3 from $D_2$. The repeated application of propagators can lead to a successive reduction of domains until reaching a fixed point where no value can be pruned. At this point, the search assigns a variable one of its values. Whenever the domain of one of the variables becomes empty, the search backtracks to explore alternatives.

Constraint programming provides a very expressive type of constraints. One can denote the predefined constraints (i.e., arithmetic constraints), constraints given in extension (list of allowed/forbidden combinations of values), and logical combination of constraints. Another kind of constraints are reified constraints, also known as meta constraints. A reified constraint $b\leftrightarrow c$ involves a boolean variable b and a constraint c, and it is equivalent to $(b=1 \wedge c)\vee (b=0 \wedge \lnot c)$. This kind of constraints is useful to express propositional formulas over constraints, formulas that are common in data mining (see Sect. 3).

3 Frequent itemset mining

This section gives a brief overview of the CP approach for itemset mining (De Raedt et al. 2008; Guns et al. 2011).

3.1 Context and definitions

Let $\mathcal {I}$ be a set of distinct literals called items and $\mathcal {T}= \{1,\ldots ,m\}$ a set of transaction identifiers. An itemset (or pattern) is a non-null subset of $\mathcal {I}$. The language of itemsets corresponds to $\mathcal{L}_{\mathcal {I}} = 2^{\mathcal {I}} \backslash \emptyset$. A transactional dataset is a set ${\mathcal {D}}$ $\subseteq \mathcal {I}\times \mathcal {T}$. Table 1 presents a transactional dataset ${\mathcal {D}}$ where each transaction $t_i$ gathers articles described by items denoted $A,\ldots ,F$. The traditional example is a supermarket dataset in which each transaction corresponds to a customer and every item in the transaction to a product bought by the customer.

Definition 5

(Coverage and Frequency) The coverage of an itemset x is the set of all identifiers of transactions in which x occurs: $cover_{{\mathcal {D}}}(x) = \{t \in \mathcal {T}| \forall i \in x, (i,t) \in {\mathcal {D}}\}$. The frequency of an itemset x is the size of its cover: ${\textit{freq}}_{{\mathcal {D}}}(x)$ = $|cover_{{\mathcal {D}}}(x)|$.

Example 2

Consider the transactional dataset in Table 1. We have for $x =BEF$ that $cover_{{\mathcal {D}}}(x) = \{t_1, t_6, t_7 \}$ and ${\textit{freq}}_{{\mathcal {D}}} (x) =3$.

Constraint-based pattern mining aims at extracting all patterns x of $\mathcal{L}_{\mathcal {I}}$ satisfying a query q(x) (conjunction of constraints), which usually define what we call a theory (Mannila and Toivonen 1997): $Th(q) = \{x \in \mathcal{L}_{\mathcal {I}} \mid {q}(x) \,\, is \,\, true\}$. A common example is the frequency measure leading to the minimal frequency constraint. The latter provides patterns x having a number of occurrences in the dataset exceeding a given minimal threshold $min_{fr}$: ${\textit{freq}}_{{\mathcal {D}}}(x) \ge min_{fr}$. Another usual constraint is the size constraint which constrains the number of items of a pattern x.

Example 3

Let us consider the following query $q(x) = {\textit{freq}}_{{\mathcal {D}}}(x) \ge 5 \, \wedge \, size(x) = 2$. It addresses all frequent patterns $(min_{fr} = 5)$, having a size equal to 2. With the running example in Table 1, we get four solutions : BE, BC, BD and CD.

Table 1 Transactional dataset ${\mathcal {D}}$

In many applications, it appears highly appropriate to look for contrasts between subsets of transactions, such as passing and failing test cases in fault localization (see Sect. 4). The growth rate is a well-used contrast measure (Novak et al. 2009). Let ${\mathcal {D}}$ be a dataset partitioned into two subsets ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$:

Definition 6

(Growth rate) The growth rate of a pattern x from ${\mathcal {D}}_2$ to ${\mathcal {D}}_1$ is:

$$\begin{aligned} m_{gr}(x)= \frac{|{\mathcal {D}}_2|\times freq_{{\mathcal {D}}_1}(x)}{|{\mathcal {D}}_1|\times freq_{{\mathcal {D}}_2}(x)} \end{aligned}$$

Emerging Patterns are those having the growth rate greater than some given threshold. Jumping Emerging Patterns are those which do not occur in ${\mathcal {D}}_2$. They are at the core of a useful knowledge in many applications involving classification features such as the discovery of suspicious statements in the program (see Sect. 5).

The collection of patterns contains redundancy w.r.t. measures. Given a measure m, two patterns $x_i$ and $x_j$ are said to be equivalent if $m(x_i) = m(x_j)$. A set of equivalent patterns forms an equivalent class w.r.t. m. The largest element w.r.t. the set inclusion of an equivalence class is called a closed pattern.

Definition 7

(Closed pattern) A pattern $x_i \in \mathcal{L}_{\mathcal {I}}$ is closed w.r.t. a measure m iff $\forall \, x_j \in \mathcal{L}_{\mathcal {I}}, \, \, x_j \supsetneq x_i \Rightarrow m(x_j) \ne m(x_i)$.

The set of closed patterns is a compact representation of the patterns (i.e we can derive all the patterns with their exact value for m from the closed ones).

Example 4

Consider the frequency measure (i.e. $m = freq$). In our running example, if we impose that ${\textit{freq}}_{{\mathcal {D}}}(x) \ge 5$, we get 9 frequent patterns which are summarized by four equivalence classes (and thus 4 closed frequent patterns). For instance, $BCD \langle 5 \rangle$ ¹ is a closed pattern for $BC \langle 5 \rangle , BD \langle 5 \rangle , CD\langle 5 \rangle , C\langle 5 \rangle$ and $D\langle 5 \rangle$. The three other equivalence classes are: $B \langle 6\rangle , E \langle 6 \rangle$ and $BE \langle 5 \rangle$.

Moreover, the user is often interested in discovering richer patterns satisfying properties involving several local patterns. These patterns define pattern sets (De Raedt and Zimmermann 2007) or n-ary patterns (Khiari et al. 2010). The approach that we present in this paper is able to deal with pattern sets such as the top-$k$  patterns.

Definition 8

(top-$k$  patterns) Let m be a measure, and k an integer. top-$k$  is the set of k best patterns according to m :

$$\begin{aligned} \begin{array}{ll} \{x \in \mathcal{L}_{\mathcal {I}}\mid&{\textit{freq}}_{\mathcal {T}}(x)\ge 1\, \, \wedge \ \not \exists y_1,\ldots ,y_k\in \mathcal{L}_{\mathcal {I}}:\ \forall 1\le j\le k,m(y_j)>m(x)\} \end{array} \end{aligned}$$

Example 5

In our running example, the top-4 closed frequent patterns (i.e., $m=freq$) are: $B \langle 6 \rangle , E \langle 6 \rangle , BE \langle 5 \rangle , BCD \langle 5 \rangle$.

3.2 CP model for the itemset mining

As defined in Sect. 3.1, let ${\mathcal {D}}$ be a dataset where $\mathcal {I}$ is the set of its n items and $\mathcal {T}$ the set of its m transactions. The set of items can be indexed by consecutive integers and thus can be referenced by their indexes; consequently, without loss of generality, the set of items $\mathcal {I}$ is supposed to be a set of n integers $\mathcal {I}=\{1, \ldots , n\}$. The transactional dataset ${\mathcal {D}}$ can be represented with a 0/1 (m,n) transactional boolean matrix d, such that

$$\begin{aligned} \forall t \in \mathcal {T}, \forall i \in \mathcal {I}, (d_{t,i}=1) \leftrightarrow (i \in t). \end{aligned}$$

Table 2 illustrates the transactional binary matrix of the transactional dataset given in Table 1, where 1 (resp. 0) means that an article is (resp. is not) in a transaction. In (De Raedt et al. 2008), the authors model an unknown pattern $M\subseteq \mathcal {I}$ and its associated dataset $\mathcal {T}$ by introducing two sets of boolean variables:

• item variables $\{M_1, M_2,\ldots , M_n\}$ where $(M_i = 1)$ iff $(i \in M)$,

• transaction variables $\{T_1, T_2,\ldots , T_m\}$ where $(T_t =1)$ iff $(M \subseteq t)$.

Table 2 Binary matrix

The relationship between M and $\mathcal {T}$ is modeled by reified constraints stating that, for each transaction t, $(T_t = 1)$ iff M is a subset of t:

$$\begin{aligned} \forall t \in \mathcal {T}: (T_t =1) \leftrightarrow \sum _{i \in \mathcal {I}} M_i \times (1 - d_{t,i}) = 0 \end{aligned}$$

(1)

Using the boolean encoding, it is worth noting that some measures are easy to encode: ${\textit{freq}}_{\mathcal {D}} (M) = \sum _{t \in \mathcal {T}} T_t$ and $size(M) = \sum _{i \in \mathcal {I}} M_i$. So, the minimal frequency constraint ${\textit{freq}}_{\mathcal {D}} (M) \ge min_{fr}$ (where $min_{fr}$ is a threshold) is encoded by the constraint $\sum _{t \in \mathcal {T}} T_t \ge min_{fr}$. In the same way, the minimal size constraint $size(M) \ge \alpha$ (where $\alpha$ is a threshold) is encoded by the constraint $\sum _{i \in \mathcal {I}} M_i \ge \alpha$.

Finally, the closedness constraint $closed_{freq}(M)$ ensures that a pattern has no superset with the same frequency; it is encoded in (Guns et al. 2011) using equation (1) as follows:

$$\begin{aligned} closed_{freq}(M) \equiv \left[ \forall i \in \mathcal {I}: (M_{i} = 1) \leftrightarrow \underset{t\in \mathcal {T}}{\sum } T_{t} \times (1 - d_{t,i}) = 0\right] \end{aligned}$$

(2)

4 Fault localization by itemset mining

In this section, we first give our modeling of the fault localization problem as an itemset mining under constraints. Then, we formalize the problem of fault localization as finding the k most suspicious patterns and we detail our algorithm for mining top-$k$  suspicious patterns. Finally, we describe how to exploit the top-k patterns to return at the end an accurate fault localization.

4.1 Modeling the fault localization as a constrained itemset mining

Let $L = \{e_{1},\ldots , e_{n}\}$ be a set of indexed statements composing a program P and $T = \{tc_1,\ldots ,tc_m\}$ a set of test cases. The transactional dataset ${\mathcal {D}}$ is defined as follows: (i) each statement of L corresponds to an item in $\mathcal {I}$, (ii) the coverage of each test case $tc_i$ forms a transaction in $\mathcal {T}$. Moreover, to look for contrasts between subsets of transactions, $\mathcal {T}$ is partitioned into two disjoint subsets ${\mathcal {T}}^+$ and ${\mathcal {T}}^-$. ${\mathcal {T}}^+$ (resp. ${\mathcal {T}}^-$) denotes the set of coverage of positive (resp. negative) test cases.

Let d be the 0/1 (m,n) matrix representing the dataset ${\mathcal {D}}$. So, $\forall t \in \mathcal {T}, \forall i \in \mathcal {I}$, $(d_{t,i}=1)$ if and only if the statement i is executed (at least once) by the test case t. Figure 1 shows the transactional dataset associated to the program Character counter. For instance, the coverage of the test case $t_{5}$ is $I_{5} = (1, 1, 1, 1, 1, 0, 0, 0, 0, 1)$. As $t_5$ fails, thus $I_{5} \in {\mathcal {T}}^{-}$.

Let M be the unknown suspicious pattern we are looking for. As detailed in Sect. 3.2, we introduce two sets of boolean variables: item variables $\{M_1, M_2,\ldots , M_n\}$ representing statements, and transaction variables $\{T_1, T_2,\ldots , T_m\}$ representing test cases. So, M will represent a suspicious set of statements.

Like for $\mathcal {T}$, transaction variables are partitioned into two disjoint subsets: variables $\{T^+_{t}\}$ representing positive test cases ${\mathcal {T}}^{+}$ and variables $\{T^-_{t}\}$ denoting negative test cases ${\mathcal {T}}^{-}$. We define also the frequency measure on ${\mathcal {T}}^{+}$ (resp. ${\mathcal {T}}^{-}$) as ${\textit{freq}}^+(M) = \sum _{t \in \mathcal {T}^+} T^+_t$ (resp. ${\textit{freq}}^-(M) = \sum _{t \in \mathcal {T}^-} T^-_t$).

To reduce the redundancy among the extracted patterns, we have to impose $closed_{freq}(M)$, which states that M must be a closed pattern w.r.t the frequency measure. In our case, this constraint is imposed on ${\mathcal {T}}^{+}$ and ${\mathcal {T}}^{-}$ to ensure that M has no superset with the same frequencies in the two sets. We encode this constraint using equation (3), which is a decomposition of the closedness constraint (2) on ${\mathcal {T}}^{+}$ and ${\mathcal {T}}^{-}$.

$$\begin{aligned}&closed_{freq}(M)\nonumber \\&\quad \equiv \left[ \forall i \in \mathcal {I}: (M_{i} = 1) \leftrightarrow \left( \underset{t\in \mathcal {T}^+}{\sum } T^+_{t} \times (1 - d^+_{t,i}) = 0 \right) \wedge \left( \underset{t\in \mathcal {T}^-}{\sum } T^-_{t} \times (1 - d^-_{t,i}) = 0 \right) \right] \end{aligned}$$

(3)

4.2 top-$k$  suspicious patterns

The intuition behind the most of fault localization methods is that statements that appear in the failing test cases are more likely to be suspicious, while the statements that appear only in the traces of passed executions are more likely to be guiltless (Eric Wong et al. 2010; Jones and Harrold 2005; Renieres and Reiss 2003). To extract the most suspicious patterns (i.e. set of statements), we define a dominance relation $\succ _\mathcal {R}$ between patterns.

Definition 9

(Dominance relation) Given a bipartition of $\mathcal {T}$ into two disjoint subsets ${\mathcal {T}}^+$ and ${\mathcal {T}}^-$, a pattern M dominates another pattern $M'$ (denoted $M \succ _\mathcal {R}M')$, iff:

$$\begin{aligned}&\left[ freq^-(M) > freq^-(M') \right] \nonumber \\&\quad \vee [(freq^-(M) = freq^-(M') ) \, \wedge (freq^+(M) < freq^+(M')) ] \end{aligned}$$

(4)

The dominance relation states that $M \succ _\mathcal {R}M'$, if M is more frequent than $M'$ in ${\mathcal {T}}^-$. If M and $M'$ have the same frequency in ${\mathcal {T}}^-$, M should have a less positive frequency to dominate $M'$.

We also define the indistinct relation $=_{\mathcal {R}}$ between patterns.

Definition 10

(Indistinct relation) Two patterns M and $M'$ are indistinct (denoted by $M=_{\mathcal {R}} M')$, iff

$$\begin{aligned}&\left[ freq^-(M) = freq^-(M') \right] \nonumber \\&\quad \wedge \left[ freq^+(M) = freq^+(M') \right] \wedge {\left[ (M \not \subset M') \wedge (M' \not \subset M) \right] } \end{aligned}$$

(5)

The indistinct relation states that two patterns can have the same level of suspiciousness. According to the dominance relation $\succ _\mathcal {R}$, we define a top-$k$  suspicious patterns.

Definition 11

(top-$k$  suspicious pattern) A pattern M is a top-$k$  suspicious pattern (according to $\succ _\mathcal {R}$) iff $\not \exists P_1,\ldots P_k,\in \mathcal {L}_{\mathcal {I}},\forall 1\le j\le k, \, \, P_j\succ _\mathcal {R}M$.

Thus, M is a top-$k$  suspicious pattern if there exists no more than $(k-1)$ patterns that dominate M. A set of top-$k$  suspicious patterns is defined as follows:

$$\begin{aligned} \{M \in \mathcal {L}_{\mathcal {I}}\mid \texttt {elementary}_{}(M) \, \, \wedge \not \exists P_1,\ldots P_k,\in \mathcal {L}_{\mathcal {I}},\forall 1\le j\le k, \, \, P_j\succ _\mathcal {R}M\} \end{aligned}$$

The constraint $\texttt {elementary}_{}(M)$ allows to specify that M must satisfy a basic property. In our case, we impose that searched suspicious patterns have to satisfy the following property:

$$\begin{aligned} \texttt {elementary}_{}(M) \equiv closed_{freq}(M) \wedge freq^-(M) \ge 1 \wedge size(M) \ge 1, \end{aligned}$$

which means that a suspicious pattern M must be closed in positive and negative test cases, must include at least one statement and must appear at least in a negative test case.

4.3 Mining top-$k$  suspicious patterns

This section shows how the top-$k$  suspicious patterns can be extracted using constraints dynamically posted during search (Rojas et al. 2014). The main idea is to exploit a dominance relation (noted $\succ _\mathcal {R}$) between sets of statements to produce a continuous refinement on the extracted patterns thanks to constraints dynamically posted during the mining process. Each dynamic constraint will impose that none of the suspicious patterns already extracted is better (w.r.t $\succ _\mathcal {R}$) than the next pattern (which is searched). This process stops when no better solution can be obtained.

Algorithm 1 extracts the top-$k$  patterns (i.e., most suspicious patterns) according to the dominance relation $\succ _\mathcal {R}$. It takes as input the positive and negative test cases (${\mathcal {T^+}}$ and ${\mathcal {T^-}}$), a positive integer k, and returns as output top-$k$  suspicious patterns. The algorithm starts with a constraint store equal to $\texttt {elementary}_{}(M)$ (line 1). First, we search for the k first suspicious patterns that are solutions of the current constraint store, using the $SolveNext({\mathcal {C}})$ function (lines 2–4). The $SolveNext({\mathcal {C}})$ function asks a CP solver to return a solution of ${\mathcal {C}}$ which is different from the previous returned solutions. Initially, the first call of $SolveNext({\mathcal {C}})$ returns the pattern $P_1$. The second call will return a pattern $P_2\ne P_1$, and so on. During the search, a list of top-$k$  suspicious patterns ${\mathcal {S}}$ is maintained. Once the k patterns are found, they are sorted according to decreasing order $\succ _\mathcal {R}$ (line 5). Thereafter, each time a new pattern is found, we remove from ${\mathcal {S}}$ the least preferred pattern w.r.t. $\succ _\mathcal {R}$ (line 10), we add the new pattern to ${\mathcal {S}}$ according to the decreasing order $\succ _\mathcal {R}$ (line 11) and we add dynamically a new constraint ($M \succ _\mathcal {R}S_{k}$) at line 7 stating that the new searched pattern M must be better w.r.t. $\succ _\mathcal {R}$ than the least pattern in the current top-$k$  list ${\mathcal {S}}$. Thus, the next solutions should verify both the current set of constraints store and the new constraints added dynamically. This process is repeated until no pattern is generated.

4.4 Fault localization by processing top-k suspicious patterns

Our top-k algorithm returns an ordered list of k best patterns ${\mathcal {S}}=\langle S_1, \ldots , S_k\rangle$. Each pattern $S_i$ represents a set of statements that can explain and locate the fault. From one to another, some statements are appearing/disappearing according to their frequencies in the positive/negative datasets ($freq^-,freq^+$).

We propose in this section an algorithm (see Algorithm 2) that takes as input the top-k patterns and returns a ranked list Loc of most accurate suspicious statements enabling to better locate the fault (line 14). The returned list Loc includes three computed ordered lists noted $\varOmega _1$, $\varOmega _2$ and $\varOmega _3$. Elements of $\varOmega _1$ are ranked first, followed by those of $\varOmega _2$, then by elements of $\varOmega _3$, which contains the least suspicious statements.

Algorithm 2 starts by merging the indistinct patterns of ${\mathcal {S}}$ (Definition 10), i.e. thus having the same frequencies in failing and passing test cases, or equivalently having the same level of suspiciousness. This treatment is achieved by the function $Merge({\mathcal {S}})$ (line 1) which returns a new list ${\mathcal {SM}}$. A pattern resulting from merging mutliple patterns is a single pattern including all statements contained in original patterns. Let us note that the returned list ${\mathcal {SM}}$ may be equal to the initial top-$k$  list ${\mathcal {S}}$ if there are no pair of patterns with the same frequencies ($freq^-,freq^+$). Then, Algorithm 2 initializes $\varOmega _1$ and $\varOmega _3$ to the empty list. $\varOmega _2$ is initialized by statements that appear in the most suspicious pattern of ${\mathcal {SM}}$ (i.e. ${\mathcal {SM}}_1$) (line 3).

From this set of most suspicious statements $\varOmega _2$, Algorithm 2 will try to differentiate these statements by taking advantage of the three following Properties 1, 2 and 3.

Property 1

Given a top-k patterns ${\mathcal {S}}$, ${\mathcal {SM}}_1$ is an over-approximation of the fault-location: $\forall S_i\in {\mathcal {S}} : (freq_1^-=freq_i^-) \wedge (freq_1^+=freq_i^+) \Rightarrow S_i \subseteq {\mathcal {SM}}_1$

Thus, ${\mathcal {SM}}_1$ contains most likely the faulty statement, i.e. statements that are most frequent in the negative dataset and less frequent in the positive dataset. However, it may also contains other statements that are suspicious for a certain degree (over-approximation). That is why, in Algorithm 2, $\varOmega _2$ is initialized to ${\mathcal {SM}}_1$ at line 3.

Property 2

Given the sets of patterns ${\mathcal {SM}}$ (resulting from top-$k$  patterns ${\mathcal {S}}$) and an over-approximation of the fault-location ${\mathcal {SM}}_1 ~ (\varOmega _2)$, some statements of ${\mathcal {SM}}_1$ will disappear in the next ${\mathcal {SM}}_i\in {\mathcal {SM}}: ({\mathcal {SM}}_1{\setminus } {\mathcal {SM}}_i) \ne \emptyset$.

In Algorithm 2, statements that disappear from $\varOmega _2$ and appear in a given ${\mathcal {SM}}_i$ are noted $\varDelta _D$ (line 5). According to the frequency values, we have two cases:

• 1. ${\mathcal {SM}}_i$ has the same frequency as ${\mathcal {SM}}_1$ in the negative dataset but ${\mathcal {SM}}_i$ is more frequent in the positive dataset than ${\mathcal {SM}}_1$. Thus, statements of $\varDelta _D$ are less frequent in the positive dataset compared with those of ($\varOmega _2 {\setminus } \varDelta _D$). So, statements of $\varDelta _D$ are more suspicious than the remaining statements in $\varOmega _2 {\setminus } \varDelta _D$ and should be ranked first (removed from $\varOmega _2$ (line 8) and added to $\varOmega _1$ (line 7)).

• 2. ${\mathcal {SM}}_i$ is less frequent than ${\mathcal {SM}}_1$ in the negative dataset. Again, statements of $\varDelta _D$ should be ranked first and added to $\varOmega _1$.

Consequently, $\varOmega _1$ contains the most suspicious statements derived from the initial state of $\varOmega _2$. The remaining statements in $\varOmega _2$ are those appearing in all patterns ${\mathcal {SM}}_i$ and are ranked second in terms of suspiciousness.

Property 3

Given the sets of patterns ${\mathcal {SM}}$, and an over-approximation of the fault-location ${\mathcal {SM}}_1$, some statements will appear in the next ${\mathcal {SM}}_i\in {\mathcal {SM}}: ({\mathcal {SM}}_i{\setminus } {\mathcal {SM}}_1) \ne \emptyset$.

According to the Property 3, the statements that are not in ${\mathcal {SM}}_1$ and that appear in a given ${\mathcal {SM}}_i$ (line 9) are noted $\varDelta _A$. So, $\varDelta _A$ should be added to $\varOmega _3$ (line 13) and ranked after $\varOmega _2$ as the least suspicious statements in the program (line 14).

In summary, the first ordered list $\varOmega _1$ ranks the statements of $\varOmega _2$ according to their order of disappearance in ${\mathcal {SM}}_2..{\mathcal {SM}}_l$ (line 4). At the end of the algorithm, $\varOmega _2$ will contain the remaining less suspicious statements as compared to the ones of $\varOmega _1$. Finally, the ordered list $\varOmega _3$ will contain statements, which do not belong to $\varOmega _2$ but appears gradually in ${\mathcal {SM}}_2$ to ${\mathcal {SM}}_l$.

5 Running example

In this section, we give an illustrative example to show the result of our method through a simple program named Character counter, introduced in (Gonzalez-Sanchez et al. 2011) and given in Fig. 1. The program contains ten executable statements, executed on eight test cases noted from $tc_1$ to $tc_8$ with failing ($tc_1$ to $tc_6$), and passing test cases ($tc_7$ and $tc_8$). In this example, the fault is introduced at line 3 where the correct statement “let += 1” is replaced by “let += 2”. Figure 1 reports the coverage of each statement with the value 1 if the statement is executed at least once by the test case, 0 otherwise. According to our approach, the coverages of failing (resp. passing) test cases form transactions of the negative (resp. positive) dataset ${\mathcal {T^-}} = \{ tc_1, tc_2, tc_3, tc_4, tc_5, tc_6 \}$ (resp. ${\mathcal {T^+}} = \{ tc_7, tc_8 \}$). Our constraint based model presented in Sect. 4 aims at extracting the k most suspicious patterns. We recall that the meaning given to the notion of suspiciousness is related to the frequency of a given statement in the negative and/or positive datasets. This means that the most suspicious statements are the ones with the highest negative frequency and/or the lowest positive frequency. In this example, we select k equals to the number of statements (i.e., $k=10$) which is sufficient to reach a good accuracy (see Sect. 6) and then we give a ranking on all statements in P from the most suspect to the guiltless ones by processing the top-$k$  patterns. Table 3 reports the top-$k$  ranking of the different patterns computed by the first step of our approach with their respective frequencies. Table 4 gives the results obtained by Algorithm 2 taking as input Table 3 as a second step of our approach.

Table 3 The top-$k$  suspicious patterns returned by Algorithm 1

Table 4 The most suspicious statements with their ranks returned by Algorithm 2

Table 5 The most suspicious statements with their ranks returned by Tarantula  and Growth rate measure

Tarantula and growth rate measures Tarantula’s formula, which computes the suspiciousness of a statement e in the considered program, is defined as follows:

$$\begin{aligned} {\textit{suspiciousness}}(e) = \frac{\frac{{\textit{failed}}(e)}{{\textit{total failed}}}}{\frac{{\textit{passed}}(e)}{{\textit{total passed}}} + \frac{{\textit{failed}}(e)}{{\textit{total failed}}}} \end{aligned}$$

(6)

Formula (6) is very similar to the growth rate formula (given in Definition 6) which measures the emergence of a given pattern from a dataset to another one (i.e., in our case, from negative test cases to positive test cases). The two formulas evaluate the amount of the negative frequency compared with the positive frequency; but Tarantula  avoids dividing by a null positive frequency. In fact, the Tarantula  values have the same increase as the growth rate, and consequently, they both give the same ranking of the statements suspiciousness, as illustrated in Table 5.

According to the Algorithm 2 (line 1), as a first step and before ranking the statements, we merge all patterns with the same frequencies (i.e., the same level of suspiciousness). From Table 3, we have $\forall i<9, {\mathcal {SM}}_i=S_i$, and the two last patterns $S_9, S_{10}$ will be merged in one pattern ${\mathcal {SM}}_9$ that will contain all statements in $S_9$ and in $S_{10}$.

By comparing the results and the ranking strategy of our method (Table 4 ) with those given by Tarantula  in Table 5 (2nd column) and the growth rate (3th column) we draw the following observations:

• First, in our results, the fault, that is introduced in $e_3$, is ranked first and is the most suspicious statement. According to our Algorithm 2, this statement is in the most suspicious pattern ${\mathcal {SM}}_1$ having frequencies ($freq_+=0, freq_-=6)$. We point out that $e_3$ disappears in the next pattern ${\mathcal {SM}}_2$ having frequencies ($freq_+=1, freq_-=6)$. Here, $e_3$ appears in ${\mathcal {SM}}_1$ and disappears in the next ${\mathcal {SM}}_i$, which means that $e_3$ must be added as a disappeared statement to $\varDelta _D$ (at line 5) and removed from $\varOmega _2$ (line 8). But, Tarantula  considers the three statements $e_3$, $e_5$, $e_7$ as the most suspicious with the same rank although these statements have different frequencies in negative test cases. In fact, Tarantula  is unable to distinguish between them.

• By using Tarantula, the statements $\{e_5, e_7\}$ are ranked before $\{e_2, e_4, e_6\}$, whereas statements $\{e_2, e_4, e_6\}$ are more suspicious since they are more present in failing test cases than $\{e_5, e_7\}$. This weak ranking is due to the low precision provided by Tarantula’s formula (6). This weakness is offset by the notion of appearing statements. Let us come back to our example, the statements $e_4$ and $e_6$ are not in the most suspicious pattern $\mathcal {SM}_1$ and they appear in the next patterns. Consequently, these statements are added as appearing statements to $\varDelta _A$ (line 9) and then added to $\varOmega _3$.

• Concerning the statements $\{e_8, e_9\}$ and $\{e_1,e_{10}\}$, Tarantula  reveals that these statements have the same suspiciousness without distinguishing them. Our approach gives the same results and the same suspiciousness because we got them in the same time (same group). In our approach the statement $e_7$ has also the same suspiciousness as $\{e_8, e_9\}$ because these statements appear in different patterns but these patterns have the same frequencies, so these statements will be in the same pattern after the merging step.

This comparison between the effectiveness of Tarantula  and our constrained mining method reveals clearly the accuracy of our method which exploits better the relationships between the statements of the program.

6 Experiments

This section reports several experimental studies. First, we present the benchmark programs we used for our experiments (see Sect. 6.1). Second, we detail our experimental protocol for evaluating our approach (see Sect. 6.2). Third, we study and discuss the influence of parameter k for mining top-$k$  suspicious patterns (see Sect. 6.3). Fourth, we compare our results with those obtained with Tarantula  (Jones and Harrold 2005) and we study the impact of varying the size of the test cases on performances of the two approaches (see Sects. 6.4 and 6.5). Finally, we study and analyze the CPU times of our approach (see Sect. 6.6).

6.1 Benchmark programs

As benchmark programs, we considered the Siemens suite, which is the most common program suite used to compare the different fault localization techniques. The suite contains seven C programs, faulty versions of these programs, and test suites for each category of program.²

Table 6 Faulty programs from the Siemens suite (111 programs)

We recall here that the Siemens programs suite is assembled for fault localization studies as well as for fault detection capabilities of control-flow and data-flow coverage criteria. In our experiments, we exclude 21 versions that are, roughly speaking, out of scope of localization task (e.g., segmentation faults).³ On the whole, we have 111 programs with faults summarized in Table 6.

6.2 Experimental protocol

First of all, we need to know which statement is covered by a given execution. For that, we use the Gcov ⁴ profiler tool to find out the statements that are actually executed by a given test case. Gcov can be used also to know how often each statement is executed. This being said, in our approach we need only the coverage matrix. Thus, we run the program P with a test case and we compare the returned result to the expected one. If the returned result matches with the expected one, we add the according test case coverage to the positive transactional dataset; otherwise we add it to the negative one.

We implemented our approach as a tool named F-CPminer. The implementation was carried out in Gecode,⁵ an open and efficient constraint programming solver. Our implementation includes Algorithm 1 for mining top-$k$  suspicious patterns (see Sect. 4) and Algorithm 2 that processes the top-$k$  patterns and returns at the end an accuracy fault localization with a ranking on statements according to their suspiciousness. All experiments were conducted on a 3.10 GHz processor Intel Core i5-2400 with 8 GB of memory, running Ubuntu 12.04 LTS.

To make a fair comparison between our F-CPminer  and Tarantula, we have implemented Tarantula  and we evaluated the statement suspiciousness as presented in (Jones and Harrold 2005). We used a common metric in fault localization, the exam   score (Wong and Debroy 2009) that measures the effectiveness of a given fault localization technique. The exam   score gives the percentage of statements that a developer will check before the one containing the fault. It is clear that the best approach is the one that has the lowest percentage of exam   score.

Tarantula  and F-CPminer  can return a set of equivalent statements in terms of suspiciousness (i.e., with the same suspiciousness degree). In this case, the effectiveness depends on which statement is to check first . For that reason, we report two exam  scores, the optimistic and the pessimistic one, denoted respectively o-exam   and p-exam. We talk about o-exam   (resp. p-exam) when the first (resp. last) statement to be checked in the set of equivalent statements is the faulty one. We also define a third metric, $\varDelta$ -exam  $=$ o-exam  $-$ p-exam, representing the margin of the exam  score. In other words, $\varDelta$ -exam  represents the distance between the optimistic and the pessimistic score.

6.3 Comparing various values of k for mining top-$k$  suspicious patterns

Our first experiment aims to select the best value of k leading to the best $\varDelta$ -exam  score. Here, a small value for $\varDelta$ -exam   means that the method gives small sets of statements with equivalent suspiciousness, which leads to an accurate localization. We recall that Algorithm 1 for mining top-$k$  suspicious patterns takes as input parameter k. For this experiment, we selected three programs from Replace, Schedule2 and Tcas of different sizes (resp. 245, 128 and 65 executable statements). We have varied the value of k from (n / 5) to ($5\times n$), where n represents the program size in terms of executable statements.

Figure 2 shows the impact of k on the precision of the returned $\varDelta$ -exam   score (i.e., the distance between the optimistic and pessimistic exam   values). The first observation that we can make is that by increasing the value of k, we reduce the distance between o-exam   and p-exam   (i.e., $\varDelta$ -exam). The second observation is that starting from a value of k greater or equal to the program size measured in executable statements (i.e., n), $\varDelta$ -exam   becomes stable. Throughout the rest of this section and according to our tests, k is fixed to the program size.

Fig. 2

Comparing various values of k

6.4 F-CPminer versus Tarantula

Table 7 gives an exam   score based comparison between F-CPminer  and Tarantula  on the 111 faulty programs of Siemens suite. For each class of program (e.g., Tcas includes 37 faulty versions), we report the averaged number of positive test cases $|{\mathcal {T^+}}|$, the averaged number of negative test cases $|{\mathcal {T^-}}|$, the value of k used in F-CPminer  for mining top-$k$  suspicious patterns (corresponding to the program size), the averaged p-exam, o-exam   and $\varDelta$ -exam  values $\pm$ the standard deviation for each class of programs.

The first observation is that F-CPminer  wins on 5 program classes out of 7 according to the reported o-exam   and p-exam   values. For instance, if we take PrintTokens2 class with its 9 faulty versions (see Table 6), using F-CPminer  the fault is localized after examining only $2.66\,\%$ of the code in the pessimistic case (p-exam) with a standard deviation less than 4 and only $1.72\,\%$ in the optimistic case (o-exam) with a standard deviation less than $3\,\%$. On the other side, Tarantula  needs to examine $16.44\,\%$ in the pessimistic case and $15.5\,\%$ of the code in the optimistic case, in both cases, the standard deviation is greater than $17\,\%$.

Table 7 F-CPminer  versus Tarantula  (exam   score comparison)

Our second observation relates to $\varDelta$ -exam   values that are better in Tarantula  than F-CPminer  in most cases. It is worth mentioning that $\varDelta$ -exam   relies heavily on the value of k (see Fig. 2). Using k equal to the program size leads us to a difference not exceeding 4 % for one program class and 1 % for the other classes comparing to Tarantula.

Table 8 Pairwise comparisons between Tarantula  and F-CPminer  

In order to complement the results given by Table 7, we report in Table 8 a pairwise comparison between Tarantula  and F-CPminer  on the 111 faulty programs. For each category of program (e.g., Tcas), we give the number of programs where Tarantula  or F-CPminer  wins by comparing the exam  scores (o-exam and p-exam). We also report the case when the exam   values are equal (i.e., tie game).

The results of Table 8 match with the results given in Table 7, where F-CPminer  is the winner on 5 out of the 7 classes. For instance, if we take the Tcas program class and by comparing the o-exam  (resp. p-exam) value, F-CPminer  is more accurate on 19 (resp. 20) faulty programs, while Tarantula  is better only on 6 (resp. 4) faulty programs. Finally, both approaches obtain the same o-exam  (resp. p-exam) on 12 (resp. 13) programs.

From Tables 7 and 8, a general observation is that F-CPminer  is highly competitive as compared to Tarantula. Indeed, F-CPminer  wins on almost 60 % of benchmark programs (61–62 out of 111 programs), while Tarantula  is doing better on 25 % of benchmark programs (24–29 out of 111 programs). Finally, the two approaches behave similarly on 15 % of the benchmark programs (21–25 out of 111 programs).

Fig. 3

Tarantula  and F-CPminer  effectiveness comparison

Figure 3 shows the effectiveness comparison, based on p-exam   and o-exam, between Tarantula  and F-CPminer. The x-axis reports the exam  values while y-axis reports the cumulative percentages of located faults on the 111 programs. Let us start with the pessimistic case (i.e. p-exam). Until 10 % of exam, both approaches behave similarly by locating more than 40 % of faults. From 10 to 20 %, we observe a difference of 10 % of located faults in favour of F-CPminer  (i.e., 60 % for F-CPminer  instead of 50 % of located faults for Tarantula). For values of exam   in the interval [20 %, 40 %], this difference is reduced up to 6 %. Between 60 and 70 %, Tarantula  arrives to catch up F-CPminer  by locating more than 84 % of the faults. However, F-CPminer  enables to detect 100 % of faults with a exam  value equal to 80 %, while Tarantula  needs to reach 100 % of exam  to locate all the faults. For the optimistic case (i.e. o-exam) showed with dashed curves, F-CPminer  is acting quickly from the beginning by locating more faults than Tarantula. It is important to stress that the two curves do not intersect and the one of F-CPminer  is always above the one of Tarantula. Let us note that after 30 % of exam, F-CPminer  in the pessimistic case detects the same percentage of faults (i.e., 74 %) than Tarantula  in the optimistic case.

In order to strengthen the previous results, we carried out a statistical test using the Wilcoxon Signed-Rank Test, where we are not able to assume a normal distribution of the population (Lyman Ott et al. 2001). Here, the one-tailed alternative hypothesis is used with the following null hypothesis (Tarantula  more efficient than F-CPminer): $H_0:$ The exam  score using F-CPminer  $\ge$ The exam  score using Tarantula. That is, the alternative hypothesis $H_1$ states that our F-CPminer  examined a fewer number of statements before locating the fault than Tarantula  (F-CPminer  more efficient than Tarantula). With this test, we are able to conclude that the use of F-CPminer  is more efficient than Tarantula  ($H_1$ accepted) with $79.99\,\%$ confidence in the pessimistic case (p-exam) and $97.99\,\%$ confidence in the optimistic case (o-exam). This test strengthens the previous results on the comparison of F-CPminer  with Tarantula.

Overall, we can conclude that F-CPminer  enables to locate most of the faults more quickly than Tarantula  in terms of effectiveness (i.e., exam   metric). Moreover, by considering the cumulative exam   over all the 111 faulty programs (i.e. the total number of executable statements that have to be checked for the whole of the 111 faulty programs), F-CPminer  has to check 2861 of statements against 3482 for Tarantula  using p-exam  (gain of 17 %). With o-exam, F-CPminer  needs to check 1808 statements against 2496 for Tarantula  (gain of 27 %).

Finally, we point out the following observations over the tested 111 programs :

• For 110 programs, the faulty statement is in the first pattern (i.e., ${\mathcal {SM}}_1$).

• For 96 programs, the faulty statement is in the first statement disappearing from ${\mathcal {SM}}_1$.

• For 14 programs, the faulty statement is located in $\varOmega _2$.

• For only one program, the faulty statement is located in $\varOmega _3$.

These observations show clearly the effectiveness of the ranking strategy adopted by Algorithm 2.

Fig. 4

Impact of the size of the datasets on the performances of F-CPminer  and Tarantula  

6.5 Impact of the size of test cases on fault localization accuracy

In this section, we study the impact of test cases on F-CPminer  and Tarantula. For that, we have varied the number of test cases given as inputs by varying the sizes of datasets ${\mathcal {T}}^+$ and ${\mathcal {T}}^-$. For each program, we reduced the size of its datasets from 100 to 10 % by removing randomly at each time 10 % of test cases. At each time, we report the exam   score (o-exam   and p-exam) for F-CPminer  and Tarantula. In this section, we selected four programs to present (PrintTokens2-v3, Tcas-v28, TotInfo-v18 and Replace-v22) that we consider quite representative in terms of program and datasets sizes. Figure 4 reports the results on the selected programs.

PrintToken2-v3 For this instance of program, when considering the full datasets (100 % of test cases), F-CPminer  and Tarantula  obtain approximately the same results in terms of exam   score. Once we start reducing the number of test cases, we observe that F-CPminer  keeps approximately the same accuracy until 10 % of test cases. In the other side, Tarantula  exhibits a chaotic behavior where the accuracy decreases (i.e (exam   score) increases) significantly after a reduction of 60 % of test cases by reaching a score of 30 % of code to exam. These observations are made on 6 versions where only one is from the same PrintToken2 class.

Tcas-v28 For this instance, F-CPminer  and Tarantula  obtain approximately the same results in terms of exam   score with a slight gain in favour of our tool. We can observe that datasets reduction have no substancial impact on the accuracy of the two tools. This result is observed on 32 versions where 14 versions belong to the same Tcas class.

TotInfo-v18 Here, F-CPminer  shows a stable behavior and more or less the same accuracy during the datasets reduction, while Tarantula  is greatly impacted by this reduction (i.e., the exam   score changes in a strange manner). The same observations are made on 22 versions where 8 of them are from TotInfo class.

Replace-v22 For this instance, we can see that the two approaches are more or less affected by reducing the size of the datasets, Tarantula  is still more stable until a reduction of 50 % of test cases. F-CPminer  is stable from 75 to 35 % of datasets reduction. For this case, the same observations (i.e., the two approaches are affected by the reduction) are made on 34 other versions from which 7 programs belong to the Replace class.

These observations are particularly informative and highlight the fact that our approach can be less sensitive to the number of considered test cases. This is especially true when we have 60 programs out of 111 where F-CPminer  behaves in the same manner (stable behavior) as the three first programs (see Fig. 4). And this is especially true where on 62 programs Tarantula  follows a chaotic behavior and only on 17 programs, the behavior of Tarantula  is more stable than F-CPminer. Thanks to the quality of our top-$k$  patterns extraction and to the processing step, which enables to analyze the dependencies between the extracted patterns. This is not the case for Tarantula  , where the adding or removing of test cases can lead to less accurate results.

6.6 Analyzing CPU times for F-CPminer

This section analyzes the CPU times of our approach. It is important to recall that Tarantula  approach evaluates the suspiciousness degree of each statement using the formula 6 without taking in account any statement dependencies. Therefore, the combinatorial explosion due to the possible combinations of statements is not tackled by Tarantula. Consequently, the CPU times obtained by Tarantula  are very shorts (in milliseconds).

Table 9 reports for each class of program both the average CPU times and the standard deviation for the two steps performed by F-CPminer  (i.e. the top-$k$  extraction corresponding to Algorithm 1 and the post-processing step corresponding to Algorithm 2).

The first observation that can be made is that extracting top-$k$  patterns is the most costly step for F-CPminer. This is in part explained by the very high number of candidate patterns (i.e. $|\mathcal{L}_{\mathcal {I}}|$). However, in our experiments, the CPU times are not exceeding 235 s for the worst case (see Replace programs) and it is less than 0.2 s in the best case (see Tcas programs). The second observation that can be made is that the CPU times spent by the post-process step for a final localization of the faulty statement is negligible (of order of milliseconds for the best and worst cases).

Table 9 Comparing the CPU times for the two steps of F-CPminer  on different programs (in seconds)

Fig. 5

CPU times variation for top-k extraction (Algorithm 1) for Replace program

Fig. 6

Impact of varying the size of the dataset and the value of k on CPU times

Figure 5 shows the CPU times variation for extracting top-k patterns for the 29 faulty versions (from v1 to v29) of the Replace program. For this class, the standard deviation of CPU time is quite large (i.e., 86.02 s) according to an average CPU time equal to 147.69 s. The deviation is not negligible due to the fact that all program versions take the same test cases but different ${\mathcal {T}}^+$ and ${\mathcal {T}}^-$ according to the introduced fault. For instance, for v5, $(|{\mathcal {T}}^-|,|{\mathcal {T}}^+|)=(271,5271)$ and F-CPminer  requires about 400 s. to extract the top-$k$  patterns. For comparison, for v24, $(|{\mathcal {T}}^-|,|{\mathcal {T}}^+|)=(3,5539)$ and F-CPminer  needs less CPU times to complete the extraction of top-$k$  pattens (22 s). In fact, extracting top-$k$  patterns from a small negative dataset (i.e. ${\mathcal {T}}^-$) and a considerable positive dataset (i.e. ${\mathcal {T}}^+$) is not time consuming. This is especially true when the extracted patterns are the more frequent ones in the negative dataset and less frequent ones in the positive dataset.

Impact of the size of test cases and parameter k on CPU times Figure 6 shows the impact of varying the size of the dataset (i.e. test case) and the value of k on the CPU times for the top-$k$  extraction. For this experiment, we have selected the program Replace(v5), which represents the worst case for extracting top-K. We can observe that CPU time decreases considerably when reducing the number of test cases (see Fig. 6a). The same trend is observed when varying the value of k (see Fig. 6b).

In fact, the extraction of top-$k$  patterns is closely related to the size of the transactional datasets (test cases coverage) and the value of k. The behavior of Fig. 6b can be explained by the fact that with a large value of k, a large number of patterns are extracted and the least patterns of the top-$k$  list have low values of frequency. This increases drastically the number of candidate patterns to be explored by Algorithm 1 and thus the CPU times. In contrast, with small values of k, the least patterns in the top-$k$  list tend to have high values of frequency. Consequently, constraints added dynamically during the mining process (line 7 of Algorithm 1) will refine the pruning condition leading to more and more powerful pruning of the search space. This explains the decreasing of CPU times.

7 Related works

In this section, we present some related works in the area of fault localization.

Using failing/passing executions As introduced previously, Tarantula  (Jones and Harrold 2005) is one of the most popular fault localization technique that records information linked to failing/passing executions in terms of how each test case covers statements. Another technique rather close to Tarantula  is the one proposed by (Cleve and Zeller 2005) and based on program states. The technique compares states of passing and failing test cases. In a previous work (Zeller 2002), Zeller shows that locating a fault just by considering the search space (variables, values) is not sufficient in general. Indeed, it is possible to return statements as faulty ones by comparing the different states in passing/failing test cases, but a fault in a program can produce a difference on all next states in the program. In (Cleve and Zeller 2005), a search during execution is performed to locate the first transition that leads to a fail. But these techniques do not differentiate between two failing (resp. passing) test cases, and consequently they ignore the dependencies between statements that can help us to locate the fault.

Using dependence analysis Other techniques take in account the cause effect chains with a dependence analysis by using, for instance, program slicing (Agrawal et al. 1993). The disadvantage here is that fault can be located in a quite large slice (static slicing) and/or can be time/space consuming (dynamic slicing). In the same perspective, Renieris and Reiss (2003) use the notion of nearest neighbor, where they confront a failing trace with the nearest passing trace. Here the distance between two traces is expressed with the difference between the set of executed statements. In the case where no nearest passing trace can be obtained, the technique builds the program dependence graph and checks the adjacent nodes of the failing trace one by one with the hope of finding the location of the fault.

Using data mining In (Cellier et al. 2009), Cellier et al. propose a data mining process DeLLIS which computes program element clusters and shows dependencies between program elements. They compute all differences between execution traces and, at the same time, gives a partial ordering of those differences. In (Cellier et al. 2008), Cellier et al. propose a methodology that combines between association rules to search for possible causes of failure and formal concept analysis to assist in fault localization. They try to identify rules between statement execution and corresponding test case failure, and then measure the frequency of each rule. (Nessa et al. 2008) generate statement subsequences of length N, referred to as N-grams, from the trace data. The failed execution traces are then examined to find the N-grams with a rate of occurrence higher than a certain threshold in the failed executions. A statistical analysis is conducted to determine the conditional probability that an execution fails given that a certain N-gram appears in its trace.

Our approach aims at exploiting recent progress on cross-fertilization between data mining and constraint programming in order to model the fault localization problem as finding the top-k patterns of statements occurring more frequently in failing executions and less frequently in the passing executions. These top-k patterns are then processed by analysing their dependencies, in order to infer a ranking on the suspiciousness degree of the statements.

8 Conclusion

In this paper we have proposed a new approach based on itemset mining and constraint programming to deal with fault localization problem. Our approach proceeds in two steps. In the first step, we have formally defined the problem of locating faults in programs as a mining task using CP for modelling and solving the arising constraints. Solving the underlying CP model enables us to get the top-k most suspicious set of statements . The second step aims at ranking in a more accurate way the whole top-k statements by taking benefit of two main observations (i) where faults are introduced in a program can be seen as a pattern (set of statements), which is more frequent in failing executions than passing ones; (ii) the difference between a more suspicious pattern and a less suspicious one is a set of statements that appears/disappears in one or the other; this difference helps us to know more about the location of the fault. We have shown how these two properties can be exploited in an ad-hoc ranking algorithm producing accurate localization. Finally we have compared experimentally our approach implemented in F-CPminer  with Tarantula  on a set of faulty programs. The results we obtained show that our approach enables to propose a more precise localization as compared to Tarantula.

As future works, we plan to experiment our approach on programs with complex faults (more than one faulty statement). We also plan to explore other observations on the behavior of a faulty program and adding them as constraints for mining the location of faults.