Mosquito-inspired distributed swarming and pursuit for cooperative defense against fast intruders

Abstract

Inspired by the swarming behavior of male mosquitoes that aggregate to attract and subsequently pursue a female mosquito, we study how random swarming motion in autonomous vehicles affects the success of target capture. We consider the scenario in which multiple guardians with limited perceptual range and bounded acceleration are deployed to protect an area from an intruder. The main challenge for the guardian (male mosquito) is to quickly respond to a fast intruder (female) by matching its velocity. We focus on the motion strategy for the guardians before they perceive the intruder, which we call the swarming phase. In the parameter space consisting of the intruder’s speed and guardians’ ability (i.e., maximum acceleration and perceptual range) we identify necessary and sufficient conditions for target capture. We propose a swarming algorithm inspired by the behavior of male mosquitoes to improve the target-capture capability. The theoretical results are illustrated by experiments with an indoor quadrotor swarm.

1 Introduction

The problem of pursuit has been studied in various contexts including missile guidance, surveillance, robot control, and animal behavior. Taxonomy and surveys of the research in the field have been presented, for example, in Robin and Lacroix (2016) and Chung and Hollinger (2011). Two ways we consider here to categorize the existing work are by the definition of target capture (intercept and tracking) and by the pursuer’s capability (dynamics and sensing).

For the missile-guidance application, the goal of the pursuit is target intercept, where the pursuer aims to collide with the target (Zarchan 2002; Moon et al. 2001; Shtessel 2009). Target intercept is also considered in pursuit–evasion games, where pursuit and evasion strategies have been studied with game-theoretic approaches (Antoniades et al. 2003; Selvakumar and Bakolas 2016). Animals also exhibit this type of pursuit behavior, exemplified by the prey capture of bats (Ghose et al. 2006) and dragonflies (Olberg et al. 2000); bio-inspired algorithms for pursuit and evasion have been studied (Wei et al. 2009; Scott and Leonard 2013).

A less aggressive pursuit scenario considered for the application to autonomous robots is target tracking, where a pursuer seeks to approach and stay close to the target without colliding with it. A path-planning algorithm to track a ground vehicle with a UAV is proposed in Lee et al. (2003). Strategies to encircle a target with a team of pursuers are proposed in Kim and Sugie (2007) and Bopardikar et al. (2009). Both target intercept and target tracking fall into the class of problems denoted as following by Robin and Lacroix (2016).

Another important aspect of pursuit problems is the capability of the pursuers. First, consider how the pursuer’s sensor is modeled. One category in the pursuit–evasion game is the so-called search problem, where pursuers have limited perceptual range (Antoniades et al. 2003; Durham et al. 2012). The objective of the pursuer is to intelligently search for the target without the knowledge of its location (pursuit before detection). On the other hand, in the missile-guidance literature and in target-tracking problems, it is assumed that the pursuer at least knows the position of the target (pursuit after detection). Second, consider how the dynamics of the pursuer are modeled. In the robotics community, there are studies on pursuit problems for the application to agents with specific constraints (Ruiz et al. 2011; Tian and Sarkar 2017). However, more generally, when the agents are treated as point particles, the majority of pursuit–evasion games assume that the pursuer has a constant speed (Antoniades et al. 2003; Lee et al. 2003; Kim and Sugie 2007; Bopardikar et al. 2009), whereas some other works consider variable speed (Moon et al. 2001; Shishika et al. 2016; Li 2017).

Wild swarms of malarial mosquitoes (Manoukis and Diabate 2009; Butail et al. 2013) show an interesting combination of these categories, which motivates the formulation of a new type of pursuit problem. Male mosquitoes aggregate and form mating swarms to attract female mosquitoes that fly faster than the males. In this stage, which we call the swarming phase, male mosquitoes do not know where the female is. They cooperate with one another to increase the chance of encounter with a female. When the female enters the swarm, male’s pursuit behavior is triggered only when the distance to the female becomes small, which we call a close encounter. This switching in the male’s behavior indicates that they have limited perceptual range to detect the female.

After the pursuit phase, the male and female exhibit coupling flight during which they fly in approximately the same direction while their separation distance oscillates—as though they are connected by a damped spring with zero rest length (Shishika and Paley 2015). For a male to achieve this flight, simply intercepting a female is insufficient; he also has to align his velocity with the female. For this reason, the objective of the mosquito pursuit is a combination of target tracking and intercept. In addition, since the female flies faster than a swarming male, a male has to accelerate after the close-encounter in order to successfully track the female. Therefore, the mosquito pursuit has to be modeled by agents with variable speed.

The combination of limited perceptual range and the dynamical model of the agent raises the importance of quick response, i.e., when a male detects a female, it has to speed up and match the velocity of a fast female in time so that the female does not escape from its perceptual range. The velocity matching may also require favorable initial conditions for the male, i.e., its initial velocity should be relatively aligned with female. This observation motivates our investigation below of continuously moving rather than static guardians.

Although the pursuit law that governs the motion of mosquitoes in the pursuit phase is an interesting topic, we focus on the swarming phase in this work [see Shishika et al. (2016) for our previous work on pursuit after detection]. A key characteristic of insect swarms is their unpolarized oscillatory motion (Butail et al. 2013), in contrast to fish schools (Becco et al. 2006), bird flocks (Cavagna et al. 2010), and formation controls inspired by those animals (Olfati-Saber and Murray 2003; Levant 2006). The oscillatory motion and the interactions between males have been previously studied (Shishika et al. 2014), and it has been suggested that this motion may increase the sensitivity to external stimuli, for example, to respond quickly to a female that enters the swarm (Attanasi et al. 2014; Shishika and Paley 2015).

Inspired by mosquito behavior, we study how swarming (unpolarized oscillatory) motion may be useful in a scenario where multiple pursuers with limited perceptual range wait for a fast target that comes from an unknown direction at an unknown time. The goal of the pursuers is to track the target, so simply blocking the target by constructing a wall-like formation will not achieve the goal. Instead, the successful pursuer also has to match its velocity with the target.

The difficulty of achieving target capture depends on the capability of the pursuer (perceptual range and maximum acceleration) relative to the target’s speed. We explore this parameter space to identify when swarming motion is necessary for the pursuer’s success. We further study what kind of swarming motion will increase the probability of successful pursuit. In addition, experiments using a small quadrotor testbed are conducted to illustrate the theoretical results. The experiments also highlight some of the challenges of real-life implementation, which in turn improve our swarming algorithm.

The contributions of this work are (1) identification of necessary and sufficient conditions related to guaranteed target capture; (2) analysis of how swarming behavior helps the pursuer’s response to the target; (3) a control law that achieves swarming motion while also avoiding collisions; and (4) experimental demonstration of the control-theoretic results. The problem studied in this work can be applied to a situation where multiple vehicles are deployed to enforce a no-fly zone, for the application to drone countermeasures, or for convoy protection. The results of this work may provide a guideline in selecting the capabilities of the vehicles for such applications, and also provide a methodology to fully utilize those capabilities [this formulation of the pursuit problem was previously introduced in Shishika and Paley (2017); a new swarming algorithm, its analysis based on numerical simulation, and new experimental results are included here for the first time].

The paper is organized as follows. Section 2 formulates the problem. Section 3 presents the results from control-theoretic analyses. Section 4 presents the swarming algorithm and simulation results. Section 5 introduces the quadrotor testbed and describes the experimental results. Section 6 summarizes the paper and ongoing and future work.

Fig. 1

Illustration of the swarming and pursuit scenario. In the swarming phase, an intruder (red) is approaching the protected region (green). The guardians (with static formation here for clarity) are deployed to wait for the intruder. Once the intruder enters the perceptual range, the guardian turns into a pursuer and the intruder becomes the target (Color figure online)

2 Problem formulation

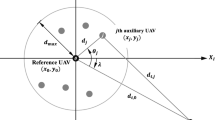
Consider a planar system of point particles with unit mass representing $N_P$ guardians and $N_T$ intruders (we use the subscripts $_T$ and $_P$ to denote the intruder/target and guardian/pursuer, respectively). The intruders seek to pass through a protected region that is known to the guardians. Figure 1 illustrates the case where only one intruder is seen in the picture. The timing and the direction of the intruder trajectories are unknown to the guardians. Once the intruder enters the perceptual range of a guardian, the roles of the agents change—the intruder becomes a target and the guardian becomes a pursuer. The goal of the pursuer is to capture the target (i.e., approach the target and stay close to it). Although the difference between target capture that occurs before and after the intrusion is important to some applications [see Shishika et al. (2017) for some preliminary analyses], we do not distinguish between those two cases in this paper.

Consider the case where the protected region is sufficiently small to be approximated as a point O. Let O to be the origin of the inertial frame; ${\mathbf {r}}_i$, ${\mathbf {v}}_i$, and ${\mathbf {a}}_i$ denote the position, velocity, and acceleration of agent i in the inertial frame. The agents have second-order dynamics, i.e., $\dot{{\mathbf {r}}}_i = {\mathbf {v}}_i$ and $\dot{{\mathbf {v}}}_i = {\mathbf {a}}_i$, where ${\mathbf {a}}_i$ is the control input. We assume the following capabilities of the guardians:

• (A1) The magnitude of the guardian’s acceleration is bounded according to $\Vert {\mathbf {a}}_P \Vert \le u_\mathrm {max}$; and

• (A2) Each guardian perceives the position and velocity of all other agents within the range $\rho _a$.

We also introduce another perceptual range that determines when the pursuit behavior is triggered:

• (A3) Each guardian becomes a pursuer once the distance to an intruder becomes less than $\rho _p$.

The threshold $\rho _p$ is inspired by the observation that the pursuit behavior of a male mosquito is triggered by the close encounter with a female. We also note that the parameter $\rho _p$ allows two interpretations. First, it can be interpreted as the limitation of the guardians to distinguish between a friendly guardian vehicle and the intruder, i.e., guardian i does not know whether an agent j (in its perceptual range) is an intruder or not if $\rho _p<\Vert {\mathbf {r}}_{j/i} \Vert < \rho _a$, where ${\mathbf {r}}_{j/i} = {\mathbf {r}}_j - {\mathbf {r}}_i$. Second, $\rho _p$ may be a control parameter that the guardian can choose; i.e., the guardian will ignore the intruder unless it is closer than the distance $\rho _p$. In either case, the value of $\rho _p$ does not exceed $\rho _a$.

In contrast to target intercept, where pursuers aim to collide into the target, we consider target tracking, defined as follows.

Definition 1

Let ${\mathbf {r}}_{T/P}={\mathbf {r}}_{T}-{\mathbf {r}}_{P}$ denote the relative position of the target with respect to the pursuer. Let $r_\mathrm {cap}>0$ denote the capture threshold. Target capture is successful if there exists $t_\mathrm {cap}$ such that $\Vert {\mathbf {r}}_{T/P}\Vert < r_\mathrm {cap}$, for all $t>t_\mathrm {cap}$.

From assumption (A2), the pursuit can last as long as the target is in the range $\rho _a$. Therefore, we choose the threshold in Definition 1 to be $r_\mathrm {cap}=\rho _a$.

Fig. 2

State transition between swarming phase and pursuit phase

Now we define the two phases of the capture problem. When a guardian has not perceived the intruder yet, it is in the swarming phase. When the intruder enters the circle with radius $\rho _p$ around a guardian, the pursuit phase starts. This reduction in the distance, i.e., $\Vert {\mathbf {r}}_{T/P}\Vert \le \rho _p,$ is defined as a close encounter. The pursuit phase continues as long as the distance remains less than $\rho _a$. When the pursuit fails, i.e., $\Vert {\mathbf {r}}_{T/P}\Vert > \rho _a,$ the guardian returns to the swarming phase.

Note that the phase is defined for each guardian. The transition between these two phases are summarized in Fig. 2. Although we discuss the control law for the pursuit phase in Sect. 3.2, the main focus of the work is on the swarming phase. The success of target capture depends on how quickly a guardian can respond (i.e., close the distance and match the velocity) to the intruder once it is in perceptual range $\rho _p$. If the response is too slow, then the target will escape from the range $\rho _a$. We seek to find a strategy for how the guardians should prepare for the intruder to maximize the probability of target capture.

To focus on the guardians’ strategy, assume that the intruder moves with a constant velocity $\Vert {\mathbf {v}}_T\Vert =v_T$ on a straight path that passes through O. (The case with a maneuvering target is discussed in Sect. 3.3) Note that even with this simplification, the intruders can choose from a variety of different strategies in terms of the directions from which they approach O and the timing of their arrival. Let $t_j^{\text {int}}$ and $\psi _j^{\text {int}}$ denote the time and azimuthal direction that the jth intruder arrives at O (assuming it is not captured), and let $T_j^{\text {int}}=t_{j+1}^{\text {int}} - t_j^{\text {int}}$ denote the time interval between two successive intruders. The sets $\{ \psi _j \}$ and $\{ T_j^{\text {int}} \}$ significantly affect the success rate of pursuit. In this paper, we study the case where $T_j^{\text {int}}$ is sufficiently large that each intruder may be considered separately. This scenario can be approximated as a single-intruder case, i.e., $N_T=1$ [the effects of $\{ \psi _j \}$, $\{ T_j^{\text {int}} \}$, and $N_T$ are subjects of ongoing work, e.g., see Shishika et al. (2017)]. Table 1 lists the parameters that are introduced in this section.

Table 1 List of system parameters and their nominal values

3 Control theoretic analysis

This section describes a condition for when the target capture fails by a static guardian and introduces nondimensional parameters that describe the difficulty of target capture. We then derive sufficient conditions for target capture, which motivate the swarming algorithms in the sequel.

3.1 Limitation of static guardian

A naive strategy is to uniformly distribute stationary guardians around the protected area as in Fig. 1 and wait for the intruder. However, if the intruder is too fast, the guardian may not react (i.e., speed up and align its velocity) in time to keep the intruder in the perceptual range. We first find the necessary condition for a static guardian to achieve target capture.

Proposition 1

A guardian who is stationary at the beginning of the pursuit phase never achieves target capture if

$$\begin{aligned} u_\mathrm {max} < \frac{v_T^2}{2(\rho _p + \rho _a)}. \end{aligned}$$

(1)

Proof

Consider the easiest case for the pursuer: the target trajectory passes through the pursuer’s position. Let $t_f = v_T/u_\mathrm {max}$ denote the time required for the pursuer to reach the speed $v_T$. The target escapes if it can travel a distance longer than $\rho _p + \rho _a + \frac{1}{2}u_\mathrm {max} t_f^2$ within time $t_f$. The inequality $v_T t_f > \rho _p + \rho _a + \frac{1}{2}u_\mathrm {max} t_f^2$ reduces to (1). $\square$

The above condition is given in terms of the intruder’s speed $v_T$ and the guardian’s capability $u_\mathrm {max}$, $\rho _a$, and $\rho _p$. To explore this parameter space efficiently in the following sections, we introduce the following two nondimensional parameters:

$$\begin{aligned} \alpha = \frac{\rho _p}{\rho _a}\;\;\;\;\;\; \mathrm {and}\;\;\;\;\;\; {\varGamma }= \frac{2u_\mathrm {max}(\rho _a+\rho _p)}{v_T^2}. \end{aligned}$$

(2)

The first parameter $\alpha \in (0,1]$ is the pursuit activation distance, which describes the ratio between the two perceptual ranges defined in assumptions (A2) and (A3). The second parameter ${\varGamma }$ is the nondimensionalized guardian acceleration, which describes the ratio between the guardian’s capability and the intruder’s speed. Noting that ${\varGamma }$ is obtained from the limiting case in (1), a static guardian will fail to capture a target if ${\varGamma }< 1$. (We introduce an augmented version of ${\varGamma }$ considering the effect of time delay in Sect. 5.3.)

For the case with infrequent intruders (or, equivalently, $N_T=1$), the difficulty of target capture can be completely described by the two nondimensional parameters $\alpha$ and ${\varGamma }$ and the number of guardians $N_P$, which we summarize in Table 2 with nominal values derived from the dimensional parameters in Table 1. For the frequent-intruders case, the number of intruders $N_T$ as well as their strategies (e.g., $\{\psi ^{\text {int}}_j \}$ and $\{T^{\text {int}}_j \}$, see Sect. 2) determine the difficulty of target capture.

Table 2 List of nondimensionalized system parameters that describe the difficulty of target capture and their nominal values

3.2 Sufficient conditions for target capture

Next, we derive a sufficient condition for target capture. Since the condition will be given for the relative velocity ${\mathbf {v}}_{T/P}$ at the time of close encounter (i.e., the initial condition of the pursuit phase), it applies to any guardian strategy in the swarming phase. Based on this general condition (Proposition 2), we consider two cases: a static swarm (Corollary 1) and a swarm with a circling motion (Corollary 2).

As a pursuit law, ${\mathbf {a}}_P = {\mathbf {F}}^\mathrm {(pursuit)}_P$, following our previous work on mosquito-inspired swarm model (Shishika and Paley 2015), consider a force resembling a damped-spring attached to the target, i.e.,

$$\begin{aligned} {\mathbf {F}}^\mathrm {}_P = c {\mathbf {r}}_{T/P} + b {\mathbf {v}}_{T/P}, \end{aligned}$$

where c and b are positive constants. With the constraint

$$\begin{aligned} 0<c<u_\mathrm {max}/\rho _a, \end{aligned}$$

(3)

the spring term alone never exceeds the acceleration limit $u_\mathrm {max}$. In this case, there always exists a scaling factor $\beta \in (0,1]$ such that

$$\begin{aligned} \Vert c {\mathbf {r}}_{T/P} +\beta b {\mathbf {v}}_{T/P} \Vert \le u_\mathrm {max}. \end{aligned}$$

(4)

In this way, the actual pursuit force is saturated as follows:

$$\begin{aligned} {\mathbf {F}}^\mathrm {(pursuit)}_P= & {} c {\mathbf {r}}_{T/P} + \beta b {\mathbf {v}}_{T/P}, \nonumber \\ \beta= & {} \left\{ \begin{array}{l r} 1 &{} \mathrm {if}\; \Vert c {\mathbf {r}}_{T/P} + b {\mathbf {v}}_{T/P} \Vert < u_\mathrm {max},\\ \beta ^* &{} \mathrm {otherwise}, \end{array}\right. \end{aligned}$$

(5)

where $\beta ^*>0$ is the maximum value of $\beta$ that satisfies the equality in (4). The value of $\beta ^*$ as a function of ${\mathbf {r}}_{T/P}$, ${\mathbf {v}}_{T/P}$, c and b can be obtained using Stewart’s theorem in geometry (see Appendix A). Although mosquitoes exhibit underdamped oscillation (Shishika and Paley 2015), for the application to guardians, a large number for b (i.e., an over-damped spring) gives good performance since velocity alignment is necessary for target capture. (Instability caused by the time delay also has to be taken into account for the gain tuning, in practice.) However, the following proposition gives a sufficient condition for target capture, which is independent of the choice of c and b as long as (3) is satisfied.

Proposition 2

Consider a pursuer under (5) with the gain c satisfying (3). Let $t_0$ denote the time when $\Vert {\mathbf {r}}_{T/P}\Vert = \rho _p$ (i.e., the time when the pursuit phase starts). The target capture is guaranteed if

$$\begin{aligned} \Vert {\mathbf {v}}_{T/P}(t_0)\Vert \le v_0 = v_T\chi , \;\;\mathrm {where}\;\; \chi = \sqrt{\frac{{\varGamma }(1-\alpha )}{2}}. \end{aligned}$$

(6)

Fig. 3

Sufficient condition on the initial velocity for target capture depicted in the velocity space. Target capture is guaranteed if the pursuer’s velocity (blue arrow) lies in the red circle at the beginning of the pursuit phase (Color figure online)

Proof

Consider the energy function

$$\begin{aligned} V = \frac{1}{2}\Vert {\mathbf {r}}_{T/P}\Vert ^2 + \frac{1}{2c}\Vert {\mathbf {v}}_{T/P}\Vert ^2. \end{aligned}$$

Since the target is not accelerating, the time derivative of V is

$$\begin{aligned} c \dot{V}= & {} c {\mathbf {r}}_{T/P}\cdot {\mathbf {v}}_{T/P} + {\mathbf {v}}_{T/P}\cdot ({\mathbf {a}}_{T}-{\mathbf {a}}_P)\\= & {} c {\mathbf {r}}_{T/P}\cdot {\mathbf {v}}_{T/P} - {\mathbf {v}}_{T/P}\cdot ( c {\mathbf {r}}_{T/P} + \beta b {\mathbf {v}}_{T/P})\\= & {} - \beta b\Vert {\mathbf {v}}_{T/P}\Vert ^2. \end{aligned}$$

Thus, V is nonincreasing for all $t>t_0$. It follows that

$$\begin{aligned} \frac{1}{2}\Vert {\mathbf {r}}_{T/P}(t)\Vert ^2 \le V(t) \le V(t_0) = \frac{1}{2}\rho _p^2 + \frac{1}{2c}\Vert {\mathbf {v}}_{T/P}(t_0)\Vert ^2. \end{aligned}$$

We obtain $\Vert {\mathbf {r}}_{T/P}(t)\Vert \le \rho _a$ for all $t>t_0$ if the right hand side of the above inequality is bounded by $\frac{1}{2}\rho _a^2$, i.e.,

$$\begin{aligned} \frac{1}{2}\rho _p^2 + \frac{1}{2c}\Vert {\mathbf {v}}_{T/P}(t_0)\Vert ^2\le & {} \frac{1}{2}\rho _a^2\\ \Vert {\mathbf {v}}_{T/P}(t_0)\Vert\le & {} \sqrt{c(\rho _a^2- \rho _p^2)} \end{aligned}$$

Noting (from definitions of ${\varGamma }$ and $\alpha$) that

$$\begin{aligned} \frac{u_\mathrm {max}}{ \rho _a}(\rho _a^2- \rho _p^2)=v_T^2\frac{{\varGamma }(1-\alpha )}{2}, \end{aligned}$$

the above inequality is equivalent to (6) with the constraint (3). $\square$

If the pursuer’s velocity ${\mathbf {v}}_P(t_0)$ at the time of close encounter lies in the circle

$$\begin{aligned} B_{v_0}({\mathbf {v}}_T(t_0)) \equiv \{ {\mathbf {v}}\; | \; \Vert {\mathbf {v}}-{\mathbf {v}}_T(t_0)\Vert \le v_0 \}, \end{aligned}$$

which is centered at ${\mathbf {v}}_T(t_0)$ with radius $v_0$ (see Fig. 3), the target capture is guaranteed. If ${\varGamma }$ is sufficiently large that the origin of the velocity space ($O_v$ in Fig. 3) is included in $B_{v_0}({\mathbf {v}}_T(t_0))$, even a static pursuer can guarantee target capture. This case is stated in the following result.

Corollary 1

Target capture is guaranteed by a pursuer that is stationary at the beginning of the pursuit phase if the following condition is satisfied:

$$\begin{aligned} {\varGamma }> \frac{2}{1-\alpha }. \end{aligned}$$

(7)

Proof

From Proposition 2 and the discussion above, the sufficient condition is $v_0 > v_T$, which reduces to (7). $\square$

One strategy to achieve the velocity alignment derived in Proposition 2 is to use a circling motion. The target capture is guaranteed if the circling motion has (i) a radius less than $\rho _p$ so that O is always in the perceptual range; (ii) sufficient speed such that $\Vert {\mathbf {v}}_P\Vert \in (v_T-v_0,\; v_T+v_0)$; and (iii) there are sufficiently many guardians so that there exists one whose direction of motion is approximately aligned with ${\mathbf {v}}_T$ when the intruder passes through O. Assuming (iii) is true, the conditions (i) and (ii) give the following result.

Corollary 2

Assuming that there are sufficiently many guardians so that there always exists one whose direction of motion is approximately aligned with ${\mathbf {v}}_T$ (see Appendix B for the required number of guardians), a circular motion around O guarantees target capture if

$$\begin{aligned} \sqrt{\frac{{\varGamma }}{2}}\left( \sqrt{\frac{ \alpha }{1+\alpha } }+\sqrt{1-\alpha } \right) > 1. \end{aligned}$$

(8)

Proof

Given the smallest required speed $v_T-v_0$ and the acceleration bound $u_\mathrm {max}$, the radius of the circular orbit has to be greater than $(v_T-v_0)^2/u_\mathrm {max}$ to be able to counteract the centrifugal acceleration. From condition (i), the radius also has to be smaller than $\rho _p$. Therefore, the condition is $\rho _p > (v_T-v_0)^2/u_\mathrm {max}$, which is equivalent to (8). $\square$

The analysis on the required number of guardians for condition (iii) to hold is presented in the Appendix.

The necessary and sufficient conditions (1), (7) and (8) are summarized in Fig. 4. Region ${{\mathscr {R}}}_1$ is where a static swarm fails to achieve target capture. Region ${{\mathscr {R}}}_3$ is where a static swarm is guaranteed to achieve target capture, assuming that the intruder encounters at least one guardian. The region ${{\mathscr {R}}}_2\cup {{\mathscr {R}}}_3$ is where a circling swarm is guaranteed to achieve target capture. The circling motion guarantees target capture with lower ${\varGamma }$ as compared to a static swarm. If ${\varGamma }$ is below the red curve in Fig. 4, guardians cannot achieve the desired circular motion, i.e., either the radius is too large or the speed is too low. Section 4 proposes strategies for the guardians so that they can achieve target capture even inside of region ${{\mathscr {R}}}_1$.

3.3 Maneuvering target

This section discusses the case where the target can change its direction of motion in an effort to evade the guardian. Our previous work (Shishika et al. 2016) proposes a robust pursuit law guaranteeing target capture in the presence of target acceleration that is bounded but unknown and time-varying. While our previous work focused on the design of pursuit algorithm, the main focus of this work is the behavior in the swarming phase. Therefore, we retain the simple pursuit law (5) and study how the condition in Proposition 2 can be modified to accommodate target maneuver.

Fig. 4

Conditions for target capture in the nondimensional parameter space: ${{\mathscr {R}}}_1$ is where the static formation never achieves target capture; ${{\mathscr {R}}}_2$ is where target capture is guaranteed by circling formation; ${{\mathscr {R}}}_3$ is where the static formation guarantees target capture (Color figure online)

Fig. 5

Deflection in target’s direction of motion by angle $\phi$

Consider the case where the target can change its direction of motion (see Fig. 5). We still assume that the target has a constant speed $v_T$, i.e., maneuver is achieved through the application of a thrust that is normal to the velocity vector. We also restrict this turning to occur in one direction, but the timing can be arbitrary—either before or after the target reaches O. We characterize the target maneuver by the net deflection angle $\phi$ shown in Fig. 5. Let ${\mathbf {v}}_T(t_1)$ and ${\mathbf {v}}_T(t_2)$ be the velocity vectors before and after the maneuver. Restricting the deflection angle to be $\phi \in [0,\pi )$, it is defined as

$$\begin{aligned} \phi = \text {acos} ({\mathbf {v}}_T(t_1) \cdot {\mathbf {v}}_T(t_2)) \end{aligned}$$

(9)

The following result gives a sufficient condition for target capture under this target maneuver.

Proposition 3

Consider a pursuer under (5) with the gain c satisfying (3). Let $t_0$ denote the time when $\Vert {\mathbf {r}}_{T/P}\Vert = \rho _p$, and $\chi$ be defined in (6). When the target can turn in one direction by a net angle $\phi$, the target capture is guaranteed if

$$\begin{aligned} \Vert {\mathbf {v}}_{T/P}(t_0)\Vert\le & {} v_0' = v_T\sqrt{\chi ^2 - 2a(1+\chi )},\;\; \mathrm {and} \end{aligned}$$

(10)

$$\begin{aligned} \chi> & {} a + \sqrt{a^2 + 2a}, \;\;\mathrm {where} \\ a= & {} \sin {\left( \frac{\phi }{2}\right) }.\nonumber \end{aligned}$$

(11)

Proof

Provided in Appendix C. $\square$

Notice that when there is no deflection (i.e., $\phi =0$), we have $a=0$, and condition (10) reduces to (6) in Proposition 2. As the angle $\phi$ increases, the constraint on the initial condition becomes more stringent (i.e., the right-hand side of (10) becomes smaller). However, the constraint remains feasible (i.e., $v_0'>0$) as long as condition (11) is satisfied.

For the case when the target continuously makes evasive maneuvers, a sufficient condition for target capture can be obtained through a Lyapunov analysis with the concept of ultimate boundedness (Khalil and Grizzle 2002). Since the analyses on the pursuit phase is not the main focus of this work, we state the result qualitatively in the following remark and refer the interested reader to Appendix D for the proof and more details.

Remark 1

Consider the case where the target has second-order dynamics with the magnitude of its acceleration bounded according to $\Vert {\mathbf {a}}_T\Vert \le u_T$. Then target capture is guaranteed if (i) $u_T$ is sufficiently small; (ii) control gains c and b in (5) are chosen properly; (iii) $u_{\text {max}}$ is sufficiently large; and (iv) ${\mathbf {v}}_{T/P}(t_0)$ is sufficiently small. The proof and the actual conditions are provided in Appendix D.

4 Algorithms and simulation results

This section considers the strategies for the guardians in the swarming phase to achieve target capture even when ${\varGamma }<1$. We first describe the probabilistic nature of the problem, and state the objectives of the swarming motion. After a brief review of our previous work on circling and radial motion (Shishika and Paley 2017), we propose a swarming algorithm that generates random oscillatory motion around O. We modify the swarming law by adding a mosquito-inspired interaction term and study the performance of the algorithms with numerical simulations.

4.1 Objectives of swarming motion

In the previous section, Proposition 2 showed that target capture can be achieved if the velocities of the guardian and the target at the time of close encounter are aligned so that the relative velocity is sufficiently small. This condition suggests the importance of the guardians maintaining sufficiently high velocity during the swarming phase. In addition, the condition prerequisite to velocity matching is that a close encounter occurs. Therefore, the two key objectives of the swarming motion are to (i) maintain high density around O where the intruder passes through; and (ii) maintain high speed that lies in the circle $B_{v_0}({\mathbf {v}}_T(t_0))$.

Note that now the problem of target capture is probabilistic. Each guardian may encounter an intruder with probability $P_{\text {e}}$, and the velocity at the time of close-encounter may lie in $B_{v_0}({\mathbf {v}}_T(t_0))$ with probability $P_{\text {a}}$. Since target capture occurs if those two occur for any of the guardians, the probability of target capture $P_{\text {cap}}$ is dictated by $P_{\text {e}}$ and $P_{\text {a}}$.

Our previous work (Shishika and Paley 2017) considered various orbiting motions around O that are generated from a central force. We used the roundness and energy of the orbiting motion as the tuning parameters of the swarming behavior studied how the optimal orbit (in terms of $P_{\text {cap}}$) varies depending on the system parameters ${\varGamma }$ and $\alpha$.

The orbiting motion enabled the guardians to capture the target even when ${\varGamma }<1$, however, the approach had two disadvantages. First, for orbits that are close to radial motion, there is a high risk of collision near the center. Second, since the orbiting motion was deterministic (except for the initial conditions), the strategy and its weaknesses may be detected by the intruders in more practical settings (e.g., the intruder may try to approach O on the side opposing the direction of rotation). To overcome these disadvantages, we present a new swarming algorithm next.

4.2 Random-swarming algorithm

The control law for the guardian is described by the combination of artificial forces that generates the desired acceleration of the agent. The overall forcing on agent i is

$$\begin{aligned} {\mathbf {F}}_i = (1-\lambda ^P_i){\mathbf {F}}^{\text {(swarm)}}_i + \lambda ^P_i{\mathbf {F}}^{\text {(pursuit)}}_i, \end{aligned}$$

(12)

where the switching parameter $\lambda _i^P\in \{0,1\}$ takes the value $\lambda _i^P=0$ (resp. 1) in the swarming (resp. pursuit) phase. The pursuit term ${\mathbf {F}}^{\text {(pursuit)}}_i$ is defined in (5). The swarming algorithm ${\mathbf {F}}^{\text {(swarm)}}_i$ consists of three forces: central, spacing, and random force, i.e.,

$$\begin{aligned} {\mathbf {F}}_i^{\text {(swarm)}} = {\mathbf {F}}_i ^{\text {(cent)}} + {\mathbf {F}}_i ^{\text {(spac)}} + {\mathbf {F}}_i ^{\text {(rand)}}. \end{aligned}$$

(13)

The central force ${\mathbf {F}}^{\text {(cent)}}_i,$ resembling a damped spring attached to O,  maintains the cohesiveness of the swarm:

$$\begin{aligned} {\mathbf {F}}_i ^{\text {(cent)}} = -k_{\text {c}} {\mathbf {r}}_i - b_{\text {c}} {\mathbf {v}}_i, \end{aligned}$$

(14)

where positive constants $k_{\text {c}}$ and $b_{\text {c}}$ are the control gains.

The spacing force ${\mathbf {F}}_i ^{\text {(spac)}}$, which also resembles a damped spring, generates attraction, repulsion, and alignment behavior between the agents:

$$\begin{aligned} {\mathbf {F}}_i ^{\text {(space)}} = -k_{\text {s}}\sum _{j\in S_i^{(\rho _s)}} \left( 1-\frac{x_0}{\Vert {\mathbf {r}}_{i/j} \Vert } \right) {\mathbf {r}}_{i/j} -b_{\text {s}}{\mathbf {v}}_{i/j}. \end{aligned}$$

(15)

The positive parameter $x_0$ denotes the rest length of the spring, and the set $S_i^{(\rho _s)}=\{\;j\;|\;\Vert {\mathbf {r}}_{i/j} \Vert \le \rho _s \}$ consists of all the agents within range $\rho _s$ from agent i. By choosing $x_0$ to satisfy $(\rho _s - x_0)/\rho _s \ll 1$, the guardians may form a crystalized formation shown in Fig. 7a [the formation is called an $\alpha$-lattice in Olfati-Saber and Murray (2003)]. However, the convergence to crystalized formations depends on the amount of energy dissipation in the system. Therefore, random swarming motion may be generated even with the selection $x_0 \approx \rho _{\text {s}}$.

The spacing term can be used to control the density of the swarm by modulating the inter-agent distance. In addition, another important purpose of the spacing term is to avoid collisions between guardians. Therefore, the selection of $\rho _{\text {s}}$ (and $x_0$) may depend on the relative size of the vehicle with respect to the perceptual range $\rho _a$, i.e., a small value of $\rho _{\text {s}}$ may be sufficient to guarantee collision avoidance if the vehicle size is small. In this work, instead of introducing another parameter to describe the vehicle size, we make a conservative choice: $\rho _{\text {s}}=\rho _{\text {a}}$.

The random force ${\mathbf {F}}_i^{\text {(rand)}}$ has a constant magnitude, $\Vert {\mathbf {F}}_i^{\text {(rand)}}\Vert = K_{\text {r}}u_{\text {max}}$, in a random direction $\theta _i$, i.e.,

$$\begin{aligned} {\mathbf {F}}_i^{\text {(rand)}} = K_{\text {r}}u_{\text {max}} [\cos \theta _i,\;\sin \theta _i]^T, \end{aligned}$$

(16)

where $K_{\text {r}}\in [0,1)$. The random variable $\theta _i$ is generated by the following process:

$$\begin{aligned} {{\dot{\theta }}} = W w_i, \end{aligned}$$

(17)

where $w_i$ denotes unit-intensity white noise and $W>0$ is a parameter describing the intensity. The intensity W determines how much (on average) the force ${\mathbf {F}}_i^{\text {(rand)}}$ changes its direction in each time step.

The main purposes of the random forcing ${\mathbf {F}}_i^{\text {(rand)}}$ are (i) to make the trajectories of the guardians unpredictable to the intruders [unlike the orbiting motion studied in Shishika and Paley (2017)]; and (ii) to propel the guardians to maintain sufficiently high speed during the swarming phase (recall the second objective of swarming stated in Sect. 4.1). For the latter purpose, we seek W that maximizes the mean speed of the guardians during the swarming phase. Figure 6 shows how the mean speed (average taken over agents and time) varies with W for different $K_{\text {r}}$. The mean velocities are obtained from numerical simulations performed with nominal parameters shown in Tables 1 and 3. Figure 6 shows that for every choice of $K_r$, there exists an optimal W that maximizes the mean speed. The figure also shows that the magnitude $K_{\text {r}}$ positively affects the mean velocity of the guardians.

Fig. 6

Mean velocity in the swarming phase as a function of the intensity of the white noise, W, that drives the direction of the random forcing. Different lines are generated from different magnitudes, $K_{\text {r}}$, of the random forcing. The red circles highlight the critical points (Color figure online)

Table 3 List of parameters in the swarming algorithm and their nominal values

Treating W as a function of $K_r$, the random force only has a single parameter $K_r$. Figure 7 shows the snapshot of the swarm with different values of $K_r$. The edges indicate the link defined by the proximity-based interaction used in ${\mathbf {F}}_i^{\text {(spac)}}$. A crystalized formation ($\alpha$-lattice) forms for small values of $K_r$, whereas the links are broken and the swarm becomes more random for larger values of $K_r$. The trajectories extending from the particles indicate the velocities that they have, i.e., guardians have higher velocities for larger $K_r$. The figure also shows that there is a tradeoff between the two objectives of the swarm—high density and high speed (although it is possible to modulate the spring constant $k_{\text {c}}$ to maintain a fixed swarm density while the speeds of the agents are increased with $K_r$, we allow the swarm density to decrease here in order to reduce the risk of collision).

Fig. 7

Snapshots of the swarm showing how the strength of random forcing, $K_r$, changes the swarm from a crystalized formation to random oscillatory motion. The edges connect the agents within the range $\rho _a$

Finally, note that the magnitude of ${\mathbf {F}}_i^{\text {(swarm)}}$ can exceed the limit $u_{\text {max}}$, in which case the control is saturated while preserving its direction, i.e.,

$$\begin{aligned} {\mathbf {F}}_i= \frac{u_{\text {max}}{\mathbf {F}}_i^{\text {(swarm)}} }{\Vert {\mathbf {F}}_i^{\text {(swarm)}} \Vert }. \end{aligned}$$

(18)

The next section studies how the random swarming motion affects the probability of target capture.

4.3 Optimal randomness

We introduced various control parameters in Sect. 4.2 that are listed in Table 3. However, we are most interested in how the random oscillatory motion plays a role in the target capture scenario. Therefore, we choose $K_{\text {r}}$ to be the independent parameter of the swarming motion and study how the random forcing affects the probability of target capture.

Numerical simulations calculate the probability of target capture $P_{cap}$ by counting the number of successful pursuits. In the simulation, the success of target capture (see Definition 1) is assessed using the energy function introduced in the proof of Proposition 2, i.e., the target is captured if the quantity $V_i = \frac{1}{2}\Vert {\mathbf {r}}_{T/i}\Vert ^2 + \frac{1}{2c}\Vert {\mathbf {v}}_{T/i}\Vert ^2$ becomes less than $\frac{1}{2}\rho _a^2$ at any point in time for any guardian i.

Fig. 8

Probability of target capture as a function of $K_r$ (the strength of random forcing). The nondimensionalized guardian acceleration ${\varGamma }$ is varied in (a), whereas the number of pursuers $N_P$ is varied in (b)

Figure 8 shows how $P_{cap}$ varies as a function of $K_r$ for different sets of parameters. The critical points are highlighted with circles. The left figure shows the effect of ${\varGamma }$ and the right figure shows the effect of $N_P$. The trend on the optimal $K_r$ can be explained by the two objectives of the swarming: density and speed (see the discussion in Sect. 4.1). For a larger $K_r$, the guardians have higher speed by sacrificing the density of the swarm, and vice versa. Therefore, the optimal $K_r$ increases with increasing $N_P$, because a larger swarm inherently has a high probability of target encounter, $P_{\text {e}}$, and is able to sacrifice density. On the other hand, the optimal $K_r$ reduces with increasing ${\varGamma }$ because guardians with higher ${\varGamma }$ do not have to rely on their initial speed for successful pursuit (i.e., they inherently have high $P_a$) and, therefore increasing the density is more important than maintaining high velocity. The specific values of $K_r$ that give optimal $P_{cap}$ vary if we tweak the other parameters in Table 3, however, the aforementioned trends are preserved.

4.4 Gain modulation

This section discusses some of the strategies for the guardians to adapt to different situations by tuning their control gains in the swarming phase.

Recall that the expression of nondimensionalized guardian acceleration ${\varGamma }$ in (2) involves target speed $v_T$, which implies that for intruders with different speeds, the value of ${\varGamma }$ will be different for each of them even if the guardians’ capabilities ($u_{\text {max}}$, $\rho _a$ and $\rho _p$) are fixed. The immediate application of the simulation results in the previous section (Fig. 8a) is to modify $K_r$ according to the prior knowledge about the speeds of incoming intruders. If the intruder is expected to be slow (i.e., ${\varGamma }>1$), the guardians should wait with a crystalized formation using $K_r=0$. On the other hand, if the intruder is expected to be fast (i.e., ${\varGamma }\ll 1$), the guardians should increase their speed by using $K_r\approx 1$.

Consider another situation where the number of guardians changes over time. For example, if the guardians leave the swarm as they successfully track the intruders, the number of guardians that remain in the swarm decreases over time. If more guardian vehicles are deployed to join the swarm, the number $N_P$ may increase over time. In either case, the guardians should modulate the gain $K_r$ according to the result in Fig. 8b; i.e., increase (resp. decrease) $K_r$ when $N_P$ increases (resp. decreases). (Estimation of $N_P$ without a centralized control system is an interesting problem, but it is out of the scope of this paper.)

Finally, consider another situation where the guardians have some prior knowledge about the azimuthal direction of the intrusion $\psi _j^{\text {int}}$; e.g., the probability density function of $\psi _j^{\text {int}}$. The guardians can increase $P_{cap}$ by modifying the central force ${\mathbf {F}}_i^{\text {(cent)}}$ as follows. Let R denote a rotation matrix

$$\begin{aligned} R({{\hat{\psi }}}) = \left[ \begin{array}{c c} \cos {{\hat{\psi }}} &{} \sin {{\hat{\psi }}} \\ -\sin {{\hat{\psi }}} &{} \cos {{\hat{\psi }}} \end{array} \right] , \end{aligned}$$

(19)

and ${\varLambda }$ denote a diagonal matrix

$$\begin{aligned} {\varLambda }(\sigma ) = \left[ \begin{array}{c c} 1/\sigma &{} 0 \\ 0 &{} \sigma \end{array} \right] , \end{aligned}$$

(20)

where additional parameter ${{\hat{\psi }}}$ describes the expected direction of intrusion and $\sigma >1$ describes the confidence in that direction. The swarm is elongated in the ${{\hat{\psi }}}$ direction by the following modification:

$$\begin{aligned} {\mathbf {F}}_i^{\text {(cent)}} = R({\hat{\psi }})^T{\varLambda }(\sigma )R(\hat{\psi }) \left( -k_c {\mathbf {r}}_i -b_c {\mathbf {v}}_i\right) . \end{aligned}$$

(21)

Figure 9 shows the snapshots from simulation. The elongated swarm increases both $P_e$ and $P_a$ if ${\hat{\psi }}$ is sufficiently close to the actual $\psi ^{\text {int}}$.

Fig. 9

Snapshots of the swarm showing how the elongation of the swarm is controlled by the parameter $\sigma$. The expected direction of intrusion is ${\hat{\psi }}=\pi /4$, and the randomness is chosen to be $K_r=0.3$

We introduced ways in which guardians can utilize prior knowledge about the intruders to maximize the probability of target capture. The next section introduces simple communication between the guardians to enable cooperation and show how it significantly improves the probability of target capture.

4.5 Velocity-alignment interaction

The swarming algorithm introduced in Sect. 4.2 focused on the individual motion of the guardians. In this section, we seek to add cooperation among the guardians to further improve the target-capture capability. In particular, we consider collaboration that is generated from a velocity-alignment behavior.

The employment of velocity-alignment behavior is inspired by swarms of male mosquitoes. In Shishika et al. (2014), we analyzed the flight data of wild mosquitoes and observed their intermittent velocity-alignment behavior. Although the reason for the velocity-alignment behavior is unknown, one hypothesis is that the male mosquitoes may be transmitting information about the presence of a female mosquito in the swarm.

Since male mosquitoes are competing against each other to mate with the female, the male that sees a female will not broadcast that information to other males. Instead, it is the other males that try to sense male behavior changes to recognize the presence of a female. On the other hand, the guardian vehicles are cooperating with each other, so it is reasonable for them to actively communicate to share the information about the presence of the intruder.

Consider a one-digit binary signal (i.e., communication of “Yes” or “No,” instead of a serial communication like “010010...”) that each vehicle can broadcast to other vehicles within the range $\rho _a$. The signal from vehicle i tells other vehicles whether it is in a regular swarming state or in an alerted state, which is the union of pursuit phase and velocity-alignment phase. In practice, the signal can be based on vision or acoustic sensing received by cameras or microphones, for example. Although there exist more sophisticated communication schemes that may carry richer information—like target position and/or velocity—we show how this one-digit binary signal can be used to significantly improve performance.

The algorithm for the velocity-alignment behavior is as follows. Let $S^{\text {(alert)}}$ be the set of guardians that are either in pursuit phase or velocity-alignment phase. A guardian i in the swarming phase switches to velocity-alignment phase if it sees any guardian in the set $S^{\text {(alert)}}$, i.e., if the following set is nonempty:

$$\begin{aligned} S_i^{\text {(align)}}=\{\;j\;|\;\Vert {\mathbf {r}}_{i/j} \Vert \le \rho _a,\; j\in S^{\text {(alert)}}\}. \end{aligned}$$

(22)

The velocity-alignment phase will terminate in one of the following two ways: (i) guardian i switches back to the swarming phase when $S_i^{\text {(align)}}=\emptyset$; or (ii) it switches to the pursuit phase when it encounters the target, i.e., $\Vert {\mathbf {r}}_{T/i}\Vert <\rho _p$.

Additional forcing for guardian i in the velocity-alignment phase is

$$\begin{aligned} {\mathbf {F}}^{\text {(align)}}_i = b_{\text {a}}\sum _{j\in S_i^{\text {(align)}}} {\mathbf {v}}_{j/i}, \end{aligned}$$

(23)

which is equivalent to changing the damping constant $b_{\text {s}}$ in the spacing term ${\mathbf {F}}^{\text {(spac)}}$ to $b_{\text {a}}$, only for those guardians in the set $S_i^{\text {(align)}}$. The constant $b_{\text {a}} \, (>b_{\text {s}})$ is sufficiently large that it dominates the other control terms during the the velocity-alignment phase.

If the guardian in pursuit phase aligns its velocity to the target and if the velocity-alignment interaction propagates through the swarm, guardians that are far from the target can start moving in the direction that matches the velocity of the target. This mechanism allows the guardians to effectively increase their perceptual range $\rho _p$ to the size of the swarm in order to gain favorable initial conditions for pursuit.

Fig. 10

Probability of target capture with velocity-alignment behavior. The nondimensionalized guardian acceleration ${\varGamma }$ is varied in (a), whereas the number of pursuers $N_P$ is varied in (b). Note that ${\varGamma }=0.7$ instead of 0.9 (see Fig. 8b) is used in (b)

Figure 10 shows $P_{cap}$ with varying $K_r$. For fixed $N_P=10$, the target is always captured (i.e., $P_{cap}=1.0$) for ${\varGamma }$ greater than 0.7. Similarly for fixed ${\varGamma }=0.7$, target capture is guaranteed for $N_P>10$. This improvement is significant compared to the results from the random-swarming case in Fig. 8 (note that ${\varGamma }=0.9$ was used for Fig. 8b). The figure also shows that $P_{cap}=1.0$ is achieved with a crystalized formation ($K_r=0$), because high connectivity is necessary for the guardians to propagate the velocity-alignment interaction.

Note, guardians perceive only the velocities of nearby agents, and this information is not transmitted through communication. Therefore, for the velocity-alignment strategy to work properly in the target-capture scenario, it is necessary that the guardians in the spanning tree of the interaction graph quickly adjust their velocities in the correct direction (i.e., the direction of target’s motion). Otherwise, the error in the direction may propagate through the interaction network, and guardians far from the target may end up accelerating in the wrong direction. (The issue of velocity-alignment in erroneous directions occurs in the experiments due to the slow response of the guardians caused by latency in the closed-loop system. In Sect. 5.5, we address this issue and augment the velocity-alignment behavior by adding a directionality constraint to their interaction.)

4.6 Relation to alternative problem formulation

This section discusses the relation between the proposed swarming algorithm and other existing research that studies search, tracking, and capturing strategies for a group of mobile agents. Although direct comparison of the performance is impossible due to the difference in the underlying assumptions, we discuss some overlapping aspects that are amenable for qualitative comparisons.

Search problem: There is a group of work that addresses the problem of detecting intruders or evaders in an unknown space using mobile robots (Kolling and Carpin 2010; Durham et al. 2012). In the so-called clearing problem a group of robots form frontier lines between “cleared” and “contaminated” regions and explores the space while guaranteeing the detection of targets that pass through the frontier. This scenario is related to the swarming phase in our work, during which the guardians do not know where the intruder is. Compared to the algorithms developed for clearing problem, the disadvantage of our algorithm is its sub-optimality and lack of theoretical guarantees in detecting the intruder, which is apparent from the probabilistic nature explained in Sect. 4.1. However, since the guardians do not need explicit motion coordination in our algorithm, our approach may be more robust to agent failures and removal of communication capabilities.

Tracking problem: A scenario that covers both the swarming phase and the pursuit phase is the tracking problem, where a team of robots coordinate their motion to maintain good estimates of the position of a moving target (Jung and Sukhatme 2002; Hausman et al. 2016). This estimation aspect is not considered in our work for simplicity. However, incorporation of estimation may be necessary for a more realistic scenario, and it may also improve the pursuit behavior enabling the guardians to continue target pursuit even when the intruder is out of its perceptual range, e.g., by using the estimated position.

Another group of work including Ferrari (2006) and Ferrari et al. (2009) addresses the problem of detection and interception of targets with multiple pursuers that have limited sensing range. To determine the control action, the robots exhaustively consider all possible trajectories of the targets. The relation between those trajectories and the pursuers’ location are taken into account in order to maximize the probability of target detection. The sensor information from one robot is used by all other robots so they can decide on their action, e.g., who should pursue which target. The main difference with our work is in the architecture. The above mentioned algorithm enables efficient deployment of the pursuers with the use of centralized information such as the location of all the robots and the targets. On the other hand, our algorithm is limited in efficiency, but is completely distributed and requires no central observer or extensive communication. In addition, the aspect of quick response is not considered in any of the above works.

Capture problem: With the assumption that the target position is known for all time, a number of works study how to encircle a target with multiple pursuers (Kim and Sugie 2007; Bopardikar et al. 2009). The notion of capture is stronger in this scenario in the sense that the target needs to be surrounded by the pursuers, instead of just one guardian staying close to the intruder. Encirclement is possible only when the pursuers are faster than the target, i.e., the region of the parameter space where the pursuers have high capabilities, which differs from the focus here.

5 Experimental results

This section experimentally demonstrates the analyses in Sects. 3 and 4 using a quadrotor swarm. Additional challenges that arise in the experimental implementation are discussed and the algorithms are augmented to overcome those challenges.

5.1 Experimental testbed

We conducted experiments using a group of small quadrotors in an indoor motion-capture environment. We used six BLADE Nano QX, a commercially available quadrotor. The architecture of the experiments is summarized in Fig. 11. The commands are computed on a desktop computer and sent to an Arduino Nano via USB serial communication. The Arduino Nano converts the received serial signal into a Pulse Position Modulation (PPM) command and sends it to the trainer port of a Spektrum DX6 transmitter that sends Radio Frequency (RF) commands to the vehicle. The OptiTrack motion-capture system tracks the position and attitude of the vehicle and streams them to the computer. When it is sent out from the computer, the control law proposed in Sect. 4.2 is converted to a desired stick input (see Zuo 2010 for details).

Fig. 11

The architecture of the experimental setup. The red numbers indicate the approximate time delay from each component. The blue box is duplicated according to the number of vehicles (Color figure online)

An additional challenge in our experimental setup is the time delay caused by the vehicle dynamics and the communication between Matlab and the Nano QX. It takes approximately 170 ms for the commands from the computer to affect the vehicle acceleration. Another limitation is the size of the test area. The horizontal footprint of the vehicle is $18.2\times 18.2 \, \hbox {cm}$, whereas the horizontal area of the volume tracked by the motion-capture system is approximately $3 \times 3 \, \hbox {m}$.

5.2 Disturbance observer

A number of techniques to track desired position, velocity, and acceleration exist in the literature (see for example Hehn and D’Andrea 2011; Mueller and D’Andrea 2013). These works assume an inner-loop controller that takes the desired acceleration and body-rotation rates as inputs and produces individual motor thrusts using feedback from Inertial Measurement Unit (IMU) data. However, the architecture shown in Fig. 11 does not allow direct control of the thrust vector and thus achieving a specified acceleration becomes a nontrivial problem for the following reasons. First, we do not have access to the IMU data on the vehicle and also the position data from motion capture system is too noisy to estimate the acceleration. Second, because of the reflective markers mounted on the vehicle, there is an offset in the position of the center of mass and trimming did not completely eliminate the effect of this offset. Third, even if each vehicle is trimmed accurately, the battery usage significantly affects the conversion from stick input to the achieved acceleration.

Therefore, we elect to use an adaptive disturbance observer to estimate the discrepancy between the desired and achieved acceleration [a more general version of this observer was introduced in Friedland and Park (1992) for the application to friction compensation in mechanical systems]. Let ${\mathbf {d}} \triangleq {\mathbf {a}}_{\text {actual}} -{\mathbf {u}}_{\text {des}}$ be the disturbance, i.e., the difference between the actual and desired acceleration of the vehicle. The goal is to estimate ${\mathbf {d}}$ and augment the control input as

$$\begin{aligned} {\mathbf {u}}_{\text {des}}' = {\mathbf {u}}_{\text {des}} - \hat{{\mathbf {d}}}, \end{aligned}$$

(24)

where $\hat{{\mathbf {d}}}$ denotes the estimated disturbance. The actual acceleration then becomes ${\mathbf {a}}_{\text {actual}} = {\mathbf {u}}_{\text {des}} + {\mathbf {d}}-\hat{{\mathbf {d}}}$. For the case where ${\mathbf {d}}$ is constant the following observer drives the estimation error ${\mathbf {e}} = {\mathbf {d}} - \hat{{\mathbf {d}}}$ to zero:

$$\begin{aligned} \hat{{\mathbf {d}}}= & {} {\mathbf {z}} + k_O {\mathbf {v}}, \end{aligned}$$

(25)

$$\begin{aligned} \dot{{\mathbf {z}}}= & {} - k_O ({\mathbf {u}}_{\text {des}} + \hat{{\mathbf {d}}}), \end{aligned}$$

(26)

where $k_O>0$ denotes the observer gain and ${\mathbf {z}}$ denotes the observer states (to derive this result use the Lyapunov function $V=\frac{1}{2}\Vert {\mathbf {e}} \Vert ^2$). Although the disturbance due to battery usage is time varying, it is sufficiently slow compared to the vehicle dynamics that we may treat this disturbance as constant.

5.3 Effect of time delay

The nondimensionalized guardian acceleration ${\varGamma }$ quantifies the difficulty of the target capture problem. Since we have time delay in the experimental testbed, the guardian can only respond to the intruder $\tau =170$ ms after the close encounter. Modifying the proof of Proposition 1, we define the augmented version of the pursuer acceleration ${\varGamma }'$ as follows.

The time it takes from the close encounter to the time that the guardian reaches the speed $v_T$ is now $t_f'=v_T/u_{\text {max}}+\tau$. The intruder has to travel the distance $\rho _a +\rho _p + \frac{1}{2}u_{\text {max}} t_f^2$ in order to escape. The condition for escape is now $v_T t_f' > \rho _a +\rho _p + \frac{1}{2}u_{\text {max}} t_f^2$, and this condition gives rise to the following time-delayed guardian acceleration:

$$\begin{aligned} {\varGamma }' \triangleq {\varGamma }- \frac{2u_{\text {max}}\tau }{v_T}. \end{aligned}$$

(27)

The effective advantage on the guardian’s side reduces in proportion to the time delay $\tau$. Extending the theoretical analysis in Sect. 3.1, we expect that a static guardian with ${\varGamma }'<1$ will never capture the target in the experiment.

This extension agrees with our previous experiment in Shishika and Paley (2017), where we concluded that ${\varGamma }>1.78$ is necessary for a static guardian waiting at O to capture the target, when the following parameters were used: $\rho _a = 0.6$, $\rho _p = 0.4$, $v_T=2.6$, and $u_{\text {max}}=6$. Using the definition (27) with the time delay in our system $\tau \approx 0.17$ s, we obtain ${\varGamma }'\approx 0.99$, which is close to 1, as expected.

5.4 Optimal randomness in swarming algorithm

We conducted experiments of the swarming and pursuit scenario with six guardians to validate the simulation results in Sect. 4.3. Based on the analysis in the previous section, we use ${\varGamma }'$ as the index to describe the difficulty of the pursuit problem. Specifically, we chose $\rho _a=1.0~\hbox {m}$, $\rho _p = 0.5~\hbox {m}$, $u_{\text {max}}=2.0~{\hbox {m/s}}^2$, and $v_T=2.23~{\hbox {m/s}}$, which corresponds to ${\varGamma }'=0.9$.

The swarming algorithm in Sect. 4.2 is extensible to three dimensions, except for the random forcing term. Since we only consider the case where the target speed has zero vertical component, pursuit behavior is considered in the horizontal direction only. Although we give guardians reference altitudes with 15 cm intervals, the spacing term ${\mathbf {F}}^{\text {(spac)}}$ is nonetheless important to ensure collision avoidance and to avoid the downwash from the vehicles above.

The perceptual ranges $\rho _a$ and $\rho _p$, as well as the intruder, are represented virtually in Matlab. The pursuit is defined to be successful if the following two conditions are satisfied: (i) a guardian is in pursuit phase when the target reaches the boundary of the motion-capture arena; and (ii) at that time, the energy function satisfies $V\triangleq \frac{1}{2}\Vert {\mathbf {r}}_{T/P}\Vert ^2 + \frac{1}{2c}\Vert {\mathbf {v}}_{T/P}\Vert ^2 < \frac{1}{2}\rho _a^2$, as considered previously in the simulation study.

We ran 30 experiments for each of 4 values of $K_r$ and obtained the probability of target capture. Due to the limitation in the motion-capture area, the values of ${\varGamma }$ greater than 0.7 could not be tested (recall that the size of the swarm increases with $K_r$). Figure 12 shows the comparison of the experimental data with the simulation results. The 6000 trials from the simulation results are partitioned into 200 sets of 30 trials to compute the expected variance in $P_{cap}$ (see the box plot in Fig. 12). For the values of $K_r$ that are tested, the experimental results show the same trend as the simulation results; i.e., the experimental results support the existence of the optimal random forcing at around $K_r=0.3$ for this set of ${\varGamma }$, $\alpha$ and $N_P$. The agreement between simulation and experimental results also supports the validity of the augmented parameter ${\varGamma }'$.

5.5 Velocity-alignment behavior

We tested the velocity-alignment behavior with a swarm of six guardians. Following the simulation results in Sect. 4.5, we study only the case with $K_r=0$, which yields the optimal performance. The sensing and communication, as well as the intruder motion are represented virtually in Matlab.

Fig. 12

Probability of target capture as a function of the strength of random forcing. For each $K_r$, experimental results are calculated from 30 trials. The animation is available at (https://youtu.be/Cnz75WZ88rI). ${\varGamma }$ greater than 0.7 are not tested due to the constraint in the motion-capture area. The box plot is obtained from computer simulation; i.e., 200 sets of 30 trials are used to see the variance that we expect from 30 experimental runs

Fig. 13

Comparison of the velocity-alignment forcing in simulation and experiment. All guardians quickly respond in the desirable direction in the simulation, whereas the guardians have forcing in various directions in the experiment. Note that the velocity vectors for guardians are scaled six times larger than the intruder for clarity

Fig. 14

Snapshot of pursuit scenario with the velocity alignment strategy. The animation is available at (https://youtu.be/Cnz75WZ88rI). An intruder approaches from the right bottom of the figure. a Guardian 3 and 4 are in pursuit phase and there is a network of velocity alignment interaction also involving guardians 1, 2, and 5. As a result, guardian 2 is already accelerating towards the top left corner (see the forcing ${\mathbf {F}}_2$), which matches with the direction of the target velocity. b At the time guardian 2 encounters the target, its velocity ${\mathbf {v}}_2$ is well aligned with the target velocity ${\mathbf {v}}_T$. Note that guardian 4 is still in pursuit phase since the target is still within the range $\rho _a$ (but not $\rho _p$). c Guardian 2 successfully tracks the target, while other guardians are returning to O (i.e., their accelerations are pointing towards O)

A major challenge in the experimental setting is highlighted in Fig. 13. In the simulation, all guardians instantaneously respond to the target through velocity-alignment behavior, and their acceleration (see the forcing vector in Fig. 13) point in the same direction that matches the target velocity. However, in the experiment, forcing vectors point in various directions (see Fig. 13b).

The velocity-alignment forcing in erroneous directions are caused by the delay in individual velocity-matching interaction. In simulation, guardians 2, 4 and 6 are already aligned with guardian 5. However, in the experiment, guardians 2, 3, and 4 are not yet aligned with guardian 6. As a result, guardian 1 is accelerating towards the right bottom at this moment, since it is matching its velocity to guardians 3, 4, and 5 who have their velocities in the wrong directions. The velocity-matching in the experiment is slower than the simulation because (i) the latency in the closed-loop system delays the response to alerted neighbors; and (ii) latency also generates velocity oscillation during crystalized formation, which may give unfavorable initial conditions, e.g., see guardian 3 in Fig. 13b.

To reduce the velocity-alignment in erroneous directions, we augment the algorithm by introducing directionality in the communication. The directionality is added to both the transmitter side and the receiver side. First, a guardian i in the alerted state now sends signal to j only if

$$\begin{aligned} \hat{{\mathbf {v}}}_j \cdot \hat{{\mathbf {r}}}_{i/j} < \cos \phi _1, \end{aligned}$$

(28)

where $\hat{}$ denotes a unit vector, i.e., $\hat{{\mathbf {v}}}={\mathbf {v}}/\Vert {\mathbf {v}}\Vert$. Second, a guardian j receives signal from an alerted guardian i only if

$$\begin{aligned} \hat{{\mathbf {v}}}_i \cdot \hat{{\mathbf {v}}}_{j} < \cos \phi _2. \end{aligned}$$

(29)

These two constraints help the guardians to propagate the signal in the desirable direction. Small values for $\phi _1$ and $\phi _2$ increase the accuracy of the velocity information carried through the interaction, but will also reduce the connectivity. Since securing sufficient connectivity is important for a small swarm, we choose $\phi _1=150^\circ$ and $\phi _2=90^\circ$ for the experimental results presented next.

Figure 14 shows the snapshots from a single experimental trial. System parameters were chosen so that ${\varGamma }'=0.90$ and $\alpha = 0.5$. Due to the velocity-alignment behavior, guardian 2 on the far side starts accelerating in the direction of the target’s motion even though it does not perceive the target itself (see the forcing ${\mathbf {F}}_2$ in Fig. 14a). This behavior generates a favorable initial condition at the time of close encounter (see ${\mathbf {v}}_2$ and ${\mathbf {v}}_T$ in Fig. 14b). This initial condition enables guardian 2 to successfully capture the target (Fig. 14c). As was done in the simulation and in the random-swarming case, we define target capture by looking at the energy function introduced in the proof of Proposition 2. It has a value $V=0.26$ for guardian 2, which is less than the criterion $\frac{1}{2}\rho _a^2=0.50$, i.e., the Lyapunov analysis in Proposition 2 predicts that the target will stay within the range $\rho _a$ of guardian 2 indefinitely.

The target was captured 15 times out of 18 trials, which gives the success rate of $P_{cap}=0.83$. This probability is lower compared to the simulation result ($P_{cap}=1.0$), mainly due to the velocity-alignment in the wrong directions caused by the latency in the system (see earlier discussion). Nonetheless, the success rate is improved as compared to the case without velocity-alignment interaction, which illustrates the advantage of utilizing communication between guardians.

6 Conclusion

This paper describes a swarming strategy for multiple guardians to defend a protected zone from an intruder. A static guardian requires high capability to guarantee target capture, whereas swarming motion relaxes the requirement. Guardians maximize the probability of target capture by balancing the swarm density and their speed.

Inspired by the swarming behavior of male mosquitoes, a random swarming motion was studied and ways in which control parameters may be optimized were discussed. In addition, velocity-alignment strategy was considered for the case where guardians communicate with each other. Even with a communication of only one digit of binary information, the probability of target capture was significantly increased when used with the velocity-alignment strategy, both in simulation and in experiment. For the experiment, directionality constraint was added to alleviate the effect of time delay.

In ongoing and future work, we are formulating the problem as a game between teams of intruders and guardians, where we distinguish between capture before and after intrusion. For this multi-intruder scenario, we are studying how the direction and frequency of intrusion affect the probability of capture. We also look at this problem from the intruder’s perspective and consider the optimal intrusion strategy.

Appendices

Appendix A: Calculation of $\beta ^*$

Figure 15 depicts the case where the damping term $b{\mathbf {v}}_{T/P}$ has to be saturated to give ${\mathbf {F}}_P^{\text {(pursuit)}} = u_{max}$. Let $n = \beta ^*\Vert b {\mathbf {v}}_{T/P}\Vert$, $m = (1-\beta ^*)\Vert b {\mathbf {v}}_{T/P}\Vert$, $A = n+m$, $B = \Vert c{\mathbf {r}}_{T/P}\Vert$, $C = \Vert c{\mathbf {r}}_{T/P}+b {\mathbf {v}}_{T/P}\Vert$, and $D = {\mathbf {F}}_P^{\text {(pursuit)}} = u_{max}$. Stewart’s theorem states that

$$\begin{aligned} B^2 m + C^2n = A(D^2+mn). \end{aligned}$$

(30)

Using (30) and $A = m+n$, we can solve for n to obtain

$$\begin{aligned} n = \frac{E\pm \sqrt{E^2 + F} }{2A}, \end{aligned}$$

(31)

where $E = A^2+B^2-C^2$ and $F = 4A^2(D^2-B^2)$. Noting that F is always positive, the solution (31) with $+$ is the only valid solution. The scaling factor is $\beta ^* = n/A$, i.e.,

$$\begin{aligned} \beta ^* = \frac{E+\sqrt{E^2 + F} }{2A^2}. \end{aligned}$$

(32)

Fig. 15

Computing the saturation factor $\beta$ to obtain the control law ${\mathbf {F}}_P^{\text {(pursuit)}}$

Fig. 16

Definitions of angles and speeds in the velocity space (Color figure online)

Appendix B: Required $N_P$ for guaranteed target capture using circling strategy

Consider a circling motion with radius $\rho _p$. Let $v_P$ denote the circling speed. Let $\theta _{T/P}=\cos ^{-1}\left( \frac{{\mathbf {v}}_T\cdot {\mathbf {v}}_P}{\Vert {\mathbf {v}}_T\Vert \Vert {\mathbf {v}}_P\Vert }\right)$ denote the difference between the direction of motion of the target and the pursuer. First, we seek to find the maximum angle $\theta ^*$ such that ${\mathbf {v}}_P \in B_{v_0}({\mathbf {v}}_T(t_0))$ (see Fig. 16 for the definitions of the relevant quantities). For a given guardian speed $v_P$, the angle $\theta ^*$ is the maximum allowable difference in the direction of motion to guarantee target capture. From Fig. 16 and the law of cosines, we have

$$\begin{aligned} \theta ^* = \cos ^{-1}\left( \frac{v_P^2 + v_T^2 - v_0^2}{2v_Pv_T} \right) . \end{aligned}$$

(33)

The angle $\theta ^*$ is maximized when the limiting ${\mathbf {v}}_P$ is tangent to the circle $B_{v_0}({\varvec{v}}_T)$, i.e., the blue dashed line in Fig. 16. This geometry is achieved when $v_P$ satisfies

$$\begin{aligned} v_P = v_P^{(1)} =\sqrt{ v_T^2 - v_0^2} = v_T \sqrt{1- {\varGamma }(1-\alpha )/2}. \end{aligned}$$

(34)

However, because of the centripetal acceleration, the achievable circling speed $v_P$ is bounded as

$$\begin{aligned} v_P \le v_P^{(2)} = \sqrt{\rho _p u_{max}} = v_T\sqrt{\frac{{\varGamma }\alpha }{2(1+\alpha )}}. \end{aligned}$$

We choose the circling speed $v_P$ to be

$$\begin{aligned} v_P = \min \left( v_P^{(1)},\;v_P^{(2)} \right) , \end{aligned}$$

(35)

i.e., use $v_P^{(1)}$ when it is achievable, otherwise, use maximum possible speed which is $v_P^{(2)}$. If the guardians are uniformly distributed on the circle, and if the number of guardians N satisfies

$$\begin{aligned} N > \frac{\pi }{\theta ^*}, \end{aligned}$$

(36)

there will be at least one guardian whose direction of motion satisfies $\theta _{T/P}<\theta ^*$. See Fig. 17 for the illustration of the case with $N_P=3$. When the target reaches the center, the velocity of the pursuer in the fan-shaped region satisfies $\theta _{T/P} < \theta ^*$. If the condition (36) is satisfied, then there is always at least one guardian in the fan-shaped region.

Fig. 17

Example of circling motion where $\theta ^*=\pi /3$. Guardians are uniformly spaced and there is always one guardian in the fan-shaped region. When the target reaches the center, the velocity of the pursuer in the fan-shaped region satisfies $\theta _{T/P} < \theta ^*$

Fig. 18

Sufficient number of guardians to guarantee target capture with circling motion

Figure 18 shows the required number of guardians obtained from conditions (33), (35) and (36). Close to the boundary $\partial _2$, the angle $\theta ^*\rightarrow 0$ and the sufficient number $N\rightarrow \infty$. Close to the boundary $\partial _3$, the angle $\theta ^*\rightarrow \pi$ and the sufficient number $N\rightarrow 2$.

Appendix C: Proof of proposition 3

For a given deflection angle $\phi$, the magnitude of normal acceleration exerted by the target increases as the time of execution ${\varDelta }t$ reduces. It is easy to see that the worst-case scenario for the guardian who is pursuing the target is when ${\varDelta }t$ approaches 0, i.e., the target makes a sudden instantaneous change in its direction of motion. This corresponds to the target applying a linear impulse with magnitude equal to $2 v_T \sin (\phi /2)$.

Consider the energy function used in the proof of Proposition 2. Let ${\varDelta }V$ denote the increase in the energy function due to the target maneuver. Then we have

$$\begin{aligned} 2c{\varDelta }V= & {} 2c V(t_2) - 2cV(t_1) \end{aligned}$$

(37a)

$$\begin{aligned}= & {} \Vert {\mathbf {v}}_{T/P} (t_2)\Vert ^2 - \Vert {\mathbf {v}}_{T/P} (t_1)\Vert ^2 \end{aligned}$$

(37b)

$$\begin{aligned}= & {} -{\mathbf {v}}_P \cdot \left( {\mathbf {v}}_T(t_2) - {\mathbf {v}}_T(t_1) \right) \end{aligned}$$

(37c)

$$\begin{aligned}\le & {} \Vert {\mathbf {v}}_P \Vert 2 v_T \sin (\phi /2) \end{aligned}$$

(37d)

$$\begin{aligned}\le & {} (v_T + v_0) 2 v_T \sin (\phi /2). \end{aligned}$$

(37e)

Target capture is guaranteed if the initial energy $V(t_0)$ is sufficiently small that the distance, $\Vert {\mathbf {r}} _{T/P}\Vert$, is bounded by $\rho _a$ even after the energy increase by ${\varDelta }V$, i.e.,

$$\begin{aligned} V(t_0) + {\varDelta }V\le & {} \frac{1}{2}\rho _a^2 \end{aligned}$$

(38a)

$$\begin{aligned} \Vert {\mathbf {v}}_{T/P}(t_0)\Vert\le & {} \sqrt{ c (\rho _a^2 -\rho _s^2)- 2c {\varDelta }V }, \end{aligned}$$

(38b)

which reduces to (10).

For feasibility of the condition, we also require that the right-hand-side of (10) is positive, i.e.,

$$\begin{aligned} \chi ^2 - 2a \chi -2a > 0, \end{aligned}$$

(39)

which reduces to (11).

Appendix D: Proof of Remark 1

For notational simplicity, let ${\mathbf {r}} \triangleq {\mathbf {r}}_{T/P}(t)$ and ${\mathbf {v}} \triangleq {\mathbf {v}}_{T/P}(t)$. Consider a Lyapunov function

$$\begin{aligned} V = 2bc\Vert {\mathbf {r}}\Vert ^2 + b\Vert {\mathbf {v}}\Vert ^2 + 2 c{\mathbf {r}} \cdot {\mathbf {v}}, \end{aligned}$$

which is positive definite if

$$\begin{aligned} 2b^2>c . \end{aligned}$$

(40)

Assuming that the control is never saturated, i.e., $\beta = 1$ (sufficient condition for this assumption is given later), the time derivative is

$$\begin{aligned} 0.5 \dot{V}= & {} -c^2 \Vert {\mathbf {r}}\Vert ^2 - (b^2-c) \Vert {\mathbf {v}}\Vert ^2 + b {\mathbf {v}} \cdot {\mathbf {a}}_T + c {\mathbf {r}} \cdot {\mathbf {a}}_T \end{aligned}$$

(41)

$$\begin{aligned}\le & {} -c^2 \Vert {\mathbf {r}}\Vert ^2 {-} (b^2{-}c) \Vert {\mathbf {v}}\Vert ^2 {+} b \left( \frac{b}{2}\Vert {\mathbf {v}}\Vert ^2 {+}\frac{1}{2b} \Vert {\mathbf {a}}_T\Vert ^2\right) \nonumber \\&+\, b \left( \frac{b}{2}\Vert {\mathbf {v}}\Vert ^2 +\frac{1}{2b} \Vert {\mathbf {a}}_T\Vert ^2\right) \end{aligned}$$

(42)

$$\begin{aligned}= & {} -\frac{c^2}{2} \Vert {\mathbf {r}}\Vert ^2 - \left( \frac{b^2}{2}-c\right) \Vert {\mathbf {v}}\Vert ^2 + \Vert {\mathbf {a}}_T\Vert ^2 \end{aligned}$$

(43)

$$\begin{aligned}\le & {} -\frac{c^2}{2} \Vert {\mathbf {r}}\Vert ^2 - \left( \frac{b^2}{2}-c\right) \Vert {\mathbf {v}}\Vert ^2 + u_T^2 \end{aligned}$$

(44)

Let $\sigma _1 = \frac{c^2}{2}$, $\sigma _2 = \frac{b^2}{2}-c$, and $D = u_T^2$. For $\sigma _2$ to be positive, we require

$$\begin{aligned} b^2>2c, \end{aligned}$$

(45)

which is stronger than (40). Also let ${\mathbf {z}} = [\Vert {\mathbf {r}} \Vert ,\; \Vert {\mathbf {v}}\Vert ]^T = [r,\;v]^T$. Then we have $\dot{V}\le 0$ for ${\mathbf {z}} \notin B_e = \{[r,v]\in {\mathbb {R}}^2\; |\; \sigma _1^2r^2+\sigma _2^2v^2\le D\}$, where $B_e$ is an ellipsoid centered at ${\mathbf {z}} = 0$, with axis length $\rho _1 = \sqrt{D/\sigma _1}$ and $\rho _2 = \sqrt{D/\sigma _2}$. Figure 19 depicts $B_e$ with other relevant regions.

Fig. 19

Definition of the regions for the proof of ultimate boundedness

If a compact set ${\varOmega }$ is such that $V\le \omega$ for ${\mathbf {z}} \in {\varOmega }$, and also $B_e \in {\varOmega }$, then by ultimate boundedness (Khalil and Grizzle 2002), we know that there exists $T>0$ such that ${\mathbf {z}} \in {\varOmega }$ for all $t > T$ (see Lemma 1 in Shishika et al. 2016).

Since it is not easy to visualize ${\varOmega }$, we introduce two compact sets ${\varOmega }_{min}$ and ${\varOmega }_{max}$ with the property ${\varOmega }_{min}\in {\varOmega }\in {\varOmega }_{max}$. Noting that $V = {\mathbf {z}}^T P {\mathbf {z}}$ where

$$\begin{aligned} P = \left[ \begin{array}{c c} 2bc &{} c \\ c &{} b \end{array} \right] , \end{aligned}$$

(46)

we obtain ${\varOmega }_{min}$ and ${\varOmega }_{max}$ to be discs with radii $\rho _{min} = \sqrt{\omega /\lambda _{max}\{P\} }$ and $\rho _{max} = \sqrt{\omega / \lambda _{min}\{P\}}$, where $\lambda _{min}\{P\}$ and $\lambda _{max}\{P\}$ are the smallest and largest eigenvalue of P.

Conditions $B_e\in {\varOmega }_{min}$ and ${\mathbf {z}}(t_0) \in {\varOmega }_{max}$ guarantee that ${\mathbf {z}}\in {\varOmega }_{max}$ for all time $t>t_0$. If $\rho _{max} = \rho _a$, then ${\mathbf {z}}\in {\varOmega }_{max}$ guarantees target capture, i.e., $\Vert {\mathbf {r}}\Vert \le \rho _a$. The latter condition determines the value of $\omega$, which defines ${\varOmega }$, as follows:

$$\begin{aligned} \omega = \rho _a^2 \lambda _{min}\{P\}. \end{aligned}$$

For $B_e\in {\varOmega }_{min}$, it is sufficient if $\max \{\rho _1, \rho _2\} \le \rho _{min}$, which gives

$$\begin{aligned} u_T \le \rho _a \sqrt{\frac{\lambda _{min}\{P\}}{\lambda _{max}\{P\}}} \big / \sqrt{2}\max \left\{ \frac{1}{c}, \frac{1}{\sqrt{b^2-2c}}\right\} . \end{aligned}$$

(47)

Equation (47) corresponds to condition (i), sufficiently small $u_T$, in Remark 1. Note that (40) guarantees that the right-hand side is positive.

Next, ${\mathbf {z}}(t_0)\in {\varOmega }_{max}$ is true if the initial condition satisfies $V(t_0)\le \omega$, which is equivalent to

$$\begin{aligned}&2bc\rho _p^2 + b\Vert {\mathbf {v}}(t_0)\Vert ^2 + 2c{\mathbf {r}}(t_0) \cdot {\mathbf {v}}(t_0)\le \omega \nonumber \\&b\Vert {\mathbf {v}}_{}(t_0)\Vert ^2 + 2c{\mathbf {r}}_{}(t_0) \cdot {\mathbf {v}}_{}(t_0) \le \rho _a^2 ( \lambda _{min}\{P\} - 2\alpha bc) \end{aligned}$$

(48)

Since ${\mathbf {r}}(t_0) \cdot {\mathbf {v}}(t_0) \le 0$ for the close encounter to occur, a conservative version of the above condition is

$$\begin{aligned} \Vert {\mathbf {v}}_{}(t_0)\Vert ^2 \le \frac{\rho _a^2}{b} ( \lambda _{min}\{P\} - 2\alpha bc) \end{aligned}$$

(49)

Equation (49) corresponds to condition (iv), sufficiently small $\Vert {\mathbf {v}}_{T/P}(t_0) \Vert$, in Remark 1. By explicitly calculating $\lambda _{min}\{P\}$, one can prove that the right-hand side of (49) is positive if

$$\begin{aligned} c \le \frac{1}{2\alpha }\left( 1 - \frac{1}{4(1-\alpha )}\right) . \end{aligned}$$

(50)

Conditions for the gain selection, which corresponds to (ii) in Remark 1, are thus (45) and (50).

For this proof, we assume that the pursuer control is never saturated, which is true if

$$\begin{aligned} u_{max}\ge \rho _{max}\max \{b,c\} = \rho _a \max \{ b,c\}, \end{aligned}$$

(51)

which corresponds to (iii), sufficiently large $u_{max}$, in Remark 1. $\square$