Incremental topological segmentation for semi-structured environments using discretized GVG

Abstract

Over the past few decades, topological segmentation has been much studied, especially for structured environments. In this work, we first propose a set of criteria to assess the quality of topological segmentation, especially for semi-structured environments in 2D. These criteria provide a general benchmark for different segmentation algorithms. Then we introduce an incremental approach to create topological segmentation for semi-structured environments. Our novel approach is based on spectral clustering of an incremental generalized Voronoi decomposition of discretized metric maps. It extracts sparse spatial information from the maps, and builds an environment model which aims at simplifying the navigation task for mobile robots. Experimental results in real environments show the robustness and the quality of the topological map created by the proposed method. Extended experiments for urban search and rescue missions are performed to show the global consistency of the proposed incremental segmentation method using six different trails, during which the test robot traveled 1.8 km in total.

1 Introduction

1.1 Motivation

Topological mapping-and-segmentation is an intuitive way to help humans to understand an environment. It is also an important approach to provide preliminary results for further semantic labeling or topological navigation. However, topological segmentation for semi-structured environments is challenging, since the definition of regions in those environments is difficult. We define a semi-structured environment as an environment where the local areas cannot be directly categorized into standard semantic labels, such as “room” or “corridor” etc. At the same time, its topology may vary due to local changes. On the contrary, a structured environment has an inherent static topology, such as a typical indoor environment can generally be decomposed and clustered into aforementioned semantic labels. Compared with indoor environments, the assessment of the segmentation quality for semi-structured environments is however vague.

As the basis of navigation and localization, mapping is of growing importance in robotics. Mapping is the process to build a representation by which robots can share with humans a common understanding of an environment. Metric maps and topological maps are the two most common types. Metric maps describe the surroundings of robots in a geometrical and measured way, usually by defining free and occupied space with occupancy grids (Elfes 1989) or distances and positions of features (Civera et al. 2008; Strasdat et al. 2010). Nevertheless, metric maps incorporate redundant information for precise mapping but usually do not handle the data in an efficient way. For example, if a robot navigates a long path based on occupancy grids, the path planning can be prohibitively slow. This shortcoming is crucial for time constrained tasks, such as search and rescue missions (Burke et al. 2004; Balaguer et al. 2009). On the contrary, topological mapping (Choi et al. 2009b; Liu et al. 2011; Choset and Nagatani 2001) shows its advantages for lightweight graph-based path planning using sparse information.

Moreover, segmentation of the working space for robots is generally required, since humans use mostly topological representation of their surroundings as well (McNamara 1986). As far as environment modeling is concerned, topological segmentation provides the basis to associate extra information to certain regions, such as the information of detected survivors in urban search and rescue (USAR) or functional areas for robots (Kruijff et al. 2012b). Related semantic labeling based on probabilistic graphical models, such as Voronoi random fields (VRF) (Friedman et al. 2007), and semi-supervised semantic learning (Shi et al. 2012) are also reported. The integration of such mapping scheme to a multi-agent system can be found in our previous works (Gianni et al. 2011; Kruijff et al. 2012a).

It is natural to decompose an indoor environment into semantic places such as “rooms”, “corridors” etc. Analytic methods such as ‘Z’ shape detection (Tomatis et al. 2003) or gateway separations (Beeson 2008) have shown good performance in such construction of topological structure. Recent work using topological graphs to fuse metric local maps showed the benefit of topological mapping in reconstructing global indoor environments (Beeson et al. 2010). Dolgov and Thrun (2009) proposed a topological navigation approach in a strongly structured environment, where crossings in a parking lot are modeled by Voronoi graph to facilitate the navigation of vehicles. However, regarding semi-structured environments, these definitions, such as “room” and “crossing”, are not obvious. Inspired by these semantic definitions, we define similar local structures for typical semi-structured environments, which are discussed in Sect. 4.4.

Semi-structured environments are typical environments for search and rescue missions (Baber et al. 2004; Balaguer et al. 2009). The topological segmentation for semi-structured environments has not been much studied because of the following two main reasons. Firstly, the lack of structure makes topological reasoning difficult. Secondly, as an extension of the first reason, no existing well-recognized criteria are applicable to justify the quality of a segmentation result.

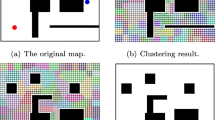
We have to recognize that the definition of inherent topology of a semi-structured environment is sometimes not even clear for humans. In the first part of this paper, we propose a metric to assess the quality of topological segmentation, by considering geometrical intuitivism.¹ After that, we present a novel approach for topological segmentation, which utilizes an incrementally generated generalized Voronoi graph (GVG) (Aurenhammer 1991; Barraquand and Latombe 1991). In order to enhance the sparseness of the representation, the spectral clustering method is then performed. Figure 1 depicts a metric map created at a parking lot and the segmentation result using the proposed method.

Fig. 1

Topological segmentation of a semi-structured environment. The raw map in a covers an area of around $50\times 50$(m$^2$). a A raw map from a parking lot, b Segmentation result

1.2 Challenges

An online incremental approach is preferable to off-line methods since the exploration of unexplored areas typically involves only small changes per iteration. First, incremental approaches are computationally more efficient. Besides, most existing clustering algorithms require the cardinality of the segmentation, which is generally impossible to define before exploration (Choi et al. 2011). In order to define a proper incremental segmentation approach, the following requirements need to be considered.

• 1. Sensitivity The approach needs to detect what changes have occurred since the last iteration. It is preferred to work only on the affected parts of the map, rather than the global map.

• 2. Modality and simplicity The segmentation should represent the inherent structure of the map at each iteration by a sufficiently small number of regions for path-planning or environment modeling. It enables the approach to be scalable at different map sizes; meanwhile it allows the use of intermediate results.

• 3. Stability The output of an incremental algorithm applied to a complete map should not differ from a segmentation obtained using the same approach in an off-line fashion.

• 4. Consistency Last but not least, the resulting topological structure ought to be consistent throughout different runs in the same environment, regardless the sequence through which the global map is created.

We describe our approach in detail in the remainder of this paper, explaining how we take these requirements into account. Especially, the stability and consistency of the segmented regions are evaluated through different runs of real experiments following an accident scenario in a tunnel.

1.3 Structure of the paper

In Sect. 2, a short overview of the state of the art is presented. Subsequently, the designed quality factor is presented before the discussion on spectral clustering, its incremental forms and the identified drawbacks. In Sect. 4, the proposed GVG extraction algorithm is introduced. Several core problems related to the GVG extraction are discussed in Sect. 5. Results and discussions are presented at the end.

2 Related work

2.1 Topological representation

Several works deal with the extraction of topological regions from metric maps as follows. Intuitively, a topological map is defined as a graph structure, which is composed of nodes and links among them. In general, there are two types of topological maps depending on what a node represents. Most existing works consider nodes in topological map as “key-points” (Ryu and Yang 1999; Choset and Nagatani 2001; Zender and Martínez Mozos 2008) in the metric map. The rest considers nodes as interesting regions (Choi et al. 2009a; Thrun 1998; Liu et al. 2011), namely region-based topological maps. Conceptually, both types describe environments by topology representations, typically by using graph structures.

There are alternative means to represent topological regions such as image-based descriptors, e.g. (Liu et al. 2009; Liu and Siegwart 2012; Tapus and Siegwart 2005), using fused information (Ranganathan et al. 2002; Liu and Siegwart 2013) or reasoning by bayesian methods (Blanco et al. 2008) or by non-parametric learning (Liu et al. 2012b). Because of their irrelevance in terms of perception pattern, we only consider those using range readings in our discussion.

2.2 Spectral clustering

Graph partition methods are widely used in this field, since topological mapping can be considered as a clustering problem over a connected graph. The most common approach is to use graph cut theories such as the Normalized Cut (Shi and Malik 2000) or Ratio Cut (Hagen and Kahng 1992). The latter may be approximated by unnormalized spectral clustering, as indicated by Luxburg (2006).

Spectral clustering is widely used in robotics to extract clusters of data which maximize the internal connectivity while minimizing the connectivity to the exterior on the adjacency graph. The spectral clustering approach however is not free of drawbacks. Nadler and Galun presented in (Nadler and Galun 2007) the difficulties to cope with multi-scale landscapes and the failure to extract regions of different sizes, namely the scaling problem. Zelnik-Manor and Perona proposed a self-tuning spectral clustering algorithm (Zelnik-Manor and Perona 2004), through which they tried to improve the scalability. In our previous work (Liu et al. 2011), we introduced an alternative topological segmentation method based on mutual information, and showed its application in regional segmentation. We also showed that how human inputs can be assistive for region generation by using a novel markov model by (Liu et al. 2012a), where we compared spectral clustering with other similar algorithms.

Besides the scaling problem, the computational complexity of spectral clustering also hinders its performance. Due to the expensive matrix inversions, different incremental variants of spectral clustering were developed to relieve the computational complexity. Brunskill et al. (2007), took a fixed number of scans and applied spectral clustering on a uniform grid with a distance adjacency function. The number of added clusters is extracted by the analysis of the eigenvalues of the adjacency matrix. Choi et al. (2010, 2011) used a quad-tree decomposition as basis for incremental spectral clustering and the number of neighboring cells as similarity indicator. Unlike Brunskill’s method, two regions were extracted for each iteration in Choi et al. (2010, 2011) and only one region of the two was added to the topological map.

2.3 Generalized Voronoi graph (GVG)

Another popular approach for the segmentation of metric maps is GVG-based segmentation as proposed by Thrun (Thrun 1998). GVG has been used in several mapping and navigation problems. However, the extraction of GVG in most of the previous work uses raw range scans instead of metric map, such as Local Voronoi Diagram proposed by Blanco et al. (2000). These methods are easily accessible for structured environments, where well-defined edges can be easily detected and the laser readings are with less noise. Based on the GVG generated by raw range scans, several works managed to achieve autonomous indoor localization (Song and Liu 2013) and navigation on GVG such as (Zwynsvoorde et al. 2000; Choset and Nagatani 2001). But it is hard to extend to semi-structured environment, where the structure is not of limited types; more important, it is inaccessible for environment modeling and constructing representations that human can easily understand. The challenge for GVG construction is that it requires the measure of the distance to different obstacles (Drysdale 1979), but obstacle designation cannot be easily handled from metric maps, where the perspective of the mobile robot is missing. In this paper, we discuss obstacle-designing problem by setting up virtual obstacles and analyzing clearance for specific examples. Please refer to Sect.  4.2 for detail.

Segmentation approaches that use GVG as the basic structure guarantee that regions are separated if they have weak connections, namely small passages, e.g. doorways. However, GVG extraction is non-trivial. An efficient algorithm called Brushfire, similar to the Dijkstra algorithm, was developed by Barraquand and Latombe (1991), originally designed for robot motion planning. Incremental Voronoi construction was proposed independently by (Karavelas 2004; Ahn et al. 2003) and (Choset 1997). The algorithm follows a computationally optimized form called Dynamic Brushfire, developed by Kalra et al. (2009). In general, because GVG is build along exact outlines of obstacles, the decomposition error introduced by space discretization is minimized. Hence, segmentation results based on GVG are more stable than those based on structured decomposition. It outperforms other decompositions which rely on global coordination, such as quad-trees, as analyzed in (Liu et al. 2011).

Some other related methods are based on thinning skeleton (Lee et al. 2007; Lau et al. 2010), which are either hard to generate region-based representation or easily over-segment the free space, leading to instability of structural analysis. Vision techniques can also be adopted such as watershed algorithms (Galindo et al. 2005), by which the structural changes in semi-structured environment can not be adapted easily.

In this paper, we treat the GVG extraction problem in a discretized space, in order to alleviate the influence of noise from metric map and allow online computation; at the same time, analytic approaches which explicitly treat special structures such as “doorway”, “corridor” and “dead end”-like local structures are implemented. They help to simplify the topology and emphasize the typical local compactness of the generated representation, leading to relatively stable region-based final representations.

2.4 Segmentation assessment

Assessing the quality of segmentation in an objective manner is extremely important when comparing different approaches. Though defining a quality measure to show the usability of a given segmentation is essential, it is difficult to do so without considering a specific application because the optimal structures are mostly task-dependent. An example of a task-dependent quality factor was given by Thrun (1998), where three criteria were proposed to evaluate the performance of the proposed algorithm, namely consistency, loss and efficiency. Zivkovic et al. (2006) compared the path-planning efficiency of different methods. In this paper, we define the criteria for more general purposes by considering the geometrical properties such as convexity.

3 Region and segmentation quality

In general, a segmentation is considered to be useful if it represents the structure of the environment efficiently and sufficiently. For instance, navigation and path-planning require topological maps to have a sufficiently small number of regions. At the same time, it is preferred to remove unnecessary information of an unsegmented occupancy grid. To this end, we consider two types of criteria: first, the quality of a well-formed region; secondly, the topology of a segmentation. The proposed criteria are mainly based on geometric intuitions.

3.1 Quality of a region

In this section, we introduce the following two criteria to define the quality of a single region.

3.1.1 Convexity

It can be represented by the area of the convex hull of the region compared to the area of the region (Latecki and Lakämper 1999; Rosin 2000). The convex hull is defined as the connected set of points extracted from the target shape such that if any two points of a set of points are connected, the segment connecting both points is contained within the convex hull (Fabri and Pion 2009).

The convexity of the $i$th region of an arbitrary segmentation can be defined as:

$$\begin{aligned} c_i = \frac{A_i}{H_i}, \end{aligned}$$

(1)

where $A_i$ is the area of the $i$th region and $H_i$ is the area of the convex hull defined by the $i$th region. The perfect region in terms of connectivity is convex and has an inter-connectivity ratio of one, whereas the quality of the region is bad if the factor is less than one and tends to zero. Figure 2 shows regions with different convexity.

Fig. 2

Two illustrations of the convexity quality factor. Solid lines delimitation of the region, dashed lines convex hull of the region. a $c = 0.88$, b $c = 0.56$

3.1.2 Compactness

The compactness of a region defines whether a region is widely spread or condensed around its center of gravity. It also indicates whether a region homogeneously reachable from neighboring regions. The compactness is normalized using the area of the region in order to have a comparable measure independent of the region size:

$$\begin{aligned} s_i = \frac{1}{M_i\,A_i} \sum _j \frac{ ( x_j - x_0 ) ^ 2 + ( y_j - y_0 ) ^ 2 }{A_i}, \end{aligned}$$

(2)

where $x_j$ and $y_j$ are the x- and y-coordinates of the mass members, and $x_0$ and $y_0$ are coordinates of the center of gravity of the region; $M$ is the number of cells in the region $i$.

In summary, the quality of a region could be represented as: $q_i = c_i - s_i$ Note that the unit for both $c_i$ and $s_i$ components are scalar. In order to emphasis different characteristics of a region, a weighting factor for each component can be further adopted.

3.2 Quality of a segmentation

The quality of a completely segmented map is a measure derived using the quality of each region while including key global characteristics of the segmentation.

3.2.1 Area coverage ratio

In the ideal case, each point on a metric map is associated to a region in the topological description. However, since a segmentation method may be based on the pre-decomposition of the global map (Choi et al. 2009b; Liu et al. 2011), the ratio of the segmented area compared to the totally available unoccupied space may not be $1$. Such a measure depicts whether a found topology may serve as a global map. The ratio is defined as follows:

$$\begin{aligned} C = \frac{\sum _{i=1}^N A_i }{A_m}, \end{aligned}$$

(3)

where $A_m$ is the total area of the map and $N$ is the number of regions.

3.2.2 Region validity ratio

The extent of a valid region needs to hold at least the footprint dimension and turning clearance of a robot, such that the robot is able to perform given tasks in the generated regions. In most cases, a validity criterion based on the accessibility is suitable. The validation criterion is defined as: being accessible by at least one open edge of minimal width $l_{min}$ and having a minimal extend $A_{min}$.

The ratio $R$ of valid regions, describing to which percentage a segmentation consists of valid regions, is defined as:

$$\begin{aligned} R = \frac{\# \; valid \; regions}{\# \; all \; free~regions}, \end{aligned}$$

(4)

where $\# \; all \; free~regions$ is the total number of regions resulting of the segmentation and $\# \; valid \; regions$ is the number of valid regions. As $l_{min}$ and $A_{min}$ are specific parameters regarding applications, this quality indicator highly depends on the task and embodiment of the robot.

3.2.3 Simplicity

An important use-case of topological segmentation is to help navigation and planning. Therefore, it is useful to penalize solutions with a large number of regions. On the other hand, if the number of regions is too small, the topological navigation will be meaningless. This component is modeled by the number of regions $N$ using: $e^{-\frac{|N-\hat{N}|}{\phi }}$. $\hat{N}$ is the expected number of regions and $\phi$ reflects the allowable difference between the expected number of regions and outcome, which are application-dependent.

3.2.4 Overall quality

Finally, evaluating the quality of a segmentation goes back to a summary of four components: the quality factors of the regions, the coverage of the map, the region validity ratio and the simplicity of the segmentation.

Overall, the quality of a segmentation is given by:

$$\begin{aligned} \varvec{Q} = \frac{CR}{N} \cdot \sum _{i=1}^N q_i + \lambda e^{-\frac{|N-\hat{N}|}{\phi }}, \end{aligned}$$

(5)

where $\lambda$ is the relative weight between raw quality and simplicity. This is the primary mean that we are going to use to assess the quality of each experimental trail.

4 GVG extraction

The interpretation of rooms and places from humans’ point of view certainly includes the concepts of narrow passages and separating obstacles. The idea behind the Voronoi decomposition for map segmentation is to extract places on the map using similar concepts. An analogous interpretation exists in semi-structured space. Even though there are no determinative corridors, obstacles may obstruct the connections between open space and thus be treated as doorway-like local structures. The resulting segmentation may not have an interpretation in terms of different places or rooms but definitely generates featured topological regions, fulfilling the needs for navigation.

We aim at an online incremental approach. Therefore it is preferred to firstly shrink the data amount from the raw map. (Thrun 1998) provided a framework to generate topological segmentation offline. However its computational complexity doesn’t allow online computing, let alone the adaptation to an incremental method. In this paper, the Voronoi decomposition of the map is based on a uniform decomposition where the cell size depends on the constraints on the precision of the map. A decomposition result is shown in Fig. 3. The blue region marks valid free space, while the red areas are removed automatically, considering connectivity.

Fig. 3

Decomposition of the raw metric map shown in Fig. 1a

Adopting the notation of Thrun (1998), we define the following components related to topological segmentation for a discretized GVG, which are also indicated in Fig. 4.

• 1. Basis Points of a free cell: the set of points in occupied space having (the same) minimal clearance to a given free cell.

• 2. Clearance of a free cell: The distance between a cell and its basis points.

• 3. Generalized Voronoi graph: The free cells which have at least two basis points.

• 4. Critical cells: The cells of the Voronoi diagram which minimize the clearance locally.

• 5. Critical lines: The line segments connecting a critical cell with its basis points.

• 6. Topological map: The regions in free space delimited by occupied space and critical lines represent topological nodes. The edges are the connections among regions.

The Voronoi decomposition is designed for applications in continuous coordinates. Nevertheless, the basic concepts remain valid but with the following adaptations.

Fig. 4

Sketch of related elements to describe a discretized GVG

4.1 Discretized Voronoi diagram

When abusing the above definition of basis points, one can observe that the Voronoi diagram is detected only when it passes the mid-way of free cells. Otherwise, a free cell will have one basis point on one side and its closest neighbor will have another basis point to the other side (see Fig. 5). In order to ensure that the Voronoi diagram is sufficiently represented by discretized cells, we have to introduce a tolerance when comparing the distances of two potential basis points: $|d_1 - d_2| < \delta \cdot C$, with $C$ the width of a grid cell. The situation for both extreme cases is illustrated in Fig. 5. As for simplicity, the width of cells is assumed to be one.

Fig. 5

Clearance tolerance for different orientations of the cells. a Horizontally oriented, b $45^{\circ }$ orientation

Figure 5a shows that the required tolerance, in order to accept both basis points (dark gray), exactly equals to $\delta = 1$. The disadvantage of this tweak is that both free cells will appear later on in the Voronoi diagram and have to be filtered out. In the situation presented in Fig. 5b, similar reflections would lead to a required tolerance of $\delta = \sqrt{2}$. Further evaluations show however that the tolerance of $\delta = 1$ is sufficient. In the presented case, the lateral cells would only get a single basis point whereas the top and bottom cells would have two basis points.

4.2 Designation of obstacles

The definition of the GVG requires that the points on the bisector of an obstacle angle have (at least) two basis points from separate obstacles. Compared with the classical GVG extraction algorithms (Aurenhammer 1991), a key issue for the application of GVG in robot mapping is the designation of obstacles. This is because most metric maps use occupancy to indicate the presence of obstacles, and the obstacles are always linked. For example, the wall surrounding a room can be considered as a single obstacle. In this case, it causes serious problems for the calculation of GVG, by using traditional algorithms, e.g. it fails in the cases that a room is surrounded by continuous walls, where the room will not be detected; it also fails at a dead-end corridor etc. In these cases, even though the region of free space is formed by a single obstacle, it is desirable to extract the surrounded region as a separated node.

It shows that the segmentation of the map is significantly influenced by the definition of the obstacles and their extension. An example is shown in Fig. 6: the boundaries of the free space form a connected obstacle. It is however desirable to separate two regions by the segment $AB$. Thus, point $A$, as a basis point, should be on a different “virtual obstacle” than $B$, even they are connected via the walls. Hereby the definition of an obstacle is extended to virtual obstacles which are used in the basis points calculations. Virtual obstacles allow two occupied cells to be the basis points of a same free cell while being member of the same physical obstacle. The designation of virtual obstacles depends on the tightness of the connectivity between two cells on obstacles, such that: two occupied cells not being part of the same obstacle are always loosely connected; two distinct occupied cells are a part of the same virtual obstacle if they are tightly connected. Please refer to Eq. (3) for further information.

In order to clearly define the tightness of a connectivity, the following definitions are used:

• 1. the linear distance between two cells $d_{linear}$

• 2. the shortest distance along the cells of the physical obstacle $d_{obstacle}$

For instance, the illustration in Fig. 6 (white color corresponds to free space) shows the difference in $d_{linear}$ and $d_{obstacle}$ in two special cases. All four points, $A$, $B$, $C$ and $D$ are candidates for being loosely connected and thus forming a virtual obstacle. $A$ and $B$ are close to each other in terms of the linear distance but further away in terms of the distance on the obstacle, hence should be considered as loosely connected, as opposed to $C$ and $D$ for which the linear distance and the obstacle distance are similar. The definition of tight and loose connection is deduced:

$$\begin{aligned} connectivity: {\left\{ \begin{array}{ll} loose, &{} \text{ if } \;\; r_{g} \cdot d_{linear} < d_{obstacle} \\ tight , &{} \text{ if } \;\; r_{g} \cdot d_{linear} \ge d_{obstacle}, \end{array}\right. } \end{aligned}$$

(6)

where $r_g$ defines the threshold ratio.² Two cells forming a virtual obstacle are not disassociated from their physical obstacle.

Fig. 6

Illustration of the definition of loss/tight connection between basis points

Note that the extraction of the connected occupied cells is simplified by only considering occupied cells which have at least one free cell as first or second order neighbor. This simplification does not affect the resulting groups but the computational expense is considerably reduced.

4.3 Grouping of critical points

Usually the local minimization of the Voronoi diagram is non-strict and the tolerance on the basis point distances leads to series of critical cells with equal clearance, shown in Fig. 7a. This effect especially occurs in corridors since they are regions of constant width of the free space. In order to account for this behavior, the critical cells are grouped in accordance with the following analysis.

Even in continuous space, perfect corridors (having exactly the same width) would give rise to a queue of critical points. However there may be more than one in the discretized setting. The redundant critical cells should be merged when they are first- or second-order neighbors of the same obstacle. We define a single virtual cell as the average of the x- and y-coordinates of the centers of both critical cells. These virtual cells are the only references that need to be considered during the critical line generation. An intuitive sketch is shown in Fig. 7b.

Fig. 7

Merging of highly similar critical cells (light gray Voronoi diagram; gray lines associated critical lines). a Raw critical cells, b Virtual critical cells

4.4 Clearance analysis

The filtering of critical cells is based on the analysis of the clearance of the grouped critical cells. If the clearance of the Voronoi diagram is plotted with respect to the internal order of the cells, the variation of the clearance can be visualized in a clearance graph. Depending on the structure of the environment, different shapes are observable as we can see in the following cases. Please note that hereby we abuse several semantic labels of these cases from structured indoor environments, which can be applicable to local areas of semi-structured environments. It does not necessarily imply that a semi-structured environment can be embedded with these semantic meanings.

4.4.1 1: Corridor-like region

A corridor is characterized by a starting point, an end point, a length and a width (see Fig. 8). Both ends are connected to cells of the Voronoi diagram with a clearance superior to the clearance in the corridor. The unique identifier of a corridor, which makes the difference to the second type “Door” is the ratio of its length to the its width. As the width of the corridor may be approximated by twice the clearance of the group of the critical cells ($c$) and the length of the corridor ($d_{c}$) can be approximated by the number of successive critical cells, the following ratio is determinative.

$$\begin{aligned} r_{cc} = \frac{c}{d_{c}} \end{aligned}$$

(7)

The value $r_{cc} = 1$ is proposed as the boundary from Case 1 to Case 2. Groups of critical cells with a length superior to their clearance are categorized as Corridors. A corridor is designed to be a distinct region connecting two or more regions, thus has a critical cell on each extremity.

Fig. 8

The clearance graph and an illustration of the situation for a corridor

4.4.2 Case 2: Door-like region

A corridor whose length tends to zero is interpreted as a door. As for the corridor, both ends are connected to cells of the Voronoi diagram with clearance superior to the clearance in the corridor. Thus a door is characterized by a start, an end and a width. After applying the ratio of Eq. (7) and respecting the threshold proposed in the previous paragraph, doors are identifiable in terms of the clearance graph. A door, as being a separator of two regions, only has a single critical cell. The center is defined as the average of the centers of the group members. The basis points are the average of the neighboring basis points of the group members.

4.4.3 Case 3: Deadend-like region

The major difference between a deadend and a corridor is the the former is lack of connectivity to the Voronoi diagram on one extremity of the clearance graph as shown in Fig. 9. A deadend is a proper region with a critical cell on the extremity connected to the Voronoi diagram.

Fig. 9

The clearance graph and an illustration of the situation for a dead end

4.5 Extraction of regions

The output of the algorithm is a region-based partition of an environment in the form of a topological graph. The nodes of the graph are regions extracted from the environment; the edges among nodes defines the relations between two nodes. The previous steps only introduced the method to extract local basis points, critical lines and corresponding clearances. An additional step is required to extract a certain region as a compact unit, containing the member cells of each region, definition of boarders and the connections to neighboring regions. Therefore, the grid introduced by the discretization of map needs to be scanned to detect the regions delimited by occupied cells and critical lines. The extraction process can be carried out as follows.

We first select a cell from all unlabeled cells as a seed. Starting with this seed cell, a queue of regional members are iteratively extracted by exploring the first-ordered neighbors of the visited cell. During this extraction process, a cell will be added to the queue only if the following three conditions are met at the same time:

• 1. The cell is within the bounds of the map;

• 2. The cell is not occupied (e.g. as an obstacle);

• 3. The cell is not crossed by any critical lines.

After the convergence of this extraction process, we define the union of all the cells in the queue as a region. The member cells of the region can further classified as bordering cells and non-bordering cells. The location and sizes of the member cells define the extent of a region. Specifically, the bordering cells are the cells with less than four first-ordered member-neighbors. Their locations determine the connections to neighboring regions.

5 Incremental Voronoi decomposition

The generation of Voronoi decomposition for robot mapping includes computationally expensive steps (e.g. the calculation of the clearance of each free cell) and less expensive steps (e.g. the generation of the Voronoi diagram). Therefore, the challenge for an incremental implementation of the Voronoi decomposition is rather not developing an efficient search for grouping algorithms, but an efficient way to determine the subset of unoccupied cells affected by the removal or addition of an occupied cell.

5.1 Dynamic brushfire

An algorithm for incremental Voronoi segmentation in dynamic and unexplored open space was developed by Kalra, Ferguson and Stentz (Kalra et al. 2009). They proposed an efficient way to update the basis points in aid of the decomposition. At the same time, they incorporated the calculation of the clearance using (Barraquand and Latombe 1991), which was known as the Brushfire algorithm. The cells, which are affected by addition or removal of an occupied cell, are marked as invalid and are thus re-evaluated according to non-incremental Voronoi decomposition algorithm.

5.1.1 Removal of an occupied cell

All the cells which are closer to a removed cell than to any other occupied cells are invalidated. The affected cells are composed of the following two groups:

• 1. the removed occupied cells;

• 2. all the free cells that used 1. to calculate their clearance.

This implies that a free cell can also be invalidated if its basis points are removed.

5.1.2 Addition of an occupied cell

Regarding the definition of Voronoi graph, adding an occupied cell affects the cells which are closer to the newly added cell than to any other occupied cell. Those cells are not as easily identifiable as the cells affected by the removal of an occupied cell. A brute force search is used in our implementation.

5.2 Incremental Voronoi segmentation with virtual obstacles

The incremental Voronoi decomposition approaches proposed in the literature are well suited in many cases. In order to extract the desired structure for optimal path planning, some modifications to the standard Voronoi decomposition algorithm were proposed such as Choset (1997). However, these methods cannot be easily extended to incremental versions, if we consider map changes instead of incrementally fed scans. The introduction of virtual obstacles removes the direct link between a cell and its basis points: loosely connected cells may be tightly connected after slight modifications of the map. The Dynamic Brushfire approach, which requires this relation, is only well suited for environments in which virtual obstacles are well defined and independent of the shape of the physical obstacles, such as the one used by Kalra et al. (2009). We propose in the next section a novel algorithm able to cope with the definition of virtual obstacles.

The idea of the proposed algorithm is to update as many free cells as required to surely catch all possibly affected cells, while keeping the number of updates as small as possible. Removing an occupied cell from a grid affects all those cells that calculated their clearance based on the removed cell. This hypothesis is valid if the group association is not re-evaluated during the basis point generation. In standard Voronoi decomposition a free cell may only have a single basis point per obstacle. However, in a discrete space, obstacles break this rule. The results are especially affected in the case of relatively large obstacles with rather complex shapes. A slight change in the structure of the obstacle may then affect multiple virtual obstacles and thus lead to additional regions. The cells that change the structure of the obstacles are not required to have a connection with all the affected free cells as required by Dynamic Brushfire (Kalra et al. 2009) or other similar algorithms.

5.3 The algorithm

Since the incremental method should deal with metric maps that are dynamically changing, we first need to identify the affected cells at each step. Moreover, the cells in their surrounding region should also be taken as affected. Then the Voronoi diagram for all the cells in the affected regions must be re-generated based on the updated critical lines. Therefore, an important feature of the incremental approach is the constant tracking of the affected elements. As a result, we need to consider the following aspects.

5.3.1 Adding occupied cells

Adding an occupied cell usually affects significant parts of the Voronoi diagram around it as it pushes the cells away from the obstacle. As a consequence, the cells containing the new obstacle and all its neighboring cells are marked as affected.

5.3.2 Removing occupied cells

The free cells that take the removed obstacle as their basis point are affected as well as the cells affected by a change in the obstacle structure.

5.3.3 Voronoi diagram

The clearance of the invalidated cells is re-computed. If a cell was marked as Voronoi cell and the basis points have changed, it is marked as affected. If it is no longer a Voronoi cell, it is removed from the Voronoi diagram and marked as affected.

5.3.4 Updating critical cells

The local minimization of the Voronoi diagram is modified but that does not affect the whole diagram. Thus local minimal are searched in the affected parts of the Voronoi diagram including the first- and second-order neighboring regions of the affected cells.

5.4 Region extraction

Finally the regions are extracted using the same algorithm as in the non-incremental approach, except that only the regions marked as affected are considered. The region generation starts with a seed cell in the set of affected cells. Each resulting region is further analyzed and categorized with respect to the following three cases:

5.4.1 No valid region was generated

Starting from the selected seed node did not result in a valid region. This implies that the region, to which the seed node was associated is no longer valid, and thus should be removed.

5.4.2 A single valid region was generated

The region with which the algorithm started is still valid and delivers a single result. No significant changes occurred in the region except a potential resize; In the case of a region resize, the old region is updated and marked as resized; otherwise, the region is marked as unchanged.

5.4.3 An arbitrary number of regions was generated

The most common case for incremental Voronoi segmentation is a regrouping in the region. In general, the bordering cells of a region are displaced, which leads to an augmentation of the available area. During the segmentation, the area of the region is rearranged into multiple regions. The named region is identified by comparing the distances among the centers of gravity of the old region and the new ones. The region with the smallest deviation is accepted as the substitution of the old region. The other newly detected regions are added as new topological nodes.

5.5 Results of incremental Voronoi decomposition

Our result of the sample experiment on semi-structured environment is shown in Fig. 10. At each step, the whole map is segmented and every valid free grid cell has a corresponding region. Green regions mark the incrementally changed areas of the map; red regions mark the affected regions. The algorithm works incrementally and topological regions defined by previous steps are updated accordingly. We must notice that the decomposition is however not perfect: the combination of grid-based segmentation with non-straight edged obstacles results in regions that are not decomposed properly. As for the example shown in Fig. 11a, corridors are frequently subject to undesired fragmentation. Therefore, post-processing of the segmentation is necessary.

Fig. 10

Incremental Voronoi decomposition on the sample map. The first row shows the incremental segmentation results. The second row shows the regions which are incrementally changed by each iteration step. The third row shows the regions where the GVG needs to be recalculated due to the incremental changes indicated by the second row respectively. The related dataset is accessible at: http://www.ece.ust.hk/~eelium/dfki_parkinglot_map.bag.tar.gz (46 MB)

Fig. 11

Fusion of pruned regions applied to the sample map. a Raw decomposition, b After pruning

6 Post-processing of a Voronoi segmentation

The following section analyzes the possibilities of reducing the complexity and increasing the quality of the Voronoi decomposition by fusing regions of high similarity. We present and discuss two different methods that we successively use.

6.1 Fusion of pruned regions

By fusing redundant topological nodes in the graph, a coarse refinement can be achieved. If a topological node has exactly two adjacent neighbors, it should be fused with one of the neighboring regions. We use a similar approach as the one described by Thrun (1998). Figure 11 depicts an instance of the fusion result, where two regions are fused if and only if each of them only has one or two neighbors.

6.2 Spectral clustering

Clustering is a way to further enhance the sparseness of topological maps. In this section, we introduce the application of spectral clustering using Voronoi decomposition results as basic structures. Spectral clustering is one of the most common algorithms for graph clustering. It is extremely flexible to different types of data structures, as the definition of the adjacency matrix $S: \{s_{ij}\}$ is open. For typical adjacency matrices, a distance metric $s_{ij}$ needs to be defined between adjacent sites $i$ and $j$. The standard spectral clustering is introduced in Algorithm 1.

6.3 Distance metrics

The construction of the adjacency matrix is the essence of spectral clustering, which is build on the distance measurement between each pair of elements in the graph. In our case, the distance can also be considered as the similarity of two regions. For standard spectral clustering approaches, please refer to Luxburg (2006). We define and evaluate four different distances for Voronoi graphs as follows, where $d_{i,j}$ denotes the Euclidean distance between the centers of cells $i$ and $j$.

6.3.1 Distance between region centers

Using the Euclidean distance between the centers of two regions is the most intuitive way:

$$\begin{aligned} s_{i,j} = K \cdot \exp \left( { - \frac{d_{i,j}^2}{\sigma } } \right) \end{aligned}$$

with $K$ and $\sigma$ weighting parameters. The results are not always satisfactory since two regions with close centers may not be well connected and small regions have a higher probability to be fused than bigger ones. Furthermore, this measure is sensitive to the choice of $\sigma$ (Nadler and Galun 2007; Zelnik-Manor and Perona 2004). Usually $\sigma$ is chosen in a way that the local cells in the range of $\sigma$ are able to hold the footprint dimension of the robot. Such that, the criteria in Eq. (2) can be optimized.

6.3.2 Maximum distance between regions

To solve the shortcoming of two loosely connected regions, we use the maximum distance between two regions:

$$\begin{aligned} s_{i,j} = K \cdot \exp \left( { - \frac{d_{i,j,max}^2}{\sigma } } \right) \end{aligned}$$

As Voronoi decomposition yields convex shapes, loosely connected regions are unlikely to have a small measure in this case. However, long and narrow regions may not be fused and this measure again depends on the choice of $\sigma$.

6.3.3 Average distance between regions

The average distance between the cells of the two regions is defined as follows.

$$\begin{aligned} s_{i,j} = K \cdot \exp { - \frac{ \left( \frac{1}{N_1 \cdot N_2} \cdot \sum _{i =1}^{N_1} \sum _{j = 1}^{N_2} c_{i,j} \right) ^2 }{\sigma } }, \end{aligned}$$

where $c_{i,j}$ is the distance between the $i$’th and the $j$’th cells of the two regions; $N_1$ and $N_2$ represent the number of cells in each region, respectively. This measure relates the compactness of the two regions to their similarity factors. Two compact regions have a small average distance between their cells.

6.3.4 Connection ratio

Another approach is to use the ratio between the length of the critical line and regional extents as their similarity:

$$\begin{aligned} s_{i,j} = K \cdot \left( \frac{ l_{c} }{ A_{1} } + \frac{ l_{c} }{ A_{2} } \right) , \end{aligned}$$

where $l_{c}$ is the length of the critical line, $A_1$ and $A_2$ denote the areas of the two regions. This metric reflects that the internal connections of the regions have to be maximized whereas the external connections are minimized. The larger the connection ratio, the better the accessibility of the regions amongst each other. Using the area or the contour length of the regions for normalization produces similar results. This criterion is the most effective metric to merge region by spectral clustering, but it is also with highest computational complexity.

6.4 Quantitative clustering results

Recall algorithm 1, the number of regions $k$ is defined by the number of strictly positive eigenvalues of the Laplacian matrix, as discussed in Sect. 7.2. The various distance matrices lead to visually rational grouping results. One example using the “Connection Ratio” criterion is shown in Fig. 1b. However, we can still compare the quality measures and other aspects as shown in Table 1. The Connection Ratio is the best candidate considering quality of the segmentation and computational complexity for this data-set. The defined ratio is independent of the map scale and does not depend on the extension of the regions. Furthermore, it doesn’t depend on parameter adjustment either, e.g. $\sigma$ in Average Distance criteria cannot easily be tuned for arbitrary semi-structured environments.

During the spectral clustering of the GVG decomposition results, small and mostly insignificant regions are fused with larger regions. Hence, the ratio of valid regions increases greatly. Additionally, observing the ratio of valid regions (i.e. usable for navigation) in the third column of Table 1, we infer that spectral clustering fuses invalid small regions into valid regions.

Table 1 Quality factor and region validity ratio

7 Discussions

In this section, we discuss several key features of the algorithm. Regarding the known shortcoming of spectral clustering, which requires the knowledge of clusters $k$, we explain how we deal with $k$ selection problem. As one of the main targets, we will now present the analysis of the algorithm consistency, as well as the test of the algorithm in a typical semi-structured environment (Fig. 12).

Fig. 12

Pictures of the tunnel accident environment. Upper row: left entrance of the tunnel, right in the middle of the environment with barrels, pallets, and damaged vehicles. Lower row: left the robot used for the tests, right a live screen during one test

7.1 Discussion on decomposition size

The proposed algorithm updates the Voronoi diagram in an incremental manner. Therefore, the performance heavily depends on the amount of data related to affected regions. The computation times for four selected incremental steps are presented in Fig. 13. It shows a high dependence on the decomposition cells size, which defines the amount of cells that need to be considered for a given updated map. The change from a cell size of 0.25 to 0.1 m, which corresponds to an augmentation from 39,000 to 245,000 cells, increases the required computation time by a factor of about $20$. With similar segmentation results, the graph additionally shows that the incremental approach outperforms the non-incremental approach, independently of the required updates.

Fig. 13

Performance of the Voronoi decomposition

7.2 Discussion on the number of regions $k$

The selection of number of regions $k$ is a key problem in nowadays clustering algorithms. It has been denoted as a major drawback of the spectral clustering algorithms as well. We propose that the number of clusters $k$ is approximated by the number of strictly positive eigenvalues. The results of the segmentation are shown in Fig. 14.

Fig. 14

Incremental Voronoi segmentation before and after applying spectral clustering using “Connection Ratio” as distance. $q$ indicates the overall quality of the segmentation result using (2). a Before ($q = 0.672$), b after ($q = 1.659$)

7.3 Experiments for consistency analysis

One of the important properties of an incremental algorithm is the consistency of the decomposition, which means that the diversity among the results of different runs at the same environment should be minimized. A too diverse decomposition would probably indicate that the method is too ambiguous to be used with human operators. In order to test this property of the proposed algorithm, we implemented a set of experiments in a tunnel environment as shown in Fig. 12. This set of experiments was carried out by 6 untrained users who drove the robot manually. Therefore, the routes by which each subject drove the robot were arbitrary. Global 2d metric maps were created incrementally using karto ³ package. Figure 15 depicts the result of each subject’s trial. Coloring is randomized, only geometry matters. It can be seen that, in each case, the global structures of the environment were extracted, which have similar topological statistical features among trials, as shown in Table 2. This similarity results in similar cost in planning and environment modeling. The main differences appear on the boundary of explored space, left or right or on the inaccessible sidewalks. Also the large central region for subjects 1, 3, and 6 can also be split for subjects 2, 4, and 5. This is due to the way the car is perceived with respect to the barrel opposite. The regions tighten slightly but it is not obvious that they should be split.

Fig. 15

Topological segmentation at the end of each subject’s trial and examples of different paths performed by subjects 5 and 6. Map size is in average $53\times 23$ m$^2$. Please refer to Table 2 for statistical results. A sample dataset of the incremental mapping process is accessible at: http://www.ece.ust.hk/~eelium/mapping_bag_tunnel_subject1.bag (117 MB)

A major difficulty to assess the quality of stability is that the ground truth is hard to be defined. It means that generic metrics using terms such as “false positive ratio” are invalid, e.g. V-measure (Rosenberg and Hirschberg 2007). More important, comparing to traditional clustering problem, the configuration space varies with each subject. Instead, we use the number of extracted regions and connections for each subject as measures. The results are shown in Table 2. All numbers are within a few units of each others. This difference can be accounted for by the sidewalks and tunnel extremities.

Table 2 Number of topological regions and connections extracted for each subject

7.4 Extended results of indoor environment

Considering that most existing work (Thrun 1998; Choset and Nagatani 2001) deal with structured environment, we also want to compare the proposed algorithm with others in the same context. We show the result from an environment which is similar to the test environments in related works. Please notice the obstacles in open areas, which are usually not considered in Thrun (1998), Choi et al. (2009a). They are usually hard to manage with GVG extraction. In this test, we only apply the algorithm to the final map once. Figure 16a shows the final metric map of a structured environment which covers an area of size $57\times 35.5$ m$^2$. Figure 16b gives the decomposition results of the raw map. Cray (light) tracks in Fig. 16b depict the GVG extracted from (a), and red (dark) dots mark the raw critical points. The final segmentation result is shown in 16(d). The overall calculation takes only 7.84 s on a Duo-Core 2.8 GHz laptop.

Fig. 16

Typical results for a structured environment. The incremental process of mapping data and other Supplementary Data are accessible at: http://www.ece.ust.hk/~eelium/ETH_HG_G_center_mapping.bag.tar.gz (912 MB). a Raw map. Map resolution is 0.025 m, b Decomposed map. Resolution is 0.25 m, c GVG by the proposed algorithm, d Final segmentation result. 50 regions

Extended results for a typical indoor environment are shown in Fig. 17.⁴ Figure17a–c show that the proposed method can reflect the ground truth segmentation in terms of traditional concepts such as “room” and “corridor”. At the same time, the result in (c) indicates there are only half the number of regions after clustering. This sparseness leads to more compact representation of the same environment and facilitates the planning task. It implies two conclusions from these results: the proposed method is able to extract the topological regions from structured metric maps correctly, with an incremental manner; Spectral clustering results in a sparse representation with minimized sufficient number of topological nodes.

Fig. 17

Results in an typical indoor environment. $q$ indicates the overall quality of the segmentation result using (2). a Raw metric map, b Voronoi decomposition (50 regions, $q=2.30$), c After clustering (25 regions, $q=3.15$)

8 Conclusion

In this paper, we proposed a novel approach to online incremental topological segmentation for metric maps of semi-structured environments. We also provided a set of general criteria to justify the quality of topological segmentation, which can potentially be used as a benchmark to evaluate related methods. Spectral clustering was used to refine the raw segmentation result from an incrementally generated Voronoi diagram, leading to a more simplified representation. The results carried out by experiment on data-sets, repetitive tests and extended tests for structured environments specifically show the simplicity, robustness and consistency of the proposed method.

Readers interested in the application of the proposed topological graph in planning, navigation and environment modeling, are invited to refer to our previous report (Kruijff et al. 2012b; Gianni et al. 2011). Topological localization and navigation in 2D and 2.5D for search and rescue robots are the next steps of our research. Preliminary results can be found by our recent report (Song and Liu 2013).