1 Introduction

Dark energy (DE) was presented to explain unexpected phase of accelerated expansion, (Riess et al. (1998), Perlmutter et al. (1999, 2003), De Bernardis et al. (2000)) in the Einstein’s general relativity framework. First candidate for dark energy is the so called cosmological constant which suffers two problems (Weinberg (1989)). First problem is the cosmological constant problem and the second one comes from the fact that its equation of state parameter (EoS), \(w\), is constant while observations reveal a small variations in that of the DE (Padmanabhan (2003), Sahni and Starobinsky (2000)). Seeking an explanation for the latter case, dynamical models of dark energy was proposed in the literature. In this category, the dark energy candidate is a live time varying component. Examples of this category are, quintessence model which is based on a self interacting scalar field (Wetterich (1988), Ratra and Peebles (1988)) and K-essence which takes a scalar field with a non-canonical kinetic term responsible for cosmic acceleration (Chiba et al. (2000), Armendarriz-Picon et al. (2000, 2001)). Also one can take a look at phantom (Caldwell et al. (2003)) and agegraphic dark energy models (Cai (2007), Wei and Cai (2008)) which are extensively investigated.

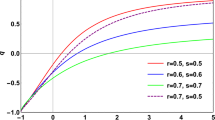
Holographic dark energy (HDE) is also another interesting model of dynamical category. HDE is an attempt to solve the cosmic acceleration which originates from the holographic principle (HP). This principle states that all the information contained in a volume, can be obtained using a theory on the boundary of that volume. Following the novel work by Cohen et al. (1999), which presented a key relation between ultra violet cutoff (UV), infra red cutoff (IR) and the entropy (S) for an effective quantum field theory, the HDE was presented in (Hsu (2004), Li (2004)). In this model, the quantum fields oscillations at the ground state level can acts as DE. Various features of the HDE is widely investigated. HDE can successfully explain some aspects of the cosmic acceleration. In (Lee et al. (2008)), the authors tried to explain the so called “coincidence problem” which simply asks that why the dark energy will be dominated at present epoches. Statefinder diagnosis is studied for the HDE in (Zhang (2005)). They found that in many versions of the HDE the statefinder variables \(\{r,s\}\) never catches \(\{1,0\}\). In some cases however acceptable values can be obtained. In addition the timeline of a flat background can not be discussed correctly through the HDE (Hsu (2004), Li (2004)). Interested reader can find a detailed review on HDE in, (Wang et al. (2017)), and references therein.

One way in curing the HDE problems is to generalize the underlying entropy relation to the non-extensive domain. One choice of the non-extensive category is the so called Tsallis entropy. Cosmological implication of the Tsallis entropy was first detailed in (Moradpour (2016)). In this paper the author considered impacts of Tsallis entropy in the DE problem. Following this paper a new version of the HDE presented in (Tavayef et al. (2018)). The authors replaced the previous entropy relation by general Tsallis entropy (\(S= \gamma A^{\delta }\)) and called the new model as Tsallis holographic dark energy (THDE). It can be seen that the THDE contains a new free parameter with respect to the standard HDE. Different choices of IR cutoff can be used to study cosmic dynamics in the framework of THDE. THDE with the Hubble cutoff was discussed in (Tavayef et al. (2018)). The future event horizon and Granda-Oliveros (GO) as IR cutoffs were performed in (Saridakis et al. (2018), Abdollahzadeh et al. (2018)). In (Sadri (2019)), the author examined the consistency of the THDE with several observational data sets. He claimed that there exist an inconsistency between the THDE and the studied data sets. Statefinder diagnosis of the model is performed in (Varshney et al. (2019)). Tsallis HDE is also studied in modified theories of gravity (Ghaffari et al. (2018, 2019), Jawad et al. (2019), Sharif and Saba (2019)). In another approach Sheykhi considered impacts of Tsallis entropy relation in emergent gravity paradigm and obtained the modified Friedmann equations (Sheykhi (2018)). The mission is done by means of the first law of thermodynamics and he showed that the resulting modified equations can solve the age problem. In the standard cosmology the dark sectors namely, DE \((\Lambda )\) and dark matter (DM) are taken as independent components. However, since the nature of both DE and DM is unknown yet, it is possible to leave a chance of interaction between these dark sectors. It is worth to note that there is not any known symmetry avoiding such an interaction in dark sectors (Wetterich (1988)). It is shown in the literature that taking an interaction between dark components can alleviate the coincidence problem. There also exists evidences which show that introducing an interaction term leads to a better consistency between theory and cosmic observations (Bertolami et al. (2007), Olivares et al. (2005)).

In this paper we mainly follow two points in THDE. At first we take a look at the cosmic dynamics through dynamical system approach. Next we try to find the impacts of adding an interaction term between dark components on the cosmic dynamics. To this end we consider different choices of interaction terms and discuss about the cosmic dynamic in every case.

The plan of this paper is as follows. Basic equations of standard cosmology are presented in Sect. 2. In the next section, we brief the Tsallis holographic dark energy model in a flat universe. In Sect. 4, we present an introduction to dynamical system approach in cosmological context and discuss about the THDE in presence of different interaction terms from a dynamical system approach. Next we consider the impacts of the interaction terms on the age of the universe. We summarize our results in Sect. 6.

2 Basic equations

In this paper our aim is to discuss the cosmic dynamics using a dynamical system method which is widely investigated in cosmology and astrophysical framework (Wainwright and Ellis (1997), Copeland et al. (2013), Amendola (2000), Xu et al. (2012), Capozziello and Roshan (2013), Landim (2015, 2016)). This technique can clarify the time line evolution of the underlying system versus evolution of different energy components of the universe. In this way we first review the basic equations governing the system. Here we assume a flat FRW background favored by cosmic observations. The first Friedmann equation takes the form

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}} \sum _{i=r,D,m}\rho _{i}, \end{aligned}$$
(1)

where “r” stands for radiation, “D” for dark energy and “m” stands for matter component which includes baryonic and dark matter. In above equation \(M_{P}=\frac{1}{\sqrt{8\pi G}}\).

Taking into account a chance of interaction between dark matter and DE components, the continuity equations can be written as

$$ \dot{\rho _{i}}+3H\rho _{i}(1+w_{i})=Q_{i}, $$
(2)

where \(Q_{i}\) denotes the chance of interaction between different components. Since the total content of the universe should satisfy the energy conservation, we expect \(\sum _{i} Q_{i}=0\). Expanding this equation separately for different components one can obtain

$$\begin{aligned} \dot{\rho }_{D}+3H\rho _{D}(1+w_{D}) =&-Q, \end{aligned}$$
(3)
$$\begin{aligned} \dot{\rho }_{m}+3H\rho _{m} =&Q, \end{aligned}$$
(4)
$$\begin{aligned} \dot{\rho }_{r}+4H\rho _{r} =&0, \end{aligned}$$
(5)

where \(Q\) represent the interaction between dark components and we used \(w_{m}=0\) and \(w_{r}=\frac{1}{3}\). Fractional density of different components can be defined as

$$ \Omega _{i}=\frac{\rho _{i}}{\rho _{cr}}, $$
(6)

where the critical energy density is \(\rho _{cr}=3M_{P}^{2}H^{2}\). Thus, the first Friedmann equation becomes

$$ \sum _{i} \Omega _{i}=1. $$
(7)

In order to obtain the dark energy EoS parameter we solve the respective conservation equation (2) for \(w_{D}\).

$$ w_{D}=-1-\frac{Q}{3H\rho _{D}}-\frac{\dot{\rho _{D}}}{\rho _{D}} $$
(8)

Taking time derivative of the first Friedmann equation (1) and using (2), we reach

$$ \dot{H}=-\frac{3}{2}\sum _{i}\frac{\rho _{i}}{3M_{p}^{2}}(1+w_{i}) $$
(9)

Dividing both sides by \(H^{2}\) and mixing with (7), one finds

$$ \frac{\dot{H}}{H^{2}}=-\frac{3}{2}\sum _{i}\Omega _{i}(1+w_{i}) $$
(10)

After a little algebra the deceleration parameter read

$$\begin{aligned} q =&-1-\frac{\dot{H}}{H^{2}}=\frac{1}{2}\sum _{i}\Omega _{i}(1+3w_{i}) \end{aligned}$$
(11)

Since we are going to discuss about the dynamical system analysis through next sections it is worth to mention evolution equation of fractional density for different components. Starting from

$$ \Omega _{i}=\frac{\rho _{i}}{3M_{P}^{2}H^{2}}, $$
(12)

and taking time derivative of above equation and after several steps we get

$$ \dot{\Omega }_{i}=\Omega _{i}\left [\frac{Q_{i}}{\rho _{i}}-3H(1+w_{i})-2H \frac{\dot{H}}{H^{2}}\right ]. $$
(13)

Replacing from (10), we obtain

$$\begin{aligned} \Omega ^{\prime }_{i} =&\frac{1}{H}\dot{\Omega }_{i} \\ =&f_{iQ}+\Omega _{i} \left [2-3(1+w_{i})+\sum _{\ell }\Omega _{\ell }(1+3w_{\ell })\right ] \end{aligned}$$
(14)

where \(f_{iQ}=\frac{Q_{i}}{3M_{P}^{2}H^{3}}\) and \(\ell \) runs over different components of the universe. The prime sign denotes derivative with respect to \(x=\ln {\frac{a}{a_{0}}}(a_{0}=1)\).

3 Tsallis holographic dark energy in a flat FRW background

Avoiding divergencies in effective field theories, UV and IR cutoffs are presented. In a subtle paper by, Cohen et al., they found that the UV and IR cutoffs are not independent (Cohen et al. (1999)). For an effective field theory with UV cutoff \(\Lambda \) in a finite universe with a size of order \(L\) (which plays the role of IR cutoff), there exist a relation between the entropy, UV and IR cutoffs as, (Cohen et al. (1999))

$$ L^{3}\Lambda ^{3}\sim S. $$
(15)

On the other hand the entire number of degrees of freedom in a spacetime (which according to holographic principle are living on the boundary of the region) does not exceed the Bekenstein-Hawking bound (Bousso (1999)). Then one obtains

$$ L^{3}\Lambda ^{3}\leq S_{BH}=\pi M_{P}^{2} L^{2}. $$
(16)

Taking to account in above inequality that \(S_{max}\cong S_{BH}^{\frac{3}{4}}\) and \(\rho _{\Lambda }\propto \Lambda ^{4}\) Cohen et al. (1999), one gets

$$ \rho _{\Lambda } \propto M_{P}^{2}L^{-2}, $$
(17)

where \(\rho _{\Lambda }\) in above relation is energy density of the standard HDE. Next step in Standard HDE is to choose a suitable IR cutoff (\(L\)). The simplest choice is the hubble scale (\(L=H^{-1}\)) which results a energy density consistent with the observed present value of the dark energy. However it was shown that this model does not yield a correct equation of state parameter (EoS) (Hsu (2004)). Curing this problem the HDE is modified through the IR cutoff parameter (\(L\)). One example is the future event horizon which was proposed in (Li (2004)). Other choices of IR cutoffs can be seen in (Wang et al. (2017)). Although modifying the IR cutoffs leads better description of the cosmic dynamic in standard HDE but still there exist problems such as stability against small perturbations. Then it seems interesting to modify the standard HDE avoiding these failures. The other chance to modify the HDE is to replace the Bekenstein-Hawking entropy relation with other forms of non-extensive entropy relations. Recently Tavayef et al. presented a new version of the HDE which is based on the Tsallis entropy relation (Tavayef et al. (2018)). The Tsallis entropy read

$$ S=\gamma A^{\delta }, $$
(18)

where \(\delta \) is non-additivity parameter and \(\gamma \) is a constant. Inserting above relation in Eq. (16), one can find

$$ \rho _{THDE}=BL^{2\delta -4}, $$
(19)

where B is an undefined parameter. It is obvious that the standard HDE is retrieved in the case \(\delta =1\).

Taking the hubble radius (\(L=H^{-1}\)) as IR cutoff the THDE energy density reads

$$ \rho _{D}=BH^{-2\delta +4}. $$
(20)

Now, we would like to obtain the governing evolution equations of a universe filled with the THDE, a pressureless cold dark matter (CDM) and a radiation component. Then the first Friedmann equation read

$$\begin{aligned} H^{2}=\frac{1}{3M_{p}^{2}} (\rho _{D}+\rho _{m}+\rho _{r}). \end{aligned}$$
(21)

The fractional density for the THDE is

$$ \Omega _{D}=\frac{BH^{2-2\delta }}{3M_{P}^{2}}, $$
(22)

and the Eq. (21) in terms of the fractional densities will be

$$ \Omega _{D}+\Omega _{m}+\Omega _{r}=1. $$
(23)

Taking time derivative of Eq. (20) and replacing in (8) get

$$ w_{D}= \frac{-1-\frac{Q}{3H\rho _{D}}-(\delta -2)(1+\frac{1}{3}\Omega _{r})}{1+(\delta -2)\Omega _{D}}. $$
(24)

One can easily check that above relation reduced to the respective one in (Tavayef et al. (2018)) for non interacting case and in the absence of radiation component. For the limiting case \(\delta =1\) and in the absence of interaction we find \(w_{D}=0\) which is expected (Hsu (2004)). Expanding Eq. (11) for different component of the universe we obtain

$$ q=\frac{1}{2}+\frac{1}{2}\Omega _{r}+ \frac{3}{2}\Omega _{D}\left [ \frac{-1+(2-\delta )\left [1+\frac{\Omega _{r}}{3}\right ]-\frac{Q}{3H\rho _{D}}}{1-(2-\delta )\Omega _{D}} \right ] $$
(25)

Another interesting feature of DE models is stability against perturbations in the cosmic fluid. Here we follow a semi-Newtonian analysis which can reveals impacts of instability in the cosmic background. To this end we start with definition of the adiabatic squared sound speed

$$ C_{s}^{2}=\frac{dP}{d\rho }=\frac{\dot{P}}{\dot{\rho }}= \frac{\rho }{\dot{\rho }}\dot{w}+w, $$
(26)

where \(P=w\rho \) and \(w\) is the effective EoS parameter of the cosmic fluid. Since the content of the universe include DE, pressureless dark matter and radiation, one easily find

$$ w=\frac{P_{r}+P_{m}+P_{D}}{\rho _{r}+\rho _{m}+\rho _{D}}=\frac{1}{3} \Omega _{r}+w_{D}\Omega _{D} $$
(27)

Combining (26), (27) and (2) one get

$$ C_{s}^{2}= \frac{-w^{\prime }}{3(1+\Omega _{D}w_{D}+\frac{1}{3}\Omega _{r})}+w. $$
(28)

It is worth mentioning that \(C_{s}^{2}\) shows the stability of total cosmic fluid and not only that of the THDE component and hence its results are a little bit different from those presented in Tavayef et al. (2018) and Abdollahzadeh et al. (2018).

Above relations at hand and the relations presented in Sect. 2 we are ready to consider the main task of this work.

4 Cosmic evolution through a dynamical system analysis

Here, we would like to consider the competitive behavior of the cosmic components. Our aim is to see whether the system evolution corresponds to observations. Running the evolution equations we expect a non-stable radiation dominated phase at beginning epoches. Next the universe should enter a long period of non-stable matter dominated era and finally the universe goes through a DE dominated epoch.

In this section we will discuss the THDE model in presence of different interaction terms. Interaction between DM and DE has long history in the literature. At first an interaction between dark components proposed to explain the large inconsistency between the observed and theoretical value the cosmological constant (Wetterich (1988, 1995)). A supporting idea of interaction between dark sector component comes from the fact that an interacting dark energy model can be equivalent to a modified gravity (De Felice and Tsujikawa (2010), He et al. (2011), Zumalacarregui et al. (2013)). Many models of DE take a linear interaction between dark component of the universe. However, there exist no reason to leave non-linear or other forms of interaction term between dark matter and energy but simplicity. An example of non-linearly interacting models is a productive relation between DM and DE densities in coupling term which seems to be consistent observationally (He and Wang (2008)). Interested reader can see a comprehensive details on interacting models of dark energy in (Bolotin et al. (2014), Wang et al. (2016)). So, in this section we consider several cases of THDE including linearly, sign changeable and non-linearly interacting models. It is worth to mention that there exist also some implications against interacting models from the stability issues (D’Amico et al. (2016)).

Now we are ready to start the main task of this note. To this end at first we bring the evolution equations of the components. Expanding Eq. (14) for DE and DM components we have

$$\begin{aligned} \Omega ^{\prime }_{D} =&f_{QD}+3\Omega _{D}\left [(\Omega _{D}-1) \left ( \frac{1-\delta -\frac{Q}{3H\rho _{D}}}{1-(2-\delta )\Omega _{D}} \right )+\frac{\Omega _{r}}{3}\right ] \\ \Omega ^{\prime }_{m} =&f_{Qm}+3\Omega _{m}\left [\Omega _{D} \left ( \frac{1-\delta -\frac{Q}{3H\rho _{D}}}{1-(2-\delta )\Omega _{D}} \right )+\frac{\Omega _{r}}{3}\right ] \\ 1 =&\Omega _{D}+\Omega _{m}+\Omega _{r} \end{aligned}$$
(29)

For a complete description of the model we introduce different versions of interaction terms and discuss the resulting dynamical systems.

4.1 Non-interacting THDE

At first we consider the THDE in the absence of interaction. Governing equations in this case are

$$\begin{aligned} \Omega ^{\prime }_{D} =& 3\Omega _{D}\bigg[(\Omega _{D}-1)\left ( \frac{1-\delta }{1-(2-\delta )\Omega _{D}}\right ) \\ &{}+ \frac{1-\Omega _{D}-\Omega _{m}}{3}\bigg] \\ \Omega ^{\prime }_{m} =& 3\Omega _{m}\bigg[\Omega _{D}\left ( \frac{1-\delta }{1-(2-\delta )\Omega _{D}}\right ) \\ &{}+ \frac{1-\Omega _{D}-\Omega _{m}}{3}\bigg] \end{aligned}$$
(30)

As we mentioned above system of equations contains three fixed points as given in Table 1.

Table 1 The admitted fixed points of THDE in the non-interacting case are listed
Full size table

The physical phase space is compact (i.e. \(0\leq \Omega _{i} \leq 1\)). The first point denotes a radiation dominated phase at the beginning of the cosmic evolution. One interesting feature about the fixed points is their stability which can be determined through their respective eigenvalues of the stability matrix. For the first point the corresponding eigenvalues are \(\lambda _{1}=1\) and \(\lambda _{2}=4(\delta -1)\). So this fixed point shows an unstable character for \(\delta >1\) and a saddle nature for \(\delta <1\). One can easily find that in this epoch \(q>0\) which shows a decelerative behavior as we expect.

Second fixed point (\(\Omega _{m}=1,\Omega _{D}=0\)), corresponds to a matter dominated phase of evolution which starts after radiation dominated one. The eigenvalues of the stability matrix are (\(\lambda _{1}=-1, \lambda _{2}=3(\delta -1)\)). This epoches could show a transient character if we take \(\delta >1\). Taking a look at Fig. 1, one easily find the decelerative nature of this era.

Fig. 1
figure 1

In the upper panel phase space diagram of the non-interacting THDE is depicted. The solid line corresponds the evolution line for \(\Omega _{D0}=0.69,\Omega _{m0}=0.30995\). In the down panel the deceleration parameter and \(\Omega _{i}\)’s are plotted against \(x=\ln {a}\) for \(\delta=1.4\)

Full size image

Last fixed point is a late time attractor (a dark energy dominated) corresponds to \(\Omega _{m}=0,\Omega _{D}=1\). Interesting point about this phase is its stability irrespective of the free parameters (\(\lambda _{1}=-3, \lambda _{2}=-4\)). It is worth to mention fate of the universe at this point. Since \(\Omega _{D}=1\), then we have

$$ \frac{BH^{2-2\delta }}{3M_{P}^{2}}=1 \Rightarrow H=( \frac{3M_{P}^{2}}{B})^{\frac{1}{2(1-\delta )}}. $$

Hence, due to the constancy of the Hubble parameter, the universe undergoes a phase of de Sitter expansion at this fixed point.

Noting to deceleration parameter one finds accelerative behavior of the universe through this phase of expansion.

As a result we find that obtaining a correct ordering of expansion phases, we should set \(\delta >1\). It is worth to mention that irrespective of the initial conditions system admits these three fixed points. Phase space diagram of (\(\Omega _{m},\Omega _{D}\)) is depicted in left part of Fig. 1.

Stability of the cosmic background could be investigated through the squared sound speed analysis. Since explicit form of \(C_{s}^{2}\) is too messy, (due to the presence of three components), we do not bring them analytically here. Evolution of the \(C_{s}^{2}\) is depicted in Fig. 2. One can easily see that for \(1\leq \delta < 2\) the model shows an unstable behavior. However for choices of \(\delta >2\) the model evolves through stable phases according to the squared sound speed analysis.

Fig. 2
figure 2

In this figure the evolution of \(C_{s}^{2}\) is plotted for non-interacting THDE case

Full size image

4.2 Interacting models

4.2.1 Linearly interacting \(Q=3b^{2}H(\rho _{D}+\rho _{m})\)

In this case the system also contains three fixed points. The fixed points are presented in Table 2. One can easily find that the first fixed point shows a radiation dominated epoch. Taking a look at the respective eigenvalues of this case, \(\lambda _{1}=3b^{2}+1\) and \(\lambda _{2}=4(\delta -1)\) reveals that the point has saddle nature for \(\delta <1\) and is unstable for \(\delta >1\). The universe is decelerating around this fixed point \(q=1\).

Table 2 Fixed points of the THDE in the presence of the linear interaction term
Full size table

Second fixed point shows a matter dominated decelerating phase of expansion. We need an unstable nature of this point for a consistent picture. The stability matrix exhibits \(\lambda _{1}=-(3b^{2}+1)<0\) and \(\lambda _{2}=3(\delta -1)(-b^{2}+1)\). The nature of the fixed point is presented in Table 2. The deceleration parameter in this point read \(q=\frac{-3b^{2}+1}{2}\). Necessity of a decelerative matter dominated epoch restrict coupling constant value to \(b^{2}<\frac{1}{3}\).

In the last fixed point (the dark energy dominated case), the first eigenvalue is \(\lambda _{1}=-4\). Second eigenvalue is \(\lambda _{2}= \frac{3(\delta -1)(-b^{2}+1)}{b^{2}(\delta -2)-(\delta -1)}\). An example is plotted in the left part of Fig. 3. Near this fix point for \(\delta >1\) the universe undergoes a phase of accelerated expansion. Then in this model the universe starts from a radiation dominated phase and exits toward a dark matter era. The dark matter era will be a transient attractor for the values in Table 2. Since more observational constraint are consistent with \(b^{2}<1\) (Sadri (2019)) and also from the necessity of the transient matter dominated epoch then we find that the case \(\delta >1\) is of cosmic interest. So in this case for a consistent history of cosmic evolution we should set \(b^{2}<\frac{1}{3}\) and \(\delta >1\). The fate of the universe is almost the same as the previous case and the universe enters a phase of de Sitter like expansion at the third fixed point. In this case the fate of the universe is called de Sitter like because the universe is not a matter free universe at the last fixed point.

Fig. 3
figure 3

Upper part shows phase space diagram of the THDE in presence of a linear interaction term. The lower part includes the deceleration parameter and \(\Omega _{i}\)s. Figures are plotted for \(\Omega _{D0}=0.69\), \(\Omega _{m0}=0.30995\), \(b=0.2\) and \(\delta =1.4\)

Full size image

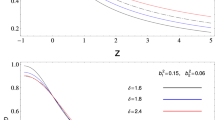
Squared sound speed analysis if Fig. 4 reveals that the cosmic fluid could be stable against perturbations for desired values in (Sadri (2019)) (\(b=0.048, \delta =2.161\)). This point is interesting because in (Sadri (2019)), the author found that the THDE component is unstable even for best fitted values of \(b\) and \(\delta \) parameters. However for some ranges of the parameters \(b\) and \(\delta \) the system shows impacts of instability.

Fig. 4
figure 4

In this figure the evolution of \(C_{s}^{2}\) is plotted for linearly interacting THDE case (b = 0.048)

Full size image

4.2.2 Sign changeable interaction term \(Q=3b^{2}H(\rho _{D}-\rho _{m})\)

The first point (\(\Omega _{D}=\Omega _{m}=0\)) with eigenvalues \(( \lambda _{1}=-3b^{2}+1, \lambda _{2}=4(\delta -1))\) shows an unstable nature provided, \(\delta >1\) and \(b^{2}<\frac{1}{3}\). For \(\delta >1\) and \(b^{2}>\frac{1}{3}\) the fixed point will be saddle. In the case \(\delta <1\), taking \(b^{2}<\frac{1}{3}\) the system provides a saddle point. If evolution of the universe starts from these possibilities in a radiation dominated epoch. It will finally approaches toward a matter dominated era. The system in this epoch experiences a decelerating evolution.

The second fixed point, \((\Omega _{m}=1,\Omega _{D}=0)\) could be a transient attractor. One can see from Fig. 5 that in this era the expansion of the universe is decelerative. One should note that the model provide a decelerative behavior at this fixed point irrespective of the values of \(\delta \) and \(b\) due to \(q(\Omega _{m}=1,\Omega _{D}=0)= \frac{3b^{2}+1}{2}\). The stability nature of this fixed point can be seen using the corresponding eigenvalues \((\lambda _{1}=3b^{2}-1,\lambda _{2}=(\delta -1)(3b^{2}+3))\). In this case the universe will exit the matter dominated phase for \(b^{2}>\frac{1}{3}\) and \(\delta >1\). This fixed point will be a saddle point taking \(\delta >1\) and \(b^{2}<\frac{1}{3}\). One can note that although the nature of this fixed point will also be saddle for the choice \(b^{2}>\frac{1}{3},\delta <1\), but these values are not consistent with the radiation dominated epoch. Since the parameters \(\delta \) and \(b\) are constants and they should be determined at first evolution steps. If we set them to \(b^{2}<\frac{1}{3},\delta <1\), then the system will exit from radiation dominated era but the matter dominated fixed point will be a stable attractor in this case. So we find that in this form of interaction term the choice \(\delta <1\) can not provide a consistent picture.

Fig. 5
figure 5

Upper panel shows phase space diagram of the sign changeable interacting THDE of the form \(Q=3b^{2}H(\rho _{D}-\rho _{m})\). In the down panel the deceleration parameter and \(\Omega _{i}\)s is plotted versus \(\ln {a}\). In above figures we used \(\Omega _{D0}=0.69,\Omega _{m0}=0.30995\), \(b=0.2\) and \(\delta =1.4\) as initial conditions

Full size image

Next the universe goes toward the third fixed point in Table 3. The future of the universe is once again a de Sitter like phase of expansion. In this case the eigenvalues of stability matrix read \(\lambda _{1}=-4,\lambda _{2}=-3\left [ \frac{2b^{4}+3b^{2}+1}{1+b^{2}\frac{\delta }{\delta -1}}\right ]\). It is obvious that for \(\delta >1\), this fixed point will be late time stable attractor. Using the deceleration parameter \(q=-\frac{3b^{2}+2(\delta -1)}{2(\delta -1)}\), it is easily seen that for \(\delta >1\) this fixed point shows an accelerative nature independent of \(b\). The history of cosmic evolution is plotted in phase portrait diagram in Fig. 5 for an example choice of free parameters. Since the universe is stable at this fixed point it is interesting to discuss about the stability against small perturbations in the cosmic fluid. Figure 6 shows that for suitable choices of the free parameters the model could be stable against perturbations.

Fig. 6
figure 6

In this figure the evolution of \(C_{s}^{2}\) is plotted for linearly sign-changeable interacting THDE case (b = 0.2)

Full size image
Table 3 Fixed points of the THDE in the presence of the sign changeable interaction term
Full size table

4.2.3 Nonlinear interaction term \(Q=3b^{2}H\frac{\rho _{D}^{3}}{\rho _{tot}^{2}}\)

For a nonlinear interaction term the dynamical system equations read

$$\begin{aligned} \Omega ^{\prime }_{D} =& - \frac{\Omega _{D}(3b^{2}\Omega _{D}^{3}+4\Omega _{D}+\Omega _{m}-4)(\delta -1)}{1+(\delta -2)\Omega _{D}} \\ \Omega ^{\prime }_{m} =&\frac{1}{1+(\delta -2)\Omega _{D}}\big[3b^{2}( \delta -2)\Omega _{D}^{4}-3b^{2}(\Omega _{m}-1)\Omega _{D}^{3} \\ +&(-3\delta +2)\Omega _{D}\Omega _{m}+\Omega _{m}(1-\Omega _{m}) \big] \end{aligned}$$
(31)

In this case also the universe contains three fixed points correspond to radiation, matter and DE dominated epoches. Setting suitable initial conditions the universe starts its evolution from radiation dominated phase (\(\Omega _{r}=1\)). In this phase the universe is decelerating according to Fig. 8. The decelerativity of this epoch is independent of the free parameter \(\delta \) and \(b\). This phase of expansion will end toward a matter dominated epoch due to the nature of this fixed point. The stability matrix eigenvalues in this case are \(\lambda _{1}=1\) and \(\lambda _{2}=4(\delta -1)\).

The second fixed point is a transient attractor for \(\delta >1\). The reason behind this choice comes from \(\lambda _{1}=-1\) and \(\lambda _{2}=3(\delta -1)\). The universe experiences a phase of slowing expansion according to Fig. 8. Once again since \(q=\frac{1}{2}\) the slowing nature of the expansion is valid for all values of the free parameter.

The third fixed point is a DE dominated phase of expansion. The explicit form of this fixed point and its stability matrix eigenvalues are a little bit messy to be presented here. Its nature is a late time stable attractor for \(\delta >1\). One should note that in this case the first eigenvalue of the stability matrix is \(\lambda _{1}=-4\). The second eigenvalue is also negative for ranges of our interest according to Fig. 7. So this fixed point will be stable which corresponds to an accelerated expansion phase for ever. However one should note that this for ever accelerated expansion leads to a de Sitter like expansion irrespective of the model parameters as mentioned before.

Fig. 7
figure 7

In this figure the \(\lambda _{2}\) is plotted for allowed region of interest in the non-linear interaction term

Full size image
Fig. 8
figure 8

In top part phase space diagram of the nonlinearly interacting THDE is plotted. In the down part the deceleration parameter and \(\Omega _{i}\)s is plotted against \(\ln {a}\). Initial condition is \(\Omega _{D0}=0.69\), \(\Omega _{m0}=0.30995\), \(b=0.2\) and \(\delta =1.4\)

Full size image

So it is obvious that for a consistent picture of cosmic evolution we need \(\delta >1\). Interesting fact about this form of interaction term is that the cosmic evolution will be consistent with what we need independent the choice of \(b\) for \(\delta >1\).

Evolution of the squared sound speed is depicted in Fig. 9. The figure reveals that a correct choice of the free parameters leave a chance of stability against perturbations. However an observational constraint on the free parameters is left and could be investigated.

Fig. 9
figure 9

This figure shows evolution of \(C_{s}^{2}\) for non-linearly interacting THDE case (b = 0.2)

Full size image

5 Age of the universe in THDE model

According to standard cosmology the age of the universe can be obtained from

$$ t_{0}=\frac{1}{H_{0}}\int _{0}^{\infty }\frac{dz}{(1+z)h(z)}= \frac{-1}{H_{0}}\int _{-\infty }^{0}\frac{dx}{h(x)}, $$
(32)

where \(h(z)=\frac{H(z)}{H_{0}}\) and \(x=\ln {a}=-\ln {(1+z)}\). One can easily check that age of the universe in the absence of the DE component is \(\frac{2}{3H_{0}}\). In (Tavayef et al. (2018)), the author found that THDE can alleviate the age problem. Here we would like to see the impacts of different choices of interaction terms on the age of the present universe. To this end we use

$$ \frac{\dot{H}}{H}= H^{\prime }=-\frac{3}{2}H\sum _{i}\Omega _{i}(1+w_{i}), $$
(33)

and solve above equation simultaneously with (14). As a result we obtain \(h(x)\). Next, replacing \(h(x)\) in (32), we can reach an evaluation of the age of the present universe. The results are summarized in Table 4 and Table 5. In obtaining the results we used the present value of the Hubble parameter \((H_{0}=67.77\pm 1.30~\mbox{km}\,\mbox{s}^{-1}\,\mbox{Mpc}^{-1})\) presented in (Macaulay (2019)).

Table 4 Age of the present universe is obtained for different values of \(\delta \) (\(b=0.2\)). In this table we used the notation \((H_{0}t_{0})^{\text{upper bound of age}}_{ \text{lower bound of age}}\) according to \(H_{0}=67.77\pm 1.30\) in Macaulay (2019)
Full size table
Table 5 Age of the present universe is obtained for different values of \(b\) (\(\delta =2.4\)). In this table we used the notation \((H_{0}t_{0})^{\text{upper bound of age}}_{ \text{lower bound of age}}\) according to \(H_{0}=67.77\pm 1.30\) in Macaulay (2019)
Full size table

6 Summary

Our goal in this paper is to discuss the THDE in the presence of interaction terms with the Hubble horizon as IR cutoff. Here, we assume a universe filled with radiation, matter and THDE. Evolution of the universe in standard cosmology starts with an unstable radiation dominated universe which is followed by another unstable matter dominated epoch. Finally a DE dominated era is favored by observations. Here we would like to see whether the interacting THDE provide such an evolution history. This issue is examined through the dynamical system analysis by means of obtaining the fixed points and a discussion about their stability. We found that in all forms of interaction terms, three expected epoches are available. Using the timeline of the fixed points, we could restrict the free parameters. In noninteracting, sign changeable and nonlinear interacting THDE cases, for \(\delta >1\), we found a consistent picture of fixed points with observations (in agreement with observational constraint presented in (Sadri (2019)) and in (Saridakis et al. (2018)) with a different IR cutoff) while the choice of \(\delta <1\) is not of cosmic interest. However in a linear interacting case apparently the model leaves home for both choices \(\delta >1\) and \(\delta <1\). However noting the necessity of a slowing phase of matter dominated epoch we reach a restriction (\(b^{2}<\frac{1}{3}\)) in the linearly interacting case. Taking this point the chance of \(\delta <1\) will also be rejected in this case.

As a result the THDE with a Hubble horizon in presence of the discussed interaction terms is just consistent with the standard cosmology for \(\delta >1\) and the case \(\delta <1\) is not cosmologically dependable. Stability of the THDE model is investigated through a squared sound speed analysis in presence of an interaction between dark sector components. The results are interesting and we find that for all choices of interaction terms there exist rooms for stability of the total cosmic fluid. However, an observational constraint on the model could be enlightening.

Next we consider the age problem in the THDE and found that the form of interaction terms can affect the age of the universe significantly.