1 Introduction

The significance of spatially homogeneous and anisotropic Bianchi models is, now, related to the discovery of an amount of anisotropy in the background radiation. This indicates that these models are more a realistic picture of past eras in the history of the universe. Also, from the theoretical point of view, anisotropic models have a greater generality than isotropic solutions of Einstein field equations for the cosmological problem. There are nine types of Bianchi space-times in literature (Taub 1951) which have been extensively used to investigate cosmological models to describe early stages of evolution of the universe in the presence of various physical distributions of matter. Here, our main concern is to present Bianchi type-(BT)-III cosmological model in the presence of dark energy fluid and an attractive massive scalar meson field.

Dark energy (DE) which is defined as the exotic negative pressure causing the accelerated expansion of the universe (Riess et al. 1988; Perlmutter et al. 1999) is attracting attention of several researchers in the recent years. In order to explain this mysterious concept two ways have been suggested. One way is to construct dark energy models and the other one is to modify Einstein’s theory of gravitation to study the corresponding anisotropic dark energy cosmological models. Significant and useful modifications of Einstein’s theory are scalar-tensor theories of gravity proposed by Brans and Dicke (1961), Saez and Ballester (1986), \(f(R)\) and \(f(R,T)\) modified theories of gravity (Nojiri et al. 2005; Harko et al. 2011). There have been several investigations on anisotropic DE models in the alternative theories of gravitation (Copeland et al. 1998; Nojiri and Odintsov 2006). In the literature, there are very nice reviews on modified theories of gravitation (Nojiri and Odintsov 2011; Capozziello et al. 2012; Clifton et al. 2012; Nojiri et al. 2017). It is important to mention, here, that the investigation of Bianchi models in the modified theories of gravitation is useful to understand the possible anisotropic nature of DE and its effects on the evolution of the universe.

Here we are interested in the study of DE models of Einstein field equations in the presence of scalar meson fields. The works of Dirac (1937), Kaluza-Klein (1921) and subsequently Brans and Dicke (1961) through their scalar-tensor theories have introduced scalar field (SF) in cosmology. Now particle physics theories confirm the presence of SFs. For example the Higgs mechanism explaining the mass of the particles is a massive SF (Zel’dovich 1986). Also, the recent scenario of accelerated expansion of the universe is explained by quintessence SF. It, also, helps to produce inflation at early stages of evolution of the universe. Scalar meson fields are of two types, namely, zero mass SFs and attractive massive SFs. Mass less SFs describes long range and massive SFs short range interactions. Several researchers have discussed, in the past, scalar meson fields associated with various physical sources (Mohanty and Pradhan 1992; Singh and Ram 1996; Singh 2005, 2008; Rahaman et al. 2002). In recent years, anisotropic DE cosmological models in the presence of massive and mass less SFs have been the subject of active investigation. BT-V dark energy model with scalar meson fields in general relativity has been obtained by Reddy (2018) while Naidu (2018) discussed BT-II modified holographic Ricci dark energy model in the presence of attractive massive SF. Aditya and Reddy (2018) discussed the dynamics of BT-III cosmological model in the presence of anisotropic DE and an attractive massive scalar meson field. Reddy et al. (2019) have investigated dark energy cosmological model in the presence of anisotropic dark energy fluid coupled with mass less SF in Kantowski-Sachs space-time in general theory of relativity. Recently, Reddy and Ramesh (2019a) presented a new DE model in five dimensional Kaluza-Klein anisotropic space-time in the presence of zero mass SFs in general relativity while Reddy and Ramesh (2019b) investigated FRW type Kaluza-Klein inflationary cosmological model in the presence of mass less SF with flat potential. Very recently, Naidu et al. (2019) discussed BT-V dark energy cosmological model in general relativity in the presence of massive SF. Aditya et al. (2019) have discussed Kaluza-Klein dark energy model in Lyra manifold in the presence of massive SF, whereas Aditya and Reddy (2019) have studied dynamics of perfect fluid cosmological model in the presence of massive SF in \(f(R,T)\) gravity. Singh and Rani (2015) obtained BT-III cosmological models in the presence of perfect fluid and an attractive massive SF in Lyra (1951) geometry using a special law of variation for Hubble’s parameter proposed by Bermann (1983). Santhi et al. (2017) have investigated Kantowski–Sachs SF cosmological models in \(f(R,T)\) theory of gravity.

The above discussion has motivated us to consider a spatially homogeneous and totally anisotropic BT-III cosmological model in the presence of DE fluid and an attractive massive SF in general theory of relativity. The scheme of this paper is as follows: Sect. 2 contains the metric and the derivation of field equations in Einstein’s theory. In Sect. 3, we obtain solutions of the field equations and present the corresponding cosmological model. In Sect. 4, some dynamical and physical aspects of our model are discussed. Finally the last section gives the summary and the results of our work.

2 Metric and field equations in general relativity

We consider the spatially homogeneous and anisotropic BT-III metric in the form.

$$ ds^{2} = dt^{2} - A^{2}dx^{2} - B^{2}e^{2x}dy^{2} - C^{2}e^{ - 2x}dz^{2} $$
(1)

where \(A\), \(B\), \(C\) are functions of cosmic time \(t\) only.

In general relativity the field equations in the presence of massive SF and anisotropic DE fluid are given by

$$ R_{ij} - \frac{1}{2}g_{ij}R = - \bigl(T_{ij}^{(\mathit{de})} + T_{ij}^{(s)} \bigr) $$
(2)

and the other symbols have their usual meaning. We use gravitational units so that \(8\pi G = c = 1\). The energy conservation equation is the consequence of Eq. (2), and is given as

$$ (T_{ij})_{;j} = 0 $$
(3)

Here the energy-momentum tensor of massive SF and anisotropic DE fluid are given by

$$ T_{ij} = T_{ij}^{(\mathit{de})} + T_{ij}^{(s)} $$
(4)

where

$$\begin{aligned}& T_{ij}^{(\mathit{de})} = (\rho _{\mathit{de}} + p_{\mathit{de}})u_{i}u_{j} - p_{\mathit{de}}g_{ij} \end{aligned}$$
(5)
$$\begin{aligned}& T_{ij}^{(s)} = \varphi _{,i}\varphi _{,j} - \frac{1}{2}\bigl(\varphi _{,k}\varphi ^{,k} - M^{2}\varphi ^{2}\bigr). \end{aligned}$$
(6)

Here \(\rho _{\mathit{de}}\) and \(p_{\mathit{de}}\) are the DE density and pressure, whereas mass of the SF \(\varphi \) is denoted by \(M\). The SF always satisfies the Klein-Gordon equation

$$ g^{ij}\varphi _{;ij} + M^{2}\varphi = 0. $$
(7)

The anisotropy of the DE in BT space-times is useful in generating arbitrary ellipsoidality to the Universe, and to fine-tune the observed CMBR anisotropies. Koivisto and Mota (2008a, 2008b) have discussed cosmological model with anisotropic EoS. They have proposed a different approach to resolve CMB anisotropy problem and it could be distorted by the direction dependent acceleration of the future Universe in such a way that it appears to us anomalous at the largest scales. They have studied a cosmological model containing a DE component which has an anisotropic EoS and interacts with the perfect fluid component. They have also suggested that cosmological models with anisotropic EoS can explain the quadrupole problem and can be tested by SN Ia data. The energy-momentum tensor of anisotropic DE fluid given by Eq. (5) can be parameterized as

$$ T_{ij}^{(\mathit{de})} = \operatorname{diag}\bigl[1, - \omega _{\mathit{de}}, - (\omega _{\mathit{de}} + \gamma ), - (\omega _{\mathit{de}} + \delta )\bigr]\rho _{\mathit{de}} $$
(8)

where we have defined the EoS parameter of DE as \(\omega _{\mathit{de}} = \frac{p_{\mathit{de}}}{\rho _{\mathit{de}}}\). \(\gamma \) and \(\delta \) are the skewness parameters which are the deviations from EoS parameter \(\omega _{\mathit{de}}\) along y and z-axes respectively.

Now using commoving coordinates and Eqs. (3)–(8) the field equations (2) and (7) for the metric can be written as

$$\begin{aligned}& \frac{\dot{A} \dot{B}}{AB} + \frac{\dot{B} \dot{C}}{BC} + \frac{\dot{C} \dot{A}}{CA} - \frac{1}{A^{2}} = \rho _{\mathit{de}} + \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(9)
$$\begin{aligned}& \frac{\ddot{B}}{B} + \frac{\ddot{C}}{ C} + \frac{\dot{B} \dot{C}}{BC} = - \omega _{\mathit{de}}\rho _{\mathit{de}} - \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(10)
$$\begin{aligned}& \frac{\ddot{A}}{A} + \frac{\ddot{C} }{C} + \frac{\dot{A} \dot{C}}{AC} = - (\omega _{\mathit{de}} + \gamma )\rho _{\mathit{de}} - \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(11)
$$\begin{aligned}& \frac{\ddot{A}}{A} + \frac{\ddot{B}}{B} + \frac{\dot{A} \dot{B}}{AB} - \frac{1}{A^{2}} = - (\omega _{\mathit{de}} + \delta )\rho _{\mathit{de}} - \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(12)
$$\begin{aligned}& \frac{\dot{A}}{A} - \frac{\dot{B}}{B} = 0 \end{aligned}$$
(13)
$$\begin{aligned}& \ddot{\varphi} + \dot{\varphi} \biggl( \frac{\dot{A}}{A} + \frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) + M^{2}\varphi = 0 \end{aligned}$$
(14)

where an overhead dot denotes differentiation with respect to time \(t\). The conservation equation (3) is given by

$$ \dot{\rho} _{\mathit{de}} + \biggl( \frac{\dot{A}}{A} + \frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) (\rho _{\mathit{de}} + p_{\mathit{de}}) = 0 $$
(15)

3 Solutions and the model

In this section, we solve the field equations (10)–(15) and present the corresponding DE model with the attractive massive SF.

From Eq. (14) we obtain

$$ A = c_{1}B $$
(16)

where \(c_{1}\) is a constant of integration which can be assumed as unity without any loss of generality so that we get

$$ A = B $$
(17)

Now using Eqs. (17), (12) and (13) we obtain

$$ \gamma = 0 $$
(18)

with the help of Eqs. (17) and (18) the field equations (10)–(15) reduce to the following independent equations:

$$\begin{aligned}& \frac{\dot{B} ^{ 2}}{B^{2}} + \frac{2\dot{C} \dot{B}}{CB} - \frac{1}{B^{2}} = \rho _{\mathit{de}} + \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(19)
$$\begin{aligned}& \frac{\ddot{B}}{B} + \frac{\ddot{C} }{C} + \frac{\dot{B} \dot{C}}{BC} = - \omega _{\mathit{de}}\rho _{\mathit{de}} - \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(20)
$$\begin{aligned}& 2\frac{\ddot{B}}{B} + \frac{\dot{B}^{ 2}}{B^{2}} - \frac{1}{B^{2}} = - ( \omega _{\mathit{de}} + \delta )\rho _{\mathit{de}} - \frac{\dot{\varphi}}{2}^{2} + \frac{M^{2}\varphi ^{2}}{2} \end{aligned}$$
(21)
$$\begin{aligned}& \ddot{\varphi} + \dot{\varphi} \biggl( 2\frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) + M^{2}\varphi = 0 \end{aligned}$$
(22)
$$\begin{aligned}& \dot{\rho} _{\mathit{de}} + \biggl( 2\frac{\dot{B}}{B} + \frac{\dot{C}}{C} \biggr) (\rho _{\mathit{de}} + p_{\mathit{de}}) = 0 \end{aligned}$$
(23)

Now Eqs. (19)–(23) are set of four independent equations in six unknowns \(B\), \(C\), \(\delta \), \(\rho _{\mathit{de}}\), \(\omega _{\mathit{de}}\) and \(\varphi \) (Eq. (23) is the consequence of the field equations). Hence to obtain a determinate solution of the field equations we need two extra conditions which are either physically or mathematically viable. So we use the following two conditions:

  1. (i)

    the expansion scalar of the model is proportional to the shear scalar so that we obtain a well-known result (Collins et al. 1980)

    $$ B = C^{n} $$
    (24)

    where \(n \ne 1\) is a positive constant. This preserves the anisotropy of the space-time.

  2. (ii)

    with a view to reduce the mathematical complexity of the field equations, we assume (Singh 2008; Singh and Rani 2015; Naidu et al. 2019)

    $$ (2n + 1)\frac{\dot{C}}{C} = - \frac{\dot{\varphi}}{\varphi }. $$
    (25)

    Now using Eq. (25) in Eq. (22) and integrating we obtain

    $$ \varphi = \exp \biggl( \varphi _{0}t - \frac{M^{2}t^{2}}{2} + \varphi _{1} \biggr) $$
    (26)

    Using Eq. (26) in Eq. (25), we get

    $$\begin{aligned}& C = \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \end{aligned}$$
    (27)
    $$\begin{aligned}& A = B = \biggl[ \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \biggr]^{n} \end{aligned}$$
    (28)

    Now using Eqs. (27) and (28) in Eq. (1) we can write the BT-III model in the present case as

    $$\begin{aligned} ds^{2} = {}&dt^{2} \\ &{}- \biggl[ \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \biggr]^{2n}\bigl(dx^{2} - e^{2x}dy^{2} \bigr) \\ &{}- \biggl[ \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \biggr]^{2}e^{ - 2x}dz^{2} \end{aligned}$$
    (29)

    with the SF in the model given by Eq. (26).

4 Kinematical parameters of the model

In this section, we compute the following kinematical parameters of the model (29) which play a significant role in the discussion of the cosmological model of the universe.

The spatial volume in the model, in view of Eqs. (17), (27) and (28), is

$$ V = a^{3} = ABC = A^{2}C = \biggl[ \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \biggr]^{2n + 1} $$
(30)

where \(a\) is the average scale factor of the universe.

The average Hubble parameter in the model is given by

$$ H = \frac{\dot{a}}{a} = \biggl( \frac{M^{2}t - \varphi _{0}}{3} \biggr) $$
(31)

The scalar expansion of the model is

$$ \theta = 3H = M^{2}t - \varphi _{0} $$
(32)

The shear scalar is given by

$$ \sigma ^{2} = \frac{1}{3} \biggl( \frac{\dot{A}}{A} - \frac{\dot{C}}{C} \biggr)^{2} = \frac{1}{3} \biggl( \frac{M^{2}t - \varphi _{0}}{2n + 1)} \biggr)^{2}(n - 1)^{2} $$
(33)

The average anisotropy parameter is

$$ A_{h} = \frac{8(n - 1)^{2}}{3(2n + 1)^{2}} $$
(34)

Using Eqs. (26)–(28) in Eq. (19) we obtain DE density as

$$\begin{aligned} \rho _{\mathit{de}} = {}&\bigl(M^{2}t - \varphi _{0}\bigr)^{2} \biggl[ \frac{n(n + 2)}{(2n + 1)^{2}} \\ &{} - \frac{(M^{2} + 1)}{2} \biggl( \exp \biggl(\varphi _{0}t - \frac{M^{2}t^{2}}{2} + \varphi _{1}\biggr) \biggr)^{2} \biggr] \\ &{}- \biggl[ \exp \biggl( \frac{\frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1}}{2n + 1} \biggr) \biggr]^{ - 2n} \end{aligned}$$
(35)

From Eqs. (26)–(28) and Eq. (20) we find EoS parameter of DE as

$$\begin{aligned} \omega _{\mathit{de}} ={}& - \frac{1}{\rho _{\mathit{de}}} \biggl[ \frac{M^{2}(n + 1)}{2n + 1} \\ &{} + \bigl(M^{2}t - \varphi _{0} \bigr)^{2} \biggl( \frac{n^{2} + n + 1}{(2n + 1)^{2}} \\ &{} - \frac{(M^{2} + 1)}{2} \biggl( \exp \biggl(\varphi _{0}t - \frac{M^{2}t^{2}}{2} + \varphi _{1}\biggr) \biggr)^{2} \biggr) \biggr] \end{aligned}$$
(36)

From Eqs. (26)–(28), (20) and (21) we can find the skewness parameter as

$$\begin{aligned} \delta ={}& \frac{1}{\rho _{\mathit{de}}} \biggl[ \frac{(n - 1)}{(2n + 1)} \bigl( M^{2} + \bigl(M^{2}t - \varphi _{0} \bigr)^{2} \bigr) \\ &{} - \biggl( \exp \biggl( \frac{M^{2}t^{2}}{2} - \varphi _{0}t - \varphi _{1} \biggr) \biggr)^{ - 2n} \biggr] \end{aligned}$$
(37)

where energy density is given by Eq. (35).

The deceleration parameter of the model is given by

$$ q = - 1 + \frac{d}{dt}\bigl(H^{ - 1}\bigr) = - \biggl( 1 + \frac{3M^{2}}{(M^{2}t - \varphi _{0})^{2}} \biggr) $$
(38)

The jerk parameter of the model is given by

$$ j(t) = q + 2q^{2} - \frac{\dot{q}}{H} = 1 + \frac{9M^{2}}{(M^{2}t - \varphi _{0})^{2}} $$
(39)

5 Discussion of the parameters

The above dynamical and physical parameters will help us to discuss their significance in the universe.

It may be observed that the spatial volume increases exponentially with cosmic time. This shows that the universe expands from a finite volume. Observation of average scale factor reveals that the model is nonsingular since the exponential function never vanishes. It may be noted that the physical parameters \(H\), \(\theta \), \(\sigma ^{2}\) all diverge when \(t\) approaches infinity and will have finite values at \(t=0\). The scalar expansion of the model is always positive for small values of \(\varphi _{0}\). Our model is totally anisotropic and spatially homogeneous since

$$ \frac{\sigma ^{2}}{\theta ^{2}} = \mbox{constant} $$
(40)

Also the average anisotropy parameter is independent of \(t\) and hence it is uniform throughout the evolution of the universe.

Scalar field

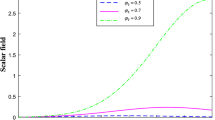
In Fig. 1, we have analyzed the behavior of the SF \(\varphi \) in terms of cosmic time for various values of \(\varphi _{0}\). For all three values of \(\varphi _{0}\), it can be observed that the SF is positive throughout its evolution. SF increases with cosmic time and reaches a maximum value at certain point of time and then decreases to vanish at later point of time. We have also observed that as \(\varphi _{0}\) increases the SF increases.

Fig. 1
figure 1

Plot of SF versus time \(t\) for \(M=0.9\) and \(\varphi _{1} = 20\)

Full size image

Energy density (\(\rho _{\mathit{de}}\))

From Fig. 2, we observe that the DE density of our model is always positive throughout the evolution for different values of \(\varphi _{0}\). It is also observed that the DE energy density increases with time, but decreases with the value of \(\varphi _{0}\). It is interesting to mention here that this behavior of energy density is quite opposite to the behavior of energy density in BT-III DE model with SF obtained by Naidu et al. (2019).

Fig. 2
figure 2

Plot of energy density versus time \(t\) for \(M=0.9\), \(n=2\) and \(\varphi _{1} = 20\)

Full size image

EoS parameter

Figure 3 describes the evolution of equation of state parameter versus time for our model. It can be seen that for various values of \(\varphi _{0}\) the model starts in the phantom region \(( \omega _{\mathit{de}} < - 1 )\) and finally reaches a constant value in the quintessence region \(( - 1 < \omega _{\mathit{de}} < \frac{ - 1}{3} )\).

Fig. 3
figure 3

Plot of EoS parameter versus time \(t\) for \(M=0.9\), \(n=2\) and \(\varphi _{1} = 20\)

Full size image

Deceleration parameter (\(q\))

This parameter plays a very important role in the description of the nature of the model obtained. For \(q>0\), the model decelerates in the standard way, when \(q=0\) we have a constant rate of expansion and for \(- 1 \le q < 0\) the model shows an accelerated expansion. For \(q = - 1\), the universe exhibits an exponential expansion and when \(q < - 1\), the model is in super exponential expansion. Figure 4 depicts the behavior of deceleration parameter versus cosmic time t for different values of \(\varphi _{0}\). For our model we observe that initially \(q\) is less than −1 and hence we obtain a universe with super exponential expansion. However, finally, the expansion is independent of \(\varphi _{0}\) and \(q\) approaches −1, i.e., the model shows exponential expansion.

Fig. 4
figure 4

Plot of deceleration parameter \(q\) versus time \(t\) for \(M=0.9\)

Full size image

Skewness parameter

Skewness parameter depicts the amount of anisotropy in the dark energy fluid. In Fig. 5, we have depicted skewness parameter versus time \(t\) for different values of \(\varphi _{0}\) and positive throughout its evolution. Also, we observe that the effect of SF on the skewness parameters, influences rapidly initially and it is independent at the present epoch.

Fig. 5
figure 5

Plot of skewness parameter versus time \(t\) for \(M=0.9\), \(n=2\) and \(\varphi _{1} = 20\)

Full size image

Jerk parameter

In can be seen from Fig. 6 that the jerk parameter is remains positive throughout the evolution for all the three values of \(\varphi _{0}\). Also, we observed that the jerk parameter is independent of \(\varphi _{0}\) at late times and approaches to a constant value, unity.

Fig. 6
figure 6

Plot of jerk parameter versus time \(t\) for \(M=0.9\)

Full size image

6 Conclusions

Investigation of dark energy models in Einstein’s modified theories of gravity is drawing the attention of several researchers in order to explain the interesting scenario of accelerated expansion of the universe. Hence, in this article, we have solved Einstein’s field equations in the presence of anisotropic dark energy and a massive SF and presented a BT-III DE universe. To construct a deterministic DE model we have considered a relation between metric potentials, and a power law between the SF and the average scale factor. We have evaluated various cosmological and kinematical parameters and presented their physical discussion in view of recent cosmological scenario and observations. The following are some conclusions:

  1. i.

    Our model represents spatially homogeneous and anisotropic BT-III DE model with an attractive massive scalar meson field in general relativity.

  2. ii.

    Our DE model with massive SF is nonsingular and exhibits an exponential expansion. Also, it shows an early inflation with finite volume.

  3. iii.

    The physical quantities \(H\), \(\theta \), \(\sigma ^{2}\) of the model are finite initially (at \(t=0\)) and tend to infinity for sufficiently large values of cosmic time.

  4. iv.

    The average anisotropy parameter of our model is constant and hence the model is anisotropic. However it may be noted that it becomes isotropic and shear free for \(n=1\).

  5. v.

    It is observed that the SF is positive throughout its evolution for all three given values of \(\varphi _{0}\). We have also observed that as \(\varphi _{0}\) increases the SF increases (Fig. 1). The energy density of DE is always positive and increasing function of time \(t\). Also as the SF increases DE density decreases (Fig. 2).

  6. vi.

    The EoS parameter of the DE model shows that the model varies in phantom region \(( \omega _{\mathit{de}} < - 1 )\), initially and it approaches to a constant value in the quintessence region \(( - 1 < \omega _{\mathit{de}} < \frac{ - 1}{3} )\) finally. Therefore our model varies in scalar field DE regions (Fig. 3). The present value of EoS parameter in our model is \(\omega _{\mathit{de}} \approx -0.642\) and it varies in the region which is in accordance with the Planck Collaboration (Aghanim et al. 2018) data as given below:

    $$\begin{aligned} \omega _{\mathit{de}} = {}&-1.56_{-0.48}^{+0.60}( \mathrm{Planck} + \mathrm{TT} + \mathrm{lowE}); \\ \omega _{\mathit{de}} ={}& -1.58_{-0.41}^{+0.52}( \mathrm{Planck} + \mathrm{TT},\mathrm{TE},\mathrm{EE}+\mathrm{lowE}); \\ \omega _{\mathit{de}} ={}& -1.57_{-0.40}^{+0.50}( \mathrm{Planck} + \mathrm{TT},\mathrm{TE},\mathrm{EE}+\mathrm{lowE} \\ &{} +\mathrm{lensing}); \\ \omega _{\mathit{de}} ={}& -1.04_{-0.10}^{+0.10}( \mathrm{Planck} + \mathrm{TT},\mathrm{TE},\mathrm{EE}+\mathrm{lowE} \\ &{} +\mathrm{lensing}+\mathrm{BAO}). \end{aligned}$$
  7. vii.

    We observe that, initially the deceleration parameter (\(q\)) of our model is less than −1 and finally approaches to −1. Hence, the model starts with super exponential expansion and finally approaches an exponential expansion (Fig. 4). The present value of \(q\) for our model is \(q \approx - 1.02\) which is in accordance with the observational data 2019 given as \(q = - 0:930 \pm 0:218\) (\(\mathrm{BAO} + \mathrm{Masers} +\mathrm{TDSL}+\mathrm{Pantheon}+{H}_{{z}}\)) and \(q=- 1:2037\pm 0.175\) (\(\mathrm{BAO}+\mathrm{Masers}+\mathrm{TDSL} +\mathrm{Pantheon} +{H}_{0}+{H}_{{z}}\)).

  8. viii.

    The skewness parameter of DE remains positive throughout its evolution. Initially, the SF influences the anisotropy of DE but the skewness is independent at the present epoch (Fig. 5). The jerk parameter remains positive and finally approaches to unity, i.e., our model approaches \(\varLambda CDM\) model at late times (Fig. 6).

  9. ix.

    It is observed that all the dynamical parameters behave in such a way that they are in good agreement with the recent experimental observation of modern cosmology.

From the above results, it may be said that at initial epochs the SF influences all the physical parameters of our model. However, at late times they are independent of the SF and approaches to a constant value. Hence, the effect of SF gradually decreases during the course of evolution of the model. It is interesting to mention, here, that the behavior of massive scalar meson field in our model is quite opposite to the behavior of SF in the BT-V DE model obtained by Naidu et al. (2019).