Lifetime of a spacecraft around a synchronous system of asteroids using a dipole model

Abstract

Space missions allow us to expand our knowledge about the origin of the solar system. It is believed that asteroids and comets preserve the physical characteristics from the time that the solar system was created. For this reason, there was an increase of missions to asteroids in the past few years. To send spacecraft to asteroids or comets is challenging, since these objects have their own characteristics in several aspects, such as size, shape, physical properties, etc., which are often only discovered after the approach and even after the landing of the spacecraft. These missions must be developed with sufficient flexibility to adjust to these parameters, which are better determined only when the spacecraft reaches the system. Therefore, conducting a dynamic investigation of a spacecraft around a multiple asteroid system offers an extremely rich environment. Extracting accurate information through analytical approaches is quite challenging and requires a significant number of restrictive assumptions. For this reason, a numerical approach to the dynamics of a spacecraft in the vicinity of a binary asteroid system is offered in this paper. In the present work, the equations of the Restricted Synchronous Four-Body Problem (RSFBP) are used to model a binary asteroid system. The main objective of this work is to construct grids of initial conditions, which relates semi-major axis and eccentricity, in order to quantify the lifetime of a spacecraft when released close to the less massive body of the binary system (modeled as a rotating mass dipole). We performed an analysis of the lifetime of the spacecraft considering several mass ratios of a binary system of asteroids and investigating the behavior of a spacecraft in the vicinity of this system. We analyze direct and retrograde orbits. This study investigated orbits that survive for at least 500 orbital periods of the system (which is approximately one year), then not colliding or escaping from the system during this time. In this work, we take into account the gravitational forces of the binary asteroid system and the solar radiation pressure (SRP). We found several regions where the direct and retrograde orbits of a spacecraft survive throughout the integration time (one year) when the solar radiation pressure is taken into account. Numerical evidence shows that retrograde orbits have a larger region initial conditions that generate orbits that survive for one year, compared to direct orbits.

1 Introduction

In the last decades, there was great interest in the exploration of asteroids that travel in the solar system (Pamela and Misra 2011). Within the solar system, there are thousands of these asteroids, which are classified taking into account the characteristics of their orbits, physical and chemical properties, mineralogical composition, etc. Until the mid-1990s, it was believed that asteroids were solitary bodies. With the evolution of the technology in the area of space exploration, it was possible to observe, in the 1990s, for the first time, a moon orbiting an asteroid. Although there were many discoveries, only in the following century spacecraft were sent to study these new celestial bodies at a shorter distances. In the year 2000, the asteroid Eros received in its surface the American spacecraft NEAR. In 2003, the Japanese spacecraft Hayabusa collected and analyzed data from the asteroid Itokawa. In the year 2012, the Dawn spacecraft was sent by the United States to the asteroid Vesta, with the goal of collecting data that would help in understanding the origin and formation of the Solar System (Pamela et al. 2013). NASA launched the Osiris-Rex spacecraft in 2016 in the direction of the asteroid Bennu (formerly 1999rq36), expected to arrive in the celestial body in 2018. The mission aims to collect asteroid data and return with samples collected in mid 2023 (Masago et al. 2017). It is estimated that $15 \pm4\%$ of the asteroids discovered until then, whose trajectory passes near the Earth, are binary, and the study of these bodies and their peculiarities provide important scientific and technological information because their exploration can provide answers to fundamental questions in space sciences (Margot et al. 2002; Merline et al. 2002). One of the fields of application for the study of asteroids is Gravitational Dynamics, where the bodies that make up the solar system are studied, considering their formation and evolution. In addition, the exploration of asteroids and their systems is ideal to test important technologies, such as the In-Orbit Demonstration experiments (IOD) (Ferrari et al. 2016). One of the most relevant topics in the asteroid area is the study of the motion of a spacecraft in the vicinity of these particular systems, which helps to design future space missions. The mission “Asteroid Impact and Deflexion Assessment” (AIDA) is one of the examples of the study of asteroids and it is a partnership between ESA and NASA (Cheng 2013; Cheng et al. 2012). This mission was created with the objective of considering two different projects: The Double Asteroid Redirection Test (DART), from NASA, which will have the function of being the kinetic impactor; and the Asteroid Impact Mission (AIM), from ESA, which will function as a binary system monitor before and after the impact, collecting asteroid data, and deploying a lander on the surface of the smaller asteroid (Ferrari and Lavagna 2015; Ferrari et al. 2016). The scientific exploration of comets and asteroids open a new horizon for the industrial activity in the area of asteroid mining (Scheeres et al. 2000).

The development of missions directed to asteroids and comets allowed the emergence of a new area of research in astrodynamics: The study and quantification of the stability and navigability of orbits of spacecraft close to irregularly rotating bodies (Scheeres et al. 2000). Studies in this area are challenging, since each of the objects we study (asteroids and comets) have their own characteristics in most diverse aspects, such as size, shape, density and rotation, which are often only discovered after the approximation and even after the landing and data collection of the spacecraft (Scheeres et al. 2000). Observational analyzes using radar astronomy have shown that several asteroids have bimodal formats, such as the Castalia and Kleopatra asteroids. This may be an indication that these objects were distinct bodies, and possibly with different densities, that later collided with each other (Scheeres 2002). Therefore, the previously planned missions must be developed with enough flexibility to cover several parameters of the body (Scheeres et al. 2000). Therefore, studies in the area of asteroid exploration are of great importance and involve multiple disciplines, among them science and technology, control, celestial mechanics and astronomy. The first phase of the study in orbital dynamics of irregular bodies is to derive a mathematical model to represent its gravitational field, because they have non-spherical shapes and peculiar rotations. It means that orbits of a spacecraft sent around these bodies do not resemble with the traditional Keplerian orbits (Masago et al. 2016, 2017; Gonçalves et al. 2013). There are several models already created to represent mathematically the gravitational potential of bodies with non-spherical shapes. One of these models is the spherical harmonic method, which was adopted to describe the gravitational potential of the asteroid Vesta (Tricarico and Sykes 2010). This model may diverge in some points (Zeng et al. 2016e). The potential of an extremely non-spherical body cannot, for example, be represented by the spherical harmonics model, because this model converges very slowly when applied to very irregular bodies, and it may even diverge, when the spacecraft is placed close to the surface of the bodies studied (Zeng et al. 2015). Another mathematical model is the ellipsoidal harmonic model, proposed by Hobson (1955), and improved by Pick et al. (1973) (Cui and Qiao 2014). There is also the model known as Restricted Full (Two or) Three-Body Problem (Scheeres 2004; Bellerose and Scheeres 2008). The word “Full” means that the mass distribution of one or both of the primaries bodies is being taken into account. Bellerose and Scheeres (2008) applied this model to the binary asteroid system 1999 KW4 and analyzed the movement of a spacecraft using zero-velocity curves, equilibrium points and the Jacobi constant. There is also the polyhedron method, developed by Werner (1994), constructed based on the image data that are obtained from radar observations and, therefore, cannot be derived analytically. Therefore, it is preferable to use simplified models to approximate the potential distribution of natural minor bodies. In this study, it is used a model based on the rotating dipole mass, initially introduced by Chermnykh (1987), and also studied by Kokoriev and Kirpichnikov, in 1988 (Kokoriev and Kirpichnikov 1988; Kirpichnikov and Kokoriev 1988). It is assumed in this model that the gravitational field of two masses located on the axis of symmetry of the body is very close to the gravitational field of an axially symmetrical body. In this paper, it is assumed that one of the asteroids of the binary system is a rotating dipole mass, thus representing an elongated body. This model was developed by Zeng et al. (2015). In the study of Ferrari et al. (2016), it was analyzed a strategy to locate trajectories in the vicinity of a binary asteroid system, where one of the asteroids is modeled as a rotating mass dipole (Zeng et al. 2016e). It also analyzed these trajectories and studied the effects of the flyby in an analytical form, finding an interesting relationship between the flyby and the Jacobi integral. The research developed in the present study uses a rotating dipole mass to represent a synchronous system of asteroids. To understand the behavior of the orbital dynamics of a spacecraft in the vicinity of a double asteroid system is fundamental to the execution of a space mission. This smallest fact motivated the present work, whose objective is to check the survival time of a spacecraft around an irregularly shaped asteroid (or around an asteroid binary system), taking into account the rotational motion of an elongated body. In the present work, we are studying a binary system of the asteroids + spacecraft. We call this problem as a Restricted Synchronous Four-Body Problem due to the fact that of one of the primaries (in this case $M_{2}$) is modeled like a mass dipole (two bodies of point masses), configuring the total system as governed by the dynamics of the four bodies. It is restricted because the mass of one of the bodies (in this case the spacecraft) is negligible. It is also assumed also that the period of rotation of the asteroid with irregular shape around its own axis and the period of movement of these asteroids around the center of mass of the system are the same, supporting the name Restricted Synchronous Four-Body Problem.

2 Methodology

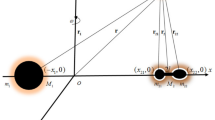
For this study, numerical tests were performed assuming that the size of the asteroid considered to be a rotating mass dipole ($M_{2}$) is $d = 500$ meters. The distance between the more massive primary asteroid, assumed to have a spherical shape (with radius $R_{1}$), and the center of mass of the dipole is $D$ and measures 3804 meters, as shown in Fig. 1.

Fig. 1

Representative image of the system of asteroids studied

Figure 1 shows the two asteroids $M_{1}$ and $M_{2}$ where $M_{2}$ is considered as a body with irregular shape. The two mass points, represented in Fig. 1 by the two white circles inside the body $M_{2}$, represent the mass dipole. These white points of masses are connected by a massless rod. The length of this rod is measured by calculating the distance between the two points of mass, and it is considered constant.

The total mass of the system is constant and measures $9.273\times 10^{12}~\mbox{kg}$. This value was inspired by the pair of asteroids $\mathit{Alpha}$–$\mathit{Gamma}$ of the triple system $2001\mathit{SN}_{263}$ (Tracy et al. 2015). $\mathit{Gamma}$ has the shape of an elongated body and has synchronous motion. The choice of this pair of asteroids is justified due to the Brazilian mission ASTER, which considers the possibility of sending a spacecraft to this asteroid system (Sukhanov et al. 2010; Prado 2014). Although the details of this system of asteroids are not the main goal of the present work, we take this system as the base to develop a general study of the problem. The present study is performed by varying the values of each of the masses of the bodies of the double system ($M_{1}$ and $M_{2}$), without changing the total mass of the system. In the first case, the mass of $M_{1}$ is 99% of the total mass of the system ($M_{1} + M_{2}$) and, consequently, $M_{2}$ has a mass of 1% of the total mass of the system. In the second case $M_{1}$ has 90% of the total mass of the system and $M_{2}$ 10%. For the next cases, a mass change of 10 percent is made, where we decrease the mass of $M_{1}$ and increase the mass of $M_{2}$ until, for the last case studied, $M_{1}$ has 60% of mass total of system and $M_{2}$ 40%.

The spacecraft is initially considered to be nearby $M_{2}$. The initial osculating semi-major axis and eccentricity of this orbit are converted to the Cartesian system, to be used in the equations of motion. The conversion is made considering $M_{2}$ as a point of mass. Once the initial conditions are established, a numerical integration is made including the mass of $M_{1}$, the shape of the body $M_{2}$ and the solar radiation pressure. Initially ($t=0$) the three bodies ($M_{1}$, $M_{2}$ and the Sun) are aligned, as shown in Fig. 2.

Fig. 2

Graphic representation of the system studied

We can note in Fig. 2 that the body $M_{2}$ have always the same face pointed to the body $M_{1}$. It occurs because the translation period of $M_{2}$ is equal to the rotation period around its own axis.

In the dynamics, a collision with $M_{1}$ is considered to occur when the position of the spacecraft is smaller or equal the radius this body. If the position of the spacecraft at any instant of time is smaller than the size of $M_{2}$ (we consider a diameter of 500 meters in the $x$ axis and 250 meters in the $y$ axis), we have a collision. We consider a discarded orbit (ejection) when the position of the spacecraft goes beyond 30 times than the distance between the primary bodies.

3 Equation of motion

In this paper, the canonical system of units is used, and it means that: (i) The unit of distance is the distance between $M_{1}$ and the center of mass of $M_{2}$ (distance D). (ii) It is also assumed that the mass of the body $M_{1}$ is greater than the mass of the body $M_{2}$. In mathematical terms, we have $m_{1}> m_{2}$ and $m_{2} = m_{21} + m_{22}$, where $m_{21} = m_{22}$. Consequently, the mass ratio is given by $\mu ^{*} = \frac{m_{21}}{(m_{1} + m_{21} + m_{22})}$, where $\mu^{*} = \frac{\mu }{2}$, with $\mu$ being the usual mass ratio used in the restricted three-body problem (Szebehely 1967; Molton 1960; Santos et al. 2017). Note that the unit of mass is chosen such that the sum of the masses is one. (iii) The unit of time is defined such that the period of the motion of the primaries is equal to $2\pi$. (iv) The gravitational constant is $G=1$ (Szebehely 1967; McCuskey 1963).

In this problem, it has been assumed that the motion of the negligible mass body $P (x, y, z)$ is governed by the gravitational forces of the primary bodies $M_{1}$ and $M_{2}$, but the body with infinitesimal mass does not affect the dynamics of the primaries. The solar radiation pressure is also taken into account. The body $M_{2}$ is modeled as a rotating mass dipole formed by two hypothetical bodies with masses $m_{21}$ and $m_{22}$, as shown in Fig. 3. The distance between the body $m_{21}$ and $m_{22}$ is $d = 0.131440$ canonical units.

Fig. 3

Coordinate system for the Restricted Synchronous Four-Body Problem

Viewed from the inertial reference, the spatial position of the body of infinitesimal mass is $P (x, y, z)$. The spatial positions of the bodies of mass $m_{1}$, $m_{21}$ and $m_{22}$, respectively, are

$$\begin{aligned} &{\begin{aligned}{} &x_{1} = - 2\mu^{*}\cos(nT), \\ &y_{1} = - 2\mu^{*}\sin(nT), \\ &z_{1} = 0, \end{aligned}} \end{aligned}$$

(1)

$$\begin{aligned} &{\begin{aligned}{} &x_{21} = \bigl(1 - d/2 - 2\mu^{*}\bigr)\cos(nT), \\ &y_{21} = \bigl(1 - d/2 - 2\mu^{*}\bigr)\sin(nT), \\ &z_{21} = 0, \end{aligned}} \end{aligned}$$

(2)

$$\begin{aligned} &{\begin{aligned}{} &x_{22} = \bigl(1 + d/2 - 2\mu^{*}\bigr)\cos(nT), \\ &y_{22} = \bigl(1 + d/2 - 2\mu^{*}\bigr)\sin(nT), \\ &z_{22} = 0, \end{aligned}} \end{aligned}$$

(3)

where $n$ is the angular velocity of the primary bodies around the center of mass and $T$ is the time. Thus, we see that the equations of motion of a body of infinitesimal mass in the plane $xy$, when viewed from an inertial reference system, is given by

$$\begin{aligned} &{\ddot{x} = - \frac{(1-2\mu^{*})(x-x_{1})}{r_{1}^{3}} - \frac{\mu ^{*}(x-x_{21})}{r_{21}^{3}}} \\ &{\phantom{\ddot{x} =}{}-\frac{\mu^{*}(x-x_{22})}{r_{22}^{3}} - P_{\mathrm{rad}x}=0,} \end{aligned}$$

(4)

$$\begin{aligned} &{\ddot{y} = - \frac{(1-2\mu^{*})(y-y_{1})}{r_{1}^{3}} - \frac{\mu ^{*}(y-y_{21})}{r_{21}^{3}}} \\ &{\phantom{\ddot{y} =}{}-\frac{\mu^{*}(y-y_{22})}{r_{22}^{3}} - P_{\mathrm{rad}y}=0,} \end{aligned}$$

(5)

$$\begin{aligned} &{\ddot{z} = - \frac{(1-2\mu^{*})(z-z_{1})}{r_{1}^{3}} - \frac{\mu ^{*}(z-z_{21})}{r_{21}^{3}}} \\ &{\phantom{\ddot{z} =}{}-\frac{\mu^{*}(z-z_{22})}{r_{22}^{3}} - P_{\mathrm{rad}z} = 0,} \end{aligned}$$

(6)

where

$$\begin{aligned} &{r_{1} = \sqrt{(x-x_{1})^{2} + (y-y_{1})^{2} + (z-z_{1})^{2}},} \end{aligned}$$

(7)

$$\begin{aligned} &{r_{21} = \sqrt{(x-x_{21})^{2} + (y-y_{21})^{2} + (z-z_{21})^{2}},} \end{aligned}$$

(8)

$$\begin{aligned} &{r_{22} = \sqrt{(x-x_{22})^{2} + (y-y_{22})^{2} + (z-z_{22})^{2}},} \end{aligned}$$

(9)

and $P_{\mathrm{rad}x}, P_{\mathrm{rad}y}$ and $P_{\mathrm{rad}z}$ represent the components $x$, $y$, and $z$ of the acceleration due to the solar radiation pressure, which is given by Masago et al. (2016), Montenbruck and Gill (2000), Beutler (2005). We have

$$ P_{\mathrm{rad}} = - C_{r}\frac{A}{m}P_{S} \frac{r_{0}^{2}}{R^{2}}{\hat{r}} $$

(10)

where $C_{r}$ is a factor that depends on the reflectivity of the spacecraft, called the $\mathit{coefficient}$ of $\mathit{radiation}$ $\mathit{pressure}$, and the value of $C_{r} = 1.5$ was used in the simulations; $P_{S}$ is the solar radiation pressure in the orbit of the Earth that measures approximately $4.55\times10^{-6}~\mbox{N/m}^{2}$; $r_{0}$ is the Sun–Earth distance; $R$ is the Sun–Spacecraft distance, ${\hat{r}}$ is the radial direction of the Sun relative to the spacecraft; $A$ is the area of the spacecraft illuminated by the sun and $m$ is the mass of the spacecraft (Masago et al. 2016; Beutler 2005; Montenbruck and Gill 2000). The value used for $A$ in the simulations is $1~\mbox{m}^{2}$ and the mass is 100 kg, so $A/m = 0.01~\mbox{m}^{2}/\mbox{kg}$.

4 Numerical investigation

Binary systems of asteroids are quite interesting, since they are systems composed of bodies that have similar masses and radii. A particle placed in the vicinity of a binary system, for example, undergoes complex perturbations, and the understanding of these perturbations is fundamental for determining the regions where there are families of orbits around the system. The determination of these families of orbits can indicate the location of possible dust around the system, which may not yet be observed. In contrast, an unstable region will have few or no dust, without the presence of any body or dust. This information is important when planning a mission for an asteroid system, because the characteristics of the system influence the positions where the spacecraft will be placed. There are regions where the spacecraft is more protected or vulnerable to the risks of collisions with particle dust (Araujo et al. 2012, 2015). A study was developed to find families of orbits in the vicinity of a binary system of asteroids, in terms of the initial Keplerian elements, within a given time period and taking into account the gravitational disturbances and the solar radiation pressure present in the system. The initial conditions adopted and the results are described next.

We will analyze the grids of initial conditions with respect to the center of mass of the rotating mass dipole. We take into account the gravitational forces of the two primary bodies, the irregular form of one of the bodies and the solar radiation pressure. The spacecraft begins in a circular orbit and vary to orbits with eccentricity up to $e = 0.99$. The semi-major axis of the spacecraft ranges from 500 meters relative to the center of mass of the elongated body up to the $\mathit{Hill}$ region Araujo et al. (2008) of the rotating mass dipole, which depend on its mass, with the addition of an extra margin of 50 meters beyond the region of influence. Then, for each initial condition with a given mass for the dipole, the sphere of influence will also be different and the variations of the initial conditions of the semi-major axis will change. In this study, we analysis planar direct orbits (inclination zero) and retrograde orbits (inclinations of 180 degrees). The total integration time is one year, which is equivalent to approximately 500 orbital periods of the system analyzed. To perform the numerical integrations, the Runge–Kutta 7/8 method is used with a time step of 0.01 canonical unit. During the integrations, we keep track of particles that have collided with any of the bodies, the particles that were ejected from the system, and the particles that survived during the integration time. Figure 4 (direct orbits) and Fig. 5 (retrograde orbits) show the results and consider a grid of initial conditions (with respect to the less massive primary) as a function of the semi-major axis and the eccentricity of the spacecraft. The color codes indicates the time the particle survives for each initial condition. The solar radiation pressure is taken into account. We can see at the top of the left side that there is a region of white color. This region is where the initial conditions are inside the body $M_{2}$, so they do not have any physical meaning. We can note that the lifetime of the spacecraft is very low (only one orbital period of system). This occurs because the mass of the body $M_{2}$ is small (only 1% of total mass of system), so the sphere of influence of this body is small also (less than twice the size of the body $M_{2}$). As a consequence, the spacecraft is released very close to the body $M_{2}$, causing it to be rapidly captured. The orbits that have a high semi-major axis and a low eccentricity are orbits that last longer, because they begin their trajectories farther from the body $M_{2}$. But they are not far enough to avoid a collision.

Fig. 4

Lifetime in the region close to $M_{2}$ (direct orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 99\%$ and mass of $M_{2} = 1\%$ of the total mass of the system. Solar radiation pressure is included

Fig. 5

Lifetime in the region close to $M_{2}$ (retrograde orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 99\%$ and mass of $M_{2} = 1\%$ of the total mass of the system. Solar radiation pressure is included

After using a mass ratio similar to the $\mathit{Alpha}$–$\mathit{Gamma}$ bodies of the asteroid $2001\mathit{SN}_{263}$, we modify the masses of the primaries, to see the effects of this parameter. As already mentioned, we will keep the total mass of the system in the value $9.273\times{10^{12}}~\mbox{kg}$. However, we will now make an analysis considering that 90% of the total mass of the system belongs to $M_{1}$ and 10% of the total mass of the system belongs to $M_{2}$ (rotating mass dipole). The mass ratio is $\mu^{*}=0.05$. Again, in this analysis, the coordinate system is centered in the center of mass of the less massive body. The order of magnitude of the mass of the body $M_{2}$ is $10^{11}~\mbox{kg}$.

The solar radiation pressure causes the spacecraft to be pushed towards $M_{2}$ (due to the initial position of the Sun and spacecraft). Since the spacecraft begins with the initial conditions very close to $M_{2}$ (as mentioned), this “push” of the solar radiation pressure causes the spacecraft to collide faster with the body $M_{2}$. It means that the solar radiation pressure reduces the lifetime of the orbits, in this case. Figures 6a and 6b show the lifetime of the spacecraft as a function of the initials semi-major axis and eccentricity, to exemplify this effect. In Fig. 6a the solar radiation pressure is not taken into account and in Fig. 6b the solar radiation pressure is included in the simulation.

Fig. 6

Lifetime in the region close to $M_{2}$ (direct orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 90\%$ and mass of $M_{2} = 10\%$ of the total mass of the system

In Figs. 6a and 6b, the semi-major axis is different from the ones shown in Figs. 4 and 5, because in the situation shown in Figs. 6a and 6b, $M_{2}$ has a larger mass, which makes its region of influence larger. When the mass of $M_{2}$ is larger, the orbits close to this body has a more intense gravitational force from $M_{2}$, making the spacecraft to collide with the body. The orbits with the semi-major axis near the extremity of the region of influence of $M_{2}$ are orbits that last longer. The direct orbits that survive throughout numerical integration in Fig. 6a, for $\mu ^{*} = 0.05$, are trajectories that orbit the center of mass of the system. No direct orbit was found orbiting around $M_{2}$.

It can be seen in Fig. 6b that, when the solar radiation pressure is taken into account in the model, the orbits last a time of 80 canonical units, approximately 3.5 months. The solar radiation pressure increases the eccentricity of the orbit, and the radius of the periapsis becomes smaller, making the spacecraft to go near the dipole and to collide with it. Note also that, due to the increased eccentricity, the apoapsis of the orbit also increases, making the spacecraft to collide with the body $M_{1}$ more frequently, or to eject from the system.

Figures 7a and 7b are a color grid, referring to Figs. 6a and 6b, respectively, indicating the initial conditions where the spacecraft collides with $M_{1}$, with $M_{2}$, survive during the total integration time or eject from the system. The red color regions in Figs. 7a and 7b indicate that the spacecraft collided with the less massive primary ($M_{2}$). The blue color region in indicates that the spacecraft collided with $M_{1}$. The yellow regions indicate that the spacecraft has ejected from the system and the black region show the initial conditions where the spacecraft survives for the entire integration time.

Fig. 7

Direct orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 90\%$ and mass of $M_{2} = 10\%$

We can see, from Fig. 7a, for the semi-major axis from 1200 meters and eccentricity below 0.1 the orbits survive (black color), orbit the system or escape (yellow colors) from the system. All direct orbits are trajectories of an artificial satellite around the system, and a small variation in the initial condition may cause the satellite to approach more or less one of the primaries. We can see, in Fig. 8, the most massive body shown in pink, the body $M_{2}$, with a mass dipole shape and two orbits. The red orbit has an initial semi-major axis of 1255 meters and an eccentricity of 0.01. The blue orbit has an initial semi-major axis of 1255 meters and an eccentricity of 0.02.

Fig. 8

Orbit ejecting from the system (blue color) and surviving orbit (red color). The solar radiation pressure is not taken into account

We can see, from Fig. 8, that the two orbits are initially superimposed, but with the passage of time (due to the sensitivity of the system) they gradually move away. At a given instant the blue orbit is closer to the primary bodies (region highlighted in the figure by a black circle), causing the orbit to gain energy and be ejected from the system. On the other hand, the red orbit is not very close to the primaries, that is, there is no gain of energy and therefore the satellite remains orbiting the system during the whole numerical integration. It is worth remembering that the two orbits are direct and that the disturbance due to the solar radiation pressure is not being considered.

Figures 9a and 9b are analyzed similarly to Figs. 6a and 6b and also has the same initial conditions. The difference is that in Figs. 9a and 9b the orbits are retrograde.

Fig. 9

Lifetime in the region close to $M_{2}$ (retrograde orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 90\%$ and mass of $M_{2} = 10\%$ of the total mass of the system

The numerical results show that there is a wider region of retrograde orbits that survive longer when compared to direct orbits.

We observed that no trajectory was found (both in the simulations where the solar radiation pressure was not considered, and where it was considered) which orbited the less massive body in direct orbits. On the other hand, all retrograde orbits that survived for 500 orbital periods in Fig. 9a surround the less massive body ($M_{2}$). All orbits that do not survive by all numerical integration are regions where the spacecraft collides with $M_{2}$.

It is possible to see, in Figs. 9b, that when the solar radiation pressure is taken into account the orbits do not last for one year (500 canonical units). But they survive longer in relation to the direct orbits shown in Fig. 6b (solar radiation pressure included).

The influence of the solar radiation pressure increases the intensity of disturbances affecting the orbits, resulting in a higher frequency of collisions with the primary bodies. Orbits that initially have semi-major axis above 1050 and eccentricity below 0.02 are orbits that collide with $M_{1}$. The remaining conditions referenced to Fig. 9b cause the spacecraft to collide with $M_{2}$.

It is notable that, when the solar radiation pressure is take into account (in Figs. 6b and 9b), both in direct and in retrograde orbits, the particles leave of survive during all numerical integration time, for a mass ratio of $\mu^{*}=0.05$.

We noticed that the inclusion of the solar radiation pressure in the simulations causes a considerable difference in the results obtained. Thus, it is necessary to use solar radiation pressure in studies involving systems with relatively weak masses, as in the case of asteroids and comets. From this point, we will only show the results taking into account the solar radiation pressure, since this is an important force that is always present in the dynamics.

Varying the masses of the bodies, but keeping the total mass of the system constant ($9.273\times{10^{12}}~\mbox{kg}$), we can study the influence of this parameter. We now make an analysis considering that 80% of the total mass of the system belongs to $M_{1}$ and 20% of the total mass of the system belongs to $M_{2}$. Again, in this analysis, the coordinate system is centered in the center of mass of the less massive body. The order of magnitude of the mass of the $M_{2}$ is $10^{12}~\mbox{kg}$ and the mass ratio is $\mu^{*}=0.1$

Figures 10 (direct orbits) and 11 (retrograde orbits) show a grid of initial conditions that relates the eccentricity, the semi-major axis, and the lifetimes of the orbits.

Fig. 10

Lifetime in the region close to $M_{2}$ (direct orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 80\%$ and mass of $M_{2} = 20\%$ of the total mass of the system. Solar radiation pressure is included

Fig. 11

Lifetime in the region close to $M_{2}$ (retrograde orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 80\%$ and mass of $M_{2} = 20\%$ of the total mass of the system. Solar radiation pressure is included

We can see, from Fig. 10, that no direct orbit survives for a year when we take into account the solar radiation pressure. Although these orbits do not survive the whole integration time, they are lasting longer compared to the previous simulations. This is because the gravitational force of $M_{2}$ gets larger and thus become comparable with the solar radiation pressure, causing the spacecraft to survive longer in orbit around $M_{2}$. From this we can deduce that, as we increase the mass of the less massive body, more orbits will last longer and, possibly, we may find directs orbits around the less massive body when taken into account the pressure of solar radiation.

On the other hand, some regions of retrograde orbits that last one year begin to appear, near the semi-major axis of 1000 meters for low eccentricities, as shown in Fig. 11.

As we increase the mass of $M_{2}$, the survival times of the orbits, when we consider the solar radiation pressure, increase as well.

We can note that there are regions where retrograde orbits survived for at least 1 year, while no direct orbit surviving the numerical integration was found. These regions are very important in the application of astrodynamics when it comes to space missions. The direct orbits are more popular regarding the existence of space dust, whereas, on the other hand, retrograde orbits hardly occur naturally. Thus, regions where direct orbits do not survive and retrograde orbits survive are great options for a spacecraft to be placed, because in such regions the probability of existence of space dust that is likely to collide with the spacecraft is less frequent. In addition, it is possible that a satellite is placed in a retrograde orbit to observe the body that we study.

The collision grids referring to Figs. 10 and 11 are shown in Figs. 12 and 13, respectively. We can see, from Figs. 12 and 13, that the influence of solar radiation pressure causes the spacecraft to collide more frequently with the primary bodies or cause the spacecraft to escape faster from the system. As the survival times of the orbits increase, the solar radiation pressure remains longer, causing disturbance in the spacecraft, making the orbit chaotic, and causing the spacecraft to escape (yellow regions in the figures) or collide with one of the primary bodies (blue and red regions).

Fig. 12

Direct orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), orbits that survived for 500 canonical units (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 80\%$ and mass of $M_{2} = 20\%$

Fig. 13

Retrograde orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), orbits that survived for 500 canonical units (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 80\%$ and mass of $M_{2} = 20\%$

We make an analysis considering that 70% of the total mass of the system belongs to $M_{1}$ and 30% of the total mass of the system belongs to $M_{2}$. The mass ratio in this case is $\mu^{*}=0.15$. Again, the grades of initial conditions have the reference in the center of mass of the less massive body. Figures 14 (direct orbits) and 15 (retrograde orbits) show a grid of initial conditions that relates the eccentricity, the semi-major axis, and the lifetimes of the orbits.

Fig. 14

Direct orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), orbits that survived for 500 canonical units (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 70\%$ and mass of $M_{2} = 30\%$

Fig. 15

Retrograde orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), the orbits that survived for 500 canonical units (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 70\%$ and mass of $M_{2} = 30\%$

Due to the larger mass of the body $M_{2}$, compared to previous cases, it is possible to find regions where direct and retrograde orbits survive all the time of the numerical integration. Note that, for the first time, regions were found where the direct orbits survive for 1 year around the less massive primary. This was predicted, as already mentioned, due to the fact that the gravitational force of the less massive body is comparable to the existing perturbations. A larger region of retrograde orbits, when compared with the previous cases, survives the whole integration time.

For space missions, it is very interesting to know these regions, where the direct orbits survive for a considerable time, because they are regions where there may exist space dust, making these regions dangerous to place a spacecraft. In this case, it would be interesting to put a spacecraft where the retrograde orbits survive, and the direct ones do not. The spacecraft would be in a safer region and could point its instruments to regions where direct orbits would survive in order to locate possible space dust.

Figures 16 and 17 show the collision grids of direct and retrograde orbits referring to Figs. 14 and 15, respectively.

Fig. 16

Direct orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), the orbits that survived for 500 canonical units (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 70\%$ and mass of $M_{2} = 30\%$

Fig. 17

Retrograde orbits. Collision region with $M_{1}$ (blue), collision region with $M_{2}$ (red), the orbits that survived for 500 canonical unit (black) and regions of ejection of the system (yellow). Solar radiation pressure is included. The white region is the region within $M_{2}$. Mass of $M_{1} = 70\%$ and mass of $M_{2} = 30\%$

Through the initial conditions for collisions of Figs. 16 and 17 we can find the final destiny of the spacecraft in the retrograde orbit. The regions black indicate the orbits that survived one year. These regions are areas where the spacecraft orbits the less massive body. The regions in red are locations where the spacecraft collides with $M_{2}$. The regions in blue are regions where the spacecraft collides with $M_{1}$. The regions in yellow are regions where the spacecraft ejects from the system and, finally, the regions in black are regions where the spacecraft orbits $M_{2}$. We realize that, as the eccentricity and the semi-major axis increase, the greater the chance of the spacecraft to orbit $M_{2}$. This occurs because the spacecraft is farthest from $M_{2}$, in regions where the gravitational pull of $M_{2}$ is smaller. Because of this, the effect of the solar radiation pressure and $M_{1}$ on the spacecraft become more significant. Because of the sensitivity of the system, these perturbative forces pull the spacecraft around $M_{2}$, causing it to collide with the second primary or ejecting from the system.

Finally, analyzing a system where 60% of the total mass is concentrated in the body $M_{1}$ and 40% of the total mass of the system is concentrated in the body $M_{2}$, we have the grids of initial lifetime conditions shown in Figs. 18 (direct orbits) and 19 (retrograde orbits). The mass ratio in this case is $\mu^{*}=0.2$. The order of magnitude of the mass of the $M_{2}$ is $10^{12}$.

Fig. 18

Lifetime in the region close to $M_{2}$ (direct orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 60\%$ and mass of $M_{2} = 40\%$ of the total mass of the system. Solar radiation pressure is included

Fig. 19

Lifetime in the region close to $M_{2}$ (retrograde orbits). The diagram shows the evolution of the lifetime of the orbit as a function of $a$ and $e$. Mass of $M_{1} = 60\%$ and mass of $M_{2} = 40\%$ of the total mass of the system. Solar radiation pressure is included

The initial condition grids that show the survival time of the spacecraft, when we consider the mass ratio of $\mu^{*} = 0.2$ (i.e., 40% of the total mass of the system is located in $M_{2}$), closely resemble the grids of condition initials shown for the previous case ($\mu^{*} = 0.15$). The difference is that in the latter case regions of orbits that survive for all time of numerical integration become larger (regions of red in Figs. 18 and 19). This is due to the fact that the gravitational field of $M_{2}$ is larger in this last situation, which increases the chance of finding orbits that survive.

The collision grids of the latter case closely resemble the collision grids shown in Figs. 16 and 17. Only the (yellow) escape and collision regions with $M_{1}$ (blue) become slightly larger for the mass ratio $\mu^{*} = 0.2$.

5 Conclusions

We investigated orbits for a spacecraft around a binary system of asteroids. The most massive asteroid was considered to have a spherical shape and, for the second (less massive) asteroid, we used the rotating mass dipole model. A series of numerical integrations were made for all models adopted, taking into account the gravitational force of the two bodies and the solar radiation pressure. A grid of initial conditions was established as a function of the semi-major axis and eccentricity to verify the lifetime and, consequently, the instability of the orbits for a spacecraft positioned in the vicinity of a binary system of asteroids.

When 99% of the mass of the system was assigned to the spherical body ($M_{1}$), no orbit survived for 1 year around the less massive primary. This occurs due to the fact that the spacecraft is released very close to $M_{2}$, causing the spacecraft to be quickly captured by the gravitational attraction of this body.

After this analysis, we verified the behavior of the system assuming 90% of the mass of the system in $M_{1}$ (more massive) and 10% of the total mass of the system in $M_{2}$. In this analysis, it was possible to find orbits that survived for one year (when solar radiation pressure is not taken into account) around the body of smaller mass (rotating mass dipole) only in retrograde orbits. On the other hand, direct orbits with a higher semi-major axis and low eccentricity also survive the whole integration time used, in this case orbiting the center of mass of the system. We realize that the system is very sensitive to the initial conditions, where a small change can cause the spacecraft to get closer to the primary bodies, receive energy and eject from the system. The orbits did not survive all numerical integrations when the solar radiation pressure is taken into account, causing the orbits to quickly collide with $M_{2}$, or $M_{1}$ or to escape from the system. Thus, it was possible to show the importance of taking into account the solar radiation pressure when investigating orbits around an asteroid binary system with a total mass of $9.273\times10^{12}~\mbox{kg}$.

We encountered unstable orbits that collide with $M_{1}$. That is, when the solar radiation pressure is taken into account, it causes the apogee radius of the orbit to become larger, causing the spacecraft to leave the orbit around $M_{2}$ and to collide with $M_{1}$. This type of orbit is also interesting. An application of some of these orbits could be to use them to observe $M_{2}$ for a short period of time and then naturally transfer the spacecraft to observe $M_{1}$. When approaching $M_{1}$, it would be necessary to use a propellant to make the spacecraft to orbit this body, instead of colliding with it.

We realize that, as we increase the proportion of mass of the body where we wish to orbit, the greater the gravitational force capable of maintaining a spacecraft around this asteroid, that is, its gravitational force happens to overcome the disturbances from the solar radiation pressure and the gravitational attraction of $M_{1}$.

We find some orbits that do not survive for one year of integration into direct orbits but remain in orbit when considering retrograde orbits. We found direct orbits that survive for up to one month and a half, generating empty regions (without dust). These regions where the retrograde orbits survive and the direct ones did not survive are indications of places where the spacecraft could be positioned in a space mission, because it is an empty region, in terms of space dust, so reducing the chance that the spacecraft will collide with a space body.

As we increase the mass of $M_{2}$, the greater is its gravitational force, so capable of maintaining a spacecraft around it. Therefore, there are more orbits that survive the numerical integration. That is to say, its gravitational force happens to overcome the disturbances of the solar radiation pressure and the gravitational attraction of the most massive primary.

It is possible to note in the figures that a high semi-major axis increases the chance of the action of the solar radiation pressure to pull the spacecraft out of the orbit around $M_{2}$, causing it to collide with $M_{1}$ or escape from the system.