1 Introduction

It is strongly believed that the Universe has entered a phase of the accelerated expansion which has been confirmed by the recent observations like supernovae Ia (Riess et al. 2007; Suzuki et al. 2012), cosmic microwave background radiation (Bennett et al. 2003; Komatsu et al. 2011), baryon acoustic oscillation (Percival et al. 2010) and Planck data (Ade et al. 2014). Within the framework of general relativity (GR), the cause of the acceleration can be attributed to the existence of a mysterious component of the Universe dubbed as “dark energy” (DE), which makes up ∼70 % of the total cosmic energy in the Universe. The \(\Lambda \)-cold dark matter (\(\Lambda\)CDM) model presents the simplest and most successful description of the recent accelerated expansion scenario and accommodates the observations very well. Despite of many attractive features, it has some theoretical problems like fine-tuning and cosmic coincidence problems (Carroll 2001; Peebles and Ratra 2003; Padmanabhan 2003). To overcome from these problems, a number of dynamical dark energy models such as scalar field (quintessence, phantom, \(k\)-essence, etc.) models (Chiba et al. 2000; Caldwell 2002; Padmanabhan 2002; Copeland et al. 2006), chaplygin gas models (Bento et al. 2002), holographic dark energy (HDE) models (Setare 2007; Xu 2009; Sheykhi and Jamil 2011), etc. have been explored in the literature.

In the recent years, the HDE models have been emerged as a viable candidates to explain the problems of modern cosmology. The HDE models explain the recent accelerated expansion as well as the coincidence problem of the Universe (Li 2004; Pavón and Zimdahl 2005). The concept of HDE is based on the holographic principle proposed by ’t Hooft (1993) and found it’s roots in the quantum field theory. Cohen et al. (1999) have shown that in the quantum field theory, the formation of black hole sets a limit which relates ultra-violet (UV) cut-off length \(\gamma \) to infra-red (IR) cut-off length \(L\). According to the authors, the quantum zero-point energy \(\rho_{h}=\gamma^{4}\) of a system of size \(L\) should not exceed the mass of a black hole of the same size, i.e., \(L^{3}\rho_{h}\leq L M_{p}^{2}\), where \(M_{p}=(8 \pi G)^{-1/2} \) is the reduced Planck mass. In a paper, Li (2004) has taken the largest allowed \(L\) to saturate this inequality and thus obtained dark energy density of the Universe \(\rho_{h}=3c^{2}M_{p} ^{2}L^{-2}\), known as HDE density. In the formalism of HDE, the Hubble horizon is a most natural choice for the IR cut-off, but it leads to a wrong equation of state (EoS) of dark energy (Hsu 2004). However, Pavón and Zimdahl (2005), and Banerjee and Pavón (2007) have shown that the viable EoS of dark energy could be achieved by taking the interaction between HDE and dark matter (DM).

On the other hand, the modified theories of gravity such as \(f(R)\) gravity (Bamba et al. 2008; Nojiri and Odintsov 2011), \(f(G)\) gravity (Nojiri and Odintsov 2005; De Felice and Tsujikawa 2009), \(f(R, G)\) gravity (Bamba et al. 2010; Elizalde et al. 2010), etc. have also been proposed to explain the recent accelerated expansion of the Universe. The \(f(R)\) gravity is one of the simplest and successful modified theories of GR, which fits with the observations very well. Recently, Harko et al. (2011) have proposed a new modified gravity theory known as \(f(R, T)\) gravity, where \(R\) as usual stands for the Ricci scalar and \(T\) denotes the trace of energy-momentum tensor. This modified theory presents a maximal coupling between geometry and matter. A number of authors (Sharif and Zubair 2012; Chakraborty 2013; Harko 2014; Singh and Singh 2014; Baffou et al. 2015; Shabani and Farhoudi 2014) have discussed the modified \(f(R, T)\) gravity in different context to explain the early and late time acceleration of the Universe. In a recent paper (Singh and Kumar 2014), the authors have discussed the viscous cosmology in this theory which shows the recent phase transition of the Universe. The HDE models have not been yet discussed in detail in the framework of \(f(R,T)\) gravity. In some papers (Houndjo and Piattella 2012; Fayaj et al. 2014), reconstruction of \(f(R,T)\) gravity from HDE and anisotropic model of HDE have been discussed.

Hsu (2004) in GR and Xu et al. (2009) in Brans-Dicke theory have shown that the Hubble horizon as an IR cut-off is not a suitable candidate to explain the recent accelerated expansion. However, Pavón and Zimdahl (2005) in GR, and Banerjee and Pavón (2007) in Brans-Dicke theory have shown that the interaction between HDE and DM can change the scenario and Hubble horizon as an IR cut-off may explain the recent accelerated expansion. In this paper our interest is to study the HDE model with Hubble horizon as an IR cut-off in \(f(R, T)\) gravity without considering the interaction between HDE and DM. As it is known, the \(f(R, T)\) gravity has coupling between geometry and matter, therefore, it will be interesting to discuss HDE with Hubble horizon as an IR cut-off in this modified theory. We show that Hubble horizon as an IR cut-off is suitable to explain the accelerated expansion in this theory without interaction between HDE and DM.

The Hubble parameter \(H\) and the deceleration parameter \(q\) are well known cosmological parameters which explain the evolution of the Universe. However, these two parameters can not discriminate among various DE models. In this context, Sahni et al. (2003) and Alam et al. (2003) have introduced a new geometrical diagnostic pair \(\{r, s\}\), known as statefinder parameters, which is constructed from the scale factor and its derivatives up to the third order. The statefinder pair \(\{r, s\}\) is geometrical in the nature as it is constructed from the space-time metric directly. Therefore, the statefinder parameters are more universal parameters to study the DE models than any other physical parameters. In a flat \(\Lambda \)CDM model, the statefinder pair has a fixed point value \(\{r, s\}=\{1, 0\}\). One can plot the trajectories in \(r\)-\(s\) and \(r\)-\(q\) planes to discriminate various DE models. We discuss the statefinder diagnostic and obtain the fixed point values of statefinder pair \(\{r, s\}=\{1, 0\}\) as in the case of \(\Lambda \)CDM model.

To be more realistic, the perfect fluid Universe is just an approximation of the viscous Universe. The dissipative processes in the relativistic fluid may be modeled as bulk viscosity. Misner (1968) was the first to use the viscosity concept in cosmology. The origin of the bulk viscosity in a physical system can be traced to deviations from the local thermodynamic equilibrium (see Maartens 1996; Brevik and Grøn 2013). In a cosmological fluid, the bulk viscosity arises any time when a fluid expands ( or contracts) too rapidly so that the system does not have enough time to restore the local thermodynamic equilibrium (Avelino and Nucamendi 2009). The bulk viscosity, therefore, is a measure of the pressure required to restore equilibrium. When the fluid reaches again the thermal equilibrium then the bulk viscous pressure ceases (Xinzhang and Spiegel 2001). Therefore, sufficient large bulk viscous pressure could make the effective pressure negative. Thermodynamic states with negative pressure are metastable and cannot be excluded by any law of nature. These states are connected with phase transitions. A phase transition in viscous early universe was discussed by Tawfik and Harko (2012).

In Weinberg (1972), the theoretical concept of the bulk viscosity in cosmology has been discussed which provides the insight into the nature of the bulk viscosity. Within the context of the early inflation, it has been known since long time ago that an imperfect fluid with bulk viscosity can produce an accelerated expansion without the need of a cosmological constant or some other inflationary scalar field (Heller et al. 1973; Zimdahl 1996). An accelerating Universe can be achieved for the right viscosity coefficient. At the late time, since we don’t know the nature of the Universe’s contents (dark matter and dark energy components) very clearly, the bulk viscosity is reasonable and can play a role as a dark energy candidate. Therefore, it is natural to consider the bulk viscosity in an accelerating Universe. It has been shown that inflation and recent acceleration can be explained using the viscous behavior of the Universe, and plays an important role in the phase transition of the Universe (Murphy 1973; Padmanabhan and Chitre 1987; Brevik and Gorbunova 2005; Hu and Meng 2006; Singh et al. 2007; Wilson et al. 2007; Kumar and Singh 2015; Sasidharan and Mathew 2015).

The concept of viscous DE has been discussed extensively in the literature (Cataldo et al. 2005; Sebastiani 2010; Setare and Sheykhi 2010). Feng and Li (2009) have shown that the age problem of the Ricci dark energy can be alleviated using the bulk viscosity. Motivated by the above works, we extend our analysis to viscous HDE with the same IR cut-off which shows the recent phase transition of the Universe. We obtain the statefinder parameters for viscous HDE which achieve the value of \(\Lambda \)CDM model and show the quintessence like behavior.

The paper is organized as follows. In the next section we discuss the formalism of \(f(R, T)\) gravity theory and present its field equations. In Sect. 3 we discuss the non-viscous HDE model and find the exact power-law solution of the scale factor which avoids the big bang singularity. We also find the cosmological parameters like deceleration parameter and statefinder parameters and discuss their behaviors. Section 4 describes the viscous HDE model and its solution. Section 5 presents the summary of our findings.

2 The formalism of modified \(f(R,T)\) gravity theory

The general form of the Einstein-Hilbert action for the modified \(f(R, T)\) gravity in the unit \(8\pi G=1\) is as follows (Harko et al. 2011; Singh and Kumar 2014):

$$ S=\frac{1}{2} \int d^{4}x\sqrt{-g}\,\bigl[f(R,T)+2\mathcal{L}_{m} \bigr], $$
(1)

where \(g\) stands for the determinant of the metric tensor \(g_{\mu \nu }\), \(R\) is the Ricci scalar and \(T\) represents the trace of the energy-momentum tensor, i.e., \(T= T^{\mu }_{\mu }\), while \(\mathcal{L}_{m}\) denotes the matter Lagrangian density. The speed of light is taken to be unity. As usual the energy-momentum tensor, \(T_{\mu \nu }\) of matter is defined as

$$ T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g} \mathcal{L}_{m})}{\delta g^{\mu \nu }}. $$
(2)

In fact, this modified theory of gravity is the generalization of \(f(R)\) gravity and is based on the coupling between geometry and matter. The corresponding field equations have been derived in metric formalism for the various forms of \(f(R, T)\).

Varying the action (1) with respect to the metric tensor \(g_{\mu \nu }\) for a simple form of \(f(R, T)=R+f(T)\), i.e., the usual Einstein-Hilbert term plus an \(f(T)\) correction (Harko et al. 2011; Singh and Kumar 2014) which modifies the general relativity and represents a coupling with geometry of the Universe, we get the following field equations.

$$ R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu }=T_{\mu \nu }- (T_{\mu \nu }+ \circleddash_{\mu \nu })f'(T)+ \frac{1}{2}f(T) g_{\mu \nu }, $$
(3)

where a prime denotes derivative with respect to the argument. The tensor \(\circleddash_{\mu \nu }\) in (3) is given by

$$ \circleddash_{\mu \nu }=-2T_{\mu \nu }+g_{\mu \nu } \mathcal{L}_{m}-2g ^{\alpha \beta }\frac{\partial^{2}\mathcal{L}_{m}}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}. $$
(4)

The matter Lagrangian \(\mathcal{L}_{m}\) may be chosen as \(\mathcal{L} _{m}=-p\) (Harko et al. 2011), where \(p\) is the thermodynamical pressure of matter content of the Universe. Now, Eq. (4) gives \(\circleddash_{\mu \nu }=-2T_{\mu \nu }-p g_{\mu \nu }\). Using this result, Eq. (3) reduces to

$$ R_{\mu \nu }-\frac{1}{2}R g_{\mu \nu }=T_{\mu \nu }+ (T_{\mu \nu }+p g_{\mu \nu })f'(T)+ \frac{1}{2}f(T) g_{\mu \nu }, $$
(5)

which are the field equations of the modified \(f(R, T)\) gravity theory.

Here, we are interested to study the behavior of HDE in this modified theory for a spatially homogeneous and isotropic flat Friedmann-Robertson-Walker (FRW) spacetime, which is expressed in comoving coordinates by the line element,

$$ ds^{2}=dt^{2}-a^{2}(t) \bigl(dx^{2}+dy^{2}+dz^{2} \bigr), $$
(6)

where \(a(t)\) stands for the cosmic scale factor. In what follows we study the non-viscous and viscous HDE models with deceleration parameter and statefinder parameters in \(f(R, T)\) gravity theory to describe the recent acceleration.

3 Non-viscous holographic dark energy cosmology

In this model, let us consider the Universe filled with HDE plus pressureless DM (excluding baryonic matter), i.e.,

$$ T_{\mu \nu }=T_{\mu \nu }^{h}+T_{\mu \nu }^{m}, $$
(7)

where \(T_{\mu \nu }^{h}\) and \(T_{\mu \nu }^{m}\) represent the energy-momentum tensors of HDE and DM, respectively. Many authors have described the recent accelerated expansion by assuming the interaction between HDE and DM in the different theories of gravity. In this paper, we consider a non-interacting matter field in \(f(R,T)\) gravity. The generalized Einstein Eqs. (5) yield

$$\begin{aligned} &3H^{2}=\rho_{m}+\rho_{h} + (\rho_{m}+ \rho_{h}+p_{h})f'(T)+\frac{1}{2}f(T), \end{aligned}$$
(8)
$$\begin{aligned} &2\dot{H}+3H^{2}=-p_{h}+\frac{1}{2}f(T), \end{aligned}$$
(9)

where \(\rho_{m}\), \(\rho_{h}\) and \(p_{h}\) denote the energy density of DM, the energy density of HDE and the pressure of HDE, respectively. An overdot denotes the derivative with respect to cosmic time \(t\). As the field equations (8) and (9) are highly non-linear, therefore, we assume \(f(T)=\alpha T\) (see, Harko et al. 2011), where \(\alpha \) is a coupling parameter. Now, the field equations (8) and (9) reduce as

$$\begin{aligned} &3H^{2}=\rho_{m}+\rho_{h} + \alpha ( \rho_{m}+\rho_{h}+p_{h})+ \frac{1}{2} \alpha T, \end{aligned}$$
(10)
$$\begin{aligned} &2\dot{H}+3H^{2}=-p_{h}+\frac{1}{2}\alpha T. \end{aligned}$$
(11)

The equation of state (EoS) of HDE is given by \(p_{h}=w_{h}\rho_{h}\) and the trace of energy-momentum tensor is given by \(T=\rho_{m}+\rho_{h}-3p _{h}\). Now, from (10) and (11), a combined evolution equation for \(H\) can be written as

$$ 2\dot{H} + (1+\alpha )\bigl[(1+w_{h})\rho_{h}+ \rho_{m}\bigr]=0. $$
(12)

In the literature, various forms of HDE (the general form is \(\rho_{h}=3c^{2}M_{p}^{2}L^{-2}\), where \(c^{2}\) is a dimensionless constant, \(M_{p}\) stands for the reduced Planck mass and \(L\) denotes the IR cut-off radius) have been discussed depending on the choices of IR cut-off such as Hubble horizon, future event horizon, apparent horizon, Granda-Oliveros cut-off, etc. In this work, we consider the Hubble horizon (\(L= H^{-1}\)) as an IR cut-off to describe the recent acceleration. The corresponding energy density \(\rho_{h}\) is given by

$$ \rho_{h}=3 c^{2}H^{2}. $$
(13)

Form (10) and (13), the energy density of DM can be obtained as

$$ \rho_{m}=\frac{3(\alpha c^{2} w_{h}-3\alpha c^{2}-2 c^{2}+2)}{(3 \alpha +2)}H^{2}. $$
(14)

Using (13) and (14) into (12), we finally get

$$ \dot{H}+\frac{3(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)}{3 \alpha +2} H^{2}=0, $$
(15)

which, on solving gives (where \(\alpha \neq -1\), \(\alpha \neq -2/3\))

$$ H=\frac{1}{c_{0}+\frac{3(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)}{3 \alpha +2} t}, $$
(16)

where \(c_{0}\) is a positive constant of integration. Equation (16) can be rewritten as

$$ H=\frac{H_{0}}{1+\frac{3 H_{0}(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w _{h}+1)}{3\alpha +2}(t-t_{0})}, $$
(17)

where \(H_{0}\) is the present value of the Hubble parameter at the cosmic time \(t=t_{0}\), the time where the HDE starts to dominate. Using the relation \(H=\frac{\dot{a}}{a}\), the cosmic scale factor \(a\) is given by

$$\begin{aligned} a &=c_{1} \biggl[1+\frac{3 H_{0}(\alpha +1)(2\alpha c^{2} w_{h}+ c^{2} w _{h}+1)}{3\alpha +2} \\ &\quad {}\times (t-t_{0}) \biggr]^{\frac{3\alpha +2 }{3(\alpha +1) (2\alpha c ^{2} w_{h}+ c^{2} w_{h}+1)}}, \end{aligned}$$
(18)

where \(c_{1}\) is an another positive constant of integration. One can rewrite \(a\) as follows

$$\begin{aligned} a &=a_{0} \biggl[1+\frac{3 H_{0}(\alpha +1)(2\alpha c^{2} w_{h}+ c^{2} w _{h}+1)}{3\alpha +2} \\ &\quad {}\times (t-t_{0}) \biggr]^{\frac{3\alpha +2 }{3(\alpha +1) (2\alpha c ^{2} w_{h}+ c^{2} w_{h}+1)}}, \end{aligned}$$
(19)

where \(a_{0}\) is the present value of the scale factor at the cosmic time \(t=t_{0}\). We obtain the power-law evolution of the Universe which avoids the big-bang singularity.

The deceleration parameter \(q\), which is defined as \(q=-a\ddot{a}/\dot{a}^{2}\), is a geometric parameter which describes the acceleration or deceleration of the Universe depending on it’s negative or positive value. In this case, the deceleration parameter is given by

$$ q=\frac{3(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)}{3\alpha +2}-1. $$
(20)

Here, we obtain a constant deceleration parameter as expected due to the power-law scale factor. The accelerated expansion may be obtained if the parameters satisfy the constraint \(\frac{3(\alpha +1)(2\alpha c^{2} w _{h}+c^{2} w_{h}+1)}{3\alpha +2}<1\). In a paper, Li et al. (2013) have studied the Planck constraints on HDE and obtained the tightest and self-consistent value of constant \(c\) from Planck + WP + BAO + HST + lensing as \(c=0.495\pm 0.039\). Therefore, let us consider here and thereafter \(c=0.5\) for further discussion which is lying in this observed range. Now, for example let’s take \(\alpha =1\) and \(w_{h}=-0.5\), we obtain \(q=-0.25\) which shows the accelerated expansion. Moreover, one may obtain the accelerated expansion even when the HDE does not violate the strong energy condition \(\rho_{h}+3p_{h}>0\) for suitable values of coupling parameter \(\alpha \). Thus, the HDE with Hubble horizon as an IR cut-off can successfully explain the accelerated expansion in the framework of \(f(R, T)\) gravity without assuming the interaction between HDE and DM in contrast to the works done in GR (Hsu 2004) and in Brans-Dicke theory (Xu et al. 2009). It is to be noted that this model does not show the phase transition as the deceleration parameter is constant.

In order to get a robust analysis to discriminate among DE models Sahni et al. (2003) and Alam et al. (2003) have introduced a new geometrical diagnostic pair \(\{r, s\}\), known as statefinder parameters, which is constructed from the scale factor and its derivatives up to the third order. The statefinder pair \(\{r, s\}\) is geometrical in nature as it is constructed from the space-time metric directly. The statefinder pair \(\{r, s\}\) provides a very comprehensive description of the dynamics of the Universe and consequently the nature of the DE. It is defined as

$$ r=\frac{\dddot{a}}{aH^{3}}, \qquad s=\frac{r-1}{3(q-1/2)}. $$
(21)

In this model, we obtain the statefinder parameters \(r\) and \(s\) as

$$\begin{aligned} & \begin{aligned} r&=\frac{18(\alpha +1)^{2}(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)^{2}}{(3 \alpha +2)^{2}} \\ &\quad {}-\frac{9(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)}{3\alpha +2}+1, \end{aligned} \end{aligned}$$
(22)
$$\begin{aligned} & \begin{aligned}[b] s &=\frac{(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)}{(3\alpha +2)[( \alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}+1)-\frac{1}{2}]} \\ &\quad {}\times \bigl[2(\alpha +1) \bigl(2\alpha c^{2} w_{h}+c^{2} w_{h}+1\bigr)-(3\alpha +2)\bigr]. \end{aligned} \end{aligned}$$
(23)

We observe that the statefinder parameters \(\{r, s\}\) are constant and the values of these parameters depend on the coupling parameter \(\alpha \), constant \(c\) and EoS parameter \(w_{h}\) of HDE. In the papers (Sahni et al. 2003; Alam et al. 2003), it has been observed that SCDM model and \(\Lambda \)CDM model have fixed point values of statefinder pair \(\{r, s\}=\{1, 1\}\) and \(\{r, s\}=\{1, 0\}\), respectively. In our work, it is observed that fixed point of \(\Lambda \)CDM model can be achieved for \(\alpha =-\frac{1+c^{2} w_{h}}{2c^{2} w_{h}}\) as a particular case of this model. Thus, for a suitable value of \(w_{h}\), which may be obtained by observations, we can find the coupling parameter \(\alpha \) for which \(\{r, s\}=\{1, 0\}\) and viceversa.

4 Viscous holographic dark energy cosmology

In the non-viscous HDE model, we have obtained the constant value of deceleration parameter which does not describe the phase transition. But, the astronomical observations show that the phase transition is an integral part of the evolution of the Universe. Therefore, in this section, it would be of interest to investigate whether a viscous HDE with the Hubble horizon as an IR cut-off could be helpful to explain the phase transition, i.e., time-dependent deceleration parameter with signature flip from positive to negative in order to elucidate the observed phase transition of the Universe.

In an accelerating Universe, it may be natural to assume that the expansion process is actually a collection of state out of thermal equilibrium in a small fraction of time due to the existence of possible dissipative mechanisms. In an isotropic and homogeneous FRW model, the dissipative process may be treated via the relativistic theory of bulk viscosity proposed by Eckart (1940) and later on pursued by Landau and Lifshitz (1987). It has been found that only the bulk viscous fluid remains compatible with the assumption of large scale homogeneity and isotropy. The other processes, like shear and heat conduction, are directional mechanisms and they decay as the Universe expands. In a cosmological context the inclusion of viscosity broadens the applicability of the theory considerably. Bulk viscosity can produce an accelerated expansion even without dark energy matter due to the presence of an effective negative pressure. A number of papers have appeared on viscous cosmology (for review, see Grøn 1990; Brevik and Grøn 2013). Recently, the present authors (Singh and Kumar 2014; Kumar and Singh 2015) have studied the effect of viscous fluid in \(f(R, T)\) gravity and discussed the recent phase transition of the Universe.

Using the Eckart formalism for dissipative fluids, we can assume that the effective pressure of HDE is a sum of the thermodynamical pressure (\(p_{h}\)) and the bulk viscous pressure (\(\varPi \)), i.e.,

$$ P_{\mathit{eff}}=p_{h}+\varPi =p_{h}-3\zeta H, $$
(24)

where \(\zeta \) is the positive coefficient of the bulk viscosity. Now, the matter Lagrangian is taken as \(\mathcal{L}_{m}=-P_{\mathit{eff}}\) for which Eq. (4) gives \(\circleddash_{\mu \nu }=-2T_{\mu \nu }-P_{\mathit{eff}}g_{ \mu \nu }\). In this model we follow the same concept as discussed in Sect. 3 to analyze the behavior of the Universe. Using \(f(T)=\alpha T\), Eq. (3) yields the field equations for viscous HDE in the framework of \(f(R, T)\) gravity as

$$\begin{aligned} &3H^{2}=\rho_{m}+\rho_{h} + \alpha (\rho_{m}+\rho_{h}+p_{h}-3\zeta H)+ \frac{1}{2}\alpha T, \end{aligned}$$
(25)
$$\begin{aligned} &2\dot{H}+3H^{2}=-p_{h}+3\zeta H+ \frac{1}{2}\alpha T. \end{aligned}$$
(26)

In this case, the trace of energy-momentum tensor is \(T=\rho_{m}+\rho _{h}-3(p_{h}-3\zeta H)\). Using this value of \(T\) into (25) and (26), a single evolution equation of \(H\) is given by

$$ 2\dot{H} + (\alpha +1) (\rho_{m}+\rho_{h}+p_{h})-3( \alpha +1)\zeta H=0. $$
(27)

From (25), we get

$$\begin{aligned} \rho_{m}=\frac{3}{(3\alpha +2)} H \bigl[\bigl(\alpha c^{2} w_{h}-3\alpha c ^{2}-2c^{2}+2 \bigr)H-\alpha \zeta \bigr]. \end{aligned}$$
(28)

Now, Using (13) and (28) into (27), we get

$$\begin{aligned} &\dot{H} + \frac{3(\alpha +1)}{3\alpha +2}\bigl(2\alpha c^{2} w_{h}+c^{2} w _{h}+1 \bigr)H^{2} \\ &\quad {}-\frac{3(\alpha +1)(2\alpha +1)\zeta }{(3\alpha +2)}H=0. \end{aligned}$$
(29)

Equation (29) is solvable for \(H\) if the coefficient of bulk viscosity \(\zeta \) is known. Many authors have studied the cosmological models by assuming the various forms of the bulk viscous coefficient (for review, see Maartens 1995). Ren and Meng (2006a, 2006b) have taken a general form \(\zeta =\zeta_{0}+\zeta_{1}H+\zeta_{2 }H^{2}\) of bulk viscous coefficient. However, in our case it is too difficult to solve Eq. (29) with this general form of \(\zeta \). Therefore, we assume the bulk viscous coefficient of the form \(\zeta =\zeta_{0}+\zeta_{1}H\) (Avelino and Nucamendi 2010; Singh and Kumar 2014) by taking \(\zeta_{2}=0\). With this form of \(\zeta \), Eq. (29) reduces to

$$\begin{aligned} &\dot{H} + \frac{3(\alpha +1)}{3\alpha +2}\bigl(2\alpha c^{2} w_{h}+c^{2} w _{h}-2\alpha \zeta_{1}-\zeta_{1}+1\bigr)H^{2} \\ &\quad {}-\frac{3(\alpha +1)(2\alpha +1)\zeta_{0}}{(3\alpha +2)}H=0. \end{aligned}$$
(30)

The solution of (30) is given by

$$ H=\frac{e^{\frac{3(\alpha +1)(2\alpha +1)\zeta_{0}}{(3\alpha +2)} t}}{c _{2}+\frac{(2\alpha c^{2} w_{h}+c^{2} w_{h}-2\alpha \zeta_{1}-\zeta _{1}+1)}{(2\alpha +1)\zeta_{0}}e^{\frac{3(\alpha +1)(2\alpha +1)\zeta _{0}}{(3\alpha +2)} t}}, $$
(31)

where \(c_{2}\) is a constant of integration. The scale factor \(a\) in the terms of cosmic time \(t\) is

$$\begin{aligned} a&=c_{3} \biggl[c_{2}+ \frac{(2\alpha c^{2} w_{h}+c^{2} w_{h}-2\alpha \zeta _{1}-\zeta_{1}+1)}{(2\alpha +1)\zeta_{0}} \\ &\quad {}\times e^{\frac{3(\alpha +1)(2\alpha +1)\zeta_{0}}{(3\alpha +2)} t} \biggr]^{\frac{3\alpha +2}{3(\alpha +1)(2\alpha c^{2} w_{h}+c^{2} w_{h}-2 \alpha \zeta_{1}-\zeta_{1}+1)}}, \end{aligned}$$
(32)

where \(c_{3}>0\) is another constant of integration. Equation (32) can be rewritten as

$$\begin{aligned} a&=a_{0} \biggl[1+\frac{(2\alpha c^{2} w_{h}+c^{2} w_{h}-2\alpha \zeta _{1}-\zeta_{1}+1)H_{0}}{(2\alpha +1)\zeta_{0}} \\ &\quad {}\times\bigl(e^{\frac{3(\alpha +1)(2\alpha +1)\zeta_{0}(t-t_{0})}{(3\alpha +2)}}-1\bigr) \biggr]^{\frac{(3\alpha +2)/(\alpha +1)}{3(2\alpha c^{2} w_{h}+c^{2} w _{h}-2\alpha \zeta_{1}-\zeta_{1}+1)}}. \end{aligned}$$
(33)

One can observe that the model avoids the big-bang singularity. In this case, the deceleration parameter is obtained as

$$\begin{aligned} q &=\frac{3(\alpha +1)}{(3\alpha +2)H_{0}} \bigl[\bigl(2\alpha c^{2} w_{h}+c ^{2} w_{h}-2\alpha \zeta_{1}-\zeta_{1}+1\bigr)H_{0} \\ &\quad {}-(2\alpha +1)\zeta_{0} \bigr] e^{\frac{3(\alpha +1)(2\alpha +1)\zeta _{0}}{(3\alpha +2)}(t_{0}-t)}-1. \end{aligned}$$
(34)

It is observed that the value of \(q\) is time-dependent which comes due to the introduction of bulk viscous term in HDE. The phase transition of the Universe can be explained using this value of deceleration parameter. The deceleration parameter must change it’s sign from positive to negative to explain the recent phase transition (deceleration to acceleration) of the Universe. In fact, \(q\) must change the sign at the time \(t=t_{0}\) because we have assumed \(t_{0}\) is the time where the viscous HDE begins to dominate. In other words, the Universe must decelerate for \(t< t_{0}\) (matter dominated epoch) and accelerate for \(t>t_{0}\) (HDE dominated epoch). We observe that the Universe shows the transition from decelerated to accelerated phase at cosmic time \(t_{0}\) if \(3(\alpha +1)[(2\alpha c^{2} w_{h}+c^{2} w_{h}-2 \alpha \zeta_{1}-\zeta_{1}+1)H_{0}-(2\alpha +1)\zeta_{0}]=(3\alpha +2)H _{0}\). Therefore, the value of coupling parameter \(\alpha \) can be obtained for a given value of \(w_{h}\), which may be obtained from the observations, or vice-versa to get the phase transition. Thus, we have shown that the bulk viscous HDE with Hubble horizon as an IR cut-off can explain the recent phase transition of the Universe in the framework of \(f(R, T)\) gravity.

Next, we discuss the another geometrical parameters, i.e., statefinder parameters. In this case, the statefinder parameter \(r\) is obtained as

$$\begin{aligned} \!\begin{aligned}[b] r &=\frac{9(\alpha +1)^{2}}{(3\alpha +2)^{2} H_{0}} \bigl[\bigl(2\alpha c^{2}w _{h}+c^{2}w_{h}-2\alpha \zeta_{1}-\zeta_{1}+1\bigr)H_{0} \\ &\quad {} -(2\alpha +1)\zeta_{0}\bigr] \\ &\quad {} \times\biggl[ \frac{(2\alpha c^{2}w_{h}+c^{2}w_{h}-2 \alpha \zeta_{1}-\zeta_{1}+1)H_{0}-(2\alpha +1)\zeta_{0}}{H_{0}e^{\frac{6( \alpha +1)(2\alpha +1)\zeta_{0}}{(3\alpha +2)} (t-t_{0})}} \\ &\quad {}+\frac{(2\alpha c^{2}w_{h}+c^{2}w_{h}-2\alpha \zeta_{1}-\zeta_{1}+1)-\frac{3 \alpha +2}{\alpha +1}}{e^{\frac{3(\alpha +1)(2\alpha +1)\zeta_{0}}{(3 \alpha +2)}(t-t_{0})}} \biggr]+1. \end{aligned} \end{aligned}$$
(35)

The second statefinder parameter \(s\) is not given here due to complexity but one can find it by using the values of \(q\) and \(r\) from (34) and (35) in \(s=\frac{r-1}{3(q-1/2)}\). Our model reproduces the fixed point value \(\{r, s\}=\{1, 0\}\) of \(\Lambda \)CDM model when the parameter \(\alpha \) satisfies the condition \(\alpha =-\frac{1}{2}(1+\frac{H_{0}}{c ^{2} w_{h}H_{0}-\zeta_{1}H_{0}-\zeta_{0}})\). For this value of \(\alpha \), the statefinder pair is independent of time and remains fixed throughout the evolution as in \(\Lambda \)CDM model. Indeed, we have obtained time-dependent statefinder pair which means that a general study of the behavior of this pair is needed.

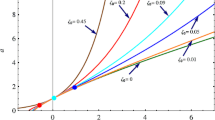
We plot the trajectories in \(r\)-\(s\) plane for some particular values of parameters \(\alpha \) and \(w_{h}\) to discriminate our model with existing models of DE. Here, we have taken \(c=0.5\), \(H_{0}=1\), \(\zeta_{0}=\zeta_{1}=0.05\) and \(t_{0}=1\). In Figs. 1 and 2, the fixed points \(\{r, s\}=\{1, 1\}\) and \(\{r, s\}=\{1, 0\}\) have been shown as SCDM model and \(\Lambda \)CDM model, respectively. It is obvious from both the figures that for any values of \(\alpha \) and \(w_{h}\), which are consistent with the model, the viscous HDE model always approaches to the \(\Lambda \)CDM model, i.e., \(\{r, s\}=\{1, 0\} \) in the late time evolution. In the early time of the evolution our model can approach in the vicinity of SCDM model for some values of \(\alpha \) as can be seen in Figs. 1 and 2. It is interesting to note that for larger negative values of \(\alpha \) the trajectories may start from \(\Lambda \)CDM in the early time and approach to the same \(\Lambda \)CDM model during the late time evolution.

Fig. 1
figure 1

The trajectories in \(r\)-\(s\) plane are plotted for \(w_{h}=-0.5\) and different values of \(\alpha \)

Full size image
Fig. 2
figure 2

The trajectories in \(r\)-\(s\) plane are plotted for \(w_{h}=-1\) and different values of \(\alpha \)

Full size image

In the quiessence model with constant EoS (\(Q_{1}\)-model) (Sahni et al. 2003; Alam et al. 2003) and the Ricci dark energy (RDE) model (Feng 2008), it has been shown that the trajectories in \(r\)-\(s\) plane are vertically straight lines. In the both models, \(s\) is constant throughout the evolution of the Universe, while \(r\) increases in RDE model and decreases in \(Q_{1}\)-model starting from the initial point \(r=1\). It has also been shown (Sahni et al. 2003; Alam et al. 2003) that the trajectories for the quintessence scalar field model (\(Q_{2}\)-model), where the scalar potential \(V(\phi )\) varies as \(V(\phi )\propto \phi^{-\beta }\), \(\beta \geq 1\), and chaplygin gas model approach asymptotically to the \(\Lambda \)CDM model in the late time. Comparing this viscous HDE model with \(Q_{1}\)-model and RDE model, we find that our viscous HDE model produces the curved trajectories which approach to \(\Lambda \)CDM model in the late time. Further, we observe that our model almost shows the similar trajectories like \(Q_{2}\)-model for some values of \(\alpha \) and \(w_{h}\) in \(r\)-\(s\) plane. For \(\alpha =-0.15\), \(w_{h}=-0.5\) and \(\alpha =-0.23\), \(w_{h}=-1\) as shown in Figs. 1 and 2, respectively, the trajectories show almost similar behavior as \(Q_{2}\)-model for \(\beta =2\).

It may be observed from Figs. 1 and 2 that for a fixed value of \(\alpha \), say \(\alpha =-0.15\), the trajectories show more deviation from the \(Q_{2}\)-model as we increase the negative value of \(w_{h}\). Further, for small negative values or positive values of \(\alpha \), the trajectories deviate more and more from the \(Q_{2}\)-model for fixed value of \(w_{h}\) (see, Sahni et al. 2003; Alam et al. 2003). We may fix \(\alpha \), and vary \(\zeta_{0}\) and \(\zeta_{1}\), the same behavior of trajectories can be observed for suitable values of \(\zeta_{0}\) and \(\zeta_{1}\).

Figures 3 and 4 plot the trajectories in \(r\)-\(q\) plane. Here, we have taken \(c=0.5\), \(H_{0}=1\), \(\zeta_{0}=\zeta_{1}=0.05\), and \(t_{0}=1\). The SCDM model and SS model (steady-state cosmology) have been shown by the fixed points \(\{r, q\}=\{1, 0.5\}\) and \(\{r, q\}=\{1, -1\}\) , respectively. We observe the signature flip in the value of \(q\) from positive to negative which explain the recent phase transition successfully. The \(\Lambda \)CDM model starting from the fixed point of SCDM model evolves along the doted line and ends at the fixed point of SS model. It can be observed from both the figures that for any values of \(\alpha \) and \(w_{h}\), the viscous HDE model always approaches to the SS model, i.e., \(\{r, q\}=\{1, -1\}\) as \(\Lambda \)CDM, \(Q_{2}\) and chaplygin gas models approach in the late time evolution. However, in the early time of evolution the model stats close to SCDM model for some values of \(\alpha \) as shown in Figs. 3 and 4. Moreover. it may start exactly from the fixed point \(\{r, q\}=\{1, 0.5\}\) of SCDM for suitable value of \(\alpha \). In \(r\)-\(q\) plane also the trajectories corresponding to our model show the \(Q_{2}\)-model like behavior. Again, comparing our viscous HDE model with \(Q_{1}\)-model, RDE model, \(Q_{2}\)-model and chaplygin gas model, we find that viscous HDE model is compatible with \(Q_{2}\)-model.

Fig. 3
figure 3

The trajectories in \(r\)-\(q\) plane are plotted for \(w_{h}=-0.5\) and different values of \(\alpha \)

Full size image
Fig. 4
figure 4

The trajectories in \(r\)-\(q\) plane are plotted for \(w_{h}=-1\) and different values of \(\alpha \)

Full size image

5 Conclusion

In GR and Brans-Dicke theory, some authors (Hsu 2004; Xu et al. 2009) have found that the Hubble horizon is not a viable candidate to explain the accelerated expansion of the Universe. However, Pavón and Zimdahl (2005), and Banerjee and Pavón (2007) have shown that the interaction between HDE and DM can describe the accelerated expansion. Therefore, it is clear that one can observe accelerated expansion if the interaction between the different matter contents is considered. In this work, we have studied non-viscous and viscous HDE models with Hubble horizon as an IR cut-off in the frame work of modified \(f(R, T)\) gravity. The \(f(R, T)\) gravity theory presents a maximal coupling between geometry and matter. Therefore, we have explored the consequences of the coupling of matter with the geometry of the Universe instead of taking the interaction between HDE and DM as many authors have studied. We have investigated the possibility whether the Hubble horizon as an IR cut-off could explain an accelerated expansion in \(f(R, T)\) gravity. We have shown that the non-viscous and viscous HDE models with Hubble horizon as an IR cut-off may explain the accelerated expansion in the frame work of this modified theory. Further, we have investigated statefinder pair \(\{r, s\}\) to discriminate our non-viscous and viscous HDE models with other existing DE models. We summarize the results of these two models as follows: in non-viscous HDE model, we have found an accelerated expansion under the constraint of parameters. In this case, we have obtained constant deceleration and statefinder parameters. Due to constant \(q\), it is not possible to analyze the phase transition of the Universe. We have found the fixed point \(\{r, s\}=\{1, 0\}\) of \(\Lambda \)CDM model as a particular case of this model. Thus, non-viscous HDE model is consistent with \(\Lambda \)CDM model.

In viscous HDE model, we have obtained the recent phase transition of the Universe as the deceleration parameter comes out to be time-dependent and shows signature flip from positive to negative. In this model, the statefinder parameters also are the function of cosmic time \(t\). These time-dependent parameters are possible due to the inclusion of bulk viscous fluid in HDE model which could explain the recent phase transition in a better way. It is interesting to note that the viscous HDE model gives the \(\Lambda \)CDM model fixed point \(\{r, s\}=\{1, 0\}\) and remains fixed in \(\Lambda \)CDM model throughout the evolution for a specific value of \(\alpha \) as discussed in Sect. 4. The statefinder diagnostic have been discussed through the trajectories of \(r\)-\(s\) and \(r\)-\(q\) planes as shown in Figs. 1–4 to discriminate our model with the existing DE models. In Figs. 1 and 2, it has been observed that some of the trajectories pass through the vicinity of SCDM during early time but ultimately all approach to \(\Lambda \)CDM model in the late time. In Figs. 3 and 4, it can be seen that the trajectories may start from SCDM model for a suitable value of \(\alpha \) in early time but all the trajectories approach to SS model in the late time evolution. It has been noticed that for some values of \(\alpha \) the trajectories of the viscous HDE model are similar to the trajectories of \(Q_{2}\)-model (Sahni et al. 2003; Alam et al. 2003). Therefore, the viscous HDE in the framework of \(f(R, T)\) gravity gives more general results in comparison to \(\Lambda \)CDM and \(Q_{2}\)-model at least at the level of statefinder diagnostic as we are able to achieve the behavior of both the models.