1 Introduction

Cosmic expansion of universe has been one of the most interesting topic of discussion in the last decade. It is thought that the current expansion of universe is accelerating and it is due to some invisible energy with strong negative pressure. Researchers call this mysterious energy as dark energy. It is expected that dark energy constitutes almost \(70~\%\) of the total energy of the universe. Einstein also defined the dark energy by using a cosmological constant in the field equations. Accelerated expansion of universe is well supported from different sources including cosmic microwave background fluctuations, galaxy clustering and supernovae experiments (Spergel et al. 2003, 2007; Riess et al. 1998, 2004; Bennett et al. 2003; Tegmark et al. 2004). Equation of state (EoS) parameter \(\omega =p/\rho\) can be used to describe the dark energy, where \(\rho\) and \(p\) represent the energy density and pressure of dark energy. It is now believed that alternative theories of gravity can be helpful to understand the dark energy and late time acceleration issues (Capozziello 2002).

Einstein’s theory of general relativity (GR) has been modified by many researchers in the recent decades. Among the various modification, \(f(R)\) and \(f(R,T)\) theories of gravity (\(R\) is the Ricci scalar and \(T\) is the trace of energy-momentum tensor) has been discussed most seriously (Starobinsky 1980; Nojiri and Odintsov 2004; Harko et al. 2011; Appleby and Battye 2007; Appleby et al. 2010; Felice and Tsujikawa 2010; Bamba et al. 2012). In particular, \(f(R)\) gravity is proved to be equivalent to scalar-tensor theory of gravity (Chiba et al. 2007). The cosmic acceleration may be justified just by involving the term \(1/R\) which is required at small curvature. It has been suggested that the modified gravity with positive powers of the curvature supports the inflationary epoch while with negative powers of the curvature serves as effective dark energy, supporting the current cosmic acceleration (Nojiri and Odintsov 2003). Future evolution of the dark energy universe in modified theories of gravity has been discussed where it is shown that the non minimal gravitational coupling can remove the finite-time future singularities (Bamba et al. 2008). Further, it has been proved that modified theories may be consistent with local tests and may provide qualitatively reasonable unified description of inflation with dark energy epoch (Nojiri and Odintsov 2011). \(f(T)\) theory of gravity (Bamba et al. 2011; Li et al. 2011; Jamil et al. 2012a,b,c) is an other alternate theory which generalizes teleparallel gravity. The interesting feature of the theory is that cosmic acceleration can be justified without involving dark energy. Modified Gauss-Bonnet (GB) gravity is another theory which has gained popularity in the last few years (Nojiri and Odintsov 2005; Congnola et al. 2006, 2007). It is also known as \(f(G)\) theory of gravity, where \(f(G)\) is a generic function of GB invariant \(G\). GB term plays an important role as it may avoid ghost contributions and helps in regularizing the gravitational action (Chiba 2005). It is hoped that this theory may describe the late-time cosmic acceleration. Moreover, the theory also passes the solar system tests for some specific choices of \(f(G)\) gravity models. Some interesting work has been done so far in this theory.

Nojiri and Odintsov (2007) developed the reconstruction techniques for \(f(G)\) gravity and it was demonstrated that how cosmological sequence of matter dominance, deceleration-acceleration transition and acceleration era could emerge by using a modified theory. Fayaz et al. (2015) investigated power law solutions with anisotropic background in \(f(G)\) gravity and it was concluded that Bianchi type \(I\) power law solutions only existed for some special choices of \(f(G)\) gravity models. Sharif and Fatima (2015) studied noncommutative static spherically symmetric wormhole solutions in modified GB gravity by considering a viable \(f(G)\) model. Abbas et al. (2015) gave the possibility for the existence of anisotropic compact stars in \(f(G)\) gravity. Cylindrical symmetry in \(f(G)\) gravity has been explored where it was shown that there existed seven families of exact solutions with three choices of \(f(G)\) models (Houndjo et al. 2014). Investigation of exact cylindrically symmetric solutions of modified field equations resulted cosmic string space-time (Rodrigues et al. 2014). Garcia et al. (2011) explored energy condition to find the viability of some specific choices of \(f(G)\) gravity models. Recently, we have discussed the dynamics of \(f(G)\) gravity in anisotropic background by studying the energy conditions and a power law \(f(G)\) model (Shamir 2016). Noether \(f(G)\) symmetries have been recently found in FRW background by Sharif and Fatima (2016a). The same authors (Sharif and Fatima 2016b) argued the role of GB term in the late time accelerated phases of the universe.

A further generalization of GB gravity named as \(f(R,G)\) gravity is also proposed recently. Felice et al. (2011) investigated the stability of Schwarzschild like solutions in \(f(R,G)\) gravity using linear metric perturbations. Wu and Ma (2015) explored the spherically symmetry by finding the exact solutions at low energy. Laurentis et al. (2015) studied the cosmological inflation in \(f(R,G)\) theory of gravity. Warm inflation has been discussed in the context of \(f(G)\) theory of gravity using scalar fields for the Friedmann-Robertson-Walker (FRW) universe model (Sharif and Ikram 2015). Energy conditions in \(f(R,G)\) gravity has been recently explored where the weak energy condition was used along with the recent experimental values of some important cosmological parameters to determine the viability of some specific choices of \(f(R,G)\) gravity models (Atazadeh and Darabi 2014). Sebastiani (2011) studied finite time singularities in modified \(f(R,G)\) gravity and it was concluded that singularities could be avoided in \(f(R,G)\) theories of gravity using the higher order curvature corrections. Thus it seems interesting to explore modified theories of gravity, in particular, the \(f(G)\) gravity.

In this manuscript, we focus our attention to investigate \(f(G)\) gravity in anisotropic background. For this purpose, we consider locally rotationally symmetric (LRS) Bianchi type \(I\) spacetime. We explore the exact solutions of the LRS Bianchi type \(I\) field equations in modified \(f(G)\) gravity. A well-known \(f(G)\) gravity model has been used to solve the set of differential equations. The paper is planned as follows: Some basics of \(f(G)\) gravity and field equations are briefly introduced in Sect. 2. In Sect. 3, the solutions of the field equations for a specific choice of \(f(G)\) model are given. Last section gives the summary and conclusion of work.

2 \(f(G)\) gravity: field equations

The action for modified GB gravity is

$$ S=\frac{1}{2\kappa} \int d^{4}x\sqrt{-g} \bigl[R+f(G) \bigr]+S_{M} \bigl(g^{\mu\nu}, \psi \bigr), $$
(1)

where \(\kappa\) is called the coupling constant and \(g\) represents determinant of the metric tensor \(g_{\mu\nu}\). Matter is minimally coupled to the metric tensor through the action \(S_{M}(g^{\mu\nu}, \psi)\), where \(\psi\) denotes the matter fields. This coupling of matter with metric tensor suggests that \(f(G)\) gravity is purely a metric theory of gravity. It is to be noted that \(f(G)\) is a general function of GB invariant \(G\)

$$ G\equiv R^{2}-4R_{\mu\nu}R^{\mu\nu}+R_{\mu\nu\sigma\rho}R^{\mu\nu\sigma \rho}, $$
(2)

where \(R\) is the Ricci scalar while \(R_{\mu\nu}\) and \(R_{\mu\nu\sigma \rho}\) denote Ricci and Riemann tensors respectively. Gravitational field equations can be obtained by varying the action (1) with respect to the metric tensor

$$\begin{aligned} &R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}+8 \biggl[R_{\mu\rho\nu\sigma}+R_{\rho\nu }g_{\sigma\mu}-R_{\rho\sigma}g_{\nu\mu}- R_{\mu\nu}g_{\sigma\rho} \\ &\quad {}+R_{\mu\sigma}g_{\nu\rho}+\frac{1}{2}R(R_{\mu\nu}g_{\sigma\rho}-R_{\rho\sigma}g_{\nu\rho})\biggr]\nabla^{\rho}\nabla^{\sigma}F \\ &\quad {}+(Gf_{G}-f)g_{\mu\nu}=\kappa T_{\mu\nu}, \end{aligned}$$
(3)

where the operator \(\nabla_{\mu}\) is used for covariant differentiation and the subscript \(G\) in \(f_{G}\) is to represent the derivative of \(f\) with respect to \(G\). A more familiar form similar to GR field equations is

$$ G_{\mu\nu}\equiv R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R=T^{\mathrm{eff}}_{\mu\nu}, $$
(4)

where

$$\begin{aligned} T^{\mathrm{eff}}_{\mu\nu} =& \kappa T_{\mu\nu}-8\biggl[R_{\mu\rho\nu\sigma}+R_{\rho \nu}g_{\sigma\mu}-R_{\rho\sigma}g_{\nu\mu}-R_{\mu\nu}g_{\sigma\rho} \\ &{}+R_{\mu\sigma}g_{\nu\rho}+\frac{1}{2}R(R_{\mu\nu}g_{\sigma\rho}-R_{\rho\sigma}g_{\nu\rho}) \biggr]\nabla^{\rho}\nabla^{\sigma}f_{G} \\ &{}-(Gf_{G}-f)g_{\mu\nu}. \end{aligned}$$
(5)

We start with the spatially homogeneous, anisotropic LRS Bianchi type \(I\) spacetime

$$ ds^{2}=dt^{2}-A^{2}(t)dx^{2}-B^{2}(t) \bigl[dy^{2}+dz^{2} \bigr], $$
(6)

where the metric coefficients \(A\) and \(B\) are known as cosmic scale factors of the universe. The corresponding GB invariant and Ricci scalar turn out to be

$$\begin{aligned} &G=8 \biggl[\frac{\ddot{A}\dot{B}^{2}}{AB^{2}}+2\frac{\dot{A}\dot{B}\ddot {B}}{AB^{2}} \biggr], \end{aligned}$$
(7)
$$\begin{aligned} &R=-2 \biggl[\frac{\ddot{A}}{A}+2\frac{\ddot{B}}{B}+ \frac{2\dot{A}\dot{B}}{AB}+\frac{\dot{B}^{2}}{B^{2}} \biggr], \end{aligned}$$
(8)

where dot represents derivative with respect to cosmic time \(t\). It is assumed that the universe is filled with perfect fluid

$$ T_{\mu\nu}=(\rho+ p)u_{\mu}u_{\nu}-pg_{\mu\nu}, $$
(9)

where \(u_{\mu}\) is the usual four-velocity vector and \(\rho\), \(p\) denote the energy density and pressure of the universe respectively. The volume scale factor \(V\) and the average scale factor \(a\) for LRS Bianchi \(I\) spacetime are given by

$$ V=AB^{2},\quad \quad a=\sqrt[3]{AB^{2}}. $$
(10)

The average Hubble parameter \(H\) is defined as

$$ H=\frac{1}{3} \biggl(\frac{\dot{A}}{A}+\frac{2\dot{B}}{B}\biggr). $$
(11)

The expansion scalar \(\theta\) and shear scalar \(\sigma\) are given by

$$\begin{aligned} &\theta = u^{\mu}_{;\mu}=\frac{\dot{A}}{A}+2 \frac{\dot{B}}{B}, \end{aligned}$$
(12)
$$\begin{aligned} &\sigma^{2} = \frac{1}{2}\sigma_{\mu\nu} \sigma^{\mu\nu} =\frac{1}{3} \biggl[\frac{\dot{A}}{A}- \frac{\dot{B}}{B} \biggr]^{2}, \end{aligned}$$
(13)

where

$$ \sigma_{\mu\nu}=\frac{1}{2} \bigl(u_{\mu;\alpha}h^{\alpha}_{\nu}+u_{\nu;\alpha }h^{\alpha}_{\mu}\bigr) -\frac{1}{3}\theta h_{\mu\nu}, $$
(14)

\(h_{\mu\nu}=g_{\mu\nu}-u_{\mu}u_{\nu}\) is known as the projection tensor. It is well known that first four time derivatives of position are termed as velocity, acceleration, jerk and snap. In a cosmology, apart from Hubble parameter, we can define some important quantities like the deceleration, jerk, and snap parameters as

$$\begin{aligned} q=-\frac{1}{H^{2}}\frac{\ddot{a}}{a},\quad \quad j=\frac{1}{H^{3}} \frac{\dddot{a}}{a},\quad \quad s=\frac{1}{H^{4}}\frac{\ddot{\ddot{a}}}{a}. \end{aligned}$$
(15)

Now using Eq. (6), the field equations (3) take the form

$$\begin{aligned} &2\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}^{2}}{B^{2}}-24\frac{\dot{A}\dot{B}^{2}}{AB^{2}}\dot{{f_{G}}}+Gf_{G}-f=\kappa\rho, \end{aligned}$$
(16)
$$\begin{aligned} &{}-2\frac{\ddot{B}}{B}-\frac{\dot{B}^{2}}{B^{2}}+16\frac{\dot{B}\ddot{B}}{B^{2}}\dot{{f_{G}}}+8\frac{\dot{B}^{2}}{B^{2}}\ddot{{f_{G}}}-Gf_{G}+f=\kappa p, \end{aligned}$$
(17)
$$\begin{aligned} &{}-\frac{\ddot{A}}{A}-\frac{\ddot{B}}{B}-\frac{\dot{A}\dot{B}}{AB}+8 \biggl(\frac{\dot{A}\ddot{B}}{AB}+\frac{\dot{B}\ddot{A}}{BA} \biggr)\dot{{f_{G}}}+ 8\frac{\dot{A}\dot{B}}{AB}\ddot{{f_{G}}}-Gf_{G} \\ &\quad{} +f=\kappa p. \end{aligned}$$
(18)

These are complicated and highly non-linear differential equations with five unknowns. Thus, some additional constraints are required to solve these equations. A physical condition that shear scalar \(\sigma\) is proportional to expansion scalar \(\theta\) can be used to give

$$ A=B^{n}, $$
(19)

where \(n\) belongs to the set of real numbers. This assumption is physically important as the recent observations of the velocity red-shift relation for extragalactic sources indicate that the expansion of universe can achieve isotropy if \(\frac{\sigma}{\theta }\) is constant (Kantowski and Sachs 1966). Collins (1977) provided the physical significance of this condition for perfect fluid with barotropic EoS. In literature (Xing-Xiang 2005; Thorne 1967; Collins and Hawking 1973; Roy and Banerjee 1995; Bali and Kumawat 2008; Sharif and Zubair 2010), many authors have used this condition to explore the solutions of field equations. Thus using Eq. (19), field equations (16)–(18) take the form

$$\begin{aligned} &(1+2n)\frac{\dot{B}^{2}}{B^{2}}-24n\frac{\dot{B}^{3}}{B^{3}}\dot{{f_{G}}}+Gf_{G}-f = \kappa\rho, \end{aligned}$$
(20)
$$\begin{aligned} &-2\frac{\ddot{B}}{B}-\frac{\dot{B}^{2}}{B^{2}}+16\frac{\dot{B}\ddot{B}}{B^{2}}\dot{{f_{G}}}+8\frac{\dot{B}^{2}}{B^{2}}\ddot{{f_{G}}}-Gf_{G}+f = \kappa p, \end{aligned}$$
(21)
$$\begin{aligned} &-(n+1)\frac{\ddot{B}}{B}-n^{2}\frac{\dot{B}^{2}}{B^{2}}+8 \biggl(2n\frac{\dot{B}\ddot{B}}{B^{2}}+n(n-1)\frac{\dot{B}^{3}}{B^{3}} \biggr)\dot{{f_{G}}} \\ &\quad {}+8n\frac{\dot{B}^{2}}{B^{2}}\ddot{{f_{G}}}-Gf_{G}+f=\kappa p. \end{aligned}$$
(22)

Now we investigate the solutions of these field equations.

3 Solutions for the power law \(f(G)\) model

We consider the \(f(G)\) model as

$$\begin{aligned} f(G)=\alpha G^{m+1}, \end{aligned}$$
(23)

where \(\alpha\) and \(m\) are arbitrary constants. This model has already been proposed by Cognola et al. (2006) and it is interesting because the Big-Rip singularity may not appear. Also, this model is compatible with the observational data and predicts the existence of a transient phantom epoch. The viability of this model has already been shown in cosmological contexts (Cognola et al. 2008; Felice and Tsujikawa 2009; Bamba et al. 2010). Moreover, this model belongs to the general class of the models without the irregular spin-2 ghosts (Tsujikawa 2010). Subtraction of Eqs. (21) and (22) yields

$$ \frac{\ddot{B}}{B}+(n+1)\frac{\dot{B}^{2}}{B^{2}}-8 \biggl(2 \frac{\dot{B}\ddot {B}}{B^{2}}+n\frac{\dot{B}^{3}}{B^{3}} \biggr)\dot{{f_{G}}}- 8 \frac{\dot{B}^{2}}{B^{2}}\ddot{{f_{G}}}=0. $$
(24)

It follows from Eq. (23),

$$\begin{aligned} f_{G}(G)=\alpha(m+1)G^{m}. \end{aligned}$$
(25)

Without loss of any generality, we choose \(\alpha=\frac{1}{m+1}\) so that Eq. (24) takes the form

$$\begin{aligned} &\frac{\ddot{B}}{B}+(n+1)\frac{\dot{B}^{2}}{B^{2}}-8 mG^{m}\biggl[ \biggl(2\frac {\dot{B}\ddot{B}}{B^{2}}+n\frac{\dot{B}^{3}}{B^{3}} \biggr)\frac{\dot{G}}{G} \\ &\quad {}-\frac{\dot{B}^{2}}{B^{2}} \biggl((m-1){\frac{\dot{G}^{2}}{G^{2}}}+\frac{\ddot{G}}{G} \biggr)\biggr]=0. \end{aligned}$$
(26)

It is worth mentioning here that many solutions can be found using this equation. Here we investigate two type of solutions.

3.1 Power law solutions

Now we consider the power law form, i.e.

$$ B(t)=\gamma t^{k} $$
(27)

where \(\gamma\) and \(k\) are arbitrary constants. Using this in Eq. (26), we obtain a constraint equation

$$\begin{aligned} &t^{2}(kn+2k-1)+32mk \bigl[8nk^{3}(kn+2k-3)\bigr]^{m}(32kn \\ &\quad {}+64k-96-128m)=0. \end{aligned}$$
(28)

This equation is satisfied for \(k=\frac{1}{n+2}\) such that

$$ m(2m+1)=0. $$
(29)

Thus, corresponding to two roots of this equation, we obtain two choices of \(f(G)\) models

$$ f(G)=G+c_{1},\quad \quad f(G)=2\sqrt{G}+c_{2}, $$
(30)

where \(c_{1}\) and \(c_{2}\) are integration constants. The first model becomes trivial for \(c_{1}=0\). The second model with square root term is important as it leads to a viable inflation in the presence of massive scalar field (Myrzakul et al. 2015). Thus, the solution metric takes the form

$$ ds^{2}=dt^{2}-\gamma^{2n}t^{\frac{2n}{n+2}}d{x}^{2}- \gamma^{2}t^{\frac {2}{n+2}} \bigl(d{y}^{2}+d{z}^{2} \bigr). $$
(31)

Using Eqs. (20)–(22), the expressions for energy density and pressure of universe turn out to be

$$\begin{aligned} &\rho=\frac{t^{2}(m+1)(2n^{2}+5n+2)\!+\!16mn(5+6m)(\frac{-16n}{t^{4}(n+2)^{3}})^{m}}{t^{4}(m+1)(n+2)^{3}\kappa}, \end{aligned}$$
(32)
$$\begin{aligned} &p=\frac{1}{t^{4}(m+1)(n+2)^{3}\kappa} \biggl[t^{2}(m+1)\bigl(2n^{2}+5n+2 \bigr) \\ &\phantom{p=} +16 \biggl(\frac{-16n}{t^{4}(n+2)^{3}}\biggr)^{m}\bigl(m^{2}n^{2}+mn^{2}+4m^{3}n+7mn \\ &\phantom{p=} +10m^{2}n+8m^{3}+12m^{2}+4m\bigr) \biggr]. \end{aligned}$$
(33)

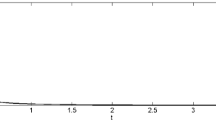
It is evident from Eqs. (32) and (33) energy density and pressure of the universe is defined for \(-\infty< n<-2\) and \(-2< n<0\) for \(m=-1/2\). The behaviour of energy density and pressure of universe can be seen from Fig. 1 for the model \(f(G)=\sqrt{G}\) with \(-2< n<0\). The Ricci scalar and GB invariant for this solution turn out to be

$$ R=\frac{2(2n+1)}{(n+2)^{2}t^{2}},\quad \quad G=-\frac{16n}{(n+2)^{3}t^{4}}. $$
(34)

The average Hubble parameter, average scale factor and volume scale factor of universe take the form

$$ H=\frac{1}{3t},\quad \quad a=\gamma^{\frac{n+2}{3}}t^{\frac{1}{3}},\quad \quad V= \gamma^{n+2}t. $$
(35)

The redshift for a distant source is directly related to the scale factor of the universe at the time when the photons were emitted from the source. The scale factor \(a\) and redshift \(z\) are related through the equation

$$ a=\frac{a_{0}}{1+z}, $$
(36)

where \(a_{0}\) is the present values of the scale factor. Using Eq. (35), we get

$$ \frac{H}{H_{0}}=\frac{t_{0}}{t},\quad \quad \frac{a_{0}}{a}=1+z=\biggl(\frac{t_{0}}{t} \biggr)^{\frac{1}{3}}, $$
(37)

where \(H_{0}\) is the present values of Hubble’s parameter. Thus the value of Hubble’s parameter in terms of redshift parameter turns out to be

$$ H=H_{0}(1+z)^{3}. $$
(38)

The deceleration, jerk and snap parameters become

$$ q=2,\quad \quad j=10,\quad \quad s=-80. $$
(39)

The expansion scalar and shear scalar turn out to be

$$ \theta=\frac{1}{t},\qquad\sigma^{2}= \frac{1}{3} \biggl[\frac {(n-1)}{(n+2)t} \biggr]^{2}. $$
(40)

The isotropy condition \(\frac{\sigma^{2}}{\theta}\rightarrow0\) as \(t\rightarrow\infty\), is also satisfied in this case. It is also observed from Eqs. (35) and (40) that the spatial volume is zero at \(t=0\) while the expansion scalar is infinite, which suggests that the universe starts evolving with zero volume at \(t=0\), i.e. big bang scenario. It is further observed that the average scale factor is zero at the initial epoch \(t=0\) and hence the model has a point type singularity (MacCallum 1971). Figure 2a shows the behaviour of EoS parameter \(\omega\) for \(-2< n<0\). It can be seen that \(\omega\) possesses negative values as well. It would be worthwhile to mention here that the phantom like dark energy is found to be in the region where \(\omega<-1\). The universe with phantom dark energy ends up with a finite time future singularity known as cosmic doomsday or big rip (Starobinsky 2000; Caldwell 2002). The behaviour of isotropy condition can be observed from Fig. 2b. The value of \(\frac{\sigma ^{2}}{\theta}\) decreases as the time goes on. It is also evident that energy \(\frac{\sigma^{2}}{\theta}\rightarrow0\) for small values of \(n\) even when \(t\) is not very large. This indicates that transition to isotropy is also possible for some suitable values of \(n\) and \(t\) (other than \(\infty\)). Now we discuss some special cases.

Fig. 1
figure 1

Behaviour of energy density and pressure for \(m=-1/2\)

Full size image
Fig. 2
figure 2

Behaviour of \(\omega\) for \(m=-1/2\) and isotropy parameter \(\frac{\sigma^{2}}{\theta}\)

Full size image

Case I: Flat FRW Solution

For a special case when \(n=1\), and \(m=-\frac{1}{2}\), space-time (31) takes the form

$$ ds^{2}=dt^{2}-\gamma^{2}t^{\frac{2}{3}} \bigl(d{x}^{2}+d{y}^{2}+d{z}^{2} \bigr), $$
(41)

which is the solution of well-known flat FRW metric. Using Eqs. (32) and (33), EoS parameter becomes

$$ \omega=\frac{115}{67}+i\frac{6\sqrt{3}}{67}. $$
(42)

The imaginary value of \(\omega\) indicates that the model \(f(G)=\sqrt{G}\) is not viable for flat FRW solution. However, for \(m= 0\), the solution is valid with \(\omega=1\) describing the stiff fluid universe (Mathew et al. 2014).

Case II: Kasner Type Solution

Putting \(n=-{1/2}\) in Eq. (31), it follows that

$$ ds^{2}=dt^{2}-\gamma^{-1}t^{-\frac{2}{3}}d{x}^{2}- \gamma^{2}t^{\frac {4}{3}} \bigl({y}^{2}+d{z}^{2} \bigr). $$
(43)

After redefining the parameters, it is exactly the same as the well-known Kasner’s metric (Cataldo and Campo 2000). Here EoS parameter takes the form

$$ \omega=-\frac{24m^{2}+29m+3}{2(6m+5)}. $$
(44)

For \(m=0\), \(\omega=-0.3\) describing accelerated expansion of universe (Hogan 2007; Corasaniti et al. 2004; Weller and Lewis 2003). Moreover, when \(m=-1/2\), EoS parameter has positive value \(\omega=1.375\). It has been shown that EoS parameter can be positive due to classical and the quantum mechanical contributions (Kim and Yoon 2007).

Now we consider one more specific \(f(G)\) model to get an idea how the solutions depend on the choice of \(f(G)\) model. We assume \(f(G)= \alpha G^{0.5}+\beta G^{m}\), where \(\alpha\) and \(\beta \) are arbitrary constants. This model has already been discussed by Nojiri et al. (2010). Moreover, this choice of \(f(G)\) model allows exact power law solutions for \(m <3/2\) (Goheer et al. 2009). Late time accelerating universe is also indicated when \(m>1\) (Nojiri et al. 2008). Here we discuss only the power law solution for the sake of comparison. Thus for \(f(G)= \alpha G^{0.5}+\beta G^{m}\), Eq. (24) yields a solution

$$ B(t)=\gamma t^{2/3},\quad \quad n=-1/2, $$
(45)

with the constraint equation

$$ 2m^{2}-3m+1=0. $$
(46)

Thus, corresponding to two roots of this equation, we obtain two choices of \(f(G)\) models

$$ f(G)=\alpha G^{0.5}+\beta G,\quad \quad f(G)=(\alpha+ \beta)G^{0.5}. $$
(47)

So many solutions can be reconstructed using different values of \(n\) and hence different choices of \(f(G)\) model are obtained. Obviously, one can work out the physical parameters like energy density, pressure etc. for this solution.

3.2 Exponential law solutions

It is noticed that Eq. (26) have an exponential solution of the form

$$ B(t)=e^{c_{3}t+c_{4}}, $$
(48)

where \(c_{3}\) and \(c_{4}\) are arbitrary constants. Here EoS parameter becomes

$$ \omega=-\frac{1}{2} \biggl[\frac{(m+1)(n^{2}+n+4)+16mn(n+2)(8n^{2}+16n)^{m}}{(m+1)(2n+1)+8mn(n+2)(8n^{2}+16n)^{m}} \biggr]. $$
(49)

It is mentioned here that the exponential solution is satisfied with the constraint equation

$$ n+2=0. $$
(50)

The solutions metric for this case turns out to be

$$ ds^{2}=dt^{2}-e^{-4(c_{3}t+c_{4})}dx^{2}-e^{2(c_{3}t+c_{4})} \bigl(dy^{2}+dz^{2} \bigr). $$
(51)

The average Hubble parameter is be zero for this solution. All other dynamical parameters expansion scalar \(\theta\), shear scalar \(\sigma\), volume scale factor of universe are constant here. EoS parameter involving energy density and pressure of the universe becomes independent of the parameter \(m\) and we get \(\omega=1\). The Ricci scalar is also constant

$$ R=-6{c_{3}}^{2}, $$
(52)

while GB invariant is zero here.

4 Summary and conclusion

This paper is devoted to investigate \(f(G)\) gravity with anisotropic background by finding the exact solutions of field equations. For this purpose, LRS Bianchi type \(I\) space-time is chosen. To our knowledge, this is the first attempt to explore the exact solutions for LRS Bianchi type \(I\) space-time. Highly nonlinear and complicated nature of the field equations restrict us to take the assumption that the shear scalar \(\sigma\) is proportional to the expansion scalar \(\theta\). This implies \(A=B^{n}\), where \(A\), \(B\) are the metric coefficients and \(n\) is an arbitrary constant. A brief summary and conclusion of the work is as follows:

  • In this work, we have considered a power law \(f(G)\) gravity model already available in literature (Cognola et al. 2006). This model is interesting because the chances of appearing Big-Rip singularity vanish. Moreover, it is compatible with the observational data predicting the existence of a transient phantom epoch. The viability of this model has already been shown in cosmological contexts (Cognola et al. 2008; Felice and Tsujikawa 2009; Bamba et al. 2010). Using this model, we have developed a general differential equation (26) which can be used to explore many solutions. Mainly we have explored the solutions of modified field equations using power law and exponential forms of metric coefficients.

  • The metric coefficients involve anisotropy parameter \(n\) for power law solution. Two \(f(G)\) gravity models are associated with this solution. The first model becomes trivial case when \(c_{1}=0\). However, the second model involves square root of GB invariant which seems more important as it leads to a viable inflation in the presence of massive scalar field (Myrzakul et al. 2015). The graphical analysis indicates that EoS parameter \(\omega\) also possesses negative values for \(-2< n<0\). It would be worthwhile to mention here that the phantom like dark energy is found to be in the region where \(\omega< -1\).

  • It can be seen from Eqs. (34) and (35) that when \(t\) is large, Ricci scalar, GB invariant and Hubble parameter approach to zero. Thus the universe becomes asymptotically flat in this case. Moreover, the solution metric (31) becomes singular at \(t=0\) for \(n<-2\). Further, Fig. 1b suggests that pressure of universe for \(n=-1/2\) falls down from infinity and gets uniform as the time goes. On the other hand, for some other value of anisotropy parameter \(n\), the behavior of pressure seems different. Also the curvature is very large at initial epoch. Thus, the solutions involving square root GB term suggests an early universe with anisotropic inflation.

  • Two special cases are discussed for power law solution. The first case corresponds to flat FRW spacetime. The solution is valid with \(\omega=1\) describing the stiff fluid universe for the first model. However, the solutions is not physical for the second model as \(\omega\) is imaginary. The second case provides the well-known Kasner’s universe and it gives the value of anisotropy parameter \(n=-1/2\).

  • Another specific model \(f(G)= \alpha G^{0.5}+\beta G^{m}\) is considered to get an idea how the solutions depend on the choice of \(f(G)\) model. This model has already been discussed by Nojiri et al. (2010). Moreover, this choice of \(f(G)\) model allows exact power law solutions for \(m <3/2\) (Goheer et al. 2009). Only the power law solutions are discussed for the sake of comparison. It is concluded that solutions provide two \(f(G)\) models, one includes linear and square root GB invariant terms.

  • The second family of solutions is obtained by exponential law assumption. It gives the average Hubble parameter zero and all other dynamical parameters like expansion scalar \(\theta\), shear scalar \(\sigma\), volume scale factor of universe constant. EoS parameter is independent of the parameter \(m\) for this solution and we get \(\omega= 1\). The Ricci scalar is constant while GB invariant is zero in this case. Thus the universe is asymptotically the de-Sitter space corresponding to an accelerating universe. Moreover, this family presents singularity free solutions.