1 Introduction

Self-gravitation is the most important phenomenon in the study of general relativity and astrophysics. Without it, stars and clusters of galaxies will dissipate through continuous expansion of matter. In self-gravitating compact objects (CO) disruption of physical parameters, like density, mass, pressure can cause expansion or collapse of relativistic objects and hence it is important to discuss such issues carefully. The study of compact stars is a hot topic not only in general relativity but also in modified theories such as \(f(T)\) (Abbas et al. 2015) and \(f(R)\) (Zubair and Abbas 2014).

The neutron stars PSR J1614-2230 (Demorest et al. 2010) and PSR J1930+327 (Freire et al. 2011) are millisecond pulsars lies in the categories of stars whose masses have been found accurately. The composition of these stars consists of the densest material exist in this universe. The radii of these stars depend upon the equation of state (EoS) i.e., how physical variables are related to each other. This relationship may be linear, quadratic, cubic etc., depends upon the model under consideration. Further, it is observed that X-ray pulsars Vela X-1, SMC X-1 and Cen X-3 with stellar companions also lies in the class of self-gravitating compact stars (Rawls et al. 2011). An X-ray pulsar composed of a neutron star in a magnetic field. This magnetic field is measured to be \(10^{8}\) Tesla that give rise to gravitation force and attract the material from its neighboring atmosphere. All this scenario gives rise to the continuous change in physical variables like density, tangential and radial pressure.

The systems of above mention neutron stars and X-ray pulsars needs to be analyze for their stability. Models of compact stars are inadequate if they are unstable against perturbation in physical variables, which can leads toward the collapse of CO. It is necessary to investigate the stability of the models for their physically validity and the important technique to do this, is cracking/overturning of CO. The initial contribution toward the stability of gravitating sphere through the criterion of adiabatic was provided by Bondi (1964). Chandrasekhar (1964) evolved the idea of Bondi and developed the formalism in this context. The idea of cracking was introduced by Herrera (1992). He discussed the concept of cracking/overturning in the study of self-gravitating objects when equilibrium state is disturbed due to change in sign of radial forces. The cracking is trigger due to change in local anisotropy of fluid or incoherent emission. Di Prisco et al. (1994) developed necessary condition for the cracking phenomenon. After few years, Herrera and Varela (1997) present the criterion of overturning for non-spherical systems. He and his coworkers presents a more recent approach by taking account anisotropic fluids with two barotropic EoS, i.e., \(p_{r}=p_{r}(\rho)\) and \(p_{t}=p_{t}(\rho)\) (Di Prisco et al. 1994). They emphasis on the effect of constant density perturbation and introduce the terms of radial and tangential sound speeds. These terms have drastic effect towards change in sign on radial forces and hence on the stability of CO (Di Prisco et al. 1997). Sharif and Azam (2012, 2013) have discussed the stability of stars in spherical and cylindrical symmetries.

In our present work we refine the idea of density perturbation by considering it effects locally i.e., non-constant density perturbation. We applied this technique to compact relativistic bodies with linear barotropic EoS (Takisa and Maharaj 2013). The radial pressure and energy density are associated with a linear relationship. The model selected here was presented by Takisa et al. (2014), that is compatible with observational values presented by Gangopadhyay et al. (2013). We use this model to study the stability of newly discovered CO PSR J1614-2230, PSR J1903+327, Vela X-1, SMC X-1, Cen X-3 (Gangopadhyay et al. 2013).

This paper is arranged as follows: In Sect. 2, Einstein field equations and hydrostatic EoS for the model is presented. Section 3 is devoted to local density perturbations to all physical variables and in Sect. 4 stability of stars is discussed. In the last section, we conclude our results.

2 The field equations and conventions

The line element for the static spherically symmetric space time is given by

$$\begin{aligned} ds^{2}=-e^{2 \nu(r)}dt^{2} +e^{2 \lambda(r)}dr^{2}+r^{2} \bigl(d\theta^{2}+ \sin^{2}\theta{d\phi^{2}}\bigr). \end{aligned}$$
(1)

The energy-momentum tensor for an anisotropic sphere is defined by

$$\begin{aligned} T^{ab}=\mathrm{diag}(-\rho, p_{r}, p_{t},p_{t}), \end{aligned}$$
(2)

where \(0\leq{\theta}\leq{\pi},\ 0\leq{\phi}<{2\pi}\), \(\rho\) represents energy density, \(p_{r}\) is the radial pressure and \(p_{t}\) is the tangential pressure of the fluid. The matter distribution of star should satisfy a barotropic EoS to grantee physically realistic star and linear EoS is given by (Takisa and Maharaj 2013)

$$\begin{aligned} p_{r}=\alpha\rho-\beta, \end{aligned}$$
(3)

where \(\beta=\alpha\rho_{\varepsilon}\). The constant \(\alpha\) is constrained by sound speed condition and \(\rho_{\varepsilon}\) gives the density at the surface \(r=\varepsilon\) (Takisa et al. 2014). For static anisotropic matter with line element (1), we have the following Einstein field equations

$$\begin{aligned} & \frac{1}{r^{2}}+e^{-2 \lambda}\biggl(2\frac{\lambda^{\prime}}{r}- \frac{1}{r^{2}}\biggr)=8\pi\rho, \end{aligned}$$
(4)
$$\begin{aligned} & \frac{1}{r^{2}}-e^{-2 \lambda}\biggl(2\frac{\nu^{\prime}}{r}+ \frac{1}{r^{2}}\biggr)=-8\pi p_{r}, \end{aligned}$$
(5)
$$\begin{aligned} & e^{-2 \lambda}\biggl(\frac{\lambda^{\prime}}{r}-\frac{\nu^{\prime}}{r} - \nu^{\prime\prime}+\nu^{\prime}\lambda^{\prime}-\bigl( \nu^{\prime}\bigr)^{2}\biggr)=-8\pi{p_{t}}, \end{aligned}$$
(6)

where “′” denotes the derivative with respect to \(r\). Here, we assume that the system under consideration is in equilibrium. Equations (4)–(6) yields

$$\begin{aligned} \frac{dp_{r}}{dr}=\frac{2(p_{t}-p_{r})}{r}-{(\rho + p_{r} )} { \nu^{\prime}}. \end{aligned}$$
(7)

Using the relation \(e^{-2 \lambda(r)}=1-2m/r\) in the above equation (Mehra 1966), we obtain the main hydrostatic equilibrium equation for anisotropic fluid, which is used to explore cracking of CO given by

$$\begin{aligned} R=-\frac{dp_{r}}{dr}+\frac{2(p_{t}-p_{r})}{r}- {( \rho + p_{r} )} {\frac{m+4\pi r^{3} p_{r}}{r^{2}-2mr}}, \end{aligned}$$
(8)

where the mass function is defined as

$$\begin{aligned} m =4\pi\int^{r}_{0} \rho(x)x^{2}dx. \end{aligned}$$
(9)

3 Localized density disruption

In this section, we will see the effects of density perturbations \(\delta \rho\) with two barotropic EoS \(p_{r}=p_{r}(\rho)\) and \(p_{t}=p_{t}(\rho)\). It can be noted from Eq. (8) that cracking take place in the inner part of the sphere when equilibrium is disturbed due to change in sign of disruption force i.e., \(\delta R <0 \rightarrow \delta R >0\) and viceversa. The density disruption causes perturbation in all variables and their derivatives and consequently the hydrostatic equilibrium is disturbed. We perturb all the physical variables through density perturbation is given by

$$\begin{aligned} &{p_{r} (\rho+\delta\rho)=p_{r} (\rho)+ \frac{dp_{r}}{d\rho}\delta\rho,} \end{aligned}$$
(10)
$$\begin{aligned} &{\frac {dp_{r} }{dr}(\rho+\delta\rho)=\frac {dp_{r} }{dr}(\rho) + \biggl[\frac{d}{dr} \biggl(\frac{dp_{r}}{d\rho} \biggr) + \frac{dp_{r}}{d\rho} \frac{d^{2} \rho}{d r^{2}} \frac{1}{ \frac{d \rho}{d r}} \biggr]\delta\rho,} \\ \end{aligned}$$
(11)
$$\begin{aligned} &{p_{t} (\rho+\delta\rho)=p_{t} (\rho)+ \frac{dp_{t}}{d\rho}\delta\rho,} \end{aligned}$$
(12)
$$\begin{aligned} &{m(\rho+\delta\rho)=m (\rho)+\frac{dm}{d\rho}\delta\rho.} \end{aligned}$$
(13)

We define the radial sound speed \({v^{2}_{r}}\) and tangential sound speed \({v^{2}_{t}}\) as

$$\begin{aligned} & {v^{2}_{r}}=\frac{dp_{r}}{d\rho}, \end{aligned}$$
(14)
$$\begin{aligned} & {v^{2}_{t}}=\frac{dp_{t}}{d\rho}. \end{aligned}$$
(15)

The perturb form of Eq. (8) is given by

$$\begin{aligned} R = R_{0}\bigl(\rho,p_{r},~ p_{r}^{\prime},~ p_{t},~m\bigr)+\delta{R}, \end{aligned}$$
(16)

where

$$\begin{aligned} \delta R =& \frac{\partial R}{\partial\rho}\delta\rho + \frac{\partial R}{\partial p_{r}}\delta p_{r}+ \frac{\partial R}{\partial p_{r}^{\prime}}\delta p_{r}^{\prime}+ \frac{\partial R}{\partial p_{t}}\delta p_{t} +\frac{\partial R}{\partial{m}}\delta{m}. \end{aligned}$$
(17)

Using density perturbation to the above equation, we have

$$\begin{aligned} \frac{\delta R}{\delta \rho} =& \frac{\partial R}{\partial\rho} + \frac{\partial R}{\partial p_{r}}{v^{2}_{r}}+ \frac{\partial R}{\partial p_{r}^{\prime}}\bigl({v^{2}_{r}}^{\prime}+{v^{2}_{r}} \rho^{\prime\prime}\bigl({\rho}^{\prime}\bigr)^{-1}\bigr) \\ &{} + \frac{\partial R}{\partial p_{t}}{v^{2}_{t}}^{\prime}+ \frac{\partial R}{\partial m}\bigl(4 \pi r^{2} \rho \bigl({\rho}^{\prime}\bigr)^{-1}\bigr). \end{aligned}$$
(18)

The derivatives involve in (18) are given by

$$\begin{aligned} &{\frac{\partial R}{\partial\rho}=-\frac{m+4\pi r^{3} p_{r}}{r^{2}-2 m r},} \end{aligned}$$
(19)
$$\begin{aligned} &{\frac{\partial R}{\partial m}=-\frac{(\rho+p_{r})(4r^{2}-16\pi r^{4} p_{r})}{(2r^{2}-4 m r)^{2}},} \end{aligned}$$
(20)
$$\begin{aligned} &{\frac{\partial R}{\partial p_{r}}=-\frac{2}{r}-\frac{2m+16 \pi r^{3} p_{r}+8\pi r^{3}\rho}{2r^{2}-4mr},} \end{aligned}$$
(21)
$$\begin{aligned} &{\frac{\partial R}{\partial p_{t}}=\frac{2}{r},} \end{aligned}$$
(22)
$$\begin{aligned} &{\frac{\partial R}{\partial p_{r}^{\prime}}=-1.} \end{aligned}$$
(23)

It is mentioned here that Eq. (18) serve as the main equation for local density perturbation.

4 The model

We apply the concept of cracking by using Eq. (18) to model given by Takisa et al. (2014). It is defined as

$$\begin{aligned} &{\rho=\frac{2b(3+ar^{2})-sa^{2}r^{4}}{16\pi(1+ar^{2})^{2}},} \end{aligned}$$
(24)
$$\begin{aligned} &{p_{r}=\alpha\frac{2b(3+ar^{2})-sa^{2}r^{4}}{16\pi(1+ar^{2})^{2}}-\beta,} \end{aligned}$$
(25)
$$\begin{aligned} &{p_{t}=p_{r}+\Delta,} \end{aligned}$$
(26)
$$\begin{aligned} &{8\pi \Delta =\frac{-b}{1+ar^{2}}-\frac{-b(1+5\alpha)}{(1+\alpha)(1+ar^{2})^{2}}} \\ &{\hphantom{8\pi \Delta ={}} + \frac{2\beta}{1+\alpha}+\frac{r^{2}[1+(a-b)r^{2}]}{(1+ar^{2})}} \\ &{\hphantom{8\pi \Delta ={}}\times \biggl\{ \frac{4a^{2}t(t-1)}{(1+ar^{2})^{2}}+\frac{8a(a-b)tn}{(1+ar^{2}) [1+(a-b)r^{2}]}} \\ &{\hphantom{8\pi \Delta ={}}+ \frac{4(a-b)^{2} n (n-1)}{[1+(a-b)r^{2}]^{2}}} \\ &{\hphantom{8\pi \Delta ={}}- \frac{a[s(1+\alpha)+2\beta](a(t+n)[1+(a-b)r^{2}]-b n)}{(a-b)(1+ar^{2})[1+(a-b)r^{2}]}} \\ &{\hphantom{8\pi \Delta ={}}+\frac{a^{2}[s(1+\alpha)+2\beta]^{2}}{16(a-b)^{2}} \biggr\} } \\ &{\hphantom{8\pi \Delta ={}}- \frac{4[1+ar^{2}(2+(a-b)r^{2})]-b(5+\alpha)r^{2}}{4(a-b)(1+\alpha)(1+ar^{2})^{3} [1+(a-b)r^{2}]}} \\ &{\hphantom{8\pi \Delta ={}} \times \bigl[-8b^{2}n+a^{3}r^{2} \bigl(-8(t+n)} \\ &{\hphantom{8\pi \Delta ={}}+ \bigl[s(1+\alpha)+2\beta\bigr]r^{2}\bigr)+a^{2} \bigl(8(t+n) \bigl(2br^{2}-1\bigr)} \\ &{\hphantom{8\pi \Delta ={}}+\bigl[s(1+\alpha)+2\beta\bigr] \bigl(2-br^{2}\bigr)r^{2}\bigr)} \\ &{\hphantom{8\pi \Delta ={}}+ a\bigl(-8 b^{2}(t+n)r^{2}+\bigl[s(1+\alpha)+2\beta \bigr]} \\ &{\hphantom{8\pi \Delta ={}}+ b\bigl(8t+16n-\bigl[s(1+\alpha)2+\beta\bigr]r^{2}\bigr)\bigr) \bigr],} \end{aligned}$$
(27)

where

$$\begin{aligned} &{t=\frac{4b\alpha -(1+\alpha)s}{8 b},} \end{aligned}$$
(28)
$$\begin{aligned} &{n = \frac{1}{8b(a-b)^{2}} \bigl\{ a^{2}\bigl((1+\alpha)s-4 \alpha \beta\bigr)2ab^{2}(1+5\alpha)} \\ &{\hphantom{n ={}}+b^{2}\bigl(-2b(1+3 \alpha)+2\beta\bigr) \bigr\} .} \end{aligned}$$
(29)

For uncharged CO \((s=0)\) radial and tangential sound speed velocities are evaluated from Eqs. (25)–(26) as

$$\begin{aligned} &{{v^{2}_{r}}=\alpha,} \end{aligned}$$
(30)
$$\begin{aligned} &{{v^{2}_{t}} =\frac{1}{\alpha_{3}} \biggl\{ \frac{\alpha a b r}{4 \pi (1+ar^{2})^{2}} -\frac{\alpha a r (6b+2abr^{2})}{4 \pi (1+ar^{2})^{3}}} \\ &{\hphantom{{v^{2}_{t}} ={}}- \frac{1}{\pi} \biggl\{ \frac{a b r}{4 (1+ar^{2})^{2}} + \frac{a b r(1+5\alpha)}{2(1+\alpha) (1+ar^{2})^{3}}} \\ &{\hphantom{{v^{2}_{t}} ={}}+ \frac{r(1+(a-b)r^{2})\alpha_{2}}{4(1+ar^{2})}+\frac{r^{3}(a-b)\alpha_{2}}{4(1+ar^{2})}} \\ &{\hphantom{{v^{2}_{t}} ={}}- \frac{r^{3}a\alpha_{2}(1+(a-b)r^{2})}{4(1+ar^{2})^{2}}} \\ &{\hphantom{{v^{2}_{t}} ={}}+\frac{r^{2}(1+(a-b)r^{2})}{8 (1+ar^{2})} \biggl\{ -\frac{16 a^{3} t (t-1)r }{(1+ar^{2})^{3}}} \\ &{\hphantom{{v^{2}_{t}} ={}}-\frac{16a^{2} b(a-b)t n r}{(1+ar^{2})^{2}(1+(a-b)r^{2})}} \\ &{\hphantom{{v^{2}_{t}} ={}}-\frac{16ab(a-b)^{2}tnr}{(1+ar^{2})(1+(a-b)r^{2})^{2}} -\frac{16(a-b)^{3}n(n-1)r}{(1+(a-b)r^{2})^{3}}} \\ &{\hphantom{{v^{2}_{t}} ={}}-\frac{4a\beta (t+n)r}{(1+ar^{2})(1+(a-b)r^{2})^{2}}} \\ &{\hphantom{{v^{2}_{t}} ={}}+ \frac{4\beta ar\alpha_{1}}{(a-b)(1+ar^{2})^{2}(1+(a-b)r^{2})}} \\ &{\hphantom{{v^{2}_{t}} ={}}+ \frac{4\beta r\alpha_{1}}{(1+ar^{2})(1+(a-b)r^{2})} \biggr\} \biggr\} \biggr\} ,} \end{aligned}$$
(31)

where \(\alpha_{1}\), \(\alpha_{2}\) and \(\alpha_{3}\) are defined as

$$\begin{aligned} &{\alpha_{1}=a(t+n) \bigl(1+(a-b)r^{2}-bn \bigr)} \\ &{\alpha_{2}=\frac{4a^{2}t(t-1)}{(1+ar^{2})^{2}}+ \frac{8a b(a-b)tn}{(1+ar^{2})(1+(a-b)r^{2})}} \\ &{\hphantom{\alpha_{2}={}}\times \frac{4(a-b)^{2}n(n-1)}{(1+(a-b)r^{2})^{2}}} \\ &{\hphantom{\alpha_{2}={}}- \frac{2\alpha_{1} \beta }{(a-b)(1+ar^{2})(1+(a-b)r^{2})}+\frac{a^{2}\beta^{2}}{4(a-b)^{2}}} \\ &{\alpha_{3}=\frac{a b r}{4 \pi(1+ar^{2})^{2}}-\frac{3b+abr^{2})ar}{2\pi (1+ar^{2})^{3}}.} \end{aligned}$$

The constants \(a,~b\) have dimension of length \((L^{-2})\) and we choose

$$\begin{aligned} \alpha=0.33, \qquad a=\frac{53.34}{\Re^{2}},\qquad b=\frac{b_{1}}{\Re^{2}}, \end{aligned}$$

where \(\Re=43.245\ \mbox{km}\) and these values are compatible with the observational values (Takisa et al. 2014).

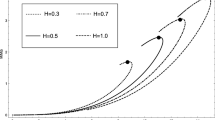
In order to observe cracking of different objects, we plot force distribution \(\frac{\partial R}{\partial\rho}\) against radius \(R\) for the objects which are as follows: PSR J1614-2230, PSR J1903+327, Vela X-1, SMC X-1 and Cen X-3. From the Figs. 1, 2, 3, 4 and 5, it is clear that SMC X-1 is the stable CO against local density perturbations. For CO under consideration the values of radii \(R_{c}\), where cracking take place are given in Table 1. Hence, at \(R_{c}\) force distribution changes its sign under the influence of local density perturbation. The above model obeys the following physical viable conditions

  • The energy density \(\rho\) of CO remain positive even after perturbation.

  • The radial pressure \(p_{r} \) vanishes at the boundary of star.

  • At \(r=0\), \(p_{r}=p_{t}= \Delta =0\).

  • \(v_{r}^{2}=\alpha>0\), is constant in the linear regime.

Fig. 1
figure 1

Cracking of PSR J1614-2230 in linear regime

Full size image
Fig. 2
figure 2

Cracking of PSR J1903+327 in linear regime

Full size image
Fig. 3
figure 3

Cracking of Vela X-1 in linear regime

Full size image
Fig. 4
figure 4

Cracking of SMC X-1 in linear regime

Full size image
Fig. 5
figure 5

Cracking of Cen X-3 in linear regime

Full size image
Table 1 Cracking of uncharged compact objects
Full size table

5 Conclusions and observations

We have used the model of Takisa et al. (2014) to check the cracking of CO in the linear regime. This model can be used to describe the observed CO PSR J1614-2230, PSR J1903+327, Vela X-1, SMC X-1 and Cen X-3. We have concluded that

  • \(v_{t}^{2}\) changes its sign from positive to negative as we move from center to the boundary of CO.

  • \(v_{t}^{2}>v_{r}^{2}\) up to \(10^{30}\) times.

  • PSR J1614-2230, PSR J1903+327, Vela X-1 and Cen X-3 shows cracking at \(R_{c}\) when perturbed.

  • SMC X-1 does not show any cracking and it is stable for local density perturbation.

  • The stability region for each stars exhibit cracking lies between \(r=0\) to \(r=R_{c}\).

The measurement of cracking radii \(R_{c}\) gives the strongest constraint of stability regions. The systems PSR J1614-2230, PSR J1903+327, Vela X-1 and Cen X-3 described by the model (Takisa et al. 2014) become ‘Potentially’ unstable due to variation in the physical variables. This stability analysis describes the sensitivity of radial forces towards local density perturbation and local anisotropy which can result in the collapse of star. In our model, the value of radial sound speed \({v^{2}_{r}}\) is always positive so overturning appears when the tangential sound speed \({v^{2}_{t}}\) counter it at \(R_{c}\).

The concept of cracking was presented by Herrera (1992) to narrate the behavior of fluid distribution just after departure from equilibrium. In this approach simultaneous and independent density disruptions may leads anisotropic matter configurations to show cracking (Di Prisco et al. 1994). In this pattern of density perturbation, constant density disruptions effect physical quantities like mass, tangential and radial pressure but leave unchanged pressure gradient.

In this work global (constant) density perturbation approach is modified by local (non-constant) density perturbations, which also effects pressure gradient and may leads towards cracking of anisotropic matter configurations. The presence of such phenomenon could badly effect the growth or decay of the system. If cracking does not take place in the system then it is potentially stable as in the case of SMC X-1, but if cracking take place system may suffer from collapse.