Schwarzschild-anti de Sitter black hole with quintessence

Abstract

In this paper, by using the effective potential for the photons, we analysis the null geodesics and all kinds of orbits corresponding to the energy levels for the Schwarzschild-anti de Sitter black hole surrounded by quintessence with $\omega_{q}= -\frac{2}{3}$ and compare our results with those obtained for the Schwarzschild black hole surrounded by quintessence matter. We also investigate the circular orbits and calculate the angle of deflection of the photons.

1 Introduction

The expansion of the Universe is a long-established fact and there are significant astronomical evidences that the Universe is expanding at an accelerating rate. The current cosmological observation predicts the existence of some form of energy which permeates all of space with a large negative pressure (Perlmutter et al. 1999; Riess et al. 1998, 1999; Spergel et al. 2007; Tegmark et al. 2004; Seljak et al. 2005), called dark energy which constitutes about 70 percent of the energy density of the Universe.

Dark energy is a complete mystery and the evidence for it is indirect and understanding the origin of this negative pressure is one of the biggest efforts in cosmology today. There are two proposed forms for dark energy. The first and the simplest explanation for dark energy is the cosmological constant (Padmanabhan 2003) with a constant equation of states ω _q =−1 and the second is the dynamical scalar field models such as quintessence (Carroll 1998), chameleon (Khoury and Weltman 2004), K-essence (Armendariz-Picon et al. 2000), tachyon (Padmanabhan 2002), phantom (Caldwell 2002) and dilaton (Gasperini et al. 2002). Basically, the difference between these models returns to the magnitude of ω _q which is the ratio of pressure to energy density of dark energy and for quintessence $-1<\omega_{q}<- \frac{1}{3}$. For more details about various models of dark energy see Fernando (2012).

Black holes surrounded by dark energy are believed to play the crucial role in cosmology. Quintessence as one candidate for the dark energy is defined as an ordinary scalar field coupled to gravity (Copeland et al. 2006). Kiselev (2003) by considering the Einstein’s field equations for a black hole charged or not and surrounded by quintessence, derived a new solution related to ω _q .

In the present work, we study the Schwarzschild-anti de Sitter black hole surrounded by quintessence matter by using the solution which obtained by Kiselev (2003) and also we analysis the geodesic structure of massless particles for this black hole and compare our results with those obtained for Schwarzschild black hole surrounded by quintessence matter which derived by Fernando (2012). By analyzing the moving particles and photons around the black hole, we can describe the gravitational field around the black hole. Studies the geodesic structure is one way to understanding the physical effects of the gravitational field and describing the effect of quintessence field on the geometry.

The outline of this paper is as follows: In Sect. 2, we briefly review the Schwarzschild-anti de Sitter black hole space-time surrounded by quintessence. In Sect. 3, we discuss the radial null geodesics structure. In Sect. 4, we use the variable change $u = \frac {1}{r}$ to analysis the geodesics. In Sect. 5, we study the deflection of light by the Schwarzschild-anti de Sitter black hole surrounded by quintessence, while a conclusion is given in Sect. 6.

2 Schwarzschild-anti de Sitter black hole space-time surrounded by quintessence

Kiselev (2003) derived a static spherically symmetric exact solution of Einstein equations for a black hole surrounded by the quintessence. The metric of the Schwarzschild-anti de Sitter black hole surrounded by quintessence can be written as (Kiselev 2003),

$$\begin{aligned} ds^{2}=-g(r) dt^{2}+g(r)^{-1} dr^{2}+ r^{2} d\varOmega^{2} \end{aligned}$$

(1)

where

$$\begin{aligned} g(r)=1-\frac{2 M}{r}- \frac{ \varLambda r^{2}}{3}-\frac{c}{r^{3\omega_{q}+1}} \end{aligned}$$

(2)

and

$$\begin{aligned} d\varOmega^{2}=d\theta^{2}+\sin^{2}\theta d \phi^{2} \end{aligned}$$

(3)

where M is the mass of the black hole and Λ is the cosmological constant. ω _q is the quintessential state parameter which has the range $-1<\omega_{q}<- \frac{1}{3}$ and c is the positive normalization factor dependent on $\rho_{q}=-\frac {c}{2}\frac{3 \omega_{q}}{r^{3(1+\omega_{q})}}$, and ρ _q is the density of quintessence which is always a positive. For more details see Kiselev (2003).

Fernando (2012) derived the geodesic structure of massless particles of the Schwarzschild black hole surrounded by quintessence matter for $\omega_{q}= -\frac{2}{3}$. In this paper, we are going to study the Schwarzschild-anti de Sitter black hole surrounded by quintessence in detail corresponds to the choice of $\omega_{q}= -\frac{2}{3}$, so that

$$\begin{aligned} g(r)=1-\frac{2 M}{r}- \frac{ \varLambda r^{2}}{3}-c r \end{aligned}$$

(4)

In this paper we only consider a case that,

$$\begin{aligned} \varLambda=\frac{1}{18} \frac{1-9Mc-\sqrt{-(6Mc-1)^{3}}}{M^{2}} \end{aligned}$$

(5)

then

$$\begin{aligned} &{g(r)=1-\frac{2 M}{r}- \frac{r^{2}(1-9Mc-\sqrt {-(6Mc-1)^{3}})}{54M^{2}} -c r} \end{aligned}$$

(6)

Therefore this metric for 6Mc<1 has two following horizons,

$$\begin{aligned} r_{\mathrm{in}} =& 3 M\biggl(-\frac{A}{2 B} +\frac{B-18 M^{2} c^{2}}{A B}+ \frac{6 M c}{B} \\ &{}+\frac{1}{2} I \sqrt{3}\biggl(\frac{A}{B}+\frac{2B-36 M^{2} c^{2}}{A B} \biggr)\biggr) \end{aligned}$$

(7)

$$\begin{aligned} r_{\mathrm{out}} =& 3 M\biggl(-\frac{A}{2 B} +\frac{B-18 M^{2} c^{2}}{A B}+ \frac{6 M c}{B} \\ &{}-\frac{1}{2} I \sqrt{3}\biggl(\frac{A}{B}+\frac{2B-36 M^{2} c^{2}}{A B} \biggr)\biggr) \end{aligned}$$

(8)

where

$$\begin{aligned} A =&\bigl(-54 M c+18 M c \sqrt{-(6 M c-1)^{3}}+4 \\ &{} -4 \sqrt{-(6 M c-1)^{3}}-216 M^{3} c^{3}+216 M^{2} c^{2}\bigr)^{\frac{1}{3}} \end{aligned}$$

(9)

and

$$\begin{aligned} B=-1+9Mc+\sqrt{-(6Mc-1)^{3}} \end{aligned}$$

(10)

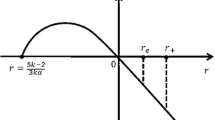
which r _out is the multiple root. Figure 1 shows the difference between horizons of the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter.

Fig. 1

Horizons of the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=1 and c=0.12

The Schwarzschild-anti de Sitter black hole surrounded by quintessence with above horizons has the Hawking temperature as,

$$\begin{aligned} T_{r_{\mathrm{in}},r_{\mathrm{out}}} =& \frac{1}{4\pi} \biggl|\frac{- 2 M}{r^{2}}+c \\ &{}+ \frac{1}{27}\frac{r(1-9Mc-\sqrt{-(6Mc-1)^{3}})}{M^{2}} \biggr|_{r=r_{\mathrm{in}, \mathrm{out}}} \end{aligned}$$

(11)

Temperature of the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter are shown in Fig. 2.

Fig. 2

Temperature of horizons for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter as a function of c with M=2

3 Radial null geodesics structure

Following Fernando (2012), the effective potential of the null geodesics can be written as

$$\begin{aligned} V_{\mathrm{eff}}=L^{2}\frac{g(r)}{r^{2}} \end{aligned}$$

(12)

The relation between energy and effective potential is defined as

$$\begin{aligned} \dot{r}^{2}+V_{\mathrm{eff}}=E^{2} \end{aligned}$$

(13)

In this section, we analysis the radial null geodesics structure in two state for angular momentum with L=0 and L≠0.

3.1 Null geodesics structure with L=0

From Fernando (2012) for a motion without angular momentum L=0, we have

$$\begin{aligned} \frac{dt}{dr}=\pm\frac{1}{g(r)} \end{aligned}$$

(14)

which for the Schwarzschild-anti de Sitter black hole surrounded by quintessence lead to

$$\begin{aligned} \frac{dt}{dr}=\pm\frac{1}{1-\frac{2 M}{r}-\frac{1}{54} \frac {r^{2}(1-9Mc-\sqrt{-(6Mc-1)^{3}})}{M^{2}}-c r} \end{aligned}$$

(15)

The coordinate time t as a function of r can be obtained by integrating the above equation as,

$$\begin{aligned} t=\pm54 M^{2}\sum_{R}\frac{R \ln(r-R)}{p}+ \mathrm{const}_{\pm} \end{aligned}$$

(16)

where

$$\begin{aligned} p =& 54M^{2} -108 cM^{2}R-3R^{2}+27 cMR^{2} \\ &{}+ 3R^{2}\sqrt{-(6Mc-1)^{3}} \end{aligned}$$

(17)

and

$$\begin{aligned} R =& \mathit{RootOf}\bigl(\bigl(-1+9Mc+\sqrt{-(6Mc-1)^{3}} \bigr)Z^{3} \\ &{}-54c M^{2}Z^{2}+54M^{2}Z-108M^{3} \bigr) \end{aligned}$$

(18)

From Fernando (2012) for the proper time we have

$$\begin{aligned} \tau=\pm\frac{r}{E}+\mathrm{const}_{\pm} \end{aligned}$$

(19)

Above equations express t tends to ∞ and $\tau\rightarrow \frac{r_{\mathrm{in}}}{E}$ if r→r _in. These results illustrate there is no difference between our results for the Schwarzschild-anti de Sitter black hole with those obtained by Fernando (2012) for the Schwarzschild black hole surrounded by quintessence.

3.2 Null geodesics structure with L≠0

For the null geodesics with L≠0, we get the corresponding effective potential from Eq. (12),

$$\begin{aligned} V_{\mathrm{eff}} =& \frac{L^{2}}{r^{2}}-\frac{2 ML^{2}}{r^{3}}-\frac {L^{2}c}{r} \\ &{}- \frac{1}{54}\frac{L^{2}(1-9Mc-\sqrt {-(6Mc-1)^{3}})}{M^{2}} \end{aligned}$$

(20)

The behavior of the effective potential depends on the parameters L, M and c and V _eff→0 if r tends to r _in and r _out. Figure 3 shows that the effective potential of the Schwarzschild-anti de Sitter black hole surrounded by quintessence is higher than for the Schwarzschild black hole surrounded by quintessence.

Fig. 3

Effective potential as a function of r for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=1, c=0.1 and L=1

Since the motion of the particles depends on the energy levels, then from Fig. 4, we can consider three cases according to different values of E (E ₁, E ₂, E _c ) for the motion as follows:

Fig. 4

Behavior of V _eff as a function of r with the different values of E. Here, M=1, c=0.12 and L=1

(1) This case denotes the value of the energy E=E ₁. In this case, the photon is allowed to starts the motion only at r<r ₁. Therefore, for all values of r, the photons will fall into the black hole.

(2) When E=E ₂, if the photons start the motion at r<r ₃, they close to r=r ₄ and fly back to r=r ₃ and oscillate between r ₃ and r ₄. If the photon starts the motion at r<r ₅, it will fall into the black hole.

(3) In this case, the energy of particle is E _c and $\dot{r}=0$, then the orbit is circular and unstable at r=r _c . If the photons start the motion at r _c <r<r ₂, then undergo unstable circular orbit at r=r _c and if start the motion at r<r _c they will fall into the black hole.

3.3 Null circle geodesics

When the energy E=E _c and $V_{\mathrm{eff}}=E_{c}^{2}$, the photon can orbit on unstable circular orbit at r=r _c as explained in previous section. We can compute the radius of the circular orbits by the equation,

$$\begin{aligned} \frac{dV_{\mathrm{eff}}}{dr}=0 \end{aligned}$$

(21)

By using the above equation and the definition of the effective potential given in Eq. (20), we obtain two circular orbits as,

$$\begin{aligned} r_{c_{1}}=\frac{1+\sqrt{1-6Mc}}{c} \end{aligned}$$

(22)

$$\begin{aligned} r_{c_{2}}=\frac{1-\sqrt{1-6Mc}}{c} \end{aligned}$$

(23)

Since $r_{c_{1}} = r_{\mathrm{out}}$, $r_{\mathrm{in}} < r_{c_{2}}< r_{\mathrm{out}}$ and we like to analysis the motion between the horizons then we consider $r_{c_{2}}$ as r _c . These results show that the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter have the same circular orbits r _c . The radius of the circular orbits as a function of c parameter for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter are shown in Fig. 5.

Fig. 5

The circular orbits as a function of c parameter for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=2

We can compute the time period for the circular orbit in proper time (T _τ ) and coordinate time (T _t ) from following equations,

$$\begin{aligned} T_{\tau}=\frac{2\pi r_{c}^{2}}{L} \end{aligned}$$

(24)

and

$$\begin{aligned} T_{t}=\frac{2\pi r_{c}}{\sqrt{g(r_{c})}} \end{aligned}$$

(25)

Figures 6 and 7 show the time periods as a function of M for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter. These figures illustrate the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter have the same T _τ , while T _t of the Schwarzschild-anti de Sitter black hole surrounded by quintessence matter for large M is smaller than for the Schwarzschild black hole surrounded by quintessence matter.

Fig. 6

T _τ as a function of M for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with c=0.05 and L=1

Fig. 7

T _t as a function of M for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with c=0.12 and L=1

We can check the instability of circular null geodesics by Lyapunov exponent λ which is given by Cardoso et al. (2009) as,

$$\begin{aligned} \lambda=\sqrt{\frac{-V^{''}_{\mathrm{eff}}(r_{c})}{2\dot{t}^{2}(r_{c})}}=\sqrt {\frac{-V^{''}_{\mathrm{eff}}(r_{c})r^{2}_{c}g(r_{c})}{2L^{2}}} \end{aligned}$$

(26)

The graphs for the Lyapunov exponent λ as a function of c for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter are given in Fig. 8. The instability of the circular orbits for large c parameter is more for the Schwarzschild-anti de Sitter black hole surrounded by quintessence in comparison with the Schwarzschild black hole surrounded by quintessence.

Fig. 8

The Lyapunov exponent λ as a function of c for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=1

3.4 Force on the massless particle

The force on the massless particle can be obtained by using the effective potential as,

$$\begin{aligned} F=-\frac{1}{2}\frac{dV_{\mathrm{eff}}}{dr}=-\frac{3ML^{2}}{r^{4}}+\frac {L^{2}}{r^{3}}- \frac{1}{2}\frac{cL^{2}}{r^{2}} \end{aligned}$$

(27)

From the above equation, we can see the Schwarzschild-anti de Sitter and the Schwarzschild black holes surrounded by quintessence matter have the same force acting on the photons. This force is attractive for the first and the third terms and is repulsive for the second term. The third term is the force due to the quintessence. The graphs for the effective force on the photons F as a function of r for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter are given in Figs. 9 and 10. Form these figures, we can see F=0 at r _c and the force on the photon for r _c <r<r _out is repulsive and for r _in<r<r _c is attractive.

Fig. 9

Behavior of F as a function of r for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=0.5, c=0.1 and L=2

Fig. 10

Behavior of F as a function of r for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=0.5, c=0.1 and L=2

4 Using the variable change $u = \frac{1}{r}$ to analysis the geodesics

In this section, we use the variable change $u = \frac{1}{r}$ to analysis the geodesics equation of motion. From Fernando (2012), the relation between ϕ and u is given by,

$$\begin{aligned} \biggl(\frac{du}{d\phi} \biggr)^{2}=f(u) \end{aligned}$$

(28)

where for the Schwarzschild-anti de Sitter black hole surrounded by quintessence matter, f(u) corresponds to,

$$\begin{aligned} f(u) =& 2Mu^{3}-u^{2}+cu+\frac{E^{2}}{L^{2}} \\ &{}+\frac{1}{54} \frac {1-9Mc-\sqrt{-(6Mc-1)^{3}}}{M^{2}} \end{aligned}$$

(29)

By using the roots of f(u)=0, we can analysis the geometry of the geodesics. Above equation illustrates for any value of M, c, L and E, f(u) tends to ±∞ if u→±∞ and $f(u) = \frac{E^{2}}{L^{2}}+\frac{1}{54} \frac{1-9Mc-\sqrt {-(6Mc-1)^{3}}}{M^{2}}$ if u=0. The roots of f(u) can be called as u ₁,u ₂ and u ₃ which u ₁ is negative real root always while the nature of u ₂ and u ₃ depends on the values of E, L, c and M. Figure 11 shows the behavior of f(u) as a function of u for general values of M, c, E and L. This figure illustrates that the behavior of f(u) for the Schwarzschild-anti de Sitter black hole is similar to what obtained by Fernando (2012) for the Schwarzschild black hole surrounded by quintessence matter. For more details about the behavior of f(u) and all possible regions of motion see Fernando (2012).

Fig. 11

Behavior of f(u) as a function of u with M=0.5, c=0.01, L=30 and E=9

5 Deflection of light by the Schwarzschild-anti de Sitter black hole surrounded by quintessence

According to general relativity, when light passes around a massive object such as a black hole, it is bent. The study of deflection of light is one of the important applications of the null geodesics. In this section, we derive the angle of deflection of light for the Schwarzschild-anti de Sitter black hole surrounded by quintessence. We first obtain the closest distance of approach r ₀ for the photon with E=E ₂. Following Fernando (2012), by finding the roots of f(r)=0, we can calculate the closest approach r ₀. From Eq. (29), the function f(r) for the Schwarzschild-anti de Sitter black hole surrounded by quintessence can be expressed as,

$$\begin{aligned} f(r) =&\frac{2M}{r^{3}}-\frac{1}{r^{2}}+\frac{c}{r}+ \frac {E^{2}}{L^{2}} \\ &{}+ \frac{1}{54}\frac{1-9Mc-\sqrt{-(6Mc-1)^{3}}}{M^{2}} \end{aligned}$$

(30)

The above equation can be written as,

$$\begin{aligned} &{ \biggl(1+\frac{1}{54}\frac{D^{2}(1-9Mc-\sqrt{-(6Mc-1)^{3}})}{M^{2}} \biggr)r^{3}} \\ &{\quad {}+cD^{2}r^{2}-D^{2}r+2MD^{2}=0} \end{aligned}$$

(31)

Here, $D=\frac{L}{E}$ is the impact parameter. The roots of the above equation are r ₃,r ₄ and r ₅ which are shown in Fig. 4. From Fig. 4, we can see the photon with E=E ₂ is allowed to starts the motion at r<r ₃ and since r ₅<r ₄<r ₃ and r ₅<r _c , therefore we choose r ₄ as a closest approach r ₀. We can obtain r ₀ from Eq. (31) as,

$$\begin{aligned} r_{0}=y-\frac{cD^{2}}{3S} \end{aligned}$$

(32)

where

$$\begin{aligned} y=2\sqrt{\frac{|p|}{3}} \cos \biggl(\frac{\theta}{3} \biggr) \end{aligned}$$

(33)

$$\begin{aligned} \theta=\arccos \biggl(\frac{-q}{2} \biggl(\frac{|p|}{3} \biggr)^{-\frac{3}{2}} \biggr) \end{aligned}$$

(34)

$$\begin{aligned} p=-\frac{D^{2}}{S}-\frac{ c^{2}D^{4}}{3S^{2}} \end{aligned}$$

(35)

$$\begin{aligned} q=\frac{2c^{3}D^{6}}{27S^{3}}+\frac{cD^{4}}{3S^{2}}+\frac{2MD^{2}}{S} \end{aligned}$$

(36)

$$\begin{aligned} S=1+\frac{1}{54}\frac{D^{2}(1-9Mc-\sqrt{-(6Mc-1)^{3}})}{M^{2}} \end{aligned}$$

(37)

Figure 12 shows the closest approach r ₀ as a function of the impact parameter D for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence.

Fig. 12

The closest approach r ₀ as a function of D for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=1 and c=0.05

This graph illustrates r ₀ for the Schwarzschild-anti de Sitter black hole surrounded by quintessence with the same D is more in comparison with the Schwarzschild black hole surrounded by quintessence.

By using a method given by Amore et al. (2006), we can obtain the angle of deflection of light α for the Schwarzschild-anti de Sitter black hole surrounded by quintessence matter. The Weyl gravity has the metric of the form (Amore et al. 2006),

$$\begin{aligned} ds^{2}=-g(r) dt^{2}+g(r)^{-1} dr^{2}+ r^{2} d\varOmega^{2} \end{aligned}$$

(38)

where

$$\begin{aligned} g(r)=1-\frac{2 \beta}{r}+\gamma r-kr^{2} \end{aligned}$$

(39)

The angle of deflection of light for the Weyl gravity which is independent of k, is defined as (Amore et al. 2006),

$$\begin{aligned} &{\alpha=\frac{4\beta}{r_{0}}-\gamma r_{0}+ \biggl( \frac{15\pi\beta ^{2}}{4r_{0}^{2}}-\frac{4\beta^{2}}{r_{0}^{2}}+\gamma\beta-\frac{3\gamma \pi\beta}{2} + \frac{\gamma^{2}r_{0}^{2}}{2} \biggr)} \end{aligned}$$

(40)

By considering $k=\frac{1}{54} \frac{1-9Mc-\sqrt {-(6Mc-1)^{3}}}{M^{2}}$, β=M, γ=−c and using above equation, we can compute α for the Schwarzschild-anti de Sitter black hole surrounded by quintessence matter. Here, r ₀ is the closest approach.

Figure 13 shows the bending angle α as a function of the impact parameter D for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence. This graph indicates α with the same D is less for the Schwarzschild-anti de Sitter black hole surrounded by quintessence in comparison with the Schwarzschild black hole surrounded by quintessence.

Fig. 13

The bending angle α as a function of D for the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter with M=1 and c=0.05

6 Conclusion

In this paper, we have investigated the null geodesics and all kinds of orbits corresponding to the energy levels for the Schwarzschild-anti de Sitter black hole surrounded by quintessence and compared our results with those obtained by Fernando (2012) for the Schwarzschild black hole surrounded by quintessence matter. By analyzing the effective potential of photons, all possible motions are discussed. The circular orbits and the Lyapunov exponent λ are studied in detail. It is shown that the Schwarzschild and the Schwarzschild-anti de Sitter black holes surrounded by quintessence matter have the same circular orbits. We also have shown that the instability of the circular orbits for large c parameter is more for the Schwarzschild-anti de Sitter black hole surrounded by quintessence in comparison with the Schwarzschild black hole surrounded by quintessence. We have used the variable change $u = \frac{1}{r}$ to analysis the geodesics equation of motion and we showed that the behavior of f(u) for the Schwarzschild-anti de Sitter black hole is similar to the Schwarzschild black hole surrounded by quintessence matter. Finally, we have calculated the angle of deflection of light and showed that the bending angle with the same D is less for the Schwarzschild-anti de Sitter black hole surrounded by quintessence in comparison with the Schwarzschild black hole surrounded by quintessence.