1 Introduction

Recently, Baňados et al. (2009) (BSW) have shown that free particles falling from rest at infinity outside an extreme Kerr black hole may collide with arbitrarily high center-of-mass (CM) energy and hence the maximally rotating black hole with the specific angular momentum a=1 might be regarded as a Planck-energy-scale collider. They have proposed that this might lead to observable signals from the ultra high energy collisions of the particles around the black holes.

In fact, near to extreme rotation is sufficient to achieve the unlimited energy for the center of the mass through the particle acceleration around rotating black holes. In the papers by Frolov (2012), Abdujabbarov et al. (2014) it has been shown that static black hole can be also particle accelerator when the black hole is immersed in the external magnetic field. Amplification of the particle acceleration by the magnetic field has been shown also for Kehagias-Sfetsos naked singularities (Stuchlík et al. 2014).

In the papers by Stuchlík and Schee (2010, 2012, 2013), Stuchlík et al. (2011), Patil and Joshi (2011a,b), Shaymatov et al. (2013) it has been shown that the center-of-mass energy of the collisions between two particles can be arbitrarily large in the field of near-extremal Kerr and Kehagias-Sfetsos naked singularities, Randall-Sundrum brane with a cosmological constant and superspinars even without need of fine turning the motion constants of colliding particles that is necessary for collisions near the black hole horizon.

Finally, it has been demonstrated by Stuchlík and Schee (2013) that ultra-high-energy radiations near the equatorial plane of near-extreme Kerr naked singularities can give strong observational signals.

One peculiar feature of string theory, which may play a role of one of the candidates for a theory of quantum gravity, is the presence of extra dimensions of space. The existence of the extra dimensions amplifies the gravity of the central object significantly. For example, in the preceding paper by Tursunov et al. (2013) we have studied particle acceleration around black strings in S 2×R 1 topology which are produced based on the string theory by adding extra dimension to the Schwarzschild and Kerr black hole spacetimes allowing enhancement of particle accelerator due to the extra dimension.

In 1969 Roger Penrose has developed and formulated new original mechanism of the energy extraction from the rotating black hole. According to the Penrose process incident particle splits into pieces in the ergosphere: one of them falls down to the black hole with negative energy, the another one goes out to infinity with positive energy (Penrose 2002). Maximum efficiency of the Penrose process for the Kerr black hole is 20.7 % (Ghosh and Sheoran 2014; Nozawa and Maeda 2005; Liu et al. 2012). In our preceding paper (Abdujabbarov et al. 2011) energy extraction by the Penrose process and its efficiency for the Kerr-Taub-NUT spacetime have been calculated.

Indeed, BSW and Penrose processes both are very relevant to each other. BSW effect occurs when the collision of the particles is happened near or on the horizon of the rotating black hole while the Penrose process occurs when the decay of the particle is happened in the ergosphere of the black hole and the value of the extracted energy increases as process occurance approaches the horizon of the black hole. In order to connect these two processes Piran, Shaham and Katz suggested collisional Penrose process (Piran et al. 1975; Piran and Shaham 1977a,b). However, in the paper by Bejger et al. (2012) it has been shown that in the collisional Penrose process energy of the extracted photon cannot be high. Zaslavskii has shown that having infinite amount of center-of-mass energy on the collision of particles near the horizon of the black hole is the generic property of the black hole (Zaslavskii 2010). Grib and Pavlov (2010) has shown that even non-extremal Kerr black hole can be particle accelerator. In the papers by Grib and Pavlov (2010), Zaslavskii (2011), Harada and Kimura (2011a,b,c), Harada et al. (2012) Kerr black hole has been investigated in different respects as a particle accelerator. Energy extraction from the extremal charged non-rotating black hole due to the BSW effect has been studied in different scenarios (Zaslavskii 2012a,b). The particle acceleration mechanism around Reissner-Nordström black hole has been studied by Nemoto et al. (2013).

It is well known that there are so-called regular black holes which do not have curvature singularity, see e.g. Toshmatov et al. (2014), Ayón-Beato and García (1998, 1999). After derivation of the Kerr solution from the Schwarzschild one by applying the Newman-Janis algorithm (NJA) (Drake and Szekeres 2000), this algorithm has been widely used to get rotational solutions of black holes, see e.g. Bambi and Modesto (2013). In our preceding research (Toshmatov et al. 2014) the rotational solution of the ABG static regular black hole (Garcia et al. 2013) has been found by using the Newman-Janis algorithm.

Static regular ABG black hole solution has been critically analyzed by Bronnikov (2000) arguing that this solution does not have the regular center with the Lagrangian \(\mathcal{L}(F)\) where F=F μν F μν, F μν is tensor of electromagnetic field. In other words in the Maxwell weak-field-limit static spherically symmetric general relativistic configurations with a nonzero electric charge cannot have a regular center. However, it has been pointed out by Bronnikov (2000) that Ayón-Beato-García solution can be found by using the alternative form of the electrodynamics in so-called P formulation (Bronnikov 2000, 2001). Afterwards, it has been shown by Burinskii and Hildebrandt (2002) that theorem described by Bronnikov (2000) on the nonexistence of regular electrically charged black holes can be circumvented and exact regular black hole solutions can be of a hybrid type that is a dual core confining a polarization of magnetic charges. It has been already shown by Toshmatov et al. (2014) that rotating regular ABG black hole solution is described by three parameters: mass M, spin parameter a and electric charge Q and it reduces to the Kerr one in the case of the absence of charge Q=0. Deducing the above statement one can assume that the Kerr solution can be considered to be the special case of the rotating ABG one. In order to study the astrophysical processes around black holes it is useful to consider more general black hole solution. In this paper we study the dynamics and the BSW and especially the Penrose processes in the gravitational field of the rotating ABG black hole as introduced by Toshmatov et al. (2014). For an alternative approach see the work of Azreg-Aïnou (2014).

The paper is organized in the following way. In Sect. 2 we study the effective potential and types of particle orbits around rotating regular black hole. The innermost stable circular geodesics around rotating regular black hole are discussed in Sect. 3. Section 4 is devoted to the energy extraction from the rotating regular black hole through the BSW mechanism. Section 5 is based on the extension of the results of study of Zaslavskii (2012b) where efficiency of the energy extraction due to the collisional version of the Penrose process for the rotating regular ABG black hole has been studied. In Sect. 6 efficiency of the energy extraction through the Penrose process from the rotating regular ABG black hole has been calculated. In Sect. 7 we summarize our main results.

In the paper, we use a spacetime signature as (−,+,+,+) and a system of geometric units in which G=1=c. Greek indices are taken to run from 0 to 3.

2 The particle orbits around rotating regular black hole

The line element in the space-time of the rotating regular black hole in the Boyer-Lindquist coordinates is given by Toshmatov et al. (2014) as

$$\begin{aligned} d s^2 =&g_{tt}dt^2+g_{rr}dr^2+2 g_{t\phi}d\phi dt+g_{\theta\theta }d\theta^2 \\ &{}+g_{\phi\phi}d \phi^2, \end{aligned}$$
(1)

with

$$\begin{aligned}& \begin{aligned} &g_{tt}=-f(r,{\theta}), \\ &g_{rr}=\frac{\varSigma}{\varSigma f(r,{\theta})+a^2\sin^2\theta}, \\ &g_{t\phi}=-a\sin^2\theta\bigl(1-f(r,{\theta})\bigr), \\ &g_{\theta\theta}=\varSigma, \\ &g_{\phi\phi}=\bigl[\varSigma-a^2\bigl(f(r,{\theta})-2\bigr) \sin^2\theta\bigr]\sin^2\theta , \end{aligned} \end{aligned}$$
(2)

where

$$\begin{aligned}& f(r,{\theta})=1-\frac{2M r \sqrt{\varSigma}}{(\varSigma+Q^2)^{3/2}}+\frac {Q^2\varSigma}{(\varSigma+Q^2)^2}, \end{aligned}$$
(3)
$$\begin{aligned}& \varSigma=r^2+a^2 \cos^2\theta, \end{aligned}$$
(4)

and M, a and Q are the total mass, the specific angular momentum and the electric charge of the black hole, respectively. The space-time metric (1) is identical to the ABG one when the specific angular momentum a=0 (Garcia et al. 2013), to the Schwarzschild one when the specific angular momentum a=0, the electric charge Q=0 and to the Kerr black hole when Q=0 (see Fig. 1). In the following we put for simplicity M=1, i.e., equivalently, we express r and t coordinates in units of mass M.

Fig. 1
figure 1

Relationship between the rotation parameters of the Kerr a Kerr and regular a ABG black holes for the different values of the electric charge Q when the radii of their event horizons coincide (\(r_{+}^{Kerr}=r_{+}^{ABG}\))

Full size image

In order to compute the trajectories of the geodesic motion of a test particle in the equatorial plane (θ=π/2) one needs the Lagrangian for this motion:

$$\begin{aligned} L=\frac{1}{2}\bigl[g_{tt}\dot{t}^2+2g_{t\phi} \dot{t}\dot{\phi}+g_{rr}\dot {r}^2+g_{\phi\phi}\dot{ \phi}^2\bigr] , \end{aligned}$$
(5)

where an overdot denotes the derivative with respect to proper time τ. Since the Lagrangian (5) does not depend on the coordinates t and ϕ, associated momenta p t and p ϕ are conserved and they are called energy E and angular momentum L of a test particle, respectively:

$$\begin{aligned}& p_t=\xi_{(t)}^\mu u_{\mu}=g_{tt}\dot{t}+g_{t\phi}\dot{\phi}=- \frac{E}{m}=-\mathcal{E}= \mbox{const} , \end{aligned}$$
(6)
$$\begin{aligned}& p_\phi=\xi_{(\phi)}^\mu u_{\mu}=g_{t\phi}\dot{t}+g_{\phi\phi}\dot{\phi}= \frac{L}{m}=\mathcal {L}=\mbox{const} , \end{aligned}$$
(7)
$$\begin{aligned}& p_r=g_{rr}\dot{r} , \end{aligned}$$
(8)
$$\begin{aligned}& p_\theta=0 , \end{aligned}$$
(9)

where m is mass of the test particle. \(\mathcal{E}\) and \(\mathcal{L}\) are the specific energy and angular momentum of the test particle per unit mass m.

The Hamiltonian is given by \(\mathcal{H}=p_{t}\dot{t}+p_{r}\dot{r}+p_{\phi}\dot{\phi}-L\). In terms of the components of the metric tensor the Hamiltonian reads

$$\begin{aligned} 2{\mathcal{H}} =&(g_{tt}\dot{t}+g_{t\phi}\dot{ \phi})\dot{t}+g_{rr}\dot{r}^2+ (g_{t\phi} \dot{t}+g_{\phi\phi}\dot{\phi})\dot{\phi} \\ =&-\mathcal{E}\dot{t}+\mathcal{L}\dot{\phi}+g_{rr} \dot{r}^2=\epsilon =\mbox{const} . \end{aligned}$$
(10)

Here parameter ϵ is equal to either −1, 0 or +1 for time-like, light-like (null) and spacelike geodesics, respectively. By solving Eqs. (6) and (7) simultaneously, one can find

$$\begin{aligned} \dot{t}=\frac{g_{\phi\phi}{\mathcal{E}}+g_{t\phi}{\mathcal{L}}}{g_{t\phi}^2-g_{tt}g_{\phi\phi}},\qquad \dot{\phi}=-\frac{g_{t\phi}{\mathcal{E}}+g_{tt}{\mathcal{L}}}{g_{t\phi }^2-g_{tt}g_{\phi\phi}} , \end{aligned}$$
(11)

where, the event horizon r + is given by the larger root of denominator of the expressions (11) \(g_{t\phi}^{2}-g_{tt}g_{\phi\phi }=0\). It can be easily verified that \(g_{t\phi}^{2}-g_{tt}g_{\phi\phi}=0 \Leftrightarrow \varSigma f(r)+ a^{2}\sin^{2}\theta=0\).

By inserting (11) into (10) and considering the particle as moving along the time-like geodesics (ϵ=−1), one can obtain the expression for the radial velocity of the particle around rotating regular black hole as

$$\begin{aligned} \dot{r}^2 =&\mathcal{E}^2- \frac{(Q^2-2\sqrt{r^2+Q^2})(a\mathcal {E}-\mathcal{L})^2}{(r^2+Q^2)^2} \\ &{}+\frac{a^2{\mathcal{E}}^2-\mathcal{L}^2}{r^2}-\frac{r^2(Q^2-2\sqrt {r^2+Q^2})}{(r^2+Q^2)^2} \\ &{}-\frac{a^2}{r^2}-1 . \end{aligned}$$
(12)

By introducing the notion of effective potential

$$\begin{aligned} V_{eff} =&\frac{(Q^2-2\sqrt{r^2+Q^2})(a\mathcal{E}-\mathcal {L})^2}{(r^2+Q^2)^2}-\frac{a^2{\mathcal{E}}^2-\mathcal {L}^2}{r^2} \\ &{}+\frac{r^2(Q^2-2\sqrt{r^2+Q^2})}{(r^2+Q^2)^2}+\frac{a^2}{r^2}+1 , \end{aligned}$$
(13)

one can write (12) as

$$\begin{aligned} \dot{r}^2=\mathcal{E}^2-V_{eff} . \end{aligned}$$
(14)

One can see from the expression (13) for the effective potential that the motion of the particle around rotating regular black hole is invariant under r⟷−r and Q⟷−Q transformations. In the flat spacetime limit (r→∞) effective potential V eff tends to 1 (V eff →1). In the opposite limiting case r→0, effective potential of the motion of the particle V eff tends to infinity (V eff →∞).

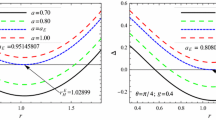
The radial dependences of the effective potential of the particle moving around rotating regular black hole for the different typical values of the electric charge Q and the rotation parameter a are presented in Fig. 2.

Fig. 2
figure 2

The radial dependence of the effective potential of the particle moving around rotating regular black hole for the different typical values of the electric charge Q (left panel) and the rotation of black hole (right panel). Q=0 (solid line in the left panel) corresponds to the effective potential of the Kerr black hole

Full size image

As it has been shown in our preceding research (Toshmatov et al. 2014) that with the increase of the value of the electric charge Q, the horizon of the black hole decreases and eventually, for the value of the charge Q>0.633M event horizon vanishes.

It is known that there are three types of particle orbits around central compact gravitating object: terminating orbit, bound orbit and escape orbit. These orbits are characterized by the angular momentum \(\mathcal{L}\) of the particle. In Figs. 3 and 4 examples of the particle orbits around black hole are given in the cases of presence and absence of the horizon of the black hole, respectively.

Fig. 3
figure 3

Examples of particle trajectories moving in the equatorial plane (θ=π/2) around Kerr (solid, Q=0) and rotating regular (dashed, Q=0.6) spacetimes in the presence of the event horizon of (no-horizon rotating regular ABG spacetimes) when the rotation parameter a=0.2: terminating orbit, bound orbit and escape orbit (from left to right). Particle starts motion from the initial position r 0=11 with the different values of the specific angular momentum \(\mathcal{L}=2.6\), \(\mathcal{L}=3.5\) and \(\mathcal{L}=4.5\)

Full size image
Fig. 4
figure 4

Examples of particle trajectories moving in the equatorial plane (θ=π/2) around Kerr (solid, Q=0) and rotating regular (dashed, Q=0.6) spacetimes in the absence of the event horizon (no-horizon rotating regular ABG spacetimes) when the rotation parameter a=0.99. Particle starts motion from the initial position r 0=11 with the different values of the specific angular momentum \(\mathcal{L}=2.6\), \(\mathcal{L}=3.5\) and \(\mathcal{L}=4.5\)

Full size image

3 Circular geodesic and innermost stable circular orbits

From the astrophysical point of view one of the most momentous type of orbits of the particle is innermost stable circular orbit (ISCO). The ISCO can be found by solving the second derivative of the effective potential V eff with respect to the radial coordinate r, i.e.

$$ \frac{d^2V_{eff}}{dr^2}=0 . $$
(15)

This equation has to be satisfied simultaneously with the equations governing the circular geodesics:

$$ \dot{r}=0, \qquad \frac{dV_{eff}}{dr}=0 . $$
(16)

Equations (16) determine the energy \(\mathcal{E}\) and angular momentum \(\mathcal{L}\) of the particle following circular geodesic orbit at a given radius r. Solving (15) and (16), we determine the ISCO radius r ISCO , energy \(\mathcal{E}_{ISCO}\) and angular momentum \(\mathcal{L}_{ISCO}\). The stable orbits are located at r>r ISCO , \(\mathcal{E}_{ISCO}\) determines efficiency of Keplerian accreation discs.

The radial profiles of the energy \(\mathcal{E}_{C}\) and angular momentum \(\mathcal{L}_{C}\) of both corotating and counter-rotating circular geodesics of the regular rotating ABG black hole spacetimes are represented in Figs. 5 and 6. The minima of the radial profiles correspond to the ISCO. The loci of stable and unstable orbits in dependence on a are given for characteristic values of Q in Fig. 7, where also the no-horizon spacetimes are taken into consideration.

Fig. 5
figure 5

Radial dependence of the specific energy and angular momentum of co-rotating (left, top and bottom) and counter-rotating (right, top and bottom) particle at the circular geodesics around black hole for the different values of the electric charge Q from left to right, respectively

Full size image
Fig. 6
figure 6

Radial dependence of the specific energy and angular momentum of co-rotating (left, top and bottom) and counter-rotating (right, top and bottom) particle at the circular geodesics around black hole for the different values of the rotation parameter a from left to right, respectively

Full size image
Fig. 7
figure 7

The regions of the circular geodesics of the particle around rotating regular BH for the different values of the electric charge Q. Gray and light gray regions represent unstable and stable orbits, respectively. Solid line represents event horizon of the BH

Full size image

As already pointed out in the previous section, when Q=0 the spacetime metric (1) coincides with the Kerr one and Q=0, a=0 with the Schwarzschild one. From the first graph of Fig. 7 one can see the following remarks:

  • In the case of extreme BH (inner and outer horizons merge into one) the radius of ISCO coincides with one of the event horizon of the BH.

  • When Q=0, a=0 the spacetime metric (1) is identical to the Schwarzschild one and the radius of ISCO is r ISCO =6 (M=1).

  • When Q=0 the spacetime metric (1) is identical to the Kerr one. The radius of ISCO of the extreme (a=1) Kerr BH is at r ISCO =1.

4 Center of mass energy of particles in collision

Now, based on the BSW (Baňados-Silk-West) mechanism in the field of rotating black holes, we calculate center of mass energy E CM for collision of the two neutral identical particles with mass m 1=m 2=m 0. We assume that particles are coming from infinity with E 1/m 0=E 2/m 0=1 and approaching the black hole with the different angular momenta L 1 and L 2. The particles motion and their collisions occur in the equatorial plane θ=π/2.

The center of mass energy can be found by using the standard formula (Baňados et al. 2009):

$$\begin{aligned} \frac{E_{CM}^2}{2m_{0}^2}=1-g_{\mu\nu}u_{1}^{\mu}u_{2}^{\nu} , \end{aligned}$$
(17)

where \(u_{1}^{\mu}\) and \(u_{2}^{\nu}\) are four velocities of the first and second particles, respectively. The four velocity of the particle that is moving around rotating black hole in the equatorial plane is given by the expressions (11) and (12). For simplicity, considering \(\mathcal{E}_{1}=\mathcal{E}_{2}=1\) and inserting the expressions (11) and (12) into (17), we get the center of mass energy as

$$\begin{aligned} \frac{E_{CM}^2}{2m_{0}^2} =&\frac{1}{\rho^4 (r^2+a^2)-r^4(2\rho -Q^2)} \\ &{}\times \bigl\{ 2\bigl(r^2+a^2\bigr)\rho^4-a r^2(\mathcal{L}_1+\mathcal{L}_2) \bigl(2\rho -Q^2\bigr) \\ &{}-\mathcal{L}_1{\mathcal{L}}_2\bigl[ \rho^4-r^2\bigl(2\rho-Q^2\bigr)\bigr] \\ &{}-r^2\bigl(r^2-a^2\bigr) \bigl(2 \rho-Q^2\bigr)-\sqrt{R_{1}}\sqrt{R_{2}} \bigr\} , \end{aligned}$$
(18)

where

$$\begin{aligned}& \begin{aligned} &\rho^2 =r^2+Q^2 \\ & R_{i}(r)=r^2\bigl(2\rho-Q^2\bigr) (a- \mathcal{L}_i)^2-\mathcal{L}_i^2 \rho ^4 +r^4\bigl(2\rho-Q^2\bigr), \end{aligned} \end{aligned}$$
(19)

and i=1,2. In absence of the electric charge Q=0 the expressions (18) and (19) will reduce to the ones for the Kerr black hole (Baňados et al. 2009).

The horizon of the black hole is determined by equation \((r^{2}+a^{2})(r^{2}+Q^{2})^{2}-r^{4}(-Q^{2}+2\sqrt{r^{2}+Q^{2}})=0\). Therefore, at the one sight it seems that the center of mass energy diverges at the horizon of the black hole. However, at this point numerator of Eq. (18) also vanishes and in order to eliminate this uncertainty one has to use L’Hopital’s rule. The radial profiles of the \(E_{CM}^{2}/2m_{0}^{2}\) are given in Fig. 8.

Fig. 8
figure 8

Radial dependence of the center of mass energy for few typical values of the rotation parameter a, electric charge Q and angular momenta of the particles \(\mathcal{L}_{1}\) and \(\mathcal{L}_{2}\). Vertical line represents the location of event horizon of the BH

Full size image

At the next step we study how much energy could be extracted from a particle slowly spiraling toward the rotating regular black hole?s horizon. For this purpose it is necessary to consider what the energy of the particle at the innermost stable circular orbit is around the rotating regular black hole. First we calculate the energy of a test particle moving along the innermost stable circular orbit. Then we use the definition of the coefficient of total amount of released energy of the test particle shifting from the outward stable circular orbit with the radius r c to the innermost stable circular orbit. Then coefficient of the energy release efficiency can be found as

$$\begin{aligned} \eta_c=100\times\frac{E(r_{c})-E(r_{ISCO})}{E(r_{c})} . \end{aligned}$$
(20)

The efficiency coefficient η in dependence on the values of the rotation parameter a and electric charge Q is shown in Table 1. The energy extraction is essentially amplified with the increase of the electric charge of the rotating regular black hole. In the limiting case when the extreme rotating black hole is uncharged one has the maximal efficiency 42 %. For the rotating black hole with smaller rotation parameter a the presence of the electric charge Q substitutes the effect of rotation of the black hole and increases the energy extraction efficiency. Physically this means that the electric charge decreases the potential of the gravitational field and particle needs less bound energy at the circular geodesics.

Table 1 The efficiency of the energy extraction η c (%) from the black hole through the particle acceleration mechanism for several values of the rotation parameter a and charge Q
Full size table

5 Energy extraction from extremal rotating Ayón-Beato-García black hole due to the collisional Penrose process

5.1 Escape to infinity

First we discuss escape of the massless particles (photons) from the rotating regular black hole to infinity. In order to escape to infinity particle coming from infinity towards the black hole must have particular values of the angular momentum L and energy E. Combining these two conservative quantities one can introduce so-called impact parameter b=L/E. Incoming particle with large value of the impact parameter b turns back to infinity at turning point. Turning point is determined by zero radial velocity of the particle (\(\dot{r}=0\)). Then solving expression (12) at the turning point for the massless particle with respect to the impact parameter b, we obtain

$$\begin{aligned} b_{\pm}= \frac{ar^2(Q^2-2M\rho)\pm\rho^2\sqrt {(r^2+a^2)\rho^4+ r^4(Q^2-2M\rho)}}{(\rho^4+r^2(Q^2-2M\rho)} , \end{aligned}$$
(21)

where we recall the notation ρ 2=r 2+Q 2, + and − signs denote the infalling and outgoing photons, respectively. In the case when Q=0 and a=M the expression (21) reduces to one for the extremal Kerr black hole (Harada and Kimura 2011a). In Fig. 9 the escape conditions of the initially infalling and outgoing photons for the several values of the electric charge Q and spin parameter a of the extremal ABG black hole are given. One can see from the last plot in Fig. 9 for the case M=1, a=0.99 and Q≈0.07 that the initially outgoing photons escape to infinity when the values of the impact parameter in the range −7≲b≲2. For the values of the impact parameter in the range b≲−7 or b≳2 any photon can escape to infinity irrespective of sign of the initial velocity. This case nearly coincides with the extremal Kerr black hole case (Bejger et al. 2012; Harada et al. 2012). From the first and second plots in Fig. 9 one can see that for the extremal cases with a=0.5, Q≈0.51 and a=0.1, Q≈0.63 escape conditions of initially outgoing and any (both initially infalling and outgoing) photons are −5.9≲b≲2.7, −4.3≲b≲4 and b≳2.7, b≲−5.9 and b≳4, b≲−4.3, respectively.

Fig. 9
figure 9

Conditions of the photon impact parameter b=L/E in case of the extreme rotating regular ABG black hole are plotted as b + (solid, black curve) and b − (solid, red curve). In order to escape the ergosphere, initially outgoing photons must have (b −)max<b<(b +)min; any photon can escape to infinity with b>(b +)min or b<(b −)max impact parameters. Gray region represents the ergosphere

Full size image

5.2 Equations of motion and conservation laws

For the convenience we write the spacetime metric (1) in the following form:

$$\begin{aligned} d s^2=-N^2 d t^2+g_{\phi\phi}(d \phi-\omega d t)^2 + r^2 d \theta^2 + g_{rr} d r^2 , \end{aligned}$$
(22)

where

$$\begin{aligned}& N^2 = \frac{(r^2+a^2)\rho^4+r^4(Q^2-2 M\rho)}{(r^2+a^2)\rho ^4-a^2r^2(Q^2-2 M\rho)} , \end{aligned}$$
(23)
$$\begin{aligned}& \omega = -\frac{a r^2(Q^2-2 M\rho)}{(r^2+a^2) \rho^4-a^2r^2(Q^2-2 M\rho )} , \end{aligned}$$
(24)
$$\begin{aligned}& g_{\phi\phi} = \frac{(r^2+a^2)\rho^4-a^2r^2(Q^2-2 M\rho)}{\rho^4} . \end{aligned}$$
(25)

Now we rewrite the equations of motion for the timelike geodesics (11) and (12) at the equatorial plane (θ=π/2) by introducing new notations as follows:

$$\begin{aligned}& m \dot{t} = \frac{X}{N^2} , \end{aligned}$$
(26)
$$\begin{aligned}& m \dot{r} = \sigma\frac{Z}{N} , \end{aligned}$$
(27)
$$\begin{aligned}& m\dot{\phi} = \frac{L}{g_{\phi\phi}}+\frac{\omega X}{N^2} , \end{aligned}$$
(28)

where

$$\begin{aligned} X=E-\omega L ,\quad\quad Z=\sqrt{X^2-N^2 \biggl(m^2+\frac{L^2}{g_{\phi\phi}} \biggr)} . \end{aligned}$$
(29)

Here parameter σ can take +1 or −1 value for outgoing or ingoing particles, respectively. One can see from the second expression of (29) that the allowed region for the particle motion is Z≥0. Condition Z=0 provides the turning points.

Assume that particles 1 and 2 collide near the black hole and produce particles 3 and 4. In this process total energy, angular momenta and radial momenta of particles are conserved:

$$\begin{aligned}& E_1+E_2=E_3+E_4 , \end{aligned}$$
(30)
$$\begin{aligned}& X_1+X_2=X_3+X_4 , \end{aligned}$$
(31)
$$\begin{aligned}& \sigma_1 Z_1+\sigma_2 Z_2=\sigma_3 Z_3+\sigma_4 Z_4 . \end{aligned}$$
(32)

5.3 Near horizon expansions

It is known that at the horizon the lapse function N=0 and in the near horizon region N is very small, namely N≪1. Then near to horizon area the angular velocity of the black hole ω and g ϕϕ component of the metric tensor cam be considered as functions of small parameter N, and we can expand them in powers of N as

$$\begin{aligned}& \omega=\omega_{H}-B_{1}N-B_{2}N^2+O \bigl(N^3\bigr) , \end{aligned}$$
(33)
$$\begin{aligned}& g_{\phi\phi}=(g_{\phi\phi})_H+(g_{\phi\phi})_1 N+ (g_{\phi\phi})_2 N^2+ O\bigl(N^3\bigr) . \end{aligned}$$
(34)

Now following to Zaslavskii (2012b) we can introduce the following notations:

$$\begin{aligned}& \begin{aligned} &b=B_1\sqrt{(g_{\phi\phi})_H},\quad\quad h= \omega_H \sqrt{(g_{\phi\phi})_H},\\ & b_2=B_2 \sqrt{(g_{\phi\phi})_H} . \end{aligned} \end{aligned}$$
(35)

5.3.1 Critical particle

It is known that the first quantity in (29) for the critical particle on the horizon tends to zero:

$$\begin{aligned} X_{H}=0 . \end{aligned}$$
(36)

Then one can derive from the expression (29) that

$$\begin{aligned} L=\frac{E}{\omega_H} . \end{aligned}$$
(37)

The forward-in-time condition \(\dot{t}>0\) gives that B 1>0. For the critical particle near the horizon expression (29), with the help of expansion (33), takes the form:

$$\begin{aligned}& \begin{aligned} &X =\frac{E N}{h}(b-b_2 N)+O\bigl(N^3 \bigr) , \\ &Z =\sqrt{\frac{E^2(b^2-1)}{h^2}-m^2}N+\frac{E^2}{2(g_{\phi\phi})_H h^2} \\ & \phantom{Z =\,\,}{}\times\frac{(g_{\phi\phi})_1-2 b b_2(g_{\phi\phi})_H}{\sqrt{\frac {E^2(b^2-1)}{h^2}-m^2}}N^2+O\bigl(N^3\bigr) . \end{aligned} \end{aligned}$$
(38)

5.3.2 Near critical particle

The near critical particle has the angular momentum

$$\begin{aligned} L=\frac{E}{\omega_H}(1+\epsilon) , \end{aligned}$$
(39)

where ϵ≪1. Considering the parameter ϵ as a function of N, we expand it near the horizon in powers of N as

$$\begin{aligned} \epsilon=C_1 N+C_2 N^2+ O \bigl(N^3\bigr) . \end{aligned}$$
(40)

Then the expressions (33) and (34) for the near critical particle can be written in the following form:

$$\begin{aligned}& X=\biggl(\frac{b}{h}-C_1\biggr)E N+\biggl( \frac{C_1 b-b_2}{h}-C_2\biggr)E N^2+O\bigl(N^3 \bigr), \end{aligned}$$
(41)
$$\begin{aligned}& Z=\sqrt{\biggl[\biggl(\frac{b}{h}-C_1\biggr)^2- \frac{1}{h^2}\biggr]E^2-m^2}N+O\bigl(N^2 \bigr). \end{aligned}$$
(42)

5.3.3 Standard particle

For the standard particle

$$\begin{aligned} X_H \neq0 . \end{aligned}$$
(43)

Therefore the expressions (33) and (34) for the standard particle are

$$\begin{aligned}& X=X_H + B_1 L N - B_2 L N^2 + O\bigl(N^3\bigr) , \end{aligned}$$
(44)
$$\begin{aligned}& Z=X-\frac{1}{2X}\biggl(m^2+\frac{L^2}{(g_{\phi\phi})_H} \biggr)N^2+O\bigl(N^3\bigr) . \end{aligned}$$
(45)

5.4 Particle collision and reaction

In this subsection based on the work of Zaslavskii (2012b) we will briefly discuss the main assumptions and possible cases. We suppose that the critical particle 1 and the standard one 2 are coming towards the horizon of the black hole from outside and therefore σ 1=σ 2=−1. As a result of the reaction occurred near horizon, a near critical particle 3 and a standard one 4 that falls into the black hole σ 4=−1 are produced. Hereafter we are interested in the energy of the particle 3 that escapes from the black hole with particular energy. By using conservation laws (31) and (32) for this collision one can get

$$\begin{aligned}& \begin{aligned} &F\equiv A_1+E_3\biggl(C_1- \frac{b}{h}\biggr)= \\ &\sigma_3\sqrt{E_3^2\biggl[\biggl( \frac{b}{h}-C_1\biggr)^2-\frac{1}{h^2} \biggr]-m_3^2} , \end{aligned} \end{aligned}$$
(46)

where

$$\begin{aligned} A_1=\frac{E_1 b-\sqrt{E_1^2(b^2-1)-m_1^2 h^2}}{h} . \end{aligned}$$
(47)

5.5 Maximum efficiency of the energy extraction

There are several possible scenarios: IN+, OUT+, IN− and OUT− according to Zaslavskii (2010, 2011, 2012a,b). Where IN and OUT denote coming σ=−1, and outgoing σ=+1, particles, respectively. “+” and “−” signs denote ϵ>0 and ϵ<0, respectively. In IN− scenario there is no energy extraction since it represents the infalling particle to the black hole. Therefore we do not consider this case. Efficiency of the extracted energy from the black hole due to the particles collision is defined by the ratio of the escaping particle’s energy E 3 and total energy of pre-reaction particles E 1+E 2 (Zaslavskii 2012a,b) as

$$\begin{aligned} \eta=\frac{E_3}{E_1+E_2}\times100~\% . \end{aligned}$$
(48)

5.5.1 Scenario IN+

IN+ scenario means that after collision the near critical particle 3 moves towards the black hole (σ=−1) and at the turning point it turns back and escapes to infinity. One can see from (48) that in order to achieve the highest efficiency of the energy extraction from the black hole energy of the escaping particle E 3 must be as high as possible:

$$\begin{aligned} \eta_{\max}=\frac{q(\sqrt{h^2+1}+1)}{q+\sqrt{h^2+1}}\times100~\% , \end{aligned}$$
(49)

where

$$\begin{aligned} q=\bigl(b+\sqrt{b^2-1}\bigr) \bigl(b- \sqrt{b^2-h^2-1}\bigr) . \end{aligned}$$
(50)

It is known that rotating regular ABG black hole solution has three independent parameters: mass M, spin parameter a and the electric charge Q of the black hole. Extremality condition requires that inner and outer horizons merge into one for the corresponding values of the parameters. For the Kerr black hole the condition a=M is enough to be extremal. However for the rotating regular Ayón-Beato-García black hole it is difficult to solve g rr →∞ with respect to r analytically. One can see from (Toshmatov et al. 2014) that infinite number of values of Q and a can satisfy extremality condition. In Table 2 several values of the maximum efficiency η max of the energy extraction through the collisional Penrose process for the extreme rotating Ayón-Beato-García black hole are given.

Table 2 Maximum efficiency of the energy extraction from the extremal rotating ABG black hole through the BSW effect in the IN+ scenario. r H is the event horizon radius of the extremal black hole
Full size table

5.5.2 Scenario OUT+

As it has been shown by Zaslavskii (2012b) for the extremal Kerr black hole, the maximum efficiency can be achieved if the mass of the pre-collisional particles E 1=m 1, m 2=0 and m 3=0 (Zaslavskii 2012b). Then

$$\begin{aligned} \eta_{\max}=b-\sqrt{b^2-1-h^2} \times100~\% . \end{aligned}$$
(51)

It has been shown by Zaslavskii (2012a,b) that in the OUT+ scenario there is no energy extraction for the Kerr black hole. Expression (51) is suitable if the following condition is satisfied:

$$\begin{aligned} \sqrt{1+h^2}< b<1+\frac{h^2}{2} . \end{aligned}$$
(52)

However the region of the values of b and h that satisfies (52) is very narrow and the efficiency is also smaller with compare to one in the IN+ scenario. In Table 3 some of the possible values of the maximum efficiency of the energy extraction η max in OUT+ scenario are given.

Table 3 Maximum efficiency of the energy extraction from the extremal rotating ABG black hole through the BSW effect in the OUT+ scenario. r H is the event horizon radius of the extremal black hole
Full size table

5.5.3 Scenario OUT−

Zaslavskii has shown that in order to extract energy with η max>100 % OUT− scenario requires that b must satisfy (52), as well as \(b<\sqrt{2}\), h<1 conditions (Zaslavskii 2012b). One can see from Table 3 that the allowed region for the condition (52) cannot satisfy \(b<\sqrt{2}\). Consequently we may consider that in OUT− scenario there is no energy extraction.

6 Energy extraction from rotating regular black hole through Penrose process

It is well known, e.g. from Penrose (2002), Ghosh and Sheoran (2014) that energy can be extracted from a rotating black hole. Energy extraction occurs not inside the event horizon of the black hole, it occurs in the region of ergosphere on account of rotational energy of the black hole. In this process massive particle enters into the ergosphere and splits into two pieces: one of them escapes from the black hole to infinity while the other one falls into the black hole. The escaping piece can possibly have greater energy than the infalling one, if the infalling piece has negative energy. As a result of this process the black hole reduces its angular momentum and consequently energy of the black hole is extracted. It derives from signature of energies of two pieces that the escaping particle has more energy than the one which entered the ergosphere.

Assume a particle enters into ergosphere of the black hole and is splitted into two labeled as 1 and 2 pieces. The first piece 1 has more energy (E 1) than the incident particle 0 and exits ergosphere while the second piece 2 is falling into the black hole with negative energy E 2 (Nozawa and Maeda 2005), i.e. according to the law of conservation of energy

$$\begin{aligned} E_{0}=E_{1}+E_{2} , \end{aligned}$$
(53)

where E 2<0, then E 1>E 0. For simplicity we assume that motion of all particles is confined to the equatorial plane (θ=π/2)

$$\begin{aligned} \upsilon=\frac{dr}{dt} ,\quad\quad \varOmega=\frac{d\phi}{dt} , \end{aligned}$$
(54)

where υ and Ω are the radial and angular velocity of the particle with respect to an observer at asymptotic infinity.

It is known that in the Penrose process energy of rotating black hole is extracted on account of decreasing black holes angular momentum. From the conservation laws of energy and angular momentum we have

$$\begin{aligned} E=-p^t A ,\quad\quad L=p^t \varOmega , \quad\quad A\equiv g_{tt}+\varOmega g_{t\phi} . \end{aligned}$$
(55)

From the Hamilton-Jacobi equation for the timelike geodesics, namely p μ p μ =−m 2, one can obtain

$$\begin{aligned} g_{tt}\dot{t}^2+g_{rr} \dot{r}^2+g_{\phi\phi}\dot{\phi}^2+2g_{t\phi} \dot {t}\dot{\phi}=-m^2 . \end{aligned}$$
(56)

Dividing both sides of (56) by \(\dot{t}^{2}\) and using (54) and (55) one can get

$$\begin{aligned} g_{tt}+g_{rr} \upsilon^2+g_{\phi\phi} \varOmega^2+2g_{t\phi}\varOmega=-m^2\biggl( \frac{A}{E}\biggr)^2 . \end{aligned}$$
(57)

As one can see the right hand side of the expression (57) is negative or equals to zero and the second term in the left hand side of the expression (57) is always positive. Due to this one can write the expression (57) in the following form (Nozawa and Maeda 2005):

$$\begin{aligned} g_{\phi\phi}\varOmega^2+2g_{t\phi} \varOmega+g_{tt}=-m^2\biggl(\frac{A}{E} \biggr)^2-g_{rr} \upsilon^2\leq0 . \end{aligned}$$
(58)

From the inequality (58) it follows that the value of Ω is in the range of Ω −≤Ω≤Ω + (Nozawa and Maeda 2005). Here Ω ± is

$$ \varOmega^\pm=-\frac{g_{t\phi}}{g_{\phi\phi}}\pm\sqrt{ \frac{g_{t\phi }^2}{g_{\phi\phi}^2}-\frac{g_{tt}}{g_{\phi\phi}}} . $$
(59)

Using the expression (55), the equations of the conservation of energy (53) and angular momentum can be written as (Nozawa and Maeda 2005)

$$\begin{aligned}& p_{(0)}^t A_{(0)}=p_{(1)}^t A_{(1)}+p_{(2)}^t A_{(2)} , \end{aligned}$$
(60)
$$\begin{aligned}& p_{(0)}^t\varOmega_{(0)}=p_{(1)}^t \varOmega_{(1)}+p_{(2)}^t \varOmega_{(2)} . \end{aligned}$$
(61)

The energy extraction from black holes and its efficiency is the momentous problem of the general relativity, see e.g. Liu et al. (2012) for its discussion. There are several means and processes which are dedicated to the determination of the efficiency of the energy extraction from the rotating black holes. One of these processes is the Penrose one and one can obtain its efficiency

$$\begin{aligned} \eta=\frac{|E_{(2)}|}{E_{(0)}}=\frac{E_{(1)}-E_{(0)}}{E_{(0)}}=\chi-1 , \end{aligned}$$
(62)

using the expression (53) and taking into account E (2)<0 (Nozawa and Maeda 2005) where χ=E (1)/E (0) and χ>1. With the help of the expressions (55), (60) and (61) we find

$$\begin{aligned} \chi=\frac{E_{(1)}}{E_{(0)}}=\frac{(\varOmega_{(0)}-\varOmega _{(2)})A_{(1)}}{(\varOmega_{(1)}-\varOmega_{(2)})A_{(0)}} . \end{aligned}$$
(63)

Following to work Nozawa and Maeda (2005) we assume that the incident particle has initial energy E (0)=1 and is splitted into a pair of two photons in the black hole ergosphere, namely their momenta are equal to zero (p (1)=p (2)=0). As one can see from the expression (63), the maximum value of the efficiency of the Penrose process in this case corresponds to the maximum value of Ω (2) and the minimum value of Ω (1) at the same time. At this moment the radial velocities of both pieces will vanish (υ (1)=υ (2)=0), namely

$$\begin{aligned}& \begin{aligned} &\varOmega_{(1)}=\varOmega^+, \\ &\varOmega_{(2)}=\varOmega^-, \end{aligned} \end{aligned}$$
(64)

and the corresponding values of the parameter A are

$$\begin{aligned} A_{(0)}=g_{tt}+\varOmega_{(0)}g_{t\phi} , \quad\quad A_{(2)}=g_{tt}+\varOmega^-g_{t\phi} . \end{aligned}$$
(65)

Consequently, the four momenta of the pieces are (Liu et al. 2012)

$$\begin{aligned} p_{\alpha}=p^{t}(1,0,0,\varOmega_{\alpha}), \quad \alpha=1,2 . \end{aligned}$$
(66)

Due to the zero radial velocity υ (α)=0, Eq. (57) takes a form

$$\begin{aligned} \bigl(g_{\phi\phi}+g_{t\phi}^2\bigr) \varOmega^2+2g_{t\phi}(1+g_{tt})\varOmega +g_{tt}(1+g_{tt})=0 . \end{aligned}$$
(67)

Angular velocity of the incident particle can be derived from (67) as in work of Nozawa and Maeda (2005)

$$\begin{aligned} \varOmega_{(0)}=\frac{-g_{t\phi}(1+g_{tt})+\sqrt{(1+g_{tt})(g_{t\phi }^2-g_{tt}g_{\phi\phi})}}{g_{\phi\phi}+g_{t\phi}^2} . \end{aligned}$$
(68)

Putting the expressions (64) and (65) into (63) we obtain the expression for the efficiency of the energy extraction in the form (Nozawa and Maeda 2005)

$$\begin{aligned} \eta=\frac{(\varOmega_{(0)}-\varOmega^-)(g_{tt}+\varOmega^+g_{t\phi})}{(\varOmega ^+-\varOmega^-)(g_{tt}+\varOmega_{(0)}g_{t\phi})}-1 . \end{aligned}$$
(69)

In order to achieve the maximum value of the efficiency the incident particle must be splitted into two pieces at the horizon of the black hole (Liu et al. 2012) and in this case the expression (69) takes a form

$$\begin{aligned} \eta_{\max}= \frac{\sqrt{1+g_{tt}}-1}{2}\bigg| _{r=r_{+}} . \end{aligned}$$
(70)

In Table 4 the values of the maximum efficiency of the energy extraction from the regular black hole by the Penrose process is given for several typical values of the rotation parameter a and the electric charge Q. According to Table 4 the maximum value of the efficiency of the energy extraction from the black hole is smaller than the one related to the Kerr black hole. When the ergosphere of the black hole vanishes, the energy extraction does not occur.

Table 4 The values of the maximum efficiency of the energy extraction η max (%) from the black hole through the Penrose process for several values of the rotation parameter a and charge Q
Full size table

One of consequences of the energy extraction from the black hole is irreducible mass of the black hole. As a result of a big number of particles infalling into the black hole with negative energy, the mass of the black hole changes by δM=E (Abdujabbarov et al. 2011). There is no upper limit on change of the mass of the black hole. However, each infalling particle with negative energy decreases the mass of the black hole until its irreducible mass. This is why there is a lower limit on the mass of the black hole.

In order to find the lower limit on δM we rewrite (10) using the expressions (6) and (7) in the form

$$\begin{aligned} \alpha E^2+2\beta E+\gamma+g_{rr}p_{r}^2+m^2=0 , \end{aligned}$$
(71)

where

$$\begin{aligned}& \alpha=-\frac{g_{\phi\phi}}{g_{t\phi}^2-g_{tt}g_{\phi\phi}} , \end{aligned}$$
(72)
$$\begin{aligned}& \beta=-\frac{g_{t\phi}L}{g_{t\phi}^2-g_{tt}g_{\phi\phi}} , \end{aligned}$$
(73)
$$\begin{aligned}& \gamma=-\frac{g_{tt}L^2}{g_{t\phi}^2-g_{tt}g_{\phi\phi}} . \end{aligned}$$
(74)

Assuming that at the horizon p r =0, m=0 and solving Eq. (71) with respect to E we get

$$\begin{aligned} E=-\frac{\beta}{\alpha} \pm \sqrt{\frac{\beta^2-\alpha\gamma}{\alpha^2}} . \end{aligned}$$
(75)

At the horizon r=r + the discriminant of Eq. (75) is equal to zero and consequently the lower limit of δM is

$$\begin{aligned} \delta M=\frac{a L}{r_{+}^2+a^2}. \end{aligned}$$
(76)

The derived limit (76) formally coincides with the expression derived for the Kerr black but in reality it is different and larger due to the different value of r + for the regular black hole.

7 Conclusion

In this paper we have studied the neutral particle motion and the energy extraction from the rotating regular ABG black hole. The dependence of the ISCO (innermost stable circular geodesics) and unstable orbits on the value of the electric charge of the rotating regular black hole is studied. In particular we have shown that with the increase of the value of the electric charge Q the radius of the ISCO decreases.

Energy extraction from the rotating regular black hole through the different processes has been examined. We have found expression of the center of mass energy for the colliding neutral particles coming from infinity, based on the BSW (Baňados-Silk-West) mechanism. In particular we have calculated the center-of-mass frame energy of two neutral particles of the same mass parameter colliding around rotating regular black hole. It has been shown that two colliding neutral particles which are at rest at infinity with different angular momenta can give arbitrarily large value of the center of mass energy. The electric charge Q of rotating regular black hole decreases the potential of the gravitational field and the particle needs less bound energy at the circular geodesics. This causes increase of efficiency of the energy extraction from rotating regular black hole through BSW process in the presence of the electric charge Q.

Efficiency of the energy extraction due to the BSW effect has been investigated based on the formalism developed by Zaslavskii (2012b). Our calculations show that energy extraction occurs from the extreme rotating ABG black hole through the collisional Penrose process with smaller efficiency than the one from the Kerr black hole. Moreover we have shown that it occurs not only in IN+ scenario but also in OUT+ one. However, as it has been pointed out by Zaslavskii (2012b), the IN+ scenario is the most favorite one to extract energy with high efficiency. OUT+ scenario has maximum efficiency with ∼112.6 %, that is smaller than for IN+ with ∼145.5 %, and it occurs in a very narrow restricted region of the values of the charge Q and the spin parameter a of the extremal rotating Ayón-Beato-García black hole.

It has been also shown that the efficiency of the energy extraction from the rotating regular black hole via the Penrose process decreases with increase of the electric charge Q and is smaller in comparison to 20.7 % which is the efficiency for the extreme Kerr black hole with the specific angular momentum a=1. It is due to the fact that on account of the nonvanishing electric charge Q the ergosphere of the black hole decreases and for the limiting value of the electric charge Q>0.634 ergoregion vanishes. After disappearance of the ergosphere, the energy extraction does not occur.