1 Introduction

It is established fact that the surfaces of most asteroids are covered with an active layer of loose unconsolidated rocks and dust, the regolith, which has formed from planetary geological processes since the solar system’s origin (Housen et al. 1979; Housen and Wilkening 1982). And the mechanisms driving these dynamical processes are collectively called space weathering, which has been widely discussed during past decades (Clark et al. 2002). Measurements of the spectra properties of asteroids provide important evidence concerning the space weathering effects (Chapman 2004), among which the most salient issue is so-called “S-type conundrum” (Feierberg et al. 1982; Gaffey et al. 1993; Chapman 1995, 1996). The discovery of infilled, degraded craters and retained marks of ejecta, obtained from in-situ explorations of spacecrafts to several specific asteroids, shows this weathering process is still at work (Sullivan et al. 1996; Carr et al. 1994; Miyamoto et al. 2007; Veverka et al. 2001a, 2001b). Generally, for these airless small bodies of solar system, the impingement by micrometeoroids and solar wind particles is considered to be the dominant role in the space weathering (Chapman 2004). The respective local interactions could be very complicated and far-reaching in dynamics: bombardment of different sizes of meteorites could be accompanied with violent physical and chemical changes such as seismic vibration, debris ejecting and reimpacting, melting, vaporization and crystallization (Clark et al. 1992); the energetic particles irradiating the surface of asteroids could cause erosional changes and chemical modification, including the iron implantation and sputtering (Moroz et al. 1996). Besides, for Near Earth Asteroids (NEA), the encounters with terrestrial planets are also considered to be a factor of regolith resetting, that the tidal gravity may expose fresh materials on the surfaces (Nesvorny et al. 2010; Richard et al. 2010). It is also shown the thermal spin-up of small bodies as a result of YORP effects can lead to regolith motion on the surface (Scheeres et al. 2007).

A detailed look at the grains’ dynamics is apparently important and necessary for understanding of above weathering processes, especially for the evolution of surface geology for specific asteroid. A list of important applications of granular dynamics in planetary science was mentioned by Richardson et al. (2011), such as granular behaviors under microgravity environment, effects of seismic vibration on regolith media, driving mechanisms for size sorting/segregation of granular etc. (Rosato et al. 1987). New particle-based numerical methods were presented and applied for the simulation of granular on small body and planetary surfaces, with hard-sphere (HSDEM) and soft-sphere (SSDEM) discrete elements employed respectively (Schwartz et al. 2012). Flow models were applied to describe impact ejecta production and deposition behavior in extremely low-gravity environment (Housen et al. 1983). And Excavation Flow Properties Model (EFPM) was developed to individual impact’s properties after the Deep Impact experiment at Comet Tempel 1 (Richardson et al. 2007). Then a detailed three-dimensional Cratered Terrain Evolution Model (CTEM) was utilized to investigate the generation retention and migration of regolith (Richardson 2009).

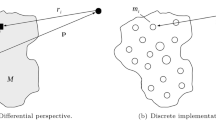
Compared with the scope of holistic behaviors of numerous particles or materials, a micro perspective is to examine the migration strategies of individual grain of the regolith during above processes, which would improve the understanding of local resurfacing effects for these physical forces. This study needs to confront the challenges of complexity of the dynamical environment and our poor knowledge on the mechanical properties of asteroid regolith. The irregular shape and heterogeneous constitution of asteroid lead to an extraordinary global gravitational field near the surface (Richardson et al. 2002; Ostro et al. 2002). The interaction of grains with the rugged non-uniform surfaces adds extreme random factors to the migrating motion, which could be a mixed routine of hopping, sliding, twisting and rolling. Under low gravity, the motion of grains might become inertia-dominated, and other spatial forces, such as solar pressure and van der Waals forces, might produce considerable effects especially on the smaller-sized grains that possess relatively higher surface area (Richardson et al. 2011; Scheeres et al. 2010; Richardson 2011). All these aspects demonstrate the great importance of models with adequate degree of sophistication; over-simplified models may lead to the loss of essential properties of the migrating process. Bellerose and Scheeres (2008) presented a general discussion on dynamics of particles on the surface of a uniformly rotating small body, which was modeled as a homogeneous ellipsoid. Analytical tools for total migration distance were developed in order to design the control laws of landing vehicles on asteroid surface, showing the great interest of modeling migrating grains for the design of landers and devices for surface exploration (Cottingham et al. 2009). Before, the initial conditions of ejecta fields generated from impacts on the asteroid surface was discussed by Geissler et al. (1996), including simulating results of landing locations of ejecta launched from the giant crater Azzurra on 243 Ida. A homogeneous polyhedral model of Ida was applied in the calculation of near-field gravity, and the migration of particles after reimpacts was neglected. Basically, numerical methods for dynamics of grains on asteroid surface are still limited to date. A major obstacle for this work is the lack of knowledge on the mechanical properties of asteroid regolith. It is hard to completely determine the mineralogy of diverse asteroids through reliance on Earth-based telescope remote sensing, because the space weathering might happen to different degrees, which has not been understood well enough. Several space missions involving in-situ analysis or sample return have been proposed or implemented (Farquhar et al. 2002; Landshof and Cheng 1995; Russel et al. 2005; Kawaguchi et al. 2005). High-resolution images of the surfaces of target asteroids (951 Gaspra, 243 Ida, 433 Eros, 25143 Itokawa and 4 Vesta) revealed remarkable details on the terrain of the regolith and size distribution of gravels (Belton et al. 1992, 1994; Zuber et al. 2000; Saito et al. 2006). Samples returned by Hayabusa mission provided information on the regolith formation of Itokawa, that the meteoroid impacts form much of the regolith particles and the seismic-induced grain motion on surface abrades them over time (Miyamoto et al. 2007). However, the mechanical features of grains are difficult to be uniformly approximated with a few parameters, which should be crucial for the accuracy of model. A feasible scheme is to correct the model by changing or adjusting the parameters with the criterion of experiments and observations. Once it is validated by successful comparison, the model can be broadly utilized in diverse practical circumstances unreachable by spacecraft or remote observations (Richardson et al. 2011).

In this paper, we present our method to model the migration of individual grain on asteroid’s surface, along with its application in the regolith movement in the steep slope of crater walls on asteroid 433 Eros. A global valid method for gravitational field’s calculation is developed by correcting possible singularities based on conventional polyhedron method. Classical Bézier Patches are employed to generate G 1 continuous surface over the polyhedral shape model of asteroid (Thomas and Stephen 2010). Then the motion of individual particle in any vicinal area is implemented by checking two routines, the orbital equations and surface equations, with a key technique called “ground tracing” in the process. In Sects. 2, 3 and 4, we introduced this method in great detail. Section 5 includes some basic tests for this method, i.e., to examine the accuracy of modified gravitational model and to check the morphology of trajectories near specific small bodies etc. We also demonstrate a possible application of this method to model regolith migration in crater Psyche of Eros and make a comparison with former observation and analysis.

2 Global gravitational field

Various methods were applied to evaluate the Newton’s volume integral of practical target objects, which are customarily approximated by ideal geometries, an aggregation of small elements or entire polyhedron (Forsberg 1984; Hubbert 1948). For asteroids of unusual shapes, Werner and Scheeres compared three typical methods to model the exterior gravitational field near them, and found a great advantage of polyhedral method on the convergence near the asteroid surface (Werner and Scheeres 1997). As a classical issue in mechanics, the procedure of computing the potential of an arbitrary polyhedron was referred to over hundred years ago (Rausenberger 1888). However, only with the improvements in digital computer technology during last decades, this methodology has been further evolved and become feasible in practice since it requires decomposition into a large number of elementary units.

Generally, there were two basic ideas for computing the attraction of arbitrary polyhedra: one is to divide the object into unit volume elements (e.g. prisms), of which the gravitational potential and attraction can be determined with analytical formulas (Nagy et al. 2000); the other is to transform the volume integral into summation of line integrals, inspired by Hubert in 1948. The latter was then brought into full development and successfully applied into the analysis of asteroid missions. Several pioneering work came from the issue on computation of gravitational and magnetic fields of planets by applying Gauss’ divergence theorem twice: first to surface and then to line integrals (Paul 1974; Plouff 1976; Barnett 1976). Analytical formulas for the gravitational potential and its derivatives of homogeneous polyhedra were presented in compact manner to suit for computer programming (Petrović 1996). And optimum expressions were presented to appropriate for efficient calculations (Pohánka 1988). Equivalent formulas of potential and derivatives up to second order were proposed through a different parameterization by Werner and Scheeres (1997), for which they induced the solid angle subtended by a face viewing from the field point (Werner 1994). These formulas were used to precisely evaluate the actual dynamical environments about specific asteroids during several in-situ explorations (Scheeres et al. 1998; Yeomans et al. 1997). Recently, this method’s application has extended to polyhedra with linearly varying density distribution (Hamayun et al. 2009).

In this section, we review the derivations of Werner and Scheeres’ formulas and pay special attention to the possible singularities in global field regime, including the field point inside, outside the polyhedra and in the polygonal faces and edges. The close forms of polyhedral potential and its 1-order derivative at arbitrary field point outside the polyhedron are

$$\begin{aligned} &{\begin{aligned}[b] U & = -\frac{1}{2} G \sigma\sum _{e \in\mathit{Edge}} \mathbf{r}_e \cdot \mathbf{E}_e \cdot\mathbf{r}_e L_e \\ &\quad {} + \frac{1}{2} G \sigma\sum_{f \in\mathit{Face}} \mathbf{r}_f \cdot\mathbf{F}_f \cdot \mathbf{r}_f \omega_f , \end{aligned}} \end{aligned}$$
(1)
$$\begin{aligned} &{ \bigtriangledown U = G \sigma\sum _{e \in\mathit {Edge}} \mathbf{E}_e \cdot\mathbf{r}_e L_e - G \sigma\sum_{f \in \mathit{Face}} \mathbf{F}_f \cdot\mathbf{r}_f \omega_f .} \end{aligned}$$
(2)

In Eq. (1) and Eq. (2), G is the gravitational constant, σ is the bulk density, an assumption of homogeneous density distribution is made in this method. r e and r f are vectors from the field point to the polyhedral points on edge e and face f, respectively. Constant edge dyad E e and face dyad F f are determined by edge unit normal vectors and face unit normal vectors, and the expressions are represented in Eqs. (7)–(8). ▽ is the gradient operator. The formulas Eqs. (3)–(4) present the edge factor L e and trigonal solid angle ω f obtained from respective integrations Eqs. (5)–(6) (Werner and Scheeres 1997).

$$\begin{aligned} &{ L_e = \ln \frac{a+b+e}{a+b-e},} \end{aligned}$$
(3)
$$\begin{aligned} &{ \omega_f =2 \arctan\frac{\mathbf{r}_1 \cdot ( \mathbf{r}_2 \times\mathbf{r}_3 )}{r_1r_2r_3 + \mathbf{r}_1 \cdot\mathbf{r}_2 r_3 + \mathbf{r}_2 \cdot\mathbf {r}_3 r_1 + \mathbf{r}_3 \cdot\mathbf{r}_1 r_2} .} \end{aligned}$$
(4)

Where a, b are the distances from the field point to the ends of the edge and e is the length of the edge; r i and r i (i=1,2,3) are the vector and distance from the field point to the three vertices of the triangular faces.

$$\begin{aligned} &{ L_e = \int_{e} \frac{1}{r} ds ,} \end{aligned}$$
(5)
$$\begin{aligned} &{ \omega_f = \int_f \frac{\bigtriangleup z}{r^3} dS .} \end{aligned}$$
(6)

Two classes of singularities might be caused during the calculation following above routines: the first is the application of Gauss’s divergence theorem with the conditions violated, which occurs when the field point locates inside the polyhedron or on its surface, making the integrated field function discontinuous at this point (Petrović 1996); the second is the numerical exceptions from Eqs. (3)–(4), resulted by the infinite integrals in Eqs. (5)–(6) when there are zero denominators in the integral area.

The second class can be corrected through examining these exceptions. The line integral Eq. (5) becomes singular only when the field point falls onto the responding edge, and then the result of Eq. (3) turns to be infinite. Back to the expressions of Eqs. (1)–(2), the multiplier of L e should be expanded as Eq. (7) to determine the actual value of the term, in which n A , n B are the unit normal vectors of two faces connected by edge e, and \(\mathbf{n}_{e}^{A}\), \(\mathbf{n}_{e}^{B}\) are the unit normal vectors of edge e, locating in faces A, B respectively. A well-known solution is to exclude a small neighborhood δ e around the zero point, and then calculate the normal integration over the remaining area e ∘ and approach the limit as δ e →0. Since the vector from the field point to the edge point re is vertical to \(\mathbf{n}_{e}^{A}\) and \(\mathbf{n}_{e}^{B}\), the value of edge related term Eq. (7) tends towards 0 vector when the field point is on the segment line of corresponding edge.

$$ \begin{aligned}[b] \mathbf{E}_e \cdot \mathbf{r}_e L_e & = \bigl( \mathbf{n}_{A} \mathbf{n}_{e}^{A} + \mathbf{n}_{B} \mathbf{n}_{e}^{B} \bigr) \cdot\mathbf{r}_e \int_{e} \frac{1}{r} ds \\ & = \lim_{\delta_e \rightarrow0} \bigl( \mathbf{n}_{A} \mathbf {n}_{e}^{A} + \mathbf{n}_{B} \mathbf{n}_{e}^{B} \bigr) \cdot \mathbf{r}_e \int_{e^{\circ}} \frac{1}{r} ds = \mathbf{0} . \end{aligned} $$
(7)

Similar operation is used to the surface integral Eq. (6), which becomes singular when the field point is inside the polygon or at the boundary. First, exclude a small neighborhood δ f around the zero point, then calculate the normal integration over the remaining area f ∘ and approach the limit as δ f →0. As shown in Eq. (8), the multiplier of ω f is determined by unit vector n f and the vector from the field point to the face point r f , which are vertical in the case of singularity stated above, thus the term Eq. (8) tends towards 0 vector.

$$ \begin{aligned}[b] \mathbf{F}_f \cdot \mathbf{r}_f \omega_f & = \mathbf{n}_{f} \mathbf {n}_{f} \cdot\mathbf{r}_{f} \iint_{f} \frac{\bigtriangleup z}{r^3} dS \\ & = \lim_{\delta_f \rightarrow0} \mathbf{n}_{f} \mathbf{n}_{f} \cdot\mathbf{r}_{f} \iint_{f^{\circ}} \frac{\bigtriangleup z}{r^3} dS = \mathbf{0} . \end{aligned} $$
(8)

Besides, since the numerator and denominator of formula Eq. (4) are both signed, Werner and Scheeres (1997) suggested to represent it as separate arguments in a computer atan2 function to calculate the solid angle, which reduce the exception cases of Eq. (4) to the points on the borders of the face polygon. Then the optimum expressions of the gravitational potential and attraction are represented by Eqs. (9)–(10) with corrections to these numerical exceptions.

$$\begin{aligned} &{ U = -\frac{1}{2} G \sigma\sum_{e \in\mathit{Edge}} \mathbf{r}_e \cdot\mathbf{P}_e (\mathbf{r} ) + \frac{1}{2} G \sigma\sum_{f \in\mathit{Face}} \mathbf{r}_f \cdot \mathbf{Q}_f (\mathbf{r} ) ,} \end{aligned}$$
(9)
$$\begin{aligned} &{ \bigtriangledown U = G \sigma\sum_{e \in \mathit{Edge}} \mathbf{P}_e (\mathbf{r} ) - G \sigma \sum _{f \in\mathit{Face}} \mathbf{Q}_f (\mathbf{r} ) .} \end{aligned}$$
(10)

Where P e (r) is vector function related affiliated with edge e and Q f (r) is vector function affiliated with face f, defined as Eqs. (11)–(12). r is field point vector; the operator—indicates taking the boundary of area; L e is calculated by formula Eq. (3), and ω f is calculated by formula Eq. (4) with atan2 as the computer function.

$$\begin{aligned} &{ \mathbf{P}_e (\mathbf{r} ) =\left \{ \begin{array}{l@{\quad}l} \mathbf{0}&\mathbf{r} \in e\\ \mathbf{E}_e \cdot\mathbf{r}_e L_e&\mathbf{r} \notin e \end{array} \right . ,} \end{aligned}$$
(11)
$$\begin{aligned} &{ \mathbf{Q}_r (\mathbf{r} ) =\left \{ \begin{array}{l@{\quad}l} \mathbf{0}&\mathbf{r} \in\bar{f}\\ \mathbf{F}_f \cdot\mathbf{r}_f \omega_f &\mathbf{r} \notin\bar{f} \end{array} \right ..} \end{aligned}$$
(12)

To detect in numeric whether a field point is on a specific edge of the polyhedron, specific numeric treatments must be performed. A finite neighborhood of edge e is carved out to declare the field point is on e if it is inside this neighborhood, which is to ensure the numerical continuity of data and the global valid computation of polyhedral method. Thus the numerical exceptions of the second class is avoided. Further, the singularities of the first class, which is more essential and influential to the determination of global gravitational field, are examined numerically. It was noticed for a long time that possible singularities may be induced due to the twice applications of Gauss’s divergence theorem (Petrović 1996), and solutions were proposed based on the formulas of pure line integrals (Tsoulis and Petrović 2001). Traditional methods of integral area division were employed and certain correction terms were taken into account to fix respective singularities. However, for the mixed formulas of line integrals and solid angles (9), (10), the theorem violation when the field point lies inside or on the polyhedron seems benign. Werner and Scheeres (1997) suspected these expressions are still correct in the interior. We present numerical proves to show these formulas could work at any field point on the surface and in the interior of polyhedron (see Sect. 5.1).

As an aside, this global valid method is crucial in the modeling of migrating granular, which provides detailed evaluation of the dynamical environment near the asteroid surface and enables us to take a special look at the granular motion under a good approximation of the actual gravitational field.

3 Bézier patches over polyhedra

Hundreds of asteroids have been detected by radar to date (Ostro et al. 2002), and tens of them got adequate coverage so that detailed three-dimensional models can be derived with reconstruction technique (Hudson 1993). Meanwhile, high-resolution images of nine asteroids have been transmitted back from in-situ explorations of spacecrafts (Farquhar et al. 2002). Based on these observations, global topography models (GTM) are exported generally in triangle-meshed polyhedron for further analysis of laboratory research (Neese 2004). These piecewise models provide rather detailed information on geology of the asteroid surface, but are still insufficient for modeling the migration of grains on asteroids. An essential barrier is the inconsistent states in two connected triangles when grains moving in the surface cross the medium edge.

The solution proposed in this section is to cover the polyhedron with patches of curved surfaces, which retain the profile of the asteroid’s shape and portray more detailed geology of its surface. G 1 continuous at the joint is required for these patches in order to keep the position and velocity consistent as the particle crossing two connected surfaces. An algorithm is developed by Shirman and Séquin (1987) to generate the local interpolated surface for meshes of cubic curves, which is directly applied to the triangle-meshed polyhedral model of asteroid. A union of geometrically continuous quartic Bézier patches is represented via two steps: first to construct the cubic curves between the polyhedral vertices and the second is to fill the mesh with Bézier patches. A brief report was published later to fix the errors of original triangular patch subdivision scheme and present an improved quadrilateral subdivision scheme (Shirman and Séquin 1991).

For arbitrary face of the polyhedral model, this algorithm starts by subdividing the face into three small triangles as shown in Fig. 1. Then 31 control points are determined on these flat subpatches to generate coplanar cubic curves with the pyramid faces. Three Bézier patches can be filled between these cubic boundaries to satisfy the geometric continuity (G 1) on them.

Fig. 1
figure 1

Subdivision of the polyhedral face △P1P2P3 and Bézier patches. Point O indicates the origin inside the polyhedron, P i (i=1,2,3) are numbers of vertices of the face, Z is the centroid of the triangle, and cubic boundaries \(\widehat{\mathrm{P}_{1}\mathrm{P}_{2}}\), \(\widehat{\mathrm{P}_{2}\mathrm{P}_{3}}\), \(\widehat{\mathrm{P}_{3}\mathrm{P}_{1}}\), \(\widehat{\mathrm{P}_{0}\mathrm{P}_{1}}\), \(\widehat{\mathrm{P}_{0}\mathrm{P}_{2}}\), \(\widehat{\mathrm{P}_{0}\mathrm{P}_{3}}\) lie in the planes OP1P2, OP2P3, OP3P1, OP0P1, OP0P2, OP0P3, respectively

Full size image

The derivation of the Bézier patches are omitted here and referred to Shirman and Séquin (1991) The expressions of these subpatches are represented in local affine frame (u,v), as illustrated in Fig. 2. Unique ID, composed of face number and patch number, is assigned to each subpatch, which is identified in turns of the vertex number of the face. Local frame (u,v) is defined with analogue orientation as Fig. 2, and the ranges of coordinates are normalized: 0⩽u⩽1, 0⩽u⩽1−v. Then the uniform expressions of the three Bézier patches over arbitrary face are represented in Eq. (13).

$$ \mathbf{r} = \mathbf{S} \bigl( u,v;\mathbf {a}_1^i, \mathbf{a}_2^i,\ldots,\mathbf{a}_{15}^i \bigr) . $$
(13)

Where subscript i=ID2=1,2,3 indicates the corresponding subpatch, the residual w=1−u−v, and \(\mathbf{a}_{1}^{i}, \mathbf {a}_{2}^{i}, \ldots, \mathbf{a}_{15}^{i}\) are vector parameters determined by the control points of face f, and their expressions are omitted here (Shirman and Séquin 1991). In addition, Eq. (13) is represented as quartic homogeneous polynomial of u, v and w, which is C ∞ continuous in the subpatches and G 1 continuous on the cubic boundaries. Actually, since the three patches of each face are coplanar for our polyhedron, the Bézier triangles are proved to be C 1 continuous on the boundaries (Wilson 2007).

Fig. 2
figure 2

Identification of the three patches of arbitrary face f and corresponding local associated local frames. The patch numbers follow the order of vertices P1, P2, P3 of face f

Full size image

These patched quartic Bézier triangles construct a global surface of asteroid out of the polyhedral model, and provide fine smoothness to meet our requirements of simulation of migrating grains on asteroids. An important reason for us to consider this tedious geometric processing is: abundant actual geographic information taken into account may help to sketch the broad outlines of what happened during the surface migration of specific asteroid. And this would give us more detailed evidences on several significant events of the asteroid evolution.

4 General strategy

In our approach, the motion paths in/above different subpatches are traced via projecting to the polyhedral surface at each integration step, thus the current ID and local coordinates are always recorded. A classical Runge-Kutta integrator with two time steps in used: the great step is adopted in the integration of orbital motion in far-field regime for efficiency, and the small one is adopted for integration of motion in and near the curved surfaces. A unit massive particle is considered for processible geometries, and its global trajectory could be seen as a chain of orbiting and sliding above/on the surface with links of instantaneous collision or liftoff. The equations of orbital motion and surface motion are represented respectively in the asteroid body-fixed frame and in the local frames associated with the subpatches. Collision searches are performed during the trajectory in near field by comparing the distances of field point and the projective point at each step. The switches between two modes, orbiting and sliding, are triggered primarily when the sign of normal contact force alternates: for a liftoff from sliding to orbiting, it is + to −; for a touchdown from orbiting to sliding, which is more complicated, the amplitude of the next hop should be first measured, when it is negligible and the contact force is +, the switch will be triggered. And due to the complex gravity field and irregular shape of surface, there is no analytical solution for the particle motion and all these operations will be conducted numerically.

4.1 Motion equations

4.1.1 Orbital motion

Considering the main perturbations in the near field, the motion equations are stated in the body-fixed frame, which is rotating uniformly about the pole axis of asteroid. Scheeres et al. (1998) presented a complete form of orbital equations of a unit massive particle around asteroid in the body-fixed Cartesian frame, which describe an autonomous system Eq. (14).

$$ \ddot{\mathbf{r}} + 2 \omega \times\dot {\mathbf{r}} + \omega \times ( \omega \times\mathbf{r} ) = -\bigtriangledown U. $$
(14)

Where ω is the angular velocity vector of asteroid. Considering the near-regime field motion, the perturbations from the sun and planets are ignored in Eq. (14). Introduce the definition of effective potential Eq. (15) which is the combination of the centrifugal and gravitational potentials, Eq. (14) is then represented by Eq. (16).

$$\begin{aligned} &{ V = -\frac{1}{2} ( \omega \times \mathbf{r} ) \cdot ( \omega \times\mathbf{r} ) + U ,} \end{aligned}$$
(15)
$$\begin{aligned} &{ \ddot{\mathbf{r}} + 2 \omega \times\dot {\mathbf{r}} = - \bigtriangledown V ,} \end{aligned}$$
(16)
$$\begin{aligned} &{ J =\frac{1}{2} \mathbf{r} \dot{\mathbf{r}} - \frac{1}{2} ( \omega \times\mathbf{r} ) \cdot ( \omega \times\mathbf{r} ) + U .} \end{aligned}$$
(17)

Noticing the dissipationless form of system Eq. (16), it can be proved to be a Hamiltonian system, and the generalized energy integral value Eq. (17) could be used as a verification of the simulation.

4.1.2 Surface motion

Obviously, the particle’s travel in the curved surface can be resolved into that of each Bézier patch in our approach. For arbitrary subpatch ID=(f,i), we define the local affine frame fixed at the contact point of the particle and surface (see Fig. 3). S u and S v indicate the partial derivatives vectors of surface equation Eq. (13) respect to the local coordinates (u,v), and n is the unit normal vector of the patch pointing out of the asteroid body, determined by Eq. (18).

$$ \mathbf{n} = \frac{\mathbf{S}_u \times\mathbf {S}_v}{\Vert \mathbf{S}_u \times\mathbf{S}_v \Vert } . $$
(18)
Fig. 3
figure 3

The local frame on surface of Bézier patch ID=(f,i). The origin locates at the position of the particle and three axis vectors point to S u , S v and n. The khaki plane indicates the tangent plane of surface at the particle position

Full size image

Note n points in the direction of the surface gradient, and S u , S v span the tangent plane and constitute its bases, so the velocity of the particle can be expressed as Eq. (19).

$$ \dot{\mathbf{r}} = \mathbf{S}_u \dot{u} + \mathbf {S}_v \dot{v} . $$
(19)

Formula Eq. (19) can be seen as the first-order time derivative of Eq. (13), and the second-order time derivative yields Eq. (20).

$$ \ddot{\mathbf{r}} = \mathbf{S}_{uu} \dot{u}^2 + 2 \mathbf{S}_{uv} \dot{u} \dot{v} + \mathbf{S}_{vv} \dot{v}^2 + \mathbf{S}_u \ddot{u} + \mathbf{S}_v \ddot{v} , $$
(20)

where S uu , S uv and S vv are the second-order partial derivatives vectors of Eq. (13). Relatively, the surface motion turns to be two-dimensional, and the contact force from the surface should be introduced to system. Thus, the motion equations in body-fixed frame of asteroid are obtained by adding terms of contact force to Eq. (16). In Eq. (21), a simplified version of rigid contact force is applied to the massive particle model, which includes one-sided supportive force and linear kinetic friction.

$$ \ddot{\mathbf{r}} + 2 \omega \times\dot {\mathbf{r}} = - \bigtriangledown V + N \mathbf{n} - \mu N \hat{\dot {\mathbf{r}}} . $$
(21)

Where N is the amplitude of normal supportive force, and μ is the coefficient of dynamic friction. The expression of Eq. (21) contains three terms of Coriolis force, potential force and the contact force, which dominates a dissipative system. Since Eq. (21) has a redundant degree of freedom, it should be represented with local coordinates (u,v). Substituting Eq. (13), Eq. (19), Eq. (20) to Eq. (21), it yields

$$\begin{aligned} &{ \mathbf{S}_u \ddot{u} + \mathbf{S}_v \ddot{v} = N \mathbf{n} - \mathbf{F} ,} \end{aligned}$$
(22)
$$\begin{aligned} &{ \begin{aligned}[b] \mathbf{F} & = \bigtriangledown V \circ \mathbf{S} + \mu N \frac{ \mathbf{S}_u \dot{u} + \mathbf{S}_v \dot{v}}{\Vert \mathbf{S}_u \dot{u} + \mathbf{S}_v \dot{v} \Vert } + 2 \omega \times ( \mathbf{S}_u \dot{u} + \mathbf{S}_v \dot{v} ) \\ &\quad {} + \mathbf{S}_{uu} \dot{u}^2 + 2 \mathbf{S}_{uv} \dot{u} \dot{v} + \mathbf{S}_{vv} \dot{v}^2 . \end{aligned}} \end{aligned}$$
(23)

Where F is a collection of terms for brevity, as presented in Eq. (23). ∘ indicates compound operation between functions. Noticing n⋅S u =0 and n⋅S v =0, Eq. (22) does dot product with S u and S v , respectively, it yields

$$ \begin{bmatrix} \mathbf{S}_u \cdot\mathbf{S}_u & \mathbf{S}_u \cdot\mathbf{S}_v \\ \mathbf{S}_v \cdot\mathbf{S}_u & \mathbf{S}_v \cdot\mathbf{S}_v \end{bmatrix} \begin{bmatrix} \ddot{u} \\ \ddot{v} \end{bmatrix} = - \begin{bmatrix} \mathbf{S}_u \cdot\mathbf{F} \\ \mathbf{S}_v \cdot\mathbf{F} \end{bmatrix} . $$
(24)

Since S u and S v are always independent, the coefficient matrix of this two-dimensional system is nonsingular, which determines the solution to Eq. (24) is unique. Therefore, Eq. (24) describes an explicit form of autonomous dynamical system, which is easy to deal with during integration.

$$ N = \mathbf{n} \cdot\mathbf{F} . $$
(25)

The normal supportive force should be calculated at every integral step to check the facility of the surface motion. Only positive value of N indicates valid motion on surface, since the constraint is one-sided. The expression of N yields Eq. (25), derived from Eq. (22) with dot product by n.

4.1.3 Collision

The condition for the particle to collide with the surface between two steps is

$$ \Vert \mathbf{r}_k \Vert > \bigl\Vert \mathbf {S} ( u_k, v_k ) \bigr\Vert \cap \Vert \mathbf{r}_{k+1} \Vert \leqslant\bigl\Vert \mathbf{S} ( u_{k+1}, v_{k+1} ) \bigr\Vert . $$
(26)

Where r k , r k+1 are the position vectors at steps t k and t k+1, (u k ,v k ) and (u k+1,v k+1) are respective local coordinates at current subpatch. This condition is inspected for every step during the orbiting motion in the near field. Since the time step is really tiny, local linear approximation is applied to determine the position and velocity at collision following routines Eqs. (27)–(31).

$$\begin{aligned} &{ \lambda_1 = \frac{ ( \Vert \mathbf{r}_k \Vert - \Vert \mathbf{S} ( u_k, v_k ) \Vert ) \Vert \mathbf{r}_{k+1} \Vert }{\Vert \mathbf{r}_k \Vert \Vert \mathbf{S} ( u_{k+1}, v_{k+1} ) \Vert - \Vert \mathbf{r}_{k+1} \Vert \Vert \mathbf{S} ( u_k, v_k ) \Vert } ,} \end{aligned}$$
(27)
$$\begin{aligned} &{ \lambda_2 = \frac{ ( \Vert \mathbf{r}_k \Vert - \Vert \mathbf{S} ( u_k, v_k ) \Vert ) \Vert \mathbf{S} ( u_{k+1}, v_{k+1} ) \Vert }{\Vert \mathbf{r}_k \Vert \Vert \mathbf{S} ( u_{k+1}, v_{k+1} ) \Vert - \Vert \mathbf{r}_{k+1} \Vert \Vert \mathbf{S} ( u_k, v_k ) \Vert } ,} \end{aligned}$$
(28)
$$\begin{aligned} &{ \bigl( u^0, v^0 \bigr) = ( 1 - \lambda_1 ) ( u_k, v_k ) + \lambda_1 ( u_{k+1}, v_{k+1} ) ,} \end{aligned}$$
(29)
$$\begin{aligned} &{ \mathbf{r}^- = \mathbf{S} \bigl( u^0, v^0 \bigr) ,} \end{aligned}$$
(30)
$$\begin{aligned} &{ \nu ^- = \lambda_2 \dot{\mathbf{r}}_k + ( 1 - \lambda_2 ) \dot{\mathbf{r}}_{k+1} .} \end{aligned}$$
(31)

Where the virtual position r 0 is used as an intermediate variant to determine the local coordinates of the contact point (u 0,v 0), and the approach is illuminated in Sect. 4.2. The position and velocity vectors at contact point is determined by Eqs. (30)–(31).

As illustrated in Fig. 4, particle impacting on the tangent plane at the contact point has an incoming velocity \(\mathbf {\nu}^{-}\) and a outcoming velocity ν +, which are coplanar with the norm direction of surface at the point. Collisions are treated as instantaneous events with a configurable amount of energy loss due to restitution and surface coupling. The normal restitution is parameterized by coefficient ε n , s.t. 0⩽ε n ⩽1, where 0 indicates perfectly inelastic collision, and 1 indicates ideal elastic collision. The tangent coupling of surface is parameterized by coefficient ε t , s.t. −1⩽ε t ⩽1, where −1 indicates reversal of tangent velocity, 0 indicates complete damping of tangent motion and 1 indicates no tangent coupling.

$$\begin{aligned} &{ \nu ^- = \nu _n^- + \nu _t^- ,} \end{aligned}$$
(32)
$$\begin{aligned} &{ \nu ^+ = -\varepsilon_n \nu _n^- + \varepsilon_t \nu _t^- .} \end{aligned}$$
(33)
Fig. 4
figure 4

Dynamics of collisions for particle on the tangent plane at the contact point. ν −, ν + are the relative velocities before and after the collision, coplanar with the normal vector n. t is the tangent vector of the surface in the velocity plane. The red arrows indicate the contact forces during collision

Full size image

Equations (32)–(33) represent the normal and tangent components of the incoming and outcoming velocities during collision. For instance, ε n =0, ε t =0 means the particle is stuck when touching the surface; ε n =1, ε t =1 means perfect bouncing by smooth surface. In practice, it is more likely that the particle has slight restitutions both in the normal and tangent directions, meaning ε n and ε t take some values between 0 and 1.

4.2 Ground trace

According to our model, the particle motion is a mixed routine of orbiting and sliding linked by instantaneous collision and liftoff. An obvious difficulty is to build a simulation scheme which enables automatic conversion between different motion modes. Since the orbital motion is represented in asteroid body-fixed frame, and the surface motion is represented with local coordinates of patches of the polyhedral surface, it is necessary to identify the subpatch beneath the particle at each step. Then the local coordinates of the particle’s projection on the Bézier subpatch can be derived and the surface motion connected with the orbital motion will continue. A barrier in numeric should be noticed that searching the subpatch ID through all the faces of the polyhedron at each step during orbiting would cost too much both because of the tiny step value and the huge number of faces for real asteroid model. In this section, we will present our solution to implement efficient global tracing of the particle motion.

Our approach is based on a class of objects called star-shaped, meaning there exists a point in the interior of the object from where the whole object is visible. In practice, most asteroid polyhedral models have this property, so it is still of wide universality. As illustrated in Fig. 5, each point of the trajectory, either on orbit or in surface, can be uniquely mapped to the two-dimensional projection on the patched polyhedral surface, named ground trace, which is evidently continuous on the triangle patches for any trajectories of the particle. It means the local coordinates of the ground trace are continuous as the particle moving, though local ID is being updated sporadically. Thus the ground trace will play as a link between different motion modes. Specifically, the sliding part of the trajectory possesses the same ID and local coordinates (u,v) with its ground trace, which adds no calculation amount; for orbiting part, it takes some cost to position its projection in ground trace: since the initial ID is provided and all the crossing events will be recorded and marked, we ensure the patch ID will never lost during the motion. Then the local coordinates (u,v) are determined by projecting formulas Eqs. (34)–(35).

$$\begin{aligned} &{ u = - \frac{\mathbf{r} \times\mathbf{p}_1 \cdot ( \mathbf{p}_3 - \mathbf{p}_1 )}{\mathbf{r} \times ( \mathbf{p}_2 - \mathbf{p}_1 ) \cdot ( \mathbf {p}_3 - \mathbf{p}_1 )} ,} \end{aligned}$$
(34)
$$\begin{aligned} &{ v = - \frac{\mathbf{r} \times\mathbf{p}_1 \cdot ( \mathbf{p}_2 - \mathbf{p}_1 )}{\mathbf{r} \times ( \mathbf{p}_3 - \mathbf{p}_1 ) \cdot ( \mathbf {p}_2 - \mathbf{p}_1 )} .} \end{aligned}$$
(35)
Fig. 5
figure 5

The ground trace (white line) of arbitrary trajectory (dark line). r is point of the trajectory, Q is the projection on the polyhedral surface, points 1, 2, 3 are the positions of crossing different patches

Full size image

Where p 1, p 2, p 3 are the vectors of three vertices of the triangle patch with the ID given. The triple product of the denominator is nonzero due to the assumption of star-shaped. Figure 5 also shows when the ground trace touches the boundaries of the triangle patches. We defined six boundaries for any patch, as illustrated in Fig. 6, and the corresponding regions of local coordinates are listed in Table 1.

Fig. 6
figure 6

Six boundaries of arbitrary patch

Full size image
Table 1 Regions of the boundaries
Full size table

B1, B2, B3 are edge boundaries and B4, B5, B6 are vertex boundaries. With current ID given, the ground trace locates in the patch only if 0⩽u⩽1 and 0⩽v⩽1−u, therefore the crossing events are detected only when this criterion is broken. The ID should be first updated with the ID of the neighbor patch sharing the same boundary, as illustrated in Fig. 7. Nevertheless, the two cases, crossing through edges (Fig. 7(a)) and crossing through vertices (Fig. 7(b)), must be treated separately. For the vertex case, because there are more than one neighbor patches at the crossing vertex, searching is required to find the real next patch that the ground trace will pass. Here a convenient way is to compare the edge vectors by projecting all neighbor patches to the current plane. After the new ID determined, the local coordinates at k+1 step should be reset back to the crossing point (u 0,v 0) to avoid skipping the real next patch, and then the new local coordinates \((u'_{k+1}, v'_{k+1})\) of crossing point could be calculated with the updated ID following the correspondences in Table 2.

Fig. 7
figure 7

Two cases when the ground trace crosses the boundary of current patch. k is the current step and k+1 is the first step to violate the inside criterion. f 1, i 1 and f 2, i 2 are the ID of the current patch and next patch, respectively

Full size image
Table 2 Local coordinates on boundaries belonging to two connected patches
Full size table

The continuous ground trace ensures consistent states of the particle when crossing between different patches. Linear interpolation is applied to approximate the states at the cross point by following Eqs. (36)–(41), respectively for orbiting part and sliding part.

$$\begin{aligned} &{ \eta= \frac{ ( u^0 - u_k ) ( u_{k+1} - u_k ) + ( v^0 - v_k ) ( v_{k+1} - v_k )}{ ( u_{k+1} - u_k ) ^2 + ( v_{k+1} - v_k ) ^2} ,} \end{aligned}$$
(36)
$$\begin{aligned} &{ \bigl( u^0, v^0 \bigr) \rightarrow \bigl( u'_{k+1}, v'_{k+1} \bigr) .} \end{aligned}$$
(37)

For surface motion, Eqs. (38)–(39) are carried out to determine the sliding velocity in local frame.

$$\begin{aligned} &{ \bigl( \dot{u}^0, \dot{v}^0 \bigr) = \eta ( \dot{u}_{k+1}, \dot{v}_{k+1} ) + ( 1 - \eta ) ( \dot{u}_k, \dot{v}_k ) ,} \end{aligned}$$
(38)
$$\begin{aligned} &{ \begin{aligned}[b] & \mathbf{S}_u \bigl( u'_{k+1}, v'_{k+1} \bigr) \dot{u}'_{k+1} + \mathbf{S}_v \bigl( u'_{k+1}, v'_{k+1} \bigr) \dot{v}'_{k+1} \\ &\quad = \mathbf{S}_u \bigl( u^0, v^0 \bigr) \dot{u}^0 + \mathbf{S}_v \bigl( u^0, v^0 \bigr) \dot{v}^0 . \end{aligned}} \end{aligned}$$
(39)

For orbital motion, Eqs. (40)–(41) are carried out to determine the position and velocity vectors in asteroid body-fixed frame.

$$\begin{aligned} &{ \mathbf{r}^0 = \eta\mathbf{r}_k + ( 1 - \eta ) \mathbf{r}_{k+1} ,} \end{aligned}$$
(40)
$$\begin{aligned} &{ \dot{\mathbf{r}}^0 = \eta\dot{\mathbf{r}}_k + ( 1 - \eta ) \dot{\mathbf{r}}_{k+1} .} \end{aligned}$$
(41)

Thus the uniform global trajectory of the particle is determined by following the ground trace between different patches. The remaining problem is to switch between orbiting and sliding modes, which will finally implement the simulation of the particle’s free motion on/around the asteroid surface. According to our model, a simple principle is adopted for a quick switch between two motion modes. As illustrated by Fig. 8, the sliding particle lifts off the surface only if N turns negative, determined by Eq. (25). Then the following trajectory should be obtained by integrating orbital equations Eq. (16), with the initial conditions determined using Eq. (13) and Eq. (19). On the other hand, collision is detected when the orbiting particle falls down to the surface, and the following motion mode depends on the normal and tangent components of the outcoming velocity ν +: the normal component \(\nu_{n}^{+}\) represents a hop in the normal direction, and the necessary condition for sliding is this hoping time should be small enough to be ignored. In our numerical operation, a comparability criterion Eq. (42) is derived with parabolic approximation, which implies the resolution of the numerical integral is insufficient to capture the shape of this slight hop. Meanwhile, if the tangent component \(\nu_{t}^{+}\) satisfies the condition of positive N, the switch will be performed.

$$ 2 \frac{\nu_n^+}{a_n} \sim\delta t . $$
(42)

Where δt is the integral step and a n is the normal component of the potential force −▽V.

Fig. 8
figure 8

Switches between the orbiting mode and sliding mode. The red line indicates the surface trajectory and the dark line indicates the orbital trajectory. The dotted line in (a) indicates a ‘tricking’ surface trajectory with negative N; the dotted line in (b) indicates a ‘tricking’ hop which is neglected in numeric

Full size image

5 Basic tests

A suite of simple tests was developed to examine the performance of the methodology proposed in this paper. Examples include testing the validity of the modified gravitational model near the surface of the polyhedron, checking the morphology of orbits in different working conditions, and applying the method to survey the seismic behaviors of regolith material on the inner walls of a specific crater.

5.1 The gravitational field of a homogeneous sphere

A homogeneous sphere is first considered for its gravitational potential and attraction are analytically determined both at exterior and interior. Figure 9 presents two polyhedral models of a unit homogeneous sphere with different surface grids. Figure 9(a) indicates a standard grid generated following the latitude and longitude, including 2114 vertices and 4224 faces, and Fig. 9(b) indicates a grid generated following a random strategy, including 2048 vertices and 4096 faces. This section will check the approximation of the modified polyhedron method with these two grids employed (both of high resolution).

Fig. 9
figure 9

The surface grids of the unit sphere generated with different divisions

Full size image

Assuming the density of the unit sphere is 1, the gravitational potential and attraction in arbitrary radial direction are

$$\begin{aligned} &{ U = \left \{ \begin{array}{l@{\quad}l} \frac{2 \pi}{3} (r^2-3 ) & r \leqslant1\\ -\frac{4 \pi}{3} & r > 1\\ \end{array} \right . ,} \end{aligned}$$
(43)
$$\begin{aligned} &{ \bigtriangledown U = \left \{ \begin{array}{l@{\quad}l} \frac{4 \pi}{3} r & r \leqslant1\\ \frac{4 \pi}{3 r^2} & r > 1\\ \end{array} \right . ,} \end{aligned}$$
(44)

where r is the distance from the center of the sphere to the field point. Figure 10 illustrates the theoretical values of the gravitational potential and radial attraction for r from 0 to 2, together with the results derived from the modified gravitational model with different surface grids.

Fig. 10
figure 10

The comparison of the gravitational potential and attraction derived from analytical formulas and modified polyhedral model. The solid line indicates the theoretical value, the crosses indicate the results from the polyhedron of standard grid, and the circles indicate the results from the polyhedron of random grid

Full size image

As shown in Fig. 10, the values at the test points are exactly consistent from the interior to the exterior, especially for the test point at the edge/face of the polyhedron where the singularity has been fixed.

5.2 Example trajectories near small bodies

This section gives some examples for trajectories near/on the surface of specific small bodies, to check the performance of our method to mimic the motions in different working conditions, and to demonstrate the possible patterns of these motions. Figure 11 illustrates the typical motions around a non-rotating homogeneous sphere (a) and those around asteroid 2063 Bacchus (b).

Fig. 11
figure 11

The typical motions near/on the surfaces of a homogeneous sphere and the model of asteroid 2063 Bacchus. The numbered trajectories marked with different colors indicate the typical motion patterns

Full size image

The polyhedral model of unit sphere with random surface grid is applied (see Fig. 9(b)). Figure 11(a) shows three trajectories initialized at the same position and with the same velocity direction: trajectory 1 indicates the escaping motion when the initial velocity exceeds the escaping speed; trajectory 2 indicates the elliptic periodic orbit surrounding the central sphere when the magnitude of the initial velocity is moderate; and trajectory 3 indicates the collisional orbit when the initial velocity is quite small, followed by hopping on the spherical surface and damped out eventually.

A normalized polyhedral model of Bacchus is used in this section, including 2048 vertices and 4092 faces. Hypothetically, take the bulk density 2.44 g/cc and the period 14.9 h, and assume the dynamic friction coefficient μ=0.6, the static friction coefficient μ S =0.7, the normal restitution coefficient ε n =0.6 and the tangent coupling of surface ε t =0.9. Figure 11(b) shows four trajectories initialized at the same position with different velocities. Trajectories 1 and 2 have similar initial velocities and experience a serious separation after collisions, which indicates a high sensitivity to the initial conditions, thus the mixed orbital motion and surface motion can be very unstable in dynamics. Trajectory 3 indicates a general conversion from orbital motion to surface motion, experiencing a transition composed of a sequence of hops, and then the test mass point stops at the bottom of a crater. Trajectory 4 indicates the conversion from surface motion to orbital motion, when the sliding speed exceeds the local separating speed and then the mass point lifts off Bacchus’ surface.

5.3 Regolith transport in crater Psyche of 433 Eros

High-resolution images of Eros from the NEAR Shoemaker spacecraft have revealed variant albedo, especially on steep crater walls (Veverka et al. 2001a, 2001b), which indicates the downslope movement of the weathered material. Meticulous survey shows several features of these bright and dark patterns such as the distribution and thickness of the weathered layer, and the general connection with the gravitational slope (Thomas et al. 2002). Analysis on the mechanism responsible for the regolith transport suggests the degree and rate to expose the bright region should be a key factor since the space weathering is meanwhile going on. The impact-related processes are considered as an important mechanism responsible for the downslope movement of regolith because the impacting event lofts local particles and causes a seismic shaking which makes wide and continuous effects on the landslide of the regolith (Mantz et al. 2004). Cheng et al. (2002) applied simplified model to demonstrate the dependence of slope failure on the strength of seismic shaking. The analysis shows the downslope motion is sensitive to the local gradient, such as on ponds and crater walls. And the observed contrast boundaries of the bright region seems more like to be formed in repeated small disturbance such as seismic shaking than in direct impacting (Mantz et al. 2004).

We survey the seismic behavior of regolith material on crater walls with our method employed. Due to the observation, the shifts of grains in regolith do not cover the entire length of long slopes, so downslope movement should be low-momentum that the migrating grains must be halted by friction of the surface before reaching the bottom of the crater. And the bright albedo regions form by accumulation during frequent seismic shaking. Richardson et al. (2004) stated the activity of impact-induced seismic on Eros surface modification process and developed global modeling method to analyze the response of regolith covered craters. In this section, the crater Psyche on Eros is examined for distinct bright and dark markings are presented in its inner walls (Mantz et al. 2004). The surface seismogram depends on the size of the impactor and the distance away from the impacting point. Comparing with the magnitude of surface gravity of Eros 10−4 g, a relatively large disturbance from seismic shaking is adopted that the initial lifting velocity is uniformly set to 10−1 m/s normal to the surface. Figure 12(a) illustrated the slope map in crater Psyche, which is determined from the gravitational attraction, centrifugal force and the local topography based on the global shape model of Eros (Gaskell and Neese 2008) with a surface resolution of ∼110 m. This colormap correlates with the bright and dark regions on large scales while not on finer scales, implying the gravity, centrifugation and topography are major factors for general trends of regolith movement and other mechanisms take effects more locally.

Fig. 12
figure 12

Map of the 5.3 km crater Psyche. Color map (a) shows the slope of the crater walls ranging (2°, 35°); gray map (b) shows the topography of Psyche and the vectors indicate the shifts of the sample particles following initial disturbance

Full size image

The critical values of friction coefficient determined from the slopes are used to estimate proper value in our model. Uniform dynamic friction coefficient μ is set as 0.6; static friction coefficient μ S is 0.7. And setting the normal restitution coefficient ε n =0.6 and the tangent coupling of surface ε t =0.9, Monte Carlo simulations are carried out throughout the crater area. ∼5000 particles are employed to sketch the regolith movement at relative high resolution. Figure 12(b) illustrates the distribution of the shift vectors at sample particles.

In Fig. 12, the distribution of the shifting vectors caused by seismic shaking is slope related: particles originally at steep slope shift farther than those at gentle slope, which is consistent with the analysis by Mantz et al. (2004); the shifting directions are generally correlated with local gradient towards the shallower of the crater. To take a detailed look at the connection between the slope and shift, sample particles are projected into a polar coordinate system. The local mean slope and mean shift at each polar area are illustrated in Fig. 13(a) and Fig. 13(b), which are in similar trend: the value (mean slope and shift) grows as the polar radius increase, and double peaks at large radius around ∼120° and ∼250°.

Fig. 13
figure 13

Histograms of slope (a) and shift (b) in polar coordinates, with mean values of data in z-axis

Full size image

The connection between high albedos and steep slopes has been established for crater walls on 433 Eros (Thomas et al. 2002; Mantz et al. 2004). Above simulations survey this problem from a view of individual particle behaviors, and the results show: the movement of regolith is primarily slope dependent, steep slopes lead to much faster shifting of the regolith material down to the shallower than gentle ones; this downslope movement caused by seismic shaking is basically low-momentum, and the steady state of the regolith is achieved as a balance with weathering effects; irregular boundaries and multiple units of the large-shifting region (similar as the high albedo region in Psyche) suggest the mobilized regolith is halted by friction and changes in topography. Consequently, the results support that seismic shaking should be a key factor in the formation of the high albedo regions in crater walls on Eros, which also work as a test of this method.

6 Conclusions

New numerical method based on the polyhedral shape data of asteroid is developed for simulating the migration of regolith material. Possible singularities on the surface in former gravitational polyhedral method are fixed and Bézier patches are used to generate geometrically continuous surface. Ground trace is employed as a numerical technology to locate the particle on and above the piecewise surface model. The validity of the modified gravitational model is verified using a homogeneous sphere, which enables a comparison with the theoretical results. Example trajectories near/on the surface of specific small bodies are generated in numeric, demonstrating the possible motion patterns in different working conditions. Applications of this method are finally discussed, especially for grains’ seismic migration on crater walls of asteroid 433 Eros, showing good match of the regolith behaviors from former analysis and observation. In summary, our approach currently is still crude for examining very detailed geographic processes on specific asteroid, since it adopted globally uniform surface parameters of mechanics and simple particle model of grains in regolith. The advantage is irregular topography and relatively precise surface gravity are introduced into modeling of the grains’ dynamics, which could be profitable for revealing the nature of regolith migration in diversified terrains.