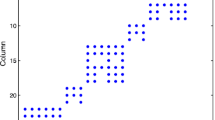1 Introduction

The distance to the Galactic center R 0 represents the most fundamental parameter for the study of Galactic structure, kinematics, and dynamics. It is also a difficult quantity to evaluate. Francis and Anderson (2013) list 135 determinations made between 1918 and 2013 with values ranging from 5.5 kpc to 16.4 kpc, with less scatter for the post-1980 values. Kerr and Lynden-Bell’s classic paper (1986) lists determinations from a low of 6.7 kpc for RR Lyrae stars to a high of 10.5 kpc for Hii regions. Perryman’s (2009) Table 9.1, more recent than Kerr and Lynden-Bell, shows values ranging from the pre-Hipparcos 7.1 kpc from H2O masers in Sgr B2 to 9.3 kpc for RR Lyrae stars calibrated from Hipparcos results.

R 0 must be determined by methods other than line of sight distance, and one should query: which method is best? Reid’s paper (1993), somewhat dated but still useful, summarizes various methods used to determine R 0. Assumptions of some sort enter into nearly all methods. One could, for example, use Galactic dynamics, but Galactic forces are complex and complicate a dynamical study of stellar motion. Any determination of the distance depends on assumptions as to the nature of the forces. Aumer and Binney (2009), for example, using parallaxes, proper motions, and line-of-sight velocities of 18 masers, find values for various Galactic models in the range 6.7–8.9 kpc. Three other recent determinations all represent more indirect methods. Gillessen et al. (2009) fit 32 stellar orbits to a point-mass potential for the black hole near the Galactic center and find R 0=8.33±0.35 kpc. Shen and Zhang (2010) use Hipparcos observations of classical Cepheids to fit radial velocity and proper motion kinematical equations and an axisymmetric model for the Galaxy to find a distance of 8.0±0.8 kpc. Sofue et al. (2011) employ kinematical relations on objects near the Galactic solar circle to determine R 0=7.54±0.77 kpc.

Galactic or stellar kinematics, which studies the movements of stars without examining the dynamics that induce the movements, obviates the need for such assumptions. Milne (1935), among others, has shown that the structure of the kinematical equations depends not on any particular dynamical theory, but merely on the hypothesis that a space-velocity frequency function exists continuous with respect to the coordinate system used. Ogorodnikov (1965, p. 73), in fact, states that one may determine R 0 without any assumptions by use of second-order kinematical equations of differential Galactic rotation. The “without any assumptions”, of course, is predicated upon there being no significant modifications to the kinematics induced by differential rotation.

My analysis depends heavily on statistics. Observational astronomers may find such use excessive and feel that a minimum of mathematics plus astronomical intuition becomes preferable. But I agree with Kurth when he asserts (1967, p. vii) that application of proper statistical tests could overturn a number of accepted hypotheses and what seem to be established facts. Trumpler and Weaver, in their classic text Statistical Astronomy (1962, p. 184), echo this sentiment and state that errors in more than one variable, what is known today as the total least squares problem and used by astronomers, had been insufficiently studied at the time, which may have compromised many important and fundamental investigations. One’s visceral instinct as to what a result should be can become compromised when confronted with solid statistics. As an example Sherill (1999) analyzes how at the beginning of the 20th century double star astronomer T.J.J. See’s overreliance on instinct lead him to carelessness and mischaracterization of results. Eichhorn and Cole (1985), moreover, maintain, by studying the compilation of star catalogs, that the very name “systematic error” is a misnomer and arises from incomplete modelization that leads to systematic trends in the residuals. Statistical tests determine whether or not the residuals are random; if they are random, there is no systematic error.

2 The reduction model

Consider a Cartesian coordinate system with x-axis directed towards the Galactic center, y perpendicular to x in the direction of increasing galactic longitude l,z perpendicular to the x–y plane and positive for positive Galactic latitude b. Let \(\dot{r}\) denote radial velocity in km sec−1, μ l proper motion in Galactic longitude in milli-arc-sec (mas) per year, μ b proper motion in latitude in the same units, κ a constant with value 4.74047 km sec−1 yr, and π the parallax in mas. The components of the solar motion are denoted by −X, −Y, −Z. Thus, X, Y, Z themselves are a reflex solar motion. Edmondson (1937) shows that \(\dot{r},\mu _{l}\), and μ b may be represented by Fourier expansions involving the 21 coefficients a 1:3,0:3, b 1:3,1:3:

$$\begin{aligned} \begin{aligned} &\dot{r}=\sum_{j=0}^{4}a_{1j} \cos jl+\sum_{j=1}^{3}b_{1j}\sin jl+ X\cos l\cos b \\ &\phantom{\dot{r}=\,\,}{} +Y\sin l\cos b+Z\sin b; \\ &\kappa \mu _{b}=\sum_{j=0}^{4}a_{3j} \cos jl+\sum_{j=1}^{3}b_{3j}\sin jl- X\cos l\sin b \\ &\phantom{\kappa \mu _{b}=\,\,}{}-Y\sin l\sin b+Z\cos b; \\ &\kappa \mu _{l}=\sum_{j=0}^{4}a_{2j} \cos jl+\sum_{j=1}^{3}b_{2j}\sin jl- X\sin l+Y\cos l; \end{aligned} \end{aligned}$$
(1)

If U,V,W are components of the velocity in rectangular coordinates x,y,z at a given point, \(U=\dot{x},V=\dot{y},W=\dot{z}\), the Fourier coefficients a,b are functions of π,b, and the first and second partial derivatives of U,V,W with respect to x,y,z. If we use rectangular coordinates Eq. (1) becomes a linear system for 30 unknowns: 9 first order partial derivatives, u x =∂U/∂x,u y =∂U/∂y,…,w z =∂W/∂z, 18 second order partial derivatives, u xx =∂ 2 U/∂x 2,u xy =∂ 2 U/∂x∂y,…,w zz =∂ 2 W/∂z 2, and the three components of the reflex solar motion. No assumptions other than the existence of the derivatives and the validity of the Fourier series enter into Eq. (2). Whittaker and Watson (1927, p. 161) discuss the conditions for a Fourier series to converge, one of which stipulates that only a finite number of discontinuities are present. This becomes important because density waves, associated with spiral arms, could induce discontinuities in the kinematical parameters. Because O and B stars are associated with spiral arms, density waves could affect the kinematics of these stars. As for the existence of the first and second-order derivatives, Branham (2002) has shown that they exist for the O and B stars by actually calculating their values.

The unknowns, however, do not involve R, the distance of the specified point from the Galactic center. If the specified point is the Sun, then R=R 0. For R to enter the equations of condition one must change to cylindrical or spherical coordinates, which permit a direct determination of the distance. Edmondson (1937) uses a cylindrical system with a total of 18 first and second order partial derivatives that include R and R 2 in the denominator. Certain symmetry assumptions bring about the reduction from 27 to 18. It thus appears as if we have a nonlinear system with 21 unknowns once the reflex solar motion is included. But such is not the situation because not all of the unknowns are independent. A singular value decomposition (SVD) demonstrates that only 10 of the unknowns are in fact independent. Edmondson may have been unaware of this defect because he nowhere employs this set of unknowns, but rather a subset of six unknowns. But it is important to realize that the genuine reduction in unknowns with cylindrical coordinates is not from 27 to 18, as one might feel upon reading Edmondson’s article, but from 27 to 10.

Consider now spherical coordinates. If O is the center of the Galaxy spherical coordinates with respect to O become x=Rcoslcosb,y=Rsinlcosb, z=Rsinb with 9 first order partial derivatives, ∂U/∂R,∂U/∂l,∂U/∂B,…,∂W/∂b and 18 second order partials, ∂ 2 U/∂R 2,∂ 2 U/∂R∂l,…,∂ 2 W/∂b 2. One might feel that we can once again employ 27 partial derivatives, but this is an illusion. It is true that one can express the spherical coordinate partials in terms of the rectangular coordinate partials and vice versa. I will not show the partials because they become complicated, especially those of second order. But in theory we have a 27×27 matrix linking the spherical partials with their rectangular counterparts and its inverse going the other way. If we consider the 27 rectangular partial derivatives a mathematical group, their representation is irreducible. But the spherical coordinates form a 27×27 block diagonal matrix with three 9×9 submatrices. The 3×3 unsymmetric submatrices in each 9×9 submatrix represent first order partials and the symmetric 6×6 submatrices second order partials. Even though these three 9×9 submatrices have differing elements, their structure is identical and their traces the same. Thus the 27×27 matrix is reducible and only 9 of the 27 variables are independent. We therefore have a total of 13 independent unknowns, 9 partial derivatives, 3 reflex solar motion, and R 0, not 31. To determine R, therefore, specifically when evaluated at the solar distance and hence R 0, one must look for a different reduction model.

Smart (1968, pp. 288–289) provides such a model. Edmondson (1937) uses equations that are basically the same in slightly different notation, which means he most likely never employed Eq. (1) reduced to cylindrical coordinates. The assumptions entering into Smart’s model are: a group of stars S is located at mean distance r from the Sun and at mean distance z from the Galactic plane; the systematic motion of S is a circular velocity V about the vertical axis through the Galactic center and parallel to the Galactic plane. If R is the distance of S from the Galactic center, c 1=1/2∂ 2 V/∂R 2, c 2=1/2∂ 2 V/∂z 2, and A and B denote the Oort constants. If W denotes velocity perpendicular to the plane then to allow for coupled motion in the plane and perpendicular to it we add two more unknowns, ∂W/∂z and ∂ 2 W/∂z 2. It would be possible to add other derivatives involving W, such as ∂W/∂y, ∂ 2 W/∂y∂z, and others, but Branham (2002) shows that these other terms are negligible compared with the first two. To obtain residuals that are highly random it is also necessary to introduce three further terms. To allow for a possible expansion of the Galaxy, which also relaxes the assumption of circular motion of S about the Galactic center, Smart (1968, pp. 303–305) introduces the terms \(e_{0}=\dot{R}_{0}/R_{0 }\) and \(\dot{e}_{0}=de_{0}/dR_{0}\). These two terms allow for bulk motion towards or away from the Galactic center, and affect the equations of condition in radial velocity and Galactic longitude. Let \(A_{1}=R_{0}\dot{e}_{0}/2\) and A 2=A 1+e 0. Finally, a further term, which can also be called an Oort constant, C may be added that indicates a displacement of the system of longitudes from the direction to the Galactic center. Ogorodnikov (1965, p. 73) introduces this term. With the C term we use in lieu of A \(\sqrt{A^{2}+C^{2}}\), and the longitude offset l 1 from the direction to the center of the Galaxy becomes \(l_{1}=1/2\tan ^{-1}(-C/\sqrt{A^{2}+C^{2}})\).

Then in lieu of Eq. (1) we have:

$$\begin{aligned} \begin{aligned} &\pi ^{2}\dot{r}=\pi A\sin 2l\cos ^{2}b \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{}+\cos ^{3}b\sin l\bigl(-A/R_{0}+c_{1} +4c_{2}\tan ^{2}b\bigr)/4 \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{}+\cos ^{3}b\sin 3l(3A/R_{0}+c_{1})/4 \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{} +\pi ^{2}(X\cos l\cos b+Y\sin l\cos b+Z\sin b) \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{}+\pi ^{2}K+\pi ^{2}\sin ^{2}b \partial W/\partial z+\sin ^{2}b\partial^{2}W/\partial z^{2}/2 \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{}+\pi A_{1}\cos 2l\cos ^{2}b+\pi A_{2}\cos ^{2}b \\ &\phantom{\pi ^{2}\dot{r}=\,\,}{}-C\cos ^{3}b\sin l\cos ^{2}l; \\ &k\pi \mu _{l}=\pi A\cos 2l+\pi B \\ &\phantom{k\pi \mu _{l}=\,\,}{}+\cos b\cos l\bigl(-3A/R_{0}+3c_{1} +4c_{2}\tan ^{2}b\bigr)/4 \\ &\phantom{k\pi \mu _{l}=\,\,}{}+\cos b\cos 3l(3A/R_{0}+c_{1})/4 \\ &\phantom{k\pi \mu _{l}=\,\,}{}+\pi ^{2}(-X\sin l+Y\cos l)-\pi A_{1}\sin 2l \\ &\phantom{k\pi \mu _{l}=\,\,}{}-C\cos ^{2}b\cos ^{3}l; \\ &\kappa \pi \mu _{b}=-\tan b\bigl[\pi A\sin 2l\cos ^{2}b \\ &\phantom{\kappa \pi \mu _{b}=\,\,}{}+\cos ^{3}b\sin l\bigl(-A/R_{0}+c_{1} +4c_{2}\tan ^{2}b\bigr)/4 \\ &\phantom{\kappa \pi \mu _{b}=\,\,}{}+\cos ^{3}b\sin 3l(3A/R_{0}+c_{1})/4 \bigr] \\ &\phantom{\kappa \pi \mu _{b}=\,\,}{}+\pi ^{2}(-X\cos l\sin b-Y\sin l\sin b+Z\cos b) \\ &\phantom{\kappa \pi \mu _{b}=\,\,}{}-\pi \sin b\cos b\partial W/\partial z+\cos b\sin ^{2}b\partial^{2}W/\partial z^{2}/2 \\ &\phantom{\kappa \pi \mu _{b}=\,\,}{} +C\sin b\cos ^{2}b\sin l\cos ^{2}l. \end{aligned} \end{aligned}$$
(2)

An unknown K has been added to the first of Eq. (2) to represent a K term, putatively significant for the early stars. There is a total of 14 unknowns in Eq. (2): the Oort constants A,B,C; the K term K; the four partial derivatives c 1,c 2,∂W/∂Z,∂ 2 W/∂z 2; the components of the reflex solar motion X,Y,Z; the terms A 1 and A 2; and the distance to the Galactic center R 0. In deriving these equations Smart makes use of symmetry considerations such as both ∂V/∂Z and ∂ 2 V/∂R∂Z are zero. Because the distance enters in the denominator, the equations become nonlinear. Notice that because of the units of \(\pi ,\dot{r},\mu _{l},\mu _{b}\), and κ, the dimensions of the residuals from Eq. (2), defined as the right-hand-side minus the left-hand-side, will be mas2 km s−1.

One should multiply both sides of Eq. (2) by R 0, which if left in the denominator exacerbates the calculated mean error for this quantity although the equations themselves remain algebraically equivalent. To see why look at the first Eq. (2), although the same line of reasoning applies if we use either of the proper motion equations. If dr T⋅r represents the error in the sum of the squares of the residuals and R 0 remains in the denominator, then dR 0 \(\propto R_{0}^{3}dr^{T}\cdot r\); the error in the sum of the squares of the residuals is multiplied by the large number \(R_{0}^{3}\) and implies a larger value for this quantity in the covariance matrix. Removal of R 0 from the denominator ameliorates its calculated mean error by making it less sensitive to the value for R 0. Upon multiplying the equations by R 0 the dimensions of the residuals become mas km s−1.

3 The observational data

Having the reduction model, several questions must be addressed. What data should I use and where can they be obtained? What are the errors in the data? How do the errors affect the results and in particular is there evidence for systematic error? Regarding the first question–the next two questions will be treated later– various catalogs are available with the necessary data. The proper motions and parallaxes up to 1 mas used in this study were taken from van Leeuwen’s version of the Hipparcos catalog (2007), henceforth called simply the Hipparcos catalog, the radial velocities from the Wilson (Nagy 1991) and Strasbourg Data center (Barbier-Brossat et al. 2000) catalogs. van Leeuwen’s catalog omits a few stars contained in the original catalog (ESA 1997). For those few stars the relevant data were taken directly from the original catalog. Any star flagged in the Hipparcos catalog as of substandard quality was omitted from consideration. The data must be consistent with the hypotheses inherent in Eq. (2). OB stars are ideal candidates because they are concentrated near the Galactic plane and hence high coupling between x–y motion and z motion becomes unlikely. Few, less than 0.4 %, of OB stars are high velocity, and these will be eliminated by the statistical filter used or, of one uses the L1 criterion their residuals will not unduly influence the solution. By confining oneself to the early stars a kinematical break between the early and the late stars, called Parenago’s discontinuity, is avoided. Some OB stars, however, are distributed about a plane different from the Galactic plane. These OB stars, called Gould belt stars, must be eliminated to enhance kinematical homogeneity. See Branham (2002) for a technique to detect and eliminate Gould belt OB stars. To extend the study beyond 1 kpc OB stars out to 3 kpc were taken from Westin’s (1985) compilation, 112 stars altogether. Proper motions for the Westin OB stars were taken from the SKYMAP catalog (Slater and Hashmall 1992), based on the Hipparcos proper motions, and the radial velocities from the two catalog already mentioned. Altogether 6347 proper motions and parallaxes and 1619 radial velocities were extracted from the various sources.

One may feel that it might be preferable to use Tycho (Høg et al. 2000) rather than Hipparcos proper motions because of their long base line, over 100 years versus a few years. van Leeuwen (2007, pp. 95–100) points out that the longer base line can actually introduce more scatter, caused by orbital motion of various years duration of binary stars, into the proper motions. I looked at 96591 Hipparcos proper motions, with bad data flagged by goodness-of-fit indicators, and 2406970 Tycho proper motions, with again bad data flagged. The former have a median error in right ascension (α) of 0.98 mas yr−1, 0.82 mas yr−1 in declination (δ), and for the total proper motion, if we assume independence of error in the two coordinates, of 1.06 mas yr−1; for the later the corresponding number are: 2.5 mas yr−1 in α, 2.3 mas yr−1 in δ, and 2.96 mas yr−1 for the total proper motion. The Hipparcos proper motions, therefore, carry over seven times more weight than the Tycho proper motions.

Smith and Eichhorn (1996) have derived a procedure to correct the observed parallaxes, and this procedure was used to transform all of the parallaxes used in this study, including the parallaxes for the Westin OB stars. An individual error is given for each Hipparcos star. For the Westin stars Westin estimates that for B5 and earlier the parallax error is 35 % and for the B6–B9 stars 5 %–18 %. Because it is often difficult to determine the exact spectral type, for the latter I used a constant 11 %. The final solution, however, does not depend critically on these corrections. Figure 1 shows the distribution of the OB stars in space, Figs. 2, 3, and 4 the distributions in the x–y, x–z, and y–z planes. The concentration towards the Galactic plane becomes manifest and confirms the assumptions used to derive Eq. (2). To emphasize this, define a symmetric moment matrix M, referred to the centroid of the distances, \(\bar{x},\bar{y},\bar{z}\), from the x i ,y i ,z i with

$$\begin{aligned}& M_{11}=\sum_{i}(x_{i}- \bar{x})^{2} \\& M_{12}=\sum_{i}(x_{i}- \bar{x}) (y_{i}-\bar{y}) \\& M_{13}=\sum_{i}(x_{i}- \bar{x}) (z_{i}-\bar{z}) \\& M_{22}=\sum_{i}(y_{i}- \bar{y})^{2} \\& M_{23}=\sum_{i}(y_{i}- \bar{y}) (z_{i}-\bar{z}) \\& M_{33}=\sum_{i}(z_{i}- \bar{z})^{2} . \end{aligned}$$

Because the matrix is symmetric

$$ M=\left ( \begin{array}{c@{\quad}c@{\quad}c} M_{11} & M_{12} & M_{13} \\ M_{12} & M_{22} & M_{23} \\ M_{13} & M_{23} & M_{33} \end{array} \right ) . $$
(3)

The eigenvalues of M, associated with the x,the y, and the z directions, are 958662, and 65; the z eigenvalue is much less prominent. Likewise, the latitude of the z-component is b=88.∘73, showing that Gould belt stars, with b≈72∘, seem to have been successfully eliminated. There is little correlation among the distances: −13.2 % between x and y, −0.01 % between x and z, and 7.7 % between y and z. These Galactic belt OB stars, therefore, form a homogeneous sample and comply with the assumptions used to derive Eq. (2).

Fig. 1
figure 1

Space distribution of OB stars

Full size image
Fig. 2
figure 2

Distribution in x–y plane

Full size image
Fig. 3
figure 3

Distribution in x–z plane

Full size image
Fig. 4
figure 4

Distribution in y–z plane

Full size image

What about the quality of the data? The Hipparcos proper motions (Branham 2009) are high quality. The parallaxes, however, contain a median error of 22 %. The effects of parallax error are ameliorated by elimination of parallaxes under 1 mas and application of correction factors for the remaining parallaxes. In my study of the M giants (Branham 2008) I found that the Smith-Eichhorn procedure seems to remove most of the parallax error; there is little indication of substantial error remaining in the parallax. Radial velocities come from disparate sources incorporated into the Wilson and the Strasbourg Data Center catalogs, but are not used alone. Rather, they are multiplied by the corrected parallaxes in the equations of condition. The effect, aside from the constant K term, will be to broaden the error distribution.

Regarding the final question, the effects of the errors and the possible presence of systematic error, the answer depends on the randomness of the residuals, which becomes a crucial test for the goodness of the kinematical model. Randomness allows one to assert that a least squares adjustment, or if the underlying error distribution is Laplacian rather than normal, an L1 adjustment is optimal. Lack of randomness indicates that systematic error is present and hence the reduction model inadequate. Two tests will be used later to check for the randomness of the residuals. A simplistic runs test measures how often a variable, distributed about the mean, changes sign from plus to negative or negative to positive, the runs, which have a mean for m data points of m/2+1 and a variance of m(m−2)/4(m−1) (Wonnacott and Wonnacott 1972, pp. 409–411). A more sophisticated runs test, based on Knuth (1981, pp. 64–67) and implemented in the IMSL Numerical Libraries “DRUNS” routine (www.roguewave.com), calculates a covariance matrix and a chi-squared statistic for the probability of the null hypothesis. The covariance matrix trivially converts to a correlation matrix that measures the correlations among a hierarchy of series of runs from longest to shortest.

The other test, the Durbin-Watson statistic, also called the mean-square successive difference d, measures the squared differences between residuals r i and r i−1:

$$ d=m\sum_{i=2}^{m}(r_{i}-r_{i-1})^{2}/ \Biggl[m\sum_{i=1}^{m}r_{i}^{2}- \Biggl(\sum_{i=1}^{m}r_{i} \Biggr)^{2} \Biggr] $$
(4)

and is 2 for a completely random distribution with variation (m−2)/m 2 (Wonnacott and Wonnacott 1972, pp. 411–413). Rather than the variance the statistic may be used by establishing upper and lower confidence limits for the calculated value of d. There seems to be a question whether the test is only applicable to a temporal series, but Durbin and Watson’s paper (1950) makes no such claim although their second paper (1951) only considers temporal data.

4 The reduction method

Equation (2) may be solved as a linear or a nonlinear system of equations. With the former we assume a set of values for R 0 and interpolate the value that minimizes the sum square of the residuals. Such a procedure incorporates risks, as the pre-Charon determinations of Pluto’s mass showed, and moreover fails to take into account the structure of the equations of condition, which form the data matrix. To consider R 0 an additional unknown and Eq. (2) as nonlinear seems preferable. Among other advantages it permits a direct determination of R 0, under the assumptions used to derive Eq. (2). Given that many nonlinear methods are available, the germane question becomes: which one? Advantages accrue to non-gradient methods. One of the best is the Nelder–Mead simplex algorithm (1965), not to be confused with the simplex algorithm for linear programming, which can be used to reduce the residuals of any vector norm. Instead of r T⋅r=min, we can choose the robust L1 norm, |r|=min, much less influenced by discordant data. I have published Fortran-77 code, since revised to Fortran-90, (Branham 1990, pp. 191–197), for the simplex algorithm. Although the method has been criticized, Cipra (2011) defends it by pointing out that it generally works in practice despite being occasionally fooled by “… cleverly concocted counterexamples… .”

I employ the robust L1 norm to calculate a first solution to R 0 with the OB stars: the few high velocity stars in the data set will have little effect on the calculated solution, thus obviating a search for an elimination criterion. After the L1 solution is calculated one may eliminate discordant residuals by a rejection criterion and then calculate a least squares solution. Various criteria are available. One may simply eliminate discordant residuals by a criterion such as Pierce’s (Branham 1990, pp. 79–80), a criterion supported by probabilistic arguments. As an alternative one can use an empirical criterion, one that has given me good results on many occasions: discard residuals greater than five times the mean absolute deviation, MAD, where \(\mathrm{MAD}=\sum_{i=1}^{m}\vert r_{i}\vert /(m-n)\) with m being the number of equations of condition and n the number of unknowns. More robust criteria assign higher weight to smaller residuals before eliminating outliers. One such criterion is the biweight (Branham 1990, p. 117), which I have used with work on comet orbits, double star orbits, and Galactic kinematics. Scale the residuals by the median of the absolute values of the residuals, r=r/median(|r|), then weight an individual residual r i by a factor w i

$$ w_{i}= \left\{ \begin{array}{l@{\quad}l} [ 1-(r_{i}/4.685)^{2} ] ^{2};& \vert r_{i}\vert \leq 4.685, \\ 0;& \vert r_{i}\vert >4.685. \end{array} \right. $$
(5)

The biweight recognizes two important characteristics of real world distributions: large residuals are most likely discordant rather than genuine residuals with a low probability of occurrence; small residuals are more probable than large residuals. Another possibility is the Welsch weighting (Branham 1990, p. 117):

$$ w_{i}=\exp (-r_{i}/2.985)^{2}, $$
(6)

with the residuals scaled as before. Although in theory Welsch weighting rejects no residuals, in practice large residuals receive such low weight as to become in effect zero. My experience has been that the biweight rejects far more residuals than does Pierce’s criterion. Stigler (1977) criticizes such extreme trimming, finding little justification for rejecting so many residuals and feels that more parsimonious trimming is preferable.

As with all nonlinear methods one needs a first approximation to the solution. For this approximation I calculated a linear solution to Eq. (2) with the L1 norm and using R 0=8.0 kpc, close to the value of 8.2 that Perryman (2009, p. 621) recommends. Because the calculations are based on the L1 norm, the MAD becomes a more natural measure of dispersion than σ(1), the mean error of unit weight. Table 1 shows this first, linearsolution.

Table 1 Linear solution for kinematic parameters for OB stars
Full size table

Certain comments should be made about this first approximation. The Oort constants seem on the high side, the solar velocity components on the low side, but nothing unreasonable. c 1 and c 2 are both negative indicating, when multiplied by a distance squared, net velocities towards, respectively, the Galactic center and Galactic plane. Thus, all of these values can serve as good first approximations, combined with R 0=8.0 kpc. For the K term I took K=5 km s−1. This value is suggested by my study of the O–B5 stars (Branham 2002), which found K=5.46±2.09 km s−1. The other constants in Eq. (2) were set to 0.

Not only does one wish to calculate a solution for the 14 unknowns of Eq. (2), but also a covariance matrix C V that permits calculation of the mean errors and the correlations among the unknowns. Because the covariance matrix does not constitute an intrinsic part of a nonlinear adjustment, it may be worthwhile to discuss the matter. The covariance matrix is derived from the Jacobian matrix J of the partial derivatives of \(R_{0}\pi ^{2}\dot{r}\) with respect to the 14 unknowns, the partials of R 0 κπμ l , and the partials of R 0 κπμ b . J is evaluated when the solution has converged to final iterates. To find J calculate the derivative of each of Eq. (2) with respect to A,B,R 0,c 1,c 2,X,Y,Z,K,∂W/∂Z,∂ 2 W/∂z 2,A 1,A 2,C. The unscaled covariance matrix becomes

$$ C_{V}= \bigl( J^{T}\cdot J \bigr) ^{-1}. $$
(7)

To obtain the scaled covariance matrix multiply Eq. (7) by a measure of dispersion such as the MAD or σ(1).

To obtain an error for the solar velocity itself, denoted by \(S_{0}=\sqrt{X^{2}+Y^{2}+Z^{2}}\), not just its components, and also e 0 and \(\dot{e}_{0}\), Rice’s procedure (1902), expressed in modern notation, calculates the mean error and uses C V . Identify the error in, for example, S 0 with its differential dS 0. Let v be the 11-vector of the partial derivatives (0 … ∂S 0/∂X ∂S 0/∂Y ∂S 0/∂Z). Then the error can be found from

$$ (dS_{0})^{2}=\sigma ^{2}(1)\mathbf{v}\cdot C_{V}\cdot \mathbf{v}^{T}, $$
(8)

or should one prefer the MAD could be used in lieu of σ(1). For the error in the circular velocity V 0=(A−B)R 0 use Eq. (8) again and put v=(∂V 0/∂A ∂V 0/∂B ∂V 0/∂R 0 … 0). By including all of the unknowns in the reduction model, one correctly models the relations among the unknowns and the calculated mean errors.

5 Results

The simplex algorithm was applied to 14313 equations of condition, 12694 in proper motion and 1619 in radial velocity, for the OB stars within 3 kpc of the Sun. A tolerance of 10−6 was used as a convergence criterion and λ=0.0001 for the initial size of the simplex; see Branham (1990, pp. 185–191) for details. After the algorithm converged to an L1 solution a new solution was computed with λ=0.01, then λ=0.001, and finally λ=0.0001. The idea becomes avoidance of a local minimum. With any nonlinear method it is difficult or impossible to know if the minimum is global. Pourbaix (1998), studying orbits of binary stars, combines a simplex with a simulated annealing algorithm and admits that simulated annealing cannot guarantee a global minimum. He follows the simulated annealing phase with several simplex iterations. I have eschewed use of simulated annealing because identifying the sum of the squares of the residuals with a “temperature” seems to be carrying the analogy between statistical mechanics and data reduction too far. Restarting the solution after convergence, however, with a new value for λ helps avoid a local minimum. Table 2 shows the L1 solution along with mean errors. Also shown are the circular velocity V 0 at R 0 and the solar motion S 0. The norm of the differences, 498, between Tables 1 and 2 far exceeds the value used for the parameter λ that increments the variables and indicates that the final solution has not fallen into a local minimum near the starting values.

Table 2 Nonlinear solutions for kinematical parameters for OB stars: L1
Full size table

Table 2 solution can be taken as is or used to calculate the residuals needed for a least squares or robust least squares solution based on the weighting function of Eqs. (5) or (6). The Gauss-Markov theorem demonstrates that a least squares solution represents the best linear unbiased estimator (BLUE). But the qualifiers rule out a nonlinear estimator, such as the median, or a biased estimator such as that given by ridge regression or total least squares. If we consider an L1 solution as one insensitive to outliers and not necessarily optimal in the least squares sense, there is no reason why the solution cannot be considered as good, robust, and without the inconvenience of having to discard outliers. Table 2 shows the L1 solution along with mean errors. How the L1 mean errors are calculated will be explained later. Also shown are the circular velocity V 0 at R 0 and the solar motion S 0.

The runs test shows that the residuals sorted by longitude have a 50.6 % chance of confirming the null hypothesis that they arise from a random distribution while the Durbin-Watson statistic, under the assumption that it can be applied to other than temporal series, gives a 19.7 % chance. Also, Eichhorn’s efficiency (Eichhorn 1990, p. 149), which varies from 0 for redundant data to 1 for independent data, becomes 0.73, showing that all of the unknowns, considered as a set, are necessary and relatively uncorrelated. For a more complete discussion of the efficiency see Eichhorn and Xu (1990). Because the residuals do not represent time series, spectral analysis cannot be applied. Figure 5 shows the residuals in latitude and longitude.

Fig. 5
figure 5

L1 residuals

Full size image

It would be possible to calculate genuine L1 mean errors, which are invariably higher than least squares mean errors, for this solution; see Branham (1986) for how to do this. It would not, however, be advisable to do so. Figure 6 gives a histogram of the residuals after 383 have been eliminated, a 2.7 % trim. The criterion for rejection was five times the MAD. This trim, although unnecessary for a robust L1 solution, permits calculation of reliable statistics for the residuals and a histogram without extremely long tails. The statistics show that the residuals are somewhat asymmetric, coefficient of skewness 0.03 (0 for the normal distribution), leptokurtic, kurtosis of 3.84 (3.0 for both the normal and the L1 distribution), and lighter tailed than a normal or L1 distribution, Q factor of 0.47 versus 2.58 for the normal and 3.11 for the L1. The Q factor is defined as

$$ Q=(U_{0.05}-L_{0.05})/(U_{0.5}-L_{0.5}), $$
(9)

where U α and L α are averages of the respective upper and lower 100α % of the data (Stigler 1977). L1 mean errors, which are sometimes appropriate, see for example Branham and Sanguin (1998), become otiose here because of the low Q factor. The mean errors for the L1 solution in Table 2, therefore, were calculated from the same covariance matrix as that used for the least squares solution of Table 3, given later, but by use of the MAD rather than σ(1) as the measure of dispersion and without scaling the matrix by the weights.

Fig. 6
figure 6

Histogram of residuals

Full size image
Table 3 Nonlinear solutions for kinematical parameters for OB stars: least squares
Full size table

This randomness also confirms that the adjustment model of Eq. (2) produces residuals without systematic trends. An earlier model did not include the last five terms: ∂W/∂z,∂ 2 W/∂z 2,A 1,A 2,C. The Durbin-Watson statistic, however, calculated, based on an L1 solution, only a 7.1 % chance of the residuals being random, symptomatic of an inferior adjustment model.

With this trim several least squares solutions were calculated: least squares based on the 2.7 % trim; least squares based on the biweight function of Eq. (5); and least squares based on the Welsch weighting of Eq. (6). The trimmed least squares solution, with a 15.3 % chance of being random as measured by a runs test and a 15.9 % chance by Durbin-Watson, becomes inferior to the L1 solution. The biweight rejects too many residuals, 14.4 % of the residuals in general and over 29 % of the residuals in radial velocity. One needs no statistical analysis to reject such profligate trimming. The Welsch weighting solution, however, seems good and is shown in Table 3. This solution calculates that 431 residuals are less than the machine ϵ and may be considered 0 and 1184 less than 0.01. The former values corresponds to a 3.0 % trim, although 8.3 % of the residuals are severely downweighted. A runs test assigns a 61.8 % chance of the residuals being random while Durbin-Watson gives 70.6 %. The runs test correlation matrix shows little evidence of correlation among runs, the highest correlation being a barely significant −53.2 %. This enhances the evidence for the randomness of the residuals. Figure 7 shows the distribution of the residuals with respect to longitude and latitude.

Fig. 7
figure 7

Residuals, Welsch weighting

Full size image

6 Discussion

Which of the two solutions, that of Table 2 or that of Table 3, is better, in some sense of the term “better”? Statistics favor the latter as do certain other indicators. The circular velocity V 0 depends on the Oort A and B constants and hence their determination becomes central to the determination of V 0. The values of A−B and −(A+B) represent controls on their determination. The former, with value 30.27, falls in of what is given in Table 4 of Branham (2011), ranging from 19.77 to 31.1. The latter, with value 1.92 also falls within the range of Table 4 of that publication, −10.52 to 4.6. The solar velocity S 0 seems a tad on the low side, but hardly discordant. In fact, Branham (2006) found 13.83±0.17 km sec−1 for just the O and B giants, but by use of a linear model and a reduction model based on semi-definite programming. I therefore consider the Welsch solution of Table 3 rather than the L1 solution of Table 2 as the better of the two. The calculated value of C implies a displacement of l 1=−3.∘14±7.∘85 of the longitudes used in this study with respect to the true longitude of the Galactic center. One may infer that longitude bias is negligible.

Table 4 Contribution of each unknown to solution
Full size table

Granted, we have calculated a solution, but how good is it? The condition number of the Jacobian matrix is 5.1⋅102, low with respect to the double-precision arithmetic, machine epsilon of 2.2⋅10−16, used for the computations. Correlations among individual unknowns are not excessive. The correlation matrix is rather large to show and is instead given as the contour plot of Fig. 8. Only three correlations exceed 50 %: −61.0 % between K and ∂W/∂z; −77.6 % between K and A 2; 88.9 % between c and C.

Fig. 8
figure 8

Correlations

Full size image

One would also like to know the contribution of each of the original unknowns to the solution. This can be obtained from an SVD of the Jacobian matrix J. Once the nonlinear algorithm has converged to a solution, this may be represented as, with d as the right-hand-side,

$$ J\cdot x=U\cdot S\cdot V^{T}\cdot x=d, $$
(10)

where U is m×m orthogonal and represents the left proper vectors, S m×n with the upper n×n part diagonal, the diagonal elements being the singular values, and V n×n orthogonal, the right proper vectors. If σ i represents the i-th singular value the decomposition can also be written as

$$ J=\sum_{i=1}^{n}\sigma _{i}u_{i}v_{i}^{T}, $$
(11)

where u i is the i-th column of U and v i the i-th row of V T. The backwards product \(u_{i}v_{i}^{T}\) is of rank 1 with unit norm. Combining Eq. (10) with Eq. (11) we see that the weight of each component of the solution x depends on the expansion of Eq. (11). The SVD, however, is not invariant to scaling. Thus, the actual values assumed by the entities in Eq. (11) will depend on the units as well as the scaling of the matrix. Standard statistical packages for the SVD, moreover, sort the singular values and associated right and left proper vectors after they have been calculated, destroying the association of index i with the corresponding unknown. I have written a C++ program that leaves the singular values unsorted and hence maintains the correspondence between index i and the unknown. Table 4 shows the percentage contribution of each unknown after the matrix J has been scaled by imposition of unit Euclidean norm on each column.

Notice that R 0 is hardly a minor contributor in the final solution. Preparing a table such as Table 3 but also including other unknowns involving W, such as ∂W/∂y or ∂ 2 W/∂x∂y, bolsters the assertion made before Eq. (2) that they remain unimportant in the solution: their percentage sum would contribute less than 1 % to the solution.

\(R_{0}^{\prime }s\) determination, although on the low side, falls within the range of the values mentioned in the first section. One should, nevertheless, discuss the difference between the L1 determination and that of the Welsch solution. Consider a sensitivity test of a residual, whether in radial velocity or proper motion, to the error dR 0. A residual for just the terms involving R 0 after Eq. (2) has been multiplied by R 0 can be represented by

$$ \vert r\vert = \Biggl\vert \sum_{i=1,i\neq 3}^{14}k_{i}R_{0} \Biggr\vert , $$
(12)

where the k i are either constant or involve l and b. Therefore, if we consider the p-th power of the residual

$$ \partial r^{p}/\partial R_{0}=p \Biggl\vert \sum _{i=1,i\neq 3}^{14}k_{i}R_{0} \Biggr\vert ^{p-1}\sum_{i=1,i\neq 3}^{14}k_{i}dR_{0}. $$
(13)

When p=2 the gradient becomes sensitive to R 0 dR 0 whereas when p=1 it is merely sensitive to dR 0. Because R 0 is substantial, a least squares solution will be more sensitive to the residuals and their exclusion than an L1 solution. Thus, the determinations of the distance can vary depending on the norm used for the reduction. Statistical tests indicate which determination is best.

That the kinematical model used embodied in Eq. (2) also seems adequate can be deduced from the randomness of the residuals as evidenced by the runs test and Durbin-Watson statistic. Systematic error, if present, must be at a level lower than the noise in the data. Thus, one cannot maintain that density waves affect the results, at least in a significant manner, because their presence would become manifest in non-random residuals.

A 1 and A 2 have been calculated, but little has been said as what this portends. From definitions given previously \(\dot{R}_{0}=R_{0}\cdot (e_{0}+\dot{e}_{0}R_{0})\). Using values from the solution of Table 3 and the conversion 1 kpc=3.09⋅1016 km I find that e 0=9.90±4.18 s−1, \(\dot{e}_{0}=-0.20\pm 0.11~\mbox{s}^{-1}~\mbox{kpc}^{-1}\), and \(\dot{R}_{0}=57.50\pm 8.52~\mbox{km\,s}^{-1}\). This implies an expansion of the OB star system at the distance R 0 of 1 kpc in 1.70⋅107±2.51⋅106 yr. Interestingly, Trumpler (1940) found from radial velocities of Galactic clusters a contraction of −4.3 km s−1 kpc−1 or −28.9 km s−1 at a distance of 6.72 kpc. This corresponds to a contraction of 1 kpc in 3.39⋅107 yr. Neither such a rapid expansion nor contraction seems likely. These values seem indicative of some sort of radial motion of the system, but one can attach little importance to the exact values. Perhaps one should interpret this as delineating the boundary between kinematics and dynamics, the latter being required to study such complex relations as bulk expansion or contraction of a stellar system.

Do the velocities calculated from the solution of Table 3 indicate serious deviations from Galactic, differential motions? This question has been addressed regarding density wave terms, but further evidence should be presented. Although there are only 1619 radial velocities available compared with 6347 proper motions, we can nevertheless calculate 6347 space velocities, \(\dot{x}\), \(\dot{y}\), \(\dot{z}\), corrected for differential motion by the values for A,B, and K in Table 3 if we are willing to perform a statistical inversion, called the pseudo-inverse, by making use of the SVD and only the proper motions. For the details of how to do this see Branham (2010), especially Eqs. (3)–(5). The medians of the calculated absolute values of the space velocities yield respective values of: 6.78, 6.49, 4.10 km s−1, also low and in rough agreement with the values in Table 2. Their norm, 10.24 km s−1 differs little from the norm of the solution of Table 2, 11.00 km s−1, especially if we keep in mind the different manner in which the respective space velocities have been calculated.

For further analysis 64 stars were rejected by use of the 5∗MAD criterion, a 1 % trim. The calculated velocities are random as measured by a runs test. For these data a runs test is superior to the Durbin-Watson statistic because some, but few, of the constructed velocities are wildly inaccurate and calculate nonsense values for the Durbin-Watson statistic. To be specific a runs test shows that the x velocities have a 68.9 % chance of being random, the y velocities a 28.9 % chance, and the z velocities a 61.4 % chance. One must remember, moreover, that for the majority of these stars the space velocities are not true space velocities but rather statistical velocities calculated from the SVD. There seem to be, therefore, no residual effects, such as possible streaming induced by other than Galactic density waves, in the velocities. This once again confirms that the solution of Table 3 seems acceptable.

7 Conclusions

The OB stars, concentrated near the Galactic plane, conform with the assumptions used to derive Eq. (2), namely that motion in the Galactic plane is relatively uncoupled from motion perpendicular to the plane and that moreover perpendicular motion is slight. The data appear to be homogeneous; there are no high correlations among the rectangular coordinates. Both Eichhorn’s efficiency and the SVD show that Smart’s model for the 14 unknowns, Oort constants, distance to the Galactic center, two second-order partial derivatives, the solar velocity, a K term and a C constant, plus four additional unknowns to represent motion perpendicular to the Galactic plane and a possible expansion of the OB stars, seems well conditioned with no redundant unknowns and, with three exception, low correlations among the individual unknowns. The model, therefore, becomes adequate. Addition of more terms, such as streaming motion induced by Galactic density waves, becomes unnecessary. Once the assumptions of the model are complied with, the calculated distance to the Galactic center becomes a direct determination with value 6.72±0.39 kpc. The residuals from the post-fit solution are highly random. Thus, the solution may be considered satisfactory.