Cylindrical thin-shell wormholes in f(R) gravity

Abstract

In this paper, we employ cut and paste scheme to construct thin-shell wormhole of a charged black string with f(R) terms. We consider f(R) model as an exotic matter source at wormhole throat. The stability of the respective solutions are analyzed under radial perturbations in the context of R+δR ² model. It is concluded that both stable as well as unstable solutions do exist for different values of δ. In the limit δ→0, all our results reduce to general relativity.

1 Introduction

Wormhole (WH) is a hypothetical tunnel, path or bridge associating two different portions of the spacetime under which observers may pass freely. Flamm (1916) was the first who found Schwarzschild solution as non-traversable WH while Einstein and Rosen (1935) investigated WH solutions with event horizon. Morris and Thorne (1988) claimed that a WH can be made traversable if it is supported by exotic matter. The existence of exotic matter at the WH throat made it a burning issue which attracted many researchers. It is interesting to mention that stability phases of the self-gravitating bodies lead to different evolutionary processes in the universe. In this context, the instability investigation for the collapsing processes has been widely performed (Herrera et al. 1989, 2012; Chan et al. 1993, 1994; Herrera and Santos 1997; Pinheiro and Chan 2013). Moreover, the stability analysis of WHs against small perturbations is also a core issue in astrophysics.

It is argued that exotic matter requirement in WHs can be refrained in modified theories of gravity (Gravanis and Willison 2007; Garraffo et al. 2008; Anchordoqui et al. 1997). Thin-shell WHs are built up by cut and paste scheme from black holes. In this technique, the exotic matter required to construct WH is settled at the shell and the matching condition is used for its analysis. The surface stresses in this framework are computed by using the Darmois-Israel formalism (Israel 1966, 1967; Papapetrou and Hamoui 1968). One can investigate the dynamical stability of thin-shell WHs either by analyzing a linearized stability procedure about a static solution (Poisson and Visser 1995; Lobo 2006), or by considering a particular equation of state (EoS) (Visser 1990; Kim 1992; Kim et al. 1993). The stability of this sort of matter distribution is being analyzed in general relativity (Barceló and Visser 2000) as well as in extended gravity theories (Anchordoqui 1998; Eiroa and Simeone 2005).

Brady et al. (1991) studied the dynamics of an infinitely thin massive shell and concluded that such stable shell has relatively larger surface energy density than pressure. Clément (1995) presented multi WH solutions in which the spacetime asymptotically inclines to the conical cosmic string spacetime. Aros and Zamorano (1997) found a solution which may be regarded as a traversable cylindrical WH within the global cosmic string core. Eiroa and Romero (2004) extended their results by invoking electric charge while Lobo and Crawford (2004) generalized this analysis with cosmological constant. Eiroa and Simeone (2004) discussed the dynamics of thin-shell WHs under non-rotating cylindrical background. The Eiroa and Simeone (2005) extended this work for charged Lorentzian WHs in the framework of dilaton gravity and calculated the total quantity of exotic matter.

Thibeault et al. (2006) investigated 5D thin-shell WHs in the scenario of modified theory. Rahaman et al. (2007) constructed thin-shell WH in the scenario of heterotic string theory and investigated its stability against perturbation. Eiroa and Simeone (2007) used Chaplygin EoS to study the stability of thin-shell WHs by introducing a new scheme. They applied this approach to analyze the stability of WHs constructed from the Schwarzschild, Schwarzschild de Sitter, Schwarzschild anti-de Sitter and Reissner-Nordström spacetimes. Sharif and Azam (2013) evaluated unstable and stable distributions of thin-shell in cylindrical symmetry.

Nojiri et al. (1999a, 1999b) found some induced WH solutions incorporating increasing red-shift function and throat radius for some specific values of initial conditions. Nojiri and Odintsov (2007) described late-time (quintessence/phantom) universe filled with dark sources arising from modified gravity theories with different choices of generic functions of f(R) and f(R,G). The Nojiri and Odintsov (2011) also presented various aspects of f(R) gravity and claimed that there is a variety of f(R) models that are well-consistent with local tests and observational data (Capozziello et al. 2009, 2010; Dev et al. 2008). Bamba et al. (2012) reviewed different dark energy cosmological models which may lead to the accelerating expansion of the universe.

Since exotic matter does not satisfy null energy condition, so researchers are interested to find realistic sources that can support WHs. Furey and DeBenedictis (2005) studied WH throats for R ⁻¹ and R ² gravity and concluded that static WHs respect null energy condition. DeBenedictis and Horvat (2012) extended these results for a model of the form f(R)=∑α _n R ⁿ. Lobo and Oliveira (2009) obtained static WH solutions for traceless matter by choosing barotropic EoS in f(R) gravity.

In this paper, we investigate the role of charge in the stability of thin-shell WH by cut and paste technique with f(R) terms. In order to check the dynamical stability, we choose Darmois-Israel matching conditions. The paper is planned as follows. In Sect. 2, we obtain general formulation required for the study of thin-shell WH. Section 3 is devoted to analyze the linearized stability of thin-shell WHs while in Sect. 4, we apply this formalism on charged black string with f(R) terms. In the last section, we conclude our results.

2 Thin-shell wormhole and f(R) gravity

The modified form of Einstein-Hilbert action in f(R) gravity can be written as

$$ \mathcal{A}_{f(R)}=\frac{1}{2\kappa}\int d^4x \sqrt{-g}f(R)+\mathcal{A}_M, $$

where $\mathcal{A}_{M}$ and f(R) are the matter action and a non-linear real function of the curvature R, respectively. The field equations are evaluated by giving variation in the above action with respect to g _αβ as follows

$$ f_RR_{\alpha\beta}-\frac{1}{2}fg_{\alpha\beta}- \nabla_{\alpha} \nabla_{\beta}f_R+g_{\alpha\beta}{ \Box}f_R=\kappa S_{\alpha\beta}, $$

where S _αβ is the energy-momentum tensor, □=∇^α∇ _α , ∇ _α  is the covariant derivative and $f_{R}=\frac{df}{dR}$. This equation can be formulated alternatively in the form of general relativity (GR) field equations as

$$ G_{\alpha\beta}=\frac{\kappa}{f_R}\bigl(S_{\alpha\beta}+ \overset{(D)}{S_{\alpha\beta}}\bigr), $$

with

$$ \overset{(D)}{S_{\alpha\beta}}=\frac{1}{\kappa} \biggl\{ \frac{f-Rf_R}{2} g_{\alpha\beta}+\nabla_{\alpha}\nabla_{\beta}f_R- \Box f_Rg_{\alpha\beta} \biggr\} . $$

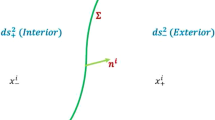
In f(R) gravity, the junction conditions over a timelike boundary surface Σ in 4D manifold can be found by projecting the above equations on the boundary surface Σ.

The extrinsic curvature linked with two portions of the hypersurface Σ is

$$ K^{\pm}_{ij}=-n^{\pm}_{\sigma} \biggl(\frac{{\partial}^2x^{\sigma}_{\pm}}{ {\partial}{\zeta}^i{\partial}{\zeta}^j}+{\varGamma}^{\sigma}_{{\alpha}{\beta}} \frac{{{\partial}x^{\alpha}_{\pm}}{{\partial}x^{\beta}_{\pm}}}{ {\partial}{\zeta}^i{\partial}{\zeta}^j} \biggr)\bigg\vert _{\varSigma}, $$

(1)

where ζ ^j, x ^σ and $\varGamma^{\sigma}_{\alpha\beta}$ are the coordinates of the hypersurface, the four dimensional manifold components and connection components related with the metric g _αβ respectively, while

$$ n^{\pm}_{\sigma}=\biggl\vert g^{\alpha\beta} \frac{{\partial}f}{{\partial} x^{\alpha}}\frac{{\partial}f}{{\partial}x^{\beta}}\biggr\vert , $$

(2)

are the unit normals (n _σ n ^σ=1). Consequently, the Lanczos equations (Musgrave and Lake 1996) with f(R) terms (Capozziello and Laurentis 2011; Sharif and Yousaf 2013a, 2013c, 2013d, 2013e) take the form

$$\begin{aligned} \frac{\kappa}{{\alpha}f_R} \bigl({\alpha}S^i_{~j}+ \overset{~~~(D)}{S^i_{~j}} \bigr) =- \bigl(k^i_j- \delta^i_jk^a_a \bigr), \end{aligned}$$

(3)

where $\alpha^{2}=\frac{\varLambda}{3}$, (Λ is the cosmological constant), $S^{i}_{~j}$ and $\overset{\quad (D)}{S^{i}_{~j}}$ are the energy-momentum tensor of the usual and effective matter on the hypersurface, respectively and $k_{ij}=K^{+}_{ij}-K^{-}_{ij}$. The GR Lanczos equations (Musgrave and Lake 1996) can be recovered from the above equation under the limit f(R)→R.

We construct a thin-shell WH of static cylindrically metric whose line element is of the form (Lemos and Zanchin 1996)

$$ ds^2=-G(r)dt^{2}+G^{-1}(r)dr^{2}+N(r) \bigl(d\phi^{2}+\alpha^2{dz^2}\bigr), $$

(4)

where

$$ G(r)=r^2{\alpha}^2-\frac{4M}{r\alpha}+ \frac{4q^2}{r^2\alpha^2}, \qquad N(r)=r^2, $$

(5)

q and M are the charge density and ADM mass, respectively. The outer and inner charged black string horizons are given by

$$ r_{h\pm}=\frac{4^{1/3}}{2} \biggl[\sqrt{s}\pm \biggl\{ 2 \sqrt{s^2-q^2 \biggl(\frac{2}{M} \biggr)^{\frac{4}{3}}} -s \biggr\} ^{\frac{1}{2}} \biggr] \frac{M^{\frac{1}{3}}}{\alpha}, $$

(6)

where

$$ s= \biggl(\frac{1}{2}-\frac{1}{2}\sqrt{1- \frac{64q^6}{27M^4}} \biggr)^{1/3} + \biggl(\frac{1}{2}- \frac{1}{2}\sqrt{1-\frac{64q^6}{27M^4}} \biggr)^{1/3}. $$

(7)

It is worth mentioning here that the given spacetime does not possess event horizon for $q^{2}>\frac{3}{4}M^{4/3}$ implying that Eq. (6) is valid only if $q^{2}\leq\frac{3}{4}M^{4/3}$. For $q^{2}=\frac{3}{4}M^{4/3}$, the outer and inner horizons merge into each other, representing extremal black string. We take radius a and choose two 4D copies $\mathcal{W}^{-}$ and $\mathcal{W}^{+}$ with radius r≥a and paste them at the boundary surface Σ defined by r−a=0, thus giving a geodesically complete new manifold $\mathcal{W}=\mathcal{W}^{-}\cup\mathcal{W}^{+}$. If the geometry is let to open at Σ, then this leads to a cylindrical thin-shell WH with two parts associated by a throat at hypersurface (flair-out condition). It is mentioned here that radius a is chosen to be greater than r _h such that there are no singularities and horizons in $\mathcal{W}$.

To investigate this traversable WH, we use the standard Darmois-Israel formalism (Israel 1966, 1967; Papapetrou and Hamoui 1968). The wormhole throat is placed at the synchronous timelike hypersurface with coordinates ζ=(τ, ϕ,z) where τ represents proper time on the boundary surface. Using Eq. (1), we obtain

$$ \begin{aligned}[c] &K^{\pm}_{\tau\tau}=\mp\frac{2\ddot{a}+G'(a)}{2\sqrt{\dot{a}^2+G(a)}},\\ &K^{\pm}_{\phi\phi}= \pm a\sqrt{\dot{a}^2+G(a)}= \frac{1}{\alpha^2}K^{\pm}_{zz}. \end{aligned} $$

(8)

The matter quantities $S^{\tau}_{~\tau}=-\sigma$ and $S^{\phi}_{~\phi}=S^{z}_{~z}=P$ turn out to be

$$\begin{aligned} & \begin{aligned}[b] \sigma&=-\frac{4f_R}{a\kappa}\sqrt{ \dot{a}^2+G(a)}+\frac{1}{{\alpha}\kappa} \biggl\{ \frac{f-Rf_R}{2}+G(a)f''_R\\ &\quad {}+G(a)f'_R \biggl(\frac{N'(a)}{N(a)} +\frac{G'(a)}{2G(a)} \biggr) \biggr\} , \end{aligned} \end{aligned}$$

(9)

$$\begin{aligned} & \begin{aligned}[b] P&=\frac{f_R}{a\kappa} \biggl( \frac{2a\ddot{a}+2\dot{a}^2+2G(a)+aG'(a)}{ \sqrt{\dot{a}^2+G(a)}} \biggr)\\ &\quad {}-\frac{1}{{\alpha}\kappa} \biggl\{ \frac{f-Rf_R}{2}+G(a)f''_R\\ &\quad {}+G(a)f'_R \biggl(\frac{N'(a)}{2N(a)}+\frac{G'(a)}{G(a)} \biggr) \biggr\} . \end{aligned} \end{aligned}$$

(10)

The stability of f(R) models is also a significant issue which is well discussed in the literature (Faraoni 2005; Faraoni and Nadeau 2005; Capozziello et al. 2004, 2006a, 2006b, 2007). We take a familiar f(R) model proposed by Starobinsky (1980)

$$ f(R)=R+\delta R^{2}, $$

(11)

with δ as a positive number. This model can explain the inflation period of the universe and is stable for δ>0 representing f _RR >0 (Noakes 1983; Sharif and Yousaf 2013b). Besides substituting for dark energy at cluster and stellar scales, f(R) gravity can be used to present as an alternate for dark matter (DM) (Capozziello et al. 2004, 2006a, 2006b, 2007). Thus the given f(R) model was claimed both as DM model with $\delta =\frac{1}{6M^{2}}$ (Cembranos 2009, 2011) and as an inflationary prospect. For DM model, M is figured out as 2.7×10⁻¹² GeV with δ≤2.3×10²² Ge/V² (Sotirou and Faraoni 2010). We are concentrated on this model to investigate WH solutions in f(R) gravity. Einstein theory is recovered if δ=0 thereby giving classically stable black hole.

The accelerated expanding behavior of the universe triggered to explore new matter that violates the strong energy condition called dark energy. Pure Chaplygin gas obey EoS $P=-\frac{B}{\sigma}$ (Kamenshchik et al. 2001; Gorini et al. 2004), where B>0. Here we are introducing this source just to solve the cumbersome set of equations. Thus we have used its simplified version instead of generalized Chaplygin gas EoS. Some authors (Hochberg et al. 1997; Nojiri et al. 1999a, 1999b) presented numerical and analytical spherically symmetric WH solution thus suggesting possibility of inducing WHs at the early universe. Here, we also try to induce WH solution at the early time universe (in the quantum era) with the help of R+δR ² model. It is well-known that if WHs are studied in the early universe then quantum effects (Duff 1994) may play significant anomaly effects. Using Eqs. (9), (10) and (11) in EoS, we obtain

$$ \begin{aligned}[b] &2a\ddot{a}+2\dot{a}^2+2G(a)+aG'(a)\\ &\quad {}= \biggl[X_P -\frac{Ba\kappa^2}{aX_{\sigma}-4f_R\sqrt{\dot{a}^2+G(a)}} \biggr] \frac{a\sqrt{\dot{a}^2+G(a)}}{f_R}, \end{aligned} $$

(12)

where

$$\begin{aligned} & \begin{aligned} X_{\sigma}&=\frac{\delta}{{\alpha}} \biggl[-\frac{R^2(a)}{2}+2G(a)R''(a)\\ &\quad {}+2G(a)R'(a) \biggl(\frac{N'(a)}{N(a)}+\frac{G'(a)}{2G(a)} \biggr) \biggr], \end{aligned} \\ & \begin{aligned} X_P&=\frac{\delta}{{\alpha}} \biggl[-\frac{R^2(a)}{2}+2G(a)R''(a)\\ &\quad {}+2G(a)R'(a) \biggl(\frac{N'(a)}{2N(a)}+\frac{G'(a)}{G(a)} \biggr) \biggr], \end{aligned} \\ & \begin{aligned} R(a)&=G''(a)+2\frac{G''(a)N(a)}{G(a)}\\ &\quad {}+\frac{G'(a)}{G(a)} \biggl(2G'(a) -\frac{G(a)N'(a)}{2N(a)} \biggr), \end{aligned} \end{aligned}$$

X _σ and X _P in Eq. (12) represent f(R) higher curvature terms. This is the required differential equation that the thin-shell WH (with throat radius a supported by an exotic matter) should satisfy. Using EoS, we can also have

$$\begin{aligned} P'=-P\frac{\sigma'}{\sigma}, \qquad \sigma'+2P'=\sigma' \biggl(1- \frac{2P}{\sigma} \biggr). \end{aligned}$$

(13)

These relations will be helpful to eliminate σ′ as well as P′ terms from the first and second derivatives of the potential function.

3 Stability analysis

In this section, we investigate the stability of static configurations of the thin-shell WH framed within f(R) gravity. In this scenario, the surface pressure, energy density and dynamical equation with static background yield

$$\begin{aligned} &P_0=\frac{(1+2{\delta}R_0)}{\kappa a_0} \biggl(\frac{2G(a_0)+a_0G'(a_0)}{\sqrt{G(a_0)}} \biggr) -\frac{X_{P0}}{\kappa}, \end{aligned}$$

(14)

$$\begin{aligned} &\sigma_0=-\frac{4(1+2{\delta}R_0)}{\kappa a_0}\sqrt{G(a_0)}+ \frac{X_{\sigma0}}{\kappa}, \end{aligned}$$

(15)

$$\begin{aligned} &2G(a_0)+aG'(a_0) \\ &\quad {}= \frac{a_0\sqrt{G(a_0)}}{(1+2{\delta}R_0)} \biggl[X_{P0} -\frac{Ba_0\kappa^2}{aX_{\sigma0}-4(1+2{\delta}R_0)\sqrt{G(a_0)}} \biggr], \end{aligned}$$

(16)

where X _σ0, X _P0 and R ₀ are evaluated at a=a ₀. The conservation equations help to examine many useful properties of the WH throat such as variation of the throat internal energy and work which internal forces in the throat has done. The energy density of the surface and isotropic pressure obeying conservation equation can be written as

$$\begin{aligned} \frac{d}{d\tau}({\varDelta }\sigma)+P\frac{d\varDelta }{d\tau}=0, \end{aligned}$$

where Δ=4πa ², giving

$$\begin{aligned} \sigma'=-\frac{2}{a}(P+\sigma). \end{aligned}$$

(17)

Equation of motion, about a=a ₀, against radial perturbation provides an efficient way to study the dynamics of thin-shell WHs. Equations (9) and (11) lead to

$$ \dot{a}^2+\varPhi(a)=0, $$

where

$$ \varPhi(a)=G(a)-\frac{\kappa^2a^2}{16(1+2{\delta}R)^2} \biggl(\frac{X_\sigma}{ \kappa}- \sigma \biggr)^2, $$

(18)

is the potential function whose first and second derivatives can be found by using Eq. (13) as

$$\begin{aligned} \varPhi'(a)&=G'(a)- \frac{\kappa^2a^2}{8(1+2{\delta}R)^2} \biggl(\frac{X_\sigma}{\kappa}-\sigma \biggr) \\ &\quad {}\times\biggl\{ \frac{X'_\sigma}{\kappa}-\frac{1}{a} \biggl(2P +\sigma-\frac{X_\sigma}{\kappa} \biggr) \\ &\quad {}+\frac{2{\delta}R'}{(1+2{\delta}R)^3} \biggl( \frac{X_\sigma}{\kappa}-\sigma \biggr) \biggr\} , \end{aligned}$$

(19)

$$\begin{aligned} \varPhi''(a)&=G''(a)- \frac{\kappa^2a}{(1+2{\delta}R)^2} \biggl[\frac{X'_\sigma}{\kappa}-\frac{1}{a} \biggl(2P+\sigma- \frac{X_\sigma}{\kappa} \biggr) \\ &\quad {} +\frac{2{\delta}R'}{(1+2{\delta}R)^3} \biggl( \frac{X_\sigma}{\kappa}- \sigma \biggr) \biggr] \biggl[ \biggl( \frac{X_\sigma}{\kappa}-\sigma \biggr) \\ &\quad {}\times \biggl( \frac{1}{4} +\frac{18{\delta}R'}{(1+2{\delta}R)} \biggr) +\frac{a}{8} \biggl\{ \frac{X'_\sigma}{\kappa}+\frac{2}{a} (\sigma+P) \biggr\} \biggr] \\ &\quad {}-\frac{\kappa^2a^2}{8(1+2{\delta}R)^2} \biggl(\frac{X_\sigma}{\kappa}-\sigma \biggr) \\ &\quad {}\times\biggl[ \frac{X''_\sigma}{\kappa}+\frac{1}{a^2} \biggl(2P +\sigma-\frac{X_\sigma}{\kappa} \biggr) \\ &\quad {}+\frac{1}{a} \biggl\{ \frac{2}{a}(P+\sigma) \biggl(1- \frac{2P}{ \sigma} \biggr)+\frac{X'_\sigma}{\kappa} \biggr\} \\ &\quad {}+\frac{2\delta}{(1+2{\delta}R)^3} \biggl\{ \biggl(\frac{X_\sigma}{\kappa}-\sigma \biggr) \biggl(R'' -\frac{3R'^2}{(1+2{\delta}R)} \biggr) \\ &\quad {}+R' \biggl(\frac{X'_\sigma}{\kappa} + \frac{2}{a}(P+\sigma) \biggr) \biggr\} \biggr]. \end{aligned}$$

(20)

Evaluating the above equation at a=a ₀ and inserting the values of P ₀ and σ ₀ from Eqs. (14) and (15) in the above equation, it follows that

$$\begin{aligned} \varPhi''_0&=G''_0- \frac{\alpha\sqrt{G_0}}{(1+{\delta} R_0)} \biggl[-{\delta}R_0R'_0+2{ \delta}\bigl(G'_0R''_0+G_0R'''_0 \bigr) \\ &\quad {}+2\delta \bigl(G'_0R'_0+G_0R'''_0 \bigr) \biggl(\frac{2}{a_0} +\frac{G'_0}{2G_0} \biggr) \\ &\quad {}+2{\delta}G_0 R''_0 \biggl( \frac{G''_0}{2G_0}-\frac{G'^2_0}{ 2G^2_0}-\frac{2}{a_0^2} \biggr) \\ &\quad {}-\frac{2}{a_0} \biggl\{ \frac{{\alpha}G'_0}{\sqrt{G_0}} (1+2{ \delta}R_0)+\frac{{\delta}R_0^2}{2}-2{\delta}G_0R''_0 \\ &\quad {}-2{\delta}G_0R'_0 \biggl( \frac{G'_0}{G_0}+\frac{1}{a_0} \biggr) \biggr\} +\frac{8{\delta}{\alpha}\sqrt{G_0}R'_0}{a_0 (1+2{\delta}R_0)^2} \biggr] \\ &\quad {} \times\biggl[1-\frac{8{\delta}a_0R'_0}{(1 +2{\delta}R_0)}- \frac{a_0^2}{\alpha\sqrt{G_0}(1+2{\delta}R_0)} \\ &\quad {}\times \biggl\{ -{\delta}R_0R'_0+2{\delta} \bigl(G'_0R''_0+G_0R''_0 \bigr) \\ &\quad {}+2{\delta} \bigl(G'_0R'_0+G_0R''_0 \bigr) \biggl(\frac{2}{a_0} +\frac{G'_0}{2G_0} \biggr) \\ &\quad {}+2{\delta}G_0R'_0 \biggl(\frac{G''_0}{2G_0}-\frac{G'^2_0}{2G^2_0}-\frac{2}{a_0^2} \biggr) \\ &\quad {} + \frac{2{\alpha^2}}{a_0^2} (1+2{\delta}R_0) \biggl(\frac{a_0G'_0-2G_0}{\sqrt{G_0}} \biggr) \\ &\quad {}+\frac{2{\delta}R'_0}{a_0^2}\bigl(2G_0-a_0G'_0 \bigr) \biggr\} \biggr] \\ &\quad {} -\frac{a_0\sqrt{G_0}\kappa}{2(1+2{\delta}R_0)} \biggl[\frac{2\delta}{ \alpha\kappa} \biggl\{ - \frac{R'^2_0}{2}-\frac{R_0R''_0}{2} \\ &\quad {} +G''_0R''_0+2G'_0R'''_0+G_0R''''_0 \\ &\quad {} +\bigl(G''_0R'_0+2G'_0R''_0+G_0R'''_0\bigr) \biggl(\frac{G'_0}{2G_0}+\frac{2}{a_0} \biggr) \\ &\quad {} +2\bigl(G'_0R'_0+G_0R''_0 \bigr) \biggl(\frac{G''_0}{2G_0} -\frac{G'^2_0}{2G^2_0}-\frac{2}{a_0^2} \biggr) \\ &\quad {}+G_0R'_0 \biggl( \frac{G''_0}{2G_0}+\frac{20}{a_0^3} +\frac{G'^3_0}{G^3_0}-\frac{3}{2} \frac{G'_0G''_0}{ G^2_0} \biggr) \biggr\} \\ &\quad {}+\frac{2}{{\kappa}a_0^2} \biggl\{ \frac{G'_0}{\sqrt{G_0}}(1+2{\delta}R_0) +\frac{{\delta}R_0^2}{2\alpha}-{\delta}G_0 \frac{2R''_0}{\alpha} \\ &\quad {} -\frac{2{\delta}G_0R'_0}{\alpha} \biggl(\frac{G'_0}{G_0} + \frac{1}{a_0} \biggr) \biggr\} \\ &\quad {}+\frac{1}{a_0} \biggl[ \biggl\{ + \frac{2{\delta}R'_0}{ {\kappa}{\alpha}a_0^2} \bigl(2G_0-a_0G'_0 \bigr) \\ &\quad {}\times\frac{2(1+2{\delta}R_0)^2}{ {\kappa}a_0^2\sqrt{G_0}} \bigl(a_0\times G'_0-2G_0 \bigr) \biggr\} [1-\chi_0] \\ &\quad {}-\frac{1}{\alpha\kappa} \biggl\{ -{\delta}R_0R'_0+2{ \delta}\bigl(G'_0R''_0+G_0R'''_0 \bigr) \\ &\quad {}+2\delta\bigl(G'_0R'_0+G_0R'''_0\bigr)\biggl(\frac{2}{a_0} +\frac{G'_0}{2G_0} \biggr) \\ &\quad {}+2{\delta}G_0 R''_0 \biggl(\frac{G''_0}{2G_0}-\frac{2}{a_0^2}-\frac{G'^2_0}{ 2G^2_0} \biggr) \biggr\} \biggr] \\ &\quad {}+\frac{8{\delta}\sqrt{G_0}}{a_0\kappa} \frac{1}{(1+2{\delta}R_0)} \biggl(R''_0- \frac{6{\delta}R'^2_0}{ (1+2{\delta}R_0)} \biggr) \\ &\quad {}+\frac{2{\delta}R'_0}{(1\,{+}\,2{\delta}R_0)^3} \biggl\{ \frac{1}{\alpha\kappa} \biggl( -{\delta}R_0 R'_0\,{+}\,2{\delta} \bigl(G'_0R''_0\,{+}\,G_0R'''_0 \bigr) \\ &\quad {} +2\delta\bigl(G'_0R'_0+G_0R'''_0 \bigr) \biggl(\frac{2}{a_0}+\frac{G'_0}{2G_0} \biggr) \\ &\quad {}+2{\delta}G_0R''_0 \biggl(\frac{G''_0}{2G_0} -\frac{2}{a_0^2}-\frac{G'^2_0}{2G^2_0} \biggr) \biggr) \\ &\quad {}+\frac{2}{{a_0^2\kappa}} \biggl(\frac{a_0G'_0-2G_0}{\sqrt{G_0}} \biggr) (1+2{\delta}R_0) \\ &\quad {}+ \frac{2{\delta}R'_0}{ a_0^2\kappa\alpha} \bigl(2G_0-a_0G'_0 \bigr) \biggr\} \biggr], \end{aligned}$$

(21)

where the subscript “0” indicates that the quantities are evaluated at a=a ₀ and χ ₀ is given by

$$\chi_0=- \biggl[\frac{(1+2{\delta}R_0)(2G_0+a_0G'_0) +a_0\sqrt{G_0}X_{P0}}{\sqrt{G_0}\{a_0X_{\sigma0}+4\sqrt{G_0} (1+2{\delta}\tilde{R}_0)\}} \biggr]. $$

For $R_{0}=\tilde{R}_{0}=\mathit{constant}$ and using Eq. (11), Eq. (9) reduces to

$$ \sigma_0=-\frac{4(1+2{\delta}R_0)}{a_0\kappa}\sqrt{G_0} -\frac{{\delta}\tilde{R}_0^2}{2{\alpha}\kappa}. $$

(22)

This shows that the energy density is negative indicating the presence of exotic matter at the throat. Moreover, Eq. (21) turns out to be

$$\begin{aligned} \varPhi''_0&=G''_0-2G'_0 \biggl(\frac{3}{a_0}+\frac{a_0G'_0-2G_0}{8a_0G_0} \biggr)- \biggl( \frac{a_0G'_0-2G_0}{a_0^2\sqrt{G_0}} \biggr) \\ &\quad {}\times \biggl[\frac{\frac{3}{2\alpha}{\delta}a_0\tilde{R}_0^2 \sqrt{G_0}+2(1+2{\delta}R_0)(4G_0+a_0G'_0)}{\frac{a_0}{2\alpha} {\delta}\tilde{R}_0^2+4\sqrt{G_0} (1+2{\delta}\tilde{R}_0)} \biggr] \\ &\quad {}-\frac{\sqrt{G_0}}{a_0} \biggl(\frac{1}{16}+\frac{3}{2} \sqrt{G} \biggr)\frac{\delta\tilde{R}_0^2}{(1+2{\delta}\tilde{R}_0)}. \end{aligned}$$

(23)

4 Charged black string thin-shell WH

Here, we devise thin-shell WH for the charged black string and investigate its stability with the static background in the context of f(R) gravity. The surface pressure and energy density, under constant Ricci scalar condition, are now obtained by using Eqs. (5), (14) and (15) as

$$\begin{aligned} &P_0=\frac{({\alpha}^3a_0^3-M)(1+2{\delta}\tilde{R}_0)}{2{\pi}a_0 \sqrt{4q^2-4M\alpha{a_0+\alpha^4a^4_0}}}+\frac{{\delta}\tilde{R}^2_0}{ 2\alpha}, \end{aligned}$$

(24)

$$\begin{aligned} &{\sigma}_0=- \biggl(\frac{1+2{\delta}\tilde{R}_0}{2\pi{a^2}_0{\alpha}} \biggr) \sqrt{4q^2-4M\alpha{a_0}+\alpha^4a^4_0}- \frac{{\delta}\tilde{R}^2_0}{ 2\alpha}. \end{aligned}$$

(25)

Equation (16) leads to

$$\begin{aligned} &4{\alpha}^2a_0^2-\frac{4M}{a_0\alpha}+ \frac{a_0{\delta} \tilde{R}_0^2}{\alpha^2(1+2{\delta}\tilde{R}_0)} \sqrt{4q^2-4M\alpha{a_0}+ \alpha^4a^4_0} \\ &\qquad {}+\frac{128a_0^2B\pi^2}{(1+2{\delta}\tilde{R}_0)} \\ &\qquad {}\times\frac{ \sqrt{4q^2-4M\alpha{a_0}+\alpha^4a^4_0}}{\{-\alpha{\delta} a_0^2\tilde{R}_0^2\,{-}\,8(1\,{+}\,2{\delta}\tilde{R}_0)\sqrt{4q^2\,{-}\,4M\alpha{a_0}\,{+}\,\alpha^4a^4_0}\}} \\ &\quad {}=0. \end{aligned}$$

(26)

This is the required dynamical equation which the charged black string WH threaded by exotic matter with throat radius a ₀ must satisfy. In this scenario, Eq. (23) yields

$$\begin{aligned} \varPhi''_0&= \frac{1}{Y_0} \biggl[ \biggl(\frac{256q^4}{a_0^5\alpha^4}+\frac{288M^2}{ a_0^3\alpha^2}+ \frac{192q^2}{a_0} \\ &\quad {}-144M\alpha-\frac{576q^2M}{ \alpha^4a_0^3} \biggr) (1+2{\delta} \tilde{R}_0) \\ &\quad {}+\frac{2{\delta} \tilde{R}_0^2\sqrt{4q^2-4M\alpha{a_0}+\alpha^4a^4_0}}{\alpha^3a_0^2} \biggl(\frac{12q^2}{a_0\alpha}-9M \biggr) \biggr] \\ &\quad {}+\frac{{\delta}\tilde{R}_0^2}{(1+2{\delta}\tilde{R}_0)} \biggl(\frac{6M}{{\alpha}a_0^2}-\frac{6M}{\alpha^2a_0^3}- \frac{3a_0\alpha^2}{2} \\ &\quad {}-\frac{\sqrt{4q^2-4M\alpha{a_0}+\alpha^4a^4_0}}{16a_0^2\alpha} \biggr) \\ &\quad {} +\frac{2\alpha^2}{(4q^2-4M\alpha{a_0}+\alpha^4a^4_0)} \\ &\quad {}\times \biggl[4q^2 \biggl( \frac{5M}{a_0^3\alpha^3} +1-\frac{4q^2}{a_0^4\alpha^4} \biggr)-6Ma_0 \biggl( \alpha +\frac{2M}{a_0^3\alpha^2} \biggr) \biggr] \\ &\quad {}+\frac{72q^2}{ a_0^4\alpha^2}- \frac{32M}{a_0^3\alpha}-10\alpha^2, \end{aligned}$$

(27)

where

$$\begin{aligned} & \begin{aligned}[b] Y_0&=\frac{\sqrt{4q^2-4M\alpha{a_0}+\alpha^4a^4_0}}{\alpha} \\ &\quad {}\times\biggl[\frac{a_0{\delta} \tilde{R}_0^2}{2\alpha}+4(1+2{\delta} \tilde{R}_0)\frac{\sqrt{4q^2-4M\alpha{a_0} +\alpha^4a^4_0}}{a_0\alpha} \biggr], \end{aligned} \\ &\tilde{R}_0=4\alpha^2 \biggl(1+\frac{2}{a_0} \biggr)+\frac{16}{ {\alpha}a_0^3} \biggl(1+\frac{1}{a_0} \biggr) \biggl( \frac{2q^2}{{\alpha}a_0} -M \biggr). \end{aligned}$$

Now, we investigate the instability and stability of the static configurations for perturbations preserving the cylindrical symmetry which is determined by Φ″<0 or Φ″>0. In all figures, the solid line indicates the stable solution of WHs due to Φ″>0 whereas Φ″<0 points unstable static WH solutions which is symbolized by dotted lines. The gray regions correspond to non-physical zone. It is worth mentioning here that the charge q _c =0.866025 determines the behavior of these solutions. This specific value is used to construct the original metric with no horizon.

In f(R) model, i.e., R+δR ², we take some specific values of δ and study the stability of black string solutions.

• 1. When δ = 0.2, 0.4, 0.6.

  • For |q|=0 and |q|=0.7q _c , i.e., |q| is not very much close to q _c , we find that there exist unstable and stable configurations for some values of Bα ² with δ=0.2, 0.4 and 0.6 as shown in Figs. 1, 2 and 3.

    Fig. 1

    

    Wormholes of a charged black string against radial perturbation for M=1=α, δ=0.2 with different charge values. The dotted and solid curves indicate unstable and stable solutions, respectively whereas the shaded zone represents non-physical case, i.e., a ₀≤r _h

    Fig. 2

    

    Wormholes of a charged black string for M=1=α, δ=0.4 with different values of charge

    Fig. 3

    

    Wormholes of a charged black string for M=1=α, δ=0.6 with different values of charge

  • For |q|≲q _c (Figs. 1–3), there is a stable WH static solution for δ=0.2, 0.4 and 0.6. Further, it is seen that horizon radius keeps on decreasing with the increase in the value of charge.

  • When δ=0.2, 0.4 and 0.6, there exist stable WH configurations corresponding to |q|>q _c as implied by Figs. 1–3.

• 2. Now we make our thin-shell WH stability analysis by reducing the equations from f(R) to GR, i.e., by taking δ=0.

  • For |q|<q _c and |q|≲q _c , there always exists stable black string WH solution for each value of Bα ². We find from Fig. 4 that αa ₀ decreases upto the horizon radius of the original manifold, and then solutions cannot be found. We also see that increment in the charge makes the radius of the horizon to decrease.

    Fig. 4

    

    Wormholes of a charged black string for M=1=α, δ=0 with different values of charge

  • There exists stable thin-shell WH solution corresponding to |q|>q _c when δ→0 as shown in Fig. 4.

5 Concluding remarks

In this paper, we have studied the stability of WH solutions of charged black string under perturbation with f(R) terms. We have computed the Darmois-Israel matching conditions on the matter shell. Wormholes are constructed using cut and paste technique framed within a well-known f(R) model (as a source of exotic matter). In this scenario, dynamical equation is formulated and stability of WH solutions (threaded by exotic matter) are investigated.

The numerical analysis is used to explore Eq. (26) for αa ₀ with different values of the dark source exponent, i.e., δ=0, 0.2, 0.4 and 0.6. The results are summarized as follows.

• 1. Figures 1–4 indicate that the radius of the WH throat decreases progressively till it reaches the radius of the charged black string horizon r _h for large values of α ⁻² B and r _h disappears for |q|>q _c . The shaded portions in the graphs indicate regions of throat radius smaller than r _h .

• 2. It is seen that stable and unstable solutions exist for δ=0.2, 0.4, 0.6 with |q|=0, 0.7q _c whereas we obtain only stable configurations for |q|=0.999q _c and |q|=1.1q _c with δ=0.2, 0.4, 0.6. The radius of horizon decreases on increasing |q|.

• 3. It is worth mentioning here that when δ=0, we find stable solutions for |q|=0, 0.7q _c , 0.9999q _c and |q|=1.1q _c which are the solutions we can expect (Sharif and Azam 2013). Thus all our results reduce to GR by taking δ→0.