1 Introduction

Nowadays we have a strong belief that our universe experiences an accelerated expansion. The complementary astronomical data gathered from SNe Ia (Perlmutter et al. 1999), WMAP (Bennett et al. 2003), SDSS (Tegmark et al. 2004) and X-ray (Allen et al. 2004) experiments confirm this cosmic acceleration. Within the framework of general relativity (GR), a dark energy component with negative pressure is introduced to explain this acceleration. Dark energy scenario have got a lot of attention in modern cosmology. In recent years a plenty theoretical models have been investigated to interpret the dynamical properties of dark energy. One can see Copeland et al. (2006), Li et al. (2011), Bamba et al. (2012) for a review of dark energy models. The holographic dark energy (HDE) model is the famous and interesting model to explain a dark energy scenario. This model is constructed based on the holographic principle in quantum gravity (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d, 2007e). According to the holographic principle, the number of degrees of freedom for a system within a finite region should be finite and should be bounded roughly by the area of its boundary. In cosmology, the holographic principle will set an upper bound on the entropy of the universe. Based on holographic principle a short distance ultra- violet (UV) cut-off is related to the long distance infra-red (IR) cut-off, due to the limit set by the formation of a black hole (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d, 2007e). In this context, the energy of a system with size L does not exceed the energy of black hole with the same size, i.e.,

$$ L^3\rho_d\leq L m_{p}^2 $$
(1)

where m p is the reduced plank mass. By saturating the inequality (1), the energy density of HDE model in cosmology is identified by Cohen et al. (1999); Li (2004)

$$ \rho_d=3c^2m_{p}^2L^{-2} $$
(2)

where c 2 is a numerical constant of order unity and the factor 3 was introduced for convenience. An interesting feature of HDE is that it has a close connection with the space-time foam (Ng 2001; Arzano et al. 2007). Another features of HDE model can be found in Sect. 3 of Zimdahl and Pavón (2007). From the observational point of view, the HDE model has been constrained by various astronomical observation (Huang and Gong 2004a; Zhang and Wu 2005; Wu et al. 2008; Ma and Gong 2009; Alam et al. 2004). Recent observational data, which have been used to constrain the HDE model, show that for the non-flat universe \(c = 0.815^{+0.179}_{-0.139}\) (Li et al. 2009), and for the flat case \(c = 0.818^{+0.113}_{-0.097}\) (Enqvist and Sloth 2004; Huang and Gong 2004b; Huang and Li 2004b; Gong 2004). Also it has been shown that the cosmic coincidence problem can be resolved by inflation in the holographic DE model, provided the minimal number of e-folding (Li 2004). The HDE model has been investigated widely in the literature (Huang and Li 2004a, 2005; Ito 2005; Enqvist and Sloth 2004; Pavon and Zimdahl 2005; Wang et al. 2005; Kim et al. 2006; Nojiri and Odintsov 2006; Elizalde et al. 2005; Hu and Ling 2006; Li et al. 2006; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d; Saridakis 2008a, 2008b, 2008c). For a recent review on different HDE models and their consistency check with observational data see (del Campo et al. 2011). It should be noted that various HDE models have been investigated via assuming different IR cutoffs. The simple choice for IR cutoff is the Hubble radius, i.e., L=H −1. In this case, the accelerated expansion of the universe can not be achieved and we get a wrong equation of state for HDE model (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d, 2007e). However, in the presence of interaction between dark matter and dark energy, the late time cosmic acceleration can be derived and the cosmic coincidence problem can be solved (Pavon and Zimdahl 2005; Zimdahl and Pavón 2007). Event horizon is the another choice for IR cutoff. Although, in this case the accelerated expansion can be achieved, but the generalized second law (GSL) does not satisfy in a universe enveloped by event horizon IR cutoff (Zhou et al. 2007; Sheykhi 2010). The other choice for IR cutoff is the particle horizon. In this case, the HDE model can not also obtain the late time accelerated expansion (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d, 2007e). Here same as Sheykhi (2011) we assume the Hubble horizon as an IR cutoff for HDE model. In this case the GSL is also satisfied in the interacting accelerating universe (Zhou et al. 2007; Sheykhi 2010). Therefore the Hubble horizon is preferred from thermodynamical point of view.

It is worthwhile to mention that the parameter c 2 in HDE model has an essential role in characterizing the properties of HDE model. For example, the HDE model can behave as a phantom or quintessence dark energy models at the future for the values of c 2 bigger or smaller than 1, respectively (Setare et al. 2007).

In all above references the HDE model was assumed to have a constant value for holographic parameter c 2. However there are no strong evidences telling us that c 2 should be a constant parameter. In general the term c 2 can be assumed as a function of time. By slowly varying function with time, \(\dot{(c^{2})}/c^{2}\) is upper bounded by the Hubble expansion rate, i.e.,

$$ \frac{\dot{(c^2)}}{c^2}\leq H $$
(3)

In this case the time scale of the evolution of c 2 is shorter than H −1 and one can be satisfied to consider the time dependency of c 2 (Radicella and Pavon 2010). It has also been shown that the parameter c 2 can not be constant for all times during the evolution of the universe (Radicella and Pavon 2010).

As was mentioned above, in the presence of interaction between dark matter and dark energy the HDE model with the Hubble horizon IR cutoff can solve the coincidence problem and late time accelerated expansion. However, another alternative approach instead of interaction between dark components is that the holographic parameter c 2 varies slowly with time to solve the coincidence problem and explain late time acceleration (Duran and Parisi 2012). It has been shown that the interacting model of dark energy in which the coincidence problem is alleviated can be recast as a noninteracting model in which the holographic parameter c 2 evolves slowly with time (Duran and Parisi 2012).

In the line of above studies, we consider the HDE model with time-varying holographic parameter c 2(z), namely: generalized holographic dark energy (GHDE, hereafter). We show that this form of HDE model can interpret the cosmic acceleration in the Hubble length without a need for interaction term. In this model, the transition from quintessence to phantom regime tacks place in near past consistently with observation. Another feature of the GHDE model under Hubble horizon is the early decelerated and late time accelerated expansions of the universe. It is worthwhile to mention that the above features for GHDE model are resulted in the Hubble length scale and also in the absence of interaction term. In this work we first investigate the GHDE model in the flat FRW universe enveloped with Hubble horizon IR cutoff (HIR, hereafter), then the evolution of EoS parameter of the model as well as the deceleration parameter have been discussed. Finally the evolution of dark energy density of the model as a function of cosmic redshift for determining the pressureless dark matter era at the early time and late-time dark energy dominated phase has been discussed.

2 Generalized holographic model in the Hubble length

In this section we obtain the evolution of GHDE model in a flat Friedmann-Robertson-Walker (FRW) universe with Hubble horizon. We first calculate the evolution of EoS parameter of the model and then obtain the evolution of dark energy density and deceleration parameter in this model.

2.1 EoS parameter

Let us start with flat Friedmann-Robertson-Walker (FRW) universe. In this case the first Friedmann equation is given by

$$ H^{2}=\frac{1}{3m_{p}^{2}}(\rho _{m}+\rho _d) $$
(4)

where ρ m and ρ d are, respectively, the energy densities of pressureless dark matter and dark energy and m p is the reduced Planck mass. For HIR cutoff, L=H −1, the energy density of GHDE model from (2) can be given by

$$ \rho_d=3m_p^2c^2(z)H^2 $$
(5)

where the holographic parameter is considered as a function of redshift.

We now define the dimensionless energy density parameters as

$$ \varOmega_{m}=\frac{\rho_m}{\rho_c}= \frac{\rho_m}{3M_p^2H^2}, \qquad\varOmega_d=\frac{\rho_d}{\rho_c}=\frac{\rho_d}{3M_p^2H^2}=c^2(z) $$
(6)

According to these definitions, the first Friedmann equation in spatially flat universe can be written as follows

$$ \varOmega _{m}+\varOmega _{\varLambda}=1 $$
(7)

The conservation equations for pressureless dark matter and dark energy, respectively, are given by

$$\begin{aligned} \dot{\rho _{m}}+3H\rho _{m}=0 \end{aligned}$$
(8)
$$\begin{aligned} \dot{\rho _d}+3H(1+w_d)\rho_d=0 \end{aligned}$$
(9)

Taking the time derivative of Friedmann equation (4) and using (7, 8, 9), one can obtain

$$ \frac{\dot{H}}{H^2}=-\frac{3}{2}[1+w_{\varLambda} \varOmega_d] $$
(10)

Also it is obvious to see that differentiating Eq. (5) with respect to time yields

$$ \dot{\rho_d}=2\rho_d\biggl( \frac{\dot{c}}{c}+\frac{\dot{H}}{H}\biggr) $$
(11)

Inserting (11) and (5) in conservation equation for dark energy (9) and using (10), we find the equation of state, w d , for GHDE model with HIR cutoff as

$$ w_d=-\frac{2c^{\prime}}{3c(1-c^2)} $$
(12)

where prime represents the derivative with respect to lna. It is clear to see that the above relation reduce to w d =0 for constant holographic parameter c. Hence, as expected, the HDE model in HIR gets a wrong equation of state for dark energy which can not describe the expanding universe. As was mentioned before, this problem for HDE model can be solved, if we consider the interaction between dark matter and dark energy (see Sheykhi (2011) for more detail). From (12) we conclude that the EoS parameter of GHDE model, in which the holographic parameter c varies with time, can get w d <0 in HIR without assuming the interaction parameter. For this aim we use the Wetterich parametrization in which the holographic parameter c is considered in terms of redshift as follows (Witterich 2004; Gong 2005)

$$ c(z)=\frac{c_0}{1+c_1\ln{(1+z)}} $$
(13)

Putting c 1=0, the above holographic parameter reduces to c=c 0 indicating the constant value for HDE model. At the present time: z→0, c(z)→c 0, and at the early time: z→∞, c(z)→0. Hence the holographic parameter varies slowly from zero to c 0 during the history of the universe. Also to have a positive energy density for dark energy, ρ d ≥0, we should take the condition: c 0>0 and c 1≥0. In numerical procedure, the present value of dark energy density parameter is chosen as \(\varOmega_{d}^{0}=c_{0}^{2}\) and matter density parameter as \(\varOmega_{m}^{0}=1-c_{0}^{2}\) in spatially flat universe. Adopting the observational values \(\varOmega_{d}^{0}=0.7\) and \(\varOmega_{m}^{0}=0.3\) in the flat universe means that here we assume c 0=0.84. In Fig. 1, by solving (12) and using (13), we plot the evolution of EoS parameter, w d , in terms of redshift z for different illustrative values of c 0 and c 1. Here we see that the EoS parameter, w d of GHDE with HIR can transit from quintessence regime (w d >−1) to phantom regime (w d <−1). The observations favor dark energy models which cross the phantom line w=−1 from up (w d <−1) to down (w d <−1) in near past (Alam et al. 2004; Shen et al. 2005; Kao et al. 2005). Therefore this model is compatible with observations. Contrary the GHDE model HIR, the EoS parameter for interacting HDE model with HIR is constant during the history of the universe (see Eq. (8) of Sheykhi (2011)). However, Sheykhi showed that by applying some restrictions on the interaction parameter b and model parameter c, the EoS parameter of the HDE model with HIR can behave as a quintessence or a phantom type dark energy. But, neither the quintessence nor the phantom alone can fulfill the transition from w d >−1 to w d <−1.

Fig. 1
figure 1

The evolution of EoS parameter of GHDE model with HIR cutoff versus redshift parameter z for different illustrative values of model parameters c 0 and c 1. Here we take \(\varOmega_{d}^{0}=c_{0}^{2}\) and \(\varOmega_{m}^{0}=1-c_{0}^{2}\)

Full size image

It is also worthwhile to indicate the singularity of the model. We know that phantom dark energy brings the universe to finite-time Big-Rip singularity and quintessence models may end up in finite-time singularity (McInnes 2002; Caldwell et al. 2003; Nojiri et al. 2005). In Nojiri et al. (2005), the possible singularities of dark energy models have been classified to four categories:

Type I (Big Rip): for t→t s , a→∞, ρ→∞ and |p|→∞.

Type II (sudden): for t→t s , a→a s , ρ→ρ s and |p|→∞.

Type III: for t→t s , a→a s , ρ→∞ and |p|→∞.

Type IV: for t→t s , a→a s , ρ→0 and |p|→0.

Here t s , a s and ρ s are constants with a s ≠0. Form Eq. (12), one can see that the EoS parameter of GHDE model with HIR cutoff tends to zero, w d →0 for c=1. In this case form Eq. (5), the energy density of the model tends to constant value ρ s at characteristic scale factor a s . The equation of state for dark energy fluid p=wρ obtains p→∞ in the case of c=1. Hence the GHDE model with HIR cut-off encounters with TypeII singularity for c=1.

2.2 Dark energy density

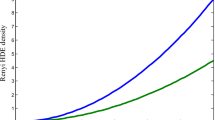
We now calculate the evolution of energy density of GHDE model described at HIR cutoff. From Eq. (6), the dark energy density of GHDE equals to square of varying holographic parameter, Ω d =c 2(z). Using (13), in Fig. 2 the evolution of dark energy density is plotted in terms of redshift for some illustrative values of model parameters c 0 and c 1. At the early time (z→∞) the parameter Ω d →0 which represents the dark matter dominated universe at the early time. Then the parameter Ω d increases to its present value \(c_{0}^{2}\) which indicates the dark energy dominated epoch. The important note is that in standard HDE model under HIR cutoff since the model parameter c is constant, the energy density Ω d =c 2 has no evolution during the history of the universe, i.e., Ω d is constant from early time to present time. Unlike the standard HDE model, in GHDE model with HIR the parameter Ω d increases from zero at the early time and tends to its present value at the present epoch. This behavior of GHDE model can interpret the dark matter dominated phase at the early time and the dark energy dominated epoch later.

Fig. 2
figure 2

The evolution of energy density of GHDE model with HIR cutoff versus redshift parameter z for different illustrative values of model parameters c 0 and c 1. Here we take \(\varOmega_{d}^{0}=c_{0}^{2}\) and \(\varOmega_{m}^{0}=1-c_{0}^{2}\)

Full size image

2.3 Deceleration parameter

Finally, we calculate the deceleration parameter q of the model. The positive value of deceleration parameter (q>0) indicates the decelerated phase of expansion and the negative value (q<0) represents the accelerated expansion epoch of the universe. The parameter q is defined as

$$ q=-1-\frac{\dot{H}}{H^2} $$
(14)

Inserting (10) in (14) and using (12) as well as Ω d =c 2, the parameter q for this model is obtained as

$$ q=\frac{1}{2}-\frac{c^{\prime}c}{1-c^2} $$
(15)

In the limiting case of standard HDE model with constant value of c, the parameter q reduces to q=1/2 which describes the decelerated phase and can not represents the accelerated expansion of the universe at all. However, including the interaction between dark components of the universe and some restrictions on the interaction parameter b and model parameter c the standard HDE model with HIR cutoff can result the negative value for deceleration parameter q (Sheykhi 2011). But it should be emphasized that the transition from decelerated to accelerated expansion can not be achieved in standard HDE model with HIR cutoff.

In Fig. 3, by solving (15) and using (13), we plot the parameter q in GHDE model with HIR cutoff as a function of redshift parameter z. We see that at the early epochs the parameter q is equal to 1/2, indicating the decelerated expansion at the dark matter-dominated universe and then the parameter q reaches to negative values, representing the accelerated phase at the dark energy-dominated universe. Daly et al. (2008), by applying a model independent analysis method showed that the transition epoch from decelerated to accelerated expansion (q=0) occurs at \(z_{t}=0.78^{+0.08}_{-0.27}\) for zero space curvature. As a comparison with the above observational fact, we obtain the transition epoch z t =0.78 in GHDE model for the selected illustrative values (c 0=0.5,c 1=0.4). Hence the GHDE model with HIR cutoff is consistent with this observational fact that the universe has entered to the accelerated phase at past times and now experiences an accelerated expansion (Daly et al. 2008).

Fig. 3
figure 3

The evolution of deceleration parameter q in GHDE with HIR model versus redshift parameter z for different illustrative values of model parameters c 0 and c 1. Here we take \(\varOmega_{d}^{0}=c_{0}^{2}\) and \(\varOmega_{m}^{0}=1-c_{0}^{2}\)

Full size image

3 Conclusion

In summery, we considered the generalized holographic dark energy model in spatially flat universe described in Hubble length an IR cutoff (GHDE with HIR cutoff). The holographic parameter c generally is not constant and can be assumed as a function of cosmic redshift. The standard HDE model described by HIR cutoff gets to wrong equation of state for dark energy (Horava and Minic 2000, 2001; Thomas 2002; Setare 2006a, 2006b, 2007a, 2007b, 2007c, 2007d, 2007e). The observations favor dark energy models which cross the phantom line w=−1 from quintessence regime (w d <−1) to phantom regime (w d <−1) in near past (Alam et al. 2004; Shen et al. 2005; Kao et al. 2005) and also the models in which the deceleration parameter transit from positive value to negative value (Daly et al. 2008). Although, including the interaction between dark matter and dark energy in standard HDE model described by HIR cutoff can solve the coincidence problem and late time accelerated expansion (Zhou et al. 2007; Sheykhi 2010, 2011), but the EoS parameter of this model behaves as a quintessence or phantom model and can not transit from quintessence regime (w d >−1) to phantom regime (w d <−1) (Sheykhi 2011). Also in the context of interacting HDE with HIR cutoff the deceleration parameter q is negative for all times in the history of the universe and therefore can not explain the transition from decelerated to accelerated expansion. However, in the case of GHDE with HIR cutoff, we obtained the EoS parameter as well as the deceleration parameter and evolution of dark energy density. Here we assumed the holographic parameter c 2 varies slowly with time instead of adding the interaction term. We showed that in this model the phantom line is crossed from up (w d >−1) to down (w d <−1) which is in agreement with observation (Alam et al. 2004; Shen et al. 2005; Kao et al. 2005). We obtained the observational transition epoch form decelerated to accelerated expansion \(z_{t}=0.78^{+0.08}_{-0.27}\) for GHDE model with HIR cut-off provided that (c 0=0.5,c 1=0.4). Therefore, in agreement with observation (Daly et al. 2008), this model can indicated the decelerated phase at the early time (q>0) and accelerated phase later (q<0). The evolution of energy density of dark energy for this model represents the pressureless dark matter-dominated universe at the early time and dark energy-dominated phase at the present time. Finally we showed that this model encounters with Type II singularity in the case of c=1.