Abstract
In this paper, we study an anisotropic Bianchi-I space-time model in f(R) theory of gravity in the presence of perfect fluid as a matter contains. The aim of this paper is to find the functional form of f(R) from the field equations and hence the solution of various cosmological parameters. We assume that the deceleration parameter to be a constant, and the shear scalar proportional to the expansion scalar to obtain the power-law form of the scale factors. We find that the model describes the decelerated phases of the universe under the choice of certain constraints on the parameters. The model does not show the acceleration expansion and also transition from past deceleration to present accelerating epoch. We discuss the stability of the functional form of f(R) and find that it is completely stable for describing the decelerating phase of the universe.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The recent developments in cosmology with the observations such as Ia supernova (Riess et al. 1998, 1999; Perlmutter et al. 1999; Tonry et al. 2003), cosmic microwave background anisotropy (Spergel et al. 2003), large scale structure (Tegmark et al. 2004; Seljak et al. 2005; Percival et al. 2007; Kamatsu et al. 2009), baryon oscillation (Eisenstein et al. 2005) and weak lens (Jain and Taylor 2003) have led to the conclusion that the universe is accelerating in the current epoch. It has been observed that a fluid known as dark energy (DE) with large negative pressure is responsible for this acceleration. Many DE models have been proposed to explain the cosmic accelerated expansion (Copeland et al. 2006). A cosmological constant Λ responsible for acceleration is the simplest candidate of DE (Sahni and Starobinsky 2000; Padmanabhan 2003), which so far best fits with the observational data. However, the observed value of the cosmological constant is much smaller (10120 orders of smaller magnitude) than any other energy (vacuum energy) predicted by quantum physics (Peebles and Ratra 2003; Carroll 2001). This problem is known as fine-tuning problem in cosmology. Therefore, there is no guiding principle for construction of a promising model of cosmological constant.
The second alternative of cosmological constant, which is not stable, is a minimally coupled scalar field ϕ, usually called quintessence. These scalar fields may be responsible for a stage of accelerated expansion (Steinhardt et al. 1999; Zlatev et al. 1999). A further interesting possibility is provided by non-minimally coupled scalar field (Amendola 1999; Chiba 2003a). It is also mentioned that energy conditions are violated in all these kind of scalar fields. Also, these models end with a finite future singularity known as Big Rip. Modification of the gravity theory is an alternative approach, for example, f(R) model (Capozziello et al. 2003; Nojiri and Odintsov 2003; Carroll et al. 2004). The f(R) model is a modified gravity model, constructed by replacing the gravitational Lagrangian with a general function of the Ricci scalar R.
The f(R) gravity provides a very natural unification of the early-time inflation and late-time acceleration. It describes the transition from deceleration to acceleration in the evolution of the universe (Nojiri and Odintsov 2007a, 2008). Over the past few years, Many works are available in literature (Capozziello and Francaviglia 2008; Abdalla et al. 2005; Nojiri and Odintsov 2007b; Bertolami and Pármos 2008; Harko 2008) addressing the well-known issues of stability (Dolgov and Kawasaki 2003), singularity problem (Frolov 2008), solar system test (Chiba 2003b), etc. The general scheme for modified gravity reconstruction from any realistic FRW cosmology have been discussed by Nojiri and Odintsov (2006). It seems that f(R) gravity models pass all known observational local test currently (Elizalde et al. 2010, 2011; Nojiri and Odintsov 2011).
Almost all of these considerations are mainly investigated in a spatially flat homogeneous and isotropic universe described by Friedmann- Robertson-Walker (FRW) metric. The theoretical studies and observational data, which support the existence of anisotropic phase, lead to consider the model of universe with anisotropic background. Since, the universe is almost isotropic at large scale, the studying of the possible effects of anisotropic universe in the early time makes the Bianchi-I type (BI) model as a prime alternative. Many authors have tried to find analytical solutions for the known functional form f(R). For examples, Barrow and Clifton (2006) have obtained exact cosmological solutions for scale invariant theories which generalize Einstein’s GR to a theory derived from the Lagrangian R 1+δ. The solutions were expanding universe of Kasner form and exist for \(-\frac{1}{2}<\delta<\frac{1}{4}\). However, these solutions were obtained for vacuum universe. Sharif and Shamir (2009, 2010a, 2010b), Sharif and Zubair (2010a), Shamir (2010), Sharif and Kausar (2011a, 2011b, 2011c), and Aktaş et al. (2012) have studied anisotropic models in f(R) theory. Recently, Yilmaz et al. (2012) have discussed quark and strange quark matter in f(R) gravity for Bianchi I and V space time models. The ordering of this approach can also be reversed. Namely, for a known scale factor, one may construct functional form of f(R) which yields such scale factors as solutions (Nojiri and Odintsov 2007c; Capozziello and Francaviglia 2008; Nojiri et al. 2009).
In this paper, we are interested to find a functional form of f(R) for a known scale factor in anisotropic locally-rotationally-symmetric (LRS) Bianchi I model with perfect fluid as a source of matter. A functional form of f(R) is obtained from the field equations by assuming the constant deceleration parameter and the shear scalar proportional to the expansion scalar. We find that the model describes the decelerated phase of the universe under the choice of certain constraints on the parameter. We discuss the stability of f(R) theory for the decelerated phase of the solution and it is found that it is completely stable for the defined constraint.
The paper is organized as follows. In Sect. 2, we present the gravitational action of f(R) gravity and the corresponding field equations. Section 3 provides the solution of the field equations. In Sect. 4 we discuss the stability condition for Bianchi model in f(R) gravity. In the last Sect. 5, summary of the finding is given.
2 Field equations for \([f(R)+\mathcal{L}_{m}]\) gravity
The gravitational action for f(R) theory of gravity coupled with matter fluid in the units 16πG=1 and c=1, takes the following form (Nojiri and Odintsov 2007c; Capozziello and Francaviglia 2008)
where R is the Ricci scalar and \(\mathcal{L}_{m}\) corresponds to the matter Lagrangian.
The field equations are obtained by varying the action (1) with respect to metric tensor g μν

where F(R)=f′(R) and T μν is the energy momentum tensor. The other symbols have their usual meanings.
The energy momentum tensor for a perfect fluid is given as
where ρ is the energy density and p is the thermodynamical pressure of the fluid. u μ is the four velocity of the fluid such that u μ u ν=1 and in comoving coordinates, \(u^{\mu}=\delta_{0}^{\mu}\).
We consider a homogeneous and anisotropic Locally-rotationally-symmetric (LRS) Bianchi type-I line element whose metric is given by
where the metric coefficients A and B are the scale factors in an anisotropic background and are functions of cosmic time t only.
The average scale factor is defined as
The rate of the expansion along x-, y-, and z-axes can be defined as,
where a dot denotes ordinary derivative with respect to cosmic time t. The average Hubble parameter (average expansion rate), which is the generalization of the Hubble parameter in an isotropic case, H is given as
The expansion scalar, θ and the shear scalar, σ 2 are respectively defined as
where

The scalar curvature for the metric (4) is given by
Using comoving coordinates, the field Eqs. (2) for the metric (4) and energy-momentum tensor (3) yield the following system of equations.

On integration of (15), we obtain
where F 0 is a constant of integration. Equation (16) represents the most general form of F(R) in terms of directional scale factors in f(R) gravity for the anisotropic LRS Bianchi-I space-time.
3 Solution of the field equations
Many authors have tried to find analytical solutions from the known functional form f(R) (Barrow and Clifton 2006). The ordering of this approach can also be reversed. Namely, for a known scale factor, one may construct functional form of f(R) which yields such scale factor as a solution (Nojiri and Odintsov 2007c; Capozziello and Francaviglia 2008; Nojiri et al. 2009). As we observe that the solution of F(R) in (16) can be found only if the scale factors are known. In this paper our aim is to find a general form of f(R) for a known scale factor and study the stability of functional form of f(R) in anisotropic model to describe the decelerated and accelerated phases of the universe.
For any physically relevant model, the Hubble parameter and deceleration parameter are the most important observational quantities in cosmology. Berman (1983), and Berman and Gomide (1988) proposed a law of variation for Hubble parameter in FRW model that yields a constant value of deceleration parameter and a power-law and exponential forms of the scale factor. In recent papers (see Refs. Singh and Kumar 2006; Singh et al. 2008; Singh 2009a, 2009b; Singh and Beesham 2010; Sharif and Zubair 2010b, 2012a) have generalized this assumption in anisotropic model. According to the assumption let us take the deceleration parameter as a constant, that is,
where n(≥0) is a constant. In the present anisotropic model, the assumption (17) yields
where c and d are positive constants of integration. For a power-law expansion (18), we must have n>0.
In view of anisotropy of the space-time, we assume that shear scalar (σ) is proportional to the expansion scalar (θ). This leads to a relation between the metric coefficients, i.e.,
where k>1 is a constant (Collins et al. 1980). For sake of simplicity, we have taken the integration constant as a unity.
Using (18) and (19), we get the metric coefficients as
From (11), (20) and (21), the expression for the Ricci scalar becomes

where \(\alpha=\frac{9\{k(k+2)+3\}-3n(k+2)^{2}}{n^{2}(k+2)^{2}}\).
Using the above background solutions into (16), we find f′(R) in terms of R as
We observe that for a real valued solution of f(R), R and α must be of opposite sign.
On integration of (23), we get
where f 0 is a constant of integration. On imposing f(0)=0, we find f 0=0, therefore, Eq. (24) gives the required form of the function f(R) as
which is basically of the form f(R)∝R λ, where \(\lambda= \frac{n+3}{2n}>0\) as n>0. For n=1, f(R)∝R 2 and for n=3, the model reduces to general relativity form, i.e., f(R)∝R. It is also clear that the power of R, i.e., λ contains only n and is independent of k.
The energy density and pressure in terms of cosmic time t are given as
For reality of the viable model, the energy density must be positive and therefore we must take n(k+2)2−3{k(k+2)+3}>0, as k>1. Equations (26) and (27) give
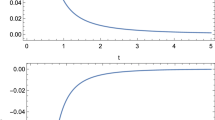
which shows that null energy condition (NEC) is satisfied for k>1. The energy density and pressure decrease with time and tend to zero for large t. The equation of state parameter ω, which is defined as \(\omega=\frac{p}{\rho}\), is given by
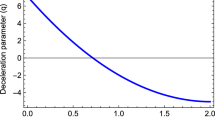
which is positive through out the evolution. This shows that the functional form of f(R) in (25) with the metric coefficients (20) and (21) describes the decelerated phases of the universe. From (17) and (29), we have the following linear relation in q and ω
which also shows that the model decelerates.
We now find the following constraints under which the model decelerates keeping in view of the positivity of energy density
or,
Therefore, we conclude that the f(R) model obtained here in (25) favors the decelerating phase of the universe under above constraints (31) and (32), which is not in according to the present day scenario of the accelerating universe. Also, the model does not show transition from decelerated to accelerated phase of the universe. In literature it can be seen that the f(R) models may imply accelerated expansion and also transition from past deceleration to present acceleration epoch. It may be noted that the anisotropic Bianchi models represent cosmos in its early stages of the evolution of the universe. In a paper (Sharif and Zubair 2012b), it is shown that some models can explain the evolutionary paradigm which would result in deceleration phase. Therefore, this functional form of f(R) can also explain some of the physical properties of the evolution of the decelerating universe.
4 Stability analysis
In Sect. 3, we have obtained a suitable functional form of f(R), which describes the decelerating phase of the universe under some defined constraints. In this section, we study the stability of a foresaid form of f(R). An acceptable cosmological model in f(R) theory is considered to be viable if it satisfies the following stability conditions
and
The conditions for the cosmological viability of f(R) models have been derived in Ref. (Amendola et al. 2007). Among those conditions the requirement of the above two are particularly important to give rise to a saddle matter era followed by a late time cosmic acceleration. The cosmologically viable f(R) models need to be close to the Λ-Cold Dark Matter (ΛCDM) model in the deep matter era, but the deviation from it becomes important around the late stage of the matter era. Several examples of such viable models were presented in Li and Barrow (2007), Amendola and Tsujikawa (2008).
The stability condition (33) always holds as k>1. To obtain the constraints which satisfy (34), we differentiate (23) with respect to R, to get
which gives
Thus, we find that out of two constraints described in (31) and (32), the constraint in Eq. (32) only favors the stability of the solution for the decelerated phases of the universe.
5 Conclusion
In this paper, we have studied f(R) theory of gravity in anisotropic LRS Bianchi-I space-time model. We have assumed the constant deceleration parameter, and a proportionality relation between shear scalar and scalar expansion to obtain exact form of f(R) and then the solution of the various cosmological parameters. We have found that the value of EoS parameter is constant, i.e., \(\omega=\frac{n}{3}\), which remains positive as n>0 throughout the evolution of the universe. This allows to describe the decelerated phases of the universe. We have obtained a linear relation between the deceleration parameter, q and EoS parameter, ω as q=3ω−1, which also describes the decelerated epoch. In Sect. 3 we have obtained some specific constraints on parameters keeping in view of positivity of the energy density under which the model exhibits decelerated universe. The model does not show transition from decelerated to accelerated phase of the universe.
We have also analyzed the stability of the functional form of f(R) and found that it is completely stable to describe the decelerated phases of the universe. We have not obtained any suitable constraints to describe the accelerated expansion and also the transition from past deceleration to present accelerating epoch of the universe in this anisotropic model. It is well known that the anisotropic models represent cosmos in its early stages of the evolution of the universe and some models can explain the evolutionary paradigm which would result in deceleration phase. It may be noted that even though the f(R) gravity describes an early-time inflation and late-time acceleration, this results shows that f(R) gravity theory is also suitable to describe the decelerated phase of the universe in anisotropic models which is stable. The approach introduced is simple and much more universal. We hope that this will make it useful in future applications of f(R) theory of gravity in anisotropic models.
References
Abdalla, M.C.B., Nojiri, S., Odintsov, S.D.: Class. Quantum Gravity 22, L35 (2005)
Aktaş, C., Aygün, S., Yilmaz, İ.: Phys. Lett. B 707, 237 (2012)
Amendola, L.: Phys. Rev. D 60, 043501 (1999)
Amendola, L., Tsujikawa, S.: Phys. Lett. B 660, 125 (2008)
Amendola, L., Gannouji, R., Polarski, D., Tsujikawa, S.: Phys. Rev. D 75, 083504 (2007)
Barrow, J.D., Clifton, T.: Class. Quantum Gravity 23, L1 (2006)
Berman, M.S.: Nuovo Cimento B 74, 182 (1983)
Berman, M.S., Gomide, F.M.: Gen. Relativ. Gravit. 20, 191 (1988)
Bertolami, O., Pármos, J.P.: Class. Quantum Gravity 25, 245017 (2008)
Capozziello, S., Francaviglia, M.: Gen. Relativ. Gravit. 40, 357 (2008)
Capozziello, S., Carloni, S., Troisi, A.: Recent Res. Dev. Astron. Astrophys. 1, 625 (2003)
Carroll, S.M.: Living Rev. Relativ. 4, 1 (2001)
Carroll, S.M., Duvvuri, V., Trodden, M., Turner, M.S.: Phys. Rev. D 70, 043528 (2004)
Chiba, T.: Phys. Rev. D 60, 083508 (2003a)
Chiba, T.: Phys. Lett. B 575, 1 (2003b)
Collins, C.B., Glass, e.N., Wilkinson, D.A.: Gen. Relativ. Gravit. 12, 805 (1980)
Copeland, E.J., Sami, M., Tsujikawa, S.: Int. J. Mod. Phys. D 15, 1753 (2006)
Dolgov, A.D., Kawasaki, M.: Phys. Lett. B 573, 1 (2003)
Eisenstein, D.J., et al.: Astrophys. J. 633, 560 (2005)
Elizalde, A., Nojiri, S., Odintsov, S.D., Gomez, D.S.: Eur. Phys. J. C 70, 351 (2010)
Elizalde, A., Nojiri, S., Odintsov, S.D., Sebastiani, L., Zerbini, S.: Phys. Rev. D 83, 086006 (2011)
Frolov, A.V.: Phys. Rev. Lett. 101, 061103 (2008)
Harko, T.: Phys. Lett. B 669, 376 (2008)
Jain, B., Taylor, A.: Phys. Rev. Lett. 91, 141302 (2003)
Kamatsu, E., et al.: Astrophys. J. Suppl. Ser. 180, 330 (2009)
Li, B., Barrow, J.D.: Phys. Rev. D 75, 084010 (2007)
Nojiri, S., Odintsov, S.D.: Phys. Rev. D 68, 123512 (2003)
Nojiri, S., Odintsov, S.D.: Phys. Rev. D 74, 086005 (2006)
Nojiri, S., Odintsov, S.D.: Phys. Lett. B 657, 238 (2007a)
Nojiri, S., Odintsov, S.D.: Phys. Lett. B 646, 105 (2007b)
Nojiri, S., Odintsov, S.D.: Int. J. Geom. Methods Mod. Phys. 4, 115 (2007c)
Nojiri, S., Odintsov, S.D.: Phys. Rev. D 77, 026007 (2008)
Nojiri, S., Odintsov, S.D.: Phys. Rep. 505, 59 (2011)
Nojiri, S., Odintsov, S.D., Saez-Gomez, D.: Phys. Lett. B 681, 74 (2009)
Padmanabhan, T.: Phys. Rep. 380, 235 (2003)
Peebles, P.J.E., Ratra, B.: Rev. Mod. Phys. 75, 559 (2003)
Percival, W.J., et al.: Mon. Not. R. Astron. Soc. 381, 1053 (2007)
Perlmutter, S., et al.: Astrophys. J. 517, 565 (1999)
Riess, A.G., et al.: Astrophys. J. 116, 1009 (1998)
Riess, A.G., et al.: Astrophys. J. 117, 707 (1999)
Sahni, V., Starobinsky, A.A.: Int. J. Mod. Phys. D 9, 373 (2000)
Seljak, U., et al.: Phys. Rev. D 71, 103515 (2005)
Shamir, M.F.: Astrophys. Space Sci. 330, 183 (2010)
Sharif, M., Kausar, H.R.: Astrophys. Space Sci. 332, 463 (2011a)
Sharif, M., Kausar, H.R.: J. Phys. Soc. Jpn. 80, 044004 (2011b)
Sharif, M., Kausar, H.R.: Phys. Lett. B 697, 1 (2011c)
Sharif, M., Shamir, M.F.: Class. Quantum Gravity 26, 235020 (2009)
Sharif, M., Shamir, M.F.: Gen. Relativ. Gravit. 42, 2643 (2010a)
Sharif, M., Shamir, M.F.: Mod. Phys. Lett. A 25, 128 (2010b)
Sharif, M., Zubair, M.: Astrophys. Space Sci. 330, 399 (2010a)
Sharif, M., Zubair, M.: Int. J. Mod. Phys. D 19, 1957 (2010b)
Sharif, M., Zubair, M.: Astrophys. Space Sci. 339, 45 (2012a)
Sharif, M., Zubair, M.: Astrophys. Space Sci. 342, 511 (2012b)
Singh, C.P.: Pramāna 72, 429 (2009a)
Singh, C.P.: Gravit. Cosmol. 15, 381 (2009b)
Singh, C.P., Beesham, A.: Int. J. Mod. Phys. A 25, 3825 (2010)
Singh, C.P., Kumar, S.: Int. J. Mod. Phys. D 15, 419 (2006)
Singh, C.P., Zeyauddin, M., Ram, S.: Int. J. Theor. Phys. 47, 3162 (2008)
Spergel, D.N., et al.: Astrophys. J. Suppl. Ser. 148, 175 (2003)
Steinhardt, P.J., Wang, L.M., Zlatev, I.: Phys. Rev. D 59, 123504 (1999)
Tegmark, M., et al.: Phys. Rev. D 69, 103501 (2004)
Tonry, J.L., et al.: Astrophys. J. 594, 1 (2003)
Yilmaz, İ., Baysal, H., Aktaş, C.: Gen. Relativ. Gravit. 44, 2313 (2012)
Zlatev, I., Wang, L.M., Steinhardt, P.J.: Phys. Rev. Lett. 82, 896 (1999)
Acknowledgements
The authors would like to thanks the anonymous referees for very valuable comments on this work. The authors also express their sincere thanks to Prof. Sami, Center for Theoretical Physics, JMI, India for useful discussion.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Singh, V., Singh, C.P. Functional form of f(R) with power-law expansion in anisotropic model. Astrophys Space Sci 346, 285–289 (2013). https://doi.org/10.1007/s10509-013-1436-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10509-013-1436-z