1 Introduction

There are growing evidences of dark energy (DE) responsible for the present expanding universe with an acceleration over the last few years. Its confirmation is made by type Ia supernovae (Perlmutter et al. 1999), galaxy redshift surveys (Fedeli et al. 2009), cosmic microwave background radiation (CMBR) data (Caldwell and Doran 2004; Huang et al. 2006a, 2006b; Keum 2007) and large scale structure (Koivisto and Mota 2006; Daniel 2008). The standard cosmology has been remarkably successful but there remain some serious unresolved issues including the search for the best DE candidate. The origin and nature of DE is still unknown except some particular ranges of the equation of state (EoS) parameter ω. In the absence of any solid argument in favor of DE candidate, a variety of models have been investigated.

Scalar field models are one of the proposed scenarios for DE. The mechanism of these models suggests that a scalar field (ϕ) provides energy with negative pressure, leading to decrease a proper potential of the field. A great number of scalar field DE models have been studied so far, including quintessence with dominating potential (Huang et al. 2006a, 2006b), K-essence with non-standard kinetic term (Armendariz-Picon et al. 2000, 2001), tachyon having negative squared mass (Sen 2002; Padmanabhan 2002), phantom keeping negative energy (Nojiri and Odintsov 2003a, 2003b), ghost condensate with no potential (Arkani-Hamed et al. 2004; Piazza and Tsujikawa 2004), quintom (Guo et al. 2005; Zhang 2005; Setare 2006) and dilaton with high energy particles (Copeland et al. 2006). There are many attempts to reconstruct potential and scalar fields by establishing a connection between different DE models with these scalar field models.

Setare (2007a, 2007b, 2007c, 2007d, 2008) studied the correspondence of HDE model with Chaplygin gas, interacting generalized Chaplygin gas, interacting phantom scalar field and tachyon scalar field model in general relativity. Ebrahimi and Sheykhi (2011) reconstructed the power-law entropy-corrected HDE by correspondence with the above mentioned scalar fields in non-flat evolving universe. Sharif and Jawad (2012) have investigated interacting HDE with new IR cutoff to develop correspondence with the scalar field models and discussed the accelerated expansion of the universe. Granda and Oliveros (2009) studied the correspondence between the quintessence, tachyon, K-essence and dilaton energy density with HDE density by taking event horizon as IR cutoff in the flat FRW universe. They reconstructed potentials and dynamics for the scalar field models, which describe accelerated expansion.

The f(T) theory of gravity (Linder 2010) is the generalized form of teleparallel gravity (Nashed 2002; Sharif and Amir 2007a, 2007b, 2008), which attracted many people to explore the accelerated expansion of the universe. Its dynamics governs the torsion scalar which takes part in this expansion. This theory uses Weitzenböck connection which inherits only torsion and zero curvature. There are many viable models (Bengochea and Ferraro 2009; Wu and Yu 2010; Yang 2011; Ferraro and Fiorini 2011; Bamba et al. 2011; Wei et al. 2012) proposed in f(T) theory to discuss DE era. Sharif and Rani (2011) extended this work for Bianchi type I universe and discussed the accelerated expansion of the universe. They also remarked that these models bear no equivalence at small scales. Daouda et al. (2012) reconstructed the HDE model in this theory and observed the crossing of phantom divide line. They also provided the unification of dark matter and DE in this scenario.

In this paper, we establish correspondence between f(T) gravity and scalar field models in the flat FRW universe and discuss them graphically. We obtain the EoS and deceleration parameters and explore their behavior for the derived scale factor using a specific f(T) model. The paper is organized as follows: In Sect. 2, the basic formalism of f(T) and the field equations are given. Section 3 explores the EoS and deceleration parameters for a particular f(T) model. In Sect. 4, we construct of f(T) scalar field models. The last section contains the summary of our results.

2 The generalized teleparallel gravity

In this section, we introduce basic formalism of teleparallel as well as its generalization f(T) theory of gravity. The basic ingredient in the structure of these theories is the vierbein field h a (x μ) (Nashed 2002; Sharif and Amir 2007a, 2007b, 2008) which forms an orthonormal basis for the tangent space at each point x μ of the manifold. Here, the Latin alphabets (a,b,…=0,1,2,3) denote the tangent space indices and the spacetime indices are represented by Greek alphabets (μ,ν,…=0,1,2,3). Each vector h a can be identified by its components \(h_{\mu}^{a}\) such that \(h_{a}=h^{\mu}_{a} \partial_{\mu}\). These tetrad are related to the metric tensor g μν by the following relation

$$ g_{\mu\nu}=\eta_{ab}h_{\mu}^{a}h_{\nu}^{b}, $$
(1)

where η ab =diag(1,−1,−1,−1) is the Minkowski metric for the tangent space and satisfy the following properties

$$ h^{a}_{\mu}h^{\mu}_{b}= \delta^{a}_{b},\qquad h^{a}_{\mu}h^{\nu}_{a}= \delta^{\nu}_{\mu}. $$
(2)

The torsion scalar is given as

$$ T=S_{\rho}{}^{\mu\nu}T^{\rho}{}_{\mu\nu}, $$
(3)

where S ρ μν and torsion tensor T ρ μν are defined as follows

(4)
(5)

and \(K^{\mu\nu}{}_{\rho}=-\frac{1}{2}(T^{\mu\nu}{}_{\rho} -T^{\nu\mu}{}_{\rho}-T_{\rho}{}^{\mu\nu})\) is the contorsion tensor. The action for f(T) gravity is given by (Bengochea and Ferraro 2009; Wu and Yu 2010; Yang 2011; Ferraro and Fiorini 2011; Bamba 2011; Wei et al. 2012)

$$ S=\frac{1}{2\kappa^2}\int d^{4}x\bigl[ef(T)+L_m \bigr], $$
(6)

where \(e=\sqrt{-g},~\kappa^{2}=8\pi G,~G\) is the gravitational constant and L m is the Lagrangian density of matter inside the universe. Here f(T) is the general differentiable function of T. The corresponding field equations are obtained by varying this action with respect to vierbein as

(7)

where f T , f TT stand for the first and second derivatives with respect to T and \(T^{\nu}_{\rho}\) is the energy-momentum tensor of the perfect fluid.

3 Some cosmological parameters

Here we discuss accelerated expansion of the universe through EoS and deceleration parameters for the flat FRW universe described by

$$ ds^{2}=dt^{2}-a^{2}(t) \bigl(dx^{2}+dy^{2}+dz^{2}\bigr), $$
(8)

where a is the time dependent scale factor. The corresponding tetrad components are \(h^{a}_{\mu}=\mathrm{diag}(1,a,a,a)\), which satisfy Eq. (2). Substituting these tetrad components in Eq. (3), the torsion scalar becomes T=−6H 2. Using these equations for a=0=ν and a=1=ν in Eq. (7), we obtain the following modified Friedmann equations

(9)
(10)

where ρ and p are the total energy density and pressure of the universe and \(H(=\dot{a}/a)\) is the Hubble parameter with dot representing the time derivative. We assume here a pressureless universe, i.e., p m =0 and κ 2=1 for the sake of simplicity. The above equations can be rewritten as

(11)
(12)

Here the subscripts m and T denote the matter and torsion contributions of energy density and pressure, and are given as follows

(13)
(14)

and satisfying the energy conservation equation

$$ \dot{\rho}_T+3H(1+\omega_T) \rho_T=0. $$
(15)

Noted that by taking f(T)=T in the modified Friedmann equations (11) and (12) which yield ρ T =0=p T and the resulting equations become the usual Friedmann equations in general relativity. Also, the energy conservation equation and its solution for dust matter are given by

$$ \dot{\rho}_m+3H\rho_m=0,\qquad \rho_{m}=\rho_{0m}a^{-3}, $$
(16)

where ρ 0m is an arbitrary constant. Using Eqs. (13) in (15), the EoS parameter for f(T) gravity is obtained as

$$ \omega_T=-1+\frac{4\dot{H}(12H^2f_{TT}-f_{T}+1)}{12H^2f_T+f-6H^2}. $$
(17)

We take the following viable power law f(T) model (Wu and Yu 2010; Wei et al. 2012) to discuss the cosmic evolution of the universe,

$$ f(T)=\mu(-T)^n;\quad \mu=\bigl(6H_0^2 \bigr)^{1-n} \biggl(\frac{\varOmega_{m0}}{2n-1} \biggr), $$
(18)

where n is a real constant and Ω m0 is the dimensionless matter energy density. The index 0 refers to the present values of the corresponding quantities. Substituting this model along with Eq. (13) in (11), we obtain the scale factor as follows

$$ a(t)= \biggl(\frac{3}{2n} \biggr)^{\frac{2n}{3}} \biggl( \frac{2\rho_{0m}}{ 6^n\mu(1-2n)} \biggr)^{\frac{1}{3}}t^{\frac{2n}{3}}. $$
(19)

We may compare this scale factor with the exact power law form of scale factor used in literature as a(t)=a 0 t m where m>0 and a 0 is a constant (Sadjadi 2006; Nojiri and Odintsov 2006). For m>1, it shows accelerating regime, while 0<m<1 corresponds to the decelerating era of the universe. Similarly, the scale factor (19) describes the expansion with acceleration and deceleration of the universe for n>3/2 and 0<n<3/2 respectively. The expansion history of the universe has experienced a rapid expansion and power law like decelerating as well as accelerating phases. Thus it would be interesting to study these kinds of scale factors in the modified gravity models. Inserting Eqs. (18) and (19) in (17), we obtain the following form of EoS parameter

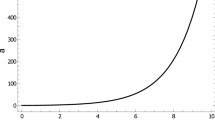
$$ \omega_T=\frac{(1-n)(3t^2)^{n-1}}{n[\mu(2n-1)(8n^2)^{n-1}+(3t^2)^{n-1}]}. $$
(20)

The graphical behavior of ω T versus time is shown in Fig. 1. We use the current values Ω m0=0.272, H 0=74.2 and assume the real constant as n=2. We examine that the EoS parameter represents the quintessence region (−1<ω≤−1/3) of the expanding universe. For the scale factor (19), the deceleration parameter is given by

$$ q_T=-1-\frac{\dot{H}}{H^2}=-1+\frac{3}{2n}. $$
(21)

The negative behavior of this parameter is achieved for n>3/2, which represents the accelerated expansion of the universe, whereas n≤3/2 corresponds to the decelerated phase of the universe.

Fig. 1
figure 1

Plot of ω T versus t

Full size image

4 f(T) scalar field models

In this section, we develop the correspondence of the f(T) model with some scalar field models like quintessence, tachyon, K-essence and dilaton field models (Setare 2007c; van der Plas 2008) in the flat universe.

4.1 f(T) quintessence model

The dynamics of quintessence scalar field is governed by an ordinary scalar field which slowly rolls down the potential. Slow-roll is the condition in which kinetic energy of the system is less than the potential energy, yielding the negative pressure. Its EoS parameter describes accelerated expansion of the universe in the interval −1≤ω q <−1/3. The energy density and pressure of quintessence scalar field are given by (Copeland et al. 2006)

where \(\dot{\phi}^{2}\) and V(ϕ) are the kinetic energy and scalar potential respectively. These take the form

(22)

where the subscript q represents the quantities corresponding to quintessence model. In order to apply the correspondence, we equate ρ T =ρ q and ω T =ω q and use Eqs. (13) and (20) in (22), it follows that

(23)
(24)

The analytical solution of Eq. (23) is difficult to determine, so we search for numerical solutions with the initial condition ϕ(0)=0. Figure 2 shows the plot of ϕ versus t for the same parameters as in the previous section. This represents an increasing behavior of the scalar field as time elapses and results the decrement in kinetic energy of the potential. Figure 3 indicates that the scalar potential is decreasing with respect to scalar field up to a certain range and then becomes zero. It corresponds to the scaling solution (V(ϕ)∝ϕ −1) (Copeland et al. 2006; Sharif and Jawad 2012) which represents the accelerated expansion of the universe. The slow-roll condition is satisfied for certain range as the kinetic energy is less than the potential energy. Hence, the scalar field ϕ slowly rolls down the scalar potential in the f(T) quintessence model (van der Plas 2008).

Fig. 2
figure 2

Plot of ϕ versus t for quintessence model

Full size image
Fig. 3
figure 3

Plot of V versus ϕ for quintessence model

Full size image

4.2 f(T) tachyon model

The tachyon scalar field model has the energy density and pressure as (Copeland et al. 2006; Setare 2007c)

(25)

leading to the EoS parameter

$$ \omega_{t}=\dot{\phi}^{2}-1. $$
(26)

This equation indicates a universe dominated by cosmological constant in the limit of vanishing kinetic energy. The correspondence of f(T) energy density and EoS parameter with tachyon model yields

(27)
(28)

Figures 4 and 5 show the evolution trajectories of scalar field and potential versus t and ϕ respectively. The scalar field indicates the increasing behavior with direct proportional to time (Sharif and Jawad 2012) leads to the continuous expansion. Figure 5 shows the same behavior of potential as for the previous model (Fig. 3). However the f(T) tachyon potential shows the expansion of the universe as it rolls down to its minimum value and corresponds to the scaling solution (Copeland et al. 2006) for a small region as compared to the f(T) quintessence model. It is noted here that interacting new holographic tachyon model also behaves like scaling models (Sharif and Jawad 2012).

Fig. 4
figure 4

Plot of ϕ versus t for tachyon model

Full size image
Fig. 5
figure 5

Plot of V(ϕ) versus ϕ(t) for tachyon model

Full size image

4.3 f(T) K-essence model

The K-essence scalar model (Copeland et al. 2006) gives the accelerated expansion of the universe with the help of kinetic energy X and its modified forms. For FRW universe, kinetic energy takes the form \(X=\frac{1}{2}~\dot{\phi}^{2}\). Also, the energy density and pressure are

(29)

The corresponding EoS parameter is

$$ \omega_{k}=\frac{1-X}{1-3X}. $$
(30)

This shows accelerating expansion of the universe with a specific range of X. For X=1/2, EoS parameter behaves like cosmological constant whereas acceleration boundary ω k =−1/3 is obtained for X=2/3. Hence, the expanding universe with acceleration corresponds to the interval 1/2≤X<2/3. Equating ρ k =ρ T and ω k =ω T for the correspondence, we obtain

(31)
(32)

The plot of X versus t shows consistent results within the interval as shown in Fig. 6. Figure 7 represents the same behavior of V(ϕ) as f(T) quintessence and new holographic tachyon model (Sharif and Jawad 2012) inherit. Also, the relation \(X=\frac{1}{2}\dot{\phi}^{2}\) yields

(33)

Its plot versus t is given in Fig. 8 which shows increasing behavior (Sharif and Jawad 2012) of scalar field with direct proportionality. It represents the continuous expansion of the universe.

Fig. 6
figure 6

Plot of X versus t for K-essence model

Full size image
Fig. 7
figure 7

Plot of V(ϕ) versus ϕ for K-essence model

Full size image
Fig. 8
figure 8

Plot of ϕ versus t for K-essence model

Full size image

4.4 f(T) dilaton model

The pressure of the dilaton scalar field model is given by (Piazza and Tsujikawa 2004)

$$ p_d=-X+b_{1}e^{b_2\phi}X^2, $$
(34)

where b 1 and b 2 are positive constants and \(2X=\dot{\phi}^{2}\). It is explained by a general four dimensional effective low-energy string action. Its dynamics is governed by negative kinetic term and higher-order derivative terms of \(\dot{\phi}\) to stable the system. The energy density of dilaton model is

(35)

Dividing Eq. (34) by (35), we obtain EoS parameter as

$$ \omega_{d}=\frac{1-b_{1}e^{b_{2}\phi}X}{1-3b_{1}e^{b_{2}\phi}X}. $$
(36)

It meets the universe in accelerated expansion for the bound \((\frac{20}{3},\frac{40}{3})\) of \(e^{b_{2}\phi}X\). Replacing ω d by ω T for f(T) dilaton model, it follows that

(37)

Figure 9 shows the graph of \(e^{b_{2}\phi}X\) versus t with b 1=0.07, b 2=6. It satisfies the criteria for accelerated expansion of the universe. Also, the solution of the above equation is as follows

(38)

Figure 10 represents the cosmic evolution of scalar field. Initially, it bears increasing negative values, however it becomes positive after a small interval of time and shows flatness with the passage of time. These types of solutions are scaling solutions due to the relation ϕ(t)∝lnt (Sharif and Jawad 2012).

Fig. 9
figure 9

Plot of \(e^{b_{2}\phi}X\) versus t for dilaton field

Full size image
Fig. 10
figure 10

Plot of ϕ versus t for dilaton field

Full size image

5 Concluding remarks

The connection of scalar field models to different DE models has gained a lot of interest due to its role in discussing accelerated expansion of the universe. In this context, we have considered the framework of f(T) gravity to connect with scalar field DE models such as, quintessence, tachyon, K-essence and dilaton. We have discussed these models graphically by taking a viable power law f(T) model. We have derived the scale factor from the first modified Friedmann equation in terms of power law form. Also, we have checked the behavior of evolution trajectory of EoS parameter and deceleration parameter of the model. The results of the paper are summarized as follows.

The EoS parameter indicates the quintessence era of the DE dominated universe whereas the deceleration parameter corresponds to this era for the real constant n>3/2 of the model. We have provided a correspondence between f(T) model and some scalar field models to analyze the accelerated expansion of the universe. The scalar field and potential are studied graphically with respect to time. These correspondences give

  1. 1.

    The scalar field graph of f(T) quintessence model represents increasing behavior while potential versus ϕ indicates scaling solution, leading to the accelerated expansion of the universe. The slow-roll condition is satisfied up to a certain region of scalar field in this case.

  2. 2.

    The plots of ϕ and V of f(T) tachyon model show the same behavior as for the previous model but for smaller region with scaling type solution.

  3. 3.

    In the f(T) K-essence model, kinetic energy shows DE region and the scalar field slowly rolls down the potential which is directly proportional to the time. It indicates an ever expanding universe.

  4. 4.

    For the correspondence between f(T) and dilaton model, the \(e^{b_{2}\phi}X\) indicates the expansion of the universe. Also, the scaling solution is obtained for its scalar field due to ϕ(t)∝lnt.

We would like to mention here that mostly HDE and its modified models are taken to make such type of correspondences (Granda and Oliveros 2009; Ebrahimi and Sheykhi 2011; Sharif and Jawad 2012) to discuss accelerated expansion of the universe. It is an effective procedure for the correspondence of scalar field models with different DE models which may help to comprehend the unknown DE candidate. It is interesting to mention here that our results are viable and consistent by comparing with those already available for other dark energy models (Setare, 2007b, 2007c, 2007d, 2008; Granda and Oliveros 2009; Ebrahimi and Sheykhi 2011; Sharif and Jawad 2012).