1 Introduction

Electron-acoustic (EA) waves have shown a great deal of interest due to their importance in interpreting the electrostatic component of the broad-band electrostatic noise observed in the cusp region of the terrestrial magnetosphere (Tokar and Gary 1984; Singh and Lakhina 2001), in the geomagnetic tail (Schriver and Ashour-Abdalla 1989), in the dayside auroral acceleration region (Dubouloz et al. 1991; Pottelette et al. 1999) etc. The idea of EA mode had been conceived by Fried and Gould (1961) during numerical solutions of the linear Vlasov dispersion equation in an unmagnetized, homogeneous plasma. Besides the well-known Langmuir and ion-acoustic waves, they noticed the existence of a heavily damped acoustic- like solution of the dispersion equation. It was later shown that with two species of electrons with widely disparate temperatures, referred to as hot and cold electrons with immobile ions, one indeed obtains a weakly damped EA mode (Watanabe and Taniuti 1977), which has different properties than Langmuir and ion-acoustic waves. Electron-acoustic waves are high frequency (in comparison with the ion plasma frequency) electrostatic modes (Stix 1992) in plasmas where a “minority” of inertial cold electrons oscillate against a dominant thermalized background of inertialess hot electrons providing the necessary restoring force (Watanabe and Taniuti 1977).

Non-extensive statistics or Tsallis statistics (Tsallis 1988), is believed to be a useful generalization of the conventional Boltzmann-Gibbs statistics, and suitable for the statistical description of long-range interaction systems, such as plasma systems (Lima et al. 2000; Silva et al. 2005; Du 2004; Liu and Du 2008; Liu et al. 2009; Tribeche et al. 2010; Amour and Tribeche 2010; Tribeche et al. 2010; Ait Gougam and Tribeche 2011; Moslem et al. 2011). Note that because of a lack of formal derivation, a non-extensive approach to kappa-distributions has been suggested (Leubner 2002). It has been shown that distributions very close to the so-called κ (kappa)-distributions are a consequence of the generalized entropy favored by non-extensive statistics. In fact, non-Maxwellian distribution is a common feature of the Earth’s atmosphere and, in general, it is turning out to be a characteristic feature of space plasmas (see e.g., Asbridge et al. 1968; Lundin et al. 1987; Hall et al. 1991; Sabry et al. 2009; Shalaby et al. 2011; Bains et al. 2011; El-Labany et al. 2012; Javidan and Pakzad 2012; Tribeche and Sabry 2012). Furthermore, since EA waves being high frequency density waves, they are trapped and modulated leading to modulation and generation of electron-acoustic envelope solitons. In high time resolution of the FAST observations, these kinds of nonlinear structures are observed (Pottelette et al. 1999).

Therefore, we shall investigate the amplitude modulation of the EA solitary wave packets in non-planar geometries as well as the role of the non-extensive parameter q beside the temperature ratio of the hot-to-cold electron species in an unmagnetized plasma consisting of cold electrons, immobile ions, and hot electrons featuring Tsallis statistics.

The present manuscript is organized as follows: The basic equations governing the nonlinear dynamics of the EA envelope solitary waves are presented and a modified nonlinear Schrödinger equation (NLSE) containing the geometrical effect is derived in Sect. 2. In Sect. 3, we discuss the stability/instability analysis and the propagation of the EA wave packets in planar as well as non-planar (cylindrical and spherical) geometries. Finally, the results are summarized in Sect. 4.

2 Derivation of the modified NLSE

The dynamics of the nonlinear electron-acoustic (EA) waves (with phase speed much larger than the cold electron thermal speed but much smaller than the hot electron thermal speed) is governed by (Shalaby et al. 2011; El-Labany et al. 2012; Tribeche and Sabry 2012)

(1)
(2)
(3)

where ν=0, for one-dimensional geometry and ν=1, 2 for cylindrical and spherical geometries, respectively. n c (n h ) is the cold (hot) electron number density normalized by its equilibrium value n co (n ho ). Here φ is the electrostatic wave potential normalized by k B T h /e, u c is the electron fluid velocity normalized by C e =(k B T h /α m)1/2, α=n ho /n co , m is the mass of the electron, θ=T h /T c , e is the electron charge and k B is Boltzmann constant, T h is the temperature of hot electrons. The space and time variables are in units of hot electron Debye length λ Dh =(k B T h /4πn ho e 2)1/2 and cold electron plasma period \(\omega_{pc}^{-1}=(m/4~\pi~n_{co}e^{2})^{1/2}\), respectively. The hot electrons are assumed to follow the q-nonextensive electron distribution (Sahu and Tribeche 2012; Tribeche and Sabry 2012), hence, the non-extensive hot electron density is given as

$$ n_{h}= \bigl[ 1+(q-1)~\varphi \bigr]^{\frac{q+1}{2(q-1)}}, $$
(4)

where the non-extensive parameter q>1. In the extensive limiting case (q→1), the non-extensive distribution function reduces to the well-known Maxwell-Boltzmann distribution.

In order to investigate the amplitude modulation of EA envelope solitary waves in the current plasma system, we employ a multiple scales perturbation technique (Taniuti and Yajima 1969). The independent variables are stretched as ξ=ϵ(r−v g  t) and τ=ϵ 2 t, where ϵ is a small (real) parameter and v g is the envelope group velocity to be determined later. The dependent variables are expanded as

$$ \boldsymbol{\Gamma}(r,t)=\boldsymbol{\Gamma}_{0}+{\sum _{m=1}^{\infty}} \epsilon^{m}{\sum_{L=-\infty}^{\infty}} \boldsymbol{\Gamma}_{L}^{ ( m ) }(\xi,\tau)\exp ( iL \varTheta ) , $$
(5)

where

k and ω are real variables representing the fundamental (carrier) wavenumber and frequency, respectively. All elements of \(\boldsymbol{\Gamma}_{L}^{ ( m ) }\) satisfy the reality condition \(\boldsymbol{\Gamma}_{-L}^{ ( m ) }=\boldsymbol{\Gamma}_{L}^{\ast ( m ) }\), where the asterisk denotes the complex conjugate. Substituting (5) into Eqs. (1)–(4) and collecting terms of the same powers of ϵ, the first-order (m=1) equations with L=1, give

and

$$ \omega=k\sqrt{\Delta+\frac{1}{k^{2}+\frac{1}{2} ( 1+q ) }} , $$
(6)

where \(\Delta=3\alpha\frac{(1+\alpha)^{2}}{\theta}\).

Solving the second-order (m=2 with L=1) using the first-order quantities, we can express the second order quantities with L=1 as;

with the compatibility condition

$$ v_{g}=\frac{\omega}{k}-\frac{ ( k^{2}\Delta-\omega^{2} )^{2}}{k\omega}=\frac{\partial\omega}{\partial k}. $$
(7)

Recall that the compatibility condition (7) is the group velocity of the envelope soliton.

The second harmonic modes (m=L=2) arising from the nonlinear self-interaction of the carrier waves are obtained in terms \([ \varphi_{1}^{(1)} ]^{2}\) as

and

$$ \varphi_{2}^{(2)}=\frac{k^{4}\alpha ( k^{2}\Delta+3\omega^{2} ) -\frac{1}{4}(q-3)(q+1) ( k^{2}\Delta-\omega^{2} )^{3}}{2 ( k^{2}\Delta-\omega^{2} )^{2} [ k^{2} ( 1+4k^{2}\Delta -4\omega^{2} ) +\frac{1}{2} ( k^{2}\Delta-\omega^{2} ) ( q+1 ) ] } \bigl[ \varphi_{1}^{(1)} \bigr]^{2}. $$
(8)

The nonlinear self-interaction of the carrier wave also leads to the creation of a zeroth order harmonic. Its strength is analytically determined by taking L=0 component of the third-order reduced equations which can be expressed as

and

$$ \varphi_{0}^{(2)}=\frac{k^{2}\alpha ( \omega^{2}+k^{2}\Delta ) +2k^{3}\alpha\omega v_{g}+\frac{1}{4}(q-3)(q+1) ( \omega^{2}-k^{2}\Delta )^{2} ( \Delta-v_{g}^{2} ) }{ ( \omega^{2}-k^{2}\Delta )^{2} [ 1+\frac{1}{2} ( q+1 ) ( \Delta-v_{g}^{2} ) ] }\bigl \vert \varphi_{1}^{(1)}\bigr \vert ^{2}. $$
(9)

Finally, the third harmonic modes (m=3 and L=1), with the aid of (9), give a system of equations, which can be reduced to the following modified NLSE:

$$ i\frac{\partial\phi}{\partial\tau}+P\frac{\partial^{2}\phi}{\partial\xi^{2}}+Q~\vert \phi \vert ^{2} \phi+i\frac{\nu}{2\tau}\phi=0, $$
(10)

where \(\phi\equiv\varphi_{1}^{(1)}\) for simplicity. The dispersion coefficient P is expressed as

$$ P=\frac{-k^{6}\Delta^{3}+3k^{2}\Delta ( -1+k^{2}\Delta ) \omega^{2}- ( 1+3k^{2}\Delta ) \omega^{4}+\omega^{6}+kv_{g} ( 4 ( k^{2}\Delta\omega+\omega^{3} ) - ( k^{3}\Delta +3k\omega^{2} ) v_{g} ) }{2k^{4}\Delta\omega-2k^{2}\omega^{3}} $$
(11)

and the nonlinear coefficient Q is given as

$$ Q=-\frac{\left [ \begin{array}{c}k^{4}\alpha^{2}\delta_{1}^{2}\left ( \begin{array}{c}-3k^{6}\Delta^{3}-20k^{4}\Delta^{2}\omega^{2}+5k^{2}\Delta\omega^{4}+2\omega^{6}\\ +kv_{g} ( -8k^{4}\Delta^{2}\omega+8\omega^{5}+ ( k^{5}\Delta^{2}+10k^{3}\Delta\omega^{2}+5k\omega^{4} ) v_{g} ) \end{array} \right ) \\ +\delta_{1}\eta_{1}-4 ( k^{8}\alpha^{2} ( k^{4}\Delta^{2}+3 ( 1+6k^{2}\Delta ) \omega^{2}-3\omega^{4} ) + ( -k^{2}\Delta+\omega^{2} )^{2}\delta_{2}\eta_{2} ) \end{array} \right ] }{ ( 4k^{2}\omega ( -k^{2}\Delta+\omega^{2} )^{2} ( k^{2} ( 1+4k^{2}\Delta-4\omega^{2} ) + ( k^{2}\Delta-\omega^{2} ) \delta_{1} ) ( 1+ ( \Delta-v_{g}^{2} ) \delta_{1} ) ) }, $$
(12)

where

$$\eta_{1}=\left [ \begin{array}{c}k^{6}\alpha^{2} ( -12k^{6}\Delta^{3}+\omega^{4}+8\omega^{6}+2k^{2}\Delta\omega^{2} ( -17+10\omega^{2} ) -k^{4}\Delta^{2} ( 3+80\omega^{2} ) ) \\ +4k^{7}\alpha^{2}v_{g} ( -2 ( k^{2}\Delta ( 1+4k^{2}\Delta ) \omega+\omega^{3}-4\omega^{5} ) +k ( k^{4}\Delta^{2}+\omega^{2}+10k^{2}\Delta\omega^{2}+5\omega^{4} ) v_{g} ) \\ -4\alpha ( k^{3}\Delta-k\omega^{2} )^{2} ( 3k^{4}\Delta^{2}+3k^{2}\Delta\omega^{2}-2\omega^{4}-kv_{g} ( -4k^{2}\Delta \omega+4\omega^{3}+ ( k^{3}\Delta+3k\omega^{2} ) v_{g} ) ) \delta_{2}\\ +12 ( k^{2}\Delta-\omega^{2} )^{5} ( \Delta -v_{g}^{2} ) \delta_{2}^{2}\end{array} \right ] $$

and

$$\eta_{2}=\left [ \begin{array}{c}k^{4}\alpha ( k^{2}\Delta ( 3+8k^{2}\Delta ) +5\omega^{2}-8\omega^{4} ) +4k^{5}\alpha\omega ( 1+4k^{2}\Delta-4\omega^{2} ) v_{g}\\ + ( -k^{2}\Delta+\omega^{2} )^{2} ( \omega^{2}+k^{2}\Delta ( -3-8k^{2}\Delta+8\omega^{2} ) +2k^{2} ( 1+4k^{2}\Delta-4\omega^{2} ) v_{g}^{2} ) \delta_{2}\end{array} \right ] , $$

while \(\delta_{1}=\frac{1}{2} ( q+1 ) \) and \(\delta_{2}=\frac {1}{8} ( q+1 ) ( 3-q )\).

3 Stability analysis and discussion

To investigate the stability/instability of the non-planar excitations, we investigate the development of the small modulation δϕ according to

$$ \phi= \bigl( \overline{\phi}_{0}+\delta\phi ( \xi,\tau ) \bigr) \exp \biggl[ -i\int_{\tau_{0}}^{\tau}\Delta \bigl( \tau^{\prime} \bigr) d\tau^{\prime}-\frac{\nu}{2}\ln\tau \biggr] , $$
(13)

where \(\overline{\phi}_{0}\) is the constant (real) amplitude of the pump carrier wave and Δ is a nonlinear frequency shift, and taking the perturbation δϕ as

$$ \delta\phi=\delta\overline{\phi}_{0}\exp \biggl[ i \biggl( K\xi-\int _{\tau _{0}}^{\tau}\varOmega \bigl( \tau^{\prime} \bigr) d \tau^{\prime} \biggr) \biggr] +c.c., $$
(14)

where \(K\xi-\int_{\tau_{0}}^{\tau}\varOmega d\tau^{\prime}\) is the modulation phase with K and Ω are the perturbation wave number and frequency of the modulation, respectively [see details in Jukui (2004)]. Using (13) and (14) into Eq. (10), one obtains the nonlinear dispersion relation (Jukui and Lang 2003; Sabry et al. 2008)

$$ \varOmega^{2}=\bigl(PK^{2}\bigr)^{2} \biggl( 1- \frac{Q}{P}\frac{2\vert \overline {\phi }_{0}\vert ^{2}}{\tau^{\nu}}\frac{1}{K^{2}} \biggr) , $$
(15)

which exactly reduces to the dispersion relation for planar geometry when ν=0. We immediately see that the modulation instability condition will be satisfied if PQ>0 and K 2≤ \(K_{c}^{2} ( \tau ) =2\frac {Q}{P}\frac{\vert \overline{\phi}_{0}\vert ^{2}}{\tau^{\nu}}\).

Experimental measurements demonstrated that small-scale coherent electrostatic structures are common in space plasma. Such structures were detected in the auroral zone on board FAST and POLAR satellites (Mozer and Kletzing 1998; Ergun et al. 1998). We choose a set of available parameters corresponding to the dayside auroral zone where an electric field amplitude E 0≃100 mV/m has been observed (Singh and Lakhina 2001; Dubouloz et al. 1993): T c ≃5 eV, T h ≃250 eV, n c0≃0.5 cm−3, n h0≃2.5 cm−3. For the case ν=0 (planar geometry), it is found that we have two stable regions (PQ<0, dark regions) beside unstable one (PQ>0, bright region), such that stable regions are found for small and high wavenumbers, as illustrated in Fig. 1.

Fig. 1
figure 1

(a) Variation of P against k, for different q, at α=5 and θ=50, (b) Variation of Q against k, for different q, at α=5 and θ=50, and (c) Variation of PQ in the parameter space (q, k), where bright regions correspond to PQ>0 (instability regions) and dark regions corresponds to PQ<0 (stability regions), for α=5 and θ=50. The solid line corresponds to, the critical wave numbers K c (i.e., PQ=0) at which the instability sets in for α=2 and θ=50, while the dashed line is for α=5 and θ=50

Full size image

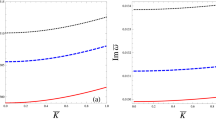
To estimate the role of the non-extensivity parameter q on the dispersion (i.e., P) and nonlinearity coefficients (i.e., Q), both of P and Q are plotted against k for different values of q, as shown in Figs. 1a and 1b. Where, it shown that increasing q increases the critical wave number at which P=0, as depicted in Fig. 1a. The same qualitative behavior is obtained for Q, as shown in Fig. 1b, but the critical wave numbers for P are shown to be higher than those for Q. In general, increasing the non-extensivity parameter q increases the critical wavenumber (K c (τ) with ν=0) at which the instability sets in. When investigating the role of the density ratio of the hot-to-cold electron species α(=n ho /n co ), on the stability/instability domains, it is found that increasing α increases stability of EA wave packets. However, for α>5, it is found that stability/instability domains remains almost without variation, as illustrated by contour lines depicted in Fig. 1c. It should be noticed that we have two contour lines at which PQ=0 (where the instability sets in), where the contour line corresponding to small critical wave numbers results from the criticality arising from the nonlinearity, while the line corresponding to large critical wave numbers is due to the criticality of the plasma arising from the dispersion.

The effect of increasing the temperature ratio of the hot-to-cold electron species θ(=T h /T c ) was found that it does not change the critical wavenumbers (i.e., K c =0) (i.e., varying θ for those values of wavenumbers satisfying the criteria PQ<0, does not affect at all on the stability of the EA envelope solitary waves) at which the instability sets in, as shown in Fig. 2. It should be noticed that the lower contour line at which PQ=0 (where the instability sets in) results from the criticality arising from the nonlinearity, while the line corresponding to large critical wave number is due to the criticality of the plasma arising from the dispersion.

Fig. 2
figure 2

Variation of PQ in the parameter space (θ, k), where bright regions correspond to PQ>0 (instability regions) and dark regions corresponds to PQ<0 (stability regions), for q=2 and α=5. The solid line corresponds to, the critical wave numbers K c (i.e., PQ=0) at which the instability sets in for q=2 and α=5

Full size image

For the non-planar geometry (ν≠0), the local instability growth rate of the nonlinear dispersion relation (15) is given by (Jukui and Lang 2003; Jukui 2004; Sabry et al. 2008),

$$ \operatorname{Im}\varOmega=PK^{2} \biggl( \frac{2Q}{P~K^{2}} \frac{\vert \overline{\phi}_{0}\vert ^{2}}{\tau^{\nu}}-1 \biggr)^{1/2}. $$
(16)

The instability growth will cease for cylindrical geometry (ν=1) when

$$ \tau\geq\tau_{\max}=\frac{2\vert \overline{\phi}_{0}\vert ^{2}}{K^{2}}\frac{Q}{P}, $$
(17)

and for spherical geometry (ν=2) when

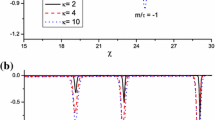
$$ \tau\geq\tau_{\max}=\frac{\vert \overline{\phi}_{0}\vert }{K} \sqrt{\frac{2Q}{P}}. $$
(18)

It is clear that there is a modulation instability period (τ) for the cylindrical and spherical wave modulation, which does not exist in the one-dimensional case. The total growth (Γ) of the modulation during the unstable period (Jukui and Lang 2003; Jukui 2004; Sabry et al. 2008) is

$$ \varGamma=\exp \biggl( {\int_{\tau_{0}}^{\tau_{\max}}} \operatorname{Im}\varOmega d\tau^{\prime} \biggr) =\exp \biggl( \frac{Q\vert \overline{\phi}_{0}\vert ^{2}}{\tau^{\nu-1}}f ( R ) \biggr) , $$
(19)

where \(R= [ 2Q\vert \overline{\phi}_{0}\vert ^{2}/ ( PK^{2}\tau_{0}^{\nu} ) ] \geq1\). For the cylindrical geometry, we have

$$ f ( R ) \equiv f_{\mathrm{cyl.}}=\arctan\sqrt{R-1}-\frac{\sqrt {R-1}}{R}, $$
(20)

while for the spherical geometry

$$ f ( R ) \equiv f_{\mathrm{sph.}}=\frac{1}{R} \biggl[ \sqrt{R}\ln \biggl( \frac{\sqrt{R}+\sqrt{R-1}}{\sqrt{R}-\sqrt{R-1}} \biggr) -2\sqrt{R-1} \biggr] . $$
(21)

We note that \(f_{\mathrm{cyl.}}\) is an increasing function in R, and \(f_{\mathrm{cyl.}}\rightarrow\pi/2\) as R→∞. This means that during the modulation instability period, the total growth increase as R does for the cylindrical case. But, for \(f_{\mathrm{sph.}}\) there is a maximum value

$$ \max f_{\mathrm{sph.}}=\frac{2\sqrt{R_{c}-1}}{R_{c}}, $$
(22)

where R c is determined by

$$ 4\sqrt{R_{c}-1}=\sqrt{R_{c}}\ln \biggl( \frac{\sqrt{R_{c}}+\sqrt{R_{c}-1}}{\sqrt{R_{c}}-\sqrt{R_{c}-1}} \biggr) . $$
(23)

For spherical geometry, the modulation instability growth rate will achieve its maximum at R=R c and then decreases as R increases further. It should be noted that the modulation instability period given by (17) for cylindrical geometry is longer than that determined by (18) for spherical geometry, meanwhile, during the unstable period, the modulation instability growth rate is always an increasing function of R in the cylindrical geometry, but not in the spherical geometry, as depicted in Fig. 3. This suggests that the spherical waves are more structurally stable to perturbations than the cylindrical waves.

Fig. 3
figure 3

Variation in f(R) against R for cylindrical and spherical geometries given by Eqs. (20) and (21), respectively

Full size image

To examine the cylindrical and spherical geometry effects on the propagation of EA envelope solitary waves, Eq. (12) may be simplified to

$$ i\frac{\partial\phi}{\partial\tau}+\frac{\partial^{2}\phi}{\partial\xi^{2}}+2\vert \phi \vert ^{2}\phi+i \frac{\nu}{2\tau}\phi=0, $$
(24)

where we have set \(\phi\rightarrow\sqrt{2/Q}\phi\) and \(\xi\rightarrow \sqrt{P}\xi\), with the conditions that P>0 and Q>0. The stationary propagation of the envelope soliton governed by Eq. (24) with ν=0 (i.e. the one-dimensional geometry), has the following general form

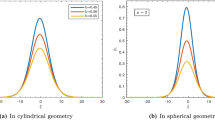
$$ \phi(\xi,\tau)=A~\psi_{1} ( \xi,\tau ) \exp \bigl[ i \psi_{2} ( \xi,\tau ) \bigr] , $$
(25)

where \(\psi_{1} ( \xi,\tau ) =\operatorname{sech} ( A\xi-2AB\tau+c_{0} ) \) and ψ 2(ξ,τ)=Bξ+(A 2−B 2)τ+c 1. While, A, B, c 0, and c 1 are arbitrary real constants. Solution (25) describes the motion of a soliton in a rapidly decaying case. Solving Eq. (24) numerically for the cylindrical and spherical geometries; where the initial solution were taken to be of the form (25) with A=0.01 and B=0, it is found that the amplitude of the EA solitary wave packets in the spherical geometry is larger than that in the cylindrical geometry for fixed time, as shown in Fig. 4. Figures 5 and 6 display the envelope electrostatic potential excitations in three-dimensional plots versus the radial and time coordinates, represented by the numerical solution of the modified NLSE (24). It is seen that the envelope soliton pulse for the cylindrical geometry is smaller than the spherical geometry.

Fig. 4
figure 4

Cylindrical and spherical waves amplitude |ϕ| against τ for ξ=0, represented by the numerical solution of the modified NLSE (24)

Full size image
Fig. 5
figure 5

Variation of the cylindrical wave amplitude |ϕ| against τ and ξ

Full size image
Fig. 6
figure 6

Variation of the spherical wave amplitude |ϕ| against τ and ξ

Full size image

4 Summary

We have investigated nonlinear wave modulation of electron-acoustic solitary wave packets in planar as well as non-planar geometry (assuming cylindrical and spherical symmetry) in an unmagnetized two temperature plasma composed of cold and hot (featuring q-nonextensive distribution) electrons with stationary ions. It is shown that in such plasma, propagation of EA wave packets is governed by a modified NLSE which accounts for the geometrical effect. It is found that the nature of the modulational instabilities would be significantly modified due to the geometrical effects. Also, there exists a modulation instability period for the cylindrical and spherical envelope excitations, which does not exist in the one-dimensional case. The instability period depends on the q-nonextensive parameter, density ratio α of the hot-to-cold electrons species as well as their temperature ratio θ. Numerical and analytical investigations reveal that the amplitude of the spherical envelope is larger than that of the cylindrical envelope for fixed time, and the growing amplitude of the spherical envelope is larger than that of the cylindrical envelope.