1 Introduction

Recently independent observations such as type Ia supernova (Riess et al. 1998; Perlmutter et al. 1999; Tonry et al. 2003), weak lens (Jain and Taylor 2003), cosmic microwave background anisotropy (Spergel et al. 2003), large scale structure (Tegmark et al. 2004; Seljak et al. 2005) and baryon oscillation (Eisenstein et al. 2005; Blake et al. 2006) current cosmic accelerated expansion. The result conflicts with general relativity prediction and consequently motivates researchers in cosmology and astrophysics to seek for alternatively models to interpolate this outstanding phenomena. Within the frame of general relativity, the cosmic acceleration may implies that the current universe is dominated by mysterious dark energy (Nojiri and Odintsov 2005; Nojiri and Odintsov 2006). A cosmological constant responsible for the dark content is the simplest explanation which so far best fits the observation data. However, the observed value of cosmological constant is unsatisfactory smaller than any theoretical estimation by a factor of 10120 (Carroll 2001; Peebles and Ratra 2003). An evolving scalar field interprets dynamical dark energy that in turn resembles the cosmological constant (Ito et al., 2011; Nojiri and Odintsov, 2011; Elizalde et al., 2004; Elizalde et al., 2008; Capozziello et al., 2006a, 2006b; Caldwell and Kamionkowski, 2004). Despite to the fact that these models provide us with initial understanding of the complexity of the problem none of them turn out to be problem-free (Huang et al. 2010).

On the other hand, one may view General Relativity as a poorly tested theory on cosmic scales and considers dark energy as an observational artifact caused by an inappropriate theory of gravity (Bean 2010). This and other issues of theoretical and observational gravity have initiated a huge interest in alternative theories of gravity (Esposito-Farese 2008). Among all, the scalar-tensor theories and in particular Brans-Dicke theory (BD) (Brans and Dicke 1961) as viable alternatives to general relativity have been triggered by many researchers to explain current universe acceleration (Bertolami and Martins, 2000; Banerjee and Pavon, 2001; Sen and Sen, 2001; Kim, 2005a, 2005b; Das and Banerjee, 2006; Chakraborty and Debnath, 2009).

In BD theory the scalar field is a fundamental element of the theory, as opposed to other scalar tensor theories in which the scalar field is postulated separately in an ad hoc way. The field plays the role of quintessence or phantom matter and lead to cosmological acceleration. The BD parameter in the range −2<ω<−3/2 violates the energy condition on the scalar field and also is inconsistent with a radiation-dominated epoch, unless ω varies with time (Banerjee and Pavon 2001) and there is a scalar potential added by hand (Sen and Sen 2001). Further models to include the so-called “chameleon fields” that allow the scalar field to interact with to matter is also studied by many researchers (Das and Banerjee 2008; Ponce de Leon 2010; Farajollahi et al. 2011b).

In this paper we study the holographic dark energy (HDE) of BD theory. The HDE which has been discussed extensively in recent years is constructed by considering the holographic principle and some features of quantum gravity theory (Amani et al., 2012; Farajollahi et al., 2011a, 2011b).

From this principle, the number of degrees of freedom which is finite in a bounded system has relations with the area of its boundary. In cosmology, one can obtain the upper bound of the entropy contained in the universe. For a system with size L and UV cut-off Λ without decaying into a black hole, it is required that \(L^{3}\rho_{\varLambda}\leq L M^{2}_{pl}\). With the largest allowed L, we obtain \(\rho_{\varLambda}=3c^{2}M^{2}_{pl}L^{-2}\), where c is a numerical constant and M pl is the reduced Planck Mass \(M^{2}_{pl}=8\pi G\). The value of parameter c determines the property of holographic dark energy. For c>1,=1,<1, the holographic dark energy behaves like quintessence, cosmological constant and phantom respectively.

A duality between UV and IR cut-offs means that L in both cases are related to the vacuum energy and the large scale of the universe respectively. The large scale of the universe can be taken as, for example Hubble horizon, event horizon or particle horizon (Hsu 2004; Li 2004). Here, following (Li 2004), we take the future event horizon (the boundary of the volume where a fixed observer may eventually observe)

$$ R_h= a\int_t^\infty \frac{dt}{a}=a\int_a^\infty\frac{da}{Ha^2}, $$
(1)

as the IR cut-off L.

2 The model

We begin with a 4-D Brans-Dicke action, given by

$$ S=\int{ d^{4}x\sqrt{g} \biggl(\frac{\phi^2}{8\omega} R- \frac{1}{2}g^{\mu\nu}\nabla_{\mu}\phi\nabla_{\nu}\phi +L_M \biggr)}, $$
(2)

where the dimensionless coupling constant, ω, determines the coupling between gravity and BD scaler field, R is 4D Ricci scaler, ϕ(x μ) is the BD scalar field and L M is the Lagrangian of matter field. In the following we assume a homogeneous and isotropic FRW geometry where the scalar field is also a function of time parameter. Therefore, variation of the action (2) with respect to metric and also scalar field yield the following field equation,

(3)
(4)
(5)

where \(H=\frac{\dot{a}}{a}\). In the above equation we assume that the matter filled the universe consists of dark matter (ρ m ) and dark energy (ρ Λ ). The conservation equations for the dark energy and matter field in the universe are respectively,

(6)
(7)

In the framework of Brans-Dicke cosmology, the holographic energy density of the quantum fluctuations in the universe is

$$ \rho_{\varLambda}= \frac{3c^2\phi^2 }{4\omega L^2}. $$
(8)

The characteristic length, L, is defined by L=ar(t) where r(t) is related to the future event horizon of the universe:

$$ \int_{0}^{r(t)}{\frac{dr}{\sqrt{1-kr^2}}}=\int _{0}^{\infty}{\frac {dt}{a}}=\frac{R_h}{a}. $$
(9)

It is important to note that in the non-flat universe the characteristic length which plays the role of the IR-cutoff is the radius L of the event horizon measured on the sphere of the horizon and not the radial size R h of the horizon. Solving Eq. (9), for the general case of the non-flat FRW universe, one yields

$$ r(t)=\frac{1}{\sqrt{k}}\sin x, $$
(10)

where \(x=\sqrt{k} R_{h}/a\). Taking derivative with respect to the cosmic time t from characteristic length, L, and using Eqs. (10) and (12) we obtain

$$ \dot{L}=HL+a\dot{r}(t)=\frac{c}{\sqrt{\varOmega_D}}-\cos x. $$
(11)

Stability analysis of the model for the best fitted model parameters will be discussed in the next section.

3 Phase space and best fit

The stability of the model is presented via phase plane analysis, by introducing the following dimensionless variables,

(12)

The system of equations in terms of new dynamical variables become,

(13)
(14)
(15)

where \(\frac{\dot{H}}{H^{2}}\) in the above is

(16)

The prime represents derivative with respect to ln(a). With the new form of Hamiltonian constraint:

$$ \varOmega_{k}-\varOmega_{m}-\varOmega_{\varLambda}+2 \alpha\biggl(1-\frac{\alpha\omega}{3}\biggr)=1, $$
(17)

the (13)–(15) now reduce to,

(18)
(19)

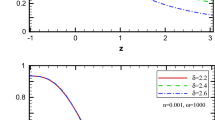
In stability formalism, solutions of the system \(\varOmega'_{m}=0\) and \(\varOmega'_{\varLambda}=0\), are critical points. On the other hand, we simultaneously best fit the system with observational data to obtain physically meaningful results. So, in the following we constraint the model parameters α, c and ω, in addition to initial conditions Ω Λ (0) and Ω m (0) with the observational data for distance modulus using χ 2 method. For simplicity, we put cosx=1 which correspond to flat FRW cosmological model. Table 1 shows the best fitted model parameters. As an example, in Fig. 1 we show the 2-dim likelihood and 3-dim confidence level for parameters c and ω.

Fig. 1
figure 1

The best fitted 2-dim and 3-dim likelihood and confidence level for c and ω

Full size image
Table 1 Best-fitted model parameters and I.C
Full size table

From stability analysis, the critical points with their stability properties are given in Table 2. The table shows that the point P 1 is stable while points P 2 and P 3 are unstable.

Table 2 Stability of the critical points
Full size table

Figure 2, illustrates phase diagram of the system. The critical points represent the state of the universe. The graph shows that with a small perturbation the universe moves from unstable states P 2 and P 3 towards stable state P 1. For the best fitted model with the observational data, the dashed red trajectory in the diagram indicates that the universe only begins from unstable state P 2 and approaches stable state P 1. At this stage, the best fitted trajectory does not possess any physical privilege as the phase space diagram shows only the state of the systems. However, in the next section that we challenge the model against observational data, the significance of the adopted best fitting analysis will also be tested.

Fig. 2
figure 2

The 2-dim phase plane corresponding to the critical point

Full size image

4 Cosmological examination

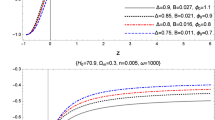
Among cosmological variables, the EoS parameter together with deceleration, jerk and snap parameters represent higher derivatives of the Hubble parameter (Harrison 1976; Caldwell and Kamionkowski 2004; Dabrowski and Stachowiak 2006). From numerical calculations, the best fitted of these parameters are obtained. Figure 3 shows the effective EoS parameters, dark energy Eos parameter and also deceleration parameter q. From effective EoS parameter graph, universe predicted to be in decelerating state in past and only recently at about z≃0.2 it turns into accelerating state. It also shows that the universe is currently in quintessence era and in near future changes into phantom era. The result can also be verified from the graph of deceleration parameter. The EoS parameter for HDE on the other hand shows that the universe is always in accelerating state. This is not surprising since DM effects not considered.

Fig. 3
figure 3

The effective EoS parameter w eff , holographic dark energy EoS parameter w Λ and deceleration parameter q plotted as functions of redshift

Full size image

The higher-order characteristics or statefinders of the model are shown in Fig. 4. The jerk and snap parameters are respectively functions of the third and forth derivative of Hubble parameter.

Fig. 4
figure 4

The graph of best fitted statefinders j−z, and k−z

Full size image

5 Summary

In this paper we have concentrated on the study of holographic dark energy in Brans-Dicke theory. Within a mathematical formulation, the stability and phase space of the theory investigated. To add physics into the formalism and support the model with observation, we also constrain the stability and model parameters with the observational data. We know that the conventional general relativity; as a limiting case of Brans-Dicke theory where ω→∞; leads to a non accelerating universe. However, the holographic dark energy in Brans-Dicke model with the best fitted BD parameter (ω=1.1) predicts universe acceleration. We examined the model by looking at cosmological parameters such as equation of state parameter in addition to deceleration, jerk and snap parameters are discussed. The results shows both universe acceleration in the past and phantom crossing in future.