A computational framework for institutional agency

Abstract

This paper provides a computational framework, based on defeasible logic, to capture some aspects of institutional agency. Our background is Kanger-Lindahl-Pörn account of organised interaction, which describes this interaction within a multi-modal logical setting. This work focuses in particular on the notions of counts-as link and on those of attempt and of personal and direct action to realise states of affairs. We show how standard defeasible logic (DL) can be extended to represent these concepts: the resulting system preserves some basic properties commonly attributed to them. In addition, the framework enjoys nice computational properties, as it turns out that the extension of any theory can be computed in time linear to the size of the theory itself.

1 Background and motivation

Recent works on agents and their societies assume that as in human societies, also in artificial societies normative concepts may play a decisive role, allowing for the flexible co-ordination of intelligent autonomous agents [Conte and Dellarocas 2001, Pitt forthcoming]. In line with this trend, in [Gelati et al. 2004] the authors of this paper and other colleagues proposed to model organisations of agents in terms of rule-based normative systems; accordingly, an organisation should be characterised by specifying the normative positions relevant to design its structure. These positions include not only duties and permissions, but also powers, as for instance powers of creating further normative positions on the head of other agents. Technically, in this paper we develop a formal machinery to capture some building blocks among those analysed in [Gelati et al. 2004]. In particular, we focus on some basic aspects of agency and institutionalised power. These concepts are embedded in a non-monotonic framework based on DL.

As in [Gelati et al. 2004], the background of this paper is Kanger-Lindahl-Pörn [Kanger 1972, Lindahl 1977, Pörn 1977] theoretical account of organised interaction (see [Elgesem 1997]). The main references here are some recent contributions [Santos et al. 1997, Jones and Sergot 1996, Jones forthcoming], which have enriched this framework with some substantial refinements. The basic idea is to describe agents’ interaction within a multi-modal logical setting. The resulting view is abstract but flexible, as social agency is captured by simply combining different modal operators, each of them corresponding to notions such as those of action, power, obligation, and belief.

The paper is confined to two basic aspects of the above line of research: the modal notion of agency and that of institutionalised power.

Despite some limitations (see [Segerberg 1992, Royakkers 2000]), modal logic of agency [Elgesem 1997] is still very much adopted thanks to its flexibility, as actions are simply taken to be relationships between agents and states of affairs. We will focus on two well-known agency notions. The first is the idea of personal and direct action to realise a state of affairs. In the mentioned logical framework, it is formalised by the modal operator E, such that a formula like $E_i A$ means that the agent i brings it about that A. Different axiomatisations have been provided for it [Governatori and Rotolo 2005]. Here we will consider two basic logical properties of this operator:¹

$$ \begin{array}{ll} E_i A \to A &(\hbox{T})\\ E_i E_j A\to \neg E_i A &(\hbox{EE}\neg \hbox{E}) \end{array} $$

Schema (T) expresses the successfulness of actions that is behind the common reading of the “bring about” concept. Schema $(\hbox{EE}\neg \hbox{E})$ is a specific axiom advanced, for example, in [Santos et al. 1997]. The brings-it-about operator expresses actions performed directly and personally. Hence, $(\hbox{EE}\neg \hbox{E})$ states a principle of rationality for modelling co-ordination in institutional organisations: it is counter-intuitive that the same agent brings it about that A and brings it about that somebody else achieves A.

The second aspect of agency considered here is that of attempt, formalised by the operator H [Santos et al. 1997, Jones forthcoming]. $H_i A$ says that i attempts to make it the case that A. The operator H _i is not necessarily successful. Here we will simply assume that each successful action is also an attempt:²

$$ E_i A\to H_i A $$

(1)

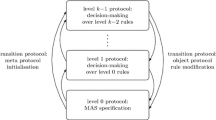
Let us focus now on the idea of institutionalised power. This notion is central for describing norm-governed organisations of agents and comes from the distinction between the practical ability to realise a state of affairs—which is not considered in this paper [Elgesem 1997, Governatori and Rotolo 2005]—and the institutional power to do this [Makinson 1986]. For example, if in an auction i raises one hand, this implies that the act of making a bid is also obtained. In principle, this kind of ability should be distinguished from the practical capacity to obtain a certain state of affairs. The attempt to make a bid may not be successful: its being successful, within the institutional context (the auction), depends on whether that institution makes it effective. It is up to institutional (constitutive) rules to establish whether i's act makes so that a bid is effective or not, namely, that i's act counts as bidding.

The logical nature of this kind of rules has been recently investigated following different directions (see, e.g., [Grossi et al. 2005, Boella and van der Torre 2004, Jones and Sergot 1996, Gelati et al. 2004]). Many of these approaches explicitly recognise that constitutive rules are defeasible. In fact, it is intuitive that, e.g., if the agent i raises one hand, this may count as making a bid but this does not hold if i raises one hand and scratches his own head. This paper will adopt the approach provided in [Gelati et al. 2004]. In that work, it is argued that constitutive rules of the form “X counts as Y in the context C” [Searle 1995] are represented within a conditional logic enjoying at least the basic properties (Reflexivity, Cut, and Cautious Monotonicity) of cumulative reasoning (system CU [Artosi et al. 2002]). In [Gelati et al. 2004] the logic was enriched by the modality D _s —originally introduced in [Jones and Sergot 1996] but with a different meaning—to represent institutional facts. In that specific perspective, the expression “A counts as B in the institution s”, formally $A\Rightarrow_s B$, was stated to be equivalent by definition to $(A\Rrightarrow D_s B)\wedge (D_s A \Rrightarrow D_s B)$, where $\Rrightarrow$ is the conditional obeying the principles of cumulative reasoning. This view is meant to capture the fact that counts-as rules may specify when (1) a brute fact (e.g., destroying the receipt) counts as a type of institutional act (e.g., freeing the debtor from his obligation), and (2) an institutional act (e.g., a contract made by person j in the name of person k) has the same effects of another institutional act (e.g., a contract made by k). D _s represents the domain of institutional facts and it corresponds to a classical non-normal modality. However, in this paper we will not consider the modality D _s , as it is mainly relevant when more institutional contexts are compared and so the modality is used to mark the different institutions where institutional facts hold. Accordingly, leaving aside D _s , the modelling of counts-as rules will simply amount in this paper to dealing with cumulative reasoning.

Notice that the framework we have just recalled is able to capture some composite concepts regarding the normative co-ordination of agents. In particular, [Gelati et al. 2004] shows that the introduction of the notion of proclamation allows to account for the ideas of declarative power and delegation [Castelfranchi and Falcone 1998, Norman and Reed 2001]. The logical representation of these ideas has a counts-as structure. Institutional proclamations are formalised by the modal operator proc: the expression $proc_i A$ means that agent i proclaims A.³ The combination of proc, agency operators, and the counts-as link enables us to capture two forms of normative delegation, intended as kinds of true representation [Gelati et al. 2004]. The first is $proc_j (proc_i A) \Rightarrow_s E_j (proc_i A)$, that is, when j proclaims that i proclaims that A, this counts as j's making so that i proclaims that A.⁴ In addition, we can have $proc_j (E_i A) \Rightarrow_s E_j (E_i A)$. This type of representation is necessary when the representative substitutes a principal which would not be able to perform directly the activity which is delegated to the representative.

Although the above building blocks supply an intermediate level of fine conceptual analysis, it seems difficult to use them directly for implementation. This is due to the inherent computational complexity of multi-modal logics (see, e.g., [Halpern and Moses 1990]). In general, the addition of modal operators to the classical propositional base leads to the increase of complexity of the logic. This is mainly due to: (1) the rules to introduce modalities, (2) the axioms governing the behaviour of modalities and their mutual interaction. But something similar applies as well to the logic of counts-as, due to the well-known computational limits of conditional logics (see, e.g., [Artosi et al. 2002]).

The main aim of this paper is to show how to introduce modalities in a (computationally oriented) non-monotonic formalism (DL), and then to apply this methodology to deal with the mentioned basic properties of institutional agency. In this perspective, some basic patterns of defeasible reasoning will be extended to account for the institutional dynamics insofar as counts-as links interact with the notions of direct action and attempt. Notice that the use of DL to model the counts-as link is immediate, as its basic form corresponds to cumulative reasoning enjoying the properties we previously mentioned [Billington 1993]. As we will see, extending DL to treat modal logic of agency requires some adjustments and integrations.

The layout of the paper is as follows. Section 2 makes provision of the basics of standard DL. In Sect. 3 we show how DL can be extended to deal with the notion of institutional agency we previously recalled; the formal system will be illustrated with the help of some simple examples. In Sect. 4 we provide some formal results of our system. Section  5 presents a discussion of some related work, while Sect. 6 provides some directions for future work. The interested reader will find an Appendix with proofs or proof sketches of the formal properties mentioned in Sect. 4.

2 Overview of defeasible logic

DL is a simple, efficient but flexible non-monotonic formalism which has been proven able to deal with many different intuitions of non-monotonic reasoning [Antoniou et al. 2000b]. Here we propose a non-monotonic logic of agency based on the framework for DL developed in [Antoniou et al. 2000a].

It is not possible to give here a complete formal description of the logic. We hope to give enough information to make the discussion intelligible and we refer the reader to [Nute 1994, Antoniou et al. 2001] for more thorough treatments. As usual with non-monotonic reasoning, we have to specify (1) how to represent a knowledge base and (2) the inference mechanism.

Accordingly a defeasible theory D is a structure $(F,R, >)$ where F is a finite set of facts, R a finite set of rules (either strict, defeasible, or defeater), and >  a binary relation (superiority relation) over R.

Facts are indisputable statements. Strict rules are rules in the classical sense: whenever the premises are indisputable so is the conclusion; defeasible rules are rules that can be defeated by contrary evidence; and defeaters are rules that cannot be used to draw any conclusions. Their only use is to prevent some conclusions. In other words, they are used to defeat some defeasible rules by producing evidence to the contrary. The superiority relation among rules is used to define priorities among rules, that is, where one rule may override the conclusion of another rule.

A rule r consists of its antecedent (or body) A(r) (A(r) may be omitted if it is the empty set) which is a finite set of literals, an arrow, and its consequent (or head) C(r) which is a literal. Given a set R of rules, we denote the set of all strict rules in R by R _s , the set of strict and defeasible rules in R by R _sd , the set of defeasible rules in R by R _d , and the set of defeaters in R by R _dft . R[q] denotes the set of rules in R with consequent q. If q is a literal, ∼q denotes the complementary literal (if q is a positive literal p then ∼q is $\neg p;$ and if q is $\neg p,$ then ∼q is p).

A conclusion of D is a tagged literal and can be either:

• $+\Updelta q$: q is definitely provable in D (i.e., using only facts and strict rules).

• $-\Updelta q$ meaning that we have proved that q is not definitely provable in D.

• $+\partial q$ meaning that q is defeasibly provable in D.

• $-\partial q$ meaning that we have proved that q is not defeasibly provable in D.

Provability is based on the concept of a derivation (or proof) in D. A derivation is a finite sequence $P=(P(1),\ldots,P(n))$ of tagged literals satisfying four conditions (which correspond to inference rules for each of the four kinds of conclusion). $P(1\ldots n)$ denotes the initial part of the sequence P of length i.

• $+\Updelta$: If $P(n+1)=+\Updelta q$ then

  • (1) $q\in F$ or

  • (2) $\exists r\in R_s[q]:\forall a \in A(r) +\Updelta a\in P(1\ldots n)$

• $-\Updelta$: If $P(n+1)=-\Updelta q$ then

  • (1) $q\notin F$ and

  • (2) $\forall r\in R_s[q] \exists a \in A(r): -\Updelta a\in P(1\ldots n)$

The intuition behind the proof conditions is to give conditions under which we can append a (tagged) literal at the end of a derivation. The definition of Δ describes forward chaining of strict rules or, in other terms, it corresponds to Modus Ponens for strict rules. Accordingly, for a literal q to be definitely provable we need to find a strict rule with head q, of which all antecedents have been definitely proved previously. To establish that q cannot be proven definitely we must establish that for every strict rule with head q there is at least one antecedent which has been shown to be non-provable.

The inference conditions for negative proof tags are derived from the inference conditions for the corresponding positive proof tag by applying the Principle of Strong Negation introduced in [Antoniou et al. 2000a]. The strong negation of a formula is closely related to the function that simplifies a formula by moving all negations to an innermost position in the resulting formula and replaces the positive tags with the respective negative tags and viceversa. For example, if in a proof condition for $+\#$ we have $\forall s(+\#_1 A(s) \wedge -\#_2 B(s))$, the strong negation of the condition is $\exists s(-\#_1\, StrongNegation(A(s))\, or\, +\#_2\, StrongNegation(B(s)))$. Accordingly, in what follows, we will often list only the positive version of the inference rules.

• $+\partial$: If $P(n+1)=+\partial q$ then either

• • (1) $+\Updelta q \in P(1\ldots n)$ or

    • (2.1) $-\Updelta\sim q \in P(1\ldots n)$ and

    • (2.2) $\exists r\in R_{sd}[q] \forall a \in A(r): +\partial a\in P(1\ldots n)$ and

    • (2.3) $\forall s \in R[\sim q]$ either

      • (2.3.1) $\exists a\in A(s): -\partial a\in P(1\ldots n)$ or

      • (2.3.2) $\exists t\in R_{sd}[q]:\, \forall a\in A(t): +\partial a\in P(1\ldots n)$ and t > s

Let us work through this condition. To show that q is provable defeasibly we have two choices: (1) We show that q is already definitely provable; or (2) we need to argue using the defeasible part of D as well. In particular, we require that there must be a strict or defeasible rule with head q which can be applied (2.2). But now we need to consider possible “attacks”, i.e., reasoning chains in support of ∼q. To be more specific: to prove q defeasibly we must show that ∼q is not definitely provable (2.1). Also (2.3) we must consider the set of all rules which are not known to be inapplicable and which have head ∼q (note that here we consider defeaters, too, whereas they could not be used to support the conclusion q; this is in line with the motivation of defeaters given earlier). Essentially each such rule s attacks the conclusion q. For q to be provable, each such rule s must be counterattacked by a rule t with head q with the following properties: (i) t must be applicable at this point, and (ii) t must be stronger than s. Thus each attack on the conclusion q must be counterattacked by a stronger rule. In other words, r and the rules t form a team (for q) that defeats the rules s. In an analogous manner we can define $-\partial q$ (see, for example [Antoniou et al. 2001]). The purpose of the $-\partial$ inference rules is to establish that it is not possible to prove $+\partial$. This rule is defined in such a way that all the possibilities for proving $+\partial q$ (for example) are explored and shown to fail before $-\partial q$ can be concluded. Thus a conclusion tagged with $-\partial$ is the outcome of a constructive proof that the corresponding positive conclusion cannot be obtained.

We illustrate how the proof conditions work with the help of the following theory:

$$ \begin{aligned} F=\{&A,C\} \\ R=\{&r_1: A \Rightarrow B, \\ &r_2: C\Rightarrow E, \\ &r_3: A,D\Rightarrow \neg B, \\ &r_4: E\Rightarrow \neg B\} \\ \{&r_3 > r_1, r_1 > r_4\} \\ \end{aligned} $$

Since $A,C\in F$, we have $+\Updelta A$ and $+\Updelta C$; by clause (1) we also have $+\partial A$ and $+\partial C$. To prove $+\partial B$ we have to ensure that its negation cannot be definitely proved (i.e., proved using only facts and strict rules). This follows immediately since $\neg B$ is not a fact and there are no strict rules for $\neg B$. r ₁ is a defeasible rule for B whose antecedent A(r ₁) is {A}, and we have already proved $+\partial A$, thus clause (2.2) is satisfied. We have two rules for $\neg B$, namely r ₃ and r ₄. Using the same reasoning we can show that $+\partial E$ (clause 2.3 for the derivation of $+\partial E$ is vacuously satisfied since there are no rules for $\neg E$). For r ₃ we have that $-\partial D$ ($D\notin F$ and there are no rules for it), so clause 2.3 is satisfied for r ₃ based on clause 2.3.1. For r ₄ we can use the superiority relation $r_1 > r_4$, to exhibit a rule (i.e., r ₁) for B which is stronger than r ₄. Thus clause 2.3 is true also for r ₄, and then we are justified to append $+\partial B$ at the end of the derivation.

Sometimes all we want to know is whether a literal is supported, that is if there is a chain of reasoning that would lead to a conclusion in absence of conflicts. This notion is captured by the following proof conditions:

• $+\Upsigma$: if $P(n+1)=+\Upsigma p$ then

  • (1) $+\Updelta p\in P(1\ldots n)$ or

  • (2) $\exists r\in R_{sd}[p]: \forall a\in A(r) +\Upsigma a\in P(1\ldots n)$

The notion of support corresponds to monotonic proofs using both the monotonic and non-monotonic parts of defeasible theories.

3 A computational framework for institutional agency

As we have seen in Sect. 1 multi-modal logics have been put forward to capture the intensional nature of (institutional) agency. Usually multi-modal logics are extensions of classical propositional logic with some intensional operators. Thus any multi-modal logic should account for three components: (1) the underlying logical structure of the propositional base; (2) the logic behaviour of the modal operators; and (3) the relationships among the modal operators. Alas, as is well-known, classical propositional logic is not well suited to deal with real life scenarios. The main reason is that the descriptions of real-life cases are, very often, partial and somewhat unreliable. In such circumstances classical propositional logic might produce counter-intuitive results insofar as it requires complete and consistent information. Hence modal logics based on classical propositional logic are doomed to suffer from the same problems.

On the other hand the logic should specify how modalities can be introduced and manipulated. Some common rules for modalities are, e.g., Necessitation (i.e., $\vdash A/\vdash \square A$) and RM (i.e., $\vdash A\to B/\vdash \square A \to \square B$) [Chellas 1980]. Both dictate conditions for introducing modalities in contrast with the analysis of institutional agency as outlined in Sect. 1. To comply with the properties of this notion, in the setting provided by DL we have to set (1) the rules describing the logical inferences and (2) the rules to introduce the modal operators of agency E _i (the agent i brings about), and H _i (the agent i attempts). Accordingly we will consider two types of rules (strict, defeasible, and defeaters): a set of rules for the notion of counts-as, and a set of rules for the notion of results-in.

Since we want to reason about actions we extend the language of DL with a set of action symbols; we will use $\alpha_i, \beta_i, \gamma_i$ to denote atomic actions. The meaning of an action symbol, for example $\alpha_i$, is that the action corresponding to it has been performed by agent i, while we use $\neg \alpha_i$ to denote that the action described by α _i has not bee performed. Given the modal operators $E_i,\,\, H_i$, and $proc_i$ we form new literals as follows: (i) if l is a literal then $proc_i l$ is a literal; (ii) if l is a literal then $E_il,\,\, \neg E_il,\,\, H_il$ and $\neg H_il$ are literals if l is different from $E_im,\,\, \neg E_im,\,\, H_im$ and $\neg H_im$, for some literal m. We will use Lit to denote the set of literals.

In this perspective a defeasible institutional action theory is a structure $I=(A,F,R^c,\{R^i\}_{i\in A}, >)$ where, A is a finite set of agents, F is a set of facts, R ^c is a set of counts-as rules (i.e., $\to_c, \Rightarrow_c, \rightsquigarrow_c$), $\{R^i\}_{i\in A}$ is a family of sets of results-in rules (i.e., $\to^i, \Rightarrow^i, \rightsquigarrow^i, \forall i\in A$), and > , the superiority relation, is a binary relation over the set of rules (i.e., $> \subseteq (R^c\cup R^A)^2$), where $R^A=\bigcup_{i\in A}R^i$.

The intuition is that, given an institution, F consists of the description of the raw institutional facts, either in form of states of affairs (literal and modal literal) and actions that have been performed. R ^c describes the basic inference mechanism internal to an institution, while R ^A encodes the transitions from state to state occurring as the results of actions performed by the agents within the organisation. The rules in R ^A are used to introduce modal operators. To capture these notions we impose some restrictions on the form of rules: literals of the form $E_il,\,\, \neg E_il,\,\, H_il$ and $\neg H_il$ are not permitted in the consequent of results-in rules for i, while actions symbols are not permitted in the consequent of results-in rules. The first restriction is motivated from the fact that (1) results-in rules are the rules to introduce the modalities and in the present context sequences of modalities for the same agent are useless⁵ (2) counts-as rules make possible the derivation of institutional actions (modalised literals) only when they follow from specific actions (intentionally) performed by the agent. The second restriction is due to the idea that results-in rules describe, as their name suggests, the results of actions, not actions themselves.

Let us see by means of some examples the intuition behind this formalism. We focus here on defeasible rules but similar remarks can be applied to the other kinds of rules. Suppose the agent i is acting in the context of an auction. Then we may have cases like the following:⁶

$$ {\mathbf{bids}}_{i},\,\, auction\_begun \Rightarrow^i offer $$

(2)

This rule is an example corresponding to the introduction of the modality E _i . In fact, agent i's fulfilment of the conditions in the antecedent produces the occurrence of offer: agent i's action of bidding has the result that i has made an offer. As we will see, if offer can be derived, this permits the introduction of E _i (offer).

$$ auction\_begun \Rightarrow^i \neg offer $$

(3)

The example above does not specify any action in the antecedent (empty action). This means that, when the auction is begun, agent i's refraining from doing any action has the result to have no offer. In logical terms, also this case can lead to the introduction of E.⁷

Now suppose that agent i is acting on behalf of agent j.

$$ {\mathbf{bids}}_{i},\,\, proc_{i}(E_j\, offer) \Rightarrow^j \, offer $$

(4)

This formula means that the fact that agent i makes a bid and proclaims that agent j makes the offer permits to introduce E _j , namely that $E_j\, offer$.

Let us consider examples of counts-as rules.

$$ {\mathbf{raises\_hand}}_{i},\,\, auction\_begun \Rightarrow_c {\mathbf{bids}}_{i}$$

(5)

This rule says that that agent i's action of raising one hand counts as agent i's action of bidding, when the auction is begun.

$$ auction\_begun,\,\, E_i (offer) \Rightarrow_c \neg {\mathbf{raises\_offer}}_{i} $$

(6)

Also here we have agent i's generic refraining from doing any action in the antecedent. This example represents the institutional connection linking such refraining, and the fact that agent i made an offer when the auction is begun, to agent i's specific refraining from raising a new offer. Notice that the same meaning is assigned to counts-as rules where the antecedent contains only non-modal literals.

$$ auction\_begun,\,\, {\mathbf{raises\_hand}}_{i} \Rightarrow_c offer $$

(7)

This rule is an example of the institutional analogous of results-in rules, where an action and a state of affairs occur respectively in their antecedent and consequent. However, in this case the result is an institutional fact and follows by convention only within the institution. In fact, that an offer is a consequence of agent i's raising one hand is not a simple matter of agent i's action results. The attempt of agent i to make an offer by raising the hand is effective only if the institution recognises this.

Let us see a couple of examples with more than one agent. As above, agent i is acting on behalf of agent j.

$$ proc_i(E_j\, offer) \Rightarrow_c E_i(E_j\, offer) $$

(8)

This rule says that if agent i proclaims that agent j makes an offer, then this counts as agent i brings it about that agent j makes such an offer.

$$ proc_{i}(E_j\, offer), {\mathbf{raises\_hand}}_i \Rightarrow_c {\mathbf{bids}}_j $$

(9)

Rule (9) expresses that agent i's proclamation that agent j makes an offer counts as agent j's action of bidding.

It is worth noting that no explicit reference is made here to the modality D _s [Gelati et al. 2004], as discussed in Sect. 1. In fact, the present setting accounts for the idea of institution in terms a special kind of defeasible theory. Each institutional action theory I encodes in itself all possible inferences that can be drawn within the domain of institutional facts relative to a given s. This means that s may be identified with I since all action results are obtained within such a domain of facts. In other words, the introduction of the modality D _s corresponds here to the general definition of derivability using counts-as and results-in rules. Technically, counts-as rules are meant to capture the case $D_s A\Rrightarrow D_s B$ mentioned in Sect. 1. Roughly speaking, on the other hand, the case $A\Rrightarrow D_s B$ will be treated as a special kind of results-in rule, where the manipulation of the consequent is made under the constraints designed to account for the idea of institutional consequence. This is just a technical device to differentiate the two cases: the logical behaviour of the counts-as link as described in [Gelati et al. 2004] is here encoded in the whole formal machinery corresponding to the definitions of the proof conditions.

Before moving to the proof conditions we have to introduce the notion of complementary literals. In standard DL two literals are complementary to each other if one is the negation of the other. This means that the two literals cannot hold at the same time. The extension with modal operators has to consider when modal literals are in conflict with each other. Since the agency operator E is successful (i.e., $E_iA\to A$), it is not possible to have together $E_iA$ for some agent i and A. In a similar way we have to capture the strong notion of agency we intend to model within our framework, i.e., where $E_iE_jA\to\neg E_iA$.

Given an atomic literal p we use Ep to denote any string $E_{i_1}\ldots E_{i_n}p$ where $E_{i_1}\ldots E_{i_n}$ is a (possibly empty) string of positive modal operators such that $\forall j,1\leq j < n, i_j\neq i_{j+1}$. Let l be a literal, ${\fancyscript{C}}(l)$ denotes the complement of l, i.e., the set of literals that cannot be true when l is.

• if l = p, then ${\fancyscript{C}}(l)=\{E\sim p\}$;

• if $l=E_ip$, then ${\fancyscript{C}}(l)=\{E\sim p, E\neg E_ip\}$;

• if $l=\neg E_ip$, then ${\fancyscript{C}}(l)=\{EE_ip\}$.

The meaning of the first condition is that if p is true then no agent prevented p; for the second condition we have that if an agent i has realised p, then no other agent prevented p and no agent prevented i from realising p. Finally if an agent i has refrained from doing p, then it is not possible that some other agents achieved that i did p.

We are now ready to give the proof conditions for institutional agency. We begin with the conditions for counts-as derivations.

• $+\Updelta_c$: if $P(n+1)=+\Updelta_cp$, then either:

  • (1) $Ep\in F$ or

  • (2) $\exists r\in R_s[Ep]:\,\, \forall a,\alpha,E_jb\in A(r), +\Updelta_ca, +\Updelta_c\alpha, +\Updelta_jb\in P(1\ldots n).$

The conditions are in essence the same as those for definite conclusions for DL given in Sect. 2. The first difference is in clause (1) where to prove a literal p we can use any fact of the form Ep, let us say, for example $E_iE_jp$. This is due to the successfulness of the E _i operator (see Sect. 1); in the limit case E is the empty sequence, and we recover the basic condition of DL. Similarly, in clause (2) we look for applicable counts-as rules for Ep instead of simply p. The last difference is that a rule is now applicable if the literals in the antecedent are proved with the right mode: $+\Updelta_c$ for unmodalised literals and action literals and $+\Updelta_i$ for modal literals whose main operator is E _i . This follows the intuition that modal rules for agent i behave as introduction rules for the modal operator E _i .

• $-\Updelta_cp$: if $P(n)=-\Updelta_cp$, then both:

  • (1) $Ep\notin F$, and

  • (2) $\forall r\in R_s[Ep]:\,\, \exists a\in A(r), -\Updelta_ca\in P(1\ldots n)$ or

    •        $\exists \alpha\in A(r), -\Updelta_c\alpha\in P(1\ldots n)$ or

    •        $\exists E_ib\in A(r), -\Updelta_ib\in P(1\ldots n).$

The intuiton for the condition for $-\Updelta_c$ is similar to that of $-\Updelta$ with the remarks about the condition for $+\Updelta_c$. The only issue we want to point out is that to reject a rule (to show that a rule cannot be applied) we have to show that there is at least one literal in the antecedent which is not provable with the appropriate mode. Finally, it is easy to verify that the condition for $-\Updelta_c$ is the strong negation of the condition for $+\Updelta_c$.

We can introduce the conditions for defeasible derivations. Again, the basic intuition is the same as in DL with the additional considerations as the conditions for strict derivations.

• $+\partial_c$: if $P(n+1)=+\partial_cp$, then:

  • (1) $+\Updelta_cp\in P(1\ldots n)$, or

  • (2.1) $-\Updelta{\fancyscript{C}}(p)\in P(1\ldots n)$ and

  • (2.2) $\exists r\in R_{sd}[Ep]\,\, \forall a,\alpha,E_ib\in A(r)$:

    •        $+\partial_ca, +\partial_c\alpha, +\partial_ib\in P(1\ldots n)$ and

  • (2.3) $\forall s\in R[{\fancyscript{C}}(p)]$: either

    • (2.3.1) $\exists a\in A(s), -\partial_ca\in P(1\ldots n)$ or

    • (2.3.2) $\exists\alpha\in A(s), -\partial_c\alpha\in P(1\ldots n)$ or

    • (2.3.3) $\exists E_ib\in A(s), -\partial_ib\in P(1\ldots n)$ or

    • (2.3.4) $\exists t\in R[Ep]\,\, \forall a,\alpha,E_ib\in A(t)$:

      •        $+\partial_ca, +\partial_c\alpha, +\partial_ib\in P(1\ldots n)$ and t > s.

The conditions for $-\partial_i$ are obtained from that for $+\partial_i$ using the mentioned principle of strong negation.

• $-\partial_c$: if $P(n+1)=-\partial_cp$, then:

  • (1) $-\Updelta_cp\in P(1\ldots n)$ and

  • (2.1) $+\Updelta_c{\fancyscript{C}}(p)\in P(1\ldots n)$ or

  • (2.2) $\forall r\in R_{sd}[Ep]:$ either

    • (2.2.1) $\exists a\in A(r): -\partial_ca\in P(1\ldots n)$ or

    • (2.2.2) $\exists \alpha\in A(r): -\partial_c\alpha\in P(1\ldots n)$ or

    • (2.2.3) $\exists E_ib\in A(r): -\partial_ib\in P(1\ldots n)$ and

  • (2.3) $\exists s\in R[{\fancyscript{C}}(p)]\,\, \forall a,\alpha,E_ib\in A(r)$:

    •        $+\partial_ca, +\partial_c\alpha, +\partial_ib\in P(1\ldots n)$ and

    • (2.3.1) $\forall t\in R[Ep]$: either $t\not > s$ or

      •       $\exists a\in A(t), -\partial_ca\in P(1\ldots n)$ or

      •       $\exists\alpha\in A(t), -\partial_c\alpha\in P(1\ldots n)$ or

      •       $\exists E_ib\in A(t), -\partial_ib\in P(1\ldots n)$.

To conclude the presentation of the proof conditions for counts-as conclusions we give the conditions for support.

• $+\Upsigma_c$: if $P(n+1)=+\Upsigma_cp$, then

  • (1) $Ep\in F$ or

  • (2) $\exists r\in R_{sd}[p]\,\, \forall a,\alpha,E_ib\in A(r)$:

    •       $+\Upsigma_ca, +\Upsigma_c\alpha, +\Upsigma_ib\in P(1\ldots n)$.

• −Σ _c : if $P(n+1)=-\Upsigma_cp$, then

  • (1) $Ep\notin F$ and

  • (2) $\forall r\in R_{sd}[p]$: either

    •       $\exists a\in A(r), -\Upsigma_ca\in P(1\ldots n)$ or

    •       $\exists \alpha\in A(r), -\Upsigma_c\alpha\in P(1\ldots n)$ or

    •       $\exists E_ib\in A(r), -\Upsigma_ib\in P(1\ldots n)$.

The conditions are the same as + Δ and −Δ; the only difference is that for support we consider both strict and defeasible rules instead of only strict rules, and the two conditions are the strong negations of each other.

The conditions for derivations involving results-in rules are more complicated since we have to cater for more possibilities. First of all we have that $I\vdash E_ip$ if either $I\vdash +\Updelta_i p$ or $I\vdash +\partial_i p$,⁸ and $I\vdash H_ip$ if $I\vdash +\Upsigma_i p$. In other words it is possible to derive $E_ip$ if we have either a strict or defeasible derivation of p using both results-in and counts-as rules, and that agent i (in an institution I) attempts $p\,\, (H_ip)$ if I supports p using counts-as ad results-in rules. The output of a results-in rule produces E _i modal literals, and we have seen in Sect. 1 that the E _i operator is a success operator; therefore we add the conditions that it is possible to derive +Δ _c p from $+\Updelta_ip$ and + ∂ _c p from $+\partial_ip$. In particular, it is worth noting that a counts-as rule can be used as it were a results-in rule if all the literals occurring in its antecedent are proved as appropriate results-in conclusions. In this case, we say that we have a conversion from a counts-as rule into a results-in rule. For example, suppose we have that

$$ auction\_begun,\,\, {\mathbf{raises\_hand}}_{i} \Rightarrow_c offer $$

If we have ${\mathbf{raises\_hand}}_{i}$ and prove auction_begun as a results-in conclusion, in particular as E _i auction_begun, then we can say that agent i brings offer about, namely that E _i offer. More on conversions can be found in [Governatori et al. 2006].

In the same way we have that −∂ _i p corresponds to $\neg E_ip$ and −Σ _i p to $\neg H_ip$ in addition to the cases where the modal literal is provable with a counts-as derivation (e.g., $I\vdash+\partial_cE_ip$). This is in agreement with the principle of strong negation used to define the inference conditions.

•  + Δ _i : if $P(n+1)=+\Updelta_ip$ then

  • (1) $EE_ip\in F$; or

  • (2) $+\Updelta_cE_ip\in P(1\ldots n)$; or

  • (3) $\exists r\in R^i_s[p]\,\, \forall a,\alpha, E_jb\in A(r)$:

    •       $+\Updelta_ia, +\Updelta_i\alpha, +\Updelta_jb\in P(1\ldots n)$ or

  • (4) $\exists r\in R^c_s[p]:\,\, \exists a\in A(r)\cap \hbox{Lit}$, and

    •       $\forall a,\alpha\in A(r):\,\, +\Updelta_ia, +\Updelta_c\alpha\in P(1\ldots n).$

To prove non-defeasible brings-it-about, we need either that it is given as a fact (or the set of facts contains a chain of brings-it-about operators where the last one is E _i ) (1), or that $E_ip$ has been proved using counts-as rules, or that we have a strict rule for results-in (an irrevocable policy) whose antecedent is indisputable (3). However we have another case (4): if an agent knows that B is an indisputable consequence of A in the institution (it is always the case that A counts as B), and it produces A, then it must realise B.

• −Δ _i : if $P(n+1)=-\Updelta_ip$ then

  • (1) $EE_ip\notin F$ and

  • (2) $-\Updelta_cE_ip\in P(1\ldots n)$ and

  • (3) $\forall r\in R^i_s[p]$: either

    •       $\exists a\in A(r), -\Updelta_ca\in P(1\ldots n)$ or

    •       $\exists \alpha\in A(r), -\Updelta_c\alpha\in P(1\ldots n)$ or

    •       $\exists E_jb\in A(r), -\Updelta_jb\in P(1\ldots n)$, and

  • (4) $\forall r\in R^c[p]$, either

    •       $A(r)\cap \hbox{Lit}=\emptyset$ or

    •       $\exists a\in A(r): -\Updelta_ia\in P(1\ldots n)$ or

    •       $\exists \alpha\in A(r): -\Updelta_c\alpha\in P(1\ldots n).$

As usual the condition for $-\Updelta_i$ is the strong negation of that for + Δ _i . The only points to notice are clause (2) where we have to consider that$E_ip$ is not provable using counts-as rules, and the first condition of clause (4) that imposes that conversions from counts-as rules to results-in rules are not possible if the antecedent of the counts-as rule does not contain any literal (even if it may contain actions). According to clause (4) of the two conditions above, given the facts $E_iA$ and β _j we can use the rule $A,\beta_j\to_cB$ to derive + Δ _i B and consequently E _i B, but not the rule $\beta_j\to_cB$.

We give now the proof condition for support for $i\,\, (\pm\Upsigma_i)$.

•  + Σ _i : if $P(n+1)=+\Upsigma_ip$ then

  • (1) $E_ip\in F$; or

  • (2) $\exists r\in R^i_{sd}[p]\,\, \forall a, E_jb, \alpha\in A(r)$:

    •       $+\Upsigma_ca,+\Upsigma_jb,+\Upsigma_c\alpha\in P(1\ldots n)$; or

  • (3) $\exists r\in R^c_{sd}[p]\,\, \exists a\in A(r)\cap \hbox{Lit}$ and,

    •       $\forall a, \alpha\in A(r): +\Upsigma_ia,+\Upsigma_c\alpha\in P(1\ldots n)$.

The inference conditions for H _i are very similar to those for strong results-in rules; essentially they are monotonic proofs using both the monotonic part (strict rules) and the supportive non-monotonic part (defeasible rules) of a defeasible institutional action theory. Given the close similarity between the conditions for + Δ _i and + Σ _i and the fact that all pairs of proof conditions for the proof tags given in this paper are in agreement with the principle of strong negation the conditions for −Σ _i are omitted.

To capture the results of defeasible actions we have to use the superiority relations to resolve conflicts. Thus the inference conditions for + ∂ _i are:

• $+\partial_i;\,\, P(n+1)=+\partial_ip$ then

  • (1) $+\Updelta_ip\in P(1\ldots n)$ or

  • (2.1) $-\Updelta{\fancyscript{C}}(E_ip),-\Updelta_iE_kp\in P(1\ldots n)$ and

  • (2.2) $\exists r\in R^i_{sd}[p]\cup R^c_{sd}[EE_ip]:\,\, \forall a,\alpha,E_jb\in A(r),$

    •       $+\partial_ca, +\partial_c\alpha, +\partial_jb\in P(1\ldots n)$ or

    • $\exists r\in R^c_{sd}[p]:\,\, A(r)\cap \hbox{Lit}\neq\emptyset$, and

    •       $\forall a,\alpha\in A(r), +\partial_ia, +\partial_c\alpha\in P(1\ldots n)$; and

  • (2.3) $\forall s\in R[{\fancyscript{C}}(E_ip)]\cup R^i[E_kp]$: either

    •       $\exists a\in A(s): -\partial_ca\in P(1\ldots n)$ or

    •       $\exists \alpha\in A(s): -\partial_c\alpha\in P(1\ldots n)$ or

    •       $\exists E_jb\in A(s): -\partial_jb \in P(1\ldots n)$, and

    $\forall s\in R^c[E_kp]$: either

    •       $A(s)\cap \hbox{Lit}=\emptyset$ or

    •       $\exists \alpha\in A(s): -\partial_c\alpha\in P(1\ldots n)$ or

    •       $\exists a\in A(s): -\partial_ia\in P(1\ldots n)$; or

    • (2.3.1) $\exists t\in R^i[p]\cup R^c[EE_ip]:\,\, t > s$ and

      • $\forall a,\alpha,E_jb\in A(t), +\partial_ca, +\partial_c\alpha, +\partial_jb\in P(1\ldots n)$ or

      • $\exists r\in R^c[p]:\,\, A(t)\cap\hbox{Lit}\neq\emptyset$, and

      •       $\forall a, \alpha\in A(t), +\partial_ia, +\partial_c\alpha\in P(1\ldots n)$

The conditions for proving the results of defeasible actions are essentially the same as those given for defeasible derivations in Sect. 2. Also here, at each stage, we have to check for two cases, namely: (1) the rule used is a results-in rule; (2) the rule is a counts-as rule. In the first case we have to verify that factual antecedents are defeasibly proved/disproved using counts-as (±∂ _c ), and brings-it-about antecedents are defeasibly proved/disproved using results-in rules (±∂ _i ). In the second case we have to remember that a conclusion of a institutional counts-as rule can be transformed (converted) into a results-in if all the literals in the antecedent are defeasibly executed. For the attack phase (clause 2.3) we have to consider all rules in ${\fancyscript{C}}(E_ip)$ as well as all results-in rules for agent i for E _k p, i.e., rules meaning that agent i does something so that agent k personally does p (again, see Sect. 1 for the motivation and intuition behind this condition). Finally, for the same reason we have to ensure that all counts-as rules for E _k $(k\neq i)$ do not behave as results-in rule for agent i. This means we have to verify that either the rule cannot be converted into a results-in rule for i (i.e., $A(r)\cap\hbox{Lit}=\emptyset$) or that the conversion is blocked, i.e., that there is a literal which is not provable for ∂ _i . This means that the event corresponding to the literal is not under the control of agent i, and so the whole conclusion, which would correspond to the delegation to agent k, is not under the influence of agent i.

For −∂ _i we have:

• −∂ _i : if $P(n+1)=-\partial_ip$ then

  • (1) $-\Updelta_ip\in P(1\ldots n)$ and

  • (2.1) $+\Updelta{\fancyscript{C}}(E_ip)\in P(1\ldots n)$ or $+\Updelta_iE_k\in P(1\ldots n)$

    • (2.2.1) $\forall r\in R^i_{sd}[p]\cup R^c[EE_ip]$ either

      •       $\exists a\in A(r): -\partial_ca\in P(1\ldots n)$ or

      •       $\exists \alpha\in A(r): -\partial_c\alpha\in P(1\ldots n)$ or

      •       $\exists E_jb\in A(r): -\partial_jb \in P(1\ldots n)$, and

    • (2.2.2) $\forall r\in R^c[p]$ either

      •       $A(r)\cap\hbox{Lit}=\emptyset$ or

      •       $\exists a\in A(r): -\partial_ia\in P(1\ldots n)$ or

      •       $\exists\alpha\in A(r): -\partial_c\alpha\in P(1\ldots n)$, or

  • (2.3) $\exists s\in R[{\fancyscript{C}}(E_ip)]\cup R^i[E_kp]:\,\, \forall a,\alpha,E_jb\in A(s)$,

    •       $+\partial_ca, +\partial_c\alpha, +\partial_jb\in P(1\ldots n)$ or

    • $\exists s\in R^c[E_kp]:\,\, \exists a\in A(s)\cap\hbox{Lit}$, and

    •       $\forall a, \alpha\in A(r), +\partial_ia,+\partial_c\alpha\in P(1\ldots n)$, and

    • (2.3.1) $\forall t\in R^i[p]\cup R^c[EE_ip]$ either $s\ngtr t$ or

      •       $\exists a\in A(t): -\partial_ca\in P(1\ldots n)$ or

      •       $\exists \alpha\in A(t): -\partial_c\alpha\in P(1\ldots n)$ or

      •       $\exists E_jb\in A(t): -\partial_jb \in P(1\ldots n)$, and

    • (2.3.2) $\forall t\in R^c[p]$ either

      •       $A(s)\cap\hbox{Lit}=\emptyset$ or

      •       $\exists a\in A(t), -\partial_ia\in P(1\ldots n)$ or

      •       $\exists\alpha\in A(t), -\partial_c\alpha\in P(1\ldots n)$ or $s\ngtr t$.

Let us examine the above conditions at work with the help of some examples. We assume the following theory:

$$ \begin{array}{l} F=\{\alpha_i, p, E_jq\},\\ R=\{r_1:\alpha_i,p,E_jq\Rightarrow^is;\quad r_2: s\Rightarrow^ir;\quad r_3: r\Rightarrow_c t\}. \end{array} $$

In this theory we are able to prove E _i t. The facts fire r ₁, thus we can prove $+\partial_is\,\, (E_is)$. Now, since s has been brought about, s is the case. We can use this to fire the rule r ₂. Hence we obtain + ∂ _i r, which is $E_ir$. This implies that all the requisites of $r_3$ have been brought about; but r ₃ states that r counts as t; this means that t has been brought about, hence + ∂ _i t and Et.

Let us replace r ₃ with $r_3^{\prime}: p, r\Rightarrow_c t$. This time we can prove + ∂ _c t, but not $E_it\,\, (+\partial_it)$. The reason is that p is the case without a specific “intention” of the agent to bring it about. Similarly, if we replace r ₃ by $r_3^{\prime\prime}: E_ir\Rightarrow_ct$ we can no longer derive E _i t. Here E _i r is understood as a mere institutional fact, and not as the successful intention of the agent to realise r in order to realise t.

In the previous example we have seen how we can argue in favour of $E_ip$ (for same literal p). Let us examine the conditions to attack it. Let I be the following institutional defeasible theory

$$ \begin{array}{l} F=\{\alpha_i,p,q\},\\ R=\{r_1: \alpha_i,p\Rightarrow^is; \quad r_2: q\Rightarrow_c r; \quad r_3: p,r\Rightarrow_c\neg s\} \end{array} $$

Clearly $E_is\,\, (+\partial_is)$ is not derivable from the given theory since there is an applicable rule for $\neg s$. r ₃ is applicable since we can derive + ∂ _c r. Similarly, if we replace r ₂ with $q\Rightarrow_i r,\,\, r_3$ is still applicable. We can prove + ∂ _i r: this means that there is a successful action resulting in r. In general to discard a rule we have to show that some of the premises cannot be derived. With a factual literal we have to show that the literal is not the case (or, in other terms, that there are no literals that count as it), and that the literal is not the result of a successful action: results of successful actions are indeed the case. Finally we replace r ₃ with $r_3^{\prime\prime}:p,r\Rightarrow^iE_js$. Again we cannot conclude E _i s; see the motivation for the principle $(\hbox{EE}\neg \hbox{E})$ in Sect. 1.

Let us now consider how to represent the following business scenario. For normal orders a company has pre-defined invoices and the finance department can delegate the preparation of the invoices to the shipping department. The preparation of an invoice requires to check that the details in it are correct and to sign it. However special orders require more care and processing, and the finance department is in charge for their invoices. Finally goods can be delivered only after the finance department has prepared the invoice. This scenario is depicted by the following institutional theory,

$$ \begin{array}{l} r_1:\,proc_{F}(E_S(invoice\_ready)), E_S(invoice\_ready) \Rightarrow^F\, invoice\_ready\\ r_2:\, special\_order, E_S(invoice\_ready) \Rightarrow_{c} \neg invoice\_ready\\ r_3:\, {\mathbf{sign\_invoice}}_X \Rightarrow^X\, invoice\_checked\\ r_4:\, invoice\_checked \Rightarrow_c\, invoice\_ready\\ r_5:\, E_F(invoice\_ready) \Rightarrow_c\, ship\_order \end{array} $$

where $r_2 > r_1$ and $r_2 > r_4$. Here rule r ₁ is the rule governing the delegation of the preparation of the invoice, where r ₂ is an exception to it. r ₃ is a schema that establishes that the act of signing an invoice by an agent (a role) X results in the invoice being checked by X. The meaning of r ₄ is that according to the business rule of the company is that once an invoice has been checked then the invoice is ready to be sent. Finally r ₅ states that items can be shipped only after their invoice has been approved by the finance department.

Let us consider the following scenario. The company receives an order. The finance department considers the order to be a standard order and it delegates the whole process to the shipping department, which processes it and a clerk in this department signs the invoice. In this case the facts are $proc_F(E_S(invoice\_ready))$, and ${\mathbf{sign\_invoice}}_S$. We can apply r ₃ to derive $E_S(invoice\_checked)$. According to rule r ₄ we have that the invoice is ready. However the invoice has been signed by a clerk in the shipping office, the result of this action is qualified as an act performed by the shipping department. This means that we carry over the qualification from the antecedent to the consequent of rule r ₄. Hence we obtain E _S (invoice_ready). Since the shipping department was delegated by the finance department to process the invoice, we can apply rule r ₁ to derive that the invoice had been prepared by the finance department via delegation $(E_F(invoice\_ready))$ and the order can be delivered. On the other hand, if an order is classified as a special order, then the only alternative is that the finance department process the invoice by itself, that is somebody in the finance department has to sign the invoice.

4 Properties of the logic

First of all, as it was mentioned in Sect. 1, it is worth noting that the consequence relation induced by the defeasible relation for the counts-as—which is characterised by proof conditions for standard DL—is a cumulative consequence relation and thus it obeys the basic properties of Reflexivity, Cautious Monotonicity and Cut we previously required for the counts-as conditional. The proof for this result can be found in [Billington 1993].

Let us see some properties of the logic we have just described.

The purpose of the −Δ and −∂ inference rules is to establish that it is not possible to prove a corresponding tagged literal. These rules are defined in such a way that all the possibilities for proving + ∂p (for example) are explored and shown to fail before −∂p can be concluded. Thus we have a constructive proof that the corresponding positive conclusion cannot be obtained.

As a result, there is a close relationship between the inference rules for + ∂ and −∂, (and also between those for + Δ and −Δ, and + Σ and −Σ). The structure of the inference rules is the same, but the conditions are negated in some sense. This feature allows us to prove some properties showing the well behaviour of DL.

Theorem 1

Let $\#=\Updelta_c, \partial_c, \Upsigma_c, \Updelta_i, \partial_i, \Upsigma_i,$ and I be an institutional action theory. There is no literal p such that $I\vdash +\# p$ and $I\vdash -\# p.$

The above theorem states that no literal is simultaneously provable and demonstrably unprovable, thus it establishes the coherence of the DL presented in this paper.

Theorem 2

Let I be an acyclic institutional action theory, and $M\in\{c,i\},\,\, i\in A.\,\, I\vdash +\partial_Mp$ and $I\vdash +\partial_M\sim p$ iff $I\vdash +\Updelta_Mp$ and $I\vdash +\Updelta_M\sim p.$

This theorem gives the consistency of DL. In particular it affirms that it is not possible to bring conflicting states about (+ ∂ _i p and $+\partial_i\sim p$) unless the information given about the environment is itself inconsistent. Notice, however, that the theorem does not cover attempts (Σ _i ). Indeed it is possible to attempt something and its negation. We will say that an institutional theory is consistent if Theorem 2 holds for the theory.

Let I be an institutional action theory I. With $\Updelta_{c}^{+}$ we denote the set of literals strictly provable using the counts-as part of I, i.e., $\Updelta^{+}_c= \{p: I\vdash +\Updelta_c p\}$. Similarly for the other proof tags.

Theorem 3

LetIbe an institutional action theory, and$M\in\{c,i\},\,\, i\in A$.

• 1. $\Updelta^{+}_{M} \subseteq \partial^{+}_M \subseteq \Upsigma^{+}_M$;

• 2. $\Upsigma^{-}_M\subseteq \partial^{-}_M \subseteq \Updelta^{-}_M$;

• 3. Let I be a consistent institutional action theory such that $I\vdash -\Updelta_ip.$ If $I\vdash +\partial_iE_jp$ then $I\vdash -\partial_ip.$

• 4. For any $i,\,\, \Updelta^{+}_i\subseteq \Updelta^{+}_{c},$ and $\partial^{+}_i\subseteq \partial^{+}_c.$

Since + ∂ _i and + Σ _i correspond to E _i and H _i , we have that that 1. and 2. correspond to the axiom $E_iA \to H_iA$. 3. is an immediate consequence of clause 2.3.2 of the inference condition for + ∂ _i . This property corresponds to the axiom $(\hbox{EE} \neg \hbox{E})$ of Sect. 1. Finally 4. corresponds to the successfulness of the E _i operator (i.e., axiom T).

To conclude this section we give a result justifying the choice of DL as our computational framework. Given an institutional action theory I, the universe of $I,\,\, U^I$ is the set of atomic propositions and action symbols occurring in it. The extension of I is the set of all proof tags derivable from I, restricted to the (modal) literals that can be built from U ^I.

Theorem 4

LetIbe an institutional action theory. The extension ofIcan be computed in time linear to the size of the theory, i.e., $O(|R|*|U^I|*|A|).$

The proof is based on a variation of the data structure used by Maher [Maher 2001] to prove that the basic DL has linear complexity, see [Governatori and Pham 2005, Governatori et al. 2006].

5 Related work

An impressive amount of literature has been devoted to agent interaction and coordination. Our work presents a rule-based system and so it fits into a long and extensive AI tradition. As regards agent interaction, we can identify in particular two recent strands: (a) a cognitive account of agents that specifies their mental attitudes; (b) modelling agents’ behaviour by means of normative concepts. In this section we simply comment some contributions which are strictly related to the specific perspective adopted here, a perspective originating from [Gelati et al. 2004] and which belongs to the research line mentioned under point (b) above. The current work is a technical extension of [Gelati et al. 2004], as it takes some of the building blocks used there and re-defines them within a computational framework, where by “computational framework” we mean a logical system which enjoys nice computational properties and which is directly designed for implementation.

Different formal theories of action have been used to deal with institutional agents. Logics such as Event and Situation Calculi, the STIT approach, Dynamic Logics—just to mention a few examples—were all proven useful in combination with normative concepts, and especially with deontic notions (for recent applications in the field, see [Demolombe and Herzig 2004, Farrell et al. 2005, Horty 2001, Broersen 2004]). However, the aim of this paper is not to develop an alternative methodology to these theories, as our approach focuses on very minimal and abstract properties of agency in the spirit of the modal logic of agency described in [Elgesem 1997]. In this specific perspective, our contribution is meant to show how such minimal properties can be embedded in DL, and so how they can be re-interpreted within a non-monotonic system specifically oriented to implementation.

A further goal of this paper was to see how agency can interplay with counts-as rules. As far as the logical nature of these rules is concerned, the literature provides different views.

In a first perspective, the institutional status of constitutive rules is directly related to some epistemic notions [Boella and van der Torre 2004]: using the metaphor of normative systems as agents, this approach attributes to them some peculiar mental attitudes. Hence, norms are considered as mental objects and constitutive rules, in particular, are modelled as beliefs.

In a second perspective, the attention is rather focused on the role of institutional rules intended as external factors constraining agents’ behaviour. Clearly, our paper draws inspiration from this second perspective. Within this view, we can mention at least two alternative options (see [Grossi et al. 2006] for a fine discussion of the different meanings of the counts-as link).

A first approach is in line with Goldman’s theory of actions generating actions [Goldman 1970]. It may be argued that the generation of institutional facts via counts-as rules is close to the idea of causality. If so, counts-as relations cannot be reflexive since “it is precisely the property of non-reflexiveness that distinguishes a generation relation as such” [Jones et al. 2003]. In [Jones and Sergot 1996], Jones and Sergot basically follow this approach and develop an analysis of the notion of institutionalised power by introducing a new (classical but not normal) conditional connective “⇒ _s ”. This connective expresses the “counts as” connection holding in the context of an institution s. In particular, when applied to action descriptions, formulas like $E_i A\Rightarrow_s E_i B$ and $E_i A\Rightarrow_s E_j B$ represent respectively i's institutional power to produce B when A is realised and i's power to perform an action as if something else were made by j (see [Jones and Sergot 1996, Jones forthcoming]).⁹ In addition, the logic for ⇒ _s is integrated by the KD modality D _s , such that D _s A means that A is a “constraint on the institution s”. The connection between ⇒ _s and D _s is characterised by the schema (A⇒ _s B)→ D _s (A→ B). This approach differs from our view, as Jones and Sergot state that the counts-as be non-reflexive and transitive, while we see it as at least enjoying Reflexivity, Cut, and Cautious Monotonicity. Reflexivity affects the meaning ascribed to the count-as link. If the defeasibility of counts-as must be accepted, we have to decide whether reflexivity must prevail over transitivity or the other way around, since transitivity and reflexivity imply monotonicity (see [Artosi et al. 2002]). As in [Gelati et al. 2004], we assume that the counts-as link has a classificatory nature, and defeasible classificatory relations, such as typicality, normally enjoy reflexivity.

A second approach, by Grossi, Meyer, and Dignum [Grossi et al. 2005], views counts-as statements as yielding contextual classifications. Hence, as we do here, it is emphasised the classificatory role of the notion of counts-as, a notion which is investigated by Grossi and colleagues by means of modal logic techniques from a semantics-driven perspective. In particular, the authors model the counts-as connection within the multi-modal logic ${\mathbf{KD45_{n}}^{i {\text -}j}}$. Despite its conceptual clarity, this analysis has two drawbacks. First, the defeasible nature of constitutive rules is disregarded. Second, contextual modalities suffer of the so-called “omniscience problem”, a problem which also affects Jones and Sergot’s D _s modality: if making_a_bid is an institutional act, this would imply in that approach that $making\_a\_bid \vee drinking\_some\_water$ holds as well within an institution. Our approach tries to avoid this difficulty, as institutional consequences are derived only if stronger reasons do not block these derivations.

6 Discussion and future work

Our aim was to develop a computational treatment of the notion of institutional agency as described in [Gelati et al. 2004]. In this perspective, our contribution does not include any explicit refinement (e.g., in terms of articulating new axioms) of what has been already proposed in [Gelati et al. 2004]. This does not mean, however, that the model presented here cannot be a potential starting point to achieve new proof-theoretical results. Let us recall that the propositional base of the modal logic of agency is classical propositional logic [Santos and Carmo 1996, Elgesem 1997]. On the other hand, any refinement to introduce non-monotonic reasoning as a crucial aspect of institutional agency has been confined both in [Gelati et al. 2004] and in [Jones and Sergot 1996, Jones forthcoming] to account only for the counts-as link. Although this paper provides a machinery to reason about actions only with regard to institutional domains, it proposes some inferential mechanisms that may be generalised to define a non-monotonic theory of agency. How to do this and which is the axiomatisation resulting from such a generalisation is a matter of future research.

The logic presented here is just one of the many logics that can be defined using the main idea of the paper. Non-monotonic reasoning is a complex phenomenon with many facets. Several variants of DL have been put forward to deal with different intuitions behind non-monotonic reasoning. Accordingly a designer of a DL of agency has to chose the most appropriate defeasible inference mechanism and the degree of provability corresponding to the modalities at hand for the intended application. Similarly, the designer can chose more or less liberal conditions to use counts-as rules to derive brings-it-about literals. For example in this paper we have assumed that we can use a counts-as rule to derive a brings-it-about literal if all the literal in the antecedent of the rule can be derived as results-in conclusions. A more liberal condition could just require that only one of them is derived in such a way.

The aim of the paper was to provide a computationally oriented framework for the notion of counts-as and institutional agency. The model was given by a multi-modal extension of DL, and we have shown that the complexity of the resulting logic is linear. At the same time it is possible to use the logic as both a conceptual and executable specification of an institution. Accordingly it is natural to ask whether the logic has been implemented. While specific implementations for the logic do not exist, [Governatori and Pham 2005] describes an implementation of a similar modal (deontic) variant of DL. The implementation follows very closely the data structures and algorithm used to prove Theorem 4. Therefore the logic presented here can be easily implemented (indeed a Python prototype for the inference engine can be implemented with a few hundred lines of code).

Finally, we suggest some conceptual refinements for our future research.

First, the model should cope with a wider range of properties and with other concepts of agency, such as those mentioned in Sect. 1, i.e. the notions of ability [Elgesem 1997] and indirect successful action. Both of them are crucial in modelling the co-ordination of agents: (a) the inference of institutional facts may be conditioned by the practical capability of an agent to do things that generate by convention these facts; (b) the characterisation of the institutionalised power may require that an agent is empowered to realise indirectly a state of affairs without specifying the chain of agents that will bring about such a state of affairs.

Another issue concerns the relations between different institutions. These relations are relevant when an action takes place in different institutional contexts and produces diverse, and possibly contradictory, results. Following [Gelati et al. 2004], multi-institutional contexts are captured by stipulating that $A\Rightarrow_s B=_{def} (A\Rrightarrow D_s B)\wedge (D_s A \Rrightarrow D_s B) \wedge (D_s A \Rrightarrow D_{s^{\prime}} B)$. They may be represented here introducing counts-as rules indexed by different institutions: the superiority relations would play an important role in settling possible contradictions between different institutional contexts. But that is not all since the matter regards the complex problem of the relation between normative systems [Prakken 1997].

We also have to develop a more accurate mechanism to deal with conflicting institutional results arising from the exercise of different powers and which lead to dropping institutional facts which were previously derived. This question requires to develop a dynamic account of the institutional mechanisms. Of course, the idea, according to which the generation of institutional facts is close to the concept of causality, is a feasible option in this regard. However, as we said, this diverges from our view of the counts-as link. An alternative possibility is thus to introduce explicit temporal dimensions, as done in [Governatori et al. 2005], in order to make explicit when an institutional fact p is cancelled by a conflicting one which results from the subsequent exercise of a different power, or even of the same power that produced p.

Finally, we have to introduce in the current framework deontic modalities, as they are, too, crucial in modelling the normative coordination of agents. Some promising results in this perspective are already provided, for example, in [Governatori et al. 2005, Governatori et al. 2006], but a more extensive work is needed in studying the properties of the system when deontic concepts are added.

Appendix

1.1 Proofs of the Theorems in Sect. 4

Theorem 1

Let$\#=\Updelta_c, \partial_c, \Upsigma_c, \Updelta_i, \partial_i, \Upsigma_i,$andIbe an institutional action theory. There is no literalpsuch that$I\vdash +\# p$and$I\vdash -\# p$.

Proof

The result is a straightforward consequence of the principle of strong negation [Antoniou et al. 2000a, Antoniou et al. 2000b] used to define the proof conditions for the logic at hand. According to the principle of strong negation the condition for + # is the constructive negation of that of −# and the other way around. Thus if the condition for + # is satisfied the condition for −# fails and the other way around.

Theorem 2

LetIbe an institutional action theory, and$M\in\{c,i\}, i\in A$. $I\vdash +\partial_Mp$and$I\vdash +\partial_M\sim p$iff$I\vdash +\Updelta_Mp$ and $I\vdash +\Updelta_M\sim p.$

Proof

We have to show that if we have both + ∂ _M p and $+\partial_M\neg p$ then the only possible derivation is one where the two are both justified by clause (1) of the proof conditions for + ∂, and combinations of justifications where one of them is justified in terms of clause (2) lead to a contradiction.

It is clear that a combination of clauses (1) does not lead to any contradiction. Thus we have that both + Δ _M p and $+\Updelta_M\neg p$.

Let us consider the cases where one is justified by clause (2). This means that clause (2.1) is satisfied thus for M = c we have $-\Updelta_c {\fancyscript{C}}(p)$, and for M = i both $-\Updelta_i{\fancyscript{C}}(E_ip)$ and $-\Updelta_iE_kp$. But both $\neg p \in {\fancyscript{C}}(p)$ and $\sim p\in{\fancyscript{C}}(E_ip)$, thus we have −Δ _M p. By Theorem 1 it is not possible that both $I\vdash+\Updelta_Mp$ and $I\vdash-\Updelta_Mp$. Thus in this case we get a contradiction.

We examine now the situation where M = c and both conclusions are justified by clause (2). This means that $\exists r^{+}\in R_{sd}[Ep]$ such that the rule is applicable (i.e., the condition of clause (2.2) is satisfied), and at the same time we have that $\exists r^{-}\in R_{sd}[E\sim p]$ such that r ⁻ is applicable. $R_{sd}[E\sim p]\subseteq R[{\fancyscript{C}}(p)]$, thus there must be a rule $t_0\in R[Ep]$ such that t ₀ applicable and $t_0 > r^{-}$ (according to clause (2.3.4)). We have two cases (i) t ₀ is maximal (i.e., $\neg \forall s > t_0$) (ii) t ₀ is not maximal. For (i) we have that $t_0\in R[{\fancyscript{C}}(\sim p)]$ and is applicable thus t ₀ satisfies clauses (2.3) of −∂ _c . Therefore, $-\partial_c\sim p$, and we have a contradiction according to Theorem 1. For (ii) let us consider the set $T_0=\{s: s > t_0\wedge s\in R[E\sim p]\}$. Notice that $r^{-}\notin T_0$, since the theory I is acyclic. From T ₀ we eliminate the rules that are not applicable for condition (2.2) of + ∂ _c , and we call the resulting set S ₀. Since we have + ∂ _c p this means that for every rule s∈S ₀ there is a rule $t^{\prime}\in R[Ep]$ such that the rule is applicable and stronger than s. Let s′ and t ₁ be such rules, If t ₁ is maximal we are done as in the previous reasoning. We build the set $T_1=\{s: s > t_1\wedge s\in R[E\sim p]\}$ and then S ₁ in the same way as S ₀. Since the theory is acyclic we have that $S_0\subset S_1$. We can repeat this construction n times for each rule in S ₀ until we reach a point where the rules we have for Ep are maximal, and we get that $-\partial_c\sim p$, from which we get again a contradiction.

For M = i we have to consider rules in $R^c[{\fancyscript{C}}(E_ip)]\cup R^i[E_kp]\cup R^c[E_kp]$ and the conditions of applicability of clause (2.2) for + ∂ _i , when we build the sets T _n and S _n , but the reasoning for ∂ _i carries over this case as well.

Theorem 3

Let I be an institutional action theory, and $M\in\{c,i\},\,\, i\in A.$

• 1. $\Updelta^{+}_{M} \subseteq \partial^{+}_M \subseteq \Upsigma^{+}_M$;

• 2. $\Upsigma^{-}_M\subseteq \partial^{-}_M \subseteq \Updelta^{-}_M$;

• 3. LetIbe a consistent institutional action theory such that$I\vdash -\Updelta_ip.$If$I\vdash +\partial_iE_jp$then$I\vdash -\partial_ip$.

• 4. For any$i,\,\, \Updelta^{+}_i\subseteq \Updelta^{+}_{c},$and$\partial^{+}_i\subseteq \partial^{+}_c$.

Proof

For 1. The inclusion $\Updelta^{+}\subseteq \partial^{+}$ is immediate given clause (1) of the the proof condition for + ∂ _M , which allows us to extend a derivation with + ∂ _M p if + Δ _M p is already in the derivation.

For the inclusion $\partial^{+}_M\subseteq \Upsigma^{+}_M$, the proof is by induction on the length of the derivation of + ∂ _M p. Notice that it is not possible to have a defeasible derivation consisting of a single step: a minimal defeasible derivation has at least two lines. We will use this case as inductive base. We have two possibilities. We have (i) $P(1)=+\Updelta_Mp$ for p = α, $\alpha\in F$ or $E_ip\in F$, and then $P(2)=+\partial_Mp$ justified by P(1); or (ii) $P(1)=-\Updelta\sim p$ (there are no strict rules for ∼ p), and $P(2)=+\partial_Mp$, justified by the fact that there is a strict or defeasible rule r in $R^M,\,\, A(r)=\emptyset$, and $R[{\fancyscript{C}}(E_ip)]\cup R[E_kp]=\emptyset$ and either $R^c[E_kp]=\emptyset$ or $\forall s\in R^c[E_kp], A(s)\cap\hbox{Lit}=\emptyset$, for $k\neq M$.

For (i) we have that the justification for P(1) corresponds to clause (1) of the proof condition for + Σ _M , thus we can create a proof for + Σ _M p. For (ii) $r\in R_{sd}[p]$ and the conditions (2) and (3) of the proof condition for Σ _M are vacuously satisfied. We can now assume that the property holds for the derivation of + ∂ _M p of length n. For the inductive step we have to consider whether + ∂ _M p is justified by clause (1) or clause (2) of the proof condition for + ∂ _M . For (1) we have two sub-cases: the conclusion is a fact and we can repeat the argument of the inductive base or either clauses (2) or (3) of + Δ _M apply. This means that by inductive hypothesis there is a strict rule that satisfies either the condition of clauses (2) or (3) of Σ _M . In case + ∂ _M p is justified by clause (2.2) of + ∂ _M , then all we have to notice is that we consider the same sets of rules as in clause (2) and (3) of + Σ _M , plus the inductive hypothesis.

For 2. The property follows immediately from 1 and the principle of strong negation.

For 3. To prove this case we have to show how to build a derivation for −∂ _i p given a derivation of $+\partial_iE_kp$, and give the appropriate conditions. If we can derive $+\partial_iE_kp$ since we have $+\Updelta_iE_kp$, then by clause (2.1) we can derive −∂ _i p. Otherwise we consider the rule r used to derive the conclusion. We have two cases (a) $r\in R^i[E_kp]\cup R^c[EE_iE_kp]$ or (b) $r\in R^c[E_kp]$. The two cases are analogous, the only difference is in the condition of applicability of the rule. We will say that r is applicable if the appropriate conditions in clause (2.2) of + ∂ _i are satisfied. We consider two exhaustive cases: (i) r is maximal, i.e., $\neg \exists s, s > r$, (ii) r is not maximal. For (i) the maximality of r ensures that clauses (2.3.1) and (2.3.2) of −∂ _i are satisfied and then the applicability of r makes clause (2.3) true. Thus in this case we can derive −∂ _i p. For (ii) if r is not maximal we consider the set of rules $S_0=\{s: s > r\}$. Let $R^{*}=R^i[p]\cup R^c[EE_ip]\cup R^c[p]$ If $S_0\cap R^{*}=\emptyset$, then clauses (2.3.1) and (2.3.2) are vacuously satisfied and again we are done. Otherwise, consider a rule s∈S ₀. If s is discarded, it meets either conditions of clause (2.3) of + ∂ _i , then we have that s satisfies also either clause (2.2.1) or (2.2.2), and we can remove s from S ₀. Otherwise if s is applicable, then there is a rule t that satisfies (2.3.3), and in particular t > s. At this stage we consider if t is maximal or not. If t is maximal we have a rule that satisfies clause (2.3) of −∂ _i , and again we are done. If t is not maximal, we consider the set $S_1=\{s: s > t\}$. Since >  is acyclic we have that $S_1\cap R^{*}\subset S_0\cap R^{*}$. We can now repeat the above reasoning for the rules in $S_1\cap R^{*}$, and we can repeat it n times for each applicable rule in the set. In this way we remove rules until we arrive at an applicable rule $t^{\prime}\in R^i[p]\cup R^c[E_ip]\cup R^c[p]$ such that it is either maximal or that all stronger rules than it in R ^* are discarded. In this way for every applicable rule in R ^* we have a rule that satisfies clause (2.3) of −∂ _i , and thus we can conclude −∂ _i p.

For 4. The proof is by induction on the length of the proof. We start with definite conclusions. For the inductive base, i.e., $P(1)=+\Updelta_ip$, either $EE_ip\in F$ or there is a rule $r\in R^i_s[p]$ such that $A(r)=\emptyset$. If $EE_ip\in F$, then $E^{\prime}p\in F\,\, (E^{\prime}=EE_i)$ and $R_s^i[p]\subseteq R_s[Ep]$, thus in both cases we can build a derivation for + Δ _c p.

For the inductive step, i.e., $P(n+1)=+\Updelta_ip$, we assume as usual that the property holds up to derivation of length n. Since $R^i_{s}[p]\subseteq R_s[Ep]$, and the conditions of applicability of strict rules in clause (3) of + Δ _i are the same as those of clause (2) of + Δ _c we have the same situation as in the inductive base. If $P(n+1)=+\Updelta_ip$ is justified by clause (4) of + Δ _i (conversion), then there is a rule $r\in R_s^i[p]$ such that $A(r)\cap\hbox{Lit}\neq\emptyset$ and $\forall\alpha\in A(r)$, $+\Updelta_c\alpha\in P(1\ldots n)$, and $\forall a\in A(r), +\Updelta_ia\in P(1\ldots n)$ are under the inductive hypothesis, thus we have that we can build a proof P′ where $\forall a\in A(r), +\Updelta_ca\in P^{\prime}(1\ldots m)$, and thus we can conclude + Δ _c p, using clause (2) of + Δ _c . If $P(n+1)=+\Updelta_ip$ is justified according to clause (2) of + Δ _i , then we have that either $EE_ip\in F$ or there is a rule $r\in R_s[E_ip]$ such that $\forall l\in A(l), +\Updelta l\in P(1\ldots n)$. In both cases we can repeat the reasoning for the inductive base to prove that there is a proof for + Δ _c p.

For ∂⁺ the proof is essentially the same as that for Δ⁺. The only differences are that we have to consider the two clauses (2.3). It is immediate to verify that (2.3.1)–(2.3.3) of + ∂ _c and (2.3) of + ∂ _i are identical; in addition we have that clause (2.3.1) of + ∂ _i (reinstatement by conversion) can be transformed into clause (2.3.4) of + ∂ _c by inductive hypothesis as we did in the case for Δ⁺. Finally, for clause (2.1) all we have to do is to notice that ${\fancyscript{C}}(p)=\{Ep\}$ and ${\fancyscript{C}}(E_ip)=\{E\sim p,E\neg E_{i}p\}$, and thus ${\fancyscript{C}}(p)\subseteq{\fancyscript{C}}(E_ip)$.

Theorem 4

LetIbe an institutional action theory. The extension ofIcan be computer in time linear to the size of the theory, i.e., $O(|R|*|U^I|*|A|).$

Proof

The proof is based on a modification of the algorithm given by Maher [Maher 2001] to show that propositional DL has linear complexity.

The main idea of the proof is to build appropriate data structure to implement a series of transformations reducing the complexity of the rules, and where each literal and modal literal is examined only once. The focal point of the transformations is based on the following properties:

• Let $D\vdash +\partial p$ then $D\cup\{rp_1, \ldots, p_n:p\Rightarrow q\} \equiv D\cup \{r: p_1, \ldots, p_n \Rightarrow q\}.$

• Let $D\vdash -\partial p$ then $D\cup\{r:p_1, \ldots,p_n p\Rightarrow q\}\equiv D$.

The properties allow us (1) to remove already proved literals from the body of rules and (2) to remove rules which have been discarded.

The algorithm has three phases. (1) A pre-processing phase where we use the transformations given in [Antoniou et al. 2001] to transform a theory into an equivalent theory without superiority relation and defeaters; the transformation is linear. (2) A rule loader that parses the theory obtained in the first phase and generates the data structure that encodes the theory. (3) The inference engine applies transformations to the data structure, where at every step it reduces the complexity of the data structure.

We set $V^I=\emptyset$, then the rule loader first scans the set of rules and extracts the set of conclusions Cn(I), and the set of atomic literals in it Lit(I). For each element $l\in Cn(I)\cup Lit(I)$ we add $l,E_il,\neg E_i$ for every i∈A to V ^I if the expressions are well formed according to the formation conditions given in Sect. 3.¹⁰ At this stage the rule loader builds a data structure where every element of V ^I is associated with four hash tables: + h the rules that can prove the elements, + h the rules that can disprove the element, + b the rules that need the element to be applicable, and −b the rules that can be discarded by the element. Each hash table depends on the type of literal it is associated to according to the following conditions.

• For α, we have:

  •  + h is the list of (pointers to) rules in R ^c[α];

  • −h is the list of rules in $R^c[\sim \alpha]$;

  •  + b is the list of rules in $\{r\in R: \alpha\in A(r)\}$;

  • −b is the list of rules in $\{r\in R: \sim \alpha\in A(r)\}$.

• For p (a plain literal), we have:

  •  + h is the list of (pointers to) rules in R[Ep];

  • −h is the list of rules in $R[E\sim p]$;

  •  + b is the list of rules in $\{r\in R: p\in A(r)\}$;

  • −b is the list of rules in $\{r\in R: E\sim p\in A(r)\}$.

• For E _i p (a modalised literal), we have:

  • $+h$ is the list of (pointers to) rules in $R^i[p]\cup R^c[EE_ip]\cup R^c[p]$;

  • −h is the list of rules in $R[E\sim p]\cup R[E\sim E_ip] \cup R^c[E_kp]\cup R^i[E_kp]$ for any k ≠ i;

  •  + b is the list of rules in $\{r\in R: E_ip\in A(r)\}\cup \{r\in R^c: p\in A(r)\}$;

  • −b is the list of rules in $\{r\in R: E\sim p\in A(r)\}\cup \{r\in R:\neg E_ip\in A(r)\}\cup \{r\in R: E_iE_kp\in A(r)\}$, for any k ≠ i.

Each results-in rule r is represented by the rule loader as a pair (h,b) where h is pointer to the head of the rule and b has pointers to the literals in A(r). On the other hand a counts-as rules is implemented as an $n+3\hbox{-tuple}$ (n = |A|, the number of agents in I) $(h,a,b,a_1,\ldots,a_n)$. h is as per results-in rules, a is the set of pointers for action literals in $A(r),\,\, b$ is the set of pointers for non action literals in A(r), and each a _i is either a set of pointers to non action literals if either $A(r)\cap\hbox{Lit}\neq\emptyset$ or there is no literal of the form $E_ip\in A(r)$; otherwise b is the special symbol nil.

The Inference Engine is based on an extension of the Delores algorithm/implementation proposed in [Maher 2001] as a computational model of basic DL. In turn

• 1. It asserts each literal l∈F as a conclusion and removes l from all rules in + b(l), and remove all rules (pointers to rules) in the hash tables for −h. For counts-as rules, if l = α we remove l from the a part of the rules; if l = p, we remove it from the p part of the b part, and if l = E _i m, then (1) we remove both m and E _i m from the rules in + b(E _i p), and (2) for counts-as rules we remove E _i m and m from the b part and p from the a _i part as appropriate.

• 2. Then it scans the set of rules for rules where b is empty. For counts-as rules it looks for rules where both a and either b or a _i are empty for some i∈A. For each of such rules it takes a(r) and E _i a(r) (only E _i a(r) for counts-as rule where a _i is empty), and it checks that −h(a(r)), −h(E _i a(r)) are empty. If so, it adds $a(r),\,\, E_ia(r)$ to the set of conclusions as appropriate.

• 3. It repeats the first step, using the conclusions obtained from the previous step.

• 4. The algorithm terminates when one of the two steps fails. On termination the algorithm outputs the set of conclusions.¹¹

Notice that all the operations described in the above steps correspond to hash functions, thus they have constant complexity O(1). It is immediate to see that the algorithm runs in linear time. Each (modal) atom/literal in a theory is processed exactly once and every time we have to scan the set of rules, thus the complexity of the above algorithm is $O(|V^I|*|R|*|A|)$.