1 Introduction

Drag in turbulent flows is much higher than that in laminar flows, and it causes an additional loss of energy in many high-speed transports such as airplanes and bullet trains. For instance, Wood [1] reported that 16% of the total energy consumed in the United States is dedicated to the aerodynamic drag deriving from transportation systems, and according to his estimation, at least 20 billion US dollars could be saved if the existing drag reduction technologies were applied to all the vehicles within the United States.

The drag in subsonic single-phase flows can be decomposed into two contributions: the pressure drag and the viscous drag. Although there are many examples in which the pressure drag is reduced, e.g. by shape optimization, there are few control methods for viscous drag reduction that can actually be used in industrial applications, excluding the polymer additives already in use for petroleum pipelines. Considering the fact that the viscous drag accounts for about half of total drag in the cruise flight of modern subsonic aircrafts [2], further development of control methods for viscous drag reduction is desired from both economical and environmental viewpoints.

In the last decades, considerable efforts have been made on the friction drag reduction in turbulent boundary layers. According to Moin and Bewley [3] and Gad-el-Hak [4], the drag reduction methods can be classified into two groups: one is the passive control such as riblets [5, 6] and superhydrophobic surfaces [7], and the other is the active control, which requires external energy input. Extensive studies have been made on the active control methods [8, 9]. Examples of the well-studied active control methods are the opposition control [10], spanwise forcing [11,12,13,14,15] and the traveling-wave of wall-normal momentum [16,17,18]. Although these methods have been reported to attain significant drag reduction effects and some of these even lead to relaminarization of turbulent flows [14, 17, 18], which has been proved to be the best scenario in terms of the net energy saving [19, 20], it remains questionable if the actuators used for these control methods can actually be fabricated and if a net power saving can be achieved using such real actuators.

Among different active control methods for friction drag reduction, uniform blowing (UB) is considered as one of the most practically realizable options because all one has to do is to impose a uniform wall-normal velocity on the wall, without the need for small-scale complicated actuators. In the recent review article by Kornilov [2], it is concluded that “utilization of the blowing through the high-technological surface, featuring low roughness and maximal requirements to orifice quality and geometry, is a reasonable way, simple, available, and reliable method of control of the near-wall turbulent flow in the aerodynamic experiment and during the numerical simulation.”

This blowing (or suction) idea originates from the primitive experiment by Prandtl [21], which initially aimed at laminar-to-turbulence transition delay. Subsequently, experiments of UB (mostly by injection of air through a permeable porous wall) have been conducted for a turbulent boundary layer [22,23,24], followed by several numerical studies [25, 26]. As a result, all of these studies confirmed that UB has a possibility to attain significant drag reduction by mitigating the viscous shear stress. Sumitani and Kasagi [26], who conducted DNS of a turbulent channel flow with UB on one wall and uniform suction (US) on the other wall, clearly showed that UB shifts the velocity profile away from the wall, while US does it in the opposite way. In addition, it turned out that the Reynolds shear stress is amplified by UB and suppressed by US, which might look contradicting with the drag reduction by UB and drag increase by US.

For more quantitative analysis, Fukagata et al. [27] derived a mathematical relationship between skin-friction drag and turbulence statistics by integrating the streamwise momentum equation. The analysis using this relationship (so-called the FIK identity) quantitatively showed that the drag reduction by UB is due to the drag-reducing contribution of mean wall-normal convection that surpasses the drag-increasing contribution of enhanced turbulence. A similar quantitative analysis based on the FIK identity was reported in the DNS study of Kametani and Fukagata [28] for a spatially developing turbulent boundary layer with UB at a relatively low Reynolds number. More recently, Kametani et al. [29] have demonstrated through large-eddy simulation (LES) that UB works equally well at moderately high Reynolds numbers. They also showed that the overall drag reduction rate is unchanged even when discrete slots are used to realize the blowing [30]. Besides, toward its use for airfoil drag reduction, some attempts to combine US to delay transition and UB to reduce turbulent drag have also been reported [31, 32].

As introduced above, turbulent drag reduction by UB has been extensively studied toward its practical implementation. However, the drag reduction effect of UB in the presence of surface roughness is still unclear, despite its importance in practical situations. Among the studies that dealt with the combined effect of roughness and UB, some [33, 34] observed drag reduction similarly to the smooth-wall cases, whereas the recent experimental study by Miller et al. [35] has shown an opposite result: UB suppresses turbulent fluctuations and increases drag in rough-wall cases. In experiments, an accurate wall-friction measurement is one of the most difficult tasks. According to Schultz and Flack [36], for instance, ± 4% of error in the friction velocity appears due to the measurement uncertainty, which may be sometimes comparable to the amount of drag modification of interest. A more serious problem may be that the friction velocity is often estimated using the Clauser plot [37] or its modified version for rough walls [38] on the assumption that the blowing does not modify the slope of the log-law (i.e., von Kármán constant). As is implied by Stevenson’s formula [39] (discussed in Section. 4.4) and also observed in the DNS result of Sumitani and Kasagi [26], the slope of log-law is actually changed by UB even in smooth-wall cases. Therefore, the possibility exists for a similar modification of log-law to happen in rough-wall cases, too, and the method for determination of friction velocity can also be considered as a possible cause for the discrepancy above.

In the present work, we perform DNS to study the drag reduction effect of UB in turbulent flow in a channel having a rough wall. The primary objective is to clarify whether UB increases or decreases the drag on a rough wall by assessing the statistics directly computed from the velocity field. The second objective is to investigate the mechanism of drag modification by decomposing the drag into the pressure and friction contributions and by examining the turbulence statistics in more detail. The paper is organized as follows. The numerical procedure is outlined in Section 2 together with the definition of the two-dimensional roughness used in the present study. In Section 3, the statistics of the base flow over a rough wall (without UB) is presented. The effect of UB on the flow is presented and discussed in Section 4. Finally, conclusions are drawn in Section 5.

2 Numerical Procedures

2.1 Direct numerical simulation

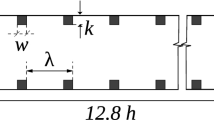
We consider an isothermal incompressible flow in a channel. As shown in Fig. 1, the bottom wall of the channel is assumed to have two-dimensional irregular roughness, while the top wall is assumed to be smooth.

Fig. 1
figure 1

Schematics of the present configuration: (a) smooth-wall case; (b) rough-wall case (only the lower surface is roughened)

Full size image

As can be found in the review articles on roughness studies [40, 41], most of such studies assume regularly distributed roughness arrays (e.g., transverse bars, packed spheres or sinusoidal wave). When it comes to the real roughness, in contrast, the heights and intervals of the bumps are randomly varying as presented in Cardillo et al. [42], who performed numerical investigation of a turbulent channel flow with measured roughness. Although three-dimensionality of roughness should be considered in practice, we chose here a two-dimensional irregular roughness as a first test case to understand the fundamental effect of UB on the irregular roughness.

We follow the method of Napoli et al. [43] to generate the two-dimensional roughness used in the present DNS (see, Fig. 2). First, we generate the normalized local wall-height at a given streamwise location x using a truncated trigonometric series, i.e.,

$$\begin{array}{@{}rcl@{}} \eta_{d}(x)={\sum\limits_{i=1}^{n}} A_{i} \sin\left( \frac{2i\pi x}{L_{x}/2}\right), \end{array} $$
(1)

where A i is the mode coefficient and L x is the streamwise length of the periodic computational domain. Subsequently, the averaged absolute deviation \(\overline {|\eta _{d}|}\) is calculated as

$$\begin{array}{@{}rcl@{}} \overline{|\eta_{d}|}=\frac{1}{L_{x}}{\int}_{L_{x}}|\eta_{d}(x)|dx. \end{array} $$
(2)

Finally, η d (x) is rescaled so that the averaged roughness height becomes the specified value. We use four modes (i = 1, 2, 4, and 8) to generate the present roughness shown in Fig. 2. The coefficient for the first mode is fixed at A 1 = 1, whereas those for i > 1 are determined by performing a Fourier transform to the roughness profile presented in Milici et al. [44] who considered the same profile as Napoli et al. [43].

Fig. 2
figure 2

Two-dimensional rough surface considered in the present study

Full size image

To deal with the flow over the rough surface defined above, we employ the boundary-fitted coordinates ξ i (i = 1,2,3) similar to Kang and Choi [45], i.e.,

$$\begin{array}{@{}rcl@{}} x=\xi_{1}, \; y=\xi_{2}(1+\eta(x))+\eta_{d}(x), \; z=\xi_{3}, \end{array} $$
(3)

where x, y and z denote the streamwise, wall-normal and spanwise coordinates in the physical space, and the local half-displacement η(x) is defined as

$$\begin{array}{@{}rcl@{}} \eta(x)=\frac{\eta_{u}(x)-\eta_{d}(x)}{2}, \end{array} $$
(4)

where η u (x) denotes the displacement of the upper surface, which is assumed flat (i.e., η u (x) = 0) except for the case used for validation (Section 2.4).

Hereafter, we interchangeably use (x,y,z;u,v,w) and (x 1,x 2,x 3;u 1,u 2,u 3) for notational convenience, and the quantities without superscript are those nondimensionalized by twice the bulk-mean velocity 2Ub∗, the channel half-width δ ∗, and the fluid density ρ ∗, where superscript ∗ denotes dimensional quantities. The bulk Reynolds number is defined as Re b = 2Ub∗δ ∗/ν ∗, where ν ∗ is the kinematic viscosity. It is also worth noting that the wall-normal coordinates in the present study are defined in the range of 0 ≤ ξ 2 ≤ 2 in contrast to Kang and Choi [45] who used − 1 ≤ ξ 2 ≤ 1.

With this nondimensionalization, the governing equations, i.e., the continuity and the Navier-Stokes equations, on the aforementioned boundary-fitted coordinates read

$$ \frac{\partial u_{i}}{\partial\xi_{i}}=-S, $$
(5)
$$ \frac{\partial u_{i}}{\partial t}=-\frac{\partial (u_{i}u_{j})}{\partial \xi_{j}}-\frac{\partial p}{\partial \xi_{i}}+\frac{1}{Re_{b}}\frac{\partial^{2}u_{i}}{\partial \xi_{j} \partial \xi_{j}}-\frac{dP}{d\xi_{1}}\delta_{i1}+S_{i}, $$
(6)

where u i and p denote the velocity components and the pressure, respectively, and (−dP/dξ 1)(t) is the instantaneous mean pressure gradient required to keep the flow rate constant [45]. The dummy indices are subjected to the summation convention.

The additional terms S and S i in Eqs. 5 and 6 appearing due to the coordinate transformation are expressed as

$$ S=\phi_{j}\frac{\partial u_{j}}{\partial \xi_{2}} $$
(7)

and

$$ S_{i}=-\phi_{j}\frac{\partial (u_{i}u_{j})}{\partial \xi_{2}}-\phi_{i} \frac{\partial p}{\partial \xi_{2}}+\frac{1}{Re_{b}}\left\{\frac{1}{2}\frac{\partial(\phi_{j}\phi_{j})}{\partial\xi_{2}}\frac{\partial u_{i}}{\partial \xi_{2}}+\phi_{j}\phi_{j}\frac{\partial^{2}u_{i}}{\partial {\xi_{2}^{2}}}+2\phi_{j}\frac{\partial^{2} u_{i}}{\partial\xi_{j}\partial\xi_{2}}\right\}, $$
(8)

where

$$ \phi_{j}=\varphi_{j}-\delta_{j2}, $$
(9)

with

$$ \varphi_{j}= \left\{ \begin{array}{ll} -\displaystyle\frac{1}{1+\eta}\left( {\xi_{2}}\frac{\partial \eta}{\partial \xi_{j}}+\frac{\partial \eta_{d}}{\partial \xi_{j}}\right), & \text{for \(j=1, 3\)},\\ \displaystyle\frac{1}{1+\eta}, & \text{for \(j=2\)}. \end{array} \right. $$
(10)

The periodic boundary condition is applied in the streamwise (x) and spanwise (z) directions. On the bottom wall (y = η d ), the boundary condition is set to allow uniform blowing (UB), i.e.,

$$ u(x,\eta_{d},z,t)=0,\; v(x,\eta_{d},z,t)=V_{w},\; w(x,\eta_{d},z,t)=0, $$
(11)

where V w is the constant wall-normal velocity of UB. On the upper wall (y = 2), a uniform suction is applied so that the mass in the channel is conserved. Three different UB amplitudes, i.e., V w /U b = 0.1%, 0.5%, and 1.0%, are considered for the controlled cases.

The present DNS code is similar to that used by Nakanishi et al. [17], who studied the streamwise traveling wave-like wall deformation. The governing equations are spatially discretized on a staggered grid system using the energy-conservative second-order finite difference scheme [46] and temporally integrated using the third-order Runge-Kutta/Crank-Nicolson scheme (see, e.g. [47]). The velocity-pressure coupling is done similarly to the SMAC method [48]. The pressure Poisson equation is solved using the fast Fourier transform in the streamwise and spanwise directions and the tridiagonal matrix solver in the wall-normal direction.

Except for the case used for validation (Section 2.4), all DNS was performed under the constant flow rate (CFR) condition [49] at the bulk Reynolds numbers of Re b = 5600 and 14000, which correspond to the friction Reynolds numbers of Re τ = uτ∗δ ∗/ν ∗≈ 180 and 400 in the smooth-wall case, respectively. These Reynolds numbers are similar to those used in the DNS of Milici et al. [44] and the LES of Napoli et al. [43]. The computational domain and the grid resolution are also set similar to the previous studies [43, 44] as summarized in Table 1. The average roughness height is set to be \(\overline {|\eta _{d}|}=0.05\delta \) and 0.024δ in the cases of Re b = 5600 and Re b = 14000, respectively, which correspond to about 10 wall units (based on the friction velocity of smooth channel) at both Reynolds numbers. The resultant local roughness height is approximately ranged within ± 0.11δ and ± 0.05δ in Re b = 5600 and Re b = 14000 cases, respectively, and its mean value is zero.

Table 1 Numerical conditions. The corresponding friction Reynolds number Re τ and wall units denoted by the superscript “ + ” are based on the friction velocity in the smooth-channel case
Full size table

2.2 Computation of drag coefficients and friction velocity

The total drag coefficient on the lower (rough) wall C D is computed as

$$ C_{D} = 2C_{D\text{ave}}-C_{Df,u} $$
(12)

where C D ave is the average of total drag on both walls and C Df,u is the friction drag coefficient on the upper smooth wall, both of which can be computed easily. Hereafter, drag coefficients without subscript “u” or “ ave” refer to those on the lower wall. The average of total drag coefficient C D ave can be computed under the present nondimensionalization as

$$ C_{D\text{ave}}=\frac{\left( -\frac{dP^{\ast}}{dx^{\ast}}\right)(2\delta^{\ast})}{\rho^{\ast} U_{b}^{\ast 2}}=8\left( -\frac{dP}{d\xi_{1}}\right). $$
(13)

In the smooth-wall case, the drag coefficient on the lower wall C D is identical to the skin friction drag coefficient C Df , i.e.,

$$\begin{array}{@{}rcl@{}} C_{Df} =\frac{1}{(1/2)\rho^{\ast} U_{b}^{\ast 2}}{\int}_{S} \mathbf{e}_{1}\cdot\mathbf{\tau^{\ast}}\cdot\mathbf{n}dS^{\ast} =8u_{\tau}^{2}=\frac{8}{Re_{b}}\left.\frac{dU}{dy}\right|_{\text{wall}}, \end{array} $$
(14)

where τ ∗ denotes the viscous stress tensor, e 1 is the unit streamwise vector, and S and n denote the surface area and its unit normal vector, respectively. (the factor “8” appears because the velocity is nondimensionalized by 2Ub∗).

In the rough-wall case, C D is a summation of C Df and the pressure drag coefficient C Dp , i.e.,

$$ C_{D}=C_{Dp}+C_{Df}, $$
(15)

where C Dp and C Df can be computed as

$$\begin{array}{@{}rcl@{}} C_{Dp} =\frac{1}{(1/2)\rho^{\ast} U_{b}^{\ast 2}}{\int}_{S} \mathbf{e}_{1}\cdot(-p_{a}^{\ast}) \mathbf{n}dS^{\ast} =\frac{8}{L_{1}L_{3}}{\int}_{0}^{L_{1}}{\int}_{0}^{L_{3}}\left.p_{a}\right|_{\xi_{2}=0} \frac{\partial \eta_{d}}{\partial \xi_{1}} dx_{1}dx_{3} \end{array} $$
(16)

and

$$\begin{array}{@{}rcl@{}} C_{Df} &=&\frac{1}{(1/2)\rho^{\ast} U_{b}^{\ast 2}}{\int}_{S} \mathbf{e}_{1}\cdot\mathbf{\tau^{\ast}}\cdot\mathbf{n}dS^{\ast} \\ &=&\frac{8}{Re_{b}}{\int}_{0}^{L_{1}}{\int}_{0}^{L_{3}} \frac{1}{1+\eta}\left[\left\{1+2\left( \frac{\partial \eta_{d}}{\partial \xi_{1}}\right)^{2}\right\}\frac{\partial u}{\partial \xi_{2}}-\frac{\partial \eta_{d}}{\partial \xi_{1}}\frac{\partial v}{\partial \xi_{2}}\right]_{\xi_{2}=0}dx_{1}dx_{3} . \end{array} $$
(17)

Note that the pressure p a in Eq. 16 is the actual pressure, which includes the component of constant pressure gradient subtracted in Eq. 6, i.e., p a = p + (dP/dξ 1)ξ 1. We have also computed C Df from the force balance, i.e.,

$$\begin{array}{@{}rcl@{}} C_{Df} &=2C_{D\text{ave}}-(C_{Dp}+C_{Df,u}) \end{array} $$
(18)

The time-averaged value of C Df directly computed from Eq. 17 was found to have 2% difference at maximum from that computed using Eq. 18 in Re = 5600 case, while the difference was negligibly small for Re = 14000 case (i.e., the case with lower roughness height). This difference is likely due to the errors in interpolation used in the computation of Eq. 17. Therefore, in the followings, we adopt Eq. 18 to compute C Df because the total drag is of primary importance here.

Similarly to Eq. 14, the friction velocity (nondimensionalized by 2Ub∗) on the rough wall can directly be computed as \(u_{\tau }=\sqrt {C_{D}/8}\). It should be emphasized that the friction velocity in the rough wall case considers both friction and pressure contributions. This is consistent with the conventional definition for rough walls, where the friction velocity is defined by the total wall stress [43].

2.3 Verification

We have carried out a grid resolution study by performing DNS of a rough channel flow without UB.

Figure 3 shows the time traces of C D computed using different grid resolutions. The reference case, i.e., \(({\Delta } \xi _{1}^{+}, {\Delta } \xi ^{+}_{2\;\min }, {\Delta } \xi ^{+}_{3}) = (4.4, 0.93, 5.9)\), gives the time-averaged value of C D = 0.0162. Halving the spanwise grid spacing to Δξ3+ = 3.0 changes C D by about 1.3% (C D = 0.0160), and halving Δξ1+ and \({\Delta } \xi _{2\;\min }^{+}\) at the same time changes C D by about 1.9% (C D = 0.0159).

Fig. 3
figure 3

Time traces of drag coefficient C D in the base flow i.e., constant flow rate (CFR) condition with one-sided roughness and without uniform blowing) at Re b = 5600, computed under different grid resolutions

Full size image

Figure 4 shows the mean streamwise velocity U + and the root-mean-square (RMS) velocity fluctuations, u rms+, v rms+, and w rms+, in wall units on the rough side. Again, the turbulent statistics in the reference case are in good agreement with those of finer grid resolutions.

Fig. 4
figure 4

Dependence on the grid resolution in the base flow (i.e., constant flow rate (CFR) condition with one-sided roughness and without uniform blowing) at Re b = 5600: (a) mean streamwise velocity U +; (b) RMS velocity fluctuations (solid line, u rms+; dotted line, v rms+; dashed line, w rms+). Black, (\({\Delta }\xi _{1}^{+},{\Delta }\xi _{2,\min }^{+},{\Delta }\xi _{3}^{+})=(4.4,0.93,5.9)\); green, (\({\Delta }\xi _{1}^{+},{\Delta }\xi _{2,\min }^{+},{\Delta }\xi _{3}^{+})=(2.2,0.93,5.9)\); blue, (\({\Delta }\xi _{1}^{+},{\Delta }\xi _{2,\min }^{+},{\Delta }\xi _{3}^{+})=(4.4,0.46,5.9)\); red, (\({\Delta }\xi _{1}^{+},{\Delta }\xi _{2,\min }^{+},{\Delta }\xi _{3}^{+})=(2.2,0.46,5.9)\). The velocities are in wall units on the rough side

Full size image

As for the temporal discretization, Δt + ≃ 0.03 is used so that the Courant number is maintained around 0.2. The time integration is done for 80000 time steps, which corresponds to the integration period about 2400 wall unit time.

2.4 Validation

Figure 5 shows the mean streamwise velocity and RMS velocity fluctuations computed for the smooth-wall and rough-wall cases. Only in this case, the constant pressure gradient (CPG) condition [49] at Re τ = 180 was used, and both walls are roughened in order to make a comparison with Milici et al. [44] under the same condition. The mean height of the roughness is used as the origin of y. Due to the ambiguity of physical origin for a rough surface, the virtual offset has often been empirically introduced in many studies in such a way that the mean velocity profile matches the log-law profile; however, as reported by De Marchis et al. [50], taking the origin at the mean height of roughness will result in a very slight difference from the case considering a virtual offset. As can be noticed in Fig. 5a, a good agreement in mean streamwise velocity can be confirmed for the rough-wall case between the present DNS result and Milici et al. [44] in addition to the excellent agreement between the present DNS result with the spectral DNS result of Moser et al. [51] for the smooth-wall case. As shown in Fig. 5b, the RMS velocity fluctuations for the smooth channel are also in good agreement with DNS data of Moser et al. [51]. In the rough-wall case, too, a reasonable agreement is found between the present DNS and Milici et al. [44]. A small difference observed near the wall could be due to some difference in the detailed numerics between the finite volume code used by Milici et al. [44] and the present DNS code based on the energy-conservative finite difference method.

Fig. 5
figure 5

Turbulence statistics computed under the constant pressure gradient (CPG) condition at Re τ = 180: (a) mean streamwise velocity; (b) RMS velocity fluctuations. Results for the smooth-wall case are compared with DNS data of Moser et al. [51]. Results for the case with rough walls on both sides are compared with DNS data of Milici et al. [44]

Full size image

The roughness function ΔU + (i.e., the velocity defect in the log-law region as compared to the smooth-wall case) is evaluated as ΔU + = 5.4. Strictly speaking, the present Reynolds number is too low for the log-law region to exist. For convenience, however, we evaluated ΔU + at y + = 60.

3 Base Flow without Uniform Blowing

The DNS results for the base flow without uniform blowing (UB) are presented in this section before discussing the effect of UB. It is worth recalling that all the results presented hereafter have been obtained under the constant flow rate (CFR) condition with a one-sided roughness, as described in Section 2.

The mean streamwise velocity U + and the RMS velocity fluctuations u rms+, v rms+, and w rms+ at Re b = 5600 are presented in Fig. 6. The vertical line drawn at y/δ ≃ 0.1 in Fig. 6b indicates the maximum height of the roughness, and the minimum range of y represents the location of the deepest valley. Below the dotted line, the average is taken only in the fluid region. This averaging procedure similar to Milici et al. [44] is different from some previous studies where the average was taken including the velocities inside the wall that are assumed to be zero (e.g., [40, 53, 54]) or the average defined in a different way (e.g., [55]). However, the present definition of average should be reasonable because the fluid velocity is the quantity of interest here.

Fig. 6
figure 6

Turbulence statistics of the base flow (i.e., constant flow rate (CFR) condition with one-sided roughness and without uniform blowing) at Re b = 5600: (a) mean streamwise velocity U + (“smooth” and “validation case” refer to those in Fig. 5); (b) RMS velocity fluctuations (black, streamwise component u rms+; blue, wall-normal component v rms+; green, spanwise component w rms+: solid line, smooth-wall case; dotted line, rough-wall case. For rough-wall case, the superscript “ + ” denotes the wall units on the rough side.

Full size image

Figure 6a shows the mean streamwise velocity profiles above the lower rough wall and the upper smooth wall. A larger downward shift is observed as compared to the two-sided rough case used for validation. The roughness function ΔU + is evaluated as ΔU + = 6.4.

Figure 6b shows the RMS velocity fluctuations in wall units on the rough side. The profiles are distorted much toward the smooth-wall side with their minimum RMS values located at y/δ ≃ 1.3. On the rough side, u rms+ is decreased and v rms+ and w rms+ are increased. These changes indicate that the turbulence has become more isotropic due to a break-up of streamwise vortices as reported by Krogstad et al. [57].

As will be shown later in Sec. 4, the base flow at Re b = 14000 is qualitatively similar to the Re b = 5600 case presented above, except that the roughness function ΔU + is smaller due to the lower roughness height, i.e., ΔU + = 3.5.

The drag coefficient on the lower wall C D in the rough-wall case as well as the smooth-wall case is presented in Fig. 7 together with its decomposition into the pressure drag coefficient C Dp and the friction drag coefficient C Df . As can be found in Fig. 7, on the rough wall, C Dp is about a half of the total C D at Re b = 5600 and about one-third at Re b = 14000. This reconfirms that the present flow is in the transitionally-rough regime [56, 58].

Fig. 7
figure 7

Decomposition of drag coefficient on the lower wall C D into the friction drag coefficient C Df and the pressure drag coefficient C Dp in the base flow (i.e., constant flow rate with roughness only on the bottom wall and without uniform blowing): (a) Re b = 5600 case; (b) Re b = 14000 case

Full size image

4 Effects of Uniform Blowing

4.1 Drag reduction effect

The drag coefficients on the lower wall (i.e., blowing side) C D at different blowing velocities V w /U b are shown in Table 2 and with their decomposition into C Dp and C Df ; these are also graphically presented in Fig. 8. Table 2 also shows the resultant friction Reynolds number Re τ = uτ∗δ ∗/ν ∗ and the uniform blowing velocity Vw+ based on the friction velocity on the lower (rough) wall uτ∗. Note that the friction Reynolds number Re τ is defined here by the original channel half-width δ ∗ to simply see the change in the friction velocity. The drag reduction rate R presented in Table 2 is defined as

$$\begin{array}{@{}rcl@{}} R=\frac{C_{D,\text{nc}}-C_{D, \text{ctr}}}{C_{D, \text{nc}}}, \end{array} $$
(19)

where subscripts “nc” and “ctr” denote the uncontrolled and controlled cases, respectively. The reduction rates for the friction and pressure drag components, R f and R p , are defined in a similar manner. From Table 2, the drag reduction rate R in the rough-wall case is found to be lower than that in the smooth-wall case for all UB amplitudes. While the reduction rate for friction drag R f , which is common in both cases, is nearly unchanged from the smooth-wall case, the reduction rate for pressure drag R p is found to be lower than that of friction comparing under the same V w /U b .

Fig. 8
figure 8

Decomposition of drag coefficient on the lower wall C D : (a, b) smooth-wall case; (c, d) rough-wall case. a, c Re b = 5600; (b, d) Re b = 14000

Full size image
Table 2 Drag coefficient on the lower wall C D and drag reduction rate R under different blowing velocity V w /U b
Full size table

Figure 9 presents a similar result, but here V w is normalized by the friction velocity on the rough wall in each case. It is observed from Fig. 9a that the drag reduction rate R for the rough-wall case is similar to, but slightly less than that in the smooth-wall case when it is scaled as a function of Vw+. While the reduction rate for the friction drag R f is similar to that of smooth-wall case, that for the pressure drag R p is lower. As can be found from the drag change ΔC D = C D,nc − C D,ctr shown in Fig. 9b, the absolute amount of drag reduction is significantly larger in the rough-wall case at Re b = 5600 because of the larger drag reduction margin due to the presence of pressure drag. The amount of pressure drag reduction reduces in the Re b = 14000 case due to the smaller pressure contribution (i.e., the smaller roughness height). This result suggests that the drag reduction effect of UB on the present two-dimensional rough wall is basically similar to that for a smooth wall when the UB amplitude is normalized by the resultant friction velocity and when the drag reduction rate is compared. Moreover, the drag reduction effect can be considered even larger for the rough-wall case in terms of the absolute amount of drag reduction.

Fig. 9
figure 9

Drag reduction effect on the lower wall as functions of Vw+: (a) drag reduction rate R; (b) drag change ΔC D . Open symbols, Re b = 5600; filled symbols, Re b = 14000

Full size image

4.2 Drag reduction mechanism

The drag reduction mechanisms for the friction drag and the pressure drag should be different from each other.

Figure 10 shows the mean streamwise velocity profiles normalized by the bulk-mean velocity U b . The velocity profile is observed to shift farther away from the wall as the blowing amplitude is increased in both cases. This modification results in the reduction of viscous shear stress as in the flat-plate turbulent boundary layer [28]. Therefore, the mechanism of friction drag reduction over the rough wall is basically similar to that of the smooth-wall case.

Fig. 10
figure 10

Mean streamwise velocity profiles under UB/US, normalized by U b : (a, b) smooth-wall case; (c, d) rough-wall case. a, c Re b = 5600; (b, d) Re b = 14000. Black, V w = 0 (uncontrolled case); green, V w /U b = 0.1%; red, V w /U b = 0.5%; blue, V w /U b = 1.0%

Full size image

Figure 11 shows the streamwise variation of the local friction drag on the lower wall C f (x) = 2τw∗(x)/(ρ ∗ Ub∗2) in V w /U b = 1.0% case. The figure indicates a high dependency on the roughness location. First, C f in the uncontrolled case is found to be nearly in-phase with the slope of roughness because of the local acceleration. Negative values following a plateau observed around valleys indicate that the flow is locally separated there. With UB, the amount of decrease in C f is found to be roughly proportional to C f in the uncontrolled case. Namely, the local friction drag reduction rate appears roughly constant.

Fig. 11
figure 11

Streamwise variation of C f at Re b = 5600: black solid line, uncontrolled rough case; red solid line, rough case with V w /U b = 1.0%. Black dotted line indicates the profile of rough wall

Full size image

The unique feature of the flow over roughness is the presence of pressure drag. Figure 12 shows the distribution of pressure averaged in time and in the spanwise direction. Alternate positive and negative high pressure regions along the bumps indicate the pressure drag deriving from roughness. As compared to the uncontrolled case (Fig. 12a), variation in pressure is reduced by UB (Fig. 12b). Strong upward motions in the regions upstream of crests observed in the uncontrolled case (Fig. 13a) are also weakened by UB (Fig. 13b); namely, the reduction of roughness-induced wall-normal velocity exceeds the increment by UB. These modifications are due to the reduced streamwise velocity near the wall. This smoothing effect by UB is more clearly illustrated by the contours of the mean stream function in the region near the wall ψ such that u = ∂ψ/∂y and v = −∂ψ/∂x, as depicted in Fig. 14. Due to UB, a region of low velocity is expanded to form a slightly smoother “virtual wall”. Also, the separation looks slightly weakened, e.g., around (x +nc,y +nc) ≃ (100,0). To sum up, the reduction of pressure drag by uniform blowing is due to the reduction in the mean velocity near the wall, which reduces the dynamic pressure acting on the rough wall.

Fig. 12
figure 12

Pressure distribution over the rough surface in wall units on the blowing (rough) side in uncontrolled case (denoted by superscript “+nc”) at Re b = 5600: (a) V w = 0; (b) V w /U b = 1.0%. Dashed lines are zero contours

Full size image
Fig. 13
figure 13

Wall-normal velocity contour over the rough surface in wall units on the blowing (rough) side in uncontrolled case at Re b = 5600: (a) V w = 0; (b) V w /U b = 1.0%. Dashed lines are zero contours

Full size image
Fig. 14
figure 14

Mean stream function ψ + in near-wall region in wall units on the blowing (rough) side in uncontrolled case at Re b = 5600: (a) V w = 0; (b) V w /U b = 1.0%. Thick lines are zero contours. For clarity, the figure is stretched in the wall-normal direction

Full size image

4.3 Turbulence statistics

Figure 15 shows the mean velocity profiles normalized by the friction velocity on the rough side in each case. In accordance to the observations in the previous studies, the velocity profile below the upper edge of roughness (y + ≃ 20 − 28 and y + ≃ 15 − 23 for Re b = 5600 and 14000 cases, respectively) significantly deviate from the law of the wall. The deviation is more pronounced for Re b = 14000 case, where the flow is considered to be attached, than Re b = 5600 case, where flow separation is observed. The slope in the “log-law” region is increased by UB in the rough-wall cases as well as the smooth-wall cases, which suggests that care should be taken when the Clauser plot is used to determine the friction velocity in experiments to study the combined effect of UB and roughness.

Fig. 15
figure 15

Mean streamwise velocity profiles with UB in wall units on the blowing (rough) side: (a) Re b = 5600; (b) Re b = 14000. Solid line, smooth-wall case; dotted line, rough-wall case; dashed line, the law of the wall. Black, V w = 0; green, V w /U b = 0.1%; red, V w /U b = 0.5%; blue, V w /U b = 1.0%

Full size image

Figure 16 shows the profiles of the RMS velocity fluctuations and the Reynolds shear stress in wall units on the lower (rough/blowing) side in the uncontrolled case. In the rough-wall case, a trend similar to that in the smooth-wall case can be observed; namely, turbulence is enhanced on the blowing side and suppressed on the suction side. While the enhancement of RMS velocities by UB is observed in all the cases, the change is less pronounced in the rough-wall cases. This can be due to the two opposing effects of UB: enhancement of turbulence and mitigation of roughness. In the smooth-wall case, the latter effect does not exist; therefore, the turbulence is simply enhanced. In the rough-wall case, in contrast, these two effects partly cancel each other to result in less modification of RMS velocities.

Fig. 16
figure 16

RMS velocity fluctuations and Reynolds shear stress in wall units on the lower (rough/blowing) side in uncontrolled case: (a) Re b = 5600; (b) Re b = 14000. Solid line, smooth-wall case; dotted line, rough-wall case. Black, V w = 0; green, V w /U b = 0.1%; red, V w /U b = 0.5%; blue, V w /U b = 1.0%

Full size image

As for the turbulence statistics, a completely opposite conclusion was drawn in the recent experimental study by Miller et al. [35]: namely, UB increases drag and suppresses velocity fluctuations in rough-wall cases. However, the present results suggest that their opposite conclusion might have possibly been mislead by the determination of the friction velocity by assuming the von Kármán constant to be unchanged under UB, which is not likely, as was shown in Fig. 15.

4.4 Outer layer similarity

Townsend’s similarity hypothesis on rough walls [60] states that there is a universal law for the outer layer, which is unaffected by the wall geometry. To investigate whether the outer layer similarity holds in the cases with UB, we examine the velocity defect profile on the rough-wall side with and without UB, as shown in Fig. 17. Here, the wall-normal axis is normalized by the distance from the wall to the place where the streamwise RMS velocity takes its minimum value, denoted as δ t . According to Bhaganagar et al. [61], this normalization is reasonable for observing outer layer for one-sided rough channel. Figure 17a presents the result of the base flow case. For y/δ t > 0.1, all the profiles collapse well regardless of the wall shape and the Reynolds number, in accordance with most of the previous roughness studies (e.g., [50, 57, 61, 62]). In the smooth-wall case with UB/US (Fig. 17b), the profile is shifted upward by UB, while it remains nearly unchanged with US. As can be observed in Fig. 17c, the profiles in the rough-wall case with UB/US (for y/δ t > 0.1) are basically similar to those in the smooth-wall case with UB/US. The larger shift in the case of Re b = 14000 can be attributed to the larger blowing velocity in wall units (see, Table 2).

Fig. 17
figure 17

Mean velocity defect Uc+ − U + in wall units on the blowing (rough) side, where Uc+= U +(δ t ) is the “centerline” velocity: (a) uncontrolled rough-wall case; (b) V w /U b = 1.0% smooth-wall case; (c) V w /U b = 1.0% rough-wall case. Solid line, smooth-wall case; dotted line, rough-wall case. Thin line, Re b = 5600; thick line, Re b = 14000

Full size image

Finally, Stevenson’s law [39] is examined as shown in Fig. 18. The equation was originally proposed for a smooth-wall turbulent boundary layer with UB/US as,

$$\begin{array}{@{}rcl@{}} \frac{2}{V_{w}^{+}}\left( \sqrt{1+V_{w}^{+}U^{+}}-1\right)=\frac{1}{\kappa}\ln{y^{+}}+B, \end{array} $$
(20)

where κ = 0.41 and B = 5 are the von Kármán constant and the log-law constant, respectively. According to the recent work by Vigdorovich [63], the log-law constant is also a function of blowing/suction velocity, i.e.,

$$\begin{array}{@{}rcl@{}} \underbrace{\frac{2}{V_{w}^{+}}\left( \sqrt{1+V_{w}^{+}U^{+}}-1\right)-\frac{C_{1}}{\kappa}V_{w}^{+}}_{U^{+S}}=\frac{1}{\kappa}\left( \ln{y^{+}}+C_{0}\right), \end{array} $$
(21)

with C 0 = 2.05 and C 1 = 3.51.

Fig. 18
figure 18

Mean streamwise velocity profiles modified by Stevenson’s law in the form of Eq. 21: (a) Re b = 5600; (b) Re b = 14000. Solid line, smooth-wall case; dotted line, rough-wall case. Black, V w = 0; green, V w /U b = 0.1%; red, V w /U b = 0.5%; blue, V w /U b = 1.0%

Full size image

As shown in Fig. 18, the profiles of U +S in Eq. 21 nearly collapse onto the lines corresponding to Vw+ = 0. This suggests that, when scaled in local wall units, the influences of blowing from one wall and suction from another wall are relatively independent of each other, although the friction velocities themselves used for the scaling are determined by their coupled effect (i.e., the force balance). It is worth noting that we have also tested different empirical constants for the Stevenson formula [2]; however, we have confirmed that the constant proposed by Vigdorovich [63] gives the best match.

The observation above further suggests that the Stevenson formula can be extended to rough walls by accounting for the roughness function ΔU + such as

$$\begin{array}{@{}rcl@{}} \frac{2}{V_{w}^{+}}\left( \sqrt{1+V_{w}^{+}U^{+}}-1\right)-\frac{C_{1}}{\kappa}V_{w}^{+}=\frac{1}{\kappa}\left( \ln{y^{+}}+C_{0}\right)-{\Delta} U^{+}. \end{array} $$
(22)

This extended formula, however, should be validated in future work by considering different roughness profiles such as three-dimensional roughness, and also at higher Reynolds numbers.

5 Conclusions

Direct numerical simulation of fully developed turbulent flow in a channel with a two-dimensional irregularly rough wall and uniform blowing (UB) was performed at Re b = 5600 and 14000 to investigate the drag reduction effect of UB on a rough surface.

The drag reduction rate is found to be slightly less than those in the smooth-wall case, owing to the smaller pressure drag reduction rate. In contrast, the absolute amount of drag reduction is found to be larger on the rough surface due to the presence of pressure drag. It was also found that the drag reduction rate is basically similar to that in the smooth-wall case when the blowing velocity is scaled in wall units, with a slight deterioration due to milder effects on the pressure drag. Similar trends were confirmed also at Re b = 14000, although the contribution of pressure drag was less due to the smaller roughness height. Therefore, as far as the present two-dimensional roughness is concerned, it can be concluded that UB on a rough wall is nearly as effective as that on a smooth wall.

The drag reduction is caused by two different mechanisms. One is the vertical shift of the mean velocity profile and turbulent structures, similar to that in smooth wall cases, which results in less friction drag. The other, which is a distinctive feature on the rough wall, is the reduced flow rate around the roughness elements (or, in other words, a smoothing effect), which decreases the pressure drag.

The examination on the outer layer similarity suggests that the effects of UB and roughness are relatively independent of each other. Accordingly, Stevenson’s law can be extended to rough walls by simply superimposing the roughness function.

In summary, the present results demonstrate that the uniform blowing is an effective drag reduction method also on a rough surface, which often appears in practical applications. Of course, the efficacy of the uniform blowing on high Reynolds number flows, on three-dimensional roughness, and in fully-rough regime should further be studied toward its practical applications. According to the drag reduction mechanisms found in the present study, however, uniform blowing is likely to be effective also in such cases.