1 Introduction

Due to its influence on the wall shear stress and hence skin friction drag, there has been considerable research effort focusing on roughness-induced turbulence (Raupach et al. 1991; Jiménez 2004; Shockling et al. 2006; Castro 2007; Langelandsvik et al. 2008; Lee et al. 2011). As with surface roughness, the effects of momentum injection or “blowing” through a surface have also received significant research attention due to its relevance for applications such as turbine blade transpiration cooling, flow separation control and turbulence control (Sumitani and Kasagi 1995; Krogstad and Kourakine 2000; Chung and Sung 2001; Haddad et al. 2006; Çuhadaroğlu et al. 2007; Dey and Nath 2010). However, there are also instances where these two phenomena coexist. For example, ablative thermal protection systems are constructed using a carbon fiber matrix impregnated with phenolic resin. Heat flux into the material is absorbed by the ablation of the surface, thus resulting in the surface acting as an insulator. As the carbon matrix ablates at a much slower rate than the resin, the surface becomes aerodynamically rough. Simultaneously, the ablating resin produces pyrolysis gases that emit from the surface, further modifying the turbulent boundary layer through mass and momentum injection. Despite coexistence of roughness and blowing boundary conditions in systems such as these, there have been relatively few investigations of how they interact (Schetz and Nerney 1977; Voisinet 1979; Gritsevich et al. 2012).

Surface roughness can be broadly characterized as being either two-dimensional or three-dimensional. Two-dimensional roughness typically consists of elements aligned perpendicular to the streamwise flow direction, whereas three-dimensional roughness includes a wide variety of actively studied geometries, ranging from closely packed beds of fine sand, to forest canopies and urban roughness. Therefore, one of the challenges in the study of surface roughness is parameterizing the roughness geometry. Typically, a roughness height, k, is used that is defined as the maximum height of the ground plane to the peak of the tallest roughness element. A number of approaches have been suggested to describe other length scales characteristic to the surface. Two-dimensional roughness has the additional length scale of the distance between roughness elements L x , in addition to k. However, three-dimensional roughness requires, by its nature, more complex parameterization such as the ratio of the frontal area per element to the ground area per element. Reviews including common methods for parameterizing surface roughness geometry are provided by Raupach et al. (1991) and Jiménez (2004).

One of the foundational hypotheses in the studies of turbulent rough-wall flow is that of wall similarity, or Townsend’s hypothesis (Townsend 1976), which is an extension of Reynolds number similarity for smooth walls. Townsend’s hypothesis states that due to the numerous interactions that occur as roughness-induced eddies are transported away from the surface, the turbulence will be dynamically similar at sufficiently high Reynolds numbers and sufficiently far from the surface to be independent of wall conditions. This condition requires that the roughness height is small relative to the layer thickness, h (i.e., h/k > 40) (Jiménez 2004). If the roughness height exceeds this limit, the roughness will disturb the log layer and consequently roughness effects will persist into the outer layer (Jiménez 2004; Krogstad et al. 1992; Flack et al. 2004).

Using the wall-similarity argument, together with k and all other length scales necessary to fully characterize the roughness, L, a description of the mean velocity of the region outside the buffer layer can be derived using an asymptotic matching analysis for a rough surface as

$$U^+(y)=\frac{1}{\kappa} \ln(y^+) + B - \Updelta U^+(k^+,L^+)+\frac{2\Uppi}{\kappa}W(y/h).$$
(1)

Here, U is the time-averaged mean velocity, y the wall-normal distance, κ the von Kármán constant, B the additive log-law constant and \(2\Uppi\kappa^{-1}W(y/h)\) a wake function describing the outer layer deviation from the log law in which the value of \(\Uppi\) may be dependent on the roughness, particularly for h/k < 60 (Jiménez 2004). The superscripted + indicates scaling using ‘inner variables’ U τ = (τ w /ρ)1/2 and ν, where U τ is the friction velocity, τ w the wall shear stress and ρ and ν the fluid density and kinematic viscosity, respectively. The parameter \(\Updelta U^+\) is the roughness function, representing the offset produced by roughness between parallel smooth- and rough-wall mean velocity and is a direct measure of the ability of the surface roughness to absorb momentum from the mean flow.

Studies incorporating blowing boundary conditions typically focus on either blowing introduced locally through a slot or series of holes (Krogstad and Kourakine 2000; Haddad et al. 2006; Çuhadaroğlu et al. 2007) or uniformly across the surface (Sumitani and Kasagi 1995; Chung and Sung 2001; Dey and Nath 2010). Generally, blowing has been found to decrease skin friction through reduction in the mean shear at the surface. Typically, studies of blowing effects focus on turbulent boundary layers, although channel flow studies have been also conducted using direct numerical simulation at low Reynolds numbers (Sumitani and Kasagi 1995; Chung and Sung 2001; Nikitin and Pavel’ev 1998; Kasagi 1998; Vigdorovich and Oberlack 2008) with blowing found to enhance turbulent motions and increase Reynolds shear stress.

In comparison with the quantity of research focused on roughness effects or blowing effects on turbulent wall-bounded flow, there have been relatively few examining their combined effects (Schetz and Nerney 1977; Voisinet 1979; Healzer et al. 1974; Holden et al. 1988). These studies limit their investigation to mean flow properties, generally observing that using roughness and blowing theory independently to predict their combined effects is ineffective. Due to the diversity of these investigations, conducted over a range of subsonic to hypersonic flow conditions for various geometries including axisymmetric bodies and flat plates, there is little consensus as to what these combined effects are. For example, an additional \(\Updelta U^+\) shift due to blowing was observed in the mean flow by Voisinet (1979); however, Schetz and Nerney (1977) observed no such shift. Furthermore, prior studies were largely limited to mean flow properties, with little to no information available about how these combined effects act to modify the turbulence, although it has been observed that blowing will increase the turbulence intensity near the wall (Schetz and Nerney 1977).

Here, we present the results from a series of experiments conducted to further our understanding of the modifications made to the structure of a turbulent wall-bounded flow by the interaction between surface roughness and blowing boundary conditions. To perform this study, a turbulent channel flow wind tunnel was modified to introduce both surface roughness and flow injection into its test section. The turbulent statistics were then measured using hot-wire anemometry over a range of both Reynolds number and blowing ratio for a single, geometrically simple, surface roughness. These statistics were then compared to those measured for a smooth surface.

2 Experiment description

The experiments were conducted in the turbulent channel flow facility (TCFF) in the University of Kentucky Experimental Fluid Dynamics Lab (EFDL). The channel has a half height of h = 50.8 mm and an aspect ratio of 9:1 to ensure quasi-2D flow at the centerline (Zanoun et al. 2003). The TCFF is powered by a 5.2-kW centrifugal blower which drives the flow through conditioning, development and test sections at bulk velocities up to \(\langle U \rangle =30\,\hbox{m/s}\); producing Reynolds numbers up to \(Re_h=h \langle U\rangle/ \nu\) = 102,000 or Re τ = h U τ/ν = 4,200.

A boundary layer trip consisting of a 50-mm-long section of 120-grit sandpaper followed by a 100-mm-long section of 60-grit sandpaper was located at the development section inlet and extended around the circumference of the channel to ensure a fixed laminar-turbulent transition point. The distance from the channel inlet to the test section is 246h, allowing the turbulence to reach a fully developed state (Monty 2005). The test section is 24h long, with an instrumentation access point located at its mid-point. Following the test section, an additional 12h long conditioning section ensures a consistent pressure gradient inside the test section.

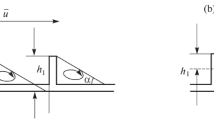
As illustrated in Fig. 1, for this set of experiments the top surface of the downstream end of the TCFF test section was replaced with a 24h long section of periodic, approximately sinusoidal roughness, whose characteristics are illustrated in Fig. 2. The roughness had a streamwise periodicity of L x  = 7 mm and amplitude of k = 1 mm. The surface had micro-cracked pores distributed uniformly over the surface that allowed mass injection through it. However, the process used to manufacture the pores disrupted the two-dimensionality of the surface and introduced a spanwise periodicity of L z  = 3.5 mm as shown in Fig. 2. To force flow through the rough surface, an apparatus was designed and constructed to produce backplane pressure on the surface. The apparatus consisted of two stages of flow conditioning screens of mesh size of M = 3.4 and 1.25 mm with over 60M recovery distance downstream of each mesh. Air was driven into the apparatus by a centrifugal blower through a fixed pattern diffuser which provided the initial flow distribution. The experimental arrangement is illustrated schematically in Fig. 1. To characterize the ratio of injected to advected momentum, we define a dimensionless blowing rate of BR = (U inj )/(U cl ) where U cl is the centerline velocity in the channel and U inj is the area-averaged velocity through the surface. To accurately determine U inj , a venturi-style flow meter (Dwyer model 2000-10-VF4) was installed downstream of the centrifugal blower to measure the mass flow rate from the blower and the area ratio used to calculate U inj , resulting in an estimated error in U inj of ±2 %.

Fig. 1
figure 1

Schematic showing experimental arrangement

Full size image
Fig. 2
figure 2

Images of the rough surface showing a xz plane and b xy view

Full size image

To measure wall-normal profiles of the fluctuating streamwise component of velocity, a single-sensor hot-wire probe was mounted on an automated traversing mechanism capable of positioning the probe with an accuracy of 0.5 μm. The hot-wire probe used was a 2.5-μm diameter platinum Wollaston wire soldered onto Auspex boundary layer type hot-wire prongs and etched to a length of ℓ = 0.5 mm. The probe was driven by a Dantec Dynamics StreamlineTM system at an overheat ratio of 1.6. The probe was calibrated at the centerline of the channel using a Pitot probe and wall-pressure tap combination. To verify the absence of voltage drift in the HWA probe, the probe was calibrated both before and after each profile measurement. The calibration data were fitted using a fourth-order polynomial following correction of the voltage for flow temperature variation.

Wall-normal profile data were digitized at 60 kHz with the acquisition time, T, for each run adjusted for each Reynolds number to capture at least 100 instances of the largest structures [estimated as \(\mathcal{O}(20h)\) (Monty et al. 2009)] in order to ensure converged statistics. Wall-normal profiles were constructed by traversing the probe from within the trough of the roughness element located 80L x from the test section inlet to y = 1.1h. Although the location of the surface relative to the probe was not able to be precisely determined, rough-walled turbulence is commonly described using a zero-plane displacement height, y d that is typically less than k. As y d can be determined a posteriori, it was therefore not essential to accurately determine the exact wall distance as all traverses initiated less than a single roughness height from the surface.

Direct measurement of wall shear stress to determine U τ was not possible in the present case. Therefore, for this set of experiments, the so-called “Clauser chart” method was used to determine the friction velocity (Clauser 1956). This method has precedence in rough-walled turbulent boundary layers (Krogstad et al. 1992; Flack et al. 2004; Perry and Li 1990; Schultz and Flack 2007; Mills and Huang 1983), but it has been noted to lack agreement with other methods (Akinlade et al. 2004). This has resulted in multiple improvements upon the basic Clauser method (Akinlade et al. 2004; Perry et al. 1986) being proposed. However, the structure of any of these methods relies on universality of the velocity-defect law. We employed a similar method to that of Perry and Li (1990). The procedure is iterative and begins by plotting U/U cl versus \(\ln(YU_{cl}/\nu)\) to determine Y = y + y d . We modified the method described in Perry and Li for the lower Reynolds number cases (Re τ < 3,000) by utilizing the streamwise Reynolds stress to determine y d whereby a value was chosen so that each profile tends toward zero at the same location as the smooth-wall cases at similar values of Re τ. This method proved very reliable at producing values of y d which also collapsed the mean profile data. An iterative procedure was then used to determine U τ by matching the slope of the mean velocity profile in the logarithmic region to that of the smooth-walled case. At higher Re τ, the near-surface peak in streamwise Reynolds stress was not sufficiently resolved to extrapolate the profile. However, it was assumed that the log region in the mean flow was large enough in this high-Re range to fit the profiles accurately using Eq. 1 with κ = 0.39 and B = 4.42 (Nagib and Chauhan 2008).

To validate the values of U τ obtained by the methodology above, a simple control volume momentum balance was performed on the mean flow which took into account the entrance and exit mass flux to the test section and the measured pressure drop along the test section. The control volume momentum equation for the streamwise equation becomes

$$\int\limits_{x_1}^{x_2} \left(\tau_w\right)_{r} \text {d}x = 2h\left(P_1-P_2\right) + \rho \int\limits_0^{2h} U_1^2 \text {d}y-\rho \int\limits_0^{2h} U_2^2 \text {d}y-\int\limits_{x_1}^{x_2} \left(\tau_w\right)_s \text {d}x$$
(2)

where the subscripted 1 and 2 indicate quantities at the entrance and exit of the control volume, and the subscripted r and s indicate the smooth and rough surface, respectively.

Solving this momentum balance required several assumptions. Additional profiles (not presented in this paper) were taken close to the entrance and exit of the rough surface, and used to determine of the net momentum of the flow entering and exiting the control volume. The streamwise dependence of the wall shear stress was assumed constant for the smooth wall and equal to that of the flow upstream of the rough surface. Finally, the streamwise development of the rough surface was not known; so, it was assumed that the value at the measurement position was approximately equal to the average shear stress along the surface. The static pressure at the inlet and outlet of the control volume was measured using Pitot-static tubes inserted into the channel.

Due to these assumptions and uncertainty in the measurement of the small pressure differences measured (typically less than 15 Pa), this method produced much more scatter in U τ when compared with the Clauser chart approach, but did provide verification of the U τ behavior exhibited when determined via the Clauser chart method.

Experiments were conducted for a range of Re τ from 650 to 7,000 and BR from 0 to 0.16 % and compared to smooth-walled measurements at Re τ from 650 to 4,200. All cases are summarized in Table 1. This table highlights two unique aspects of this data set, the high Reynolds number achieved with roughness present and the matched blowing rates across multiple Reynolds numbers.

Table 1 Nominal parameters for experiments
Full size table

3 Results and discussion

3.1 Mean flow

The variation of the friction coefficient \(C_f= \tau_w/(0.5 \rho \langle U \rangle^2)\) is presented in Fig. 3 as a function of Re h . For the cases with flow injection, \(\langle U \rangle\) was calculated over the area extending from the wall to the location of maximum velocity to account for slight asymmetry in the mean velocity profile. Generally, this asymmetry was small, with the maximum value of U found to be within 2 % of U cl in location and value.

Fig. 3
figure 3

Coefficient of friction as a function of bulk Reynolds number: multiple sign smooth-wall cases; diamond BR = 0 %; square BR = 0.10 %; triangle BR = 0.13 %; and circle BR = 0.16 %. Solid line indicates the smooth-wall correlation of 0.073(2Re h )−0.25 (Dean 1978), and dashed lines indicate modifications to BR = 0 % cases following Eq. 4 for BR = 0.10 %, BR = 0.13 %, BR = 0.16 %

Full size image

If we first examine the results for the BR = 0 % condition, the deviation of C f from the smooth-wall curve follows typical surface roughness behavior, with the lowest Reynolds number appearing to be transitional and the highest Reynolds numbers indicating fully rough conditions. Interestingly, for nonzero BR, the skin friction was observed to increase with increasing BR and the Reynolds number behavior of C f is similar to that expected for increasing roughness effects. This is in contrast to results from blowing studies with smooth walls as well as prior turbulent boundary layer roughness and blowing results (Schetz and Nerney 1977; Voisinet 1979), where any amount of flow injection was observed to result in a reduction in skin friction when roughness was present. Potentially, this deviation from the expected behavior could be related to the specifics of the surface geometry used in the present study, for example through the periodic nature of the roughness in the streamwise direction or through the spacing of the pores used for momentum injection. However, without more detailed investigation of the flow structure near the wall, we can only speculate as to the reason for the C f behavior in the present case.

The inner-scaled streamwise mean velocity profiles for all cases listed in Table 1 are presented in Fig. 4a. As expected, due to the method used to obtain U τ, the roughness and blowing boundary conditions do not appear to significantly affect the logarithmically scaled region in the flow.

Fig. 4
figure 4

Streamwise mean velocity plotted in inner coordinates: diamond Re τ ≈ 600; square Re τ ≈ 2,000; triangle Re τ ≈ 4,000; circle Re τ ≈ 5,000; and inverted triangle Re τ ≈ 7,000. White symbols indicate BR = 0 %; light gray symbols indicate BR = 0.10 %; dark gray symbols indicate BR = 0.13 %; and black symbols indicate BR = 0.16 %. Solid lines indicate smooth-walled cases, and dashed line indicates log law

Full size image

Focusing first on BR = 0 cases, the profiles show the expected increase in \(\Updelta U^+\) with increasing Reynolds number and corresponding increase in wall shear stress. Furthermore, corresponding to the C f behavior, additional blowing at fixed Reynolds number causes an increase in \(\Updelta U^+\). Thus, as with C f , the impact of blowing on the mean flow appears as an effective increase in roughness effects.

This behavior is further reflected by the defect-scaled presentation of the mean velocity profiles, as shown in Fig. 4b. Collapse is evident among all cases including smooth, rough and rough-with-blowing. This figure also indicates that the impact of the different boundary conditions on the mean flow is confined to the near-wall region and affects the outer region only through the wall shear stress, consistent with Townsend’s hypothesis.

To further explore the dependence of \(\Updelta U^+\) on BR and roughness Reynolds number k +, this quantity is presented in Fig. 5. Figure 5 shows that the results span a wide range of k + values from 13 to 145. Comparison with the BR = 0 % cases with the Colebrook relation shows that for \(k^+\,\gtrapprox\,60\) the \(\Updelta U^+\) behavior follows the expected logarithmic increase for fully rough conditions with k s  ≈ 1.8k. As mentioned previously, an increase in BR results in an increase in \(\Updelta U^+\), analogous to an effective increase in roughness effects. However, these results also show that this effective increase cannot simply be treated as an increase in roughness height, as the BR > 0 cases follow separate \(\Updelta U^+(k^+)\) trends for each BR. Following the roughness analogy, this behavior is similar to that expected for a change in roughness geometry.

Fig. 5
figure 5

Roughness function plotted with respect to the roughness Reynolds number, k +: diamond BR = 0 %; square BR = 0.10 %; triangle BR = 0.13 %; and circle BR = 0.16 %. Filled symbols are the original data and hollow symbols show BR > 0 data corrected using Eq. 3. Solid line is the Colebrook relation

Full size image

It was also found that a simple empirical correction of

$$\Updelta U_{\rm corrected}^+=\Updelta U^+ (1-1.2BR)$$
(3)

where BR is in %, resulted in collapse of the BR data to a single roughness function. As shown in Fig. 5, the \(\Updelta U^+\) values for BR > 0 modified following Eq. 3 collapse onto the BR = 0 curve for the highest, fully rough, Reynolds numbers. Although the formulation is simplistic, and purely empirical, it does suggest that the effects of roughness and blowing can potentially be treated in succession, at least for the mean flow.

Noting, that \(C_f=2\langle U^+ \rangle^{-2}\), Eq. 3 can be combined with Eq. 1 to modify the C f relationship for the rough-walled surface to account for blowing effects such that

$$C_{f_{\rm blowing}}=2\left(\sqrt{\frac{2}{C_f}} + \Updelta U^+\left[\frac{1.2BR}{1-1.2BR}\right]\right)^{-2}$$
(4)

where C f and \(\Updelta U^+\) are the values for the rough-walled case at a particular Reynolds number and BR is expressed as a percent. As shown in Fig. 3, although this correction does not capture the transitionally rough behavior, it is effective at predicting the blowing effects on C f under fully rough conditions.

3.2 Turbulence statistics

The previous section demonstrated that the effects of BR on the mean flow are analogous to an increase in roughness. We now shift our attention to exploring how the boundary conditions affect the turbulence statistics, in particular the streamwise Reynolds stress. In Fig. 6, the wall-normal profiles of inner-scaled and outer-scaled streamwise Reynolds stress, u 2 +, are presented. Note that the highest Reynolds number cases can be expected to be subject to spatial filtering (Hutchins et al. 2009) which will artificially reduce the magnitude of the measured streamwise Reynolds stress. Spatial filtering effects can generally be considered to be minimal for ℓ+ = ℓ U τ/ν ≈ 20 (Ligrani and Bradshaw 1987), which is the case for the two lowest Reynolds numbers in the current study. Due to the dependence of the spatial filtering effects on the transverse Taylor microscale (Segalini et al. 2011) existing spatial filtering corrections for smooth-walled flows are potentially inaccurate for rough-walled flows. Therefore, no spatial filtering corrections were applied. However, it is expected that spatial filtering was confined to the near-wall region only (Smits et al. 2011) and that the magnitude of the spatial filtering will not change significantly between different BR cases measured at similar Reynolds number. Segalini et al. (2011) note that 95 % of the variance is recovered when the wire length is 50 % of the transverse Taylor microscale. Using estimated values of the Taylor microscale (calculated from the dissipation spectrum assuming local isotropy), the wire length was greater than 50 % of the transverse Taylor microscale for Y + < 20 (Y/h < 0.01) at Re τ ≈ 2,000; for Y + < 100 (Y/h < 0.025) at Re τ ≈ 4,000; for Y + < 300 (Y/h < 0.06) at Re τ ≈ 5,000; and Y + < 500 (Y/h < 0.07) at Re τ ≈ 7,000.

Fig. 6
figure 6

Streamwise Reynolds stress for Re τ < 1,000 shown in a using inner units and b using outer units. The same profiles for 1,000 < Re τ < 3,000 are shown in c and d and for Re τ > 3,000 in e and f. Symbols as in Fig. 4

Full size image

Figure 6 shows that surface roughness with BR = 0 serves to decrease the relative magnitude of the near-wall peak compared with the smooth-walled cases. The BR > 0 cases exhibit similar trends, with increasing BR further reducing the magnitude of the inner peak relative to the corresponding BR = 0 case. At the lowest Reynolds number measured, Fig. 6a, k +≈ 13 and the inner peak appears at Y + = 15, suggesting that the near-wall turbulence production cycle in the transitionally rough regime is largely similar to that for smooth-walled flows. However, for the fully rough cases, the near-wall peak moves away from the wall in inner units, consistent with the peak location scaling with the physical scale of the roughness elements, rather than the viscous length, ν/U τ. This is demonstrated in Fig. 6d and f, which shows that for BR = 0 and k + ≥ 40, the near-wall peak occurs at Y/h = 0.01 (Y ≈ 0.5k). When BR > 0, the peak moves to Y/h ≈ k, with a slight increase in distance from the wall observed with increasing BR.

As with the mean flow, the addition of blowing therefore appears to act as an increase in surface roughness, and Fig. 6a and c reveals that the effects of roughness and blowing on \({u^{2}}^+\) are greatest in the near-wall region with little effect on the far outer flow except as enacted through the change to U τ. The roughness and BR behavior of \({u^2}^+\) are therefore similar to that of the mean velocity profiles, which followed the behavior predicted by Townsend’s hypothesis. Given that the relative roughness height of h/k = 51 in the present case exceeds the minimum value of h/k = 40 cited by Jiménez (2004) for validity of Townsend’s hypothesis, we would expect that the effect of roughness should be confined to the inner layer and thus wall-similarity would hold for the Reynolds stresses, as well as the mean flow. As indicated in Fig. 6b, d and f, the results for the rough-walled cases do not collapse with the smooth-walled profiles in the outer layer, which themselves collapse using this scaling for Re τ ≥ 3,000. This lack of agreement with the smooth-walled results is not surprising in the present experiment given that the flow is still developing over the surface in the rough-walled cases, whereas it is fully developed for the smooth-walled cases. However, as is illustrated in Fig. 6d, the highest Reynolds number BR = 0 cases are self-consistent, scaling within the outer layer of Y/h > 0.1. However, the BR > 0 cases were found to only follow this scaling behavior for Y/h > 0.5, well into the outer layer.

To provide further insight into the source of this modification of the scaling behavior, we can investigate the power spectral density, ϕ uu calculated each wall-normal position. Here, we employ Taylor’s frozen flow hypothesis and examine the spectra pre-multiplied by the streamwise wavenumber, k x , and presented as spectral maps (Hutchins and Marusic 2007). These spectral maps illustrate the dependence of the pre-multiplied spectral energy on wall distance and wavelength, λ and have the advantage of allowing identification of the wavelengths that have the greatest contribution to \({u^2}^+\) as regions of high pre-multiplied spectral value. These results are presented for the smooth-walled and BR = 0 cases for Re τ ≈ 700, 2,200 and 4,000 in Fig. 7.

Fig. 7
figure 7

Pre-multiplied power spectra results for Re τ ≈ 700, Re τ ≈ 2,000 and Re τ ≈ 4,000 for the smooth-walled case and BR = 0.0 %. Also shown are the contours of \(\Updelta \left(k_x \phi_{uu}^+\right)\) for BR = 0.10 % and BR = 0.16 %. Short- and long-dashed lines indicate where LSM and VLSM signatures, respectively, can be observed in the smooth-walled results

Full size image

At Re τ ≈ 700, the spectral maps of both smooth- and rough-wall cases are dominated by the wavelengths which form the near-wall peak in Reynolds stress, with a local maxima at λ/h ≈ 1 and Y/h = 0.025. At this low, transitional, k + value the effect of roughness is confined to suppression of this peak. However, for the two higher, fully rough, Reynolds number cases (Re τ ≈ 2,000 and 4,000), there is a much greater difference between the smooth-wall and rough-wall spectral maps. As noted with the Reynolds stress profiles, the near-wall peak for the rough case shifts to Y/h ≈ 0.01. Furthermore, it is composed of much smaller eddies than the near-wall peak for the smooth-walled case, having λ/h ≈ 0.02, or λ ≈ k. This is consistent with the near-wall turbulence production transitioning from being driven by the wall shear and therefore scaling with the viscous length for transitionally rough conditions to being driven by the roughness geometry and scaling with k under fully rough conditions.

Also, evident further from the wall for the higher Re τ cases is the signature of what Monty et al. (Monty et al. 2007) termed the “dominant energy modes.” In the spectral maps, this signature appears as ridges in the contours, which have been highlighted for the smooth-walled case in Fig. 7 using dashed lines. These modes have been associated with the occurrence of large- and very large-scale motions (LSMs and VLSMs) (Hutchins and Marusic 2007; Kim and Adrian 1999; Zhou et al. 1999; Guala et al. 2006; Balakumar and Adrian 2007; Bailey et al. 2008; Bailey and Smits 2010). Although also evident in the Re τ ≈ 700 spectral map, due to the shift of the near-wall peak to smaller wavelengths which occurs at higher Reynolds numbers, these modes become more evident for the higher Re τ cases.

Notably, these dominant energy modes exhibit very different behavior between the smooth wall and BR = 0 cases, with the the long-wavelength VLSM mode dominating the smooth-walled spectral map far away from the wall and the shorter-wavelength LSM mode dominating the spectral map for the rough-walled case. The streamwise evolution of these modes from the start of the surface roughness is therefore the source of the differences between the scaled smooth-walled and rough-walled Reynolds stress profiles presented in Fig. 6. Comparison with the spectral maps of the different Reynolds numbers but identical boundary conditions indicates that the structure and magnitude of the outer layer structures are Reynolds number independent for the smooth-walled and rough-walled cases.

To investigate the effect of nonzero BR, the differences between the BR = 0.10 % and BR = 0 % spectral maps are shown in Fig. 7 as contours of \(\Updelta(k_x \phi_{uu}^+\)) and the differences between the BR = 0.16 % and BR = 0 % spectral maps are also shown in Fig. 7. For the lowest, transitionally rough, Reynolds number case (Re τ ≈ 700) the additional effects of blowing appear to be largely confined to the suppression of kinetic energy of the near-wall peak eddies, as with the effect of roughness, with increased suppression occurring with increasing BR. Also noticeable, however, was a slight increase in energy at wavelengths corresponding to k and in the outer layer, suggesting a shift toward increased influence of the roughness elements.

This suppression is also evident for the two higher, fully rough, Reynolds number cases (Re τ ≈ 2,000 and 4,000) near the wall, with the additional blowing suppressing wavelengths of scales ranging from k to h. This suppression corresponds to the resulting decrease in \({u^2}^+\) in the near-wall peak observed in Fig. 6. More interesting, however, is that the decrease in \({u^2}^+\) observed into the outer layer appears to be due to reduction in the strength of the LSM, suggesting that the additional blowing disrupts the formation of LSM. The magnitude of this disruption increases with increasing BR. The VLSM wavelengths, conversely, appear largely unaffected by blowing, although there is a suggestion of some enhancement of the VLSM at Re τ ≈ 2,000 and BR = 0.10 %.

The imperviousness of the VLSM scaling to suppression of the LSM modes indicates that the two phenomena may be unrelated, contrary to what has been proposed previously (Guala et al. 2006; Balakumar and Adrian 2007). Instead, it would appear that the LSM are driven by the wall boundary condition which in the present case is significantly altered by the addition of blowing, whereas the VLSM is produced by the outer layer mean flow shear, which was demonstrated to scale with outer variables, regardless of blowing rate.

4 Conclusions

The scaling effects of combined roughness and blowing boundary conditions were examined in turbulent channel flow for a Reynolds number range of Re τ = 700–4,500. It was observed that the addition of blowing through the surface resulted in an increase in skin friction, rather than the decrease observed for blowing under smooth-wall surface conditions. The effects of roughness on the mean velocity were found to be confined to the near-wall region, and the addition of blowing was found to be analogous to an increase in roughness effects, allowing for a simple empirical correction for its effects on the mean profile and skin friction coefficient. Although the mean profile followed behavior predicted by Townsend’s hypothesis, the Reynolds stresses did not, and modifications to the Reynolds stress profile were observed well into the outer layer with the addition of blowing boundary conditions. This lack of scaling, which occurred simultaneously with suppression of the near-wall peak in Reynolds stress, was found to be associated with blowing rate dependent suppression of the outer-scaled LSM mode.