A Stochastic Backscatter Model for Grey-Area Mitigation in Detached Eddy Simulations

Abstract

A new stochastic backscatter model is proposed for detached eddy simulations that accelerates the development of resolved turbulence in free shear layers. As a result, the model significantly reduces so-called grey areas in which resolved turbulence is lacking after the computation has switched from a Reynolds-averaged Navier–Stokes simulation to a large eddy simulation. The new stochastic model adds stochastic forcing to the momentum equations with a rate of backscatter from the subgrid to the resolved scales that is consistent with theory. The effectiveness of the stochastic model is enhanced by including spatial and temporal correlations of the stochastic forcing for scales smaller than the cut-off scale. The grey-area mitigation is demonstrated for two canonical test cases: the plane free shear layer and the round jet.

1 Introduction

Detached Eddy Simulation (DES) has been conceived as a way to improve the accuracy of the simulation of turbulent flows with significant flow separation, which are still beyond the grasp of Reynolds-Averaged Navier–Stokes (RANS) turbulence models, without the high expense of a full Large Eddy Simulation (LES). In DES the attached boundary layers are captured with RANS while the separated flow regions are captured with LES. These RANS and LES regions are not specified a priori as in a zonal hybrid RANS–LES approach, but are determined by comparing the turbulence length scale of the RANS model to the subgrid length scale or filter width of LES. Thus, no a priori knowledge of the flow topology is strictly required, which is one of the advantages of the method. Since its original proposal by Spalart et al. [1], DES has seen much development, including improvements such as Delayed DES [2] to shield the boundary layers captured with RANS from so-called shear-stress depletion and Improved DDES [3, 4] to extend DES towards wall-modelled LES, as well as several variants such as ZDES [5] and X-LES [6].

The success of a DES computation depends on the speed of development of resolved turbulence in the separated flow regions captured with LES. In some cases, a substantial so-called grey area exists immediately after flow separation, consisting of a stable free shear layer containing no or little resolved turbulence even though the computation is in LES mode [7, 8]. This grey-area problem is most pronounced in flows with little or no recirculation of turbulence back to the separation onset where it could destabilize the shear layer. For example, the prediction of the noise generated by turbulent jets using DES will fail due to this problem, but it also limits the accuracy of other DES computations involving separated thin shear layers. Therefore, tackling the grey-area issue is important if DES is to fulfil its potential for extending the domain where accurate and affordable CFD computations can be performed towards strongly separated flows and in particular towards to the borders of the flight envelope for aeronautical applications.

One approach to overcome the grey area is to add synthetic turbulence at the RANS–LES interface [9,10,11]. This is a natural approach in a zonal RANS–LES method, but fits less well with the original non-zonal concept of DES where the location of the RANS–LES interface is generally not known. Thus, there is a need to look for alternative approaches to mitigate the grey-area issue.

Generally, two lines can be followed for non-zonal grey-area mitigation: reducing the level of subgrid stresses in the initial free shear layer, allowing 3D instabilities to develop, or inducing the development of 3D instabilities more directly by adding some form of stochastic forcing.

In DES, the subgrid stresses are typically modelled by an eddy-viscosity subgrid-scale (SGS) model and are therefore proportional to the product of the eddy viscosity and the rate of strain. As shear layers are initially very thin, they contain high values of the mean velocity gradient, and therefore of the rate of strain, which leads to high values of the subgrid stresses. Any instability of the initial shear layer may then be damped by these high stresses, thus delaying the development of resolved turbulence. A first approach to reduce these high subgrid stresses consists of reducing the eddy viscosity by defining the subgrid length scale as the cube root of the cell volume instead of the maximum of the mesh size (which is standard in DES), making use of the slender cells typically present in initial free shear layers, as proposed in the original ZDES [5]. Another approach that uses the slender cells, sensitizes the subgrid length scale to the direction of the vorticity vector, essentially excluding the mesh size in that direction from the definition of the filter width [10, 12, 13]. There is something to be said, however, for more generic methods that are less dependent on the specific shape of the grid cells. The subgrid stresses can also be significantly reduced in the initial shear layer by removing the dependence on the high velocity gradients in the mean flow through a High-Pass Filtered (HPF) SGS model [14]. A similar effect can be obtained by using algebraic eddy-viscosity SGS models that deliver zero eddy viscosity in case of pure shear or nominally 2D flows such as the WALE and σ models [15, 16] as proposed by Mockett et al. [17] . Finally, Shur et al. [13] recently proposed to use a kinematic measure, based on the rate-of-strain tensor and the vorticity vector, to identify nominally 2D flows to reduce the subgrid length scale. All these approaches have shown some success in mitigating the grey-area issue, but room for improvement clearly remains. Here, the HPF model is used as a baseline approach for reducing the level of subgrid stresses, as it is independent of the shape of the grid cells and as the methods of Mockett et al. and of Shur et al. were not yet available when this work was performed.

This paper focusses on inducing 3D instabilities through a stochastic SGS model. The stochastic model is included in the X-LES method, which is a k– ω based DES method, but it can be used in other DES methods as well. In earlier work, a simple stochastic eddy-viscosity model had been proposed and tested [7]. This model had been formulated ad hoc and consisted of multiplying the eddy-viscosity coefficient (in LES regions) with a stochastic variable ξ ² (where ξ has a standard normal distribution).

Here, a new stochastic SGS model is proposed that has a more physical grounding. It is based on the stochastic models of Leith [18] and Schumann [19]. These models include energy backscatter from the subgrid scales to the resolved scales at a rate consistent with theory such as EDQNM (see for example Lesieur [20]): for wave numbers κ smaller than the cut-off wave number, the power spectrum of backscatter scales as κ ⁴. As a consequence, the backscatter will mainly affect the resolved scales close to the cut-off wave number. If the stochastic forcing is formulated as the gradient of a stochastic variable that is uncorrelated in space, as is the case in the Leith and Schumann models, then the correct scaling of the backscatter rate is obtained. Note that the stochastic eddy-viscosity model, although formulated ad hoc, also essentially consisted of the gradient of a stochastic variable and therefore had the correctly scaled backscatter rate as well.

An additional reason for replacing the stochastic eddy-viscosity model is that it was less effective when combined with the HPF SGS model that reduces the level of subgrid stresses [14]. Reducing the subgrid stresses also reduced the stochastic forcing as it was part of the same subgrid stress tensor. The new stochastic model adds an additional stochastic forcing term, independent of the deterministic subgrid stress and therefore does not have this disadvantage.

The new stochastic backscatter model is based on the model of Leith, but includes aspects of the Schumann model as well as other modifications to combine it with the X-LES method and to make it suitable for grey-area mitigation. The main advantage of the Leith model is that the stochastic forcing is solenoidal and therefore does not function as a noise source. To determine the velocity scale of the stochastic subgrid stresses, the Leith model uses the magnitude of rate of strain and the filter width Δ. As the X-LES method employs a k-equation SGS model, with k the subgrid kinetic energy, it is more natural to use $\sqrt {k}$ as velocity scale, as is also done by Schumann.

As the stochastic forcing represents the backscatter effect of the subgrid scales, which are by definition not resolved on the computational grid, it is natural to define the stochastic variables to be uncorrelated in space. Leith also defines them to be uncorrelated in time, but Schumann introduces temporal correlation for time scales smaller than the subgrid time scale or eddy turn-over time ${\Delta }/\sqrt {k}$, using a Langevin-type stochastic differential equation. Schumann’s main argument is that typically the numerical time step (based on a Courant number of order one) will be significantly smaller than the subgrid time scale. Along the same line, spatial correlation should be introduced when the mesh size is significantly smaller than the subgrid length scale or filter width Δ, which is the case for the slender grid cells typically used to capture shear layers. Furthermore, as noted by Schumann, only the subgrid scales close to the cut-off wave number contribute significantly to backscatter, because backscatter decreases rapidly with increasing wave number of the subgrid scales (as κ ⁻⁶ in the inertial subrange). Thus, a backscatter model will be most effective if the spectrum of the stochastic variables is not uniformly distributed (white noise), but is concentrated near the cut-off wave number (that is, if the stochastic variables are spatially correlated over distances smaller than the filter width). In the new stochastic backscatter model, spatial correlation is obtained by an additional, purely spatial, stochastic differential equation that effectively applies implicit smoothing to a spatially uncorrelated stochastic variable. At present, this implicit smoothing is defined by factoring in the three spatial directions, which makes it very efficient on structured grids. To make the method applicable to unstructured grids, a non-factored formulation would have to be defined, for which a suggestion is made.

Although this is not the aim of the present work, stochastic forcing may also be used to resolve the log-layer mismatch when using DES as a wall model in LES, as shown by Piomelli et al. [21, 22]. Their formulation of the stochastic forcing, however, differs from the present approach in that it is not based on the gradient of a spatially uncorrelated stochastic variable, but rather on the stochastic variable itself, and therefore does not have the proper scaling of the backscatter rate.

The baseline detached eddy simulation method employed here, X-LES, is briefly described in Section 2, together with the high-pass filtered SGS model. Then, the stochastic backscatter model is presented, both in continuous and discretized forms, in Section 3. Finally, the effectiveness of the stochastic method in mitigating the grey-area issue is considered in Section 4 for two test cases: the plane free shear layer and the round jet. These two cases suffer strongly from the grey-area problem, as there is no turbulence recirculating back to the onset of the shear layer that could diminish the grey area by destabilizing the shear layer. In that sense, they form essential test cases for any method for grey-area mitigation. The proposed method, however, is applicable to more complex test cases. First, promising results have been obtained for a delta wing at high angle of attack [23, 24] and a three-element airfoil [23, 25], with both computations displaying no significant grey areas in the separating shear layers.

2 Detached Eddy Simulation: X-LES

In non-zonal DES methods such as X-LES [6], a single set of turbulence-model equations is used to model both the Reynolds stresses in RANS mode and the subgrid-scale (SGS) stresses in LES mode. An eddy-viscosity model is used for these stresses, which are then given by the Boussinesq hypothesis:

$$ \tau_{ij} = 2 \nu_{t} \left( S_{ij} - \tfrac{1}{3} \partial_{k} u_{k} \delta_{ij} \right) - \tfrac{2}{3} k \delta_{ij} $$

(1)

(using the summation convention), with ν _t the eddy viscosity, $S_{ij} = \tfrac {1}{2} (\partial _{j} u_{i} + \partial _{i} u_{j} )$ the rate-of-strain tensor, u _i the velocity vector, k the turbulent or subgrid-scale kinetic energy, and δ _{i j} the Kronecker delta.

The X-LES method in particular is based on the TNT k– ω model [26]. The method switches to LES when the RANS length scale, $l = \sqrt {k}/\omega$, exceeds the LES length scale C ₁Δ (with C ₁ a model constant). The RANS length scale is then replaced by the LES length scale in the expression for the eddy viscosity as well as in the expression for the dissipation of turbulent kinetic energy ε:

$$\nu_{t} = l_{b} \sqrt{k} , $$

and

$$\varepsilon = \frac{ \beta k^{3/2} }{ l_{b} } , $$

with β = 0.09 and l _b = min{l,C ₁Δ} . The filter width Δ is defined at each grid point as the maximum of the mesh width in all directions. Note that effectively a k-equation SGS model is used in LES mode (where l _b = C ₁Δ), as ω drops out of the expressions for ν _t and ε. In practical simulations, the shielding function f _d as defined for Delayed DES must be employed to protect the (attached) boundary layers from inadvertently switching to LES (with f _d varying between 0 inside attached boundary layers and 1 away from the wall; see Spalart et al. [2] for the precise definition of f _d ). The shielding function is included in (delayed) X-LES by redefining the blended length scale as

$$l_{b} = (1-f_{d}) l + f_{d} \min\{ l , C_{1} {\Delta} \} = (1-\tilde{f}_{d}) l + \tilde{f}_{d} C_{1} {\Delta} \, $$

with

$$\tilde{f}_{d} = \left\{ \begin{array}{ll} 0 & \text{ if } l \leq C_{1} {\Delta} \, , \\ f_{d} & \text{ if } l > C_{1} {\Delta} \, . \end{array} \right. $$

The modified shielding function $\tilde {f}_{d}$ is identical to zero in the original RANS zones. It is used as an indicator to effectively distinguish between RANS mode ($\tilde {f}_{d} \rightarrow 0$) and LES mode ($\tilde {f}_{d} \rightarrow 1$), allowing to switch on specific modifications of the SGS model only in LES mode.

As a first step to mitigate the grey-area issue, a high-pass filter (HPF) is applied to the velocity field prior to computing the subgrid stresses [14]. Thus, the subgrid stresses essentially depend on the gradient of the velocity fluctuations and not on the gradient of the mean velocity field. As a result, the subgrid stresses are substantially reduced in thin free shear layers which are characterized by high mean velocity gradients. The high pass filter consists of subtracting the running time average of the velocity from the instantaneous velocity:

$$u^{\prime}_{i}(x,t) = u_{i}(x,t) - \tilde{f}_{d} \bar{u}_{i}(x,t) , $$

with the running time average given by

$$\bar{u}_{i}(x,t) = \frac{1}{t} {{\int}_{0}^{t}} u_{i}(x,s) \mathrm{d} s . $$

The (subgrid) stresses given by Eq. 1 are then computed from the filtered velocity $u^{\prime }_{i}$ instead of the instantaneous velocity u _i . In LES mode ($\tilde {f}_{d} \rightarrow 1$), the filtered velocity equals the velocity fluctuations, whereas in RANS mode ($\tilde {f}_{d} \rightarrow 0$) the filter is effectively switched off. A similar HPF approach has been followed by Stolz [27] and by Lévêque et al. [28] using a spatial filter instead of a temporal filter in order to improve the Smagorinsky model for LES of wall-bounded flows. High-pass filters have also been used in the context of the structure-function model [29]. It should be stressed that as the HPF approach already effectively reduces the subgrid stresses in initial shear layers, there is no need to use the alternative definitions of the filter width Δ that were mentioned in the introduction.

A limitation of the current HPF is that it does not filter out any low-frequency oscillations that are outside of the turbulence spectrum. For example, in the case of smooth-surface separation, the shear layer may oscillate as a whole. This leads to a lower time-averaged velocity gradient compared to a non-oscillating shear layer and therefore the filtering gives a less strong reduction of the subgrid stresses. Nevertheless, also in these case the HPF approach results in some grey-area mitigation and it has been applied to cases with smooth-surface separation such as a bump in a square cylinder [30], a tandem cylinder [31], and a three-element airfoil [23]. A possible improvement would consist of using high-pass filters that filter out all frequencies below a certain cut-off frequency. For the objective of the present work, however, the time-average based HPF suffices as a baseline to test the stochastic backscatter model, in particular because in the essential test cases considered below, the shear layers do not oscillate.

The model constant C ₁ has been calibrated to a value of 0.08 for decaying isotropic homogeneous turbulence using a fourth-order numerical method. In particular, a fourth-order low-dispersion symmetry-preserving finite-volume scheme [32, 33] is used for X-LES computations. This method is based on the skew-symmetric form of convection, ensuring the exact, discrete conservation of kinetic energy by convection, even for compressible flow. Thus, numerical errors stemming from the discretized convection terms do not interfere with the dissipation of kinetic energy by the subgrid stresses. Additionally, the numerical dispersion of the method has been minimized, along the lines of the DRP scheme of Tam and Webb [34], allowing accurate capturing of acoustic and vorticity waves with only eight grid cells per wavelength.

3 Stochastic Backscatter Model

A new stochastic backscatter model is considered that is based on the models of Leith [18] and Schumann [19]. These models include energy backscatter at the correct rate. The subgrid stress tensor is redefined as

$$\tau_{ij} = 2 \nu_{t} \left( S_{ij} - \tfrac{1}{3} \partial_{k} u_{k} \delta_{ij} \right) - \tfrac{2}{3} k \delta_{ij} - \tilde{f}_{d} R_{ij} , $$

with R _{i j} a random stress tensor that is responsible for the backscatter. This tensor is not modelled directly, but, following Leith, its divergence is modelled as the curl of a stochastic vector potential,

$$ \nabla \cdot \boldsymbol{R} = \nabla \times (C_{B} k \boldsymbol{\xi}) , $$

(2)

with C _B a model constant (C _B = 1 by default) and ξ(x,t) a vector of three independent stochastic variables with standard normal distribution: ξ _i = N(0,1).

The additional stochastic term f = ∇⋅R is effectively a random acceleration that is added to the momentum equation. As it is solenoidal, it does not induce pressure fluctuations and therefore will not function as a noise source. This can be understood from Lighthill’s acoustic analogy [35], in which a wave equation for the density perturbation ρ ^′ relative to the far-field density is obtained from the Navier–Stokes equations (without any approximation), given by

$$\frac{\partial^2 \rho^{\prime}}{\partial t^2} - {c_{0}^{2}} \frac{\partial^2 \rho^{\prime}}{\partial x_{i} \partial x_{i}} = \frac{\partial^2 T_{ij}}{\partial x_{i} \partial x_{j}} - \frac{\partial f_{i}}{\partial x_{i}} \, , $$

with c ₀ the far-field speed of sound, T _{i j} the Lighthill stress tensor, and f any acceleration added to the right-hand side of the momentum equation. In this analogy, all aerodynamic noise sources are contained in the terms on the right-hand side. When f is solenoidal, it drops from the right-hand side of this equation and therefore it will not produce any acoustic fluctuations.

Note that the magnitude of the backscatter term is proportional to the subgrid kinetic energy k. In X-LES, a single equation is solved for k in the entire flow domain. Thus, the value of k in an initial shear layer will be influenced by the value of k in the upstream, attached boundary layer. This boundary layer is typically in RANS mode and therefore k will represent the total turbulent kinetic energy there. A high value of k will be convected into the initial shear layer if the upstream boundary layer is turbulent, whereas k will be practically zero if the boundary layer is laminar. In the former case, the stochastic model may destabilize the shear layer, whereas in the latter case the stochastic model will be effectively switched off, allowing a natural laminar-to-turbulent transition of the shear layer.

Another consequence of the scaling with k is that when a fully developed shear layer is well resolved by LES, implying low subgrid kinetic energy, then the backscatter term will be relatively small. Hence, also only a relatively weak effect of the backscatter model is expected there. Remember that the aim of the present work is in the first place to mitigate the grey area and not to accurately model backscatter in a well-resolved LES. Nevertheless, the backscatter model will also be active in such regions and therefore the theoretical consistency of the backscatter model, as discussed in the introduction, is required so that the backscatter model behaves appropriately there.

To ensure the backscatter model is switched off when in RANS mode, the tensor R _{i j} is multiplied with the shielding function $\tilde {f}_{d}$. The shielding itself is not directly impacted by the backscatter model. There may be an indirect effect, as the backscatter is intended to induce fluctuations in the LES regions. If strong fluctuations are induced close to the effective RANS–LES interface, diffusing to some extent into the RANS region, then the value of f _d may be influenced, as it depends on the magnitude of the velocity gradient (both directly and indirectly through the eddy-viscosity coefficient). This influence can only be assessed in practice. In the first computations for more complex test cases indicated at the end of the introduction, no significant impact on the shielding was observed.

By construction, each stochastic variable ξ _i will be uncorrelated in space over distances larger than the filter width Δ and uncorrelated in time over time intervals larger than the subgrid time scale $\tau \sim {\Delta }/\sqrt {k}$. When the filter width is defined as the maximum of the mesh width in all directions, however, then the distance between grid points can be smaller than the filter width. In particular, this is the case for grid cells with high aspect ratios as typically found in initial shear layers. As motivated in the introduction, for distances smaller than the filter width, the stochastic variables will be correlated. Similarly, temporal correlation is introduced when the time step is smaller than the subgrid time scale τ, as is the case for the Schumann model. These correlations are obtained by solving stochastic differential equations for the stochastic variable ξ, as detailed below. Essentially, these stochastic differential equations result in the following spatial and temporal correlations, which rapidly decay for distances larger than the filter width and time intervals larger than the subgrid time scale:

$$ \left\langle \xi_{i}(\boldsymbol{x},t) \xi_{j}(\boldsymbol{y}, s) \right\rangle = \delta_{ij} \mathrm{e}^{-d^{2}/2} \mathrm{e}^{-\left|t-s\right|/\tau} , $$

(3)

with d = |x −y|/b, $b = \sqrt {C_{\Delta }} {\Delta }$, and $\tau = C_{\tau } {\Delta }/\sqrt {k}$, and with 〈.〉 the expectation of a stochastic variable. As stressed by Schumann, for the model to be Galilean invariant, this correlation should be interpreted in Lagrangian sense, i.e., x and y are the time-dependent coordinates of fluid particles. The default values for the model constants are C _Δ = 0.1 and C _τ = 0.05. These default values, including the value of C _B given above, have been calibrated in practice for the plain free shear layer considered in Section 4.2 below. Subsequently, the same values have been used for the round jet.

The stochastic subgrid-scale models of Leith and Schumann include energy backscatter at a rate that scales as κ ⁴ for wave numbers κ smaller than the cut-off wave number. Introducing spatial correlation may possibly alter this backscatter rate. For the spatial correlation of Eq. 3, this is not the case, as is shown in Appendix A.

3.1 Continuous stochastic differential equations

To create a stochastic variable ξ _i with temporal and spatial correlation, a stochastic Langevin-type differential equation is solved, given by

$$ \xi_{i} \mathrm{d} t + \tau \left( \frac{\partial \xi_{i}}{\partial t} + \boldsymbol{u}\cdot\nabla\xi_{i} \right) \mathrm{d} t = \sqrt{2\tau} \mathrm{d} W_{i} , $$

(4)

with dW _i (x,t) the differential of a Wiener process W _i (x,t) with the properties

$$\mathrm{d} W_{i}(\boldsymbol{x},t) = N(0,\mathrm{d} t) $$

and

$$ \left\langle \mathrm{d} W_{i}(\boldsymbol{x},t) \mathrm{d} W_{j}(\boldsymbol{y},s) \right\rangle = \delta_{ij} \mathrm{e}^{-d^{2}/2} \delta(t-s) \, \mathrm{d} t \, \mathrm{d} s . $$

(5)

Loosely speaking, dW _i is an infinitesimally small stochastic variable, with zero mean and variance dt, that is correlated in space but uncorrelated in time. Using the continuity equation, the Langevin equation can also be written in conservative form:

$$\rho\xi_{i} \, \mathrm{d} t + \tau \left( \frac{\partial \rho\xi_{i}}{\partial t} + \nabla\cdot(\rho\boldsymbol{u}\xi_{i}) \right) \mathrm{d} t = \sqrt{2\tau} \rho \, \mathrm{d} W_{i} . $$

To create a stochastic differential dW _i with the spatial correlation of Eq. 5, a purely spatial stochastic differential equation is solved, given by

$$ \mathrm{d}\boldsymbol{x} \left( I - b^{2}\frac{\partial^2}{\partial x_{1}^2} \right) \left( I - b^{2}\frac{\partial^2}{\partial x_{2}^2} \right) \left( I - b^{2}\frac{\partial^2}{\partial x_{3}^2} \right) \mathrm{d} W_{i} = 8 b^{3/2} \, \mathrm{d} V_{i} , $$

(6)

with I the identity operator and dx = dx ₁dx ₂dx ₃. The stochastic differential dV _i (x,t) has the properties

$$\mathrm{d} V_{i}(\boldsymbol{x},t) = N(0,\mathrm{d}\boldsymbol{x}\,\mathrm{d} t) $$

and

$$ \left\langle \mathrm{d} V_{i}(\boldsymbol{x},t) \mathrm{d} V_{j}(\boldsymbol{y},s) \right\rangle = \delta_{ij} \delta(\boldsymbol{x}-\boldsymbol{y}) \delta(t-s) \, \mathrm{d}\boldsymbol{x} \, \mathrm{d}\boldsymbol{y} \, \mathrm{d} t \, \mathrm{d} s , $$

(7)

that is, it is completely uncorrelated both in space and time.

In practice, one will start with drawing values for the stochastic differential dV _i independently at each spatial location (i.e., grid point) and at each time instance. Then, the stochastic differential dW _i is determined by solving (6) and finally the stochastic variable ξ _i is obtained by solving (4).

It is shown in Appendix B that the solution ξ _i of these stochastic differential equations essentially has the spatial and temporal correlation as defined in Eq. 3, interpreted in Lagrangian sense.

Note that Eq. 6 can be seen as an approximation of the following equation using the Laplacian operator:

$$\mathrm{d}\boldsymbol{x} \left( I - b^{2} \left( \frac{\partial^2}{\partial x_{1}^2} + \frac{\partial^2}{\partial x_{2}^2} + \frac{\partial^2}{\partial x_{3}^2} \right) \right) \mathrm{d} W_{i} = 8 b^{3/2} \, \mathrm{d} V_{i} , $$

with an error of order $\mathcal {O}(b^{4}) = \mathcal {O}({\Delta }^{4})$. Although more expensive to solve, this equation would be applicable to any type of grid, either structured or unstructured. Before using this formulation, however, the spatial correlation of its solution would have to be verified, similar to Appendix B, which is not a trivial matter.

3.2 Discretized stochastic differential equations

The stochastic differential equations are discretized in space and time by the following algorithm. First, a vector of three independent stochastic variables $\boldsymbol {\zeta }_{i,j,k}^{n} = N(0,1)$ is defined on a structured grid, with (i,j,k) the grid cell indices and n the time-step index. At each time step, new values of the three components ζ _m of $\boldsymbol {\zeta }_{i,j,k}^{n}$ are drawn at each grid cell, independently of the values of ζ _m at previous time steps and at other grid cells, so that they have the property

$$\left\langle (\zeta_{m})_{i,j,k}^{n} (\zeta_{m^{\prime}})_{i^{\prime},j^{\prime},k^{\prime}}^{n^{\prime}} \right\rangle = \delta_{mm^{\prime}} \delta_{ii^{\prime}} \delta_{jj^{\prime}} \delta_{kk^{\prime}} \delta_{nn^{\prime}} , $$

that is, they are uncorrelated both in space and time. This stochastic variable constitutes the discrete equivalent of the stochastic differential dV _m , which is approximated by

$$\mathrm{d} V_{m}(\boldsymbol{x}_{i,j,k},t^{n}) \approx \sqrt{\delta_{i} x \, \delta_{j} x \, \delta_{k} x \, \delta t} \, (\zeta_{m})_{i,j,k}^{n} , $$

with δ t the time step and δ _i x the mesh size in i-direction. For notational simplicity, the subscript m for the three components of $\boldsymbol {\zeta }_{i,j,k}^{n}$ will be dropped in the remainder of this section.

Next, at each time step, a spatially correlated stochastic variable $\eta _{i,j,k}^{n}$ is obtained by smoothing the stochastic variable $\zeta _{i,j,k}^{n}$ in space. This is done by solving the following set of implicit difference equations:

$$ (I-\beta_{i}{\delta_{i}^{2}})(I-\beta_{j}{\delta_{j}^{2}})(I-\beta_{k}{\delta_{k}^{2}}) (\lambda_{i,j,k} \eta_{i,j,k}^{n}) = \zeta_{i,j,k}^{n} , $$

(8)

with I the identity operator, β _i = (b/δ _i x)² the smoothing coefficient in i-direction, λ a suitable scaling coefficient defined below, and ${\delta _{i}^{2}}$ the second-order difference operator in i-direction,

$${\delta_{i}^{2}} f_{i,j,k} = f_{i+1,j,k} - 2 f_{i,j,k} + f_{i-1,j,k} . $$

The implicit smoothing requires solving a tridiagonal system per computational direction, which can be done efficiently using the Thomas algorithm. At the boundaries, Dirichlet boundary conditions (η = 0) are applied.

Equation 8 is in fact a discretization of the spatial stochastic differential (6) by central differences, with the stochastic differential dW approximated by

$$\mathrm{d} W(\boldsymbol{x}_{i,j,k},t^{n}) \approx \sqrt{\delta t} \eta_{i,j,k}^{n} , $$

implying that η essentially has the same spatial correlation as dW. Furthermore, it implies that η should have zero mean and a variance equal to one, just like ζ. Thus, the implicit smoothing operator should preserve both the mean value and the variance of ζ. The mean of η satisfies (8) with zero right-hand side and homogeneous boundary conditions, and therefore is equal to zero. Preserving the variance, independent of the mesh size, is ensured by defining λ as

$$\lambda_{i,j,k} = \frac{ (1+4\beta_{i})^{3/4} (1+4\beta_{j})^{3/4} (1+4\beta_{k})^{3/4} } { (1+2\beta_{i})^{1/2} (1+2\beta_{j})^{1/2} (1+2\beta_{k})^{1/2} } , $$

as is shown in Appendix C. Discretizing (6) and substituting the approximations for dV and dW by ζ and η, it follows that Eq. 8 forms a consistent discretization if λ satisfies

$$\lambda_{i,j,k} \rightarrow \frac{ 8 b^{3/2} }{ \sqrt{\delta_{i} x \, \delta_{j} x \, \delta_{k} x} } = 8 (\beta_{i}\beta_{j}\beta_{k})^{1/4} , $$

in the limit for zero mesh size (that is β _i →∞), which is indeed the case for the expression given above.

Note that strictly speaking, the discrete equation (8) is only a consistent discretization of the continuous equation (6) if the grid lines are orthogonal or, alternatively, if the three coordinates (x ₁, x ₂, and x ₃) are considered to be coordinates in the computational space instead of the physical space. The latter interpretation means that the distance d in Eq. 3 should also be measured in computational space. This distance is still properly defined and is of the same order as the distance in physical space. In fact, the distances in computational and physical space between two points lying on the same grid line are equal. Thus, non-orthogonality of the grid essentially does not influence the correlation between two points on the same grid line, but only between two points that are on different grid lines. But even for these points, the correlation as defined in Eq. 3 will still rapidly go to one for distances smaller than the filter width and to zero for distances larger than the filter width. This is the essential behaviour of the model and it is not altered by non-orthogonality. Nevertheless, one should avoid grids that are very skewed as this may still introduce some grid dependence in the computational results. Alternatively, the more generic Laplacian form discussed above (end of Section 3.1) could be used in the future to become fully independent of grid skewness.

Finally, a spatially and temporally correlated stochastic variable $\xi _{i,j,k}^{n}$ is obtained from the variable $\eta _{i,j,k}^{n}$ by taking one time step for the Langevin-type equation (4) in conservative form. This equation is discretized with a second-order central scheme in time (mid-point rule):

$$ (\rho\xi)_{i,j,k}^{n} + \frac{\tau}{\delta t} \left( (\rho\xi)_{i,j,k}^{n+1/2} - (\rho\xi)_{i,j,k}^{n-1/2} \right) + \tau \nabla_{i,j,k} \cdot \left( (\rho\boldsymbol{u})^{n} \xi^{n} \right) = \sqrt{\frac{2\tau}{\delta t}} \rho_{i,j,k}^{n} \eta_{i,j,k}^{n} , $$

(9)

where ∇ _i,j,k represents the discretized gradient operator. The values of the conservative variables (ρ, ρ u, and ρ ξ) at time t ⁿ are computed as

$$f^{n} = \tfrac{1}{2} (f^{n+1/2} + f^{n-1/2}) . $$

The convection term in the Langevin-type equation needs to be discretized in space. For this, a central skew-symmetric finite-volume discretization is used, consistent with the discretization of the flow equations [32]. The advantage of using central discretizations, both in time and space, is that the variance of ξ will be conserved and equal to the variance of η (that is, equal to one), as is demonstrated in Appendix D. If non-central discretizations are used, then the variance is not conserved and the coefficient of the right-hand side of Eq. 9 will have to be adapted to correct this effect.

The stochastic variable ξ as needed in Eq. 2 is a 3-component vector and therefore three temporal Langevin equations need to be solved. This can be done simultaneously with the main flow and turbulence-model equations. These three equations are solved in the complete flow domain, with the right-hand side $\boldsymbol {\eta }_{i,j,k}^{n} = 0$ when in RANS mode and at all external boundaries.

To test the effect of introducing spatial and temporal correlations, three different variants of the stochastic backscatter model will be considered: the basic backscatter model in which ξ is completely uncorrelated both in space and time, that is, it is equal to ζ; the backscatter model including only spatial correlations through (8), that is, ξ is equal to η; and finally the complete model including both spatial and temporal correlations through (8) and (9).

A final point in this section concerns the computational costs of the stochastic backscatter model. For the basic, uncorrelated model, the additional costs are negligible. Introducing the spatial and temporal correlations, however, does come at a price. For the spatial correlations, Eq. 8 needs to be solved only once per time step and due to the factoring in the three directions it can be solved efficiently with the Thomas algorithm. Thus, it only requires a few percent of additional computational effort. The temporal correlations are more expensive, as three additional transport equations equations need to be solved, increasing the total number of transport equations from seven to ten (an increase of 43%). Fortunately, the additional transport equations have a simpler structure than the basic flow equations (e.g., no diffusion terms) and are therefore less expensive. In practice, an increase of at most 25% is observed.

4 Results

4.1 Decaying isotropic homogeneous turbulence

Most DES methods have been calibrated for the decay of isotropic homogeneous turbulence, ensuring that the energy spectrum is captured with a − 5/3 slope. Likewise, this has been done for the baseline X-LES method, leading to a coefficient of C ₁ = 0.08 when using the low-dissipation fourth-order discretization. As a first step, it needs to be assessed that the stochastic backscatter model does not disrupt this calibration.

Computations have been performed on a 64³ grid and have been based on the experiment of Comte-Bellot and Corrsin [36]. In this experiment, the turbulence was generated by a grid with mesh size M = 5.08 cm and with an onset velocity of U ₀ = 10 m/s. The Reynolds number based on these scales is R e ₀ = U ₀ M/ν = 34,000. In the computations, a cubic box of size L = 11M is used with periodic boundary conditions. The initial solution consists of a random velocity field generated from the experimental energy spectrum at time t ⁺ = t U ₀/M = 42. The precise details of the computational set-up are given by Rozema [33].

Two X-LES computations in LES mode are considered: without stochastic model (baseline) and with the complete stochastic backscatter model (including both temporal and spatial correlations). For this case, the decay of turbulence in time implies that temporal high-pass filtering is not appropriate. Instead, filtering in one of the spatial directions could be applied, which is actually equivalent to filtering in time in the experimental set-up, in which the turbulence decay occurs in stream-wise direction and not in time. However, spatial filtering would have no effect as the mean velocity gradient equals zero and therefore no filtering is applied.

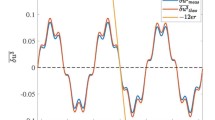
Figure 1 shows the computed energy spectra at the initial time t ⁺ = 42 and at two subsequent time levels t ⁺ = 98 and t ⁺ = 171. The spectra are compared to the experimental data of Comte-Bellot and Corrsin as well as to the − 5/3 Kolmogorov law for the last time instance. These results clearly show that for this case, with the cut-off well within the inertial range, the stochastic backscatter has little impact on the spectrum and does not lead to a pile-up of energy near the cut-off as might be feared. Thus, it appears that the backscatter model can be applied safely in well-resolved LES regions. Note that with the coefficient calibrated to C ₁ = 0.08, the computations match the − 5/3 slope at the last time instance, whereas the experimental data shows a somewhat lower slope.

Fig. 1

Energy spectrum at three subsequent time instances (t ⁺ = 42, 98, and 171) for decaying isotropic homogeneous turbulence computed with X-LES in LES mode on a 64³ grid without (baseline) and with the stochastic backscatter (SBS) model (with $E_{\text {tot}}^{0}$ the total kinetic energy at the initial time t ⁺ = 42)

4.2 Plane free shear layer

As a first test case to demonstrate the effectiveness of the stochastic backscatter model in mitigating the grey-area issue, the plane free shear layer from the experiment of Delville [37] is considered. As shown previously [7, 10], standard detached eddy simulations fail for this case, displaying an essentially 2D shear layer that is void of any resolved 3D turbulence even though the method is in LES mode. The simple stochastic eddy-viscosity model was used with some success to trigger 3D instabilities in the shear layer, eventually leading to full 3D turbulence downstream [7]. A further improvement was obtained by the high-pass filter (HPF) subgrid-scale model, substantially reducing the subgrid stresses in the initial shear layer, and as a result allowing instabilities to develop further upstream [14]. Subsequently, other authors have also used this case to test their approaches for grey-area mitigation [10, 13, 17].

In the experiment of Delville [37], the free shear layer starts from the trailing edge of a flat plate with free-stream velocities u ₁ = 41.54 m/s and u ₂ = 22.40 m/s at the different sides of the flat plate and with fully developed turbulent boundary layers at the trailing edge. The Reynolds number based on the momentum thickness at the high-speed side is R e _𝜃 = 2900 at the trailing edge. The shear layer develops in a 0.3 m × 0.3 m square test section of length 1.2 m. A self-similar flow with fully developed turbulence is reached well within the test section.

A computational domain is used with a length of 2.5 m (x-direction), a height of 2 m (y-direction) and a width of 0.15 m (z-direction). To obtain the correct velocity profiles at the trailing edge of the flat plate, the same settings are employed as proposed by Deck [10]: on the upper side the plate has a length of 820 mm and transition is triggered at 708 mm upstream of the trailing edge, while on the lower side the plate has a length of 460 mm and transition is triggered at 388 mm before the trailing edge.

A computational ‘test section’ is defined with a length of L = 1 m after the trailing edge and with a uniform grid in the x- and z-directions. Note that the grid deliberately has not been stretched in x-direction towards the trailing edge. Thus, the grid is more representative of the situation when a priori one does not know the location where the shear layer separates.

Most computations have been performed on a grid with 1.71 million cells and a mesh size h = 3.125 mm in x- and z-direction in the test section. The fourth-order, low-dispersion, symmetry-preserving finite-volume method has been used together with the second-order mid-point rule for the time integration. Time steps have been taken of size δ t = 8 ⋅10⁻⁴ L/u ₁, implying a convective CFL number, based on the maximum velocity u ₁, equal to CFL = u ₁ δ t/h = 1/4. Also a fine grid has been considered with half the mesh size and 13.7 million cells and using also half the time step. For all computations, the total time computed was at least 11.2L/u ₁ (14,000 time steps on the coarse grid) and the statistics have been gathered over the last 5.6L/u ₁.

Different stochastic models have been tested in combination with the HPF SGS model on the coarse grid of 1.71 million cells. For consistency with the previous computational results [7, 14], the X-LES coefficient is set to C ₁ = 0.05. A qualitative impression of the effect of the different models on the grey area is given in Fig. 2 in terms of instantaneous iso-surfaces of the Q-criterion. The left-hand side shows the complete ‘test section’ of 1 m, while the right-hand side shows a close-up of the initial shear layer. In the baseline computation (subfigure a), which only employs the HPF SGS model [14], a substantial part of the shear layer (about one quarter of the test region) essentially remains two dimensional, displaying only a Kelvin–Helmholtz type instability. Nevertheless, this already formed a significant improvement over standard X-LES or DES, which showed no 3D turbulence at all [7, 10]. The stochastic eddy-viscosity model [7] (subfigure b) gives some improvement over the baseline, with the onset of 3D instabilities shifting closer to the flat-plate trailing edge. This effect is more pronounced for the stochastic backscatter model (subfigure c), especially when the spatial and temporal correlations are introduced through the stochastic differential equations (subfigure d). In the latter case, the 3D instabilities start immediately after the trailing edge.

Fig. 2

Instantaneous iso-surfaces of $Q = {\Omega }^2 - S^2 = 500~ u_1^2/L^2$, coloured with the vorticity magnitude Ω, for the spatial shear layer computed with X-LES using different SGS models on the coarse grid (1.71 million cells)

Resolving the 3D instabilities closer to the trailing edge has a clear impact on the initial thickness and the growth rate of the shear layer as can be seen in Fig. 3. Both the initial thickness and the growth rate further downstream improve for each successive step starting from the baseline without any stochastic model and ending with the stochastic backscatter model with both spatial and temporal correlations. For the latter model, the momentum thickness lies close to the experiment beyond x = 0.2 m, while the vorticity thickness matches the experiment over the entire length of the shear layer. In the very initial shear layer, it appears that there is a better comparison between the computations and the experiment for the vorticity thickness than for the momentum thickness. The momentum thickness is an integral quantity and therefore depends on the complete velocity profile of the shear layer, whereas the vorticity thickness depends only on the maximum velocity gradient. Thus, although the maximum gradient may match the experiment in the very initial shear layer, this is apparently not the case for the complete velocity profile (as is also confirmed in Fig. 4a below for the velocity profile at x = 0.2 m).

Fig. 3

Thickness of the spatial shear layer computed with X-LES using different SGS models on the coarse grid (1.71 million cells) (SEV = stochastic eddy-viscosity model; SBS = stochastic backscatter model; SBS-spatial = SBS with spatial correlations; SBS-full = SBS with spatial and temporal correlations)

Fig. 4

Profiles of mean velocity, resolved normal stress, and resolved shear stress of the spatial shear layer computed with X-LES using different SGS models on the coarse grid of 1.71 million cells (y _1/2 is the location where the velocity u = (u ₁ + u ₂)/2) (abbreviations: see Fig. 3)

The reduced extent of the grey area, as well as its impact further down stream, is also visible in the profiles of the mean velocity and the resolved stresses, presented in Fig. 4. The lack of resolved turbulence in the baseline HPF result at the first station (x = 0.2 m) leads to a velocity profile with a local minimum, still showing an imprint of the two upstream boundary layers, contrary to the experimental results. At the stations further downstream, the baseline HPF computation strongly overpredicts the turbulence levels (both normal and shear stresses), which causes the shear layer to grow too rapidly. The stochastic backscatter model strongly improves the turbulence level at the first station and as a consequence the local minimum in the velocity profile at that station is completely removed and also the turbulence levels as well as the velocity profiles match the experiment more closely further downstream. The peak level of the stresses is now overpredicted at the first station, but approaches the experiment at the other stations, with exception of the normal stress at x = 0.95 m (possibly an upstream effect of the grid coarsening starting at x = 1 m). By including the spatial and temporal correlations in the model, both the velocity profile and the stress levels get closer to the experiment, in particular at the upper and lower tails of the profiles. The main difference with the experiment that remains, is a higher mean velocity at the upper side at the first station. This may be attributed to a lack of resolved turbulence coming from the upper boundary layer (which is thicker than the lower one), which could probably only be remedied by adding synthetic turbulence at the flat-plate trailing edge.

The power spectra of the velocity component u in x-direction are compared to the experiment at two stations along the shear-layer centreline (x = 0.2 m and x = 0.8 m) in Fig. 5. A very strong impact is seen at the first station (subfigure a). Without any stochastic model, the energy level is much too low over the complete frequency range. Using the stochastic eddy-viscosity model, the solution is still dominated by two-dimensional span-wise vortices, giving a narrow band in the spectrum. This is clearly improved by the stochastic backscatter model, again in particular when the correlations are included, giving a broader spectrum and a result close to the experiment, until the cut-off frequency (corresponding to the filter width) is reached. At the second station, where the shear layer is fully developed, the impact of the stochastic models is much weaker, which is consistent with the results for decaying isotropic homogeneous turbulence. The power spectrum lies close to the experiment for all models, except for a small increase at the lowest frequencies when no stochastic model is included (subfigure b). Since the integral of the power spectrum is equal to the normal stress, this increase is in-line with the overprediction of the normal stresses that can be seen in Fig. 4b. This is caused by the larger grey area in the initial shear layer when no stochastic model is used, which influences the further development of the shear layer far downstream.

Fig. 5

Power spectral densities (PSD) of the velocity component u in x-direction for the spatial shear layer computed with X-LES using different SGS models (abbreviations: see Fig. 3)

To assess the grid sensitivity of the results, computations with the new stochastic backscatter model have been performed on the two grid levels, using the X-LES coefficient as calibrated for decaying isotropic homogeneous turbulence (C ₁ = 0.08). On the fine grid of 13.7 million cells, small-scale instabilities are captured in the initial shear layer immediately downstream of the trailing edge (Fig. 6), showing that the effectiveness of the stochastic backscatter model is maintained. The shear-layer thickness and the energy spectra on the two grid levels are compared in Figs. 7 and 8, including also the coarse-grid result with the old X-LES coefficient (C ₁ = 0.05) for completeness. Overall, the grid dependence of the results (as well as the sensitivity to the coefficient) is clearly weaker than the variation in results of the different subgrid-scale models on the coarse grid as shown above. The strongest grid dependence is seen in the energy spectra for which the tail starts to drop at higher frequencies on the fine grid due to the smaller filter width, as it should. Also, there is some grid dependence in the momentum thickness: the growth rate of the shear layer is consistent with experiment on the fine grid and on the coarse grid with the lower C ₁ value, but it is somewhat overpredicted with the higher C ₁ value.

Fig. 6

Instantaneous iso-surfaces of $Q = 500~ u_1^2/L^2$ for the spatial shear layer computed with X-LES using the stochastic backscatter HPF SGS model with spatial and temporal correlations on the fine grid (13.7 million cells)

Fig. 7

Thickness of the spatial shear layer computed with X-LES using the stochastic backscatter HPF SGS model with spatial and temporal correlations on different grid levels and with different values of the X-LES coefficient C ₁

Fig. 8

Power spectral densities (PSD) of the velocity component u in x-direction for the spatial shear layer computed with X-LES using the stochastic backscatter HPF SGS model with spatial and temporal correlations on different grid levels and with different values of the X-LES coefficient C ₁

Finally, to illustrate how the backscatter model works, the distribution of the first component of the stochastic vector ξ is shown in Fig. 9 for both grid levels. The variable is multiplied with the sub-grid kinetic energy k, as that is how it appears in the stochastic forcing term of Eq. 2. Visually, the spatial structures are dominated by scales ranging between the filter width Δ = 3.125 mm and a width of about 10 mm on the coarse grid. These scales are reduced by a factor two on the fine grid. Furthermore, the spatial structures are essentially locally isotropic. Both the sizes and the isotropy of the structures are consistent with the spatial correlations as defined by Eq. 3. As a consequence, the stochastic forcing will generate disturbances with similar isotropic scales. Without the spatial correlations, non-isotropic structures would have resulted with scales of the order of the filter width in the x-direction and of the order of the mesh width in the y-direction, which is much smaller than the filter width at the centre of the initial shear layer. Then, the stochastic forcing also would have generated disturbances of (much) smaller size in y-direction, which are less effective in influencing the development of the initial shear layer.

Fig. 9

Distribution of the stochastic variable ξ ₁ (multiplied with sub-grid kinetic energy k) in a plane y = constant for the spatial shear layer computed with X-LES using the stochastic backscatter HPF SGS model with spatial and temporal correlations on two grid levels

In conclusion, the stochastic backscatter model with spatial and temporal correlations is capable of strongly reducing the grey area for this case and clearly outperforms the stochastic eddy-viscosity model. It shows that a substantial improvement can be made for grey-area mitigation methods that rely on reducing the subgrid stresses, such as the HPF model, by adding stochastic forcing to enhance the development of instabilities. Potentially, the stochastic backscatter model can also be added to and further improve the results of other recent proposals, such as those of Mockett et al. [17] and Shur et al. [13]. In particular, the results of Mockett et al. were comparable to those of the HPF model without stochastic forcing on a practically identical coarse grid. Naturally, the results show some dependence on the grid level and the X-LES coefficient, but without reducing its effectiveness in grey-area mitigation.

4.3 Round jet at Mach 0.9

A second case that strongly suffers from the grey-area problem for standard detached eddy simulations, as shown for example by Spalart [8], is the computation of a plain round jet. Like for the plane shear layer, there is no recirculation of turbulent flow that could destabilize the initial shear layer of the jet. Here, a cold, compressible jet is considered with a Mach number of 0.9 and a Reynolds number R e _D = 1.1 ⋅ 10⁶ based on the nozzle diameter D and the nozzle exit velocity U _jet. A range of experimental data is available for this case, including Arakeri et al. [38], Bridges et al. [39], Lau et al. [40, 41], and Simonich et al. [42].

The definition of this test case follows the lines of Shur et al. [43]. A computational domain is used that has a conical shape extending from 10D upstream of the nozzle exit to 70D downstream, with the outer boundary growing from 15D to 30D. Three multi-block structured grids are employed (labelled G1, G2, and G3) with respectively 1.5, 4.2, and 8.4 million grid cells. Grids G2 and G3 only differ in the number of cells in circumferential direction (80 and 160). More details of the grids are given by Shur et al. [43]. The interior domain of the nozzle is not represented in the computational domain. Instead, profiles of velocity, k, and ω are prescribed at the nozzle exit. These have been obtained from a precursor SST k– ω RANS computation of the nozzle interior.

X-LES computations have been performed using the fourth-order low-dispersion symmetry-preserving scheme, explicit fourth-order Runge–Kutta time integration, and an X-LES coefficient of C ₁ = 0.05. Time steps have been used of 0.002D/U _jet on all three grids. The total time computed equalled 1100D/U _jet, with statistics gathered over the last 500D/U _jet.

Three different approaches have been tested: a baseline without any grey-area mitigation, the HPF SGS model, and the HPF SGS model extended with the stochastic backscatter model with spatial and temporal correlations. Without mitigation, the jet displays essentially the same grey-area problem as the plane shear layer, but less severe, as can be seen in Fig. 10a. Initially, the jet shear layer shows hardly any vortical structures, then it starts to develop large-scale vortex rings which eventually develop into full 3D turbulence. The HPF model (Fig. 10b) considerably accelerates this process, with the vortex rings starting close to the nozzle and rapidly breaking up into small scale structures. Finally, the stochastic backscatter model even further reduces the grey area, with the vortex rings breaking up almost immediately at the nozzle lip.

Fig. 10

Instantaneous iso-surfaces of $Q = {\Omega }^2 - S^2 = 20~ U_{\text {jet}}^2/D^2$, coloured with the vorticity magnitude Ω, for the Mach 0.9 jet computed with X-LES using different SGS models on the fine grid G3

The profiles of the mean velocity and the velocity fluctuations along the jet centreline (r = 0) are compared to the different experimental results in Fig. 11. The baseline computation clearly underpredicts the length of the potential core, even on the fine grid G3. Furthermore, it shows a significant disturbance of the centreline velocity in the core. Using the HPF model increases the length of the potential core on the fine grid, consistent with the experimental results, but it still shows a small disturbance of the velocity in the core. Using the stochastic backscatter model, the length of the potential core is not only consistent with experiment on the finest grid, but it is also not much smaller on the coarser grids. The mean centreline velocity lies within the experimental range on all grids downstream of the end of the potential core. The velocity fluctuations also lie within the experimental range on the fine grid. On the two coarse grids, although the peak of the velocity fluctuations is predicted further upstream, it has clearly shifted closer to the experiments compared to the results with only the HPF model. Furthermore, the disturbance in the core is fully removed, even on the coarsest grid G1. Clearly, the weakest grid dependence is found with the stochastic backscatter model.

Fig. 11

Mean velocity and velocity fluctuations (RMS value) along jet centreline computed with X-LES using different SGS models and on different grids

The radial velocity profiles at four stations (Fig. 12) essentially show the same tendency as the centreline profile. The best comparison to the experiment, and the weakest grid dependence, is found with the stochastic backscatter model. Underprediction of the mean centreline velocity for the baseline results is accompanied by a too strong thickening of the jet as well as an overprediction of the velocity fluctuations at the first two stations and an underprediction at the latter two. These effects are diminished with the HPF model and even more so with the stochastic backscatter model, especially on the coarser grids G1 and G2.

Fig. 12

Mean velocity and velocity fluctuations (RMS value) at four stations computed with X-LES using different SGS models and on different grids (mean velocity offset with 0.5, 1, and 1.5 and velocity fluctuations offset with 0.2, 0.4, and 0.6 at x = 8, 12, and 16D, respectively)

The impact of the stochastic backscatter model is the strongest close to the nozzle lip, as could already be seen from the instantaneous iso-surfaces of Q. It can also be seen from the velocity profiles along the lip line r = R (Fig. 13), where substantial velocity fluctuations are present immediately after the lip with the backscatter model, while they need some distance (one or two nozzle diameters) to grow with the baseline and HPF models, ending in a sharp peak in the velocity fluctuations themselves as well as leading to a peak in the mean velocity. The peak in the velocity fluctuations is substantially reduced with the backscatter model, while the peak in the mean velocity is completely removed, leading to an overall better comparison with the experiment.

Fig. 13

Mean velocity and velocity fluctuations (RMS value) along jet lip line computed with X-LES using different SGS models on the fine grid G3

5 Conclusions

A new method has been presented for accelerating the development of resolved turbulence in free shear layers in the context of non-zonal detached eddy simulations. In standard DES, this development may be unrealistically slow, in particular when there is no significant recirculation of resolved turbulence back to the onset of flow separation, and a substantial so-called grey area may be present in which significant resolved turbulence is lacking, even though the computation is in LES mode. In order to induce the development of 3D instabilities in the initial free shear layers, stochastic forcing is added in the form of a stochastic backscatter model with spatial and temporal correlations for scales smaller than the subgrid scales. This approach is combined with a high-pass filtered SGS model that reduces the level of subgrid stresses in the initial shear layers.

The new method strongly reduces the grey area as has been demonstrated both for the plane free shear layer and for the round jet, giving a clear improvement over computations that only reduce the level of subgrid stresses through the HPF SGS model. For the free shear layer in particular, 3D instabilities start immediately at the trailing edge, instead of being delayed for one quarter of the test section. This leads to a broad energy spectrum, indicating fully developed turbulence, already at 20% of the test section as well as a correct growth rate downstream of that location. Furthermore, the new model is also effective on relatively coarse grids, reducing the grid dependence compared to computations using only the HPF SGS model. As the stochastic backscatter model gives improved results when added to the HPF approach, it also has the potential to further improve the results of other recently proposed methods [13, 17] that reduce the level of subgrid stresses and that give similar results to the HPF approach.

Finally, there are several directions open for future research. First of all, application to more complex test case is on-going [23,24,25]. Second, for the jet case, the assessment of the far-field noise is of interest. Although the backscatter model has been formulated analytically such that it should not generate noise artificially, this is not necessarily maintained by the numerical discretization and therefore needs to be verified in practice. The last question is whether the stochastic backscatter model will also be beneficial for wall-modelled LES. This is not unlikely as others have used stochastic forcing to resolve the log-layer mismatch. In wall-modelled LES the RANS–LES interface is located well within the boundary layer, and it may be expected that close to this interface high values of the (subgrid) kinetic energy k will diffuse from the RANS zone into the LES zone. Thus, the stochastic backscatter model will then be active there (as it scales with k), possibly mitigating a potential lack of resolved turbulence. Further research would be needed to evaluate this in practice, possibly requiring reassessment of the model coefficients.

Appendices

Appendix A: Rate of Backscatter

The new stochastic backscatter model includes spatial correlation in the stochastic variables, contrary to the models of Leith and Schumann. In this section, it is shown that this spatial correlation does not alter the scaling of the rate of backscatter as κ ⁴ for wave numbers κ → 0.

Consider a homogeneous stochastic forcing term f _i (x,t) added to the right-hand side of the momentum equation:

$$\frac{\partial u_{i}}{\partial t} + {\ldots} = f_{i}(\boldsymbol{x},t) , $$

with its spatial Fourier transform $\hat {f}_{i}(\boldsymbol {\kappa },t)$ given by

$$\hat{f}_{i}(\boldsymbol{\kappa},t) = {\int}_{\mathbb{R}^{3}} f_{i}(\boldsymbol{x},t) \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}\cdot\boldsymbol{x}} \mathrm{d}\boldsymbol{x} . $$

Let C _{i j} (r,t) be the two-point correlation of f _i ,

$$C_{ij}(\boldsymbol{r},t) = \left\langle f_{i}(\boldsymbol{x},t) f_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle , $$

which is independent of x due to homogeneity, and let $\hat {R}_{ij}(\boldsymbol {\kappa },t)$ be the covariance of $\hat {f}_{i}$,

$$\hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) = \left\langle \overline{\hat{f}_{i}(\boldsymbol{\kappa},t)} \hat{f}_{j}(\boldsymbol{\kappa}^{\prime},t) \right\rangle . $$

The two-point correlation and the covariance are related by

$$ \begin{array}{llllllll} \hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) &= {\int}_{\mathbb{R}^{3}} {\int}_{\mathbb{R}^{3}} \left\langle f_{i}(\boldsymbol{x},t) f_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle \mathrm{e}^{\mathrm{i}\boldsymbol{\kappa}\cdot\boldsymbol{x}} \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}^{\prime}\cdot(\boldsymbol{x}+\boldsymbol{r})} \mathrm{d}\boldsymbol{x} \, \mathrm{d}(\boldsymbol{x}+\boldsymbol{r}) \\ &= {\int}_{\mathbb{R}^{3}} \mathrm{e}^{\mathrm{i}(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime})\cdot\boldsymbol{x}} \mathrm{d}\boldsymbol{x} {\int}_{\mathbb{R}^{3}} \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}^{\prime}\cdot\boldsymbol{r}} C_{ij}(\boldsymbol{r},t) \mathrm{d}\boldsymbol{r} \\ &= 2\pi\delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) \hat{C}_{ij}(\boldsymbol{\kappa}^{\prime},t) \end{array} $$

(10)

so that

$$ \hat{C}_{ij}(\boldsymbol{\kappa},t) = \frac{1}{2\pi} {\int}_{\mathbb{R}^{3}} \hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) \mathrm{d}\boldsymbol{\kappa}^{\prime} . $$

(11)

The rate of backscatter at a wave number κ is determined by the spectrum function $\hat {F}(\kappa ,t)$ of f _i [44]. Here, $\hat {F}$ is defined analogous to the energy spectrum function E(κ) of the velocity field as defined in Pope, section 6.5 [45]:

$$\hat{F}(\kappa,t) = \oint_{S_{\kappa}} \hat{C}_{ii}(\boldsymbol{\kappa},t) \mathrm{d} S_{\kappa} $$

with S _κ the sphere around the origin with radius κ. The spectrum function $\hat {F}$ should scale as κ ⁴ for wave numbers smaller than the cut-off wave number κ _c ≈ π/Δ.

If f _i is directly defined as a spatially uncorrelated stochastic variable, then C _{i j} = C δ _{i j} Δ³ δ(r) (with C constant in case of homogeneity), implying $\hat {C}_{ij} = C{\Delta }^{3}\delta _{ij}$ and $\hat {F} = 12\pi C{\Delta }^{3}\kappa ^{2}$ (as δ _{i i} = 3 and the surface of a sphere equals 4π κ ²). Thus, such an approach would give the wrong scaling of the power spectrum.

The correct scaling is obtained if f _i is defined as the gradient of a spatially uncorrelated stochastic variable ξ _i , formulated in case of the Leith model as

$$f_{i}(\boldsymbol{x},t) = \varepsilon_{ijk}\frac{\partial \xi_{k}}{\partial x_{j}} , $$

with ε _{i j k} the alternating symbol. In this case, the Fourier transform of the two-point correlation D _{i j} of ξ _i is given by $\hat {D}_{ij} = D{\Delta }^{3}\delta _{ij} = \tfrac {1}{3} \hat {D}_{kk} \delta _{ij}$ and its covariance by $\hat {S}_{ij} = \tfrac {2}{3} \pi \hat {D}_{kk} \delta _{ij}\delta (\boldsymbol {\kappa }-\boldsymbol {\kappa }^{\prime })$, according to Eq. 10. One then finds that

$$\begin{array}{llllllll} \hat{R}_{ii}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) &= \varepsilon_{ijk}\varepsilon_{ilm}(-\mathrm{i}\kappa_{j})(\mathrm{i}\kappa^{\prime}_{l}) \hat{S}_{km}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) \\ &= (\delta_{jl}\delta_{km} - \delta_{jm}\delta_{kl})\kappa_{j}\kappa^{\prime}_{l} \tfrac{2}{3}\pi\hat{D}_{ii} \delta_{km} \delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) = \tfrac{4}{3}\pi\hat{D}_{ii} \kappa^{2} \delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) , \end{array} $$

which implies upon substitution in Eq. 11 that

$$\hat{C}_{ii} = \tfrac{2}{3} \hat{D}_{ii} \kappa^{2} = 2D {\Delta}^{3} \kappa^{2} . $$

It follows that the power spectrum $\hat {F} = 8\pi D{\Delta }^{3}\kappa ^{4}$ has the correct scaling.

Finally, consider the case that ξ _i is spatially correlated according to

$$D_{ij} = \left\langle \xi_{i}(\boldsymbol{x},t) \xi_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle = D \delta_{ij}\mathrm{e}^{-d^{2}/2} , $$

with d = |r|/b and $b = \sqrt {C_{\Delta }} {\Delta } \approx \sqrt {C_{\Delta }} \pi / \kappa _{c}$. Taking the Fourier transform of D _{i j} gives

$$\hat{D}_{ij} = D \delta_{ij} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

so that

$$\hat{C}_{ii} = \tfrac{2}{3} \hat{D}_{ii} \kappa^{2} = 2D \kappa^{2} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

following the same derivation as above, and finally

$$\hat{F} = 8\pi D\kappa^{4} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

which again scales as κ ⁴ for κ ≪ κ _c .

Appendix B: Correlations of Solutions of the Stochastic Differential Equations

Consider the Langevin-type equation (4) and the spatial stochastic differential equation (6). In this appendix, it is shown that the solution of these equations has the desired spatial and temporal correlation of Eq. 3, interpreted in Lagrangian sense, in case of a uniform flow.

Let G(x,t) be the Green’s function satisfying the equation

$$G + \tau \left( \frac{\partial G}{\partial t} + \boldsymbol{u}\cdot\nabla G \right) = \delta(\boldsymbol{x}) \delta(t) , $$

for a constant velocity u. Applying Fourier transformations of this equation both in space and time results in the following expression for the Fourier transform $\hat {G}$ of G:

$$\hat{G}(\boldsymbol{\kappa},\omega) = \frac{1}{(2\pi)^{2}} \frac{1}{1 + \mathrm{i}\tau\omega + \mathrm{i}\tau\boldsymbol{u}\cdot\boldsymbol{\kappa}} \, , $$

with κ the spatial wave number vector and ω the angular frequency. Applying inverse Fourier transforms, first in time and then in space, gives

$$G(\boldsymbol{x},t) = \frac{1}{\tau} H(t) \mathrm{e}^{-t/\tau} \delta(\boldsymbol{x}-\boldsymbol{u}t) . $$

Using the Green’s function, a general solution of Eq. 4 for arbitrary dW _i can be written as

$$\begin{array}{llllllll} \xi_{i}(\boldsymbol{x},t) &= {\int}_{\mathbb{R}^{3}} {\int}_{-\infty}^{\infty} G(\boldsymbol{x}-\boldsymbol{x}^{\prime},t-t^{\prime}) \sqrt{2\tau} \, \mathrm{d}\boldsymbol{x}^{\prime} \, \mathrm{d} W_{i}(\boldsymbol{x}^{\prime},t^{\prime}) \\ &= {\int}_{-\infty}^{\infty} \sqrt{\tfrac{2}{\tau}} H(t-t^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \, \mathrm{d} W_{i}(\boldsymbol{x}-\boldsymbol{u}(t-t^{\prime}),t^{\prime}) . \end{array} $$

Given the spatio-temporal correlation of dW _i defined by Eq. 5, the following spatio-temporal correlation is found for ξ _i :

$$\begin{array}{llllllll} \left\langle \xi_{i}(\boldsymbol{x},t) \xi_{j}(\boldsymbol{y},s) \right\rangle &= {\int}_{-\infty}^{\infty} {\int}_{-\infty}^{\infty} \tfrac{2}{\tau} H(t-t^{\prime}) H(s-s^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \mathrm{e}^{(s^{\prime}-s)/\tau} \\ &\qquad \left\langle \mathrm{d} W_{i}(\boldsymbol{x}-\boldsymbol{u}(t-t^{\prime}),t^{\prime}) \, \mathrm{d} W_{j}(\boldsymbol{y}-\boldsymbol{u}(s-s^{\prime}),s^{\prime}) \right\rangle \\ &= {\int}_{-\infty}^{\infty} {\int}_{-\infty}^{\infty} \delta_{ij} \tfrac{2}{\tau} H(t-t^{\prime}) H(s-s^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \mathrm{e}^{(s^{\prime}-s)/\tau} \delta(t^{\prime}-s^{\prime}) \\ &\qquad \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s-t^{\prime}+s^{\prime})\right|^{2} \right) \mathrm{d} t^{\prime} \, \mathrm{d} s^{\prime} \\ &= \delta_{ij} \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s)\right|^{2} \right) {\int}_{-\infty}^{\min(t,s)} \tfrac{2}{\tau} \mathrm{e}^{(2t^{\prime}-t-s)/\tau} \mathrm{d} t^{\prime} \\ &= \delta_{ij} \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s)\right|^{2} \right) \mathrm{e}^{-|t-s|/\tau} , \end{array} $$

which is indeed equivalent with Eq. 3 with x and y replaced by the Lagrangian coordinates x −u t and y −u s.

Next, let G(x) be the 1D Green’s function satisfying the equation

$$\left( 1 - b^{2} \frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} \right) G = \delta(x) , $$

which is given by

$$G(x) = \frac{1}{2b} \mathrm{e}^{-\left|x\right|/b} . $$

A general solution of Eq. 6 for arbitrary dV _i can then be written as

$$\mathrm{d} W_{i}(\boldsymbol{x},t) = {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) 8 b^{3/2} \, \mathrm{d} V_{i}(\boldsymbol{x}^{\prime},t) , $$

with $G_{3}(\boldsymbol {x}-\boldsymbol {x}^{\prime }) = G(x_{1}-x^{\prime }_{1}) G(x_{2}-x^{\prime }_{2}) G(x_{3}-x^{\prime }_{3})$. If dV _i is completely uncorrelated both in space and time, as defined by Eq. 7, then it follows that

$$\begin{array}{llllllll} \left\langle \mathrm{d} W_{i}(\boldsymbol{x},t) \mathrm{d} W_{j}(\boldsymbol{y},s) \right\rangle &= 64 b^{3} {\int}_{\mathbb{R}^{3}} {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) G_{3}(\boldsymbol{y}-\boldsymbol{y}^{\prime}) \left\langle \mathrm{d} V_{i}(\boldsymbol{x}^{\prime},t) \mathrm{d} V_{j}(\boldsymbol{y}^{\prime},s) \right\rangle \\ &= 64 b^{3} \delta_{ij} \delta(t-s) {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) G_{3}(\boldsymbol{y}-\boldsymbol{x}^{\prime}) \mathrm{d} \boldsymbol{x}^{\prime} \\ &= b^{-3} \delta_{ij} \delta(t-s) {\prod}_{m=1}^{3} {\int}_{\mathbb{R}} \mathrm{e}^{-\left|x_{m}-x^{\prime}_{m}\right|/b} \mathrm{e}^{-\left|y_{m}-x^{\prime}_{m}\right|/b} \mathrm{d} x^{\prime}_{m} \\ &= \delta_{ij} \delta(t-s) {\prod}_{m=1}^{3} \left( 1 + \tfrac{1}{b}\left|x_{m}-y_{m}\right| \right) \mathrm{e}^{-\left|x_{m}-y_{m}\right|/b} \\ &= \delta_{ij} \delta(t-s) \left( \mathrm{e}^{-\left|\boldsymbol{x}-\boldsymbol{y}\right|^{2}/(2b^{2})} + \mathcal{O}(\left|\boldsymbol{x}-\boldsymbol{y}\right|^{3}) \right) . \end{array} $$

For small distances, this is the spatio-temporal correlation of dW _i as defined by Eq. 5 up to third order in the distance. For large distances, this correlation rapidly decays, ensuring the correct scaling of the rate of backscatter.

Appendix C: Preservation of the Variance in the Discretized Spatial Stochastic Differential Equation

Consider the 1D stochastic differential equation

$$(1-{\beta\delta_{i}^{2}}) \eta^{\prime}_{i} = \zeta_{i} , $$

with i the grid-cell index, β the smoothing coefficient, and ${\delta _{i}^{2}}$ the second-order difference operator. The stochastic variable ζ _i = N(0, 1) is spatially uncorrelated,

$$\left\langle\zeta_{i} \zeta_{j}\right\rangle = \delta_{ij} . $$

We wish to determine the variance of the smoothed variable η ^′.

Let G _i be the discrete Green’s function satisfying the equation

$$(1-{\beta\delta_{i}^{2}}) G_{i} = \delta_{i0} . $$

Then, the general solution of the 1D stochastic differential equation (assuming periodicity) is given by

$$\eta^{\prime}_{i} = {\sum}_{j} G_{i-j} \zeta_{j} , $$

so that the variance of $\eta ^{\prime }_{i}$ is given by

$$\left\langle(\eta^{\prime}_{i})^{2}\right\rangle = {\sum}_{j} {\sum}_{k} G_{i-j} G_{i-k} \left\langle\zeta_{j} \zeta_{k}\right\rangle = {\sum}_{j} G_{i-j}^{2} = N \left|G\right|^{2} , $$

with N the number of grid cells and |G| the L ² norm of G.

Consider the discrete Fourier transform $\hat {G}_{k}$ of the Green’s function

$$\hat{G}_{k} = \frac{1}{N} {\sum}_{i} G_{i} \mathrm{e}^{-\mathrm{i} \theta_{k} i} $$

with 𝜃 _k = 2π k/N. Applying the Fourier transform to the equation for the Green’s function, one finds

$$\hat{G}_{k} = \frac{1}{N} (1 + 2\beta(1-\cos\theta_{k}) )^{-1} . $$

Thus, the variance of $\eta ^{\prime }_{i}$ is given by

$$\left\langle(\eta^{\prime}_{i})^{2}\right\rangle = N {\sum}_{k} \left|\hat{G}_{k}\right|^{2} = \frac{1}{N} {\sum}_{k} (1 + 2\beta(1-\cos\theta_{k}) )^{-2} . $$

In the limit for zero mesh size (i.e., δ 𝜃 = 2π/N → 0), this summation becomes an integral over the wave number 𝜃, so that

$$\begin{array}{llllllll} \left\langle(\eta^{\prime}_{i})^{2}\right\rangle &= \frac{1}{2\pi} {\int}_{0}^{2\pi} (1 + 2\beta(1-\cos\theta) )^{-2} \mathrm{d}\theta = \frac{1}{\pi} {\int}_{0}^{\pi} (1 + 2\beta(1-\cos\theta) )^{-2} \mathrm{d}\theta \\ &= \frac{1}{\pi} \frac{2}{1+4\beta} \left[ \frac{ \beta \sin\theta }{ 1 + 2\beta (1+\cos\theta) } + \frac{ 1 + 2\beta }{ \sqrt{1+4\beta} } \arctan\left( \sqrt{1+4\beta} \tan\left( \tfrac{1}{2}\theta\right) \right) \right]_{0}^{\pi} \\ &= \frac{ 1 + 2\beta }{ (1+4\beta)^{3/2} } \end{array} $$

Finally, it follows that to obtain a stochastic variable with unit variance, $\eta ^{\prime }_{i}$ should be scaled as

$$\eta_{i} = \frac{ (1+4\beta)^{3/4} }{ (1 + 2\beta)^{1/2} } \eta^{\prime}_{i} . $$

In 3D, this scaling should be applied for each computational direction.

Appendix D: Preservation of the Variance in the Discretized Langevin-Type Equation

Consider the Langevin-type equation in primitive form, discretized as

$$\xi^{n} + \frac{\tau}{\delta t} \left( \xi^{n+1/2} - \xi^{n-1/2} \right) + \tau \boldsymbol{u}^{n} \cdot \nabla\xi^{n} = \sqrt{\frac{2\tau}{\delta t}} \eta^{n} , $$

with $\xi ^{n} = \tfrac {1}{2} (\xi ^{n+1/2} + \xi ^{n-1/2})$.

First, no flow (u = 0) is considered, in which case

$$\left( 1 + \frac{\delta t}{2\tau} \right) \xi^{n+1/2} = \left( 1 - \frac{\delta t}{2\tau} \right) \xi^{n-1/2} + \sqrt{\frac{2\delta t}{\tau}} \eta^{n} . $$

Given that 〈(η ⁿ)²〉 = 1 and 〈η ⁿ ξ ^n−1/2〉 = 0, and assuming that 〈(ξ ^n−1/2)²〉 = 1, it follows that

$$\left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left\langle(\xi^{n+1/2})^{2}\right\rangle = \left( 1 - \frac{\delta t}{2\tau} \right)^{2} + \frac{2\delta t}{\tau} , $$

so that

$$\left\langle(\xi^{n+1/2})^{2}\right\rangle = 1 . $$

Thus, if the initial variance of ξ equals one, then this variance is locally conserved by the central time discretization.

Including the convective term, local conservation of the variance cannot be easily proven. However, one can show global conservation up to third order in the time step. Let ξ be the vector with the values of ξ at all grid points as its components. The Langevin-type equation, discretized both in space and time, can then be written as

$$\boldsymbol{\xi}^{n} + \frac{\tau}{\delta t} \left( \boldsymbol{\xi}^{n+1/2} - \boldsymbol{\xi}^{n-1/2} \right) + \tau \boldsymbol{C}(\boldsymbol{u}^{n}) \boldsymbol{\xi}^{n} = \sqrt{\frac{2\tau}{\delta t}} \boldsymbol{\eta}^{n} , $$

with C the discretized convection operator. For a symmetry-preserving discretization, this operator is skew-symmetric, that is, ξ ^T C ξ = 0 for any ξ. Rewriting the equation as

$$\left( \boldsymbol{I} + \frac{\delta t}{2\tau}\boldsymbol{I} + \tfrac{1}{2}\delta t\boldsymbol{C} \right) \boldsymbol{\xi}^{n+1/2} = \left( \boldsymbol{I} - \frac{\delta t}{2\tau}\boldsymbol{I} - \tfrac{1}{2}\delta t\boldsymbol{C} \right) \boldsymbol{\xi}^{n-1/2} + \sqrt{\frac{2\delta t}{\tau}} \boldsymbol{\eta}^{n} , $$

and taking the square of the L ²-norm of the left-hand and right-hand sides, one finds

$$\begin{array}{@{}rcl@{}} &&\left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left|\boldsymbol{\xi}^{n+1/2}\right|^{2} + \tfrac{1}{4}(\delta t)^{2} \left|\boldsymbol{C}\boldsymbol{\xi}^{n+1/2}\right|^{2} = \left( 1 - \frac{\delta t}{2\tau} \right)^{2} \left|\boldsymbol{\xi}^{n-1/2}\right|^{2} \\ &&+ \tfrac{1}{4}(\delta t)^{2} \left|\boldsymbol{C}\boldsymbol{\xi}^{n-1/2}\right|^{2} + \frac{2\delta t}{\tau} \left|\boldsymbol{\eta}^{n}\right|^{2} + (\ldots) \boldsymbol{\xi}^{n-1/2} \cdot \boldsymbol{\eta}^{n} , \end{array} $$

if C is skew-symmetric. This time, given that 〈|(η ⁿ)²|〉 = N and assuming that 〈|(ξ ^n−1/2)²|〉 = N, with N the total number of grid points, it follows that

$$\begin{array}{@{}rcl@{}} \left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left( \left\langle\left|\boldsymbol{\xi}^{n+1/2}\right|^{2}\right\rangle - N \right) = \tfrac{1}{4}(\delta t)^{2} \left( \left\langle\left|\boldsymbol{C}\boldsymbol{\xi}^{n-1/2}\right|^{2}\right\rangle - \left\langle\left|\boldsymbol{C}\boldsymbol{\xi}^{n+1/2}\right|^{2}\right\rangle \right) . \end{array} $$

This equation allows for the global conservation of the variance of ξ, that is, 〈|(ξ ^n+1/2)²|〉 = N, if either conservation of the variance of C ξ is also assumed or the right-hand side, which is of $\mathcal {O}((\delta t)^{3})$, is neglected. Note that if the discretization is not symmetry-preserving, then a right-hand side of $\mathcal {O}(\delta t)$ is found that leads to considerable dissipation of the total variance of ξ.