Theories, algorithms and applications in tensor learning

Abstract

Due to the accelerated development and popularization of Internet, mobile Internet, and Internet of Things and the breakthrough of storage and communication technologies, the amount of data obtained in the fields of health care, social media, and climate science is increasing, showing complex high-dimensional, multimodal, and heterogeneous characteristics. As the expansion of a vector and matrix, a tensor is the natural and essential mode of representation for this kind of data. The theory of tensor algebra provides a powerful mathematical tool and an extensible framework for learning algorithms for processing data with high-dimensional heterogeneity and complex dependence. In recent years, tensor theory and its applications have become a research hotspot, from new tensor models and scalable algorithms in academia to industry solutions. The article shows its advances in tensor theories, algorithms, and applications. Firstly, tensor operation, classical tensor decomposition theory, and t-product tensor theory are introduced. Secondly, tensor supervised learning, tensor unsupervised learning, and tensor deep learning are discussed from the perspective of tensor decomposition and t-product, and then their application research is summarized. Finally, the opportunities and challenges of tensor learning are briefly discussed.

1 Introduction

Humans have never stopped collecting data for the purpose of restoring human history since data was first used to record history. In recent years, due to the accelerated development of the Internet, mobile Internet, Internet of Things, and communication technologies, the cost of collecting data is getting lower and lower, and the amount of data is getting larger and larger, showing explosive growth. A large amount of data has been accumulated in various aspects of scientific research and social life. Machine learning, as a key tool for exploring the value of data, plays an extremely important role in big data research.

However, most of the data in the real world contains a lot of attributes or features, frequently involving complex high-dimensional correlations, which is a huge challenge to traditional vector- or matrix-based machine learning. High-dimensional data samples are usually represented as vectors or matrices even though they are naturally expressed in high dimensions. For example, for a grayscale image, the gray value of pixels is used as its feature, and it is rearranged into a vector for the image. However, when the image is represented as a vector, it will produce a very large dimension, such as when a 100×100 image corresponds to a vector of 10000 dimensions. A number of issues arise when multidimensional data are expanded into a vector for analysis [1, 2]:

• (1) Vectorization or matricization will result in the curve of dimensionality and the small size problem.

• (2) The multi-linear structure may be destroyed, which results in sub-optimal performance in processing. For example, the images collected by multimedia sensor networks need to be unfolded into vectors for processing, which will destroy the internal structure information of the image and may cause key information loss.

• (3) The distance between any two sample points of many datasets would be large due to the sparsity of high-dimensional space, and may be basically the same, which invalidates most traditional distance learning algorithms. With an increase in data dimensions, the time and space complexity of machine learning algorithms increases. Therefore, such vectorization or matricization greatly reduces the accuracy and efficiency of machine learning algorithms.

In a nutshell, multidimensional data have exposed the limitations of machine learning techniques based on vectors or matrices, as well as the need to transition to more appropriate data analysis tools. Tensors are multi-dimensional arrays, which are a generalization of vectors and matrices, and they are a natural representation for high-dimensional data. Machine learning techniques based on tensor computation can prevent the loss of multi-linear data structures found in their traditional matrix-based counterparts. Furthermore, the computational complexity in tensor subspaces may be considerably lower than in the original form. Therefore, the symbiotic relationship between data complexity and computational power has enabled methods based on tensor computation to gain popularity. Tensor-based algorithms provide the potential to capture latent features more effectively than vector- or matrix-based machine learning methods by keeping the intrinsic data structure. Multi-dimensional operations and approaches based on them are utilized in a number of data-related applications, such as signal processing (e.g., speech, radar), machine learning (e.g., subspace learning, neural networks), and experimental sciences (e.g., psychometrics, chemometrics).

There are some excellent tutorials and summaries that present various viewpoints on particular topics. One of them was the highly-cited overview [3] which was published in SIAM Review. It does a good job of covering the fundamental concepts and methods; however, it doesn’t delve deeply into topics like uniqueness, complex algorithms, or estimation theory. In a recent tutorial on tensors [4], tensors are viewed as mappings from one linear space to another in which the coordinates undergo multilinear transformations when the basis is changed. Instead of discussing how to apply tensors in science and engineering, this article is more suited to those who are interested in tensors as a mathematical idea. The recent overview [5] focuses on data fusion and scalability; it doesn’t delve in-depth on topics like tensor rank, identifiability, decomposition under restrictions, or statistical performance. The highly-cited Chemometrics overview [6] provides a simple introduction to tensor decompositions. From a signal processing standpoint, a worthy tutorial [7] to tensor decompositions is offered. It includes algebraic foundations, computational aspects, and promising applications, but it also includes many fundamentals beyond the basics from the viewpoint of machine learning. The highly-cited overview [8] provides the fundamental applications of tensor decompositions in signal processing as well as the continually expanding toolbox of tensor decomposition methods. It does not, however, delve deeply into the latest tensor decompositions and machine learning techniques.

None of the aforementioned sources provides a comprehensive overview that dives deep enough into tensor methods and applications in deep learning and machine learning. This paper provides a basic coverage of tensor notions, preliminary operations, main tensor decompositions, and the t-product. From the perspective of machine learning, a series of tensor learning algorithms are presented as multi-linear extensions of classic vector- or matrix-based approaches. The applications of tensor computation are summarized, and some challenges in tensor learning are briefly discussed. Graduates can use it as an article to learn how to approach the majority of tensor learning methods. It can be used by researchers to keep up with the state of the art for these particular techniques.

The following describes how this paper is organized. Firstly, this paper discusses the basic theory of tensor algebra, namely tensor decomposition and the t-product tensor. Then the tensor learning algorithms based on tensor decomposition and t-product are summarized and analyzed, and their application research in related fields is summarized. Finally, the future research direction is outlined. The main structure of a review is shown in Fig. 1.

Fig. 1

The basic structure of a review

2 Basic theory of tensor algebra

Tensor algebra is the theoretical basis of tensor learning and its applications. The following is an overview of tensor decomposition and the t-product tensor. It is worth mentioning that the tensor in this paper differs from tensors (e.g., stress tensors) in physics and engineering. The latter are often called tensor fields in mathematics [9].

2.1 Tensor decomposition

We briefly review some basic knowledge of tensors. Readers should refer to references [3, 10] for additional information on the tensor basis.

2.1.1 Tensor notations

Definition 1 (tensor)

: The n-order tensor $\mathcal {X}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{N}}}}$ is an n-way data array whose elements are expressed as ${{x}_{{{i}_{1}}{{i}_{2}}{\cdots } {{i}_{n}}}},{{i}_{n}}\in \{1,2,{\cdots } ,{{I}_{n}}\},1\le n\le N$. Tensor is a generalized form of scalar, vector, and matrix. As a result, as shown in Fig. 2, a scalar, vector, and matrix can be thought of as the oth-, first-, and second-order tensors, respectively.

Fig. 2

Instance of a vector (first-order), matrix (second-order) and 3rd-order tensor

2.1.2 Tensor operations

Definition 2 (Output product)

: The outer product of N vectors ${{a}^{\left (i \right )}}\in {{\Re }^{i\times 1}},i=1,2,{\cdots } ,n$ is written as (1), and the result is an n-order tensor:

$$ {{a}^{\left( 1 \right)}}\circ {{a}^{\left( 2 \right)}}\circ {\cdots} \circ {{a}^{\left( n \right)}}=\mathcal{A} $$

(1)

Definition 3 (Rank-one tensor)

: If the n-order tensor can be expressed by an outer product of N vectors, it has rank 1, that is

$$ \mathcal{X}={{x}^{(1)}}\circ {{x}^{(2)}}\circ {\cdots} \circ {{x}^{(N)}}=\prod\limits_{n=1}^{N}{\circ {{x}^{(n)}}} $$

(2)

Definition 4 (Tensor Matricization)

: A tensor is arranged tensor fibers into a matrix. The n-mode matrix ${{X}_{\left (n \right )}}$ of a tensor is to take the n-mode fiber as the column of the matrix.

Definition 5 (N-mode product)

: The product of an n-order tensor$\ \in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{N}}}}$ and an J × I_n n-mode matrix U is expressed as×_nU. This is an I₁ × I₂ ×⋯ × I_n− 1 × J × I_n+ 1 ×⋯ × I_Ntensor whose elements can be given by

$$ {{\left( {\mathcal{X}_{{{\times }_{n}}}}U \right)}_{{{i}_{1}}{{i}_{2{\cdots} {{i}_{n-1}}j{{i}_{n+1{\cdots} {{i}_{N}}}}}}}}=\sum\limits_{i_{n}=1}^{I_{N}} {{x}_{{{i}_{1}}{{i}_{2{\cdots} {{i}_{N}}}}}}{{u}_{{{j}_{1}}{{i}_{n}}}} $$

(3)

Or,

$$ \mathcal{Y}=\mathcal{X}{{\times }_{1}}U\Leftrightarrow {{Y}_{\left( n \right)}}=U{{X}_{\left( n \right)}} $$

(4)

Figure 3 visually illustrates the mode-1 product between the third-order tensor and the matrix.

Fig. 3

N − mode product of tensor $\mathcal {X}$and U

2.1.3 Classical tensor decomposition

Tensor decomposition was put forward by Hitchcock in two papers [11, 12] published in the Journal of Mathematics and Physics in 1927. The canonical multivariate decomposition, which decomposed a tensor into a sum of finite rank-1 tensors, was demonstrated.

CP Decompositions (CPD): Let $\mathcal {X}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{N}}}}$ be a tensor and R be a positive integer. A CPD represents $\mathcal {X}$ as a linear combination of rank-1 tensor in the form

$$ \begin{array}{@{}rcl@{}} \mathcal{X}&=&\sum\limits_{r=1}^{R}{a_{r}^{(1)}\circ a_{r}^{(2)}\circ {\cdots} \circ a_{r}^{(N)}} \\ &=&\left[ \lambda ;{{A}^{\left( 1 \right)}},{{A}^{\left( 2 \right)}},{\cdots} ,{{A}^{\left( N \right)}} \right]=\sum\limits_{r=1}^{R}{\prod\limits_{n=1}^{N}{\circ a_{r}^{(n)}},} \end{array} $$

(5)

where $\lambda =diag\left ({{\lambda }_{1}},{{\lambda }_{2}},{\cdots } ,{{\lambda }_{R}} \right )$, and ${{A}^{\left (n \right )}}=\left [ a_{1}^{\left (n \right )},a_{2}^{\left (n \right )},{\cdots } ,a_{R}^{\left (n \right )} \right ]\in {{\Re }^{{{I}_{n}}\times R}}$. Figure 4 shows the CPD of the 3rd-order tensor. The minimal value of R for which (5) holds precisely is referred to as the tensor rank.

Fig. 4

CPD of the 3rd-order tensor, which is the sum of rank-1components

Equation (5) is a nonconvex optimization problem and can be resolved by alternating least squares (ALS).

Partly due to its simplicity of interpretation, CPD is one of the most widely used tensor decompositions. In the data, each rank-one component of the decomposition acts as a latent “category” or cluster. The vectors of component r can be seen as soft memberships to the r-th latent cluster. Therefore, it is appropriate for exploratory data mining.

Tucker Decomposition (TD): Let $\mathcal {W}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{N}}}}$ be an n-order tensor, it can be expressed as

$$ \begin{array}{@{}rcl@{}} \mathcal{W}&=&\mathcal{G}{{\times }_{1}}{{U}^{\left( 1 \right)}}{{\times }_{2}}{{U}^{\left( 2 \right)}}{\cdots} {{\times }_{N}}{{U}^{\left( N \right)}} \\ &=&\left[ \mathcal{G};{{U}^{\left( 1 \right)}},{{U}^{\left( 2 \right)}},{\cdots} ,{{U}^{\left( N \right)}} \right] \end{array} $$

(6)

with the core tensor of $\ \in {{\Re }^{{{R}_{1}}\times {{R}_{2}}\times {\cdots } \times {{R}_{N}}}}$. Its elements represent the correlation degree of each mode of the tensor, and $\left \{ {{U}^{\left (i \right )}}\in {{\Re }^{{{I}_{i}}\times {{R}_{i}}}} \right \}_{i=1}^{N}$ is the factor matrices of each mode of the tensor. It can be regarded as the principal component of each mode. The matrix form of (6) is

$$ \begin{array}{@{}rcl@{}} {{W}_{\left( n \right)}}&=&{{U}^{\left( n \right)}}{{G}_{\left( n \right)}}\left( {{U}^{\left( N \right)}}\otimes {\cdots} \otimes {{U}^{\left( n+1 \right)}}\right. \\ && \left. \otimes {{U}^{\left( n-1 \right)}} \otimes {\cdots} \otimes {{U}^{\left( 1 \right)}} \right)^{T} \end{array} $$

(7)

The tucker decomposition example is shown in Fig. 5. The Kronecker product of M matrices is

$$ {{U}_{\otimes }}={{U}^{\left( M \right)}}\otimes {{U}^{\left( M-1 \right)}}\otimes {\cdots} \otimes {{U}^{\left( 1 \right)}}. $$

(8)

Equation (8) can be transformed into (9) form:

$$ \begin{array}{@{}rcl@{}} {{W}_{\left( n \right)}}&=& {{U}^{\left( n \right)}}{{G}_{\left( n \right)}}\left( {{U}^{\left( N \right)}}\otimes {\cdots} \otimes {{U}^{\left( n+1 \right)}} \right.\\ &=& \left.\otimes {{U}^{\left( n-1 \right)}}\otimes {\cdots} \otimes {{U}^{\left( 1 \right)}} \right)^{T}{{U}^{\left( n \right)}}{{G}_{\left( n \right)}}{{\overline{U}}^{T}} \end{array} $$

(9)

Fig. 5

TD of a 3rd-order tensor

Tensor-Train Decomposition (TTD) : TTD [13] can deal with the “Curse of Dimensionality” problem of higher-order tensors without prior knowledge. It can decompose a high-order tensor into a product of core tensors and matrices, and it can connect adjacent core tensors using the reduced mode R_i (common reduced mode).

For the d th-order tensor, the tensor train decomposition is to represent the elements of a tensor as the entries of the 2nd- or 3rd-order tensors:

$$ \begin{array}{@{}rcl@{}} &&\mathcal{X}\left( {{i}_{1}},{{i}_{2}},{\cdots} ,{{i}_{d}} \right)=\sum\limits_{{{r}_{1}},{\cdots} ,{{r}_{d-1}}}{{G_{1}}\left( {{i}_{1}},{{r}_{1}} \right)}{{\mathcal{G}}_{2}}\left( {{r}_{1}},{{i}_{2}},{{r}_{2}} \right) \\ &&\qquad {\cdots} {\mathcal{G}_{d-1}}\left( {{r}_{d-2}},{{i}_{d-1}},{{r}_{d-1}} \right){{G}_{d}}\left( {{r}_{d-1}},{{i}_{d}} \right), \end{array} $$

(10)

where $\mathcal {X}\left ({{i}_{1}},{{i}_{2}},{\cdots } ,{{i}_{d}} \right )$ is the entry at index $\left ({{i}_{1}},{{i}_{2}},{\cdots } ,{{i}_{d}} \right )$ of an dth-order tensor$\mathcal {X}.{\mathcal {G}_{n}}\in {{\Re }^{{{R}_{n}}\times {{I}_{n}}\times {{R}_{n+1}}}},n=2,{\cdots } ,d-1\left ({{R}_{1}}={{R}_{d-1}}=1 \right )$ are and the 3rd-order core tensors. ${{G}_{1}}\in {{\Re }^{{{I}_{1}}\times {{R}_{1}}}},{{G}_{d}}\in {{\Re }^{{{R}_{d-1}}\times {{I}_{d}}}}$are the 2th-order core tensors. Figure 6 shows the tensor-train decomposition of the 4th-order tensor.

Fig. 6

TTD of a 4th-order tensor. The variables in circles stand for the reduced dimension that connects the core tenors

Tensor Ring Decomposition (TRD) [14]: The main disadvantage of TTD is that the first and last rank must be set to 1, which limits its expressiveness and flexibility. The best alignment is an important and challenging problem for TTD.

Compared with TTD, the important modification of TR is that the first core is connected with the last kernel tensor, which looks like a ring structure. We set r₀ = r_d = r for a d-order tensor $\mathcal {X}$, and the tensor ring decomposition is as follows:

$$ \begin{array}{@{}rcl@{}} &&\mathcal{X}\left( {{i}_{1}},{{i}_{2}},{\cdots} ,{{i}_{d}} \right)\\ &&=\sum\limits_{{{r}_{1}},{\cdots} ,{{r}_{d-1}}}{{{G}_{1}}\left( {{i}_{1}},{{r}_{1}} \right)}{\mathcal{G}_{2}}\left( {{r}_{1}},{{i}_{2}},{{r}_{2}} \right) \\ &&{\cdots} {\mathcal{G}_{d-1}}\left( {{r}_{d-2}},{{i}_{d-1}},{{r}_{d-1}} \right){{G}_{d}}\left( {{r}_{d-1}},{{i}_{d}} \right). \end{array} $$

(11)

2.2 T-product framework

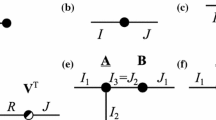
In order to establish the t-product tensor framework, Kilmer et al. [15, 16] put forward some new concepts and definitions. Given a l × m × n fixed tensor ${\mathscr{B}}$, its third order is frontal slices ${{B}^{\left (k \right )}}$, which is a l × m matrix, k = 1,2,⋯ ,n. The second order of the fixed tensor is the lateral slices ${{\overrightarrow {A}}_{j}}$, which is the l × n matrix, j = 1,2⋯ ,M. Keeping the first and second order unchanged is tubes, which is a n × 1 vector, i = 1,2,⋯ ,l,j = 1,2,⋯ ,n. The like-matrix framework is shown in Fig. 7.

Fig. 7

Tensor of t-product framework. Tube, lateral, and tensor are similar to scalar, vector, and matrix, respectively

2.2.1 Basic concepts and definitions

Definition 6 (Unfold and fold operations)

: Let ${\mathscr{B}}\in {{\Re }^{l\times m\times n}}$ be a tensor, unfold and fold operations are defined as

$$ unfold\left( \mathcal{B}\right)={\left( \begin{array}{l} {{B}^{\left( 1 \right)}} \\ {{B}^{\left( 2 \right)}} \\ {\vdots} \\ {{B}^{\left( n \right)}} \end{array}\right)_{nl\times m}}fold\left( unfold\left( \mathcal{B} \right) \right)=\mathcal{B} $$

(12)

$unfold\left ({\mathscr{B}} \right )$ is regarded as a block vector whose elements are composed of frontal slices of a tensor.

Definition 7 (Block circulant operation, Bcirc)

: Given a tensor ${\mathscr{B}}\in {{\Re }^{l\times m\times n}}$, the bcirc operation is to convert a tensor into the following block circulant matrix.

$$ bcirc\left( \mathcal{B} \right)=\left( \begin{array}{ccccc} {{B}^{\left( 1 \right)}} & {{B}^{\left( n \right)}} & {\cdots} & {{B}^{\left( 3 \right)}} & {{B}^{\left( 2 \right)}} \\ {{B}^{\left( 2 \right)}} & {{B}^{\left( 1 \right)}} & {{B}^{\left( n \right)}} & {\cdots} & {{B}^{\left( 3 \right)}} \\ {{B}^{\left( 3 \right)}} & {{B}^{\left( 2 \right)}} & {{B}^{\left( 1 \right)}} & {\ddots} & {\vdots} \\ {\vdots} & {\ddots} & {\ddots} & {\ddots} & {{B}^{\left( n \right)}} \\ {{B}^{\left( n \right)}} & {\cdots} & {{B}^{\left( 3 \right)}} & {{B}^{\left( 2 \right)}} & {{B}^{\left( 1 \right)}} \end{array}\right) $$

(13)

The first column of the cyclic matrix is the front slice, and the subsequent columns are obtained by circulant movement.

2.2.2 Discrete fourier transformation

A normalized discrete fourier transform (DFT) can realize the diagonalization of a circulant matrix. This idea is applied to a block circulant matrix to realize its diagonalization [15]. Therefore, DFT plays a critical role in t-product framework. An $\widehat {x}={{F}_{n}}x$ is the DFT of x ∈Rⁿ. The Fourier matrix ${{F}_{n}}\in {{\mathbb {C}}^{n\times n}}$was defined by

$$ {{F}_{n}}=\left[\begin{array}{ccccc} 1 & 1 & 1 & {\cdots} & 1 \\ 1 & \omega & {{\omega}^{2}} & {\ldots} & {{\omega}^{\left( n-1 \right)}} \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & {{\omega }^{n-1}} & {{\omega }^{2\left( n-1 \right)}} & {\cdots} & {{\omega }^{\left( n-1 \right)\left( n-1 \right)}} \end{array}\right] $$

(14)

where ω = e^−j2π/n and $j=\sqrt {-1}$ is an imaginary unit. Suppose $\widehat {{\mathscr{B}}}$ be DFT of tensor ${\mathscr{B}}\in {{\Re }^{{{n}_{1}}\times {{n}_{2}}\times {{n}_{3}}}}$ along the third order of tensor, whose (i, j)th tube is computed by $\widehat {{\mathscr{B}}}\left (i,j,: \right )={{F}_{{{n}_{3}}}}{\mathscr{B}}\left (i,j,: \right )$. In the Matlab, there are $\widehat {{\mathscr{B}}}=fft\left ({\mathscr{B}},[],3 \right )$ and ${\mathscr{B}}=ifft\left (\widehat {{\mathscr{B}}},[],3 \right )$.

Let $\widehat {B}\in {{\mathbb {C}}^{{{n}_{1}}{{n}_{3}}\times {{n}_{1}}{{n}_{3}}}}$ be a block diagonal matrix whose kth elements are calculated by the frontal slice matrix ${{\widehat {B}}^{\left (k \right )}}$ of $\widehat {{\mathscr{B}}}$ in the Fourier domain. The form is as follows

$$ \widehat{B}=bdiag\left( \widehat{\mathcal{B}} \right)=\left[\begin{array}{cccc} {{\widehat{B}}^{\left( 1 \right)}} & & & \\ & {{\widehat{B}}^{\left( 2 \right)}} & & \\ & & {\ddots} & \\ & & & {{\widehat{B}}^{\left( {{n}_{3}} \right)}} \end{array}\right] $$

(15)

We can use DFT to transform a block circulant matrix into a block diagonal matrix, that is,

$$ \left( {{F}_{{{n}_{3}}}}\otimes {{I}_{n{}_{1}}} \right)circ\left( \mathcal{B} \right)\left( F_{{{n}_{3}}}^{H}\otimes {{I}_{n{}_{2}}} \right)=\widehat{B}, $$

(16)

where ${{F}_{{{n}_{3}}}}$ is the normalized n₃ × n₃ DFT matrix, $F_{{{n}_{3}}}^{H}$is the conjugate transpose matrix of ${{F}_{{{n}_{3}}}}$, and⊗ represents the Kronecker product.

2.2.3 T-product algorithm

Definition 8 (t-product)

: Suppose $\mathcal {X}\in {{\Re }^{l\times p\times n}}$ and $\mathcal {Y}\in {{\Re }^{p\times m\times n}}$ are two tensors, the t-product operator is defined as

$$ \begin{array}{@{}rcl@{}} \mathcal{Z}&=&\mathcal{X}*\mathcal{Y} \\ &=&fold\left( bcirc\left( \mathcal{X} \right)\bullet unfold\left( \mathcal{Y} \right) \right),\mathcal{Z}\in {{\Re }^{l\times m\times n}} \end{array} $$

(17)

where “∗” is the t-product operator. For the convenience of derivation, the t-product is changed into a frontal slice form:

$$ \begin{array}{@{}rcl@{}} {{Z}^{\left( k \right)}}&=&{{X}^{\left( k \right)}}\bullet {{Y}^{\left( 1 \right)}}+\sum_{i=1}^{k-1}{{{X}^{\left( i \right)}}\bullet {{Y}^{\left( k-i+1 \right)}}} \\ &&+\sum_{i=k+1}^{n}{{{X}^{\left( i \right)}}\bullet {{Y}^{\left( n-i+1 \right)}}},\text{ }k=1,2,{\cdots} ,n \end{array} $$

(18)

Suppose it’s a2 × 2 × 3 tensor $\mathcal {X}$ whose front slice is ${{X}^{\left (1 \right )}}=\left [\begin {array}{cc} 1 & 0 \\ 0 & 1 \end {array} \right ]{{X}^{\left (2 \right )}}=\left [\begin {array}{cc} 0 & 2 \\ 2 & 0 \end {array} \right ],{{X}^{\left (3 \right )}}=\left [\begin {array}{cc} 0 & 3 \\ -3 & 0 \end {array} \right ]$$\overrightarrow {\mathcal {y}}$W is the lateral slice (vector) whose value is ${{\overrightarrow {Y}}^{\left (1 \right )}}=\left [\begin {array}{c} 1 \\ 1 \end {array} \right ]{{\overrightarrow {Y}}^{\left (2 \right )}}=\left [\begin {array}{c} 0 \\ -2 \end {array}\right ]{{\overrightarrow {Y}}^{\left (3 \right )}}=\left [ \begin {array}{c} 0 \\ 3 \end {array}\right ]$.

So their t-product is

$$\begin{aligned} &\overrightarrow{\mathcal{Z}}=\mathcal{X}*\overrightarrow{\mathcal{Y}}=fold(bcirc(\mathcal{X})\bullet unfold(\overrightarrow{\mathcal{Y}} ) ) \\ & \quad= \left[\begin{array}{cccccc} 1 & 0 & 0 & 3 & 0 & 2 \\ 0 & 1 & -3 & 0 & 2 & 0 \\ 0 & 2 & 1 & 0 & 0 & 3 \\ 2 & 0 & 0 & 1 & -3 & 0 \\ 0 & 3 & 0 & 2 & 1 & 0 \\ -3 & 0 & 2 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} 1 \\ 1 \\ 0 \\ -2 \\ 0 \\ 3 \end{array}\right] \end{aligned}$$

In this way, $\overrightarrow {\mathcal {Z}}=\mathcal {X}*\overrightarrow {\mathcal {Y}}$ is equal to the following: ${{\overrightarrow {\mathcal {Z}}}^{\left (1 \right )}}=\left [\begin {array}{c} 1 \\ 1 \end {array}\right ]{{\overrightarrow {\mathcal {Z}}}^{\left (2 \right )}}=\left [\begin {array}{c} 11 \\ 0 \end {array}\right ]{{\overrightarrow {\mathcal {Z}}}^{\left (3 \right )}}=\left [\begin {array}{c} -1 \\ 0 \end {array} \right ]$.

Definition 9 (Facewise product)

: given two tensors, $\mathcal {X}\in {{\Re }^{l\times p\times n}}$ and $\mathcal {Y}\in {{\Re }^{p\times m\times n}}$, “” represents the facewise product operator. It multiplies frontal slice of $\mathcal {X}\textit {and}\mathcal {Y}$, which is as follows:

$$ \mathcal{Z}=\mathcal{X}\vartriangle \mathcal{Y}\equiv \text{ }{{Z}^{\left( i \right)}}={{X}^{\left( i \right)}}\bullet {{Y}^{\left( i \right)}} $$

(19)

The effective algorithm of T-Product is as follows:

Algorithm 1

T-product.

2.2.4 Tensor Singular Value Decomposition (T-SVD)

Definition 10 (Transpose)

: Given a 3rd-order tensor ${\mathscr{B}}\in {{\Re }^{{{n}_{1}}\times {{n}_{2}}\times {{n}_{3}}}}$, its transpose ${{\mathscr{B}}^{T}}$is n₂ × n₁ × n₃ tensor calculated by transposing each of the frontal slices, and then reversing the order of obtained frontal slices 2 through n₃.

Definition 11 (Identity tensor)

: A tensor is an identity tensor $\mathcal {I}\in {{\Re }^{n\times n\times m}}$ if its first frontal slice is an n × n identity matrix and other frontal slices are zero entries.

Definition 12 (F-diagonal tensor)

: A tensor is F-diagonal if each of its frontal slices is a diagonal matrix.

Definition 13 (Orthogonal tensor)

: A tensor $\mathcal {O}\in {{\Re }^{n\times n\times m}}$is orthogonal if it satisfies${\mathcal {O}^{T}}*\mathcal {O}=\mathcal {O}*{\mathcal {O}^{T}}=\mathcal {I}$.

Theorem 1 (T-SVD)

Given a real valued tensor $\mathcal {A}\in {{\Re }^{{{n}_{1}}\times {{n}_{2}}\times {{n}_{3}}}}$, it can be decomposed into:

$$ \mathcal{A}=\mathcal{U}*\mathcal{S}*{\mathcal{V}^{T}} , $$

(20)

where $\mathcal {U}$ is an orthogonal tensor of n₁ × n₁ × n₃, $\mathcal {S}$ is a F-diagonal tensor, andis an orthogonal tensor of n₂ × n₂ × n₃, and (20) is called T-SVD.

Algorithm 2

T-SVD.

3 Tensor based algorithm

3.1 Tensor supervised Learning

3.1.1 Tensor regression

In recent years, to take advantage of tensor decomposition and machine learning, many researchers have extended the vector-based learning algorithm to tensor space in order to form a tensor learning algorithm.

Linear regression has played a significant role in regression analysis. Although a few complicated systems are hard to accurately approximate with linear regression, it is nonetheless frequently employed in industries due to its efficiency and simplicity, especially when exact accuracy is not crucial. When it comes to multidimensional data analysis and prediction problems, linear tensor regression models have emerged as the leading research area.

Linear tensor regression models: Standard linear regression model had been naturally expanded to tensor regression. Given a d th-order $\mathcal {X}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{d}}}}$ and the regression tensor (also called the weight tensor) $\mathcal {W}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } \times {{I}_{d}}}}$. The tensor regression can be formulated as

$$ y=\left\langle \mathcal{W},\mathcal{X} \right\rangle +b, $$

(21)

where b is the bias and the predicted y is a scalar. The model involves high-dimensional $\prod _{i=1}^{d}{{{I}_{i}}}$ parameters, which is larger than the typical sample size. Therefore, the weight tensor is represented approximately in a suitable tensor decomposition, such as CP, tucker, or tensor train, which plays an important role in model performance. To reduce the dimensionality, reference [17] proposed utilizing CP to decompose the weight tensor $\mathcal {W}$ in the following form

$$ \mathcal{W}=\sum_{r=1}^{R}{u_{r}^{\left( 1 \right)}\circ }u_{r}^{\left( 2 \right)}\circ {\cdots} u_{r}^{\left( n \right)}, $$

(22)

where R is the rank of CP. The number of parameters is reduced to $R\sum _{i=1}^{n}{{{I}_{i}}}$. It is called CP tensor regression, which can be solved by ALS. Similarly, upon the application of tucker decomposition, it exists tucker tensor regression [18, 19]. Hoff et al. [18] proposed a new form of the multilinear tucker model, which supposed the replicated observations $\left \{ \left ({\mathcal {X}_{1}},{\mathcal {Y}_{1}} \right ),\left ({\mathcal {X}_{2}},{\mathcal {Y}_{2}} \right ),{\cdots } ,\left ({\mathcal {X}_{n}},{\mathcal {Y}_{n}} \right ) \right \}$, and can be stacked two (N + 1) order tensor $\mathcal {X}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}{\cdots } \times {{I}_{K}}\times N}}$ and $\mathcal {Y}\in {{\Re }^{{{J}_{1}}\times {{J}_{2}}{\cdots } \times {{J}_{K}}\times N}}$. It is formalized as follows

$$ \mathcal{Y}=\mathcal{X}{{\times }_{1}}{{W}_{1}}{{\times }_{2}}{{W}_{2}}{\cdots} {{\times }_{K}}{{W}_{K}}{{\times }_{K+1}}{{I}_{N}}+\mathcal{E}, $$

(23)

where I_N is an N × N diagonal matrix, ${{W}_{k}}\in {{\Re }^{{{J}_{k}}\times {{I}_{k}}}}$ are the weight matrices, and denotes a zero-mean residual tensor of the same order as $\mathcal {Y}$.

Compared to the CP regression model, the Tucker regression model has a number of advantages. It has more concise modeling capability and a more compact model, particularly given the small number of samples that are available, and the ability to select a different rank for each mode allows one to fully leverage multi-linear ranks.

We suppose that the input of a multivariate regression is a vector and the response is a tensor structure (sample$\left \{ \left ({{x}^{\left (n \right )}},{{\mathcal {Y}}^{\left (n \right )}} \right ) \right \}_{n=1}^{N}$). For this regression task, it can be solved by vectorizing each output tensor and performing standard low-rank regression on $\left \{ \left ({{x}^{\left (n \right )}},vec\left ({{\mathcal {Y}}^{\left (n \right )}} \right ) \right ) \right \}_{n=1}^{N}$. This method would lead to the loss of structural information of the output tensor in the vectorization, and ignored possible higher-level dependencies in the output with a tensor-structure. To overcome the problems, reference [20] proposed a low-rank tensor responses regression and higher-order Low-rank regression. Reference [21] proposed sparse tensor response regression (STORE). Specifically, it was formulated as follows:

$$ \mathcal{Y}={{\mathcal{W}}^{*}}{{\times }_{n+1}}{{x}_{i}}+{{\mathcal{E}}_{i}}, $$

(24)

where ${{\mathcal {W}}^{*}}\in {{\Re }^{{{d}_{1}}\times {\cdots } \times {{d}_{n}}\times p}}$ denotes a (n + 1)th-order tensor coefficient, ${{\mathcal {W}}^{*}}$ is an error tensor that is independent of x_i. The intercept term is set to zero without loss of generality in order to simplify the expression. Reference [21] incorporated the sparity and rank-R CP structure, and proposed to solve

$$ \left\{\begin{array}{l} \underset{\overset{{w}_{r},{\beta}_{r,k}}{r\in \left[ R \right],k\in \left[ d+1 \right]}}{\min} 1/m \sum_{i=1}^{m}\left\| \mathcal{Y}_{i}-\sum_{r=1}^{R}{{w}_{r}} \right. \\ \left.\left( \beta_{r,d+1}^{T}{{x}_{i}} \right){{\beta }_{r,1}}\circ {\cdots} \circ {{\beta }_{r,d}} \right\|_{F}^{2}\\ subject\quad to\ {{\left\| {{\beta }_{r,k}} \right\|}_{2}}=1,{{\left\| {{\beta }_{r,k}} \right\|}_{0}}\le {{s}_{k}} \end{array}\right., $$

(25)

where s_k is the sparsity parameter. In order to solve (25), alternating updating algorithm was proposed. More recently, references [22,23,24] describe additional tensor regression methods.

Algorithm 3

Multilinear tucker regression.

There are some unaddressed issues with tensor response regression. One is how to use the CP structure to generate a reliable estimator of the rank R. More crucially, when examining the asymptotic attributes, it is still possible to calculate the relevant convergence rate and incorporate the estimated rank with the subsequent estimator of ${{\mathcal {W}}^{*}}$. The currently available solutions primarily serve R as known from asymptotic researches. Recent works have mostly concentrated on parameter estimation, and parameter inference for tensor response regression remains a challenging subject, especially when the sample size is small.

Nonlinear tensor regression models: Linear tenor regression models may lack predictive power in the presence of complex nonlinear correlation between input and output tensorial variables, whereas nonlinear tensor regression models can effectively deal with these issues. In the reference [25], tensor is applied to a Gaussian process to generate a tensor Gaussian process. Given a dth-order tensor $\mathcal {X}\in {{\Re }^{{{I}_{1}}\times {{I}_{2}}\times {\cdots } {{I}_{d}}}}$, y and ε are returned as scalar and Gaussian noise, respectively.

$$ y=f\left( \mathcal{X} \right)+\varepsilon , $$

(26)

where $f\left (\mathcal {X} \right )$ denotes a nonlinear function, which is modeled by a Gaussian process

$$ f(\mathcal{X}) \sim GP (m(\mathcal{X}), k(\mathcal{X}, \bar{(\mathcal{X})} \mid \theta ) $$

(27)

𝜃 is the associated hyperparameter vector, $k\left (\mathcal {X},\overline {\mathcal {X}} \right )$ denotes a kernel function, and $m\left (\mathcal {X} \right )$ denotes a zero mean function. It is important to design an appropriate tensor kernel that can explore the multiway correlations of tensorial data.

Reference [26] proposed a nonlinear tensor model as follows:

$$ \begin{array}{@{}rcl@{}} {{y}_{i}}&=&{{T}^{*}}\left( {{\mathcal{X}}_{i}} \right)+{{\varepsilon }_{i}}=\sum_{{{j}_{1}}=1}^{{{m}_{1}}}{{\cdots} }\sum_{{{j}_{d}}}^{{{m}_{d}}}{f_{{{j}_{1}}{\cdots} {{j}_{d}}}^{*}}\\ &&\left( {{\left[ {{\mathcal{X}}_{i}} \right]}_{{{j}_{1}}{\cdots} {{j}_{d}}}} \right)+{{\varepsilon }_{i}}, \end{array} $$

(28)

where the sample $\left \{ {{y}_{i}},{{\mathcal {X}}_{i}} \right \}_{i=1}^{n}$ is subject to independent identically distribution, $\left \{ {{\varepsilon }_{i}} \right \}_{i=1}^{n}$ are i.i.d. observation noises, and ${{\left [ {{\mathcal {X}}_{i}} \right ]}_{{{j}_{1}}{\cdots } {{j}_{d}}}}$ is the (j₁,⋯,j_d) th entry of the tensor. $f_{{{j}_{1}}\cdots {{j}_{d}}}^{*}\left (\bullet \right )$ is some smooth function that can be approximated by spline series expansion [27, 28],

$$ \begin{array}{@{}rcl@{}} {{T}^{*}}({\mathcal{X}}_{i})&\approx& \sum_{j=1}^{{d}_{1}}\cdots \sum_{{j}_{n}=1}^{{d}_{n}}\sum_{h=1}^{H}\\ &&{\beta_{{{j}_{1}}{{j}_{2}}\cdots {{j}_{d}}h}^{*}}{{\psi}_{{{j}_{1}}{{j}_{2}}\cdots {j}_{d}h}}\left( {[{{\mathcal{X}}_{i}}]}_{{{j}_{1}}{{j}_{2}}\cdots {j}_{d}} \right), \end{array} $$

(29)

where H is the number of spline series.

Define ${{\left [ {\mathcal {F}}_{h}\left (\mathcal {X} \right ) \right ]}_{{{j}_{1}}{{j}_{2}}{\cdots } {{j}_{d}}}}={{\psi }_{{{j}_{1}}{{j}_{2}}{\cdots } {{j}_{d}}h}}\left ({{\left [ {{\mathcal {X}}_{i}} \right ]}_{{{j}_{1}}{{j}_{2}}{\cdots } {{j}_{d}}}} \right )$ and ${{\left [{~}_{h}^{*} \right ]}_{{{j}_{1}}{{j}_{2}}\cdots {{j}_{d}}}}=\beta _{{{j}_{1}}{{j}_{2}}{\cdots } {{j}_{d}}h}^{*}$, a compact tensor representation of the model is

$$ {y}_{i}=\sum_{h=1}^{H}{\langle \mathcal{B}_{h}^{*},{\mathcal{F}}_{h} \rangle}+{\varepsilon}_{i}. $$

(30)

When ${{\psi }_{{{j}_{1}}{{j}_{2}}{\cdots } {{j}_{d}}h}}(\mathcal {X})=\mathcal {X}$ and H = 1, (28) becomes the linear tensor regression model (21).

3.1.2 Support matrix machines

In many practical classification problems, such as EEG, data can naturally be represented by a matrix [29], which is a better method to exploit the structure information. For the matrix $\left \langle W,W \right \rangle =tr\left ({{W}^{T}}W \right )$, the soft margin support matrix machine [15] is formalized as follows:

$$ \left\{\begin{array}{l} \underset{W,b,\zeta }{{\min }} \frac{1}{2}tr\left( {{W}^{T}}W \right)+C\sum_{m=1}^{M}{{{\zeta }_{m}}} \\ s.t.{{y}_{m}}\left( tr\left( {{W}^{T}}{{X}_{m}} \right)+b \right)\ge 1-{{\zeta }_{m}},\\ {{\zeta }_{m}}\ge 0,m=1,2,{\cdots} ,M \end{array}\right. $$

(31)

When $w=vec\left ({{W}^{T}}\right )$,

$$ \left\{\begin{array}{l} tr\left( {{W}^{T}}{{X}_{m}} \right)=vec{{\left( {{W}^{T}} \right)}^{T}}vec\left( {X_{m}^{T}} \right)={{w}^{T}}{{x}_{m}} \\ tr\left( {{W}^{T}}W \right)=vec{{\left( {{W}^{T}} \right)}^{T}}vec\left( {{W}^{T}} \right)={{w}^{T}}w \end{array}\right., $$

(32)

Then (32) is essentially equivalent to a support vector machine. This vectorization does not exploit the correlation in the matrix structure. By introducing a kernel norm, the correlation between rows or columns of the data matrix can be included, so that the problem becomes:

$$ \left\{\begin{array}{l} \underset{W,b,\zeta }{{\arg \ \min }} \frac{1}{2}tr\left( {{W}^{T}}W \right)+\tau {{\left\| W \right\|}_{*}}+C\sum_{m=1}^{M}{{{\zeta }_{m}}} \\ s.t.\ {{y}_{m}}\left( tr\left( {{W}^{T}}{{X}_{m}} \right)+b \right)\ge 1-{{\zeta }_{m}},{{\zeta }_{m}}\ge 0 \\ m=1,2,{\cdots} ,M \end{array}\right. $$

(33)

The solution of (31) is

$$ \overline{W}={{D}_{\tau }}\left( \sum_{m=1}^{M}{\overline{{{\beta }_{m}}}{{y}_{m}}{{X}_{m}}} \right) . $$

(34)

${{D}_{\tau }}\left (\centerdot \right )$ denotes the singular value threshold operator that controls singular values under τ to zero. ${\Omega } =\sum _{m=1}^{M}{\overline {{{\beta }_{m}}}{{y}_{m}}{{X}_{m}}}$ is a combination of X_m and non-zero $\overline {{{\beta }_{m}}}$, named support matrix.

3.1.3 Support tensor machines

We extend the standard support vector machine from vector to tensor space. The support tensor machine is established by CPD, TD, and TTD.

A supervised tensor learning framework for processing tensor data was proposed by Tao et al. [30] in 2005, where support tensor machines were formed by expanding support vector machines to tensor space. Similarly, tensor Fisher discriminant analysis method was established based on the tensor. Cai et al. Proposed tensor space oriented support tensor machines and tensor least square linear classifiers in reference [31]. In reference [32], the supervised tensor learning framework was applied to various typical support vector machines, such as C-SVM, v-SVM. Kotsia proposed support Tucker machine (STuM) and high rank support tensor machine (HR-STM) in 2011 [33] and 2012 [34], respectively. However, these supervised tensor learning frameworks are nonconvex optimization problems. As a result, the adopted algorithms for solving the original problem of the support tensor machine are alternating iterative optimization. Solving the nonconvex optimization problem is not only time-consuming and computationally expensive, but also the solution may be the local optimal solution. In order to overcome these shortcomings, combined with the dual problem of the support vector machine, the kernel method, and the advantages of tensor rank-one decomposition, a linear support higher-order tensor machine (SHTM) was introduced by Hao et al. [35]. The alternative iterative method is avoided to solve SHTM so as to reduce the solution time, and the easy solution is the global optimal solution.

$$ \left\{\begin{array}{l} \qquad\underset{{{\mathcal{W}}^{\left( k \right)}},b,\xi }{{\min }}\frac{1}{2}\left\| {{\mathcal{W}}^{\left( k \right)}} \right\|_{F}^{2}+C\underset{i=1}{\overset{M}{\sum }}{{\xi }_{i}} \\ s.t.{{y}_{i}}\left( vec{{\left( {{\mathcal{W}}^{\left( k \right)}} \right)}^{T}}{{x}_{i}} \right)\ge 1-{{\xi }_{i}}, \\ {{\xi }_{i}}\ge 0,i=1,{\cdots} ,M, \end{array}\right. $$

(35)

The CP decomposition of a tensor is adopted, so the computational complexity is increased in the solution process. There are massive actual data points that limit the expressive ability of the rank-1 tensor. In order to overcome this limitation, Cong Chen et al. established the support tensor train machine (STTM) by replacing CP decomposition with tensor train decomposition in the literature [36]. The weight tensor W of TTD can be obtained by solving (35).

3.1.4 Kernel support tensor machines

Most supervised tensor learning methods are proposed, which cannot maintain complex multi-way structure information or extract the nonlinear relationship of tensor data. To solve this problem, using the kernel method, the linear tensor model is extended to the nonlinear tensor model, and the kernel support tensor machine is established. A cumulant based kernel method was suggested by Signorette et al. [37] to classify multichannel data. A kernel tensor partial least square regression method was proposed by Zhao et al. [38]. Since the method in reference [37, 38] is to reshape the tensor into a matrix, they can only capture the unidirectional relationship in the tensor data. Before constructing the core, the multi-channel structure information in the tensor data was lost. Different from these methods, reference [39] built a tensor kernel to maintain tensor structure, wherein each tensor in the input space can be mapped to another tensor in the feature space while maintaining the tensor structure by using the dual tensor mapping function. Reference [40] proposed multi-way multi-level kernel (MMK) . The kernel CP decomposition is used to extract the nonlinear representation of tensor data. In the decomposition, the kernel matrix of each mode is shared, and then the extracted representation is embedded into the dual-preserving kernel. Reference [41] proposed a kernelized support tensor-train machine (KSTTM) that accepts tensorial data.

3.1.5 Tensor compressed sensing

The traditional compressed sensing theory depends on vector representation, but in lots of real-world applications the data is tensor form, such as color images, video sequences, and multi-sensor networks. When compressed sensing theory is utilized to high-order tensor data, it must be transformed into vectors to form a large sampling matrix, resulting in high computational cost and memory load. References [42, 43] proposed a generalized tensor compressive sensing (GTCS) for high-order tensor data to decrease the calculation complexity of reconstruction while keeping the internal structure information of tensor data. References [44, 45] proposed a compressed sensing framework with mixed vectors and tensors that can be compatible with real devices according to the requirements of acquisition and reconstruction.

3.2 Tensor unsupervised learning

3.2.1 Tensor clustering

Clustering can be used to research the key underlying data structures. Vectorization is necessary to cluster tensor data by vector-based clustering methods, which could lead to decreased clustering accuracy and more expensive or even difficult calculations. Many tensor clustering algorithms have been proposed.

Clustering via tensor factorization: Given M copies of nth-order tensor, ${{\mathcal {X}}_{1}},{\cdots } ,\mathcal {X},\in {{\Re }^{{{d}_{1}}\times {\cdots } \times {{d}_{n}}}}$, reference [46] intended to reveal potential cluster structures of the M samples. This is

$$ \underbrace{\left( 1,{\cdots} ,1, \right.}_{l\ samples}\underbrace{2,{\cdots} ,2,}_{l\ samples}{\cdots} \underbrace{\left. ,K,{\cdots} ,K \right)}_{l\ samples}, $$

(36)

with K clusters and l samples, and l = N/K for every cluster. In order to cluster these tensor samples, firstly, they were stacked into an (n + 1)th-order tensor, $\mathcal {T}\in {{\Re }^{{{d}_{1}}\times {\cdots } \times {{d}_{n}}\times N}}$, and then $\mathcal {T}$ was decomposed. Finally, to obtain the cluster assignment, the routine clustering algorithm of K-means was applied to the matrix from the decomposition corresponding to the last mode. Concretely, let $\mathcal {T}$ be a noisy tensor, and $\mathcal {T}={{\mathcal {T}}^{*}}+\mathcal {E}$, where ${{\mathcal {T}}^{*}}$ denotes a true tensor with rank-R CP composition and $\mathcal {E}$ denote an error tensor. ${{\mathcal {T}}^{*}}$ is given by

$$ {{\mathcal{T}}^{*}}=\sum_{r=1}^{R}{w_{r}^{*}}\beta_{1,r}^{*}\circ {\cdots} \circ \beta_{n+1,r}^{*}, $$

(37)

where $\beta _{j,r}^{*}\in {{\Re }^{{{I}_{j}}}}$, ${{\left \| \beta _{j,r}^{*} \right \|}_{2}}=1,w_{r}^{*}>0, j=1,\ldots ,(n+1), r=1,\ldots ,R.$ Then the matrix $B_{m+1}^{*}$stacked the decomposition factors is as follows

$$ \begin{array}{@{}rcl@{}} B_{n+1}^{*}&=&\left( \beta_{n+1,1}^{*},{\cdots} ,\beta_{n+1,R}^{*} \right) \\ &=&\underbrace{\left( \mu_{1}^{*T},{\cdots} ,\mu_{1}^{*T}, \right.}_{l\quad samples}{\cdots} \underbrace{\left. ,\mu_{K}^{*T},{\cdots} ,\mu_{K}^{*T} \right)}_{l\ samples}\in {{\Re }^{N\times R}},\\ \end{array} $$

(38)

where $\mu _{k}^{*}:=\left (\mu _{k,1}^{*},{\cdots } ,\mu _{k,R}^{*} \right )\in {{\Re }^{R}}, k=1,\ldots ,K$. The true cluster means can be represented as

$$ \begin{array}{@{}rcl@{}} &&\underbrace{{{\mathcal{M}}_{1}}:=\sum_{r=1}^{R}{w_{r}^{*}\beta_{1,r}^{*}\circ {\cdots} \circ \beta_{n,r}^{*}\mu_{1,r}^{*}}}_{cluster\quad center\mathcal{ 1}},\cdots, \\ &&\underbrace{{{\mathcal{M}}_{K}}:=\sum_{r=1}^{R}{w_{r}^{*}\beta_{1,r}^{*}\circ {\cdots} \circ \beta_{n,r}^{*}\mu_{K,r}^{*}}}_{cluster\quad center\mathcal{ K}}. \end{array} $$

(39)

To obtain the sparsity and dynamics of the tensor samples, Reference [46] further proposed a dynamic tensor clustering that fused the sparse and smooth fusion structure with tensor decomposition. All of the aforementioned tensor clustering theoretical analyses made the assumption that the actual number of clusters was known. When the number of clusters is assessed, it is very important to analyze the tensor clustering characteristic.

In the reference [47], an essential tensor learning approach based on t-product was proposed to exploit high-order correlations for multi-view data. Firstly, the view-specific similarity matrix and the corresponding multi-view transition probability matrix were calculated, and then a transition probability tensor was established on this basis. The essential tensor was learned by t-SVD and tensor nuclear norm minimization, which were utilized as inputs to the standard markov chain method for spectral clustering. In reference [48], multiview data was represented as a 3rd-order tensor, and a low-rank multiview clustering byt-linear combination was proposed.

3.2.2 Tensor graphical model

The data that needs to be processed can be in tensor form in more general situations. The tensor will lose important structural information if it is simply rearranged into a matrix or vector, producing disappointing results. Additionally, reshaping the tensor data directly to fit in the vector- or matrix-based graphical model will necessitate a massive precision matrix, which is computationally expensive.

The goal of a tensor graphical model is to explore the dependency structure of each mode of tensor-valued data. Similar to the vector- or matrix-based value graphic model, a tensor graphical model has been proposed [49,50,51,52,53,54]. Given the D th-order tensor $\mathcal {T}\in {{\Re }^{{{I}_{1}}\times {\cdots } \times {{I}_{D}}}}$ from a tensor normal distribution with zero mean and covariance matrices Σ₁⋯,Σ_D, i.e. $\mathcal {T}\sim TN\left (0;{{\Sigma }_{1}}{\cdots } ,{{\Sigma }_{D}} \right )$, its PDF is

$$ \begin{array}{@{}rcl@{}} && \Pr ob\left( \mathcal{T}\mid {{\Sigma }_{1}}{\cdots} ,{{\Sigma }_{D}} \right) \\ &&={{\left( 2\pi \right)}^{{-I}/{2} }}\left\{ \prod_{d=1}^{D}{{{\mid {{\Sigma }_{d}} \mid}^{{-I}/{\left( 2{{I}_{d}} \right)} }}} \right\} \\ &&\exp \left( -\left\| \mathcal{}\times {{\Sigma }^{{-1}/{2} }} \right\|_{F}^{2}{\Sigma }/{{2}} \right) \end{array} $$

(40)

Where $I=\prod _{d=1}^{D}{{{I}_{d}}}$, and ${{\sum }^{{-1}/{2} }}=\left \{ {\sum }_{1}^{{-1}/{2} },{\cdots } ,{\sum }_{D}^{{-1}/{2} } \right \}$. When D = 1, it transforms into a vector normal distribution with zero mean and covariance Σ₁.

The tensor data is supposed to follow a tensor normal distribution, according to all publicly available studies. Relaxing this normal distribution constraint, extending to the higher-order nonparanormal distribution, and utilizing a reliable rank-based probability estimator are reasonable further initiatives. In addition to the above methods, there are other learning algorithms [55, 56].

3.3 Tensor deep learning

The main reason for introducing tensor algebra theory into deep learning (DL) is that traditional DL has the following problems:

• 1) The traditional DL structure is arranged into layers. The special structure needs to convert non-vector inputs (e.g., matrices and tensors) into vectors, which has the following challenges: First, in the vectorization process, spatial information between data elements may be lost. Second, the solution space becomes very large; therefore, the requirements of network parameters are complex, and the calculation cost is also very high.

• 2) DL involves millions of parameters. Training a DL model typically requires huge memory and an expensive computational cost. Therefore, it is challenging to apply DL to low-end devices.

3.3.1 Compressing deep neural network based on tensor

References [57,58,59] proposed a low-rank approximation of tensor decomposition for the convolutional layers of a convolutional neural network (CNN). CP decomposition was utilized for the convolutional layers [58], whereas Tucker decomposition was used on each kernel tensor of CNN, and then fine-tuning was used to recover accumulated loss of accuracy [60]. Reference [61] proposed a tensor decomposition framework for efficient multidimensional convolutions of higher-order CNN that unified tensor decomposition and efficient architectures, such as MobileNet or ResNet’s Bottleneck blocks.

There are fully connected layers to connect the outputs in traditional CNN architecture, which result in tremendous parameters. For instance, the parameters of the connected layers account for about 80% of the whole CNN in the VGG-19 network [62]. Based on these reasons, the tensor-train decomposition [63], the block-term decomposition [64], and the Tucker decomposition [65] are used to decrease the number of parameters for completely connected layers in CNN.

In addition to respectively compressing the convolutional and fully connected layers, another method is to compress all layers of CNN. Reference [66] proposed the randomized tensor sketching method and used it to design a general scheme to approximate the operation of both the convolution layers and full connection layers in CNNs. Reference [67] proposed tensorizing the entire CNN with a single high-order tensor and using it to capture CNN structure information.

Recurrent neural networks (RNNs) are a kind of neural network for processing sequence data, showing promising performances. Reference [68] proposed that the tensor train format was used to decompose the input-to-hidden weight matrix for the high-dimensional inputs. The block-term decomposition was utilized to approximate the weight matrices with low-rank tensors, which can effectively reduce the number of CNN and RNN [69,70,71].

The theoretical features of the tensor-based DNN compression algorithms have demonstrated considerable empirical effectiveness; however, they remain unclear. Furthermore, low-rank structures have been the main focus of existing techniques for dimension reduction. To further minimize the number of parameters and enhance the interpretability of the tensor layers in CNNs or RNNs, it may be beneficial to take into account additional sparsity structures, such as the sparse tensor factorization.

3.3.2 Deep learning theory based on tensor approaches

Although there is a lot of empirical evidence that deep hierarchical networks have more expressive power than shallow ones, theoretical justifications are limited so far. Reference [72] proposed using tensors as an analytical tool to exploit the expressive power of deep neural networks and established equivalence between neural networks and tensor decomposition. The shallow and deep networks correspond to CPD and hierarchical Tucker decomposition, respectively. With the corresponding connection, it is also demonstrated that for all functions that can be implemented by a deep network of polynomial size, an exponential network size is required to approximate or realize the function with a shallow network.

Based on the tensor tool, reference [73] extended the research on expressive efficiency to the overlapping architecture of deep networks. In the reference [74], the connection between recurrent neural networks and tensor-train decomposition was established, and it was proved that a shallow network with an exponentially large width is needed to simulate a recurrent neural network. The corresponding relationship between tensor and deep learning is shown in Table 1.

Table 1 The connection of between tensor and deep learning

Reference [75] utilized tensor decomposition methods to obtain a series of data that can effectively describe the compressibility and generalizability of NNs. Many other connections between deep neural networks and tensor decompositions were established [76,77,78].

The theoretical underpinnings for the relationship between learning a one-hidden-layer neural network and tensor factorization are provided by the literature mentioned above. It is possible to extend this relationship to deeper neural network topologies and broader data distributions. The theoretical findings of [75] can be used to examine the compressibility and generalizability of further deep neural network architectures.

3.4 Learning algorithm based on t-product tensor

CP decomposition is a concise tensor decomposition method, but solving the best approximation to the original tensor is an ill-posed issue. The widely used TD can extract the multilinear relationship of tensor data, but its solution is a suboptimal approximation and difficult to explain. Tensor train decomposition can compress high-order tensor data efficiently, but it lacks interpretability and provable optimality. Therefore, the tensor decomposition based tensor neural network has problems in proving optimality, interpreting compression, and parallelization. In order to solve these problems, researchers have preliminarily explored the learning algorithm based on the new tensor algebra t-product.

Newman et al. [79] proposed to parameterize the neural networks on the basis of tensor and t-product for efficient feature extraction. YIN, Ming [80] applied t-product to construct multiview clustering method for the 3th-order tensor data. Based on t-product and convolutional sparse coding (CSC), reference [81] proposed tensor convolutional sparse coding (TCSC), which allows coding the high-order correlation between features/channels and helps to learn high-capacity dictionaries. In reference [82], the problem of tensor robust principal component analysis (TRPCA) is investigated. In order to accurately describe TRPCA, tensor kernel norm, tensor spectral norm, and tensor averaged rank will be derived from t-product. Using the novel tensor kernel norm, the TRPCA problem is solved by solving convex programming, which provides a theoretical guarantee for the accurate solution of the TRPCA problem. Based on the t-product, reference [83] designed two neural networks to approximate a 3rd-order tensor. By integrating the Bayesian framework with low-tubal-rank structures, Reference [84] proposed Bayesian low-tubal-rank robust tensor factorization. The approach can automatically settle tubal and multi-rank components while obtaining the trade-off between low-rank and sparse components. Generalized transformed t-product [85] is used for tensor completion.

3.5 Experimental comparison

In order to thoroughly compare different classical algorithms based on tensors, we selected a number of the classical methods to classify the instantaneous cognitive states from StarPlus fMRI data. The methods being contrasted include: SVM [86], STM [87], TT classifier [88], STuM [33], DuSK [39], and KSTTM [41].

We have 300 fMRI images: half for picture stimuli and half for sentence stimulus. Each fMRI image is in size of 64 × 64 × 8, which contains 25-30 anatomically defined regions (called “regions of interest”, or ROIs). Following the selection of those ROIs, the data from each sample is normalized. The primary goal of this work is to develop classifiers that can identify whether a subject is looking at a sentence or a picture. 130 photographs are chosen at random for training, 50 for validation, and the remaining subjects for testing.

The accuracy is used as the evaluation indicators. The values in the subject column of Table 2 represent corresponding data. For example, 04847 is data for subject 04847. Table 2 displays the classification outcomes for the SVM, STM, STuM, TT classifier, DuSK, and KSTTM algorithms. The very high dimensionality and sparsity of the data prevent SVM from finding appropriate hyperparameters, and the classification accuracy is poor. The CP-based STM cannot reach adequate classification performance because finding the best approximation is an ill-posed problem, and fMRI data are exceedingly complex. The rank-1 CP’s simplicity prevents it from extracting complicated structure from an fMRI image. The kernel-CP-based DuSK and Tucker-based STuM perform better than SVM and STM. The KSTTM and TT classifiers, which are efficient for removing the redundant information in the original data and providing a more compact data representation by lowering the dimensionality of the input data, both produce good results. Consequently, we can say that tensor classification techniques outperform their rivals for high-dimensional data.

Table 2 Classification accuracy of different approaches

4 Application of tensor

The tensor is a generalization of the matrix to a higher order, which is a good representation for high-dimensional multi-aspect data, and can be helpful for representing different kinds of data. In contrast to their traditional matrix-based counterparts, tensor learning techniques can prevent the loss of multi-linear structure information, and tensor subspaces can have substantially lower computing complexity than the initial format. The recent advances in tensor algebra theory have greatly promoted the development of tensor learning and its applications. In this subsection, we discuss a wide range of such situations, including healthcare applications, urban computing, Internet of Things, remote sensing, recommendation systems, and intelligent transportation systems.

4.1 Healthcare applications

Electronic health records (EHR) consist of a variety of data, including structured information (such as diagnosis, drugs, and laboratory data), molecular sequences, social network data, and unstructured clinical records. It is increasingly obvious that the EHR is a valuable clinical research resource, but it is difficult to use because of its health care business operation, cross-business system heterogeneity, and high missing or wrong records. In addition, the interaction between different data sources in EHR makes modeling challenging, and the traditional analysis framework cannot be used to solve this problem. Researchers have made various efforts to get concise and meaningful phenotypes or concepts from EHR data. Sun team [89] is using deep learning and tensor learning research to solve these problems, and they intend to develop a generalized computing framework to extract meaningful phenotypes from EHR data, requiring only a small amount of professional guidance.

Ho et al. [90] used tensor technology to automatically obtain phenotypic candidates from electronic health records. The author proposed a CP model based tensor decomposition in which each candidate phenotype is a rank-1 component of CPD (patient, diagnosis, and procedure). The resulting phenotypes are brief, understandable, and comprehensible. This method reduces the number of nonzero elements by at least 42.8% while maintaining classification-related predictive power. It has also been applied to EHR to predict heart failure [91], using a tensor model (drugs × patient × diagnosis).

Tensors are also used in bioinformatics to simulate and diagnose disease using microarray gene expression tensors (genes × sample × Time) [92]. Recently, tensor decomposition has been used to detect disease outbreaks in epidemiology [93, 94]. The author proposes to use space for monitoring (tasks × time × index) third-order tensor (Fig. 8).

Fig. 8

Tensor decomposition for phenotypes from EHR data [90]

4.2 Urban computing

Urban computing is the term for a group of computer applications that examine how people move around and interact with their environment in cities with the aim of making them more livable.

To predict areas where criminal activities may occur in the future, reference [95] represents crime data as a 4-order tensor, which is composed of longitude, latitude, time, and other related incidents, e.g., residential theft data, social events, and criminal data. Tucker decomposition was utilized to approximate the 4-order tensor for discriminative information, and then the empirical discriminative tensor analysis was applied to forecast potential crime activity. The proposed tensorial algorithm outperforms the vector-based method and the methods that learn the discriminative information and minimize the empirical risk, respectively. Reference [96] proposed a coupled matrix tensor decomposition for the GPS trajectories, one of which was the third-order tensor with (road segment, driver, time slot), the other was a matrix (road segment, geographical features), and the third was a (time slot, time slot) matrix.

To identify the main noise pollution sources in New York City in different periods of a week by analyzing the noise complaint data, reference [97] models the noise complaint data as a third-tensor, where the three orders represent locations, noise types, and time slots, respectively. It was coupled with matrices with additional information.

4.3 Internet of things

A tensor is a multilinear mapping across vector spaces that is a generalization of a vector and a matrix. It can effectively represent heterogeneous heterogeneous data, overcome vector defects, and has special compression properties. Tensor has been widely used in the field of Internet of things (IoT) [98,99,100,101,102,103,104,105,106,107]. IoT data is composed of structured, unstructured, and semi-structured data, which are expressed as three sub-tensors in reference [98], and then they were mapped to a unified and concise tensor model, which Tucker decomposition was utilized to obtain the high-quality core data. The tensor model successfully addresses the following two issues: how to represent heterogeneous IoT data as a concise and unified model and extract the essential core data that are smaller for transmission but contain the most valuable information; and how to control network devices globally and flexibly and dynamically reallocate bandwidth to improve communication link utilization ratio. The unified representation of Internet of Things data is shown in Fig. 9.

Fig. 9

Unified representation of the IoT big data [98]

Data recovery is critical in wireless sensor networks (WSNs). However, the recovery accuracy of most approaches cannot meet the actual needs, due to the multimode features of sensor data. To address the correlation among multimode data, reference [108] modeled the multimode sensor data as a low-rank third-tensor.

4.4 Remote sensing

Spectral images in different spectral ranges can be captured, and multiple images of scenes or objects can be created with hyperspectral imaging technology, which can be used for remote sensing. To detect and classify targets [109,110,111] or identify space object material [112], hyperspectral images can be modeled as a 3rd-order tensors with (spatial row × spatial column × wavelength). In reference [113], a 5th-order tensor is selected to model remote sensing images, which are processed by a support tensor machine for target recognition.

In reference [114], a remote sensing image is represented as a data cube, which was preprocessed by a multilinear principal component analysis [115] for alleviating the tensorial data redundancy, and then a multiclass support tensor machine was utilized to identify the information classes in tensor space.

4.5 Recommendation system

Tensor is widely used in recommendation systems [116,117,118,119,120,121,122]. Based on CP decomposition, reference [116] proposed a bayesian probabilistic tensor factorization (BPTF, Fig. 10), which was utilized in a recommendation system with temporal information. Experiments demonstrate that BPTF surpasses Bayesian probabilistic matrix factorization (BPMF). It is helpful to recommend the use of time information and its high-order structure on data. Symeonidis et al. [123] introduced the tensor into the social tag systems and represented users, items, and tags as a 3rd-order tensor by utilizing Tucker decomposition for dimensionality reduction and semantic analysis. Utilizing two actual datasets, they conducted an experimental comparison of the proposed approach against two cutting-edge tag recommendation systems. Their results demonstrate significant gains in efficiency according to recall/precision.

Fig. 10

The graphical model for BPTF [116]

Although the Tucker decomposition model has shown higher label recommendation quality compared with other methods, the core tensor is still three-dimensional, which leads to the high time complexity of model training and prediction, so the Tucker decomposition model cannot be well applied to large- and medium-sized datasets. To solve this problem, reference [124] proposed a pairwise interaction tensor factorization (PITF) decomposition model. It simplifies the decomposition by ignoring the interaction between users and items, resulting in a linear model with significantly reduced algorithm complexity. Compared with other recommendation algorithms, the recommendation quality had been greatly improved.

4.6 Intelligent transportation system

Tensor is a powerful tool for modeling and analyzing traffic data that has been widely used in intelligent transportation systems [125,126,127,128,129,130,131,132,133]. To solve the problem of random missing values, the iterative tensor decomposition (ITD) was proposed by reference [126], which completes missing data using the inherent correlation of traffic data. Experimental studies were conducted to investigate the cases of excessive missing (missing days vary from 1 to 21 days) and random missing (missing ratio ranges from 10% to 90%). The findings demonstrate that, for various missing ratios, ITD surpasses a number of cutting-edge tensor-based techniques. Reference [127] takes advantage of the traffic data by modeling it as a dynamic tensor. A proposed dynamic tensor completion method was utilized to impute the traffic data.

4.7 Brain data analysis

Every mental action that takes place over a certain amount of time is controlled by various brain areas; therefore, the brain is one of the complex systems that produces a rich source of tensorial data. Tensors are used to brain data analysis [134,135,136,137,138]. In order to pinpoint the seizure’s cause, [134] examine electroencephalogram (EEG) data from epileptic patients. To achieve this, authors preprocessed the EEG recordings by a wavelet transformation, and modeled the data as a 3th-order tensor (time samples × scales × electrodes). They utilized the CP deomposition to analyze the EEG tensor. Researchers [135] modelled fMRI data from nine different individuals after showing them 60 distinct simple English nouns as a 3rd-order tensor (noun × voxel × person). In order to locate latent clusters of nouns, voxels, persons, and noun qualities, they applied coupled matrix-tensor factorization.

4.8 Other application

Tensors are also widely used in Signal processing [139,140,141,142,143,144], cyber-physical-social systems [145,146,147,148,149], Web mining [150,151,152], image processing, computer vision [153,154,155], and tensor completion [156, 157], and so on. Tensor decomposition has been applied in seismology, and reference [158] established spatial × time × frequency the third-order tensor, which is used to predict the ground motion after an earthquake.

5 Prospects

Tensor is an effective representation for complex, high-dimensional, and multi-modal data. Researchers have made a more in-depth exploration of tensor learning theory and its application and obtained some research results. However, there are many theoretical and application problems worthy of our in-depth exploration of tensor learning. To sum up, there are mainly the following research points:

• (1) How to design efficient methods based on tensor computing for dealing with big data.

  Developing distributed tensor learnings, online decomposition, and high-performance tensor learning techniques is a possible approach to solving this issue. A promising approach to speeding up the calculation of the tensor operator is to develop some novel quantum circuits. In addition, the combination of tensor decomposition theory and randomization algorithms are also promising methods.

• (2) Learning algorithms based on t-product are promising research directions.

  Tensor decomposition is inconsistent with matrix theory. CPD is a concise tensor decomposition method, but solving the best approximation to the original tensor is an ill-posed problem. TD can extract the multi-linear relationship of tensor data and has been effectively used in many areas, but its solution is a sub-optimal approximation and difficult to explain. TT-SVD can compress high-order tensor data efficiently, but it lacks interpretability and provable optimality. Therefore, the tensor decomposition method has problems in provable optimality and parallelization. It is necessary and worthwhile to research a learning algorithm based on t-product.

• (3) Research on DL theory by tensor approaches.

  Although preliminary results have been obtained by using tensor method to investigate DL theory. Compared with the experimental success of DL, there is still very little understanding of their theoretical properties. It is necessary to further study the expressive force, compressibility and generalization of DL by tensor method.

• (4) Nonlinear tensor models.

  The linear model is uncomplicated and has good generalizability; however, it cannot naturally match the local characteristics. Since they are capable of good fitting, nonlinear models have attracted a lot of attention recently. An unsolved issue in kernel learning is how to create a suitable tensor kernel function that can take advantage of the data’s multidimensional structure while simultaneously making calculations simpler.

• (5) More research is needed on the combination algorithms of tensor theory and neural networks, particularly t-product and deep learning, as well as generation countermeasure networks, which are used to solve a variety of practical problems.

• (6) Research on the application of the extended tensor learning algorithm. The tensor learning method is applied to practical problems, e.g., mechanical fault diagnosis, chemical fault diagnosis, network security, intelligent medical treatment, sensor networks, and so on.