A reference vector adaptive strategy for balancing diversity and convergence in many-objective evolutionary algorithms

Abstract

Decomposition-based multiobjective evolutionary algorithms (MOEA/D) have achieved great success in the field of evolutionary multiobjective optimization, and their outstanding performance in solving for the Pareto-optimal solution set has attracted attention. This type of algorithm uses reference vectors to decompose the multiobjective problem into multiple single-objective problems and searches them collaboratively, hence the choice of reference vectors is particularly important. However, predefined reference vectors may not be suitable for dealing with many-objective optimization problems with complex Pareto fronts (PFs), which can affect the performance of MOEA/D. To solve this problem, we introduce a reference vector initialization strategy, namely, scaling of the reference vectors (SRV), and also propose a new reference vector adaptation strategy, that is, transformation of the solution positions (TSP) based on the ideal point solution, to deal with irregular PFs. The TSP strategy can adaptively redistribute the reference vectors through periodic adjustment to endow that the solution set with better convergence and a better distribution. Both strategies are introduced into a representative MOEA/D, called 𝜃-DEA-TSP, which is compared with five state-of-the-art algorithms to verify the effectiveness of the proposed TSP strategy.

1 Introduction

Multiobjective evolutionary algorithms (MOEAs) have received extensive attention in recent decades. Due to their superior performance in both research and practical problem optimization, they have been widely used in the fields of engineering [1,2,3,4] and scientific research [5,6,7,8]. In these fields, an increasing number of multiobjective optimization problems (MOPs) are emerging in which it is necessary to optimize three or more conflicting objectives simultaneously. Therefore, studying such many-objective optimization problems (MaOPs) has important practical significance.

Without loss of generality, the minimum MOP can be defined as:

$$ \begin{aligned} &minimize\ F(x)=\left( f_{1}(x),f_{2}(x),\cdots,f_{m}(x)\right)^{T}\\ &Subject\ to\ x \in {\Omega} \end{aligned} $$

(1)

where x=(x₁,x₂,⋯ ,x_m)^T is the decision vector, f_i(x) represents the i-th objective function in the objective space, m denotes the number of objective functions, and Ω is the feasible region in the decision space. An MOP can also be called an MaOP if m> 3 [9,10,11]. So-called PFs are generated by these MOEAs to help decision-makers choose a solution that strikes a desirable balance among the various conflicting objectives.

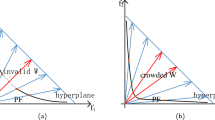
In recent years, the emergence of many excellent algo rithms, such as the adaptive-reference-point-based nondominated sorting genetic algorithm (ANSGA-III) [12], MOEA/D [13], and the reference-vector-guided evolutionary algorithm (RVEA) [14], has enabled many MaOPs to be solved. In paticular MOEA/D, which was first proposed by Zhang, has been a trending research topic in recent decades. Without prior knowledge, this algorithm generates a series of uniformly distributed reference vectors in the first quadrant. The algorithm then uses this set of predefined reference vectors to decompose the problem into several subproblems. Reference vectors in different directions are used to search different areas of the objective space. As described by Liu [15], the predefined reference vectors are constructed from a set of reference points on the hyperplane ${\sum }_{i=1}^{m} f_{i}=1$ in the normalized m-dimensional objective space, called the normal boundary intersection (NBI) [16]. The basic assumption of MOEA/D is that a uniform distribution of the reference vectors can ensure the diversity of the solution set, as shown in Fig. 1(a).

Fig. 1

Ten uniformly distributed reference vectors on a regular PF, a concave PF, and a convex PF. (a) Ten uniformly distributed reference vectors on a regular PF. (b) Ten uniformly distributed reference vectors on a concave PF. (c) Ten uniformly distributed reference vectors on a convex PF.

However, such predefined reference vectors do not allow satisfactory handling of MaOPs with irregular PFs. Because the generated reference vectors are not evenly distributed along the true PF, the performance of MOEA/D can be greatly affected. Under the assumptions that the PF is symmetric and the m objectives have been normalized to 0<f_i< 1, the curvature of the PF can be expressed as ${f_{1}^{p}}+{f_{2}^{p}}+\cdots +{f_{n}^{p}}=1$, where p> 0. When p> 1, the PF is concave, and most of the solutions obtained are sparse in the central area and dense at the corners. When p< 1, the PF is convex, and most of the solutions obtained are dense in the center area and sparse at the corners. For the concave and convex cases, the solutions specified by ten uniformly distributed reference vectors on the PF of a simple two-objective problem are shown in Fig. 1(b) and (c) respectively.

According to Pan [17], irregular PFs also include discontinuous and degenerate Pareto surfaces. A discontinuous PF is defined as a PF whose geometry is incomplete and the PF of a degenerate MOP has fewer than m-1 dimensionals.

Therefore, to solve such problems, many scholars have set out to study how to ensure that the reference vectors in MOEA/D are evenly distributed on the real PF.

The improved MOEA/D (MOEA/D-TPN) proposed by Jiang [18] adopts a two-phase strategy. In the first phase, the unevenness of the PF of the MOP is judged, and then the reference vectors are adjusted in accordance with the results of the first stage and a corresponding decision on how to allocate computational resources, however, this algorithm introduces too many parameters, making it heavily dependent on the values of these parameters.

Dong [19] proposed an adaptive reference vector adjustment strategy based on chain segmentation, in which a chain topology relationship is established for the subproblems, the step length between adjacent individuals is calculated to divide the chain equally, and then, the positions of the reference vectors are determined through a distance strategy and the calculation of the ratios between two adjacent individuals. Finally, vector addition is used to obtain a more uniformly distributed reference vector set. However, the structure assumed for the topological relationship is suitable only for two-dimensional and three-dimensional MOPs.

Qi [20] proposed an improved MOEA/D with adpative weight adjustment (MOEA/D-AWA), in which the reference points are dynamically adjusted during the optimization process. The entire optimization process is also divided into two stages to balance convergence and diversity. Specifically, a sparsity level calculation formula is introduced to calculate the sparsity of each subproblem; then, overcrowded subproblems are periodically deleted in accordance with a preset value, and new reference vectors are generated in relatively sparse positions. However, the external archive mechanism and the complicated sparsity level calculation seriously affect the efficiency of the algorithm.

On the other hand, some scholars have combined machine learning methods to generate new reference vectors. Gu [21] proposed a reference point design method based on a self-organizing map (SOM). This method uses the weights of the neurons as the reference vectors and uses the objective vector of the nearest population to periodically train an SOM network of N neurons. Wu [22] proposed a learning decomposition method to adaptively determine the reference vectors. This method is divided into a learning module and an optimization module. Specifically, in the learning module, the current nondominated solutions are used as training data, and Gaussian process (GP) regression is used to train an analysis model. In the optimization module, feature vectors are extracted to adjust the reference vectors. However, the learning process is time consuming and can easily lead to overfitting.

For MaOPs with convex, concave, degenerate, or discontinuous PFs, many algorithms based on reference vectors may not be able to solve them well or may require considerable computational resources to solve them [23]. To solve such problems more effectively, we propose our TSP strategy, which can be combined with other decomposition-based MOEAs.

The main contributions of this paper can be summarized as follows.

• 1. The proposed TSP strategy can be easily integrated into other algorithms to improve the convergence of the population.

• 2. 𝜃-DEA-TSP is proposed, which incorporates the TSP strategy and considers the diversity and convergence of the population throughout the whole execution of the algorithm, instead of focusing on the diversity of the population at the end of the algorithm, to avoid the algorithm falling into a local optimum in the early stage. At the same time, the algorithm has lower computational complexity.

• 3. This research is expected to provide better solutions for MaOPs facing similar problems.

The rest of this paper is organized as follows. In Section 2, we introduce the background of our work, including the SRV strategy and the previously proposed strategy for the transformation of the solution locations (TSL), as well as the motivation for our work. In Section 3, we describe in detail the framework of the proposed TSP strategy and 𝜃-DEA-TSP. In Section 4, our experimental results illustrate the effectiveness of the proposed strategy and the comprehensive performance of 𝜃-DEA-TSP on MaOPs with complex PFs. Finally, in Section 5, this paper is summarized, and future research topics are proposed.

2 Related work

To solve MaOPs with complex PFs, Liang [24] proposed the SRV and TSL strategies for modifying the reference vectors.

Specifically, the SRV strategy scales the reference vectors generated via the NBI method on the basis of a predesignated center vector, to ensure that the reference vectors can be evenly distributed on PFs that are concave or convex in nature.

In the NBI method, the number of reference vectors N is counted as follows:

$$ \qquad\qquad N=(^{H+m-1}_{m-1}) $$

(2)

where m is the number of objectives, and H represents the the number of divisions on each axis. The N reference points are evenly distributed on the entire normalized hyperplane with m objectives.

Therefore, the reference points are mostly generated near the boundary, and only a few points are generated on the inner part of the hyperplane, where H ≥ m. In the SRV stragety, divides the boundary and inner layers are divided using values of as H₁ and H₂, respectively, to generate two-layer reference points. The N reference vectors are then generated as follows:

$$ \qquad\qquad N=(^{H_{1}+m-1}_{m-1}) +(^{H_{2}+m-1}_{m-1}) $$

(3)

However, when the intent is to solve an MaOP with a concave or convex PF, the reference vectors thus generated still will not be evenly distributed on the PF, especially in the case of MaOPs. Therefore, a scaling function (SF) is applied to the original reference vectors, as expressed below:

$$ \begin{array}{@{}rcl@{}} \qquad\qquad W_{i}=\frac{W_{i}{\circ}r_{i}+V_{c}{\circ}(1-r_{i})}{||W_{i}{\circ}r_{i}+V_{c}{\circ}(1-r_{i})||} \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \qquad\qquad r_{i}={p^{k}_{i}} \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \qquad\qquad p_{i}=\frac{max{|W_{i}-V_{c}|}}{max_{i=1}^{N}\{max\{|W_{i}-V_{c}|\}\}} \end{array} $$

(6)

Here, i = 1,2,⋯ ,N, W_i represents the i-th reference vector. V_c represents the designated center vector. The ∘ operator denotes the Hadamard product and ||⋅|| denotes the calculation of the norm. r_i is the scale of the i-th reference vector, and p_i ∈[0,1] represents the similarity between the i-th reference vector and the center vector.

To solve MaOPs with degenerate and discontinuous PFs, Liang [24] also proposed the TSL strategy. Specifically, this strategy consists of comparing the Euclidean distances between pair of solutions, filtering out less diverse solutions based on their the Euclidean distances, removeing the overcrowded solutions and transforming the remaining highly diverse solutions into a new set of reference vectors to deal with the degenerate or discontinuous PF. This strategy solves the problem that the reference vectors cannot be evenly distributed on the PF in the case of complex MaOPs. However, we have found that the TSL strategy considers only the diversity of the solutions when deleting overcrowded solutions. It ignores the convergence of the solutions, leading to population degradation. In the proposed algorithm 𝜃-DEA*, the TSL strategy is applied at the end of the algorithm to increase the diversity of the solution set. However, this can cause the algorithm to fall into a local optimum early.

In this article, to solve the problem that the TSL strategy results in degeneration of the population in the face of complex MaOPs, we propose the TSP strategy as an alternative. In the TSP strategy, when a new set of reference vectors is being constructed two solutions to be deleted are compared with the current ideal point by calculating the Euclidean distance, and the better solution is retained to prevent population degradation. In addition, the TSP strategy is applied to adjust the reference vectors throughout the whole execution of 𝜃-DEA-TSP, thereby guaranteeing good diversity of the population while improving convergence.

3 Methodologies

In this section, we describe the TSP strategy. Specifically, to better deal with MaOPs with degraded or discontinuous PFs, the positions of solutions are converted into new reference vectors to prevent the degradation of the population while maintaining its diversity. This strategy can be integrated along with the SRV strategy into popular MOEAs based on reference vectors to enhance the evolutionary search process.

3.1 Transformation of solution positions based on the ideal point solution

Oriented toward MaOPs with degenerate or discontinuous PFs, we propose the TSP strategy to fit an irregular PF by transforming the position of a solution with good distribution and convergence characteristics to obtain a new reference vector. Specifically, in the TSP strategy, the distances between pairwise solutions are initially calculated. If such a distance is less than a preset threshold, then the corresponding solution with poorer diversity is selected to calculate the Euclidean distance between this solution and the ideal point. Solutions with larger Euclidean distances, that is, poorer convergence are deleted, and the remaining solutions are converted into reference vectors.

The TSP process is shown in Algorithm 1. First, the algorithm initializes a population archive PA as the entire population, in which each individual is normalized. Second, the Euclidean distances Dist of the pairwise solutions in PA are calculated. The Euclidean distance is expressed as follows:

$$ \begin{aligned} \qquad\qquad&D(X,Y)=\sqrt{{\sum}_{m}^{i=1}(x_{i}-y_{i})^{2}}\\ &Subject\ to\ X,Y \in \omega \end{aligned} $$

(7)

where X=(x₁,x₂,⋯ ,x_m)^T and Y=(y₁,y₂,⋯ ,y_m)^T are the decision vectors, and ω is the feasible region in the decision space. Lines 3-10 of the algorithm filter out the two solutions corresponding to the minimum Euclidean distance based on Dist, calculate the Euclidean distances between these two solutions and the current ideal point, and delete the solution corresponding to the larger distance. This process is repeated until Dist_min is greater than the threshold 𝜖. The aim of Lines 11-15 is to find the solution among the remaining solutions that is nearest to be better solution of each solution pair processed as described above and generate a new solution S at the midpoint of the two. The new solution S is stored in PA, Dist is updated, and the process is repeated until the number of solutions in PA is N. In Lines 17-19, the solutions in PA are converted into new reference vectors to guide the generation of new offspring.

To illustrate the process more clearly, we present an example in Fig. 2. In Fig. 2(a), the algorithm finds four points corresponding to two Euclidean distances smaller than our preset threshold 𝜖, namely, points B and C and points D and E. Second, the Euclidean distances between B, C, D and E, and the current ideal point Z^∗ are calculated, as shown in Fig. 2(b). Next, the algorithm deletes the individuals farther from the ideal point between B and C and between D and E, that is, B and D, as shown in Fig. 2(c). Finally, the individuals closest to B and D other than C and E are found, namely, A and F. New individuals $B^{\prime }$ and $D^{\prime }$ are generated at the midpoints between A and C and between E and F, as shown in Fig. 2(d).

Fig. 2

An example illustrating the whole process of screening, deleting, and generating solutions in accordance with the TSP strategy

3.2 The framework of 𝜃-DEA-TSP

The SRV and TSP strategies are two independent strategies that can be easily integrated into MOEAs. The algorithm framework is shown in Algorithm 2. First, the population Pop is initialized and reference vectors W are generated using the NBI method. In Lines 2-3, the SRV strategy mentioned in Section 2 is used to scale the reference vectors, and then, the objective normalization flag is set. Lines 4-14 are the main part of the algorithm. The purpose of line 5 is to generate N offspring. Then, based on the Boolean value of the objective normalization flag, it is judged whether it is necessary to deal with the problem of different ranges for each objective. Subsequently, the SRV strategy is used to adjust the generated reference vectors. We introduce a frequency parameter f_r to control the frequency of application of the TSP strategy so that it will be applied throughout the entire execution of the algorithm instead of taking effect only at the end of the algorithm. Finally, N individuals are obtained through environmental selection.

3.3 Computational complexity

Since it is still necessary to calculate the Euclidean distances between pairs of solutions, the computational complexity of the TSP strategy is the same as that of the original TSL strategy, which is O(N²). However, the overall algorithm frameworks differ between the TSL and TSP strategies. In the overall framework of 𝜃-DEA^∗, the TSL strategy takes effect every constant generation at the end of the algorithm, and the algorithm complexity is O($N^{2}* \frac {T_{max}-0.75*T_{max}}{C}$), where T_max is the maximum number of function evaluations (FEs), and C is the preset constant of the algorithm. In contrast, this article introduces the frequency parameter f_r, and the complexity of 𝜃-DEA-TSP is O(N₂ ∗$\frac {T_{max}}{f_{r}*T_{max}})$. In the case of many FEs, the TSL strategy will take effect frequently. Therefore, in this case, the complexity of 𝜃-DEA-TSP will be better than that of 𝜃-DEA^∗.

4 Experiment study

In this section, we combine the proposed strategy with 𝜃-DEA to obtain the resulting 𝜃-DEA-TSP algorithm for comparison with several typical algorithms: 𝜃-DEA* [24], ANSGA-III [25], RVEA [14], and the guided nondominated sorting genetic algorithm (gNSGA-II) [26]. 𝜃-DEA* is the algorithm proposed by Liang, which integrates the SRV and TSL strategies into 𝜃-DEA. 𝜃-DEA* is an algorithm based on decomposition. It incorporates the TSL strategy and selects a set of excellent solutions to guide the reference vectors for self-adaptation, enabling some improvements in solving MaOPs. ANSGA-III is adaptive in the dynamic deletion and inclusion of new reference points. It is an algorithm proposed by Deb based on the nondominated sorting genetic algorithm version II (NSGA-II) framework for solving MaOPs, providing denser PFs under the same computational workload and demonstrating excellent performance in dealing with constrained and unconstrained MaOPs. RVEA is also an optimization algorithm based on decomposition. It applies an adaptive strategy for dynamic adjustment of the reference vector distribution in accordance with the objective function, and reference vector regeneration strategies are used to deal with irregular PFs. Many papers have proven its effectiveness in solving MaOPs. gNSGA-II is an evolutionary algorithm based on dominance that introduces the concept of g-dominance. Through comparisons with this algorithm, the performance of the g-dominance method for solving MaOPs has been proven. Since DTLZ1 is an MOP with a regular PF, we test the above mentioned 5 algorithms on DTLZ2-7 [27]. Each test problem is run independently 20 times, and the average and standard deviation are taken. The above tests are all carried out on the PlatEMO [28] platform. To ensure fairness, the parameters of the algorithms mentioned above are all set to their default values in PlatEMO.

In the following sections, we first give the parameter settings for the simulation experiments. Second, we briefly introduce the evaluation metrics used in the comparative study. Then, we analyze the influence of the value of the parameter f_r on the performance of our algorithm. Finally, we compare the experimental results obtained by independently running each algorithm 20 times on each test problem. In these comparisons, the symbol “-” indicates that 𝜃-DEA-TSP is significantly better than the other algorithm considered for comparison, the symbol “+” indicates that 𝜃-DEA-TSP is significantly inferior to the other compared algorithm, and the symbol “≈” indicates that the result obtained is not significantly different from that of the other algorithm.

4.1 Parameter setting

The parameters of all algorithms considered for comparison are set as follows: In 𝜃-DEA-TSP, 𝜃-DEA^∗, ANSGA-III, RVEA, and gNSGA-II, the simulated binary crossover (SBX) operator and polynomial mutation are used to solve the test problems, and the detailed settings are shown in Table 1. To ensure fairness, the default parameters values are used for binary crossover and polynomial mutation. The relevant parameter settings of the test function are summarized in Table 2, where M is the number of objectives; D is the number of decision variables, and k is a parameter used to artificially change the length of a decision variable.

Table 1 Parameter settings for crossover and mutation

Table 2 Parameter settings for the test problems

4.2 Performance metrics

In the experiments, we measure the performance of various algorithms on the test problems. We use the following three metrics to evaluate the convergence and comprehensive performance of the solution set.

(1) Generation Distance (GD) [34]

The GD metric is used to calculate the distance between the obtained solution set and the true Pareto solution set, which is defined as follows:

$$ \qquad\qquad GD={\frac{{\sum}_{i=1}^{n}({d_{i}^{p}})^{\frac{1}{p}}}{n}} $$

(8)

where n denotes the number of obtained solutions, d_i is the Euclidean distance between the obtained solution i and its nearest true solution, and p denotes the number of objectives. The smaller the GD value is, the stronger the algorithm performance.

(2) Inverse Generation Distance (IGD) [35]

The IGD indicator is calculated as the average value of the distance from each reference point to the nearest solution, and can be used to simultaneously evaluate the convergence and distribution of the solution set calculated by an algorithm. The indicator is defined as follows:

$$ \qquad\qquad IGD(P, P^{*})=\frac{\sum\limits_{x^{*}\in P^{*}}d(x^{*},P)}{|P^{*}|} $$

(9)

where P represents the solution set obtained by the algorithm, P^∗ denotes the solution set of the ideal PF, and d(x^∗, P) denotes the minimum Euclidean distance from x^∗ to P. The smaller the IGD value is, the stronger the algorithm performance.

(3) Hypervolume Distance (HV) [36]

HV is another way to measure the comprehensive performance. It calculates the volume of the objective space enclosed by the reference points and the i-th non-dominated solution. The larger the HV value, the better the comprehensive performance. The metric can be defined as follows:

$$ \qquad\qquad HV(S) = \textit{volume}(\bigcup\limits_{{i=1}}^{|S|}a^{i}) $$

(10)

where aⁱ is the hypercube formed by the solution x and the origin of the coordinate axes as diagonal lines. The space covered by aⁱ is volume(aⁱ).

Notably, the widely used evaluation metric HV is not selected for the DTLZ problems because HV and IGD show certain contradictions on concave PFs [37]. For MaOPs whose PFs are nonconvex, HV has a certain error [36]. The PF of DTLZ2-6 is concave, as shown in Table 2. GD is an indicator of convergence and, can still measure the convergence of an algorithm even if the diversity of the solution set is not good. To prove the effectiveness of the convergence enhancement strategy, we choose the GD and IGD metrics to evaluate the results on the DTLZ problems.

4.3 Sensitive analysis of parameter f _r

f_r is an important parameter in the reference vector adaptation strategy. Its value will affect the frequency of reference vector adaptation, and thus, in turn, affect the convergence and distribution of the solution set found by the algorithm. To study the impact of this parameter on the algorithm performance, with f_r= 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1, we tested the algorithm on DTLZ2-7 with 6, 8, 10, and 15 objectives, and all parameters except f_r remaining unchanged. Fig. 3 shows the comprehensive performance on the test problems when f_r takes each value. With taking different values of f_r, the IGD ranking of 𝜃-DEA-TSP fluctuates greatly on the DTLZ2-7 test problems. However, it can be seen from Fig. 3 that when f_r= 0.1 and M= 8, 𝜃-DEA-TSP has the best IGD ranking on the DTLZ2-7 test problems. Therefore, for the comparative experiment, we choose f_r= 0.1 as the value of the frequency parameter of 𝜃-DEA-TSP.

Fig. 3

The IGD performance of 𝜃-DEA-TSP on the 6-, 8-, 10-, and 15-objective versions of DTLZ2-7 when f_r is 0.1-1

4.4 Comparison experience

4.4.1 Test problems

In this section, 𝜃-DEA-TSP is compared with 𝜃-DEA^∗, ANSGA-III, RVEA, and gNSGA-II on DTLZ2-7 [38], IDTLZ1-2 [12] and DTLZ5IM [33]. Here, the numbers of objectives (m values) of DTLZ2-7 are 6, 8, 10, and 15. Tables 3 and 4 show the performance of the algorithms in terms of the GD metric and the IGD metric, respectively, on DTLZ2-7.

Table 3 The average GD values of the 𝜃-DEA-TSP algorithm and other algorithms on the DTLZ2-7 test problems

Table 4 The average IGD values of the 𝜃-DEA-TSP algorithm and other algorithms on the DTLZ2-7 test problems

Experiments were run 20 times independently on the DTLZ2-7 test problems to compare the convergence performance of 𝜃-DEA-TSP, 𝜃-DEA^∗, ANSGA-III, RVEA, and gNSGA-II as represented by the GD metric. The mean and variance of the GD values are listed in Table 3. In Table 3, the average GD value of 𝜃-DEA-TSP is better than those of the other algorithms on 50% of the 24 problems tested. In particular, 𝜃-DEA-TSP shows obviously superior performance on DTLZ4-7. Especially for the concave and multipeak DTLZ6 problem [39], the results for the 6-, 8-, 10-, and 15-objective versions of this problem are all better than those of the other four algorithms. On 8-objecitve DTLZ6, the GD value of 𝜃-DEA-TSP is 64% lower than that of the second-ranking algorithm 𝜃-DEA^∗. On the 10-objective DTLZ6 problem, the GD value of 𝜃-DEA-TSP is 54% lower than that of the second-ranking algorithm 𝜃-DEA^∗.

The experimental results in terms of the IGD values on DTLZ2-7 are shown in Table 4. We can see that when solving DTLZ4-7, 𝜃-DEA-TSP exhibits excellent performance. Even when the number of objectives is large, the IGD value of this algorithm is still better than those of the other algorithms. It is not difficult to see that 𝜃-DEA-TSP is highly very competitive on such problems. In addition, it can be seen from the experimental results that RVEA shows excellent performance on DTLZ2 and DTLZ3 and on other test problems with regular PFs. However, on DTLZ5-7, which have discontinuous or degraded PFs, the performance of our algorithm is significantly better than the other four, thus proving the effectiveness and pertinence of the TSP strategy proposed in this article. To more intuitively illustrate the performance of the five algorithms on DTLZ2-7 for different numbers of objectives, we plot their ranking histograms in Fig. 4. The x-axis represents the number of objectives, the y-axis represents the algorithm, and the z-axis represents the average ranking. The lower the column height in this figure, the higher the ranking of the corresponding algorithm, and the better its performance. We can see that the performance of the 𝜃-DEA-TSP and RVEA algorithms is relatively stable, while the ranking of 𝜃-DEA^∗ fluctuates greatly for problem with 8 objectives and 15 objectives. The performance of the ANSGA-III worsens as the number of objectives increases. Compared with the other four algorithms, gNSGA-II performs poorly on these problems. The optimization results of the 5 compared algorithms for 15-objective DTLZ5 and 6-objective DTLZ7 are shown in Figs. 5 and 6.

Fig. 4

Bar chart of the average rankings of the five algorithms considered for comparison in terms of the IGD metric on the 6-, 8-, 10-, and 15-objective versions of the DTLZ2-7 test problems

Fig. 5

The solutions obtained by the five compared algorithms on 15-objective DTLZ5

Fig. 6

The solutions obtained by the five compared algorithms on 6-objective DTLZ7

𝜃-DEA* selects excellent solution sets only in the middle and late stages of the algorithm and generates reference vectors to guide the algorithm. A strategy for screening the solution sets that places too much emphasis on diversity may result in the degradation of the solution set. RVEA optimizes the reference vectors globally, which is not beneficial for subregion-specific solution sets. Although ANSGA-III modifies the traditional concept of dominance applied in NSGA-II, it also introduces extreme point calculation and target normalization strategies to enhance the convergence of the algorithm. However, the experimental results are still not very good. When 𝜃-DEA-TSP solves a problem whose PF has degenerate or discontinuous characteristics, it will dynamically screen the excellent solution set throughout the whole process, delete locally inferior solutions, and generate reference vectors from the results to better guide the evolution of the algorithm. Hence, the 𝜃-DEA-TSP algorithm performs better on DTLZ2-7 in terms of both the GD and IGD evaluation metrics.

In Fig. 5, on the one hand, we can see that the convergence of gNSGA-II, ANSGA-III, and 𝜃-DEA^∗ is poor, which may be because they lack convergence improvement methods or place too much emphasis on the diversity of the solution set. On the other hand, RVEA has poor diversity on this problem, which may be because, in high-dimensional situations, its current reference vectors tend to be excessively concentrated in a certain location, and its adaptive reference vector strategy dose not improve this situation. In comparison, 𝜃-DEA-TSP does not fully converge, but because it considers both convergence and diversity, it performs significantly better than the algorithms. In Fig. 6, with an increase in the number of dimensions, the selection pressure of the dominance-based algorithms decreases sharply, preventing them from converging to the optimal PF, and gNSGA-II does not fully converge. In contrast, the convergence and diversity performance of 𝜃-DEA-TSP, 𝜃-DEA^∗, RVEA and ANSGA-III on 6-objective DTLZ7 are all good, and 𝜃-DEA-TSP is slightly better than the other two.

To further analyze and compare the experimental results, we present boxplots of the experimental results for some test problems, namely, 8-objective DTLZ5, 10-objective DTLZ5, 8-objective DTLZ6, and 10-objective DTLZ7 in Fig. 7. The average IGD values of our algorithm on 8-objective DTLZ5 and 10-objective DTLZ5 are significantly better than those of the other four algorithms. It is not difficult to see in Fig. 6(a) and (b) that the stability of 𝜃-DEA- TSP is also significantly better than that of the other four algorithms. It can be seen from the boxplot for 8-objectives DTLZ6 that the IGD values of 𝜃-DEA-TSP, 𝜃-DEA*, and RVEA are relatively close and the fluctuations of the IGD values of these three algorithms are relatively small. The boxplot for 10-objective DTLZ7 shows that, except for the outliers, the IGD values of 𝜃-DEA-TSP are relatively close to those of ANSGA-III. Among the compared algorithms, the fluctuation in the performance of gNSGA-II on this test problem is particularly obvious. In addition, RVEA yields too many outliers, although the fluctuation in the IGD values is similar to that of the other three algorithms.

Fig. 7

Boxplots of the IGD values of the five compared algorithms on the 8-objective DTLZ5, 10-objective DTLZ5, 8-objective DTLZ6, and 10-objective DTLZ7 test problems

The experimental results for the IGD values on DTLZ5IM and IDTLZ1-2 for all dimensionalities are shown in Table 5. For these test problems in all numbers of dimensions, 58.33% of the experimental results of 𝜃-DEA-TSP are better than those of the other algorithms considered for comparison. Especially for DTLZ5IM and 6-objective IDTLZ2, 𝜃-DEA-TSP shows excellent performance. A feature of IDTLZ1-2 is that many reference points created on the standardized hyperplane do not have a Pareto optimal advantage. 𝜃-DEA-TSP, 𝜃-DEA* and ANSGA-III all benefit from their adaptive strategies for adaptively screening reference points and reallocating them to obtain Pareto-optimal solutions. Therefore, they perform well on these two test problems. However, gNSGA-II and RVEA lack strategies for local adaptation, leading to unsatisfactory results.

Table 5 The average IGD values of the 𝜃-DEA-TSP algorithm and other algorithms on other many-objective test problems

The experimental results for the HV values on DTLZ5IM and IDTLZ1-2 for each dimensionality are shown in Table 6. The experimental results of 𝜃-DEA-TSP are better than those of the other compared algorithms on half of these test instances. The PF of DTLZ5IM is nonconvex. By comparing the experimental HV and IGD results, it can be seen that the HV and IGD values may contradict each other in the testing of the PF. Nearly half of the HV values for gNSGA-II are 0, because all obtained solutions do not form a supervolume with the lowest point.

Table 6 The average HV values of the 𝜃-DEA-TSP algorithm and other algorithms on other many-objective test problems

4.4.2 Real world problem

To verify the performance of the proposed algorithm on real problems, we also conduct a comparative analysis of this algorithm on the multipoint distance minimization problem (M-DMP) [40]. The problem of minimizing the distance between a point and a set of predetermined fixed target points has many advanced applications in navigation and layout optimization [30]. In this section, the D value of the problem is set to 2, and the upper and lower bounds are 100 and -100 [40], respectively. The other experimental parameters are the same as above. For real problems, we usually choose HV to measure the quality of the solution set.

The experimental results for versions of M-MDP with different numbers of dimensions are shown in Table 7. It can be seen that the proposed algorithm performs very well on this real problem, and the experimental results of gNSGA-II are also surprisingly good, perhaps because the changes to the traditional concept of dominance introduced by the g-dominance concept applied in this algorithm allow it to perform only slightly worse than 𝜃-DEA-TSP on this problem. In contrast, because 𝜃-DEA* and ANSGA-III sacrifice their convergence to preserve the diversity of the solution set, their solution sets do not form a hypervolume with the reference point of the HV metric for 15-objective M-DMP, resulting in a result of 0.

Table 7 The average HV values of the 𝜃-DEA-TSP algorithm and other algorithms on M-DMP

5 Conclusion

We propose the TSP strategy to balance the convergence and diversity of the population during evolution and correspondingly propose the 𝜃-DEA-TSP algorithm. The proposed algorithm has a lower computational cost on MaOPs, and can better solve problems with complex PFs and balance the convergence and diversity of the solution set throughout the whole execution of the algorithm. For classic test problems, recent test problems and a real world problem with different numbers of objectives, the GD, IGD and HV values are better than those of other algorithms on at least half the tested problem instances, although some of the algorithms considered for comparison already perform extremely well on MaOPs, thereby confirming the effectiveness of the proposed MOEA. However, as described by Aggarwal [41], in the case of high dimensions, the Euclidean distance is not a good metric. Therefore, we must admit that in MaOPs, the proposed TSP strategy will still have shortcomings. In future work, we need to find another method of measuring the diversity and convergence between individuals to replace the calculation of the Euclidean distance in the TSP strategy.