Stochastic optimization for bayesian network classifiers

Abstract

How to reduce the complexity of network topology and make the learned joint probability distribution fit data are two important but inconsistent issues for learning Bayesian network classifier (BNC). By transforming one single high-order topology into a set of low-order ones, ensemble learning algorithms can include more hypothesis implicated in training data and help achieve the tradeoff between bias and variance. Resampling from training data can vary the results of member classifiers of the ensemble, whereas the potentially lost information may bias the estimate of conditional probability distribution and then introduce insignificant rather than significant dependency relationships into the network topology of BNC. In this paper, we propose to learn from training data as a whole and apply heuristic search strategy to flexibly identify the significant conditional dependencies, and then the attribute order is determined implicitly. Random sampling is introduced to make each member of the ensemble “unstable” and fully represent the conditional dependencies. The experimental evaluation on 40 UCI datasets reveals that the proposed algorithm, called random Bayesian forest (RBF), achieves remarkable classification performance compared to the extended version of state-of-the-art out-of-core BNCs (e.g., SKDB, WATAN, WAODE, SA2DE, SASA2DE and IWAODE).

1 Introduction

Classification is a fundamental issue in machine learning and data analysis that requires to learn a classifier or a function, which can assign the right class labels to different instances represented by an attribute vector [1]. Bayesian network classifiers (BNCs) [2] describe data in the form of directed acyclic graph (DAG) in which nodes represent the attributes in a given domain and edges connecting the respective nodes indicate the dependencies between these attributes. However, learning a full Bayesian network classifier is very time consuming and quickly becomes an NP-hard problem with the increasing number of attributes [3].

In consequence, how to learn restricted BNCs has attracted a lot of research interest in the past decades [4,5,6,7]. Numerous supervised BNCs have been proposed, such as Naive Bayes (NB) [8, 9], tree-augmented Naive Bayes (TAN) [10] and k-dependence Bayes (KDB) [11, 12]. However, these BNCs can only represent a limited number of conditional dependencies, which are always the most significant [13]. Information-theoretic metrics, e.g., mutual information (MI) and conditional mutual information (CMI), are commonly applied to roughly quantify the mutual or conditional dependence between the attributes. However, due to the limitation in structure complexity and computation complexity, the biased estimate of high-order conditional probability may result in poor performance especially when processing small data.

To address this issue, researchers propose to learn ensemble of classifiers [14,15,16] which combines multiple learning models’ decisions to classify new examples by (weighted) voting. Ensembles are more likely to include more hypothesis, and often perform better than the single classifiers that make them up. Ensemble learning does not require the learned BNC to represent high-order dependencies, and the network topology of each member is relatively simpler, thus high-confidence estimate of low-order conditional probability helps approximate the true target function [17]. Boosting [18] and bagging [19] are the two most popular ensemble learning approaches, each of them trains classifiers with different subsets of the training data [20].

The key issue for constructing an ensemble is how to vary the results of the member classifiers, and keep the covariance between the (varied) classifiers low, but not raise the bias of the base classifier [21]. The instances from the training dataset may not follow the same probability distribution, thus the (conditional) dependency relationships between variables may vary greatly for different instances, and these relationships should be fully represented by committee members of the ensemble. Boosting and bagging vary the learned (conditional) dependency relationships by resampling, whereas that may potentially lose information implicit in the data as a whole. The estimate of conditional probability distribution will be biased and when applied to compute MI or CMI, insignificant rather than significant dependency relationships may be introduced to the network topology of BNC.

According to Bayes theorem and chain rule of the joint probability, BNC assumes predictive attribute X_j as the candidate parent of attribute X_i and represents conditional dependence between them in the network topology only when j < i holds. That is, for attribute order {X₁, X₂,⋯ ,X_n} given implicitly or explicitly, attribute X_j should appear before X_i. For different instances, predictive attributes may take specific values, thus the attribute order and the dependency relationships may vary greatly. Although significant dependency relationships appear much more often than insignificant ones, the latter may also appear for specific instances.

Breiman [19] reveals that ensemble learning improves classification accuracy for “unstable” learning procedure where small changes in the training set may result in large changes in models. To systematically create multiple BNCs using the same dataset, we propose to apply stochastic optimization to make the learned BNCs unstable. Different BNCs can represent dependency relationships from different aspects and then generalize their classification in complementary ways. The main contributions and innovations of this paper can be highlighted as follows:

• Following the principles of stochastic optimization, we propose to learn the attribute order and conditional dependencies by applying random sampling. The resulting highly scalable algorithm, called RBF (random Bayesian forest), combines the low variance of ensemble learning with the low bias of high-dependence topology.

• We compare the classification performance of RBF with extended version of other state-of-the-art BNCs (e.g., SKDB, WATAN, WAODE, SA2DE, SASA2DE and IWAODE) on 40 datasets, ranging in size from 5 to 60 attributes and 57 to 164,860 instances. We show that our algorithm shows competitive classification performance in terms of zero-one loss, root mean squared error(RMSE), bias-variance decomposition and Friedman test.

The paper is organized as follows: we review the background and provide a brief introduction to ensemble learning in Section 2. Section 3 describes in detail our base learning algorithm, called random Bayesian classifier (RBC), and then the ensemble of RBC, called random Bayesian forest (RBF). Section 4 presents the experimental evaluation and compares the performance of RBF with related BNCs. Section 5 draws the conclusions.

2 Related work

2.1 Bayesian network classifier

The Bayesian network (BN) defines a pair $(\mathcal {G},{{\varTheta }})$ that encodes a joint probability distribution over a set of attributes $\textbf {X}=\{X_{1}, \dots , X_{n}\}$ and class variable Y. It consists of two parts: (1) a DAG $\mathcal {G}=\{\mathcal {V},\mathcal {E}\}$ whose nodes $\mathcal {V}$ represent attributes, and edges $\mathcal {E}$ represent attribute dependencies, and (2) the parameters Θ which quantifies the network topology. BNC approximates joint probability distribution with a factorization according to a BN. Given a specific instance $\textbf {{x}}=\{x_{1}, x_{2}, \dots , x_{n}\}$, BNC ${\mathscr{B}}$ assigns the maximum a posteriori (MAP) class (simply y^∗) to x by

$$ \begin{array}{ll} y^{*}&=\arg \max_{y\in Y}P_{\mathcal{B}}(y|\textbf{{x}})=\arg \max_{y\in Y} \frac{P_{\mathcal{B}}(\textbf{{x}},y)}{P_{\mathcal{B}}(\textbf{{x}})} \varpropto \arg \max_{y\in Y} P_{\mathcal{B}}(\textbf{{x}},y)\\&=\arg \max_{y\in Y} P(y)\prod\limits_{i=1}^{n} P(x_{i}|\pi_{i}^{\mathcal{B}},y) \end{array} $$

(1)

where $\pi _{i}^{{\mathscr{B}}}$ represents the parent attributes of X_i in ${\mathscr{B}}$. Thus the problem of learning posterior probability $P_{{\mathscr{B}}}(y|\textbf {{x}})$ for classification turns to be the problem of learning joint probability $P_{{\mathscr{B}}}(\textbf {{x}},y)$ for data fitting. Equation (1) implicitly requires to learn an attribute order first so that attribute X_i can only select parents from attributes before it in the order. To make the network topology of BNC fit data, each factor (i.e., $P(x_{i}|\pi _{i}^{{\mathscr{B}}},y)$) in (1) should help maximize the estimate of $P_{{\mathscr{B}}}(\textbf {{x}},y)$. For full BNC, the i-th attribute may have at most i − 1 candidate parents, whereas high-order dependencies will lead to biased estimate of conditional probability. We take the dataset magic ¹ from the UCI repository of machine learning as an example for experimental study. Dataset magic contains the result of simulated registration of high energy gamma particles in an atmospheric Cherenkov telescope with 19,020 instances, 10 attributes and 2 class labels (Fig. 1).

Figure 1(a)$\sim$1(f) respectively visualize the distribution of values of P(x₂|x_i, y) (i = 1, 3, 4, 7, 9, or 10). The Y-axis in Fig. 1 represents the values of P(x₂|x_i, y) sorted in descending order when x₂ = 4 and y = 1, the X-axis represents the index number of values of X_i, and the dotted line represents the value of P(x₂|y). As shown in Fig. 1, for different values of X_i, there exist instances corresponding to P(x₂|y) > P(x₂|x_i, y) although they may appear less often. That is, X_i may be independent from X₂ and thus the lower-order probability P(x₂|y) is more reasonable than higher-order probability P(x₂|x_i, y) in some cases.

Fig. 1

The distributions of values of P(x₂|x_i, y) on dataset magic

NB is the simplest BNC with a strong independence assumption that all the attributes are independent given class variable Y, thus NB doesn’t need to learn the attribute order and conditional dependencies. However, the conditional independence assumption of NB may hold only while dealing with sparsely distributed datasets, so its estimates of conditional probabilities are often suboptimal. In contrast, KDB provides a highly scalable learning approach that alleviates some of NB’s independence assumption by allowing each non-class attribute to have up to k parents. KDB first computes mutual information I(X_i;Y ) to sort attributes. Each attribute X_i can have at most k parent attributes with the highest values of I(X_i;X_j|Y ) according to the current topology. Flexible KDB (FKDB) [22] takes an efficient heuristic learning strategy to sort attributes by comparing conditional entropy. To control the structure complexity, FKDB selects a subset of π_i, which can minimize the conditional entropy of attribute X_i, and learns significant causal relationships from data. Selective KDB (SKDB) [23] evaluates and selects candidate parents for X_i from all possible attribute subsets {x₁,⋯ ,x_i− 1}, and chooses the value of k up to the maximum capacity available. Thus it is highly scalable and achieves a good tradeoff between structure complexity and classification accuracy.

2.2 Ensemble learning

As discussed above, the same conditional probability distribution may fit different instances to different extents. Ensemble learning improves the performance of single learners by training multiple learners to encode possible probability distributions and then combine them. To learn ensemble of BNCs and combine the decisions of committee members, Webb et al. [24] propose the averaged one-dependence estimators (AODE), which respectively chooses each attribute as the parent of all the other attributes, and then averages all superparent one-dependence estimators (SPODEs). Jiang et al. [25] propose the weighted AODE (WAODE) to assign different weights to SPODEs. Kong et al. [26] propose the averaged tree-augmented one-dependence estimators (ATODE), which adds the augmented edges for each SPODE by identifying causality between attributes. Jiang et al. [27] propose the averaged tree augmented naive Bayes (ATAN), which selects each attribute as the root node to build a one-dependence maximum weighted spanning tree, and then averages all of the spaning TAN classifiers. Hellman et al. [28] introduce the ensembled continuous Bayesian networks (ECBNs), which predict values for continuous random variables and discover salient dependence relationships. Geiger and Heckerman [29] propose the Bayesian multinet to learn a single network for different partitions of the class label, and then use multiple networks to encode asymmetric independence assertions.

Bagging and boosting are popular ensemble learning approaches that combine arbitrary number of base-learners, and are applicable to different machine learning algorithms. By manipulating the training data given to a “base” learning algorithm, bagging [19] uses the bootstrap [30] (i.e., sampling with replacement) to broaden “independency” among the component classifiers [31]. The outputs of the subclassifiers are finally combined by averaging or voting. Boosting [18, 32] iteratively trains subclassifiers on weighted training data. A “weak” classifier (e.g., NB) is built first and then a succession of classifiers are built iteratively. The data points misclassified by the previous classifier are given more weight. AdaBoost [33] is the most popular boosting algorithm.

Diversity in training data or learning procedure helps to build diverse learners, and randomness provides an efficient and effective way to introduce diversity. Ho [34] proposes random subspace method (RSM) to randomly select a subset of attributes. Kunwar et al. [35] propose Random Bayesian Network (RBN) which trains on a different set of training samples (Bagging) and attribute set (RSM). Ma et al. [36] propose Bagging-MultiTAN to respectively train different TAN classifiers on different training subsets. Breiman [37] proposes Random Forest (RF) which uses bagging to aggregate multiple decision trees that are each grown using a process that involves a stochastic element to increase diversity.

3 Random bayesian forest

3.1 Our motivation and structural learning framework

Information-theoretic metrics, e.g., mutual information I(X_i;Y ) or conditional mutual information I(X_i;X_j|Y ) defined as follows, are widely applied to measure (conditional) dependency relationships for BNC learning.

$$ \left \{ \begin{aligned} &I(X_{i};Y)= \sum\limits_{X_{i}, Y} P(x_{i},y)\log\frac{P(x_{i},y)}{P(x_{i})P(y)}= \sum\limits_{X_{i}, Y} P_{i}\log\delta_{i}\\ &I(X_{i};X_{j}|Y)= \sum\limits_{X_{i}, X_{j}, Y} P(x_{i},x_{j},y)\log\frac{P(x_{i},x_{j}|y)}{P(x_{i}|y)P(x_{j}|y)}= \sum\limits_{X_{i}, X_{j}, Y}P_{ij}\log\delta_{ij} \end{aligned} \right. $$

(2)

I(X_i;Y ) measures the direct mutual dependence between predictive attribute X_i and class variable Y, and thus it can also measure the extents to which X_i is effective for classification. For restricted BNCs, all the predictive attributes depend on a common class variable Y, and augmented edges measured by I(X_i;X_j|Y ) are added to represent conditional dependence between attributes only. Given specific instance x = {x₁, x₂,⋯ ,x_n}, if P(x_i, y) > P(x_i)P(y) then x_i and y are mutually dependent rather than independent in term of probability theory. The higher the value of δ_i, the stronger the probability-theoretic dependence between x_i and y. As shown in (2), significant mutual dependence needs to satisfy two requirements: stronger probability-theoretic dependence measured by δ_i, and higher probability measured by P_i when the dependence happens. Similarly, significant conditional dependence also needs to satisfy two requirements: stronger probability-theoretic conditional dependence measured by δ_ij, and higher probability measured by P_ij when the conditional dependence happens.

Given an attribute order {X₁, X₂,⋯ ,X_n}, implicitly or explicitly, X_i is the candidate parent for attributes {X_i+ 1,⋯ ,X_n} in the order. If the first few attributes in the order are relatively independent from the rest of attributes, less conditional dependencies will be introduced for them and that may bias the estimates of conditional probabilities. To achieve the bias-variance tradeoff for structure learning, we propose to apply heuristic search strategy to flexibly learn the significant conditional dependencies, and then the attribute order is determined implicitly.

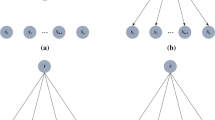
The learning framework of proposed RBF is depicted in Fig. 2. RBF is an ensemble of RBCs which are obtained by applying stochastic optimization. For given dataset $\mathcal {D}$ after preprocessing, RBC selects one attribute X_r as the root node which is assumed to be dependent on class variable only, and then it will be added to the network topology $\mathcal {G}$. Then RBC recursively selects the next attribute X_i and adds it to $\mathcal {G}$. X_i is assumed to be dependent on all the attributes already in $\mathcal {G}$, or all the attributes in $\mathcal {G}$ are candidate parents of X_i. Due to the restriction in structure complexity, X_i can only selects limited number of attributes as its parents π_i. Thus during the learning procedure, RBC needs to select X_r, X_i and π_i, and RBC selects by performing random sampling based on the probability distribution. After that RBCs vote for the most possible class label.

Fig. 2

The learning framework of RBF

3.2 RBF learning algorithm

3.2.1 Random selection of root node X _r

For full BNC there exists directed edge $X_{j} \rightarrow X_{i}$ between attributes X_j and X_i when j < i. That is, the root attribute X_r is the only one that is dependent on class variable Y, whereas the other attributes are dependent on X_r to different extents. Thus similar to KDB, mutual information I(X_i;Y ) is introduced to measure the significance of attribute X_i. Higher value of I(X_i;Y ) corresponds to stronger mutual dependence related to attribute X_i. Thus X_i with the highest value of I(X_i;Y ) is considered in priority as the candidate root attribute. We first normalize the values of I(X_i;Y ) for different attributes and transform them into the form of probability. Then the attributes are listed in descending order of the normalized probability. To introduce diversity and mitigate the negative effect of overfitting, as described in Algorithm 1, we perform random sampling based on the probability distribution to select root attribute from the list, and then add it to the network topology. The root attribute is also the first candidate parent attribute for the other attributes.

3.2.2 Random selection of children node X _i

The attributes already in the network topology $\mathcal {G}$ constitute candidate parents for the newly added children attributes, or the children attributes should have strong conditional dependence on the parent attributes. Thus children correlation criterion $CCC(X_{i}|\mathcal {G})$ is introduced to select the children attribute as follows.

$$ CCC(X_{i}|\mathcal{G})= \sum\limits_{X_{j}\in\mathcal{G},i\neq j}I(X_{i}; X_{j}|Y) $$

(3)

The values of $CCC(X_{i}|\mathcal {G}) (X_{i}\notin \mathcal {G})$ are normalized first and transformed into the form of probability. Then the corresponding attributes are sorted into list △CCC in descending order of the normalized probability. As described in Algorithm 2, we perform random sampling to select children node from the list, and then add it to the network topology. But note that, if the candidate children attributes are assumed to be independent from the attributes already in $\mathcal {G}$, i.e., $CCC(X_{i}|\mathcal {G})=0(X_{i}\notin \mathcal {G})$, then one of them will be randomly selected as the children attribute.

3.2.3 Random selection of parents node π _i

Due to the restriction in computational complexity and structure complexity, each children attribute X_i can only select limited number of parent attributes, or more precisely, at most k parents for k-dependence BNC. Thus conditional mutual information I(X_i;X_j|Y ) is introduced to select parent attributes for X_i as follows. Similar to the learning procedure described in Algorithm 2, Algorithm 3 applies random sampling to select parents from attributes in $\mathcal {G}$. For k-dependence topology, Algorithm 3 will perform random sampling and select at most k parents for attribute X_i. Corresponding directed edges will be added to $\mathcal {G}$. If X_i is independent from all the attributes in $\mathcal {G}$ then its parents will be selected randomly.

3.2.4 RBF learning algorithm

The network topology $\mathcal {G}$ is represented in the form of tree and contains three parts: root node, branch node (including parent attribute or children attribute) and directed edge between them. The proposed algorithm, called random Bayesian classifier (RBC), applies random sampling to select them at different learning phases. Algorithm 4 describes the learning procedure of RBC.

Introducing randomness to the learning procedure of BNC will build an “unstable” topology, and that helps avoid overfitting and reduce variance. On the other hand, the training data is just a sample from the complete dataset, that may result in potentially lost information implicated. One single BNC cannot encode by coincidence the most significant dependency relationships in its topology, that would result in suboptimal classification performance.

Ensemble of classifiers performs better than its committee members on average. Different attribute orders and augmented edges will form different BNCs. It also shows that the classification performance of different BNCs varies and, in some cases, varies greatly. Randomness helps to independently learn RBCs which describe the true Bayesian network from different aspects. The wrong prediction from BNC A may be corrected by BNC B. In this paper, we adopt RBC as the base algorithm and then the different classifiers are obtained by applying stochastic optimization. After that they vote for the most possible class label. Algorithm 5 gives the general learning framework for the ensemble of RBC.

Introducing randomness to the learning procedure of BNC will build an “unstable” topology, and that helps avoid overfitting and reduce variance. On the other hand, the training data is just a sample from the complete dataset, that may result in potentially lost information implicated. One single BNC cannot encode by coincidence the most significant dependency relationships in its topology, that would result in suboptimal classification performance.

Ensemble of classifiers performs better than its committee members on average. Different attribute orders and augmented edges will form different BNCs. It also shows that the classification performance of different BNCs varies and, in some cases, varies greatly. Randomness helps to independently learn RBCs which describe the true Bayesian network from different aspects. The wrong prediction from BNC A may be corrected by BNC B. In this paper, we adopt RBC as the base algorithm and then the different classifiers are obtained by applying stochastic optimization. After that they vote for the most possible class label. Algorithm 5 gives the general learning framework for the ensemble of RBC.

3.3 Classification process and complexity analysis

For subclassifier RBC_m, given the testing instance x, RBC_m assigns the MAP class to x by

$$ y_{m}^{*}=\arg \max_{y\in Y} P(y) \prod\limits_{i=1}^{n} P(x_{i}|\pi_{i}^{\text{RBC}_{m}},y) $$

(4)

After training a set of learners, ensemble learning combines multiple learning models’ predictions appropriately. Thus, in practice, the class-membership prediction produced by RBF are simply voted as follows:

$$ y^{*}=\arg \max \{F(y_{1}),F(y_{2}),\cdots,F(y_{q})\} $$

(5)

where y^∗ is the predicted class label, F(y_i) is the number of models whose prediction results are y_i in all models and q is the number of class labels.

During the training phase, the time complexity of forming the frequency table from which the probability estimates by RBF is $\mathcal {O}(tn^{2})$, where t and n respectively denote the number of training instances and the number of attributes. Calculating I(X_i;Y ) and I(X_i;X_j|Y ) respectively need $\mathcal {O}(cnv)$ and $\mathcal {O}(c(nv)^{2})$ time, where v is the maximum number of values of discrete attributes and c is the number of classes. The procedure of randomly selecting the root attribute needs $\mathcal {O}(n)$ time. The time complexity of randomly selecting attributes and conditional dependencies is $\mathcal {O}(n(n^{2}+kn))$, where k is user-defined. Finally, the computational complexity of RBF is $\mathcal {O}(tn^{2}+cnv+c(nv)^{2}+p(n+n(n^{2}+kn)))$, where p is the number of RBCs. During the testing phase, classifying a test instance using RBF only needs $\mathcal {O}(pnck)$ time.

4 Experimental results

We perform experiments on 40 benchmark datasets from the UCI repository of machine learning [38] and summarize the characteristics of datasets in Table 1, including the name of dataset, the number of instances, attributes, and classes. The results of RBF using MDL (Minimum Description Length) discretization [39] to preprocess numerical attributes. The missing values in the datasets are processed into a distinct value in all cases, m-estimation (m = 1) [40] is used for base probability estimation. Each algorithm is processed with 10 rounds of 10-fold cross validation. The following algorithms are introduced for comparison with our proposed RBF:

Table 1 Datasets

⋅ SKDB [23], selective KDB with k = 5.

⋅ WATAN [27], weighted averaged TAN.

⋅ WAODE [25], weighted AODE.

⋅ SA2DE [41], selective A2DE which uses both MI and CMI to directly rank the attributes.

⋅ SASA2DE [42], sample-based attribute selection A2DE whose sample size is 50k.

⋅ IWAODE [43], instance-based weighting AODE.

The primary loss functions are zero-one loss, RMSE, bias and variance, and the detailed results in Tables 8, 9, 10 and 11 are shown in the Appendix. We use the Win/Draw/Loss (WDL) records where each cell’s W/D/L in the table indicates that one classifier is better than another on W datasets, equal on D datasets and worse on L datasets to show the classification performance. A summary table of the statistics employed is shown in Table 2.

Table 2 A summary table of the statistics employed

To illustrate how to determine the number of committee members of RBF, in Fig.3 we present learning curves for all the datasets (which are described in Table 1). As can be seen, lower bias delivered by large number of committee members and lower variance by random sampling result in lower error for RBF, while as the number increases to some extent the zero-one loss doesn’t change significantly. When RBF selects 30 classifiers as an ensemble it can substantially reduce error across all the datasets, thus we take 30 as the default number of members for RBF.

Fig. 3

The changes in RMSE and zero-one loss as the number of committee members of the ensemble increases

4.1 Diversity of the classifier generated by RBF

To use ensembling well, we need good performing learners with lower correlation. Dietterich [49] has measures of dispersion of an ensemble and notes that more accurate ensembles have larger dispersion. Breiman’s [37] results indicate that the generalization error of random forests depends on the strength of the individual trees in the forest and the correlation between them.

In order to investigate the diversity of classifiers generated by RBF, statisticians have developed several measures of agreement (or disagreement) between classiers. The most widely used measure is the Kappa statistic (K statistic) [49]. We show the diversity of the classifiers on some datasets by k-error diagrams, which help visualize the accuracy and diversity of the individual classifiers constructed by the RBF classifier.

Given two classifiers g₁ and g₂. Suppose there are W classes, and let H be a W × W square array such that H_ij contains the number of test examples assigned to class i by g₁ and into class j by g₂. The K statistic is defined as:

$$ \begin{aligned} k = \frac{{{\varTheta}}_{1}-{{\varTheta}}_{2}}{1-{{\varTheta}}_{2}}, \end{aligned} $$

(13)

where Θ₁ be an estimate of the probability that the two classifiers agree, and Θ₂ be an estimate of the probability that the two classifiers agree by chance. They are respectively defined as follows:

$$ \begin{aligned} {{\varTheta}}_{1}=\frac{{\sum}_{i=1}^{W}H_{ii}}{m}, \end{aligned} $$

(14)

$$ \begin{aligned} {{\varTheta}}_{2}= \sum\limits_{i=1}^{W}( \sum\limits_{j=1}^{W}\frac{H_{ij}}{m}\cdot \sum\limits_{j=1}^{W}\frac{H_{ji}}{m}), \end{aligned} $$

(15)

where m is the total number of test examples. k = 0 when the agreement of the two classifiers equals that expected by chance, and k = 1 when the two classifiers agree on every example. Negative values occur when agreement is weaker expected by chance—that is, there is systematic disagreement between the classifiers.

We choose 12 datasets (hepatitis, sonar, chess, car, kr-vs-kp, dis, hypo, nursery, magic, adult, connect-4 and localization) from Table 1. We run RBF on every dataset and obtain 30 classifiers. For each pair of classifiers, we compute their K statistic value according to equation (13). We then construct a scatter plot in which each point corresponds to a pair of classifiers. Its x coordinate is the diversity value (k) and its y coordinate is the mean accuracy of the classifiers. Figure 4 shows the mean accuracy and K statistic value between every two classifiers. The classifiers generated by RBF have larger diversity on some datasets (e.g. chess, kr-vs-kp, dis and localization), but have smaller diversity on some other datasets (e.g. hypo, nursery and connect-4). In some datasets (e.g. hepatitis and sonar), some quite agreement classifiers are generated. However, there exist the diversity in the majority of classifiers.

Fig. 4

the k-error diagrams of the classifiers generated by RBF on twelve datasets

4.2 Comparison in terms of zero-one loss and RMSE

Tables 3 and 4 show WDL records summarizing the relative zero-one loss and RMSE of the different algorithms. The p value following each WDL record is the outcome of a two-tailed binomial sign test and represents the probability that RBF would obtain the observed or more extreme ratio of wins to losses. We assess a difference is significant if p ≤ 0.05, and all such p values are changed to boldface corresponding tables.

Table 3 Win/Draw/Loss records of zero-one loss on all, small and large datasets

Table 4 Win/Draw/Loss of RMSE on all, small and large datasets

As can be seen from Tables 3 and 4, RBF achieves the advantage in terms of zero-one loss and RMSE over all the other BNCs, and the difference between them is statistically significant on all datasets. Generally, variants of AODE, e.g., WAODE, SA2DE, SASA2DE and IWAODE, assume different independence assumptions for different SPODE members and the complementary characteristic help fully represent all possible conditional dependencies. In contrast, SKDB and WATAN apply conditional mutual information to identify dependency relationships, which may be information-theoretic rather than probability-theoretic significant. The experimental results show that our heuristic search and random sample strategies provide high accuracy. For example, RBF beats SKDB on 31 datasets whereas it beats IWAODE on 26 datasets in terms of zero-one loss. RMSE-wise, RBF beats SKDB on 25 datasets whereas it beats IWAODE on 18 datasets.

The complexity of problem domains makes ever more urgent the need for scaling-up of existing learning algorithms to deal with datasets of different sizes. To clarify the effectiveness of heuristic search strategy and random sampling, we categorize datasets in terms of their sizes. For example, datasets with less than 2,000 instances (25 datasets) and more than 2,000 instances (15 datasets) are denoted as small size and large size respectively. On smaller datasets RBF has a better zero-one loss performance and RMSE than other BNCs, and most achieved a significant advantage. On larger datasets RBF has significantly better zero-one loss than WATAN (13 wins and 0 loss), WAODE (10 wins and 1 loss), IWAODE (11 wins and 2 losses). RBF is comparable to SKDB, SA2DE and SASA2DE in terms of zero-one loss and RMSE on large datasets. We claim that RBF’s improved performance on small size datasets is very encouraging.

To further illustrate that heuristic search strategy and random sampling are powerful methods to improve the performance of ensemble models. Figures 5 and 6 respectively present the scatter plots of the comparison results of RBF against other BNCs in terms of zero-one loss and RMSE, and the dotted line means that RBF performs almost the same as the alternative BNC. Note that some outlier points are removed for significance analysis. We can observe that most data points are located above the dotted line, that means RBF performs better than other BNCs much more often, and the advantages are obvious and significant.

Fig. 5

Scatter plot of comparisons in terms of zero-one loss

Fig. 6

Scatter plot of comparisons in terms of RMSE

4.3 Comparison in terms of bias-variance decomposition

Tables 5 and 6 respectively show the W/D/L comparison results using bias and variance. In general, lower bias means that model can capture fine detail in the training data. But this low bias may has potentially higher variance, which leads to greater changes in the topology learned from sample to sample. SKDB and WATAN try to fully represent the most significant conditional dependencies and build more robust topologies, that often result low bias and high variance. In contrast, variants of AODE inherit the tradeoff between bias and variance due to its impractical independence assumptions for different SPODE members and ensemble learning strategy. Significant and insignificant conditional dependencies are indiscriminately represented in the SPODE members. RBF also reduces bias by applying ensemble learning strategy, whereas it reduces variance by applying random sampling to randomly select conditional dependencies from all possible significant ones. Compared to SKDB, RBF achieves the advantage in terms of bias although less often (19 wins and 11 losses). Variance-wise, high-dependence BNCs may have high variance, leading to overfitting training data. Thus RBF obtains lower variance significantly more often than SKDB (32 wins and 4 losses). Compared with WATAN, RBF has a more significant advantage in bias (20 wins and 8 losses) and variance (31 wins and 6 losses). RBF achieves lower bias and variance more often than variants of AODE, except for IWAODE in variance. The reason might be that IWAODE applies weighting approach to improve the estimates of conditional probabilities while retaining the basic topologies of all SPODEs, and the weaker independence assumptions help avoid overfitting.

Table 5 Win/Draw/Loss comparison results of bias on all, small and large datasets

Table 6 Win/Draw/Loss comparison results of variance on all, small and large datasets

From Tables 5 and 6, when dealing with small datatsets, RBF is comparable to other BNCs in terms of bias. RBF has significantly better variance performance than SKDB (20 wins and 2 losses), WATAN (21 wins and 3 losses) and SA2DE (18 wins and 4 losses). IWAODE is a low variance high bias learner, it should be suitable for small data. This can be seen in Table 6 where IWAODE has significantly better variance than RBF (18 wins and 4 losses) on small datasets. When dealing with large datasets, most of the results are not significant, except for WATAN (9 wins and 1 loss) in terms of bias and SKDB (12 wins and 2 losses) and SA2DE (11 wins and 2 losses) in terms of variance.

4.4 Difference among all the classifiers

The average ranks of the algorithms obtained by applying the Friedman test with respect to zero-one loss, RMSE, bias and variance are shown in Table 7. The Friedman statistic F_F is distributed according to the F distribution with t − 1 = 6 and (t − 1)(D − 1) = 234 degrees of freedom. The critical value of F(6,234) for α = 0.05 is 2.14. At the bottom of Table 7, we could see that the F_F statistics for zero-one loss, RMSE, bias and variance are 50.5600, 40.1800, 19.3100 and 73.7900 respectively. Therefore, we can reject the null hypothesis, indicating that there are significant differences among those 7 algorithms.

Table 7 Average ranks of the algorithms

In order to further explore the significant difference among algorithms, we perform the Bonferroni-Dunn test and show the comparison results in terms of zero-one loss, RMSE, bias and variance in Fig. 7, where the middle line corresponds to the average level of different algorithms. For α = 0.05 with 7 algorithms and 40 datasets, q_α is 2.638 and the value of CD is 1.274. The CD interval is marked to the left and right of the average rank of RBF.

Fig. 7

The comparison results of the Bonferroni-Dunn test in terms of zero-one, RMSE, bias and variance on 40 datasets. CD = 1.274

As can be seen from the Fig. 7, RBF enjoys a significant advantage over other algorithms in terms of zero-one loss. RBF ranks first in terms of RMSE whereas it doesn’t have a significantly higher score than SASA2DE, WAODE and IWAODE. With respect to bias, the performance of RBF is comparable to other BNCs. With respect to variance, the performance of RBF is comparable to SASA2DE, WAODE and IWAODE, significantly better than WATAN, SA2DE and SKDB.

5 Conclusions

Ensemble learning can lead to performance improvement for “unstable” learning algorithms. State-of-the-art approaches, e.g., Bagging and Boosting, use resampling from the training set to produce very different models. To mitigate the negative effect caused by biased estimate of probability distributions, we propose to apply heuristic search strategy and random sampling to randomly select strong dependency relationships. In return for this extra random sampling during training, the proposed algorithm, RBF, provides well-calibrated posterior class probability estimates and always improves classification accuracy by reducing the structure complexity. RBF reduces bias by applying ensemble learning strategy and reduces variance by applying random sampling, thus it achieves the tradeoff between bias and variance. As shown in the experimental results, RBF attains lower error than the other out-of-core BNCs considered.

RBF provides an efficient and effective solution to potentially large problem space in learning Bayesian network classifier (BNC). This solution allows it to capture and take advantage of the additional fine-detail that is inherent in very large data while its efficiency makes it feasible to deploy. We take the dataset localization² from the UCI repository of machine learning as an example. Dataset localization contains recordings of five people performing different activities and each person wore four sensors (tags) while performing the same scenario five times. Dataset localization has 164,860 instances, 5 attributes (Sequence Name, Tag identificator, x coordinate of the tag, y coordinate of the tag and z coordinate of the tag) and 11 class labels (walking,falling, ‘lying down’, lying, ‘sitting down’, sitting, ‘standing up from lying’, ‘on all fours’, ‘sitting on the ground’, ‘standing up from sitting’ and ‘standing up from sitting on the ground’). As shown in Fig. 4, the classifiers generated by RBF have significant diversity on dataset localization. RBF significantly reduces misclassification rate (0.2672) compared to SKDB (0.3013), WATAN (0.3575), WAODE (0.3566), SA2DE (0.3078), SASA2DE (0.2735) and IWAODE (0.3593).

Future directions for research include:

Table 8 Experimental results of zero-one loss

1. Weighting approaches to combining the predictions from committee members of the ensemble in a more reasonable and efficient way;

2. More appropriate loss functions to tackle RBF’s tendency to overfit or underfit training sets;

3. Customized selection of edges and numbers of parents for different attributes in a discriminative manner.

Appendix

Table 9 Experimental results of RMSE

Table 10 Experimental results of bias

Table 11 Experimental results of variance