Green supplier selection based on probabilistic dual hesitant fuzzy sets: A process integrating best worst method and superiority and inferiority ranking

Abstract

China’s equipment manufacturing industry is increasingly important due to the development of economic globalization. Selecting the proper suppliers, taking into consideration the economic and environmental benefits, is strategic due to its impacts on the operation and competitiveness of an enterprise. Uncertainty in the selection of suppliers creates challenges for managers. The probabilistic dual hesitant fuzzy sets (PDHFSs) are powerful and effective tools to handle uncertain information, which integrate the strengths of both the dual hesitant fuzzy sets and probabilistic hesitant fuzzy sets. Considering that the best worst method (BWM) is an efficient weight-determination method, which can simplify the calculation process and improve the consistency degree of the results. The superiority and inferiority ranking (SIR) integrates the strengths of most multi-criteria decision making methods in handling unquantifiable, cardinal and ordinal data. In this paper, we developed an integrated group BWM and SIR to help managers select the optimum suppliers in which the evaluation is expressed in PDHFSs. In this multi-criteria group decision making (MCGDM) problem, the BWM with PDHFSs is investigated to obtain the weights of experts and criteria. A consistency reaching method based on the input-based consistency ratio is proposed to overcome the barrier of the low consistencyrelied on the pairwise comparison and reduce the computation complexity. Furthermore, with the weights of criteria and experts acquired by the PDHFS-BWM, the SIR is extended to the probabilistic dual hesitant fuzzy information environment. A numerical example is given to verify the validity and feasibility of the proposed method, and comparison are conducted to show its advantage.

1 Introduction

Insupplier selection problems, the managers of an enterpriseinvite a group of experts from different fields to give evaluations based on the specified criteria. After aggregating the assessment information, a final ranking of the alternative suppliers can be made. It has been figured out that manufacturing firms are responsible for global warming, resource depletion, environmental pollution and so on [9]. Green supply chain management (GSCM) is an excellent and effective way to reduce damage to the environment. In the GSCM, the purchasing of raw materials is the primary activity, which forms the basis of operations such as manufacturing and employment. It is necessary to pay attention to protecting the environment and reducing environmental pollution from the beginning of the green supply chain [5]. During the last decade, with the growing outsourcing businesses, the industry has relied greatly on the suppliers. For the company, selecting the proper green suppliers not only can improve the protection of the environment, it also can provide an opportunity to promote the corporate image and corporate competitiveness. So developing an efficient method by which to select green suppliers is necessary.

For many years, the managers only considered the purchasing cost when choosing suppliers. With the growing awareness of the need for environmental protection, the environmental performance of the suppliers should be considered. The managers generally invites a group of experts from the related areas to assist them to in making the proper choice, which indicates that the green supplier selection problem is a multi-criteria group decision-making (MCGDM) problem. Due to the complexity of MCGDM problems and the different expertise levels, experience and time pressure of experts, the uncertainty appears in the decision-making processes. In these cases, uncertain techniques were introduced. The intuitionistic fuzzy sets (IFSs) [43] include the membership function and the non-membership function, which could reflect both the positive and negative information. In order to avoid losing original information, Torra [46] proposed the hesitant fuzzy sets (HFSs), which take the multiple values of the membership functions and are widely used in different fields [25, 27]. Zhu [50, 53] proposed the dual hesitant fuzzy sets (DHFSs) integrating the advantages of the IFSs and the HFSs. It can accurately reflect the gradual cognitive uncertainty of unknown objects [11]. Although the HFSs contain all possible evaluation values provided by the experts, which assume that all evaluation values are of the same importance. In fact, due to the complexity and uncertainty of actual problems, there are often differences in the importance of different assessment values. To overcome this deficiency, the probabilistic hesitant fuzzy sets (PHFSs) are born at the right moment. It adds the corresponding probability to the element that is included in the experts’ preference. To aggregate the advantages of the above fuzzy sets and reduce loss of information, the probabilistic dual hesitant fuzzy sets (PDHFSs) were proposed [11], which show both the positive and negative attitude of experts with their preference of multiple values in the membership and non-membership part. It improves the decision accuracy to a great extent. Therefore, the features of considered problems could be more accurately presented under the probabilistic dual hesitant fuzzy information environment. The researches about the PDHFSs [6, 7] have provided the foundation and motivation for our research.

In this problem, we consider that the senior manager evaluates the expertise of the experts while the experts decide the weights of criteria and evaluate the alternatives, which is similar to the structure in [10]. In the study of Hafezalkotob et al. [10], the senior manager assigns a weight for each expert. However, the experts from different departments are accomplished in different fields. Experts from the purchasing department are more knowledgeable about the cost related criteria, than they are about the environmental related criteria. It is obvious their judgments about the fields in which they are skilled are more reliable than their evaluation of unfamiliar fields. Assigning different weights for experts with respect to the criteria could reflect the familiarity of the experts with the relevant fields. It is necessary to explore methods by which to settle different weights for experts with respect to the criteria.

Determining the weights of experts and criteria are crucial steps in MCGDM problems. Many methods have been proposed to allocate weights of criteria, like the correlation coefficient and standard deviation (CCSD) [28] and criteria importance though inter-criteria correlation (CRITIC) [21]. They both heavily rely on the decision matrix of the alternatives on the criteria, which may cause one-sidedness. What’s more, it can not reflect the degree of importance that the experts decided on the criteria. Sometimes, the final weights may be quite different from the actual importance of the criteria. The best worst method (BWM) allows the experts to express their preference on the criteria, and it is widely used and shows marvelous performance in weight-getting process [9, 10, 19, 20], which is proposed by Rezaei [40] as an enhanced version of the traditional analytic hierarchy process (AHP). It has two obvious advantages over AHP. The first advantage is fewer comparisons. It takes the best and worst objects as reference points, then compares other objects with the best and the worst. The times of pairwise comparison in the BWM is 2n − 3, which is smaller than the times of pairwise comparison in the AHP with n(n − 1)/2. The larger n is, the bigger the difference is. The second advantage is higher consistency; since the times of comparisons are reduced, the consistency is increased. In view of the relatively few comparisons and high consistency in the BWM, it is chosen in this paper to deduce the weights of experts and criteria. The different levels of expertise and the different experiences of experts lead to the emergence of uncertain information. Handling uncertain information is of great importance in the BWM. Several uncertain techniques have been integrated with the BWM, such as fuzzy sets, IFSs [32], the HFSs [31], the PHFSs [22] and so on. Considering the PDHFSs contain more information and avoid loss of information, we investigated the BWM under the probabilistic hesitant fuzzy information environment in this paper. In the former researches about the BWM, the consistency ratio is derived at the same time the weights are obtained. The consistency ratio, which attracts many scholarships’ attention, was first defined by Razaei [40]. Fuzzy related consistency researches have been conducted. Guo and Zhao [8] provided the definition of the fuzzy BWM consistency ratio. The consistency indices of the membership and non-membership were considered separately and the preference values were adjusted to improve the consistency ratio [33]. The consistency ratio and consistency reaching process (CRP) of the hesitant fuzzy linguistic-BWM were designed [24]. The above results about the CRP were derived after calculating the optimal models. If the evaluation information is modified, the optimal models are calculated again, which increases the complexity. The input-based consistency ratio, which checks the consistency of the preference before the optimal models are solved, was proposed [23]. Since the input-based consistency ratio is on the basis of the input preference, there is no need to conduct the whole process, which reduce the computational complexity. It does not rely on optimization models. Furthermore, it can offer instant feedback because it can locate the most inconsistent judgement accurately and provide guidelines for the experts to regulate their opinions. Inconsistent information should be modified to avoid inaccurate results. Until now, there is no paper concentrating on the CRP with regard to the input-based consistency ratio, which is put forward in this paper.

After getting the weights of criteria and experts, we need to evaluate the performance of each alternative on the criteria and then get a final rank. Several methods performed well in outranking have been used to rank the alternatives, such as the TOPSIS [20] and VIKOR [26]. The TOPSIS measures the distance between the alternatives with the ideal solutions as the score of the alternatives, while the VIKOR determines compromise solutions with the maximum values of ‘group utility’ and the minimum values of ‘individual regret’. In both methods, the extreme values are the critical references, which may lead to a biased result as if the extreme values are not properly settled [31]. To overcome this barrier, the superiority and inferiority method (SIR) is proposed, which is a valid extension of the PROMETHEE method [47]. The SIR compares alternatives under each criterion to build the superiority flow and the inferiority flow. Another advantage of the SIR is that it can accurately adjust the aggregation process in accordance with experts’ preferences. The SIR method has aggregated with fuzzy sets to solve various problems, such as to select the IT service management software with the triangular fuzzy numbers [41], to select the engineering investment with interval-valued IFSs [15], to choose the overseas outstanding teachers with the HFSs [30], and to pick up sustainable energy technologies with hesitant fuzzy linguistic sets [48]. Considering the PDHFSs could properly express the decision information in the green supplier selection problem, exploring the SIR with the PDHFSs is essential.

With the above analysis, this paper investigates the BWM with the PDHFSs to perform the weight-determining process, and integrate with the SIR method under the probabilistic dual hesitant fuzzy information environment to handle the supplier selection problem. We take full consideration of the good performance of the BWM in weight-determining and the SIR in outranking. The main contributions of this paper are summarized in the following:

• (1) In view of the advantages of the PDHFSs in showing the uncertain and imprecise information relying in the green supplier selection problem, this paper proposes the group best worst method under the probabilistic dual hesitant fuzzy information in which the multiple values in the membership and the non-membership with their probability are given by the manager and experts.

• (2) The experts’ weights are determined by the senior manager with probabilistic dual hesitant fuzzy best worst method (PDHF-BWM) who knows them deeply. We assign different weights to the experts in different areas with the BWM, which reflects his/her expertise on the criteria.

• (3) Since the former researches adjusted the inconsistent preferences after solving the optimal models, it is necessary to check and improve the consistency ratio before calculating the optimal models is necessary. This can decrease the computing difficulties and increase the efficiency. According to the definition of the input-based consistency ratio and the expertise of the experts in the areas related to the criteria, we design the CRP before solving the optimal models to modify the inconsistent preferences.

• (4) We investigate the group SIR with probabilistic dual hesitant fuzzy information. The general distance measures of the PDHFSs are applied to show the deviation between alternatives. The PDHF-BWM is combined with the SIR, and the probabilistic dual hesitant fuzzy group best worst superiority and inferiority ranking (PDHF-GBW-SIR) is proposed to solve the MCGDM problem.

This paper is organized as follows:

The next section shows the details about how to derive experts’ weights and the criteria weights with the BWM, and the CRP is also presented in this part. In addition, the whole steps of the PDHF-GBW-SIR are proposed. In Section 4, the formulated method is applied to the supplier selection of the equipment manufacturing industry, including case background, implementation, comparison and discussion. The final part outlines the conclusions and possible directions for further study.

2 Preliminaries

Several necessary concepts with regard to the PDHFSs, the BWM and the SIR are reviewed in this section.

2.1 Probabilistic dual hesitant fuzzy sets

In consideration of the complexity of the real-world problems, the experts give several possible values to express their opinions under uncertainty. First, the concepts of the HFSs and the DHFSs are introduced. The HFSs introduced by Torra [46] contain a set of values to express the evaluation information. The mathematical expression is:

$$ H=\{\langle x,h(x)\rangle |x\in X\} $$

(1)

where h(x) means several different values in [0,1], which is called a hesitant fuzzy element (HFE).

The HFSs only show the positive values of the evaluation, while sometimes the negative information is easier to get and can also reflect the epistemic uncertainty. Zhu et al. [53] put forward the DHFSs which contain the membership degrees and the non-membership degree. The mathematical expressions can be denoted as:

$$ D=\{\langle x,h(x),g(x)\rangle |x\in X\} $$

(2)

where the h(x) and g(x) indicate the membership and the non-membership functions. Every value in h(x) and g(x) is in [0,1].

The PHFSs [52] add the probability of each element and the mathematical expression is:

$$ P=\{\langle x,h(x)|p(x)\rangle |x\in X\} $$

(3)

where the h(x) means several different values in[0,1] and the p(x) refers to the corresponding probability of the h(x).

To inform the probabilistic information in the fuzzy sets and include as much decision information as possible, Hao et al. [11] proposed the concepts of the PDHFSs in view of the membership degrees, the non-membership degrees and the probabilistic information simultaneously, whose mathematical expression is as follows:

$$ P=\{\langle x,h(x)|p(x),g(x)|q(x)\rangle |x\in X\} $$

(4)

where h(x)|p(x) and g(x)|q(x) represent the membership and the non-membership degrees with their corresponding probabilistic information, which satisfies

$$ 0\leq\gamma,\eta\leq1,0\leq\gamma^{+}+\eta^{+}\leq 1 $$

(5)

and

$$ p_{i}\in [0,1],q_{j}\in [0,1],\sum\limits_{i=1}^{\# h}p_{i}=1,\sum\limits_{i=1}^{\#g}q_{i}=1 $$

(6)

where γ ∈ h(x), η ∈ g(x), $\gamma ^{+}=\bigcup _{\gamma \in h(x)}$ max {γ}, $\eta ^{+}=\bigcup _{\eta \in h(x)}$ max {η}, p_i ∈ p(x) and q_j ∈ q(x), #h and #g indicate the number of elements in γ ∈ h(x) and η ∈ g(x). In order to compare and compute with the PDHFSs, the basic operational laws and score functions are given [11]. Suppose that P, P₁, P₂ are three probabilistic dual hesitant fuzzy elements (PDHFEs), P = (h|p,g|q), P₁ = (h₁|p₁,g₁|q₁), and P₂ = (h₂|p₂,g₂|q₂), then

$$ \begin{array}{@{}rcl@{}} P_{1} \oplus P_{2}&=&\bigcup\limits_{\gamma_{1}\in h_{1},\eta_{1} \in g_{1},\gamma_{2}\in h_{2},\eta_{2} \in g_{2}}\\ &&\times\{\{(\gamma_{1}+\gamma_{2}-\gamma_{1}\gamma_{2})|p_{\gamma_{1}}p_{\gamma_{2}}\},\{(\eta_{1}\eta_{2})|q_{\eta_{1}}q_{\eta_{2}}\}\} \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} P_{1} \otimes P_{2}&=&\bigcup\limits_{\gamma_{1}\in h_{1},\eta_{1} \in g_{1},\gamma_{2}\in h_{2},\eta_{2} \in g_{2}}\\ &&\times\{\{(\gamma_{1}\gamma_{2})|p_{\gamma_{1}}p_{\gamma_{2}}\},\{(\eta_{1}+\eta_{2}-\eta_{1}\eta_{2})|q_{\eta_{1}}q_{\eta_{2}}\}\} \end{array} $$

(8)

Let P = (h|p,g|q) be a PDHFE, then the score function can be defined as:

$$ s=\sum\limits_{i=1,\gamma\in h}^{\# h}\gamma_{i}\cdot p_{i}- \sum\limits_{j=1,\eta \in g}^{\# g}\eta_{i}\cdot q_{j} $$

(9)

Let P = (h|p,g|q) be a PDHFE, then the standard deviation degree is defined as:

$$ \sigma =\sqrt{\sum\limits_{i=1,\gamma\in h}^{\# h}(\gamma_{i}-s)^{2}\cdot p_{i}+ \sum\limits_{j=1,\eta \in g}^{\# g}(\eta_{i}-s)^{2}\cdot q_{j}} $$

(10)

where s is the score function of the PDHFE.

The real preference value of Υ, (Υ = (γ₁,γ₂,⋅⋅⋅,γ_n,) ∈ [0,1]), is:

$$ RPV ({{\varUpsilon}})=2mean({{\varUpsilon}})*rpd(\hat{{{\varUpsilon}}}) $$

(11)

where mean(Υ) is the mean value of all values in the set Υ, $\hat {{{\varUpsilon }}}=\{\gamma _{i}/ {\sum }^{n}_{i=1}{\gamma _{i}}, (i=1,2,\cdot \cdot \cdot ,n)\},rpd(\cdot )$ is the real preference degree in [38], which is denoted as

$$ rpd(\widetilde{h})=\left\{\begin{array}{l} {\sum}^{\sharp\widetilde{h}}_{i=1}\widetilde{\gamma_{i}}(\frac{\sharp\widetilde{h}-i}{\sharp\widetilde{h}-1}), if mean (h)<0.5;\\ 1-{\sum}^{\sharp\widetilde{h}}_{i=1}\widetilde{\gamma_{i}}(\frac{\sharp\widetilde{h}-i}{\sharp\widetilde{h}-1}), if mean (h)>0.5;\\ 0.5, if mean (h)=0.5; \end{array}\right. $$

(12)

where $\widetilde {h}={\widetilde {\gamma }=\gamma _{i}/sum(h)\mid \gamma _{i}\in h}$ is the normalized HFE.

Based on the above definitions, Ren et al. [39] proposed a new comparison method, synthetical score function considering the mean value and the stability of information at the same time. The specific expression is:

$$ ss(P)=(RPV(\gamma_{i})-\sigma(\gamma_{i}|p_{i}))-\theta(RPV(\eta_{j})-\sigma(\eta_{j}|q_{j})) $$

(13)

in which RPV (γ_i) and RPV (η_j) mean the real preference values of the membership and non-membership degree. 𝜃 reflects the sensibility degree of experts of the non-membership. The higher the value of 𝜃 is, the experts pay more attention on the negative information. σ(γ_i|p_i) and σ(η_j|q_j) are the standard deviation values of the membership and the non-membership.

2.2 Best worst method

Best worst method is a relatively new MCDM method proposed by Rezeai in 2015 [40], which is more efficient than the typical pairwise comparison-based MCDM method AHP. On account that the pairwise comparisons of n criteria in AHP are n(n − 1)/2 while the comparisons in BWM are 2n − 3. The basic steps of BWM are described as follows:

Step 1

Determine a set of decision criteria. In this step, the criteria related to the problem should be figured out, and the set is always indicated as {C₁,C₂,⋯ ,C_n}.

Step 2

Make a choice of the best and worst criteria. The experts select the best (most important) and the worst (least important) criteria. If there is more than one criterion considered as the best or the worst, one can be chosen randomly.

Step 3

Determine the preference of the best criterion over all the other criteria and all the criteria over the worst criteriaon. The best-to-others vector is BO = (a_B1,a_B2, ⋯ ,a_Bn) and the others-to-worst vector would be OW = (a_1W,a_2W,⋯ ,a_nW).

Step 4

Find the optimal weights through the programming method. The optimal weights for the criteria satisfy the equations ω_B/ω_j = a_Bj and ω_j/ω_W = a_jW. In order to achieve it, the maximum absolute differences $| \frac {\omega _{B}}{\omega _{j}}-a_{Bj}|$ and $| \frac {\omega _{j}}{\omega _{W}}-a_{jW}|$ for all j is minimized. And the following optimization model is formulated:

Model 1

$$ \begin{array}{@{}rcl@{}} \begin{array}{ll}min max_{j}&\{| \frac{\omega_{B}}{\omega_{j}}-a_{Bj}|, | \frac{\omega_{j}}{\omega_{W}}-a_{jW}|\}\\ &s.t.\\ & \sum\limits_{j}\omega_{j}=1\\ & \omega_{j}\geq 0, j=1,2,\cdots, n \end{array} \end{array} $$

(14)

The model 1 can be transformed into model 2:

Model 2

$$ \begin{array}{@{}rcl@{}} \begin{array}{ll}min&\ \xi\\ &s.t.\\ &| \frac{\omega_{B}}{\omega_{j}}-a_{Bj}|\leq \xi, j=1,2,\cdots,n\\ &| \frac{\omega_{j}}{\omega_{W}}-a_{jW}|\leq \xi,j=1,2,\cdots,n\\ & \sum\limits_{j}\omega_{j}=1\\ & \omega_{j}\geq 0, j=1,2,\cdots, n \end{array} \end{array} $$

(15)

After solving the model 2, the optimal weights $(\omega ^{*}_{1},$ $\omega ^{*}_{2},\cdots ,\omega ^{*}_{n})$ and the minimum maximum absolute difference ξ^∗ can be obtained.

2.3 Superiority and inferiority ranking

The SIR [47], as an extension of the PROMETHEE [30], taking the uncertain and undetermined information into account, ranks the alternatives by comparing the superiority matrix and the inferiority matrix. The classical SIR method is reviewed as follows:

Step 1:

Form the decision matrix. Determine the criteria and the alternatives of the MCDM problem. Gather the assessment information.

Step 2:

Establish the superiority and the inferiority matrices.

Step 2.1:

Compare the criteria values of different alternatives on each criterion. Define the deviation between each two alternatives as regards to any criteria, which could be the difference between the attribute values with the accurate numbers. To reflect the intensity of preference of any two alternatives over a criterion, an appropriate generalized criterion function should be developed. Brans and Vincke [3] introduced six generalized criteria, including the true criterion, quasi criterion, criterion with linear preference, level criterion, criterion with linear preference and indifference area and Gaussian criterion.

Step 2.2:

For each alternative, calculate its superiority index and inferiority index about each criterion.

Step 2.3:

Formulate the superiority and the inferiority matrices which represent the comparison results from different aspects.

Step 3:

Get the superiority flow and inferiority flow. Derive the superiority flow and the inferiority flow through some aggregation procedures. It should be noted that different aggregation methods may lead to various kinds of flows. So, choosing a proper aggregation method is needed in this step.

Step 4:

Get the net flow of each alternative.

Step 5:

Acquire the final ranking according to the net flow.

3 The PDHF-GBW-SIR method

In this section, the PDHF-GBW-SIR method is introduced. The description of the MCGDM problem is presented in the first part. Considering the advantages of the BWM in less comparison and higher consistency, the weights of the experts and criteria based on the BWM are obtained in the next part. Afterward, the CRP of the BWM about the input-based consistency ratio is proposed. When giving evaluation to the experts and the criteria, it is easy to figure out the best and worst ones. While it is not easy to select the best alternative without other methods, the probabilistic dual hesitant fuzzy superiority and inferiority ranking (PDHF-SIR) based on the decision matrix is carried out. The whole procedure is presented in the last part of this section. In this section, the PDHF-GBW-SIR method is introduced. The description of the MCGDM problem is presented in the first part. Considering the advantages of the BWM in less comparison and higher consistency, the weights of the experts and criteria based on the BWM are obtained in the next part. Afterward, the CRP of the BWM about the input-based consistency ratio is proposed. When giving evaluation to the experts and the criteria, it is easy to figure out the best and worst ones. While it is not easy to select the best alternative without other methods, the probabilistic dual hesitant fuzzy superiority and inferiority ranking (PDHF-SIR) based on the decision matrix is carried out. The whole procedure is presented in the last part of this section.

3.1 Problem description

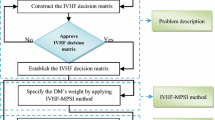
For the green supplier selection problem, we assume that one senior manager invites a group of experts e_k(k = 1,2,⋯ ,t) to evaluate the alternatives A_l(l = 1,2,⋯ ,m) with reference to the criteria C_i(i = 1,2,⋯ ,n). The senior manager and experts express their preference and evaluation information with the PDHFSs. The senior manager takes charge of giving evaluation to the experts for the criteria in accordance of their performance and his cognition of the experts. He/she picks up the best and worst experts with i − th criterion, which are denoted as ${e^{B}_{i}}$ and ${e^{W}_{i}}$. Then he can get the matrix of the weights of experts, which is n × t. The k − th expert selects the best criterion ${C^{B}_{k}}$ and the worst criterion ${C^{W}_{k}}$, and conduct the further comparison to get the weights of criteria,which is the second matrix in Fig. 1. The structure of getting the weights of experts and criteria can be seen in Fig. 1.

Fig. 1

The general framework of deriving the weights of experts and criteria

Then the experts assess the alternatives. After calculation with the SIR method, a final ranking of the alternatives is obtained. The rest of this section presents the detail process of the PDHF-GBW-SIR method.

3.2 The weight-deriving method

Due to the diversity of experience, knowledge and background of different experts, the attitude, motivation and understanding of the same problem vary from individuals to individuals. The criteria values are more objective and accurate when experts evaluate the familiar aspects, while the criteria values are less reliable facing the unfamiliar criteria. Rather than a single weight assigned to an expert, a vector which contains different weights based on the criteria and the expert’s contributions are considered. In this paper, a senior manager is considered to provide assessments on the experts with regard to the given criteria. The senior manager assigns different weights to the experts based on the chosen criteria with the BWM. Under each criterion, we can derive the vector of an expert’s weights, then the weight matrix of experts is t × n. The steps of the weight deriving method are as follows:

Stage 1:

Determine the experts’ weight vectors with the BWM.

Step 1:

The senior manager selects several experts in the expert group.

Step 2:

Determine the best and worst experts related to the criteria by the senior manager. The best expert set $B_{e}=\{{e^{b}_{1}},{e^{b}_{2}},\cdots ,{e^{b}_{n}}\}$ and the worst expert set $W_{e}=\{{e^{w}_{1}},{e^{w}_{2}},\cdots ,{e^{w}_{n}}\}$ are built, in which the same experts may be the best (worst) experts of different criteria.

Step 3:

Evaluate the experts’ expertise degree.

Step 3.1:

Specify the preference degree in the PDHFE $P^{ei}_{Bk}=(h^{ei}_{Bk}|p^{ei}_{Bk},g^{ei}_{Bk}|q^{ei}_{Bk})$, which represents the comparison of the best expert over the k − th expert with respect to the i − th criterion. The best-to-others vector of the i − th criterion is: $B{O^{e}_{i}}=(P^{ei}_{B1},P^{ei}_{B2},\cdots ,P^{ei}_{Bt})$. The other vectors based on different criteria can be got in the same way.

Step 3.2

Set the preference degree $P^{ei}_{kW}=(h^{ei}_{kW}|p^{ei}_{kW},$ $g^{ei}_{kW}|q^{ei}_{kW})$ of the k − th expert to the worst (least expertise) expert in the related area. The others-to-worst vector of the i − th criterion is described as: $O{W^{e}_{i}}=(P^{ei}_{1W},P^{ei}_{2W},$ $\cdots ,P^{ei}_{tW})$. This method is also used to get the vectors of the rest criteria. For the sake of further calculation, the $B{O^{e}_{i}}$ and $O{W^{e}_{i}}$ vectors should be handled. The priority degree pd is introduced to reflect the differences between the assessment information in the PDHFSs, which is similar to the definition of the priority degree of dual hesitant fuzzy elements proposed in [37]. What should be emphasized is that the parameter α shows the importance between the membership and non-membership, which could reflect the experts’ attitude towards the positive and negative sides. And the α grows larger when the experts are concerned more about the membership.

Step 4:

Check the consistency with the input-based consistency ratio and modify the inconsistent preference. The detailed explanation and modified rules are presented in Section 3.3.

Step 5:

With the consistent information, we calculate the following model to get the optimal vectors:

$$ \begin{array}{@{}rcl@{}} \begin{array}{ll} min max &\{|\omega^{ei}_{B}-p^{ei}_{Bk}\omega^{ei}_{k}|,|\omega^{ei}_{k}-p^{ei}_{kW}\omega^{ei}_{W}|\} \\ &s.t.\\ &\sum\limits^{t}_{k=1}\omega^{ei}_{k}=1\\ & \omega^{ei}_{k}\geq 0 \end{array} \end{array} $$

(16)

where the $\omega ^{ei}_{B}$ means the weight of the best expert for the i − th criterion. $p^{ei}_{Bk}$ is the preference degree of the best expert over the k − th expert for the i − th criterion. $\omega ^{ei}_{k}$ is the weight of the k − th expert for the i − th criterion. $p^{ei}_{kW}$ is the preference degree of the k − th expert over the worst expert for the i − th criterion. Model 3 can be transformed into the following model:

$$ \begin{array}{@{}rcl@{}} \begin{array}{ll} min \ &\xi_{i}\\ &s.t.\\ &|\omega^{ei}_{B}-p^{ei}_{Bk}\omega^{ei}_{k}|\leq \xi_{i}\\ & |\omega^{ei}_{k}-p^{ei}_{kW}\omega^{ei}_{W}|\leq \xi_{i} \\ &\sum\limits^{t}_{k=1}\omega^{ei}_{k}=1\\ & \omega^{ei}_{k}\geq 0 \end{array} \end{array} $$

(17)

The optimal weight vector $(\omega ^{ei}_{1},\omega ^{ei}_{2},\cdots ,\omega ^{ei}_{t})$ can be obtained, while the corresponding value $\xi ^{*}_{i}$, as a significant component of the output-based consistency ratio, is derived simultaneously. We can check the consistency again with the parameter $\xi ^{*}_{i}$. If $\xi ^{*}_{i}=0$, then the preference relations are fully consistent. In most cases, $\xi ^{*}_{i}\neq 0$, it should be within the consistency threshold value. After solving all the models, the experts’ weight matrix W_e can be derived which is n × t.

Stage 2:

Derive the weights of criteria.

In this stage, the experts should decide the weights of criteria. Since multiple experts are invited to give evaluations, the group best worst method (GBWM) is conducted. In the GBWM, several ways have been studied to choose the best and worst criteria of the group [42]. In this paper, the experts have enough freedom to select the best and worst criteria according to their expertise. Each expert can directly or use some other method, for example, graph theory [33], to select the best and worst criteria themselves. We just take one expert as an example to illustrate the process. Then the preference vectors $B{O^{C}_{k}}$ and $O{W^{C}_{k}}$ can be derived, where $P^{Ck}_{Bj}$ denotes the probabilistic dual hesitant fuzzy preference degree of the best criterion C_B over C_j. And $P^{Ck}_{jW}$ means the probabilistic dual hesitant fuzzy preference degree of the criterion C_j over the worst criterion C_W. The vectors can be expressed as:

$$ \begin{array}{@{}rcl@{}} &B{O^{C}_{k}}=\{P^{Ck}_{B1}, P^{Ck}_{B2}, P^{Ck}_{B3},\cdots, P^{Ck}_{Bn} \} \\ &O{W^{C}_{k}}=\{P^{Ck}_{1W}, P^{Ck}_{2W}, P^{Ck}_{3W},\cdots, P^{Ck}_{nW} \} \end{array} $$

(18)

Then the priority degree is calculated and the input-based consistency ratio is checked. The inconsistency repairment is conducted before the optimal models are solved, which is introduced in Section 3.3. For the other n − 1 criteria, the similar models can be established and solved in the same way. After solving the proposed n model, a t × n criteria weight matrix is derived, which can be expressed as W_C. Since the experts’ weights with regard to criteria and the weights of criteria decided by experts have been obtained, the aggregation procedures are performed. To better reflect the influence of the experts’ strengths and weaknesses, the weighted average operators are selected. and the computational formula can be shown as follows:

$$ \begin{array}{@{}rcl@{}} {\omega^{C}_{i}}=\sum\limits_{k=1}^{t}\omega^{ei}_{k}*\omega^{Ck}_{i} \end{array} $$

(19)

where ${\omega ^{C}_{i}}$ is the weight of criteria i, $\omega ^{ei}_{k}$ is the weight of the k − th expert for the i − th criterion. $\omega ^{Ck}_{i}$ is the weight of the i − th criterion decided by the k − th expert. If the ${\sum }_{i=1}^{n}{\omega ^{C}_{i}}$ is more than 1, then the standardization steps should be carried out based on Eq. 20.

$$ \begin{array}{@{}rcl@{}} \omega^{C\ast}_{i}=\frac{{\omega^{C}_{i}}}{{\sum}_{i=1}^{n}{\omega^{C}_{i}}} \end{array} $$

(20)

Then the experts assess the alternatives. After calculation with the SIR method, a final ranking of the alternatives is obtained. The rest of this section presents the detail process of the PDHF-GBW-SIR method.

3.3 The consistency reaching process of the PDHF-GBWM

To improve the reliability of the final results, the detailed inconsistency improving method in the MCGDM scenario is proposed. The inconsistency improving process under the uncertain situation based on the output-based consistency ratio with the hesitant fuzzy linguistic has been presented [24], while the CRP with accordance to the input-based consistency ratio of the BWM is still a question, which is investigated in this part.

The input-based consistency ratio is taken into consideration, which has been proven highly monotonically related to the defined output-based consistency ratio based on the original consistency [23]. The concepts of the input-based consistency ratio are:

$$ \begin{array}{@{}rcl@{}} CR^{Ik}=max_{j}\{CR^{Ik}_{j}\} \end{array} $$

(21)

having

$$ \begin{array}{@{}rcl@{}} CR^{Ik}_{j}=\left\{ \begin{array}{cl} \frac{|a_{Bj}\times a_{jW}-a_{BW}|}{a_{BW}\times a_{BW}-a_{BW}},&a_{BW}>0.1,\\ 0,&a_{BW}=0.1, \end{array} \right. \end{array} $$

(22)

where the CR^Ik is the consistency ratio of the k − th expert, the $CR^{Ik}_{j}$ means the consistency level related with criterion j and a_BW represents the preference of the best expert over the worst expert. The experts modify their preference until the preference vectors satisfy the consistency requirement. Previous researches obtained the consistency level after the entire optimization process was completed. In that case, once the evaluation information is modified, the optimal process needs to be repeated again. However, checking the consistency before solving the optimal models could reduce the computation process and make the method easier to conduct. It is difficult to achieve the absolute consistency, therefore, a threshold indicating the experts’ acceptance level should be determined. If the obtained consistency ratio is larger than the threshold, the results lack of reliability. If the CR^Ik is smaller than the threshold, we take the preference vectors as the reliable ones. Through statistical analysis, the thresholds for different combinations of criteria and evaluation grades are calculated [23].

The adjustment of the experts’ preference should be conducted to achieve acceptable consistent results [45]. Several approaches have been put forward to improve the consistency such as the automatic improving method [44] and the feedback-based improving method [13]. Since the experts own the right to participate in the CRP, they can choose to change their evaluation freely with our suggestions. In this paper, the feedback-based improving approach is taken into consideration. The method mainly consists of two stages: the identification stage and the adjusting stage [34, 49] In the first stage, we find out which experts’ judgment and which criteria lead to the largest deviation and need adjustment [16]. In the second stage, we take measures to modify the preferences or weights according to the designed guide rules. The CRP is presented in the following:

Stage 1:

Identification stage.

In this stage, the biggest deviation of criteria should be figured out. Since the former calculation has derived the maximum absolute difference of all criteria. If the ξ_i is bigger than the thresholds assigned, then the corresponding criterion C_j is picked out and the evaluation on it should be revised. After finding out the criterion which needs to repair, the repair procedures are introduced in the next stage.

Stage 2:

Direction stage.

In this stage, the following direction rules are stated to modify the inconsistency and revise the evaluations of the chosen criterion.

Rule 1: The deviation between the best and worst criteria is not changed. It is a significant influence factor of the threshold. If the biggest deviation changes, then the threshold may changes accordingly [23]. Further, the changes may cause the increase of the number of assessment value that needs to be adjusted.

Rule 2: The sequence of the criterion which needs adjustment should not be changed, which confirms the ranges of the evaluation to be adjusted. If the orders of the $B{O^{e}_{i}}$(or $B{O^{C}_{k}}$) and $O{W^{e}_{i}}$(or $O{W^{C}_{k}}$) vectors are not the same, pick up one to revise until the orders of both vectors are the same.

Rule 3: The consistency ratio should satisfy the threshold. The experts choose to change one or both of the a_Bj and a_jW and preferentially adjust one parameter. If the a_Bj and the a_jW can both be modified, we choose to change the less deviation one.

Rule 4: When the evaluation of more than one criterion needs modification, the most inconsistent one would be adjusted first, then the second large one, until all the inconsistent criteria are repaired.

Next, the algorithm to illustrate the process of checking and improving consistency is given in Table 1:

Table 1 The consistency checking and improving algorithm

3.4 The procedure of the PDHF-GBW-SIR method

Based on the above analysis and the hesitant fuzzy linguistic prioritized SIR method [48], the PDHF-GBW-SIR method is proposed to solve the MCGDM problems in which the experts express their preferences and evaluations in the PDHFSs. In addition, the weights of the experts are vectors related to the criteria rather than a single element. What should be emphasized before showing the procedures of the whole decision making process is presented in the following:

Firstly, we invite the experts to give their judgements of the alternatives with the PDHFSs. The individual assessment matrices are integrated into group matrix with the PDHFWA operators as follows:

$$ \begin{array}{@{}rcl@{}} Pg_{li}=\oplus^{t}_{k=1}\omega^{ei}_{k} P^{k}_{li} \end{array} $$

(23)

in which the $\omega ^{ei}_{k}$ means the weight value of the k − th expert on the i − th criterion and $P^{k}_{li}$ is the evaluation to the l − th alternative on the i − th criterion given by the the k − th expert. The aggregated matrix is

$$Dg=\left[\begin{array}{cccc} Pg_{11} & Pg_{12} &\cdot\cdot\cdot &Pg_{1n} \\ Pg_{21} & Pg_{22} &\cdot\cdot\cdot &Pg_{2n}\\ \cdot\cdot\cdot & \cdot\cdot\cdot &\cdot\cdot\cdot &\cdot\cdot\cdot\\Pg_{m1} & Pg_{m2} &\cdot\cdot\cdot &Pg_{mn} \end{array}\right] $$

For the alternatives A_a and A_b, we adopt the general distance measure developed by Ren [39] to calculate the deviation related to the criterion C_i:

$$ \begin{array}{@{}rcl@{}} d(Pg_{ai},Pg_{bi})&=&vEPD(Pg_{ai},Pg_{bi})\\ &&+(1-v)\frac{|ss(Pg_{ai})-ss(Pg_{bi})|}{1+\theta} \end{array} $$

(24)

where the EPD means the equiprobability distance measure, which is explicitly explained in [39]. And the ss refers to the synthetical score function. v ∈ [0,1] indicates the experts’ preferences of the equiprobability distance measure and the synthetical score function. 𝜃 ∈ [1,10] reflects the experts’ sensitivity towards the non-membership degree. Pg_ai and Pg_bi represent the evaluation information in the aggregated matrix of alternatives A_a and A_b.

Next, the calculation of intensity that the alternative A_a is non-inferior to A_b with respect to the criterion C_i is:

$$ \begin{array}{@{}rcl@{}} PA_{i}(A_{a},A_{b})=f_{i}[d(Pg_{ai},Pg_{bi})] \end{array} $$

(25)

where f_i is a monotone-nondecreasing function in [0, 1] picked up by experts from the given six functions in [47], which is expressed as:

$$ \begin{array}{@{}rcl@{}} f_{i}(x)=\left\{ \begin{array}{cl} 1,&x>1,\\ x,&0<x\leqslant1,\\ 0,&x\leq0 \end{array} \right. \end{array} $$

(26)

and the x is the priority degree which represents the possibility of Pg_ai being superior to Pg_bi.

Then, for the alternative A_a, the non-inferiority index S_i(A_a) related to the criterion C_i is defined as:

$$ \begin{array}{@{}rcl@{}} S_{i}(A_{a})&=&\frac{1}{m}\sum\limits^{m}_{b=1} PA_{i}(A_{a},A_{b})\\ &&=\frac{1}{m}\sum\limits^{m}_{b=1} f_{i}[d(Pg_{ai},Pg_{bi})] \end{array} $$

(27)

and the non-superiority index I_l(x_i) could be obtained in the similar way and be expressed as:

$$ \begin{array}{@{}rcl@{}} I_{i}(A_{a})&=&\frac{1}{m}\sum\limits^{m}_{b=1} PA_{i}(A_{b},A_{a})\\ &&=\frac{1}{m}\sum\limits^{m}_{b=1} f_{i}[d(Pg_{bi},Pg_{ai})] \end{array} $$

(28)

The matrix S represents the information about the intensity of superiority of each alternative with regard to each criterion, and the matrix I means the information about the intensity of inferiority. They are shown in the following:

$$ S=S_{i}(A_{a})_{m\times n}=\left[\begin{array}{llll} S_{1}(A_{1}) & S_{2}(A_{1}) &\cdot\cdot\cdot &S_{n}(A_{1}) \\ S_{1}(A_{2}) & S_{2}(A_{2})&\cdot\cdot\cdot &S_{n}(A_{2})\\ \cdot\cdot\cdot & \cdot\cdot\cdot &\cdot\cdot\cdot &\cdot\cdot\cdot\\S_{1}(A_{m}) & S_{2}(A_{m})&\cdot\cdot\cdot &S_{n}(A_{m}) \end{array}\right]$$

$$I=I_{i}(A_{a})_{m\times n}=\left[\begin{array}{llll} I_{1}(A_{1}) & I_{2}(A_{1}) &\cdot\cdot\cdot &I_{n}(A_{1}) \\ I_{1}(A_{2}) & I_{2}(A_{2})&\cdot\cdot\cdot &I_{n}(A_{2})\\ \cdot\cdot\cdot & \cdot\cdot\cdot &\cdot\cdot\cdot &\cdot\cdot\cdot\\I_{1}(A_{m}) & I_{2}(A_{m})&\cdot\cdot\cdot &I_{n}(A_{m}) \end{array}\right] $$

Furthermore, the non-inferiority flow φ^>(A_a) is:

$$ \begin{array}{@{}rcl@{}} \varphi^{>}(A_{a})=\sum\limits\limits^{n}_{i=1}\omega_{i}S_{i}(A_{a}) \end{array} $$

(29)

the non-superiority flow φ^<(A_a) is:

$$ \begin{array}{@{}rcl@{}} \varphi^{<}(A_{a})=\sum\limits^{n}_{i=1}\omega_{i}S_{i}(A_{a}) \end{array} $$

(30)

the net flow is defined as:

$$ \begin{array}{@{}rcl@{}} \varphi(A_{a})=\varphi^{>}(A_{a})-\varphi^{<}(A_{a}) \end{array} $$

(31)

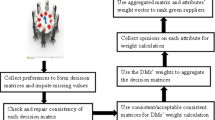
After comparing the values of the net flows, the final ranking of the alternatives is obtained. The overall process is summarized in Fig. 2.

Fig. 2

The flowchart of the proposed PDHF-GBW-SIR method

4 Case study

Given the previous introduction of the PDHF-GBW-SIR method, In this section, a supplier selection problem is utilized to indicate the applicability and practical process of the proposed method. Some comparison analysis with other MCGDM methods is given to demonstrate the verification and effectiveness of the PDHF-GBW-SIR method.

4.1 Background

The former researches figured out that quality and price are crucial determinants [14], which is also taken into consideration in this case. China’s equipment manufacturing industry has become a significant role in the global market [2]. They outsource some critical business, so the equipment manufacturing enterprise relies much on the suppliers. Choosing the proper green suppliers not only brings the financial benefits but also enhances the environmental performance. Sometimes with the unique requirement, the factory needs to order some customized components, timely delivery has an impact on the assembly efficiency, and affects the final delivery time. While the unqualified components lead to incompetent products and delay in delivery, which reduces the credibility of the company and increases the economic cost, further may cause safety accidents in the operational process. Finding the best suppliers for purchasing the components is a key means for the equipment enterprise. Incorporating with the actual situation of the enterprise, the following factors are analyzed:

• (1) C₁: Technology level. Since the enterprise provides customized products based on the customers’ demands, it may have special requirements on the components manufactured by the suppliers, such as: the specific size, the fixed intensity. So the product development, technical and improvement capability of the suppliers are significant [4]. Advanced production technology ensures the product quality. The test facilities and capabilities are another guarantee of the qualified products.

• (2) C₂: Quality. The products should strictly meet the requirements, the material, the size, the craft and so on [17]. Besides, the quality system of the suppliers could also reflect their ability and their product quality.

• (3) C₃: Price. The cost comes first to the mind when an enterprise considers purchasing problems [12]. Choosing products with high quality and low price is the goal of all purchasing personnel. The current price and cost reduction factors are regarded.

• (4) C₄: Service. It mainly refers to these aspects: deliverability, rate of delivery in time, inquiry information timeliness, timely rate of after-sales service and quality information timely response rate, etc. [18]. The time-oriented indicators are of great importance in this part. Just-in-time supply reflects that the suppliers own satisfactory production capacity. And the just-in-time delivery has a strongly influence on shortening the lead time of purchase and enhance the delivery rate. In addition, the contents contained in the after-sales service also affect a lot.

• (5) C₅: Environmental consistences. Since the growing concern about the environmental problems, many enterprises pay attention to the environmental issues, not only in the productive processes, but also in the supplier selection process. The environmental consciousness of the alternative suppliers is taken into consideration. Using the environmentally friendly technology, taking the environmental management and training the staff with eco-friendly philosophy could reflect the alternatives’ environmental consistencies [35].

The evaluation of the suppliers according to the above criteria is a complex and significant process. Some necessary methods should be developed to help choose suppliers that provide high quality products and service at reasonable price, willing to a long-term cooperation and achieving win-win development. But the evaluation of the suppliers in terms of the above criteria are full of uncertainty. It is not appropriate to judge the performance of suppliers with accurate data. The experts may hesitate between several values and for each value, they have their preferences. Sometimes, they have trouble in expressing judgement from the positive aspects, but it is convenient in indicating the negative information. The PDHFSs is a proper tool to solve the above problem, which contain the positive and negative information and model the imprecise and subjective evaluation of suppliers in a direct way. Considering the above criteria, the manager invites experts from the technical, production, purchasing and environmental department to give evaluations. They are less knowledgeable about other aspects of the suppliers, so it is necessary to adopt their strengths and avoid their weaknesses. The PDHF-GBWM could solve this problem. It is not easy to figure out which alternative is the best or the worst as the reference, so the method based on the decision matrix is applied. The PDHF-SIR are conducted to get the rank of alternatives.

In order to obtain reliable information with respect to the given criteria, 4 participants from relevant departments are selected. They work together to judge the 4 alternative suppliers, and give a final rank of the alternatives.

4.2 Implementation

In this part, the proposed PDHF-GBW-SIR method is conducted to solve the supplier selection problem with probabilistic dual hesitant fuzzy information. The calculation process results are presented:

Stage 1: Determine the weights of experts.

In this stage, the weight vectors of the experts are acquired.

Step 1: A senior manager picks up 4 experts from technology, production, purchasing and environmental departments. We assume that the senior manager knows the experts comprehensively and deeply, he can give the evaluation fairly.

Step 2: Identify the best and worst experts of the fixed criteria, which is shown in Table 2.

Step 3: Acquire the BO and OW vectors under each criterion. Table 2 presents the details of the preference.

To better reflect the differences between the assessment information in the PDHFSs, the priority degree is introduced, which is similar to the priority degree of the DHFSs [37]. The importance of membership and non-membership is considered the same, so the parameter α is set as 0.5. Table 3 presents the priority degree between the evaluations of the experts over the best and the worst ones.

Step 4: Check the input-based consistency ratio and modify the inconsistent ones. In [23], the highest evaluation grades of the best and worst is between 3-9, so a transformation function is applied to transform [0.5,1] to 1-9. The specific expression is:

$$ \begin{array}{@{}rcl@{}} pt=16x-7, x\in [0.5,1] \end{array} $$

(32)

where the x is the priority degree. The transformed numbers and the input-based consistency ratio is shown in Table 4. From the table, it is obvious that the e₄ of C₁, e₁ and e₃ of C₂, e₂ of C₃, e₃ and e₄ of C₄, e₁ of C₅ need modification. With the CRP rules proposed in Section 3.3, the priority degree and the input-based consistency ratio of the revised evaluation information is in Table 5.

Step 5: Solve the optimization model to get the weights. The results are shown in Table 6.

After getting the experts’ weights related to the criteria, the processes of deriving the criteria’ weights are performed.

Stage 2: Decide the weights of criteria.

Get the preference matrices of the 4 experts for the 5 criteria, since they come from different departments, their most and least concerns differ. The best and worst criteria determined by each expert are different. The first expert comes from the technical department, he concerns about the technique most and service takes the least attention. For the second expert from the production department, he thinks the quality is the most favourable criterion and price is the least important one. The third expert thinks the price is the best criterion and the environmental consistences is the worst one. The last expert from environmental department pays most attention to the environment, and least attention to price. The BO vectors and the OW vectors are shown in Table 7. The priority degrees are shown in Table 8. The input-based consistency are checked before the mathematical models are applied to obtain the optimal weights. The transformed information and the input-based consistency ratios are presented in Table 9. Referred to the consistency thresholds for different combinations, we can obtain that the threshold of this case is 0.3062. While the input-based consistency ratios of the three experts are all beyond the thresholds, so the CRP is undertaken.

Table 2 The evaluation information of the experts by the senior manager

Table 3 The priority degree of the experts

Table 4 The transformed information and consistency ratio

Table 5 The priority degree and input-based consistency ratio of the revised evaluation information

Table 6 The weights with regard to the criteria of experts

Table 7 The preference of the criteria

Table 8 The priority degree of the experts’ evaluation information

Table 9 The transformed information and input-consistency ratio

First of all, the inconsistent judgements are found out. For the first expert, it is obvious that the assessment information of C₃ and C₅ needs adjustment. As for e₂, the related information of C₁ and C₄ should be improved. The judgement information of the C₁ of the e₃needs orientation. If the $a^{3}_{B1}$ remains unchanged, the priority degree of $a^{3}_{1W}$ should be less than 3.848 but more than 3.594. If the $a^{3}_{1W}$ stays the same, then the $a^{3}_{B1}$ should be less than 3.928 and more than 3.422. For the e₂, we modify the C₄ first, and when $a^{2}_{B4}$ stays stable, the $a^{2}_{4W}$ should be no more than 4.091 but larger than 3.667. If we modify the $a^{2}_{B4}$, it would be less than 4.025. However, it is less than the $a^{2}_{B1}$, which may cause the change of order. So we choose to adjust $a^{2}_{4W}$. $a^{2}_{B1}$ could turn into 3.595 and more than 1, when $a^{2}_{1W}$ keeps no change. $a^{2}_{1W}$ may be in the range of (4.091,6.433) when $a^{2}_{B1}$ remains invariability. According to the rule 3, the evaluation value of C₃ should be firstly improved. $a^{1}_{3W}$ would be in (1,4.603), at the same time $a^{1}_{B3}$ has no change. $a^{1}_{B3}$ is modulated smaller than 4.148, which is smaller than 6.87, and this scheme is abandoned. For C₅, only adjusting $a^{1}_{B5}$ satisfies the rules, and it would be in (2.05,4.518). The experts modify their assessment information based on the given ranges. The consistent evaluation information is shown in Table 10.

Table 10 The priority degree and input-based consistency ratio of the modified information

After all the evaluation values satisfy the consistent requirement, the optimization models are solved by lingo to obtain the optimal weights, and the results are shown in Table 11.

Table 11 The optimal weights and output-based consistency ratio

In line with (19) and normalization, the final optimal weights of the criteria are W = (0.2244, 0.2562, 0.2514, 0.0500, 0.2180). It is noticeable that the experts pay the most attention to the quality and concerns least on the service. The weights of the experts and criteria have been acquired. The alternative ranking process is undertaken in the following. The 4 experts evaluate the candidates A_l with regard to the criteria C₁ to C₅ and build the PDHFS decision matrices in Table 12.

Table 12 The PDHFS decision matrices for criteria by experts

Step 1: Using the weighted aggregation operators to integrate the individual opinions into group opinions. With the weight vectors of experts, the normalized integrated group decision matrix is shown in Table 13.

Step 2: Calculate the deviation between two alternative suppliers under each criterion based on (24) with the information in Table 13. For convenience, we set the v = 0.5 and 𝜃 = 5 which means the experts pay equivalent attention on the positive and negative judgements, and the sensitivity on negative information is on medium level. The deviation of A_i(i = 1,2,3,4) to A_j(j = 1,2,3,4) about C₁ is:

$$\left[\begin{array}{cccc} 0 & 0.2493&0.1123&0.1609 \\0.2493 & 0&0.3617&0.4102\\0.1123& 0.3617&0&0.0588\\0.1609&0.4102&0.0588&0 \end{array}\right] $$

Step 3: For each criterion, (25) and (26) are used to get the non-inferior intensity of each alternative over the other alternatives. We take the A₁ and A₄ of the criterion C₁ for example. With the priority degree, we can clearly get the degree of a₁₁ which is superior to a₄₁ is 0.6513. The non-inferior intensity of A₁ over A₄ of C₁ is:

$$ \begin{array}{@{}rcl@{}} P_{1}(A_{1},A_{4})&=&f_{1}[p(a_{11}\succ a_{41})]\cdot gd(a_{11}\succ a_{41})\\ &&=f_{1}(0.6513\times 0.1609)=0.1048 \end{array} $$

We still take A_i(i = 1,2,3,4) to A_j(j = 1,2,3,4) about C₁ as an example, the results are:

$$\left[\begin{array}{cccc} 0 & 0.0843&0.0714&0.1048 \\ 0.1650 & 0&0.3220&0.2831\\0.0410& 0.0397&0&0.0303\\0.0561&0.1272&0.0285&0 \end{array}\right]$$

Other non-inferior intensities can be obtained in the same way.

Step 4: Use (27) and (28) to get the non-inferiority and non-superiority indexes. For example, as for the A₂, the non-inferiority index for C₁ is:

$$ \begin{array}{@{}rcl@{}} S_{1}(A_{2})&=&\frac{1}{4}\sum\limits^{4}_{j=1}P_{1}(A_{2},A_{j})\\ &&=\frac{1}{4}(0.1650+0+0.3220+0.2831)=0.1925 \end{array} $$

The associated non-superiority index is:

$$ \begin{array}{@{}rcl@{}} I_{1}(A_{2})&=&\frac{1}{4}\sum\limits^{4}_{j=1}P_{1}(A_{j},A_{2})\\ &&=\frac{1}{4}(0.0843+0+0.0397+0.1272)=0.0628 \end{array} $$

Similarly, the non-inferiority and non-superiority indexes of other suppliers for the criteria are exhibited in the following matrices:

$$ [NI_{i}(A_{l})]_{5\times4}=\left[\begin{array}{cccc} 0.0651 & 0.1925&0.0277&0.0529 \\ 0.0178& 0.1607 & 0.0937& 0.0638\\ 0.0343&0.0304 &0.0223 &0.0246\\ 0.0296& 0.1741 &0.0556& 0.1466\\ 0.2219&0.0432 &0.0384& 0.0926 \end{array}\right]$$

$$[SI_{i}(A_{l})]_{5\times4}=\left[\begin{array}{cccc} 0.0655&0.0628& 0.1055& 0.1045\\ 0.1883& 0.0426 &0.0376& 0.0675\\ 0.0119& 0.0599& 0.0229& 0.0170\\ 0.2064& 0.0364& 0.1268& 0.0364\\ 0.0414& 0.1444& 0.1323& 0.0781 \end{array}\right]$$

Step 5: The WA operator is applied to gather the non-inferiority flows of the suppliers:φ^>(A₁) = 0.2244 × 0.0651 + 0.2562 × 0.0178 + 0.2514 × 0.0343 + 0.0500 × 0.0296 + 0.2180 × 0.2219 = 0.0776φ^>(A₂) = 0.1101, φ^>(A₃) = 0.0469, φ^>(A₄) = 0.0619

The non-superiority flows are: φ^<(A₁) = 0.2244 × 0.0655 + 0.2562 × 0.1883 + 0.2514 × 0.0119 + 0.0500 × 0.2064 + 0.2180 × 0.0414 = 0.0853 φ^<(A₂) = 0.0734, φ^<(A₃) = 0.0742, φ^<(A₄) = 0.0638

Step 6: The net flows of the suppliers are: φ(A₁) = φ^>(A₁) − φ^<(A₁) = − 0.0077, φ(A₂) = 0.0367, φ(A₃) = − 0.0273, φ(A₄) = − 0.0019

So the final ranking of the suppliers is A₂ > A₄ > A₁ > A₃.

From the above computation process, it can be clearly seen that the best supplier is A₂ and the worst choice is the supplier A₃. The results indicate that the PDHF-GBW-SIR method can be conducive for manufacturing industry managers to evaluate and select the proper supplier considering different criteria from the economic, environmental, time and quality aspects.

Table 13 The normalized aggregated PDHFS decision matrix

4.3 Sensitivity analysis

In this part, we conduct the sensitivity analysis to highlight the impact of the parameters α, ν and 𝜃 on the solutions to this case.

• (1) First, we consider the parameter α in the priority degree changes while the others are not changed. In our model, the parameter α shows the different attitude of the experts towards the membership and non-membership in the priority degree. When α= 0.5, it indicates that the experts pay the same attention to both sides. If α ∈ [0,0.5), it means that the experts concern more on non-membership. Furthermore, if α ∈ [0.5,1), it shows that the experts care more about the membership. According to the definition in [37], α changes from 0 to 1 with a step width of 0.1. We can see the variation trend in Fig. 3a. We can see that the ranking of the alternatives does not change except when α ≤ 0.9. A₁ and A₃ exchange their position when α = 1. As the value of α becomes bigger, the value of A₁, A₃ and A₄ tend to increase. On the contrary, as the value of α increase, the value of A₂ shows a trend of decrease.

  Fig. 3

  

  Sensitivity analysis

• (2) For the parameter ν in the general distance measure, it usually changes from 0 to 1 based on the existing study. Therefore, we set 0.1 as the step width and α = 0.5, 𝜃 = 5. Then we can obtain the result in Fig. 3b. The ranking of the alternatives keeps the same in most cases, only when ν < 0.1,A₁ and A₄ exchange. It is obvious that the net flows of the A₂, A₃ and A₄ increase with the growth of ν. However, the net flow of the A₁ goes down as ν goes up.

• (3) For the parameter 𝜃 in the synthetical score function, it is in the range of 1 to 10. We set 1 as the step width and α = 0.5, ν = 0.5. The result is shown in Fig. 3c. It is obvious that the ranking of the alternatives does not change when the value of 𝜃 changes.

Table 14 Results of the PDHF-GBWM, HF-BWM and GBWM

4.4 Comparison and discussion

To aid in further elucidating the advantages of the proposed method, comparison and discussion are provided. This subsection is divided into two parts: The comparison of the PDHF-GBWM with BWM in different information environment and contrast of the PDHF-GSIR with other outranking decision making methods.

4.4.1 Comparison of the PDHFS-GBWM with other weight-determining methods

In this section, the comparative analysis of the PDHF-GBWM, the GBWM [42] and the hesitant fuzzy BWM [31] are provided. And the weights acquired are presented in Table 14. Since the weights of the experts in the GBWM are crisp value, we just normalize and gather the weight matrix to derive a comprehensive weight of each expert, which is ω_e = (0.2065,0.3305,0.2396,0.2233) and the 𝜃 is set as 1 which reflects the model sensitivity. The hesitant fuzzy BWM is a multi-criteria decision making method. To get the final weight of the criteria, the aggregation process is conducted and the weights of experts are the same in the PDHF-GBWM.

It is obvious that the results from different methods vary. In Table 14, CR^O means the output-based consistency ratio. The PDHF-GBWM owns the highest consistency ratio and the GBWM has the lowest consistency ratio.We analyse the computational process and explore the reasons which are summarized from the next perspectives:

• (1) The method we proposed allows more flexibility for the experts to express their attitude on selecting the best and the worst criteria. The traditional GBWM requires the experts to make their judgments on the condition that the best and worst criteria are decided before they provide the preference information, which may contradict their intention. This is a significant factor why the consistency we achieved is higher than the value gotten by the GBWM.

• (2) The weights of experts may be another factor. We occupy the weights of experts related to the criteria, which could show the strengths and weaknesses of the experts. In the aggregation process, the weights united to each evaluation value, reflecting their expertise in the fields of the criteria. However, in the GBWM, the weights of experts appear in the objective function and multiply with the consistency ratio. The integrated experts’ weights can not reflect their real levels in different areas and may affect the final results.

• (3) The differences in original information effect the final results. The PDHFSs contain both the membership and non-membership information with the corresponding probability, while the HF-BWM includes the multiple values that the experts assigned. As for the GBWM, the evaluation is expressed by crisp values, which contain the least information. It is obvious that the more information, the high consistency and the more complex the computing process.

• (4) The CRP contributes to higher consistency. In the GBWM and HF-BWM, the CRP is not conducted.

4.4.2 Compare the PDHFE-SIR with other MCGDM methods

In this part, the comparison with other MCGDM methods, such as the PDHF-TODIM [36], aggregation operator-based MCGDM of the PDHFSs [11], the TOPSIS [20], and the hesitant fuzzy SIR (HF-SIR) [30], is implemented.

With the decision matrix shown in Table 13 and the weights of criteria gained by the PDHF-GBWM, the PDHF-TODIM, the PDHFSs aggregation operator-based MCGDM, TOPSIS, and HF-SIR are conducted. The ranking results are shown in Fig. 4.

Fig. 4

The comparison results of the PDHF-TODIM, PDHF-WA operators, PDHF-GSIR, TOPSIS and HF-SIR methods

The ranking result derived by the PDHF-TODIM is the same as the ranking acquired by the PDHF-GBWM (S₂ > S₄ > S₁ > S₃), which demonstrates the validity of the proposed method. The SIR method provides more options in the aggregation process. However, the result of the aggregation operators-based method, TOPSIS and the HF-SIR has a little distinction of the presented method, the orders of the S₄ and S₁ exchange while the first and last positions are the same. The reason for the differences is that the SIR method calculates the deviation based on the decision matrices but the aggregation operators-based method just integrates the information and finally ranks the alternatives according to the score function. And the information forms also influence the ranks of alternatives.

The PDHF-GBW-SIR method integrates the SIR method and the BWM in the probabilistic dual hesitant information environment to deal with the MCGDM problem. The CRP is designed based on the experts’ strengths and weaknesses as well as the input-based consistency ratio. The PDHF-GBWM contains more preference information and provides a new method to adjust the inconsistent information which also enhances the BWM.

5 Conclusions

In this paper, we have focused on the MCGDM problem under the probabilistic dual hesitant information environment, in which the experts express their opinions in both positive and negative aspects as the membership and non-membership with multiple values and their corresponding probability. We have put forward an extension of the BWM, namely the PDHF-GBWM, on the strength of the PDHFS preference vectors. the PDHF-GBWM has been applied to derive the weights of experts and weights. Considering experts from related fields concentrate more on the solution with respect to the criteria that he/she is familiar with and pay less attention to the unacquainted criteria, we assigned different weights to the experts for each criterion. And the CRP of the PDHF-GBWM has been designed referring to the experts’ weight vectors and the input-based consistency ratio to improve decision efficiency. The PDHF-SIR has been introduced to deal with the ranking of the alternatives based on the decision matrices and general distance measures. An integrated PDHFS-GBW-SIR method was developed to solve the green supplier selection problem. The comparison analyses have been conducted to demonstrate the effectiveness of the PDHF-GBW-SIR method. In the future, we can use the proposed method to solve other practical problems, such as the investment projects selection. Furthermore, It may be feasible to think of related models since not always the information has a probabilistic nature. In particular, we might be faced with non-probabilistic (dual, hesitant and fuzzy) [1, 29, 51] information for which we want to keep track of what elements have been multiply submitted.