1 Introduction

Nowadays, manufacturers have turned out to be extremely worried about environmental issues because of expanded pressure from regulation and public awareness regarding the environment. This implies adjusting economic and environmental exhibitions turned into critical sympathy towards manufacturers (Boiral 2006; Jabbour and Jabbour 2009). They have connected different ways to deal with ecological concepts in the last decade (Shen et al. 2013; Dobos and Vörösmarty 2019; Tseng et al. 2019; Yang et al. 2019).

Green supply chain management (GSCM) focuses on the guarantee of incorporating new manufacturing theory with the possibility to accomplish higher environmental execution (Kuo et al. 2010; Fernando et al. 2019; Liou et al. 2016). Noci (1997) brought up that organizations ought to develop proficient administration conditions and underlined on incorporating the connection amongst customers and suppliers. Organizations could deliver green products together with suppliers as common participation relationship was produced. Besides, in the GSCM, complicated mechanisms were employed to the integration and factory level to appraise or enhance environmental outcomes (Srivastava 2007; Gavronski et al. 2011; Gitinavard et al. 2018). Vachon and Klassen (2006) brought up that through the association amongst suppliers and consumers, manufacturers could build and practice a compelling arrangement programme while confronting environmental challenges.

Green supplier selection problem (GSSP) is regarded as a fundamental segment of a GSCM procedure. Supplier selection in light of environmental factors has pulled in the consideration of numerous researchers. There are numerous studies that have concentrated on GSSPs. For instance, Hsu and Hu (2009) introduced an analytic network process (ANP) for GSSPs in an electronics company. Chen and Lee (2010) built up an IT2F-TOPSIS technique to manage group decision problems. Large and Thomsen (2011) used information from German organizations and found that the level of appraisal and joint effort straightforwardly could impact a company’s performance.

A review by Baskaran et al. (2012) was done on the incorporation of sustainability factors in Indian textile industry. Govindan et al. (2013) investigated sustainable supply chain activities and displayed a fuzzy multicriteria way to deal with a viable model for supplier selection in view of the economic, environmental, and social contemplations. Hashemi et al. (2015) regarded a model for GSCM with the ANP and grey relational analysis (GRA) with an application to the automotive industry. Kannan et al. (2014) concentrated on a five-phase approach to appraising the suppliers in the GSCM by fuzzy TOPSIS technique. Kuo et al. (2015) provided MCDM approach to deal with the assessment of the carbon execution of suppliers in a green chain network utilizing the fuzzy ANP and fuzzy TOPSIS techniques.

Awasthi and Govindan (2016) considered the evaluation problem of green supplier development programmes by NGT and VIKOR techniques with fuzzy conditions. Keshavarz-Ghorabaee et al. (2017a) reviewed MCDM techniques for the GSSPs under fuzzy conditions. Govindan et al. (2017) presented a decision approach by PROMETHEE and compromise ranking methods within the GDM for GSSPs in food supply chain. Yazdani et al. (2017) introduced an approach for taking account of inter-relationships between the customer requirements, building a relationship structure and assessing candidate suppliers for the GSSPs by DEMATEL, QFD and COPRAS. Gavareshki et al. (2017) developed an integrated approach by interpretive structural modelling, fuzzy MICMAC analysis, AHP and VIKOR to handle GSSPs.

Jiang et al. (2018) regarded a variant of DANP, named grey DANP, for solving the GSSPs by providing a case study to illustrate its expediency. Chatterjee et al. (2018) proposed rough DEMATEL, ANP, and MAIRCA methods for GSSPs and implemented GSCM in electronics industry. Zhu and Li (2018) provided a hybrid framework for GSSPs under the hesitant fuzzy linguistic environment via group decision making. Wang et al. (2018) considered models for GSSPs with some 2-tuple linguistic neutrosophic operators. Wan et al. (2018) dealt with GSSPs by Pythagorean fuzzy sets via extending an uncertain mathematical programming method. Banaeian et al. (2018) presented a green supplier evaluation model that considered the fuse of fuzzy sets into TOPSIS, VIKOR and GRA strategies in agri-food industry.

The literature on the GSSPs shows that this problem is the MAGDM framework for the supply chain networks and is regarded as a new research area. In practice, several evaluation factors or criteria can influence the appraisements. This research presents a novel coordinated approach in view of weighted aggregated assessment and ranking strategies, to manage MAGDM problems in the GSCM with interval type-2 fuzzy sets (IT2FSs). This approach depends on administrators of interval type-2 trapezoidal fuzzy sets (IT2TrFSs), a few alterations in traditional compromise solution techniques, and another strategy for computations of criteria weights. For the criteria weights, this research consolidates the subjective weights communicated by decision makers (DMs) with objective weights that came about because of entropy technique to get more realistic weights. To illustrate the pertinence of proposed model in real MAGDM issues, a green supplier selection is utilized. The IT2FSs approach along with statistical concepts (SCs) ought to be more fitting and powerful than conventional decision-making methods, and proposed model can be effectively utilized as a part of the different application areas of MAGDM in the GSCM.

Major innovations of this research for GSSP in supply chain networks are as follows:

  1. 1.

    A new MAGDM model is proposed under IT2TrFNs by some possibilistic mean (PM) and possibilistic standard deviation (PSD) metrics.

  2. 2.

    New relations are presented to take ideal solutions with possibilistic statistical (PS) information with IT2TrFNs.

  3. 3.

    A new PM and PSD entropy method is extended for the weights of factors by PS concepts.

  4. 4.

    A new weighting method of experts within a group decision-making (GDM) process is developed by some PS metrics.

  5. 5.

    A new ranking process based on relative-closeness coefficients is presented to rank all candidates with IT2TrFNs.

Finally, this research presents an illustrative example in supply chain networks from the recent literature to regard the green supplier candidates by the proposed model along with the comparison to a recent decision method.

The remainder of the research is organized as below. Section 2 provides definitions for IT2TrFNs and PS approach. Presented approach is described in Sect. 3 for handling the GSSP. In Sect. 4 of this research, the presented model is discussed with an application example. Conclusions are given in Sect. 5.

2 Preliminary knowledge of IT2TrFNs

A trapezoidal IT2FS is demonstrated as \( \tilde{A}_{1} = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) = \left( {\left( {a_{11}^{U} ,a_{12}^{U} ,a_{13}^{U} ,a_{14}^{U} ;h_{1}^{U} } \right),\left( {a_{11}^{L} ,a_{12}^{L} ,a_{13}^{L} ,a_{14}^{L} ;h_{1}^{L} } \right)} \right) \) and \( \tilde{A}_{2} = \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) = \left( {\left( {a_{21}^{U} ,a_{22}^{U} ,a_{23}^{U} ,a_{24}^{U} ;h_{2}^{U} } \right),\left( {a_{21}^{L} ,a_{22}^{L} ,a_{23}^{L} ,a_{24}^{L} ;h_{2}^{L} } \right)} \right) \) where \( \tilde{A}_{i}^{L} \) and \( \tilde{A}_{i}^{U} \) are indeed type-1 fuzzy sets. \( a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ,a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} \text{and } a_{i4}^{L} \) can be reference points of IVT2FS \( \tilde{A}_{i} \)\( H\left( {\tilde{A}_{i} } \right) \) regarded as a membership value. An IT2TrFN is presented in Fig. 1.

Fig. 1
figure 1

Interval type-2 trapezoidal fuzzy number (Baležentis and Zeng 2013)

Full size image

Basic algebraic operations of IT2TrFNs are as follows (Mendel 2001; 2007; Baležentis and Zeng 2013):

$$ \tilde{A}_{1} = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) = \left( {\left( {a_{11}^{U} ,a_{12}^{U} ,a_{13}^{U} ,a_{14}^{U} ;h_{1}^{U} } \right),\left( {a_{11}^{L} ,a_{12}^{L} ,a_{13}^{L} ,a_{14}^{L} ;h_{1}^{L} } \right)} \right) $$
(1)
$$ \tilde{A}_{2} = \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) = \left( {\left( {a_{21}^{U} ,a_{22}^{U} ,a_{23}^{U} ,a_{24}^{U} ;h_{2}^{U} } \right),\left( {a_{21}^{L} ,a_{22}^{L} ,a_{23}^{L} ,a_{24}^{L} ;h_{2}^{L} } \right)} \right) $$
(2)

Definition 2.1

Addition operation:

$$ \begin{aligned} \tilde{A}_{1} \oplus \tilde{A}_{2} & = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \oplus \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ & = \left( {\left( {a_{11}^{U} + a_{21}^{U} ,a_{12}^{U} + a_{22}^{U} ,a_{13}^{U} + a_{23}^{U} ,a_{14}^{U} + a_{24}^{U} ;{ \hbox{min} }\left( {h_{1}^{U} ,h_{2}^{U} } \right)} \right),} \right. \\ & \quad \left. {a_{11}^{L} + a_{21}^{L} ,a_{12}^{L} + a_{22}^{L} ,a_{13}^{L} + a_{23}^{L} ,a_{14}^{L} + a_{24}^{L} ;\hbox{min} \left( {h_{1}^{L} ,h_{2}^{L} } \right)} \right) \\ \end{aligned} $$
(3)

Definition 2.2

Multiplication operation:

$$ \begin{aligned} \tilde{A}_{1} \otimes \tilde{A}_{2} & \approx \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \otimes \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ & = \left( {\left( {a_{11}^{U} \times a_{21}^{U} ,a_{12}^{U} \times a_{22}^{U} ,a_{13}^{U} \times a_{23}^{U} ,a_{14}^{U} \times a_{24}^{U} ;{ \hbox{min} }\left( {h_{1}^{U} ,h_{2}^{U} } \right)} \right),} \right. \\ & \quad \left. {a_{11}^{L} \times a_{21}^{L} ,a_{12}^{L} \times a_{22}^{L} ,a_{13}^{L} \times a_{23}^{L} ,a_{14}^{L} \times a_{24}^{L} ;\hbox{min} \left( {h_{1}^{L} ,h_{2}^{L} } \right)} \right) \\ \end{aligned} $$
(4)

Definition 2.3

Multiplication with a scalar \( \lambda \)≥ 0:

$$ \begin{aligned} \lambda \cdot \tilde{A}_{1} & = \lambda \cdot \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) = \left( {\left( {\lambda \cdot a_{11}^{U} ,\lambda \cdot a_{12}^{U} ,\lambda \cdot a_{13}^{U} ,\lambda \cdot a_{14}^{U} ;h_{1}^{U} } \right), \left( {\lambda \cdot a_{11}^{L} ,\lambda \cdot a_{12}^{L} ,\lambda \cdot a_{13}^{L} ,\lambda \cdot a_{14}^{L} ;h_{1}^{L} } \right)} \right) \\ \end{aligned} $$
(5)

Definition 2.4

PM value of IT2TrFN is (Gong et al. 2017):

$$ \begin{aligned} M\left( {\tilde{A} } \right) & = \frac{{\left( {h^{U} } \right)^{2} }}{24}\left( {a_{1}^{U} + 5a_{2}^{U} + 5a_{3}^{U} + a_{4}^{U} } \right) \\ & \quad + \frac{{\left( {h^{L} } \right)^{2} }}{24}\left( {a_{1}^{L} + 5a_{2}^{L} + 5a_{3}^{L} + a_{4}^{L} } \right) \\ \end{aligned} $$
(6)

Definition 2.5

Possibilistic variance value of IT2TrFN is (Gong et al. 2017):

$$ \begin{aligned} {\text{var}}\left( {\tilde{A}} \right) & = \frac{{\left( {{\fancyscript{m}}^{U} } \right)^{2} + 6{\fancyscript{m}}^{U} {\fancyscript{n}}^{U} + 17\left( {{\fancyscript{n}}^{U} } \right)^{2} }}{48}\left( {h^{U} } \right)^{2} \\ & \quad + \;\frac{{\left( {{\fancyscript{m}}^{L} } \right)^{2} + 6{\fancyscript{m}}^{L} {\fancyscript{n}}^{U} + 17\left( {{\fancyscript{n}}^{L} } \right)^{2} }}{48}\left( {h^{L} } \right)^{2} \\ \end{aligned} $$
(7)

where \( {\fancyscript{m}}^{U} = a_{4}^{U} - a_{1}^{U} \), \( {\fancyscript{m}}^{L} = a_{4}^{L} - a_{1}^{L} \), \( {\fancyscript{n}}^{U} = a_{3}^{U} - a_{2}^{U} \) and \( {\fancyscript{n}}^{L} = a_{3}^{L} - a_{2}^{L} \).

The standard deviation of \( \tilde{A} \) is defined by:

$$ {\text{SD}}_{{\tilde{A}}} = \sqrt {{\text{var}}\left( {\tilde{A}} \right)} $$
(8)

3 Proposed selection approach

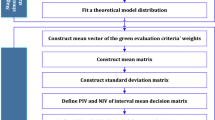
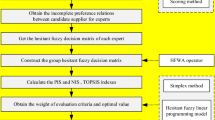
To make the model more understandable, this research illustrates a framework demonstrated in Fig. 2. As can be seen, the proposed model has 12 main steps. In step 1, identifying the proper criteria to select the green supplier is the primary purpose. Then, the decision matrices are formed based on the DMs in step 2. Each DM’s opinion on each alternative according to each attribute may vary according to his/her personality (e.g., Dorfeshan et al. 2019; Ebrahimnejad et al. 2012; Vahdani et al. 2013). Linguistic terms are assigned to their preferences into IT2TrFNs which are widely and commonly used in the related literature (e.g., Qin et al. 2017; Keshavarz-Ghorabaee et al. 2016, 2017a, b; Haghighi et al. 2019; Mohagheghi et al. 2019; Eshghi et al. 2019). In step 3, the IT2TrF-decision matrices transformed into normalized IT2TrF-decision matrices based on the principle criteria category, benefit or cost (Qin et al. 2017). For instance, if the neutral DM expresses his/her opinion about a benefit criterion very poor (VP), the opinion can be regarded as very good (VG) on the complementary linguistic variable for a cost criterion. Calculating the importance weight of criteria is extended based on a new PM and PSD entropy method in steps 4 and 5. Aggregating the DMs’ opinions regarding weights of criteria which is obtained in two previous steps is the aim in step 6. PIV and NIV of PM and PSD for the GSSP are defined in step 7. It can be comprehending the distance between PIV and NIV from DMs by computing separation measures according to steps 8 and 9. Respectively, steps 10 and 11 present a novel idea for calculating and computing relative coefficient degrees and closeness coefficient. In the end, step 12 will rank the green supplier towards the decreasing scores.

Fig. 2
figure 2

Flowchart of new presented group decision approach

Full size image

A new interval type-2 trapezoidal fuzzy decision model for solving the GSSP is introduced. We assume:

  • \( DM = \left\{ {\left. {DM^{\fancyscript{s}} } \right|{\fancyscript{s}} = 1, \ldots ,\fancyscript{p}} \right\} \): a set of experts

  • \( {\mathcal{A}} = \left\{ {\left. {{\mathcal{A}}_{i} } \right|i = 1, \ldots ,\fancyscript{q}} \right\} \): a set of alternatives

  • \( {\mathcal{O}} = \left\{ {\left. {{\mathcal{O}}_{j} } \right|j = 1, \ldots ,\fancyscript{t}} \right\} \): a set of selection attributes

The GSSP with IT2TrFNs, GDM, and SCs provided by DMs is presented below:

(9)

where IT2TrFNs \( \tilde{X}_{\fancyscript{s}} \) and \( \left( {\left( {\tilde{X}_{ij}^{\fancyscript{s}} } \right)^{U} ,\left( {\tilde{X}_{ij}^{\fancyscript{s}} } \right)^{L} } \right) = \left( {\left( {\left( {x_{ij}^{\fancyscript{s}} } \right)_{1}^{U} ,\left( {x_{ij}^{\fancyscript{s}} } \right)_{2}^{U} ,\left( {x_{ij}^{\fancyscript{s}} } \right)_{3}^{U} ,\left( {x_{ij}^{\fancyscript{s}} } \right)_{4}^{U} ;\left( {h_{ij}^{\fancyscript{s}} } \right)U} \right),\,\left( {\left( {x_{ij}^{\fancyscript{s}} } \right)_{1}^{L} ,\,\left( {x_{ij}^{\fancyscript{s}} } \right)_{2}^{L} ,\left( {x_{ij}^{\fancyscript{s}} } \right)_{3}^{L} ,\left( {x_{ij}^{\fancyscript{s}} } \right)_{4}^{L} ;\left( {h_{ij}^{\fancyscript{s}} } \right)^{L} } \right)} \right) \)

  • Step 1 Regard attributes for the GSSP.

  • Step 2 Consider IT2TrF-decision matrices of green supplier alternatives for each DM.

  • Step 3 Convert IT2TrF-matrix into a normalized matrix.

We have:

$$ \begin{aligned} & \left( {\left( {\tilde{N}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{N}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\left( {\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right), } \hfill & {\quad {\text{for benefit criteria }}C_{j} \in \varOmega_{\text{benefit}} } \hfill \\ {\left( {\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{c} ,} \hfill & {\quad {\text{for cost criteria }}C_{j} \in \varOmega_{\text{cost}} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(10)

where \( \left( {\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{c} \) is the complement of \( \left( {\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{X}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right) \). Then, we form the normalized decision matrix \( \tilde{N}_{k} \) according to (Qin et al. 2017); \( \varOmega_{\text{benefit}} \) and \( \varOmega_{\text{cost}} \) are regarded as sets of benefit and cost attributes, respectively.

$$ \tilde{N}_{{\fancyscript{s}}} = \left[ {\left( {\left( {\tilde{N}_{ij}^{{\fancyscript{s}}} } \right)^{U} ,\left( {\tilde{N}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)} \right]_{{\fancyscript{q} \times \fancyscript{t}}} $$
(11)

Step 4 Determine weights of criteria with PM and PSD entropy measures.

Step 4.1 To determine assessment criteria’ weights, build PM and PSD matrixes of IT2TrFNs \( \tilde{N}^{{\fancyscript{s}}} , \) respectively, according to Definitions 2.4 and 2.5.

$$ \begin{aligned} \bar{\fancyscript{m}}_{ij}^{{\fancyscript{s}}} & = \left( {\frac{{\left( {\left( {h_{ij}^{{\fancyscript{s}}} } \right)^{U} } \right)^{2} }}{24}\left( {\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{1}^{U} + 5\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{2}^{U} + 5\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{3}^{U} + \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{4}^{U} } \right)} \right. \\ & \quad \left. { + \frac{{\left( {\left( {h_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{2} }}{24}\left( {\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{1}^{L} + 5\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{2}^{L} + 5\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{3}^{L} + \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{4}^{L} } \right), \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p}} \right) \\ \end{aligned} $$
(12)

We have:

$$ \begin{aligned} \bar{M}_{{\fancyscript{s}}} & = \left[ {\bar{\fancyscript{m}}_{ij}^{{\fancyscript{s}}} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}l} {\bar{\fancyscript{m}}_{11}^{{\fancyscript{s}}} } \hfill & {\bar{\fancyscript{m}}_{12}^{{\fancyscript{s}}} } \hfill & \cdots \hfill & {\bar{\fancyscript{m}}_{1t}^{{\fancyscript{s}}} } \hfill \\ {\bar{\fancyscript{m}}_{21}^{{\fancyscript{s}}} } \hfill & {\bar{\fancyscript{m}}_{22}^{{\fancyscript{s}}} } \hfill & \cdots \hfill & {\bar{\fancyscript{m}}_{2t}^{{\fancyscript{s}}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\bar{\fancyscript{m}}_{q1}^{{\fancyscript{s}}} } \hfill & {\bar{\fancyscript{m}}_{q2}^{{\fancyscript{s}}} } \hfill & \cdots \hfill & {\bar{\fancyscript{m}}_{qt}^{{\fancyscript{s}}} } \hfill \\ \end{array} } \right],\quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} \\ \end{aligned} $$
(13)

and

$$ \overline{sd}_{ij}^{{\fancyscript{s}}} = \sqrt {\left( {\frac{{\left( {\left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)^{U} } \right)^{2} + 6\left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)^{U} \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)^{U} + 17\left( {\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)^{U} } \right)^{2} }}{48}\left( {\left( {h_{ij}^{{\fancyscript{s}}} } \right)U} \right)^{2} + \frac{{\left( {\left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{2} + 6\left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)^{L} \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)L + 17\left( {\left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{2} }}{48}\left( {\left( {h_{ij}^{{\fancyscript{s}}} } \right)^{L} } \right)^{2} } \right)} , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(14)

where \( \left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)_{ij}^{U} = \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{4}^{U} - \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{1}^{U} \), \( \left( {\fancyscript{m}_{ij}^{{\fancyscript{s}}} } \right)^{L} = \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{4}^{L} - \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{1}^{L} \), \( \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)^{U} = \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{3}^{U} - \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{2}^{U} \) and \( \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)^{L} = \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{3}^{L} - \left( {\fancyscript{n}_{ij}^{{\fancyscript{s}}} } \right)_{2}^{L} \).

We have:

$$ \begin{aligned} \overline{SD}_{{\fancyscript{s}}} & = \left[ {\overline{sd}_{ij}^{{\fancyscript{s}}} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {\overline{sd}_{11}^{{\fancyscript{s}}} } & {\overline{sd}_{12}^{{\fancyscript{s}}} } & \cdots & {\overline{sd}_{{1\fancyscript{t}}}^{{\fancyscript{s}}} } \\ {\overline{sd}_{21}^{{\fancyscript{s}}} } & {\overline{sd}_{22}^{{\fancyscript{s}}} } & \cdots & {\overline{sd}_{{2\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \vdots & \vdots & \ddots & \vdots \\ {\overline{sd}_{{\fancyscript{q}1}}^{{\fancyscript{s}}} } & {\overline{sd}_{{\fancyscript{q}2}}^{{\fancyscript{s}}} } & \cdots & {\overline{sd}_{{\fancyscript{q}\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \end{array} } \right], \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} \\ \end{aligned} $$
(15)

Step 4.1.1 Calculate PM and PSD entropy of each assessment attribute (Foroozesh and Tavakkoli-Moghaddam 2018).

$$ E\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} = - \frac{1}{{Ln\left( {\fancyscript{q}} \right)}}\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \overline{\fancyscript{m}}_{ij}^{{\fancyscript{s}}} Ln\left( {\overline{\fancyscript{m}}_{ij}^{{\fancyscript{s}}} } \right) , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(16)

and

$$ E\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} = - \frac{1}{{Ln\left( {\fancyscript{q}} \right)}}\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \overline{sd}_{ij}^{{\fancyscript{s}}} Ln\left( {\overline{sd}_{ij}^{{\fancyscript{s}}} } \right), \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(17)

Step 4.1.2 Determine modified entropy importance by PM and PSD.

$$ D\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} = 1 - E\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} ,\quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(18)

and

$$ D\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} = 1 - E\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(19)

Step 4.1.3 Determine weights of criteria based on PM and PSD.

$$ W\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} = \frac{{D\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} }}{{\mathop \sum \nolimits_{j = 1}^{n} D\left( {\overline{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} }} ,\quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(20)

and

$$ W\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} = \frac{{D\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} }}{{\mathop \sum \nolimits_{j = 1}^{n} D\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} }} , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{q} $$
(21)

Step 4.2 Aggregate weights of criteria based on PM and PSD obtained from step 4.1.3.

$$ W\left( {\text{Total}} \right)_{j}^{{\fancyscript{s}}} = \gamma \times W\left( {\bar{\fancyscript{m}}} \right)_{j}^{{\fancyscript{s}}} + \left( {1 - \gamma } \right) \times W\left( {\overline{sd} } \right)_{j}^{{\fancyscript{s}}} $$
(22)

Step 5 Determine proposed extended weights of supply chain DMs or experts.

Step 5.1 For PM and PSD matrixes of each expert by some importance of assessment criteria based on Eqs. (18) to (20), weighted normalized decision matrixes are built as:

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} & = W\left( {\text{Total}} \right)_{j}^{{\fancyscript{s}}} \times \overline{M}_{{\fancyscript{s}}} \\ {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} & = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{11}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{12}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{1\fancyscript{t}}}^{{\fancyscript{s}}} } \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{21}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{22}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{2\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}1}}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}2}}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \end{array} } \right],\quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} \\ \end{aligned} $$
(23)

and

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}} & = W\left( {\text{Total}} \right)_{j}^{{\fancyscript{s}}} \times \overline{SD}_{{\fancyscript{s}}} \\ {\mathcal{G}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}} & = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{sd} } \right)_{11}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{12}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{1\fancyscript{t}}}^{{\fancyscript{s}}} } \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{21}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{22}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{2\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}1}}^{{\fancyscript{s}}} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}2}}^{{\fancyscript{s}}} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}\fancyscript{t}}}^{{\fancyscript{s}}} } \\ \end{array} } \right],\quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} \\ \end{aligned} $$
(24)

Step 5.1.1 Obtain an average of group decision matrix based on a new extension of the literature (Yue 2011, 2013) under an interval type-2 trapezoidal fuzzy statistical environment; the best results of group deciding ought to be the typical matrix of a group decision. In other words, a DM is a higher decision level as a result of his/her opinion is nearer to the average:

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)^{*} & = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{*} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{11}^{*} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{12}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{1\fancyscript{t}}}^{*} } \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{21}^{*} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{22}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{2\fancyscript{t}}}^{*} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}1}}^{*} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}2}}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}\fancyscript{t}}}^{*} } \\ \end{array} } \right] \\ \end{aligned} $$
(25)

and

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{sd} } \right)^{*} & = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{*} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{sd} } \right)_{11}^{*} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{12}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{1\fancyscript{t}}}^{*} } \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{21}^{*} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{22}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{2\fancyscript{t}}}^{*} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}1}}^{*} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}2}}^{*} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}\fancyscript{t}}}^{*} } \\ \end{array} } \right] \\ \end{aligned} $$
(26)

where \( {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{*} = \frac{1}{{\fancyscript{p}}}\mathop \sum \nolimits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} \); \( {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)^{*} = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{*} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) and \( {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{*} = \frac{1}{{\fancyscript{p}}}\mathop \sum \nolimits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} \); \( {\mathcal{G}}\left( {\overline{sd} } \right)^{*} = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{*} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) are denoted as the PIS of experts.

Step 5.1.2 Worst outcome of GDM is the outcome of maximum separation from left negative ideal decision (L-NID) (Yue 2011, 2013).

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{l} & = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{l} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{11}^{l} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{12}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{1\fancyscript{t}}}^{l} } \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{21}^{l} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{22}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{2\fancyscript{t}}}^{l} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}1}}^{l} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}2}}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}\fancyscript{t}}}^{l} } \\ \end{array} } \right] \\ \end{aligned} $$
(27)

and

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{sd} } \right)_{l} & = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{l} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{sd} } \right)_{11}^{l} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{12}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{1\fancyscript{t}}}^{l} } \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{21}^{l} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{22}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{2\fancyscript{t}}}^{l} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}1}}^{l} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}2}}^{l} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}\fancyscript{t}}}^{l} } \\ \end{array} } \right] \\ \end{aligned} $$
(28)

where \( {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{l} = \mathop {\hbox{min} }\limits_{{1 \le \fancyscript{s} \le \fancyscript{p}}} \left\{ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} } \right\} \); \( {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{l} = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{l} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) and \( {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{l} = \mathop {\hbox{min} }\limits_{{1 \le \fancyscript{s} \le \fancyscript{q}}} \left\{ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} } \right\} \); \( {\mathcal{G}}\left( {\overline{sd} } \right)_{l} = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{l} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) are denoted as the NID of experts.

Step 5.1.3 Worst outcome of GDM is the outcome of maximum separation from right negative ideal decision (R-NID) (Yue 2011, 2013).

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{r} & = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{r} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{11}^{r} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{12}^{r} } & \cdots & {{\fancyscript{g}}\left( {\fancyscript{m}} \right)_{{1\fancyscript{t}}}^{r} } \\ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{21}^{r} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{22}^{r} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{2\fancyscript{t}}}^{r} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left({\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}1}}^{r} } & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}2}}^{r} } & \cdots & {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{q}\fancyscript{t}}}^{r} } \\ \end{array} } \right] \\ \end{aligned} $$
(29)

and

$$ \begin{aligned} {\mathcal{G}}\left( {\overline{sd} } \right)_{r} & = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{r} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \\ & = \left[ {\begin{array}{*{20}c} {{\fancyscript{g}}\left( {\overline{sd} } \right)_{11}^{r} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{12}^{r} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{1\fancyscript{t}}}^{r} } \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{21}^{r} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{22}^{r} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{2\fancyscript{t}}}^{r} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}1}}^{r} } & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}2}}^{r} } & \cdots & {{\fancyscript{g}}\left( {\overline{sd} } \right)_{{\fancyscript{q}\fancyscript{t}}}^{r} } \\ \end{array} } \right] \\ \end{aligned} $$
(30)

where \( {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{r} = \mathop {\hbox{max} }\limits_{{1 \le \fancyscript{s} \le \fancyscript{p}}} \left\{ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} } \right\} \); \( {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)_{r} = \left[ {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{r} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) and \( {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{r} = \mathop {\hbox{max} }\limits_{{1 \le \fancyscript{s} \le \fancyscript{p}}} \left\{ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} } \right\} \); \( {\mathcal{G}}\left( {\overline{sd} } \right)_{r} = \left[ {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{r} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} \) are denoted as the NID of experts.

Step 5.1.4 Determine separations of an expert in terms of ideal decision.

$$ {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{*} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{*} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(31)

and

$$ {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{*} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{*} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(32)

Similarity, the separations from the NIS are given as:

$$ {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{l} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{l} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(33)

and

$$ {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{l} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{l} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(34)
$$ {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{r} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{\fancyscript{m}}} \right)_{ij}^{r} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(35)

and

$$ {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{r} = \sqrt {\mathop \sum \limits_{i = 1}^{{\fancyscript{q}}} \mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {{\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{{\fancyscript{s}}} - {\fancyscript{g}}\left( {\overline{sd} } \right)_{ij}^{r} } \right)^{2} } , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(36)

Step 5.1.5 Compute relative closeness of each expert via \( {\mathcal{G}}\left( {\overline{\fancyscript{m}}} \right)^{*} \) by:

$$ {\mathcal{C}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} = \frac{{{\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{l} + {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{r} }}{{{\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{*} + {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{l} + {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{r} }} , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(37)

and

$$ {\mathcal{C}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}} = \frac{{{\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{l} + {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{r} }}{{{\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{*} + {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{l} + {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{r} }} , \quad \fancyscript{s} = 1, \ldots ,\fancyscript{p} $$
(38)

Since \( {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{l} \ge 0 \), \( {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{r} \ge 0 \), \( {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\overline{{\fancyscript{s}}} }}^{*} \ge 0 \)\( {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{l} \ge 0 \), \( {\mathcal{S}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}}^{r} \ge 0 \), \( {\mathcal{S}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}}^{*} \ge 0 \) and \( {\mathcal{S}}\left( {\overline{d}} \right)_{{\fancyscript{s}}}^{*} \ge 0 \), then, clearly, \( {\mathcal{C}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} \in \left[ {0,1} \right] \) and \( {\mathcal{C}}\left( {\overline{d}} \right)_{{\fancyscript{s}}} \in \left[ {0,1} \right] \) for all \( \fancyscript{s} \).

Step 5.1.6 Provide a ranking order of experts and choose the suitable one.

$$ \vartheta \left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} = \frac{{{\mathcal{C}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} }}{{\mathop \sum \nolimits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} {\mathcal{C}}\left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} }} ,\quad \forall \fancyscript{s} $$
(39)

and

$$ \vartheta \left( {\overline{sd} } \right)_{{\fancyscript{s}}} = \frac{{{\mathcal{C}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}} }}{{\mathop \sum \nolimits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} {\mathcal{C}}\left( {\overline{sd} } \right)_{{\fancyscript{s}}} }} ,\quad \forall \fancyscript{s} $$
(40)

Denoted weight of \( \fancyscript{s} \) th expert; \( \vartheta \left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} \ge 0, \vartheta \left( {\overline{sd} } \right)_{{\fancyscript{s}}} \ge 0 \) and \( \mathop \sum \limits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} \vartheta \left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} = 1, \mathop \sum \limits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} \vartheta \left( {\overline{sd} } \right)_{{\fancyscript{s}}} = 1 \).

Step 5.2 Aggregate weights of criteria based on PM and PSD obtained from step 5.1.6.

$$ \vartheta \left( {\text{Total}} \right)_{{\fancyscript{s}}} = \varphi \times \vartheta \left( {\overline{\fancyscript{m}}} \right)_{{\fancyscript{s}}} + \left( {1 - \varphi } \right) \times \vartheta \left( {\overline{sd} } \right)_{{\fancyscript{s}}} $$
(41)

Step 6 For the supply chain DMs’ weight vector \( \vartheta \left( {\text{Total}} \right) = \left( {\vartheta \left( {\text{Total}} \right)_{1} ,\vartheta \left( {\text{Total}} \right)_{2} , \ldots ,\vartheta \left( {\text{Total}} \right)_{{\fancyscript{s}}} } \right)^{\text{T}} \) by Eq. (39), PM and PSD decision matrices (step 5.2). are combined into a collective matrix by:

$$ \overline{M}\prime = \left[ {\overline{\fancyscript{m}}_{ij}^{\prime} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\left( {\frac{1}{{\fancyscript{p}}}\mathop \sum \limits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} \vartheta \left( {\text{Total}} \right)_{{\fancyscript{s}}} \times {\overline{\fancyscript{m}}}_{ij}^{{\fancyscript{s}}} } \right)} \right]_{{\fancyscript{q} \times \fancyscript{t}}} $$
(42)

and

$$ \overline{SD} \prime = \left[ {\overline{sd}_{ij}^{\prime} } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\left( {\frac{1}{{\fancyscript{p}}}\mathop \sum \limits_{{\fancyscript{s} = 1}}^{{\fancyscript{p}}} \vartheta \left( {\text{Total}} \right)_{{\fancyscript{s}}} \times \overline{sd}_{ij}^{{\fancyscript{s}}} } \right)} \right]_{{\fancyscript{q} \times \fancyscript{t}}} $$
(43)

PM and PSD matrixes are built for the GSSP as:

$$ \overline{M}^{\prime } = \left[ {\overline{\fancyscript{m}}_{ij}^{\prime } } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\begin{array}{*{20}c} {\overline{\fancyscript{m}}_{11}^{{^{\prime} }} } & {\overline{\fancyscript{m}}_{12}^{\prime} } & \cdots & {\overline{\fancyscript{m}}_{{1\fancyscript{t}}}^{\prime} } \\ {\overline{\fancyscript{m}}_{21}^{\prime} } & {\overline{\fancyscript{m}}_{22}^{\prime} } & \cdots & {\overline{\fancyscript{m}}_{{\fancyscript{t}}}^{\prime} } \\ \vdots & \vdots & \ddots & \vdots \\ {\overline{\fancyscript{m}}_{{\fancyscript{q}1}}^{\prime} } &{\overline{\fancyscript{m}}_{{\fancyscript{q}2}}^{\prime} } & \cdots & {\overline{\fancyscript{m}}_{{\fancyscript{q}\fancyscript{t}}}^{\prime} } \\ \end{array} } \right] $$
(44)

and

$$ \overline{SD}^{\prime } = \left[ {\overline{sd}_{ij}^{\prime } } \right]_{{\fancyscript{q} \times \fancyscript{t}}} = \left[ {\begin{array}{*{20}c} {\overline{sd}_{11}^{{^{\prime} }} } & {\overline{sd}_{12}^{\prime} } & \cdots & {\overline{sd}_{{1\fancyscript{t}}}^{\prime} } \\ {\fancyscript{m}_{21}^{\prime} } & {\fancyscript{m}_{22}^{\prime} } & \cdots & {\overline{sd}_{{\fancyscript{t}}}^{\prime} } \\ \vdots & \vdots & \ddots & \vdots \\ {\overline{sd}_{{\fancyscript{q}1}}^{\prime} } & {\overline{sd}_{{\fancyscript{q}2}}^{\prime} } & \cdots & {\overline{sd}_{{\fancyscript{q}\fancyscript{t}}}^{\prime} } \\ \end{array} } \right] $$
(45)

Step 7 Regard positive-ideal and negative-ideal vectors (PIV and NIV) of PM and PSD for the GSSP.

$$ \overline{M}_{j}^{\prime*} = \left\{ {\overline{M}_{1}^{\prime*} , \overline{M}_{2}^{\prime*} , \ldots ,\overline{M}_{{\fancyscript{t}}}^{\prime*} } \right\} = \left\{ {\left. {\mathop {\hbox{max} }\limits_{i} {\overline{\fancyscript{m}}}_{ij}^{\prime}} \right|i = 1,2, \ldots ,\fancyscript{q}} \right\} $$
(46)
$$ \overline{M}_{j}^{\prime - } = \left\{ {\overline{M}_{1}^{\prime - } , \overline{M}_{2}^{\prime - } , \ldots ,\overline{M}_{{\fancyscript{t}}}^{\prime - } } \right\} = \left\{ {\left. {\mathop {\hbox{min} }\limits_{i} {\overline{\fancyscript{m}}}_{ij}^{\prime}} \right|i = 1,2, \ldots ,\fancyscript{q}} \right\} $$
(47)
$$ \overline{Sd}_{j}^{\prime*} = \left\{ {\overline{Sd}_{1}^{\prime*} , \overline{Sd}_{2}^{\prime*} , \ldots ,\bar{M}_{{\fancyscript{t}}}^{\prime*} } \right\} = \left\{ {\left. {\mathop {\hbox{max} }\limits_{i} \fancyscript{m}_{ij}^{\prime} } \right|i = 1,2, \ldots ,\fancyscript{q}} \right\} $$
(48)

and

$$ \overline{Sd}_{j}^{\prime - } = \left\{ {\overline{Sd}_{1}^{\prime - } , \overline{Sd}_{2}^{\prime - } , \ldots ,\overline{Sd}_{{\fancyscript{t}}}^{\prime - } } \right\} = \left\{ {\left. {\mathop {\hbox{min} }\limits_{i} \overline{Sd}_{ij}^{\prime}} \right|i = 1,2, \ldots ,\fancyscript{q}} \right\} $$
(49)

Step 8 Calculate separation measures of candidate via the PM and PSD from the PIV (\( \bar{M}_{j}^{\prime*} \) and \( \overline{Sd}_{j}^{\prime *} \)), respectively.

$$ {\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime*} } \right) = \sqrt {\mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {\left( {m_{j}^{\prime *} } \right) - {\overline{\fancyscript{m}}}_{ij}^{\prime} } \right)^{2} } $$
(50)
$$ {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime*} } \right) = \sqrt {\mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {\left( {Sd_{j}^{\prime*} } \right) - \overline{Sd}_{ij}^{\prime} } \right)^{2} } $$
(51)

Step 9 Calculate separation measures of candidate via the PM and PSD from the NIV (\( \overline{M}_{j}^{\prime - } \) and \( \overline{Sd}_{j}^{\prime - } \)), respectively.

$$ {\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime - } } \right) = \sqrt {\mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {\left( {m_{j}^{\prime - } } \right) - {\overline{\fancyscript{m}}}_{ij}^{\prime} } \right)^{2} } $$
(52)
$$ {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime},\overline{Sd}_{j}^{\prime - } } \right) = \sqrt {\mathop \sum \limits_{j = 1}^{{\fancyscript{t}}} \left( {\left( {Sd_{j}^{\prime - } } \right) - \overline{Sd}_{ij}^{\prime} } \right)^{2} } $$
(53)

Step 10 Compute proposed new relative coefficient degrees.

$$ {\mathfrak{H}}_{i}^{ + } = \sqrt {\frac{{{\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{*} } \right) \times {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime*} } \right)}}{{{\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{ - } } \right) \times {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime - } } \right)}}} $$
(54)
$$ {\mathfrak{H}}_{i}^{ - } = \sqrt {\frac{{{\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime - } } \right) \times {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime - } } \right)}}{{{\Im }_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime*} } \right) \times {\Im }_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime*} } \right)}}} $$
(55)

Step 11 Calculate proposed closeness coefficient \( {\mathfrak{C}}_{{\mathfrak{i}}} \) for the GSSP.

$$ {\mathfrak{C}}_{{\mathfrak{i}}} = \frac{{\sqrt {\frac{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime - } } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime - } } \right)}}{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime *} } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime *} } \right)}}} }}{{\sqrt {\frac{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime},\overline{M}_{j}^{*} } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime *} } \right)}}{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime - } } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime - } } \right)}}} + \sqrt {\frac{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime - } } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime - } } \right)}}{{\Im_{i} \left( {\overline{\fancyscript{m}}_{ij}^{\prime} ,\overline{M}_{j}^{\prime*} } \right) \times \Im_{i} \left( {\overline{Sd}_{ij}^{\prime} ,\overline{Sd}_{j}^{\prime *} } \right)}}} }} $$
(56)

Step 12 Rank each green supplier candidate, sorting by the values \( {\mathfrak{C}}_{\text{i}} \) in decreasing order.

4 Application

Regarding the continuous advancement of financial globalization and condition assurance, the GSCM has assumed a critical part in promoting monetary, which specifically affects the fabricates and condition execution. The automobile manufacturing industry needs to actualize green methodology for phases of production procedure and urge suppliers to enhance the ecological practices. GSSP is regarded as a standout amongst the vital issues in the networks. Taken a choice issue in automobile industry, which expects to look for a suitable supplier for acquiring critical parts of new equipment from the literature (Qin et al. 2017).

With the improvement of GSCM, the company must start to actualize some regulatory checks and projects to guarantee that suppliers could give products via an ecological approach. Many automobiles’ parts can be manufactured by suppliers; in this regard, evaluations in main decision problem in light of green growth and influential factors could enhance the company’s ecological outcomes.

In this problem, automobile equipment suppliers (\( {\mathcal{A}}_{1} , {\mathcal{A}}_{2} , {\mathcal{A}}_{3} , {\mathcal{A}}_{4} \)) are taken regarding the assessments. The application is related to the company. As indicated by the company strategies, the request capability is made by IS0 9001 and 14001. Other than the ecological issues, they regarded conventional factors by focusing on quality, cost, delivery, and service.

Besides, ten green factors ought to be considered because of the immense ecological weight. The GS-assessment factors are reported by different methods. These factors in the appraisement procedure can be (Qin et al. 2017):

  • \( {\mathcal{O}}_{1} \): Green item advancement;

  • \( {\mathcal{O}}_{2} \): Green picture;

  • \( {\mathcal{O}}_{3} \): Use of naturally benevolent innovation;

  • \( {\mathcal{O}}_{4} \): Resource utilization;

  • \( {\mathcal{O}}_{5} \): Green capabilities;

  • \( {\mathcal{O}}_{6} \): Environment administration;

  • \( {\mathcal{O}}_{7} \): Quality administration;

  • \( {\mathcal{O}}_{8} \): Total item life cycle cost;

  • \( {\mathcal{O}}_{9} \): Pollution creation; and

  • \( {\mathcal{O}}_{10} \): Staff ecological preparing.

Three experts (\( DM_{1} \), \( DM_{2} \), \( DM_{3} \)) with some risk preferences (i.e., D1: averse; D2: neutral; D3: appetite) will be welcome for assessments, and e = (0.2, 0.4, 0.4) will be a vector of weights. Experts can utilize the IT2FSs appeared in Table 1. DMs use the linguistic variables (i.e., 7-scale) for their assessments; then, these variables are expressed by the corresponding IT2TFNs according to Table 1 (Qin et al. 2017). Also, complementary relations for IT2FSs are given in Table 2 (Qin et al. 2017). Then, decision matrix from three experts is provided in Table 3.

Table 1 Linguistic variables
Full size table
Table 2 Complementary relations
Full size table
Table 3 Decision matrix from three experts
Full size table

\( {\mathcal{O}}_{1} ,{\mathcal{O}}_{2} ,{\mathcal{O}}_{3} ,{\mathcal{O}}_{5} ,{\mathcal{O}}_{6} ,{\mathcal{O}}_{7} ,{\mathcal{O}}_{10} \) are regarded as benefit factors, and \( {\mathcal{O}}_{4} ,{\mathcal{O}}_{8} ,{\mathcal{O}}_{9} \) are regarded as cost factors; decision matrices are normalized by Eq. (8).

Table 4 The PM of IT2TrFNs and weight of each factor by entropy measure respect to each decision maker based on step 4
Full size table
Table 5 The PSD of IT2TrFNs and weight of each factor by entropy measure respect to each decision maker based on step 4
Full size table

The results of step 4 are given in Tables 4 and 5. Then, Aggregated weights of factors based on PM and PSD are obtained from step 4.2 as:

$$ \begin{aligned} W\left( {\text{Total}} \right)_{j}^{1} & = \left\{ {0.179,0.032, 0.057,0.117,0.108,0.064,0.119,0.110,0.076,0.139} \right\} \\ W\left( {\text{Total}} \right)_{j}^{2} & = \left\{ {0.129,0.137,0.091,0.093,0.141,0.067,0.088,0.104,0.075,0.075} \right\} \\ W\left( {\text{Total}} \right)_{j}^{3} & = \left\{ {0.110,0.154,0.117,0.055,0.094,0.081,0.086,0.110,0.118,0.073} \right\} \\ \end{aligned} $$

Aggregated weights of factors based on PM and PSD are obtained from step 5.2 as:

$$ \vartheta \left( {\text{Total}} \right) = \left( {\vartheta \left( {\text{Total}} \right)_{1} ,\vartheta \left( {\text{Total}} \right)_{2} ,\vartheta \left( {\text{Total}} \right)_{3} } \right)^{\text{T}} = \left( {0.320, 0.343, 0.337} \right) $$

According to Table 6, it can be observed that the result is adopted to the recent literature for the GSCM.

Table 6 Ranking results of the proposed model
Full size table

4.1 Sensitivity analysis

This research wants to study on weights of DMs which are calculated according to step 5.2. of the proposed approach. The idea of this analysis is to change the pairwise weights of DMs in Table 7. The results indicate no changes in the ranking of green suppliers.

Table 7 Result of sensitivity analysis on DMs’ weights
Full size table

In comparison with other methods in the literature, as mentioned in the introduction the decision information can be lost within the GDM and in the aggregating process; therefore, in introduced MAGDM model to overcome this drawback, a new approach with IT2TrFNs along with PM and PSD is presented to avoid the aggregations in decision process of the GSCM.

5 Conclusion

GSCM can be a new idea employed by manufacturing companies. Different industries look for enhancements in the obtaining of raw materials, fabrication, allocation, and transportation effectiveness with a view towards accomplishing environment aims and decreasing expenses in the manufacturing procedure. Consequently, the GSCM has effects from an academic scholarly point of view, and additionally, from the perspective of industrial managers since associations benefit when they are socially mindful notwithstanding being proficiently managed. The main strategies of green supplier selection (GSS) are changed. Different industries ought to concern suppliers from both economic and ecological perspectives since suppliers could impact manufacturing firms’ execution and partners. The GSS is a vital and complex decision issue, requiring assessment of numerous financial and natural factors by fusing unclearness and imprecision with the inclusion of a gathering of specialists. Although various reviews have utilized financial elements in the GSS, limited papers have considered economic and ecological factors concurrently. Notwithstanding, with an aggregation of data in the group decision process of the GSCM, some data might be lost. The point of this research was to display a precise procedure staying away from data loss for the GDM under uncertain environments. In this research, judgments of decision makers have been taken on the basis of IT2TrFNs. In introduced approach, both economic and environmental criteria have been considered concurrently. Then, the importance of criteria with PS metrics was obtained by presented entropy measures. Also, a new weighting method for supply chain DMs was proposed based on PS concepts of mean and standard deviation. Besides, a new ranking method has been introduced for the ranking green supplier alternatives. Finally, the proposed approach was employed to deal with real problems in the GSCM. Outcomes illustrated that the model could be advantageous in the GSSP for manufacturing companies. The application indicated that the computational procedure was efficient in practice to take into account uncertain environments for the GSSP. There is an idea that could be strengthened the proposed method by using a data collection method for words and then mapping that data into a trapezoidal FOU. Recently, an example of this idea is reviewed and summarized in (Mendel 2016). Interval approach (IA), enhanced interval approach (EIA), and Hao–Mendel approach (HMA) are three methods that are proposed in the related literature to estimate an IT2FS model for a word beginning with data that are collected from a group of subjects, or from a single subject. Moreover, this idea could be extended by taking some references for the aggregation of several numerical values into single representative one (Grabisch et al. 2009, 2011a, b; Pap 1997).