1 Introduction

Subspace clustering methods find clusters within multiple subspaces of unlabeled data. As a result, four major groups of studies on subspace clustering have persisted over the years, namely applied statistics [25, 30, 42], factorization [8, 13, 29, 31, 45], algebraic [32, 33, 35], and spectral clustering [4, 14, 15, 38, 50]. However, the spectral-type, which requires constructing a similarity matrix using data’s low dimensional representation, has become increasingly popular in the last decade. Thus, low-rank representation (LRR) [19] and sparse subspace clustering (SSC) [10] approaches are known to be efficient in constructing the similarity matrix [1, 20]. The reason is that both of them utilize the self-expressiveness property of data to represent each data sample as a linear combination of others. Therefore, several studies inspired by SSC and LRR have surfaced more recently. In [5], Chen et al. proposed a collaborative representation method using the LRR recovery technique. In [46], Zhang et al. proposed a hyperspectral remote sensing image representation method based on SSC. Other studies, such as [22, 37] presented various subspace methods, combining LRR and SSC approaches. Similarly, Shen and Li [28] proposed the NLRR method by combining LRR and matrix factorization.

Notwithstanding, the above are two-phase methods, which require post-processing of the similarity matrix via spectral clustering algorithm [26]. That means the clustering performance of these methods depends on the accuracy of the predefined similarity matrix. Regarding this limitation, the studies in [17, 21, 27] proposed methods, which learn the similarity matrix cooperatively to improve clustering performance. Even so, these methods obtain similarity between data samples by assuming that similar samples reside near each. Therefore, they often do not perform well in practical cases when a given data has an arbitrary distribution. This drawback exists because two data samples may seem similar by their spatial location yet belong to different subspaces [39], which means two unrelated data samples can then reconstruct one another. Although the methods presented in [23, 40, 41, 49] utilize nonnegative constraints to encourage the similarity matrix to be block diagonal, they also follow a two-phase procedure to obtain the clustering structure. So, these methods’ discrimination ability would degrade when the similarity matrix produced in the first phase fails to hold an accurate block diagonal shape

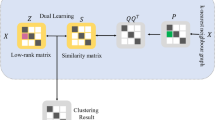
To this end, we propose a novel method, which guarantees an ideal clustering structure through coupled low-rank representation to enhance clustering performance. First, our method obtains a manifold recovery structure, which corrects inadequacy in the low-rank representation of data using the k-block-diagonal regularizer [23]. This manifold recovery structure is directly useful for the subspace clustering task because our method can instantly find a clustering projection matrix that obeys the k-block diagonal property by utilizing it. Unlike the common block diagonal property learned by spectral-based methods, the k-block diagonal property acquired through the clustering projection matrix guarantees the within-cluster consistency and independence between clusters. Hence, our method finds an ideal similarity matrix that approximates the clustering projection matrix with a rank constraint on the normalized Laplacian matrix to ensure that it denotes our clustering structure with an accurate k number of connected components. This approach avoids k-means post-processing of the low dimensional embedding matrix, which is inherent in spectral clustering algorithms. Additionally, we couple our method to allow the clustering structure to approximate the low-rank representation adaptively in order to capture a more accurate manifold structure of data. Therefore, the proposed method can achieve better performance in practice since the cleaner low-rank matrix guarantees a better clustering structure.

The main contributions are as follows:

  1. 1)

    We propose a new method, which learns an ideal similarity matrix through a clustering projection matrix. This approach guarantees more discrimination ability than existing subspace methods, which learn the similarity matrix in advance by utilizing a low dimensional representation obtained directly from the original data. Besides, our method avoids k-means spectral post-processing of the low-dimensional embedding matrix by imposing a rank constraint on the normalized Laplacian matrix to allow the similarity matrix to denote our clustering structure explicitly with k connected components.

  2. 2)

    Furthermore, we couple our method to allow mutual capturing of the data’s manifold structure by the clustering structure and the low-rank representation.

  3. 3)

    To evaluate our method, we perform a wide range of experiments on several benchmark datasets. The results show that our method outperforms similar state-of-the-art methods in six evaluation metrics.

The rest of this paper is structured as follows. Section 2 provides the background and a review of the related works. In Section 3, we present the proposed method. Section 4 demonstrates the effectiveness of the proposed method. Then, Section 5 gives the conclusion.

2 Background and related work

In this section, we provide the main notations and a review of the related works.

2.1 Notation

In this paper, we denote matrices with an uppercase letter. ∥ .∥∗ denotes nuclear norm, ∥ .∥1 denotes L1-norm, ∥ .∥F denotes Frobenius norm, ∥ .∥k denotes k-block diagonal inducing regularizer, ∥ .∥2,1 denotes L2,1-norm, and Tr(.) denotes the trace of a square matrix. Furthermore, we denote the (i,j)th entry of a matrix Z by Zi,j, where i and j represent the ith row and jth column. Z ≥ 0 implies that all entries of Z are nonnegative. Diag(Z) denotes a diagonal matrix whose element is the ith diagonal entry of Z. Then I denote an identity matrix.

2.2 Related work

Given an unlabeled dataset X = {x1,…,xn}∈ Rd×n drawn from a union of subspaces, the SSC approach uses L1-norm regularization to find a sparse representation of the data samples. However, the L1-norm does not capture a global data structure since it obtains a sparse representation independently for each data sample [2]. LRR approach, on the other hand, captures a global data structure using the nuclear norm regularization as follows:

$$ \begin{array}{c} {\min_{Z,E}}\parallel Z{\parallel_{*}} + \lambda\parallel E{\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, \end{array} $$
(1)

where Z denotes the low-rank representation, X denotes the self-dictionary, E denotes the error matrix. λ is a parameter to balance the first and second terms, and the ∥ .∥2,1 norm used in (1) is very efficient when only a part of the samples is contaminated by noise. Zi,j can then correctly capture the data’s local manifold structure when only similar data samples xi and xj belonging to the same cluster reconstruct one another. Therefore, considering its robustness, several studies inspired by LRR, such as [5, 6, 9, 18, 28, 34, 49], have been conducted over the years. In [34], Vidal and Favaro proposed a method, which attempts to find a clean low-rank matrix by decomposing a data matrix into three matrices: a noise-free matrix, a corrupted matrix, and an error matrix. In [28], Shen and Li proposed a method, which factorizes a nuclear norm regularized matrix to capture the exact similarity between data samples. In [49], Zheng et al. proposed a method named SinNLRR, which imposes a non-negative constraint on the low-rank matrix to ensure that only similar data samples are connected while unrelated data samples are not connected. Also presented is a low-rank local embedding representation (LRLER) method [9]. LRLER uses local manifold embedding constraint to enforce a global low-rank representation since most data often do not hold a linear structure. So, a method named LRLTSER was introduced together with LRLER to handle neighborhood aliasing distortion in data. Besides, Lu et al. [23] introduced the Block Diagonal Representation (BDR) method, which uses the k-block diagonal regularizer to encourage a proper low dimensional matrix.

Upon learning the low-dimensional representation of data, the above methods can directly construct a similarity matrix. Afterward, a spectral clustering algorithm such as [26] is applied to obtain the clustering structure. Thus, it is easily noticeable that the accuracy of the clustering structure learned in the two-phase process will depend entirely on the quality of the similarity matrix obtained in the first phase. Towards this end, many other studies, such as [21, 27, 40], proposed methods, which learn a similarity matrix cooperatively in search of an optimum solution. For example, given an initial similarity matrix A, the Constrained Laplacian Rank (CLR) [27] can obtain an ideal similarity matrix S by learning S and A simultaneously. Similarly, the Extreme Learning Machine (ELM-CLR) [21] and the Implicit Block Diagonal Low-Rank Representation (IBDLR) [40] can find an ideal similarity matrix by adapting it on dual data representations where one data representation relies on the actual data, and another on its affine space. Meanwhile, Yang et al. [44] proposed a model based on a low-rank variation dictionary (LRVD) to improve performance accuracy. This approach constructs the dictionary independently using variations of data. In [47], Zhang et al. presented a method named CMC by applying nonnegative matrix factorization. CMC mainly focuses on capturing actual similarity between data samples even with limited samples.

The proposed method is comparable to IBDLR since they both apply the same k-block diagonal regularizer [23] and LRR approaches to solve the subspace segmentation problem. However, our approach can guarantee a more discriminating ability with explicit block diagonal clustering structure through coupled LRR without spectral post-processing procedure. Furthermore, a coupling strategy was used in a previous study in [48], but it relied on additional k-means post-processing to obtain the clustering results.

3 The proposed method

In this section, we present our proposed method based on coupled low-rank representation. First, we formulate the model in Section 3.1. Then propose an efficient optimization method to solve it in Section 3.2.

3.1 Model formulation

3.1.1 Relationship between data

LRR based methods or any other subspace method would efficiently find a low dimensional matrix that preserves the relationship between data samples when underlying data is clean. Because only similar data samples will reconstruct one another using the data’s self-expressiveness property. On the other hand, the self-expressiveness property alone will not guarantee an accurate low dimensional matrix when the data is noisy. The reason is that two unrelated data samples, xi and xj, may be selected to reconstruct themselves where the singular value Zij is non-zero instead of 0. Assuming this to be the case, it means the similarity matrix learned after using the low-dimensional matrix would be fallible— and the goal of subspace clustering to partition the data samples into k appropriate clusters will then be defeated. The ideal is for only similar samples from the same class to be connected, while the samples from different classes should not stay together. To this end, we consider a block diagonal compliant model directly such that a manifold recovery structure obtained can correct a possible inadequacy in the low-rank representation of data as follows:

$$ \begin{array}{c} {\min_{Z,E,L}}\parallel Z{\parallel_{*}} + \lambda_{1}\parallel E{\parallel_{2,1}} + \lambda_{2}\parallel L {\parallel_{k}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2, Diag(L) = 0,L \ge 0, \end{array} $$
(2)

where X ∈ Rd×n represents the self-dictionary. Z ∈ Rn×n denotes the low-rank representation. L ∈ Rn×n is the manifold recovery structure. Diag(L) = 0 and L ≥ 0 are non-negative constraints to enforce a diagonal block structure on L. E ∈ Rd×n is the error matrix whose columns are encouraged to be zero by ∥ .∥2,1, assuming that the data corruption is precise. As such, this error matrix is incredibly efficient since noise, or noise-free element, is generally not known in advance. Thus, most subspace methods, such as LRR in (1), usually estimate Z using X. However, when X is noisy, Z’s estimation becomes biased, which means Z cannot effectively capture the similarity between the data samples. The core idea in (2) attempts to recover the actual manifold structure from Z through the k-block diagonal regularizer defined below so that Lij is only 0 for two unrelated data samples, i and j.

Definition 1 [23] (k-Block Diagonal Regularizer): For any similarity matrix L ∈ Rn×n the k-block diagonal regularizer is defined as the sum of the smallest k eigenvalues of LL, i.e.

$$ \parallel L {\parallel_{k}} = \sum\limits_{i = n-k+1}^{n} \lambda_{i}(L_{L}),\\ $$
(3)

where LL = Diag(L1) − L is the Laplacian matrix of L. λi(LL) is ith eigenvalue of LL in the descending order. This k-block diagonal regularizer performs two functions: First, it encourages L to be block-diagonal with nonnegative constraints mentioned above. Secondly, it ensures that there is k exact number of connected blocks in L.

3.1.2 Clustering Structure with constrained Laplacian rank

Ideally, an optimal L by (2) denotes the similarity matrix of existing methods, made possible by L = (|Z| + |ZT|)/2. On the contrary, our method obtains the similarity matrix through a clustering projection matrix to guarantee more discrimination capability. Thus, considering that L has an inherent Laplacian structure LL by definition in (3), the clustering projection matrix is obtained directly from it in the following way:

$$ \begin{array}{c} {Tr(H^{T}LH)},\\ s.t.,{\kern 1pt} {\kern 1pt} {H^{T} H=I} \end{array} $$
(4)

Apparently, H is similar to the primary output of a spectral clustering algorithm in the two-phase methods. Nonetheless, let us consider that the k-block diagonal regularization on L may not guarantee an exactly k-block diagonal structure as suggested in [40]. Then it is easy to see that the constraint HTH = I only enforces the common block diagonal property on H. That also means HTH = I can only guarantee within-cluster consistency without considering overlapping between clusters. To mitigate against this problem, we observe that the binary matrix HHT obeys the k-block-diagonal property by itself, which hints that HHT can guarantee both the within-cluster consistency and independence between clusters. As a result, an ideal similarity matrix \(S={\{{s_{i}^{T}},\ldots ,{s_{n}^{T}}}\}\in {R^{n \times n}}\) is redefined, which is not only approximate to HHT but denotes our clustering structure with rank(Ls) = n − k through the following theorem.

Theorem 1: if S is non-negative, the multiplicity k of the zero eigenvalue of the graph Laplacian Ls corresponds to the number of connected components in the graph associated with S.

Theorem 1 implies that if rank(Ls) = n − k, then S becomes an ideal similarity matrix from which the data samples can be partitioned into k clusters explicitly without spectral post-processing of S. The proof of Theorem 1 can be found in [7, 36].

Hence, we have the following formulation:

$$ \begin{array}{@{}rcl@{}} {\min_{L,H,S}}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} + \lambda_{3}{Tr(H^{T}LH)},\\ s.t.,{\kern 1pt} {\kern 1pt} {H^{T} H=I}, S1=1, S\ge 0, rank(L_{s} )=n-k, \end{array} $$
(5)

where S1 = 1 ensures that each data sample can only belong to one cluster, then LS = DS − S denotes the normalized Laplacian matrix because DS ∈ Rn×n represents the diagonal matrix whose ith entry \({\sum }_{j} S_{i,j}=1\). Besides, HHT denotes the clustering projection matrix, where (HHT)ij is 1 if hi = hj and 0 otherwise. In other words, (HHT)ij = 1 indicates that xi and xj belongs to the same cluster.

3.1.3 Coupled low rank representation

Achieving the objective of (5) may still be challenging since the manifold structure is pre-captured analogously to the two-phase methods such as SinNLRR [49], BDR [23], and IBDLR [40]. Thus, the idea of dynamic approximation is introduced into our model using the coupling term \(\parallel S-Z {{\parallel _{F}^{2}}}\) to allow for joint capturing of the data’s manifold structure by both S and Z. I.e., \(\parallel S-Z {{\parallel _{F}^{2}}} \rightarrow 0 \) as much as possible, leading to the problem of coupled low-rank representation and subspace clustering:

$$ \begin{array}{c} {\min_{Z,H,L,S,E}}\parallel Z {\parallel_{*}}+ \lambda_{2}\parallel L {\parallel_{k}} +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} + \lambda_{1}\parallel E {\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2,Diag(L) = 0, L \ge 0,\\{H^{T} H=I}, S1=1, S\ge 0, rank(L_{s} )=n-k, \\ . \end{array} $$
(6)

where parameters λ1,λ2,λ3,λ4, and λ5 controls the tradeoff between the terms, respectively.

The goal of the above objective function is to make a perfect subspace segmentation more possible by simultaneously learning S and Z. Therefore, our method uses the coupling term \(\parallel S-Z {{\parallel _{F}^{2}}}\) to measure the effect of the k-block diagonal representation on S. Because once the obtained Z varies largely to S, it indicates that Z is not clean enough. In that case, our method finds a cleaner Z that captures a more accurate manifold structure of the data so that S can then also capture a better manifold structure correspondingly. Besides, this term allows S and Z subproblems to be strongly convex, making convergence analysis very easy.

3.2 Optimization

We propose an efficient optimization method based on Augmented Lagrange Multiplier (ALM) [16] to solve (6). First, (6) is not easily solvable because of the non-convex nature of ∥ L∥k. So, following Ky Fan’s theorem [12], ∥ L∥k is reformulated as a convex problem in the following way:

$$ \begin{array}{c} { \parallel L {\parallel_{k}}={\min_{W}}(L_{L}, W)},\\ s.t.,{\kern 1pt} {\kern 1pt} 0 \le W \le I,Tr(W)=k, \end{array} $$
(7)

By substituting (7) in place of ∥ L∥k, we rewrite (6) as:

$$ \begin{array}{c} {\min_{Z,W,H,L,S,E}}\parallel Z {\parallel_{*}}+ \lambda_{2}(Diag(L1)-L, W) +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} + \lambda_{1}\parallel E {\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2,Diag(L) = 0, L \ge 0,\\{H^{T} H=I}, S1=1, S\ge 0, rank(L_{s} )=n-k, \\0 \le W \le I,Tr(W)=k, \\ . \end{array} $$
(8)

Equation 8 may still be hard to solve because rank(Ls) = n − k is not linear. Resolving this problem, we denote the i-th smallest eigenvalue of Ls as 𝜃i(Ls). Then given a large enough λ6, (8) is the same as:

$$ \begin{array}{c} {\min_{Z,W,H,L,S,E}}\parallel Z {\parallel_{*}}+ \lambda_{2}(Diag(L1)-L, W) +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} +\lambda_{6}\sum\limits_{i = 1}^{k} \theta_{i}(L_{s}) + \lambda_{1}\parallel E {\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2,Diag(L) = 0, L \ge 0,\\{H^{T} H=I}, S1=1, S\ge 0, \\0 \le W \le I,Tr(W)=k, \\ . \end{array} $$
(9)

where 𝜃i(Ls) ≥ 0 since Ls is positive semidefinite matrix. Thus, when λ6 is large enough, \({\sum }_{i=1}^{k} \theta _{i}(L_{s})=0\) to satisfy the constraint rank(Ls) = n − k. According to Ky Fan’s theorem, we know that \({\sum }_{i=1}^{k} \theta _{i}(L_{s})\) is equivalent to minimizing Tr(FTLsF) subject to FTF = I, so we get:

$$ \begin{array}{c} {\min_{Z,W,H,L,S,E}}\parallel Z {\parallel_{*}}+ \lambda_{2}(Diag(L1)-L, W) +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} +\lambda_{6} Tr(F^{T} L_{s} F) + \lambda_{1}\parallel E {\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2,Diag(L) = 0, L \ge 0,\\{H^{T} H=I}, S1=1, S\ge 0, F^{T} F=I, \\0 \le W \le I,Tr(W)=k, \\ . \end{array} $$
(10)

where F is a low dimensional embedding matrix the same as H. Except that, S has an inherent k-block diagonal structure already by approximating HHT. As such, λ6 doesn’t need tuning like the other parameters [27]. It may only turn low or high when the number of connected components is larger or smaller than k.

Moreover, we take a clue from [49] by introducing an intermediate term J to relax (10) further as follows:

$$ \begin{array}{c} {\min_{Z,W,H,L,S,E}}\parallel J {\parallel_{*}}+ \lambda_{2}(Diag(L1) - L, W) +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} +\lambda_{6} Tr(F^{T} L_{s} F) + \lambda_{1}\parallel E {\parallel_{2,1}},\\ s.t.,{\kern 1pt} {\kern 1pt} X = XZ + E, L = (|Z| + |{Z^{T}}|)/2,Diag(L) = 0, L \ge 0,\\J=Z, {H^{T} H=I}, S1=1, S\ge 0, F^{T} F=I, \\0 \le W \le I,Tr(W)=k.\\ . \end{array} $$
(11)

The Lagrangian function of (11) is given below:

$$ \begin{array}{c} \mathcal{L}= \parallel J {\parallel_{*}}+ \lambda_{2}(Diag(L1)-L, W) +\lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} \\+ \lambda_{3}{Tr(H^{T}LH)} + \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} +\lambda_{6} Tr(F^{T} L_{s} F) + \lambda_{1}\parallel E {\parallel_{2,1}}\\ +Tr[{M_{1}^{T}}(X-XZ-E)] + Tr[{M_{2}^{T}}(J-Z)] \\+ \frac{\mu }{2}(\parallel X-XZ-E {{\parallel_{F}^{2}}} + \parallel J-Z {{\parallel_{F}^{2}}}), \end{array} $$
(12)

M1,M2 are Lagrange multipliers. Now, we divide (12) into several subproblems by denoting each variable as a subproblem. By doing so, we remove the terms not connected to each subproblem to obtain an optimal solution by fixing others as follows:

J subproblem:

$$ \begin{array}{c} {\min_{J}} \frac{1}{\mu } \parallel J {\parallel_{*}} + \frac{1}{2}\parallel J-(Z+\frac{M_{2}}{\mu }) {{\parallel_{F}^{2}}}. \end{array} $$
(13)

Then, denoting the singular value thresholding [3] of Sμ[M] as \(U{{{\mathscr{H}}}_{\mu } }[{\Sigma } ]V^{T}\) the optimal solution of (13) is given as:

$$ \begin{array}{c} J = {S_{{1}/{\mu }}}[{Z}+\frac{M_{2}}{\mu }].\\ {{\mathcal{H}}_{\mu} }[{\Sigma} ] = \min(0,{\Sigma} +\mu ) + \max(0,{\Sigma} -\mu ). \end{array} $$
(14)

W subproblem:

$$ \begin{array}{c} {\min_{w}}\lambda_{2}(Diag(L1)-L ,W),\\ s.t.,{\kern 1pt} {\kern 1pt} 0 \le W \le I,Tr(W)=k. \end{array} $$
(15)

Similar to [40] we can obtain a close form solution for W as follows:

$$ \begin{array}{c} W=UU^{T}, \end{array} $$
(16)

where U ∈ Rn×k holds the k connected components corresponding to the k eigen vectors associated with k smallest eigen values of LL.

H subproblem:

$$ \begin{array}{c} {\min_{H}} \lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}} + \lambda_{3}{Tr(H^{T}LH)},\\ s.t.,{\kern 1pt} {\kern 1pt} {H^{T} H=I}. \end{array} $$
(17)

Since (17) is unique for different i, we rewrite it as:

$$ \begin{array}{c} {\min_{H}} {Tr(H^{T}(L+2\lambda_{4}S)H)},\\ s.t.,{\kern 1pt} {\kern 1pt} {H^{T} H=I}. \end{array} $$
(18)

Therefore, the optimal H in (18) is derived by the k eigenvectors of the corresponding topmost k highest eigenvalues of (L + 2λ4S).

Z subproblem:

$$ \begin{array}{c} {\min_{Z}} \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}} +Tr[{M_{1}^{T}}(X-XZ-E)] + Tr[{M_{2}^{T}}(Z-J)] \\ + \frac{\mu }{2}(\parallel X-XZ-E {{\parallel_{F}^{2}}} + \parallel J-Z {{\parallel_{F}^{2}}}). \end{array} $$
(19)

By setting the derivative \( \frac {\partial }{\partial Z } =0 \), we obtain:

$$ \begin{array}{c} Z = {[(\frac{2}{\mu }+1)I + X^{T}X]^{- 1}} ((X^{T}X-{X^{\prime}} * E + J)\\ + {(2\lambda_{5}S + X^{T}M_{1}-M_{2})}/\mu). \end{array} $$
(20)

S subproblem:

$$ \begin{array}{c} {\min_{S}} \lambda_{4}\parallel S-{HH^{T}} {{\parallel_{F}^{2}}}+ \lambda_{5}\parallel S-Z {{\parallel_{F}^{2}}}+\lambda_{6} Tr(F^{T} L_{s} F),\\ s.t.,{\kern 1pt} {\kern 1pt} S1=1, S\ge 0, F^{T}F=I. \end{array} $$
(21)

Equation (21) can be rewriting it as:

$$ \begin{array}{c} {\min_{S}} \parallel S-(\lambda_{4}{HH^{T}} + \lambda_{5}Z) {{\parallel_{F}^{2}}}+\lambda_{6} Tr(F^{T} L_{s} F),\\ {\min_{S}} \parallel S {{\parallel_{F}^{2}}} - 2\langle\lambda_{4}{HH^{T}} + \lambda_{5}Z,S \rangle+\lambda_{6} Tr(F^{T} L_{s} F),\\ s.t.,{\kern 1pt} {\kern 1pt} S1=1, S\ge 0, F^{T}F=I. \end{array} $$
(22)

Then, denoting 2(λ4HHT + λ5Z) by G, we obtain the following:

$$ \begin{array}{c} {\min_{S}} \parallel S {{\parallel_{F}^{2}}} - Tr(GS^{T})+\lambda_{6} Tr(F^{T} L_{s} F),\\ s.t.,{\kern 1pt} {\kern 1pt} S1=1, S\ge 0, F^{T}F=I. \end{array} $$
(23)

Same as (4), the optimal solution of F in (23) contains eigenvectors of the corresponding k smallest eigenvalue of LS. Upon that, we rewrite (23) as:

$$ \begin{array}{c} {\min_{S_{j}}} (\lambda_{6}\parallel f_{i}-f_{j} {{\parallel_{2}^{2}}}-g_{ij})s_{ij} + {s_{j}^{T}}s_{j}, \\ s.t.,{\kern 1pt} {\kern 1pt} s_{j}\ge 0, 1^{T}s_{j}=1. \end{array} $$
(24)

Then, denoting \(\lambda _{6}\parallel f_{i}-f_{j} {{\parallel _{2}^{2}}}-g_{ij}\) as qij, (24) is simplified as:

$$ \begin{array}{c} {\min_{S_{j}}} \frac{1}{2}\parallel s_{j}+\frac{q_{j}}{2} {{\parallel_{2}^{2}}}, \\ s.t.,{\kern 1pt} {\kern 1pt} s_{j}\ge 0, 1^{T}s_{j}=1. \end{array} $$
(25)

Similar to Eq. 30 in [27], we obtain sj as follows:

$$ \begin{array}{c} s_{j}=\left( -\frac {q_{j}}{2} + \eta 1 \right)_{+}. \end{array} $$
(26)

L subproblem:

$$ \begin{array}{c} {\min_{L}} \lambda_{3}Tr(H^{T}LH) + \lambda_{2}(Diag(L1)-L ,W),\\ s.t.,{\kern 1pt} {\kern 1pt} L = (|Z| + |{Z^{T}}|)/2, Diag(L) = 0, L \ge 0. \end{array} $$
(27)

The optimal solution L is:

$$ \begin{array}{c} L = \frac {1}{2}\parallel \lambda_{3}({HH^{T}}) + \lambda_{2}[Diag(W) * 1^{T} - W] {\parallel^{2}} \end{array} $$
(28)

Furthermore, by denoting A = λ3(HHT) + λ2[Diag(W) ∗ 1T − W)], \( \hat {\mathrm {A}} = A - diag(diag(A))\), we rewrite (28) as follows:

$$ \begin{array}{c} L={[\thinspace(\hat{\mathrm{A}} + \hat{\mathrm{A}}^{T})/2 \thinspace ]}_{+}. \end{array} $$
(29)

E subproblem:

$$ \begin{array}{c} E = {\min_{E}}\frac {\lambda_{1}}{\mu}\parallel E {\parallel_{2,1}} + \frac {1}{2} \parallel E -\left( X-XZ+ \frac{Y_{1}}{\mu}\right){{\parallel_{F}^{2}}}. \end{array} $$
(30)

Algorithm 1 outlines the complete solution of our method.

figure d

3.3 Complexity analysis

Our method’s complexity depends on three key components: matrix multiplication required to solve Z and E subproblems, matrix inversion required to solve Z subproblem, and eigendecomposition required to solve W, H, and S subproblems. For each matrix multiplication, the inverse of a matrix, and eigendecomposition, the time complexity is O(n3). But notice that the Z subproblem needs more than one multiplication. So, it takes (k + 1)O(n3), which may be problematic in large-scale datasets. In that case, one can perform inverse and multiplication operations using a graphics processing unit (GPU) device or apply large-scale techniques such as Accelerated LRR [11] to speed up our method. Besides, (25) takes O(n) since it requires Euclidean projection onto simplex space. Overall, each iteration’s time complexity is O(3n3 + (k + 1)n3 + n).

4 Experiments

In this section, we demonstrate the effectiveness of our method. To begin with experiment settings, we describe six benchmark datasets, nine state-of-the-art compared methods, and six standard metrics utilized to evaluate our proposed method. We then present the experimental results with analysis in Section 4.2.

4.1 Experiment settings

4.1.1 Data set

To assess our method’s performance, we conduct widespread experiments on six benchmark datasets, namely UCI Digits, USPS, ORL, Yale, COIL-20, and Caltech101-07 datasets.

  • UCI digitsFootnote 1: dataset has 2000 data samples of handwritten digits from 0 to 9. Each data sample has 240 features or pixels that describe each digit.

  • USPSFootnote 2: dataset has 1854 data samples of handwritten digits from 0 to 9, where 256 features describe each digit.

  • ORLFootnote 3: dataset comprises 400 images of 40 different subjects. Each subject contains 10 distinct images taken under various conditions such as lights, facial expressions (smiling or not smiling), and facial details (with glasses or without glasses). Besides, each image has 1024 features to describe it.

  • YaleFootnote 4: dataset contains 165 gray-scale images of 15 individuals with 6750 Gabor features for each image. I.e., every individual contributes 11 images taken with different facial settings such as glasses, without glasses, happy mood, sad mood, and sleepy mood.

  • COIL-20Footnote 5: dataset contains 20 classes with a total of 1440 images. For each class, there are 72 images, which corresponds to 1024 features per image.

  • Caltech101-07Footnote 6: dataset covers 101 classes of images. However, we selected the commonly used seven classes and obtained 1474 images with 1984 HOG features.

    Table 1 gives a summary of the datasets, while Fig. 1 provides a pictorial view of Yale and COIL-20 datasets.

Fig. 1
figure 1

Example images of Yale and COIL-20 datasets

Full size image
Table 1 Summary of the datasets
Full size table

4.1.2 Compared methods

We compare our method with nine state-of-the-art subspace clustering methods: LRR [19], SSC [10], CASS [22], S3C [17], ELM-CLR [21], SinNLRR [49], BDR [23], IBDLR [40], and FGNSC [43]. Most of these methods were selected for comparison because they use a similar approach as our proposed method. For example, IBDLR, SinNLRR, CASS, and our proposed method uses LRR’s nuclear norm regularization approach to find a low dimensional representation of data.

Therefore, each method’s parameters are tuned following the corresponding literature to achieve the best clustering performance. Accordingly, we give a brief description of the different methods below.

  • LRR [19]: This method uses the nuclear norm to pursue a low-rank matrix of data from which it obtains a similarity matrix.

  • SSC [10]: This method finds a sparse representation of data independently using the L1 norm.

  • CASS [22]: This method encodes the grouping effect of LRR and the sparsity nature of SSC.

  • S3C [17]: This method extends SSC by learning a similarity matrix and data segmentation simultaneously.

  • ELM-CLR [21]: This method obtains a similarity matrix adaptively through dual data representations. One representation is based on the actual data, while another relies on the data’s affine space.

  • SinNLRR [49]: This method uses nonnegative constraints to ensure that similar data samples are connected while unrelated data samples are not connected.

  • BDR [23]: This method employs the k-block diagonal regularizer to encourage a block diagonal similarity matrix.

  • IBDLR [40]: This method also uses the k-block diagonal regularizer by BDR to find a proper similarity matrix. Besides, it adapts the similarity on dual data representations similar to ELM-CLR.

  • FGNSC [43]: This method makes use of post-processing technique to optimize both sparsity and connectivity of self-representation simultaneously to find good neighbors.

Table 2 Clustering performance of different algorithms on handwritten digits
Full size table

Note that all the compared methods except ELM-CLR apply a spectral clustering algorithm on the learned similarity matrix to obtain a clustering structure. Meanwhile, ELM-CLR can obtain a cluster structure explicitly with a rank constraint on the similarity matrix’s Laplacian matrix, the same as our proposed method. Furthermore, we adopt the best value from [0.001,0.01,0.1,...,1000] using a grid search strategy for our tunable parameters. Hence, to ensure no generalization loss, we perform each experiment ten times and report the mean and the standard deviation of the clustering performance.

4.1.3 Evaluation metrics

Six conventional metrics, namely Accuracy (ACC), Normalized Mutual Information (NMI), F-score, Recall, Precision, and Adjusted Rand index (AR), are used to evaluate the clustering performance of each method. These metrics capture different aspects whose values are directly proportional to the clustering performance. For example, ACC measures the percentage of correctly clustered data samples in the learned clustering structure compared with the ground truth labels. NMI refers to the amount of information that one can extract from shared random variables. F-score is a measure of an experiment’s accuracy calculated from the experiment’s Precision and Recall values. AR computes a similarity measure between two clusterings by considering all data samples’ pairs and counting pairs assigned in the same or different clusters of the learned clustering structure and ground truth labels.

4.2 Result and analysis

We present the clustering performance of different algorithms on six benchmark datasets in Tables 1, 2, 3 and 4. In each table, the values in bold symbolize the best performance.

Table 3 Clustering performance of different algorithms on face images
Full size table
Table 4 Clustering performance of different algorithms on object images
Full size table

Table 2 shows the clustering performance of different methods on UCI Digits and USPS handwritten datasets. It is easy to see that our method achieves the best clustering performance in all evaluation metrics. Also, FGNSC achieves better performance than others, followed closely by ELM-CLR, which may be due to the adaptive nature of learning the similarity matrix. On the contrary, the S3C method has the worst performance than SinNLRR and CASS, which obtains a similarity matrix uncooperatively. Arguably, SinNLRR may benefit from nonnegative constraints imposed on the low-rank matrix, which seems useful for relatively low dimensional UCI Digits and USPS datasets. Moreover, CASS combines the grouping effect of LRR and SSC’s sparsity nature to enhance its performance. S3C, on the other hand, appears limited by the L1-norm low dimensional matrix, which does not capture the data’s global structure.

Notwithstanding, UCI Digits’ results clearly show that our method outperforms FGNSC by over 9.44%, 0.49%, 8.28%, 10.18%, 5.4%, and 12.34% in ACC, NMI, F-score, Recall, Precision, and AR evaluation metrics, respectively. Furthermore, FGNSC, SinNLRR, and IBDLR have comparable performances on the USPS dataset, better than the rest methods. Still, our method consistently outperforms these methods in all evaluation metrics on this dataset. Table 3 tabulates the clustering performance on ORL and Yale face image datasets. Thus, our method maintains the best performance on Yale dataset with 72.12%, 73.61%, 58.38%, 62.91%, 54.46%, and 55.47%, in ACC, NMI, F-score, Recall, Precision, and AR, respectively. Similarly, on ORL dataset, our method has better performance in all metrics except Recall. This performance is only slightly higher than that of BDR by 0.95%, 1.94%, 1.09%, 0.34%, 1.68%, 1.12%, in ACC, NMI, F-score, Recall, Precision, and AR, respectively, perhaps because BDR also applies the k block diagonal regularizer. Additionally, ELM-CLR outperforms S3C by 2.62% and 13.58% just in ACC and Recall evaluation metrics, respectively. In contrast, S3C outperforms ELM-CLR in all evaluation metrics on the Yale dataset. Nevertheless, the standard deviation indicates that ELM-CLR is more stable than S3C on face image clustering. Moreover, ELM-CLR and S3C have better performances than SSC, LRR, CASS, SinNLRR, and FGNSC in most evaluation metrics to demonstrate adaptive similarity matrix’s effectiveness. Furthermore, our method outperforms ELM-CLR in ACC by over 3% on ORL datasets even as the nonlinear data structure of ORL favors ELM-CLR since it learns the similarity matrix on the actual data and the affine space of the data simultaneously. That being the case, Fig. 2 provides a visual comparison of similarity matrices of the different methods to demonstrate more superiority of our proposed method on ORL dataset. Thus, we can see that most methods, including CASS, IBDLR, and FGNSC, obtained similarity matrices with much density, which means the clusters in these matrices are not independent.

Fig. 2
figure 2

Visualization of similarity matrices of different methods

Full size image

On the other hand, Fig. 2 shows that the similarity matrix obtained by our proposed method has exactly k connected components, which means that our method can capture an accurate block diagonal property. We can also observe that the similarity matrix S and the low-rank matrix Z of our proposed method are very close, confirming our coupled learning effectiveness.

Table 4 compares our method with six state-of-the-art methods using COIL-20 and Caltech101-07 object datasets. On COIL-20 dataset, our method outperforms FGNSC, BDR, and ELM-CLR only slightly in NMI, F-score, and Precision, and AR, respectively. Whereas it performs better than its closest competitor, LRR, by over 5%, 2%, 7%, and 3% in ACC, F-score, Recall, and Precision, respectively, on Caltech 101-07 dataset. We note that ELM-CLR achieves better performance than our method by 3.76% in Precision, which perhaps is due to significant class imbalance in this dataset. However, ELM-CLR fails to maintain the same performance in other metrics. For example, our method outperforms ELM-CLR by over 20% and 19% in ACC and Recall, respectively. Besides, excluding SinNLRR and SSC, it is easily noticeable that the other methods also perform better than ELM-CLR and S3C methods.

Additionally, Fig. 3 shows the robustness of our method against noise on USPS and Caltech-07 datasets. We use random noise following uniform distribution between -0.5 and 0.5, similar to ELM-CLR [21], to perform this experiment. In particular, we adopt two experimental settings in each dataset. Firstly, 10% of the original pixels of sample images are replaced with random values in the range above. Then, 20% in the second case. Thus, one may observe that all methods have degrading performance, increasing the noise level. However, our proposed method is generally more robust against noise when compared to the other methods.

Fig. 3
figure 3

Performance comparison of different methods w.r.t. ACC on USPS and Caltech-07 datasets with 10% and 20% levels of noise

Full size image

4.2.1 Parameter analysis

Figure 4 shows our proposed method’s clustering performance by varying λ4 and λ5 while fixing other on UCI digits, ORL, and COIL-20 datasets. Note that λ6 does not need tuning like the other parameters because a similar approach in [21, 27] is followed to obtain its best value in a heuristic way to accelerate the process. Initially, we set λ6= 1 and automatically multiply it by two or divide it by two in each iteration when the number of connected components is smaller or larger than k. It is easy to see from Fig. 4 that our proposed method is relatively stable on all datasets by varying λ4 and λ5 in a range of [0.001,0.01,0.1,1]. Therefore, our proposed method can ensure good clustering performance by finding a suitable combination of both parameters.

Fig. 4
figure 4

Visualization of the clustering performance of our method w.r.t. ACC and NMI evaluation metrics by fixing other parameters and varying-parameters λ4 and λ5 on UCI Digits dataset, ORL dataset, and COIL-20 dataset

Full size image

4.2.2 Computational runtime analysis

Here we investigate the computational time of different methods on all six datasets. Specifically, we ran each method using MATLAB 2016b installed on Windows 10 CORE i5 computer system to perform this experiment. Accordingly, Table 5 displays the computational time obtained by different methods. Notice that the computation time is excessively high for most methods, which performs k-means spectral post-processing of the low dimensional embedding matrix, such as CASS, S3C, and SinNLRR. However, it is not surprising to see that CASS has a much higher computational time than LRR and SSC since it combines both approaches to learn the similarity matrix. Besides, IBDLR has three times more computation time than the similar BDR method in most datasets— the reason is not far-fetched because IBDLR learns a similarity matrix on dual data representations. We can also observe that our method has comparable computational time with ELM-CLR since both methods obtain the clustering structure explicitly without k-means spectral post-processing step. Thus, both methods converge very quickly, making their computational time much lesser than others. Nonetheless, when one considers that our method has six subproblems to update in each iteration as against a few by ELM-CLR, it may then be seen that our proposed method has a relatively good computational time in all six datasets

Table 5 The computational runtime (in seconds) of different methods on six benchmark datasets
Full size table

4.2.3 Convergence analysis

According to Liu et al. [19] and Luo et al. [24], the convergence of the inexact Augmented Lagrange Multiplier (ALM) method with more than three sub-problems is still not easy to theoretically prove. As a result, the relative error of the term \(\parallel S-Z {{\parallel _{F}^{2}}}\) is computed to illustrate our method’s convergence behavior using Figs. 5 and 6. As expected, one may see from Fig. 6 that the difference between the clustering structure and the low-rank representation reduces by each iteration step before convergence because our method learns cleaner low-rank representation in successive iteration circles. Therefore, Fig. 5 shows that our method converges within ten iterations on all six benchmark datasets, which means it is very stable.

Fig. 5
figure 5

Visualization of the clustering performance of our method at different stages of iterations

Full size image
Fig. 6
figure 6

Visualization of the convergence behavior of our coupled method (\(\parallel S-Z {{\parallel _{F}^{2}}}\)) at different stages of iterations

Full size image

5 Conclusion

This paper proposed a novel method that guarantees better clustering performance through coupled low-rank representation. To achieve that, we considered the practical case where a given data may have arbitrarily distribution, in which two unrelated samples are likely to reconstruct themselves. Therefore, we learned a manifold recovery structure to correct any incorrectness in the data’s low-rank representation. Then we obtained an ideal similarity matrix through this manifold structure differently from existing subspace clustering methods, which construct the similarity matrix by utilizing the low-dimensional representation acquired directly from original data. Furthermore, we ignored k-means spectral post-processing of the low-dimensional embedding matrix by imposing a rank constraint on the similarity matrix’s Laplacian matrix to obtain the clustering structure explicitly. Besides, we found that our proposed method can learn a more accurate clustering structure by incorporating the clustering structure into the low-rank representation. Comprehensive experiments on six benchmark datasets show that our method outperforms similar state-of-the-art methods in Accuracy, Normalized Mutual Information, F-score, Recall, Precision, and Adjusted Rand Index evaluation metrics. In future work, we will extend our proposed method to Multi-view learning.