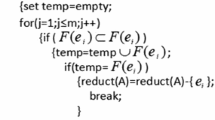A new parameter reduction algorithm for soft sets based on chi-square test

Abstract

Redundancy is an extremely significant challenge in data integration and decision making based on the model of soft set which is able to process data under uncertainty. There are four available methods which are designed to reduce the redundant parameters of the soft set. But there is a very low success rate on a large number of data sets obtained from practices by these methods. In order to overcome the inherent weakness, we propose a parameter reduction method based on chi square distribution for the model of soft set. Experimental results on two real-life application cases and thirty randomly generated data sets demonstrate that our algorithm largely improves the success rate of parameter reduction, redundant degree of parameter, and has higher practicability in comparison with the four existing normal parameter reduction algorithms.

1 Introduction

Uncertainty is pervasive in many realistic fields such as economics, engineering, environmental governance, social sciences, business management, etc. Facing these uncertainties, researchers have introduced many mathematical tools, including probability theory, fuzzy set, rough set, etc. However, these mathematical tools have their own shortcomings [1]. Until 1999, Molodtsov, D. [1] put forward a novel soft set theory, which compensates for disadvantages of the insufficient parameterization about classic mathematical methods. It is known to all that soft set is a new powerful mathematical tool for uncertainty.

At present, There are two main aspects in the study of soft set such as theoretical and application research. These articles such as [2,3,4] discuss some related definitions, properties and operations of soft sets. There has been a growing interest in addressing the extended models based on soft set. We can list some popular combination models as diverse as fuzzy soft set [5, 6], interval-valued fuzzy soft set [7, 8, 27], integration of the 2-tuple linguistic representation and soft set [9], belief interval-valued soft set [10], confidence soft sets [11], linguistic value soft set [12], separable fuzzy soft sets [13], dual hesitant fuzzy soft sets [14], Z-soft fuzzy rough set [15], Fault-tolerant enhanced bijective soft set [16], and soft rough set [28].

Fortunately, more and more researchers have the resulting interests on developing the applications of soft sets in many areas. Demonstrations of soft set in real applications are easily displayed in the following fields such as information system data analysis [17], decision processing [18,19,20], conflict processing [21, 22], resource discovery [23], text classification, data mining [24,25,26] and medical diagnosis so on. In this paper, we address an associated parameter reduction problem for decision making under soft set. Redundancy is an important consideration in data, and parameter reduction is essential for the application of soft set in decision making. Many pioneer researchers have done a lot for this issue. It was firstly suggested in [29] that parameter reduction of soft set was necessary and the related concept was described. Chen et al. [30] improved the parameter reduction of soft sets in [29]. However, the method in [30] has the weakness of ignoring the added parameters. So Kong et al. initiated [31] the normal parameter reduction idea without neglecting the newly added parameters. To decrease the computational complexity of this algorithm, the improved methods were created in [32, 33]. However, three above methods for the normal parameter reduction are not appropriate for the large data sets. So a normal parameter reduction algorithm by particle swarm optimization which is suitable for large data sets was expressed in [34, 35]. Next, facing up to the inaccuracy of the method in paper [34], Han et al. [36] again proposed four 0–1 linear programming models. In this paper, we find out that due to its restrictions on special conditions about normal parameter reduction, probability of finding the reduction results and redundant level of parameter on a large number of data sets is very low by means of the above algorithms in [31, 33, 34, 36]. Consequently, we propose a parameter reduction algorithm based on chi square distribution for the soft set, which greatly improves the success rate, redundant degree of parameter and practicality of parameter reduction.

The rest of this paper is structured as follows. Section 2 reviews the basic concepts of soft set theory and four existing methods. Section 3 creates a new parameter reduction method based on chi-square distribution. In Section 4, the proposed chi-square distribution parameter reduction algorithm is applied in real life, and further compared with the four existing algorithms. Finally, the research conclusions are given in Section 5.

2 Basic concepts and the existing normal parameter reduction methods

In this section, we will briefly review the basic concept of soft set theory, which is described through an example and the existing normal parameter reduction methods.

Definition 2.1 (See [1])

Assume that U is a non-empty initial universe of objects, E is a set of parameters in relation to objects in U, and A be a subset of E, ξ(U) is the power set of U. A pair (F, A) is called a soft set over U, where F is a mapping given by

$$ F:A\to \xi (U) $$

(1)

In the above definition, the soft set over U is a parameterized family of subsets of the universe U. Let’s walk through an example on what is the soft set.

Example 2.1

An elderly person has a plan to reserve a comfortable nursing house which provides the wonderful old-age service facilities. This elderly person takes into consideration six top nursing houses. Let U = {h₁, h₂, h₃, h₄,h₅, h₆} be the six top nursing houses, suppose that E = {e₁, e₂, e₃, e₄, e₅} be the five parameters to express the situation of six nursing houses. Here e_i (i = 1,2,3,4,5) represents “good daily life assist”, “high-quality service for the wealthy”, “excellent food service”, “good education”, “home service” respectively. Table 1 represented by soft set depicts six top nursing houses from five above respects. From this table, we should discover that the structure of a soft set can classify the candidates into two categories. “1” and “0” stand for “yes” and “no”, respectively. For instance, this elderly person thinks that the nursing house h₁ has the good daily life assist, low-quality service for the wealthy and has the satisfactory screen, excellent food service, poor education and good home service from Table 1.

Table 1 Tabular representation of a soft set in example 2.1

We can apply soft set to solving decision making. However, there are some redundant parameters which should be reduced for decision making. Kong et al. initiated [31] the normal parameter reduction idea without neglecting the newly added parameters. Aiming to reduce the computational complexity, the method in [31] was improved [33]. However, these methods for the normal parameter reduction are not appropriate for the large data sets. So Kong et al. [37] proposed a normal parameter reduction algorithm based on particle swarm optimization for large data sets. Next, three types of linear programming algorithms for normal parameter reductions of soft sets are proposed in [39]. It is clear that the above four methods are created in the framework of normal parameter reduction.

Definition 2.2 (See [31])

For soft set (F, E),E = {e₁, e₂, ⋯, e_m}, if there exists a subset $A=\left\{{e}_1^{\prime },{e}_2^{\prime },\cdots, {e}_p^{\prime}\right\}\subset E$ satisfying f_A(h₁) = f_A(h₂) = ⋯ = f_A(h_n), then A is dispensable, otherwise, A is indispensable. B ⊂ E is a normal parameter reduction of E, if the two conditions as follows are satisfied

• (1) B is indispensable

• (2) f_E − B(h₁) = f_E − B(h₂) = … = f_E − B(h_n)

However, Due to its special conditions, that is, for all of objects, the parameters in subset A must satisfy f_A(h₁) = f_A(h₂) = ⋯ = f_A(h_n). This condition is not easily satisfied on the most of datasets. That is, for normal parameter reduction, probability of finding the reduction results and redundant level of parameter on a large number of data sets is very low by means of the above algorithms in [31, 33, 34, 36]. For instance, we can not find the parameter reduction results by the above methods in Table 1. In order to improve probability of finding the reduction results and redundant level of parameter on a large number of data sets and practicality, we propose a parameter reduction method based on chi square distribution for the model of soft set. The main idea of our method is to reduce the redundant parameter when two parameters have the similar parameter values for all of objects. For instance, for e₁ and e₃, that is “good daily life assist” and “excellent food service”, the two parameters have the high similarity. That is, except for h₃, for all of other objects, the two parameters have the same values. Thus, we think that the two parameters are similar. We only choose one parameter as representation while the other parameter is redundant. Based on the reduced parameter sets, the decision ability is not changed.

3 Parameter reduction method based on chi square distribution for soft set

The parameter reduction method of chi square distribution based on soft set mainly detects redundant parameters by analyzing the correlation between two parameters. In order to obtain the correlation value between the two parameters, we must first calculate the practical correlation frequency and the expected correlation frequency. Next, we will discuss the whole calculation process of the chi square distribution parameter reduction algorithm.

Let the soft set (F, E) including a set of the object set U = {p₁, p₂, …, p_n}and the parameter set E = {e₁, e₂…, e_m}, e_αand e_β represent any two parameters in the parameter set E, and f (e_i)(f (e_i) ∈ 0v1) indicates that the entity value of the soft set. To calculate the practical correlation frequency between parameters e_α and e_β, we first construct the correlation tables for each pair of parameter e_αand e_β, that is, fourfold table as shown in Table 2.

Table 2 2*2 fourfold table of each pair parameter e_αand e_β

In this table, the parameterse_αand e_βthat satisfy the number of entity values f (e_i) = 0 and f (e_i) = 1 are used to form a row (r) or a column (c), the number of parameters e_αand e_β satisfying the entity values f (e_i) = 0 and f (e_i) = 1 respectively is constructed into a row (r) or column (c), which is represented as ${N}_{f\left({e}_i\right)}$, that is, the practical correlation frequency between each pair of parameters. For example, the number of parameters that meet the entity value f (e_α) = 0 and f (e_β) = 0 between the parameters e₁ and e₂ is 2 in the dataset of Example 2.1, hence the practical correlation frequency ${N}_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=0\end{array}}$, between them is 2. The fourfold between e₁ and e₂ is shown in Table 3. Considering the subsequent work, we use the formula (2) to calculate the degrees of freedom V in the fourfold table.

$$ V=\left(r-1\right)\ast \left(c-1\right) $$

(2)

Table 3 Tabular representations of the soft set (F, E)

From the above fourfold table, it can be seen that the table is a data table with two rows and two columns, and then the degree of freedom V = 1. According to the calculation results of the above fourfold table, a definition of the chi-square distribution for the correlation between the two parameters is given in detail below.

Definition 3.1 The correlation between two parameters

The correlation between parameters e_α and e_β is defined as:

$$ {\displaystyle \begin{array}{l}{X}_{{\mathrm{e}}_{\alpha, \beta}}^2=\overset{c}{\underset{\alpha =i}{\varSigma }}\overset{r}{\underset{\beta =j}{\varSigma }}\frac{{\left({N}_{f_{\left({e}_i\right)}}-{T}_{f_{\left({e}_i\right)}}\right)}^2}{T_{f_{\left({e}_i\right)}}}\\ {}=\frac{{\left({N}_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=0\end{array}}-{T}_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=0\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=0\end{array}}}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=1\end{array}}-{T}_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=1\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_{\alpha}\right)=0\\ {}f\left({e}_{\beta}\right)=1\end{array}}}\\ {}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=0\end{array}}-{T}_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=0\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=0\end{array}}}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=1\end{array}}-{T}_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=1\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_{\alpha}\right)=1\\ {}f\left({e}_{\beta}\right)=1\end{array}}}\end{array}} $$

(3)

According to the above-mentioned fourfold table, we can know that ${N}_{f\left({e}_i\right)}$is the practical correlation frequency between the parameterse_αand e_β; ${T}_{f\left({e}_i\right)}$ is the expected correlation frequency between the parameters e_αand e_β, in other words, ${T}_{f\left({e}_i\right)}$ is the theoretical correlation value between each pair of parameter under the entity values entity values f (e_i) = 0 and f (e_i) = 1, which can be calculated by the following formula:

$$ {T}_{f\left({e}_i\right)}={T}_{f\left({e}_{\alpha, \beta}\right)}=\frac{T^{\prime}\times {T}^{\hbox{'}\hbox{'}}}{T} $$

(4)

Combined with the fourfold table,T^′ = {T₁, T₂}and T^″ = {T₃, T₄} respectively indicate the total value of row and column in the case of entity values f (e_i) = 0 and f (e_i) = 1. T is the number of the objects in the soft set. For example 2.1, there are 6 object sets, the T value is 6.

Here, we still use example 2.1, to illustrate the calculation process of formula (3) and (4) in practical applications. Suppose we calculate the correlation between e₁ and e₂ again, we must calculate the the practical correlation frequency value ${N}_{f\left({e}_i\right)}$ and expected correlation frequency value ${T}_{f\left({e}_i\right)}$ a of each pair of parameters before calculating the correlation value ${X}_{e_{\alpha, \beta}}^2$ between the two parameters. Since the actual value of each pair of parameters has been calculated in Table 3. Next, we can calculate the expected value of each pair of parameters, as shown below:

$$ {\displaystyle \begin{array}{c}{T}_{f\left({e}_{1,2}\right)}={T}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}\frac{T_1\times {T}_3}{T}=\frac{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}\right)\times \left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}\right)}{T}\frac{2\times 4}{6}=\frac{8}{6}=\frac{4}{3}\\ {}{T}_{f\left({e}_{1,2}\right)}={T}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}\frac{T_1\times {T}_4}{T}=\frac{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}\right)\times \left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\right)}{T}\frac{2\times 2}{6}=\frac{4}{6}=\frac{2}{3}\\ {}{T}_{f\left({e}_{1,2}\right)}={T}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}\frac{T_2\times {T}_3}{T}=\frac{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\right)\times \left({N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}\right)}{T}\frac{4\times 4}{6}=\frac{16}{6}=\frac{8}{3}\\ {}{T}_{f\left({e}_{1,2}\right)}={T}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\frac{T_2\times {T}_4}{T}=\frac{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\right)\times \left({N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}+{N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\right)}{T}\frac{4\times 2}{6}=\frac{8}{6}=\frac{4}{3}\end{array}} $$

Finally, combining with the two parameters of e₁ and e₂ in Table 3, we get the correlation between the two parameters as follows:

$$ {\displaystyle \begin{array}{c}{X}_{{\mathrm{e}}_{1,2}}^2=\overset{c}{\underset{\alpha =1}{\varSigma }}\overset{r}{\underset{\beta =1}{\varSigma }}\frac{{\left({N}_{f_{\left({e}_i\right)}}-{T}_{f_{\left({e}_i\right)}}\right)}^2}{T_{f_{\left({e}_i\right)}}}\\ {}=\frac{{\left({N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}-{T}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}-{T}_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=1\end{array}}}\\ {}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}-{T}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=0\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_1\right)=0\\ {}f\left({e}_2\right)=0\end{array}}}+\frac{{\left({N}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}-{T}_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}\right)}^2}{T_{\begin{array}{c}f\left({e}_1\right)=1\\ {}f\left({e}_2\right)=1\end{array}}}\\ {}=\frac{{\left(2-\frac{4}{3}\right)}^2}{\frac{4}{3}}+\frac{{\left(0-\frac{2}{3}\right)}^2}{\frac{2}{3}}+\frac{{\left(2-\frac{8}{3}\right)}^2}{\frac{8}{3}}+\frac{{\left(2-\frac{4}{3}\right)}^2}{\frac{4}{3}}\\ {}=\frac{9}{6}\end{array}} $$

Definition 3.2 correlation matrix

The correlation matrix stores a suite of correlation of all N parameters in Fig. 1, and the correlation between each pair of parameters is represented by ${X}_{e_{\alpha, \beta}}^2$.

Fig. 1

Correlation matrix between the parameters

According to the correlation calculation formula between the above two parameters, the correlation between each pair of parameters in example 2.1 is shown in Fig. 2.

Fig. 2

Correlation matrix between the parameter e1 and e2

For the sake of simplicity, we name our proposed parameter reduction algorithm of chi square distribution as C-SDPR of which detailed steps are given as follows.

3.1 Our Algorithm: parameter reduction algorithm based on chi square distribution for soft set (C-SDPR)

• Step 1: Input U = {p₁, p₂, ⋯, p_n} and E = {e₁, e₂, ⋯, e_m};

• Step 2: Calculate the correlation matrix between all two parameters, and check the correlation between parameters.

• Step 3: Access to the rejection hypothesis value D corresponding to the confidence level under the degree of freedom V = 1. Suppose the correlation between the parameters e_α and e_β is higher than D, which are strong correlation between the two parameters. So one of the parameter e_α and e_β can be reduced.

• Step 4: Get the new soft set (F, E) after parameter reduction.

In our algorithm, the confidence level depends on the decision maker itself. The rejection hypothesis value D for judging the correlation between the two parameters is taken from the critical value table of the chi-square distribution, which can usually be found in any statistics textbook. Assuming that the correlation between the two parameters is high, it is sufficient to indicate that the similarity between the two parameters is very high. Hence we can keep one parameter and reduce the other one. In order to interpret our algorithm, we will describe it in detail through an example below.

Example 3.1

Assume the object set U = {p₁, p₂, p₃, p₄, p₅} and parameter set E = {e₁, e₂, e₃, e₄, e₅}, the mapping relationship of the soft set (F, E) is shown in Table 3.

According to our method, the following process is shown.

• Step 1: Input the data in the instance.

• Step 2: calculate the fourfold table of each pair of parameters, as shown Tables 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. Combine the practical correlation frequency value between each pair of parameters in the fourfold table with formula (4) to calculate the corresponding expected frequency value, which is indicated in brackets of each table. Finally, the correlation between each pair of parameters is calculated by formula (3), and represented in matrix format, as shown in Figs. 3 and 4 respectively.

Table 4 Fourfold table of e₁, e₂

Table 5 Fourfold table of e₁, e₃

Table 6 Fourfold table of e₁, e₄

Table 7 Fourfold table of e₁, e₅

Table 8 Fourfold table of e₂, e₃

Table 9 Fourfold table of e₂, e₄

Table 10 Fourfold table of e₂, e₅

Table 11 Fourfold table of e₃, e₄

Table 12 Fourfold table of e₃, e₅

Table 13 Fourfold table of e₄, e₅

Fig. 3

The correlation between each pair of parameters

Fig. 4

Correlation matrix for Example 3.1

• Step 3: when the degree of freedom v = 1, we take the confidence level as 0.05 and the corresponding rejection hypothesis D is 3.843 by consulting the chi-square distribution table. From Fig. 3 above mentioned, we can notice that the correlation value of the parameter e₁ and e₅ is${\mathrm{X}}_{{\mathrm{e}}_{1,5}}^2=5>3.843$. Accordingly, the two attributes are strong correlation. That is, e₁ or e₅ can be reduced.

• Step 4: In the end, we will get the new soft set (F, E) after parameter reduction as {e₁, e₂, e₃, e₄} or {e₂, e₃, e₄, e₅}.

4 The comparison result

In this section, we compare the proposed algorithm with the normal parameter reduction algorithms in [31, 33, 34, 36] on two practical cases in our life and thirty randomly generated datasets, and finally show the comparison results of the five algorithms in tabular form. In short, we term the normal parameter reduction algorithm in [31] as NPR, the algorithm in [33] as NENPR, the normal parameter reduction in soft set based on particle swarm optimization algorithm in [34] as NPR-PSO, the method in [36] as NPR-LP, respectively. In detail, we make comparison among five methods from two aspects: redundant degree of parameter and success rate.

• A. Case 1: Weather index dataset in different areas

The weather station wants to predict the weather quality of some areas according to the weather index of different areas in the same period. We collect the meteorological data of some areas from China weather network and transform these data into the style of soft set, which is shown in Table 14. Among them, U represents five different areas in the same period and U = {p₁, p₂, p₃, p₄, p₅}={Lhasa, Dali, Dunhuang, Qingdao, Luoyang}. E is a set of parameter sets considered and E = {e₁, e₂, e₃, e₄, e₅, e₆}={air pollution index, tourism index, sports index, UV index, temperature index, weather humidity index}. Next, we will discuss the results of the five algorithms for the above datasets.

• (1) Parameter reduction by our algorithm

• Step 1: Input the soft set as shown in Table 14;

• Step 2: According to the given formula and definition, the correlation values between all two parameters are calculated and indicated in matrix form in Fig. 5.

• Step 3: Suppose we take the confidence level is 0.2. When the degree of freedom is 1, the corresponding rejection hypothesis value D is 1.64 by consulting the chi square distribution table. We find that the correlation between parameter e₁ and e₅, e₂ and e₃, e₂ and e₅, e₄ and e₅are higher than 1.64, so the parameter e₁ or e₅, e₂ or e₃, e₂ or e₅, e₄ or e₅ can be reduced. After the simplification, the parameters {e₁, e₂, e₄} or {e₃, e₅} can be reduced.

• Step 4: Finally, we get the new soft set for minimizing after parameter reduction is {e₃, e₅, e₆}.

Table 14 Soft set for case 1

Fig. 5

Correlation matrix for case 1

• (2) Parameter reduction by NPR, NENPR, NPR-PSO and NPR-LP

When the soft set for case 1is input, we can not discover the parameter subset which satisfies the condition of ${\sum}_{e_k\in A}{\mathrm{p}}_{1k}={\sum}_{e_k\in A}{p}_{2k}=\dots ={\sum}_{e_k\in A}{p}_{5k}$. Therefore, we can not find the parameter reduction result by the methods of NPR, NENPR, NPR-PSO and NPR-LP.

• (3) Comparison results on case 1.

From the above discussion, the comparison results of the five algorithms are analyzed and presented in Table 15. Here, we give two assessment criteria such as redundant degree of parameter and success rate.

• 1) Redundant degree of parameter

Table 15 Comparison results on case 1

Definition 4.1

For soft set (F, E) including a set of the object set U = {p₁, p₂, …, p_n}and the parameter set E = {e₁, e₂…, e_m}, the redundant degree of parameter is defined by

$$ \mathrm{g}=\frac{\mathrm{s}}{\mathrm{m}} $$

(5)

Where m denotes the number of parameters and s expresses the number of reduced parameter. Redundant degree of parameter g represents the ratio of the number of reduced parameter to all of parameter. Notice that the higher value of g means the higher efficiency of reduction and vice versa.

In case 1, there are six parameters, therefore, m = 6; we can reduce the parameters{e₁, e₂, e₄}by our method, which means s = 3. As a result, g=$\frac{\mathrm{s}}{\mathrm{m}}=\frac{3}{6}$=50%. For NPR, NENPR, NPR-PSO and NPR-LP, there is no reduced parameter, which means s = 0. Therefore, g = 0 by the existing four methods.

• 2) Success rate

Definition 4.2

For soft set (F, E) including a set of the object set U = {p₁, p₂, …, p_n}and the parameter set E = {e₁, e₂…, e_m}, the success rate of parameter reduction is defined by

$$ \kern0.5em \mathrm{d}=\frac{\mathrm{a}}{\mathrm{t}} $$

(6)

Where t denotes the number of datasets expressed by soft set and a expresses the number of datasets on which we can find the parameter reduction results. Success rate of parameter reduction d represents the probability of finding parameter reduction on all of datasets. Notice that the higher value of d means the higher success rate of reduction and vice versa.

In case 1, there is one dataset, therefore, t = 1; we can find the parameter reduction as {e₃, e₅, e₆}by our method, which means a = 1. As a result, d=$\frac{\mathrm{a}}{\mathrm{t}}=\frac{1}{1}$=100%. For NPR, NENPR, NPR-PSO and NPR-LP, we can not find the parameter reduction result, which means a = 0. Therefore, d = 0 by the existing four methods.

From Table 15, it is easy to find that our algorithm is superior to the four existing algorithms on case 1.

• B. Case 2: Online hotels evaluation dataset

In order to verify our algorithm, we have collected data of five-star hotels.

Among them, U = {p₁, p₂, …, p₁₀, …p₁₅, p₁₆} represents 16 hotels such as “JW Marriott Hotel”, “Millennium Hotel”, “Royal Palace Hotel”, “Royal Juran Hotel”,” Trade Hotel”, “Maya Hotel”, “Pacific Regency Suite Hotel”, “Renaissance Hotel”, “Mandarin Oriental Hotel”, “G Tower Hotel”, “Ritz Carlton Galaxy”, “Sunway Prince Hotel”, “Crown Plaza Pearl Hotel”, “Hilton Hotel”, “Garden St. Giles Icon Hotel” and “Mi Casa All-Suite Hotel”, respectively. E = {e₁, e₂, e₃, e₄, e₅, e₆} indicates the parameters as diverse as “clean”, “comfortable”, “geographic location”, “service”, “staff quality” and “cost-effective”. Customers want to choose the best hotel among sixteen hotels. The collected dataset is expressed by the model of soft set as shown in Table 16. Before making decision, we should reduce the redundant parameters.

• (1) parameter reduction for Chi-Square Distribution

• Step 1: Input the soft set as shown in Table 16;

• Step 2: Calculating the correlation value between each pair of parameters, the results are expressed in the form of the matrix of Fig. 6;

• Step 3: Assume that the confidence level is taken as 0.025, the corresponding rejection assumption is about 5.024 under the degree of freedom as 1. Discovering the correlation between parameter e₁ and e₂, e₁ and e₃, e₁ and e₆ are more than 5.024, then the parameter e₁ or e₂, e₁ or e₃, e₁ or e₆can be reduced. After simplification, the parameter set {e₁} or {e₂, e₃, e₆} can be reduced.

• Step 4: Finally, we get the new soft set for minimizing after parameter reduction is {e₃, e₅, e₆}.

Table 16 Dataset for case 2

Fig. 6

Correlation matrix for case 2

• (2) Parameter reduction by NPR, NENPR, NPR-PSO and NPR-LP

It is pity that we can not find the parameter reduction result by the methods of NPR, NENPR, NPR-PSO and NPR-LP on case 2.

In case 2, there are six parameters, therefore, m = 6; we can reduce the parameters {e₁, e₂, e₄} by our method, which means s = 3. As a result, g=$\frac{\mathrm{s}}{\mathrm{m}}=\frac{3}{6}$=50%. For NPR, NENPR, NPR-PSO and NPR-LP, there is no reduced parameter, which means s = 0. Therefore, g = 0 by the existing four methods.

In case 2, there is one dataset, therefore, t = 1; we can find the parameter reduction as {e₃, e₅, e₆} by our method, which means a = 1. As a result, d=$\frac{\mathrm{a}}{\mathrm{t}}=\frac{1}{1}$=100%. For NPR, NENPR, NPR-PSO and NPR-LP, we can not find the parameter reduction result, which means a = 0. Therefore, d = 0 by the existing four methods.

The comparison results of the five algorithms on case 2 are presented in Table 17. It is clear that our method outperforms NPR, NENPR, NPR-PSO and NPR-LP.

Table 17 Comparison results on case 2

• C. The results of the experiment on thirty randomly generated datasets

Here, thirty soft-set datasets are randomly generated to test our proposed method and four existing methods such as NPR, NENPR, NPR-PSO and NPR-LP. The confidence level is taken as 0.05, degree of freedom is 1, and the corresponding the rejection hypothesis D is 3.843. As a result, we can discover the reduction results on 22 datasets by our method. Meanwhile we can find the reduction results on 2 datasets by NPR, NENPR, NPR-PSO and NPR-LP. Therefore, the success rate of our method is computed as 22/30 = 73.3%. Meanwhile the success rates of NPR, NENPR, NPR-PSO and NPR-LP are 2/30 = 6.7%, respectively. From Fig. 7 and Table 18, our method is much better than NPR, NENPR, NPR-PSO and NPR-LP about success rate of parameter reduction and average redundant degree of parameter. Compared with the four existing methods, the improvement of average redundant degree of parameter of our method on thirty datasets is up to 90.7%; success rate is improved to 90.9%.

Fig. 7

Success rate of five methods

Table 18 Comparison results on thirty datasets

5 Conclusion

In this paper, we propose a new parameter reduction method based on chi square distribution for the model of soft set. The motivation of this idea is to improve the success rate of finding reduction for the existing methods such as NPR, NENPR, NPR-PSO and NPR-LP. Because of the very low success rate and redundant degree of parameter, the four existing methods are not practical in the real-life applications. On two real cases, success rate of our method is up to 100%, the redundant degree of parameter is up to 50%, in contrast, success rate and redundant degree of parameter of the four existing methods are 0, respectively. The improvement of average redundant degree of parameter of our method on thirty random generated datasets is up to 90.7%; success rate is improved to 90.9% compared with the four existing methods. Finally, we can draw the conclusion that the proposed method has much higher success rate, redundant degree of parameter and then practicability compared the existing four approaches.