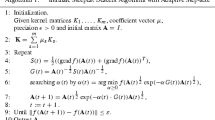Metric transfer learning via geometric knowledge embedding

Abstract

The usefulness of metric learning in image classification has been proven and has attracted increasing attention in recent research. In conventional metric learning, it is assumed that the source and target instances are distributed identically, however, real-world problems may not have such an assumption. Therefore, for better classifying, we need abundant labeled images, which are inaccessible due to the high cost of labeling. In this way, the knowledge transfer could be utilized. In this paper, we present a metric transfer learning approach entitled as “Metric Transfer Learning via Geometric Knowledge Embedding (MTL-GKE)” to actuate metric learning in transfer learning. Specifically, we learn two projection matrices for each domain to project the source and target domains to a new feature space. In the new shared sub-space, Mahalanobis distance metric is learned to maximize inter-class and minimize intra-class distances in target domain, while a novel instance reweighting scheme based on the graph optimization is applied, simultaneously, to employ the weights of source samples for distribution matching. The results of different experiments on several datasets on object and handwriting recognition tasks indicate the effectiveness of the proposed MTL-GKE compared to other state-of-the-arts methods.

1 Introduction

Today, variety of web technologies, social media and digital devices continuously generate enormous amount of visual data such as images and videos in increasing manner [1].This case confront us with one of the challenging subjects of big data problem such as data management, in the rising stream of novel applications and corresponding data generation. A prerequisite for big data management is labeling and classification of existing data. However, the researchers confront with an entirely sparse labeled data, which is not enough for training an accurate classifier. On the other hand, labeling this enormous amount of data may require an expert to use an expensive way.

In such circumstances, transfer learning and domain adaptation methods [2, 3] can be used to utilize previous source labeled data to create a classifier and apply it on new task in target data. Conventional machine learning methods have the assumption of same distribution of source and target samples, while this assumption in real world application is not considered anymore and the cross-domain problem arises. Hereupon, domain adaptation with the aim of reducing the destructive impact of cross domain problem on the classification accuracy and learning a domain invariant model from training data, is introduced. However, state-of-the-arts have three established methods to mitigate cross domain problems under elimination of distribution divergence between domains as follows [4]: 1) instance-based methods [5,6,7,8] which use more related source samples for training a predictive classifier for target data via re-weighting procedure. By doing so, distribution difference between domains can be decreased. Instance-based methods have two assumptions. First, with allocating more weights to those more related samples, only some of the source instances are used to learn a classifier [9]. Second, the source and target domains should have the same conditional distribution; however, they could have different marginal distribution [10]; 2)metric-based methods [11,12,13,14,15] also called distance metric learning (DML) algorithms, aim to learn an optimal distance metric for measuring sample pairs similarity or dissimilarity by exploiting meaningful correlations between source and target data; 3) feature-based methods [16,17,18] with the aim of distribution divergence and classification error minimization and also preservation of important properties of data, attempt to learn a latent sub-space by discovering the shared features of source and target data with small distribution gap.

The established researches in domain adaptation (DA) has three main line of approaches. The first line consists of metric learning methods, e.g., Consistent distance metric learning (CDML) [19] that attempts to learn a consistent distance metric under covariate shift [20] and utilize Euclidean distance metric to determine sample pairs correlation. The learned metric under Euclidean distance is then used in target task classifier to facilitate the classification problem by measuring the (dis)similaritly of samples, where it may cause the learned classifier finds suboptimal solutions because of Euclidean distance limitations. In the other words, the intra-class distance decreases while the inter-class distance does not increase optimally. The second line e.g., Visual domain adaptation (VDA) [21] seeks a subspace representation, which uncovers discriminant and domain invariant features and projects samples from original source and target domains into achieved sub-space by only one projection matrix. The third line of researches, for an example Metric transfer learning framework (MTLF) [4], in order to minimize the distribution gap between domains, attempt to assign less weights for those samples of source domain, which are far from target distribution to avoid from negative transfer. In MTLF sample reweighting is performed by statistical analysis such as direct importance estimation [22], which requires expensive distribution density estimation.

The proposed approach in this paper, called Metric Transfer Learning via Geometric Knowledge Embedding (MTL-GKE), uncovers metric-based methods with learning an appropriate distance metric alongside finding a new feature representation and utilizes a novel instance reweighting approach with graph optimization in order to address the aforementioned issues and bridge the distributional and geometrical divergences between domains as well as maximizes sample discrepancy for accurately classifying target samples. Specifically, MTL-GKE learns two projection matrices for each of source and target domains via a graph Laplacian to map samples from both domains into particular sub-spaces. Since the geometrical structure of samples plays crucial role in landmark selection [23], MTL-GKE utilizes constructed Laplacian graph to select more related samples. In this way, instead of performing the complex mathematical operations on matrices, simple arithmetic operations are performed on an integer. For better classification on target task followed by better labeling of unknown data, we need to maximize the sample discrepancy to decrease the expected error of learned model in classification. For this purpose, we take advantage of metric learning methods with learning an appropriate distance metric. However, if most of the training samples are inappropriate for training a target model, using a distance metric that does not take the correlation of samples into consideration, an accurate model cannot be learned. As a result, we employ the Mahalanobis distance metric [24], which considers the dependency of samples in measuring the similarity or dissimilarity of samples.

In general, the contributions of our work are as follows.

• 1) In order to perform more accurately classification, MTL-GKE minimizes the distance within each class and maximizes distance between classes via Mahalanobis distance metric in which the correlations between each sample pairs affect their computed value distance. As a result, if the sample pairs are more related, the distance between them will be smaller.

• 2) In this paper, we utilize a novel instance reweighting strategy that construct a Laplacian graph with extraction of samples into vertices of graph and try to optimize the formed graph to minimize the distribution differences of domains. Therefore, more efficient classification is performed.

• 3) Since in optimization problem, learning both source samples weights and distance metric are performed, simultaneously, in a pipelined framework and their values are updated after each other in an iterative manner, this makes it possible that Mahalanobis distance metric is learned under a more accurate source sample weights, which leads to develop an optimal discrepancy between samples.

In the rest of this paper, we briefly review some related work from recent literature in Section 2. The details of our proposed method as well as the required definitions are presented in Section 3. In Section 4, we propose a theoretical optimization problem and in Section 5 the results of our experiments on several datasets are compared. Eventually, in Section 6 we discuss about the conclusion and future works.

2 Related work

In this section, we review the previous studies that are related to our work. According to the available literature review [2], since different types of knowledge can be transferred across domains, there are various approaches for knowledge transfer in domain adaptation. This knowledge can be either each of instances, feature representation, relational knowledge across domains or a combination of them. In this section, we interest to review the most related works to our method that can be sorted into metric-based, feature-based and instance-based transfer learning.

In the first class, the goal is to improve the performance of classification task by learning a distance metric for target task. Soleimani et al. [25] proposed a deep multi-task metric learning (DMML) for offline signature verification. DMML with the use of deep neural networks, considers the separated layers for each authentic signer and also a shared layer for all authors, and utilizes squared Euclidian distance in top layer for measuring the similarity between different pairs of signatures to distinguish genuine signature from its forgery. As another work, a discriminative distance metric learning with label consistency [26] was proposed for high spatial resolution remote sensing image classification. In this approach, at first the features of images are extracted and then the distance metric was learned for maintaining the intra-class density and inter-class discrepancy as well as label consistency. Ding et al. [27] proposed a robust transfer metric learning framework, which discovers the low-rank metric to mitigate both marginal and conditional distribution divergences and attempts to discover a robust metric to facilitate the learning of target domain. A semi-supervised metric learning method was proposed as semi-supervised multi-view distance metric learning [28], which learns a distance metric from different extracted feature sets and quantifies dissimilarity of different cartoon characters under the graph-based learning.

In the second class, sub-space learning is applied to adapt the source and target domains. Zhu et al. [29] proposed a semantic subspace learning in which the source and target domains are in text and image format, respectively. They expanded the representation of target images with semantic concept that extracted from source text via collective matrix factorization technique [30]. Gong et al. proposed a geodesic flow kernel (GFK) [31] for unsupervised domain adaptation. The geodesic flow is created under source domain subspaces to target domain with different representations to extract those sub-spaces that are domain invariant. Wang et al. [32] proposed a transfer feature representation method via multi-kernel learning that combines multiple kernels to create a reproducing kernel Hilbert space [33] and projects samples to the achieved space with linear transformation. Xu et al. [34] proposed an unsupervised transfer representation method with Takagi-Sugeno-Kang (TSK) Fuzzy system [35] as (TRL-TSK-FS). In TRL-TSK-FS, TSK Fuzzy system is used as feature mapping, which discovers nonlinear transformation without kernel functions and creates a shared feature space between domains. It also uses principle component analysis and linear discriminative analysis to preserve the intrinsic information of samples. Also, Long et al. [36] proposed to use deep convolutional neural network for representation of transfer learning. In fact, they embed task-specific features of higher layers into a reproducing kernel Hilbert space to make them safely transferable for kernel matching across domains. Rossiello et al. [37] proposed a model to transfer the relational representation of entity pairs of textual corpora. Specifically, they used Siamese network to learn similarity between instance pairs and then tried to minimize the difference between different paraphrases among the similar entity pairs.

In the third category, Chattopadhyay et al. [5] proposed a multi-source domain adaptation that obtains a set of weight vectors for each source domain and incorporates various source domain data with weight vectors. Moreover, the weights are used to obtain pseudo labels of target data. Labeled and pseudo labeled target samples are then used to learn a target classifier. Gong et al. [38] proposed an unsupervised instance-based domain adaptation that selects multiple sets of landmarks where each of which obtains from different perspective. The landmarks are then used to create auxiliary tasks that are resulted in domain invariant features for each task and finally integrates all resulted features for original domain adaptation problem. Aljundi et al. [39] attempted to discover a set of landmarks from source and target domains by assigning a value to each sample based on the Gaussian kernel [40] and compare it with predefined threshold. As a result, if it is greater than the threshold, the sample can be considered in landmark set. Finally, the landmarks are used to find a new representation of source and target domains.

Our study is more associated with the work proposed by Cao et al. [19] named consistent distance metric learning (CDML) that mitigates the problem of domain shift in metric learning framework. It is noteworthy that we use sample reweighting and landmark selection in the same concept and are interchangeably. The basic idea behind CDML and our proposed MTL-GKE is similar in decreasing the distribution gap between the source and target tasks, but MTL-GKE is different from following three aspects: 1) in CDML the importance of source instances for sample reweighting is determined by density ratio estimation [22] as well as KL-divergence [41]. In contrast, in MTL-GKE, landmark selection is employed on geometrical structure of samples and performed based on the graph Laplacian instead of complex mathematical operations. 2) While in CDML the source samples are weighted first and then Mahalanobis distance metric is then learned under those reweighted samples, in MTL-GKE these two steps are learned, simultaneously, in an alternative framework. As a result the distance metric learning is performed with an appropriate weighted source samples. 3) Finally, in the proposed MTL-GKE, we utilize two projection matrices via a graph Laplacian for mapping the source and target data into a shared subspace, one for each domain. Therefore, in the latent space, the source and target data are distributed identically and the sample structures are preserved consistently.

3 Proposed method

3.1 Problem definition

• A. Notations in this paper, we supposed to represent matrices with bold uppercase letters and vectors via bold lowercase letters. The weight of source samples is a vector and is indicated by w, and a sample set is indicated by X = {x_i,y_i|i = 1,2,...,n} where x_i is the i^th sample vector and y_i is the correspondence label vector and n denotes the number of samples. Similarly, we denote X_s to represent the source samples and X_t to represent the target samples. We denote A to be the Mahalanobis matrix, and P, K, ${\mathscr{L}}$ and M to represent the projection, kernel, Laplacian and MMD (Maximum Mean Discrepancy) [42] matrices, respectively. The ℓ_2,1 − norm of the assumptive matrix M is denoted by $\|\textit {\textbf {M}}\|_{1,2}={\sum }_{j}\sqrt {{\sum }_{i}(\textit {\textbf {M}}_{ij})^{2}}$ and it’s Frobenius norm is denoted by $\|\textit {\textbf {M}}\|_{F}=\sqrt {{\sum }_{i}\delta _{i}(\textit {\textbf {M}})^{2}}$ in which δ(M) is the singular value of matrix M.

• B. Definitions

  Definition 1

  Domain D consists of an m-dimensional feature space X and a probability distribution P(x) where x ∈X. For a given domain D, task T can be defined as a composition of label set Y and a predictive classifier f(x) where T = {Y, f(x)}.

  Definition 2

  Mahalanobis distance metric is a measure to compute the similarity between pairs of x_i and x_j samples that incorporates the correlation between samples in its computation via inversed covariance matrix as follows:

  $$ MD=\sqrt{(\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})^{T}\boldsymbol{{C}} (\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})} $$

  where C is an inversed covariance matrix. As a result for more similar sample pairs, the value of distance metric decreases. C. Problem statement In our transfer learning setting, we consider two different distributions of labeled source domain D_s and a mostly unlabeled target domain D_t, where the marginal distribution of domains are different, i.e., P_s(X)≠P_t(X) and the conditional distribution of the source and target samples are similar, i.e., P(y_s|X_s) ≈ P(y_t|X_t). In this situation, the learned metric with source domain may not be appropriate for target domain. On the other hand, we have a few labeled target data for learning a desired target metric. In this paper, we are supposed to minimize the distribution gap between source and target domains, and learn an optimal distance metric with labeled source domain.

3.2 Overall framework

The aim of domain adaptation methods is to transfer information and knowledge across different distributed domains. For this purpose, we have to learn a distance metric and find a shared feature representation on which domains could be well aligned together. As a result, we introduce an approach for simultaneously learning the Mahalanobis distance metric A for target domain, new feature representations K_s and K_t for source and target domains, and a predictive function f to label the unseen target samples. The proposed objective is written as follows:

$$ \underset{\boldsymbol{A},\boldsymbol{P},\textit{f}}{\min \mathcal{J}}= \mathnormal{r}(\boldsymbol{A})+\mathnormal{\varphi}(\boldsymbol{P}_{s}, \boldsymbol{P}_{t})+ \eta\ell(\textit{f}, \boldsymbol{A}, \boldsymbol{w}) $$

(1)

where η > 0 is a trade-off parameter for balancing the effect of various terms in objective function. Also, the first term provides to manage the propagation error of the learned metric A. The second term provides the knowledge adaptation and feature matching in which P_s and P_t are projection matrices to project the samples of source and target domains onto a common feature spaces, respectively. The third term ℓ is introduced as a loss function for predictive function f under the learned Mahalanobis metric A and instance weight w. The specific definition of each part of the objective function will be explained in the rest.

3.2.1 Metric learning

In this section, we deal with learning a Mahalanobis distance metric for target domain, which is defined as follows:

$$ dist_{ij}=\sqrt{(\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})\boldsymbol{{M}} (\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})^{T}} $$

where x_i and x_j are the sample pairs, $\textit {\textbf {M}}\in \mathbb {R}^{d \times d}$ is a positive semi-definite matrix with d dimension, where it can be decomposed as M = A^TA in which $\textit {\textbf {A}}\in \mathbb {R}^{d \times d}$. Therefore, learning a Mahalanobis matrix M can be substituted by learning the matrix A. The aim of the first term of objective function is to minimize the propagation error of the learned metric specified as A, which is defined as follows:

$$ \mathnormal{r}(\boldsymbol{A})=\textit{tr}(\boldsymbol{A}^{T}\boldsymbol{A}) $$

(2)

where tr(.) denotes the trace of matrix.

3.2.2 Feature and distribution matching

The aim of domain adaptation methods is to reduce the distribution gap across domains. For this purpose, we need a data transition to latent space as well as transferring some intrinsic and geometric structure of samples and selecting some latent features that are useful for classification. In this way, we define φ(P_s,P_t) as follows:

$$ \mathnormal{\varphi}(\boldsymbol{P}_{s}, \boldsymbol{P}_{t})= (\boldsymbol{X}_{s}\boldsymbol{P}_{s}, \boldsymbol{X}_{t}\boldsymbol{P}_{t})_{\mathcal{H}}+(\boldsymbol{P}_{s}^{T}\boldsymbol{K}_{s}, \boldsymbol{P}_{t}^{T}\boldsymbol{K}_{t}) $$

(3)

where the first part mitigates the domain shift problem in which P_s and P_t are projection matrices and the subscript ${\mathscr{H}}$ shows the distribution matching that is performed in Hilbert space. Moreover, the second part shares some latent factors between domains, i.e., structure consistency and feature selection in which K_s and K_t are new well aligned representations for source and target domains, respectively. In the rest, we specify the details of each part.

• A. Distribution matching In domain adaptation methods, we generally encounter with different distributed source and target samples. In this section, we attempt to find a shared subspace for both X_s and X_t with no distribution difference, any more. Recent researches utilize MMD to match two distributions based on the empirical means of domains in a reproducing kernel Hilbert space as follows:

  $$ \begin{array}{@{}rcl@{}} \textit{D}_{\textit{MMD}}(\boldsymbol{X}_{s},\boldsymbol{X}_{t})=\|\frac{1}{n_{s}}\sum\limits_{i=1}^{n_{s}}\boldsymbol{Z}_{s}^{T}\boldsymbol{X}_{s,i}- \frac{1}{n_{t}}\sum\limits_{j=1}^{n_{t}}\boldsymbol{Z}_{t}^{T}\boldsymbol{X}_{t,j}\|_{\mathcal{H}}^{2} \end{array} $$

  (4)

  where n_s and n_t are the number of source and target samples, and Z_s and Z_t are the transformation matrices onto a latent space, one for each domain. To show whether these projection matrices correctly project the source and target samples into a common space, we combine two projection matrices to learn them, simultaneously. In this purpose, we introduce data matrix X as $\textit {\textbf {X}}=\binom {\textit {\textbf {X}}_{s}}{\textit {\textbf {X}}_{t}}$ and projection matrix Z as $\textit {\textbf {Z}}=\binom {\textit {\textbf {Z}}_{s}}{\textit {\textbf {Z}}_{t}}$. Therefore, (4) can be written in closed form as:

  $$ \textit{D}_{\textit{MMD}}(\boldsymbol{{X}}_{s},\boldsymbol{{X}}_{t})= \textit{tr}(\boldsymbol{{Z}}^{T}\boldsymbol{{XMX}}^{T}\boldsymbol{{Z}}) $$

  (5)

  where M defines the MMD matrix and is computed as follows:

  $$ \textbf{\textit{M}}_{ij}=\begin{cases} \frac{1}{n_{s}n_{s}}, & \text{if } \boldsymbol{{x}}_{i},\boldsymbol{{x}}_{j}\in \boldsymbol{{X}}_{s} \\ \frac{1}{n_{t}n_{t}}, & \text{if } \boldsymbol{{x}}_{i},\boldsymbol{{x}}_{j}\in \boldsymbol{{X}}_{t} \\ \frac{-1}{n_{s}n_{t}}, & \text{otherwise}. \end{cases} $$

  Since the distribution matching is performed in an RKHS space [33], we consider kernel matrix K = ϕ(x)^Tϕ(x), in which ϕ(x) is a kernel mapping. In this paper, we use Z = ϕ(x)P to kernelize PCA (principle component analysis) [43] to map samples into a common space via a nonlinear mapping ϕ(x) and perform a linear PCA in common space. Hence, Eq. (5) can be rewritten as:

  $$ \textit{D}_{\textit{MMD}}(\boldsymbol{X}_{s},\boldsymbol{X}_{t})_{\mathcal{H}}= \textit{tr}(\boldsymbol{P}^{T}\boldsymbol{KMK}^{T}\boldsymbol{P}) $$

  (6)

  where $\textit {\textbf {P}}=\binom {\textit {\textbf {P}}_{s}}{\textit {\textbf {P}}_{t}}$ is a transformation matrix for both kernelized PCA and also mapping K onto a common subspace.

• B. Structure consistency In this study, we consider an assumption that takes into account the intra-class compactness and inter-class separability. According to [44], samples with same class labels tend to stay close with each other and are connected on a graph. In this way, to increase the effectiveness of distribution matching, it is more useful to keep this structure of samples during transformation and distribution adaptation. In this way, let 𝜗_i be the new representation of feature vector x_i in common space. According to [45], the following equation is minimized for structure preservation:

  $$ \frac{1}{2}\sum\limits_{i,j=1}^{n}\|\vartheta_{i}-\vartheta_{j}\|^{2}\boldsymbol{W}_{ij} $$

  (7)

  where W is adjacency matrix and W_ij defines the correlation between each sample pair. In this paper, to acquire W we use cosine similarity as follows:

  $$W_{ij}=\begin{cases} cosine(\boldsymbol{{x}}_{i},\boldsymbol{{x}}_{j}) & \text{if \ } \boldsymbol{{x}}_{i}\in Nearest_{k}(\boldsymbol{{x}}_{j}) \\ 0, & \text{otherwise} \end{cases}$$

  where Nearest_k(x_j) denotes the k-nearest neighbors of $\textit {\textbf {x}}_{j}^{th}$ sample with same class as x_i. Given 𝜗 = P^TK, (7) can be rewritten as follows:

  $$ \begin{array}{@{}rcl@{}} &&\frac{1}{2}\sum\limits_{(i,j=1)}^{n}\|\vartheta_{i}-\vartheta_{j}\|^{2}\boldsymbol{{W}}_{ij}\\&=& \frac{1}{2}\sum\limits_{(i,j=1)}^{n}\|\boldsymbol{{p}}^{T}\boldsymbol{{K}}_{i}- \boldsymbol{{P}}^{T}\boldsymbol{{K}}_{j}\|^{2}\boldsymbol{{W}}_{ij}\\&=& \sum\limits_{i=1}^{n}\boldsymbol{{P}}^{T}\boldsymbol{{K}}_{i} \boldsymbol{{D}}_{ii}\boldsymbol{{K}}_{i}^{T}\boldsymbol{{P}}- \sum\limits_{i,j=1}^{n}\boldsymbol{{P}}^{T}\boldsymbol{{K}}_{i}\boldsymbol{{W}}_{ij} \boldsymbol{{K}}_{j}^{T}\boldsymbol{{P}}\\ &=&\textit{tr}(\boldsymbol{{P}}^{T}\boldsymbol{{K}}\mathcal{L}\boldsymbol{{K}}^{T}\boldsymbol{{P}}) \end{array} $$

  (8)

  where ${\mathscr{L}}=\textit {\textbf {D}}-\textit {\textbf {W}}$ denotes the graph Laplacian and $\textit {\textbf {D}}_{ii}={\sum }_{j}\textit {\textbf {W}}_{ij}$ is a diagonal matrix that its i^th diagonal entry is the sum of i^th row of W.

• C. Feature selection As discussed in previous sections, we utilize multiple projections to map high dimensional features onto a low dimensional common space. However, latent subspace may include numerous features that are not really important for domain adaptation. For alleviate useless features in this part and select domain invariant features that are beneficial for domain adaptation and distribution matching, we apply ℓ_2,1 − norm to the projection matrix in the form of ∥P∥_2,1. This leads to select the efficient and domain invariant features in the shared space. Moreover, during the distribution matching for knowledge transfer, information loss may occur. To mitigate this problem, we propose to introduce PCA regularization that preserves the intrinsic information of target samples as follows:

  $$ \|\boldsymbol{K}_{t}-\boldsymbol{P}_{t}{\boldsymbol{P}}_{t}^{T}\boldsymbol{K}_{t}\|_{\mathcal{F}}^{2} $$

  (9)

  where it can be rewritten as follows:

  $$ -tr((\boldsymbol{{P}}_{t}^{T}\boldsymbol{{K}}_{t}) (\boldsymbol{{P}}_{t}^{T}\boldsymbol{{K}}_{t})^{T})= -tr(\boldsymbol{{P}}^{T}\boldsymbol{{K}}\ddot{I}\boldsymbol{{K}}^{T}\boldsymbol{{P}}) $$

  (10)

  where $\ddot {I}$ is a diagonal matrix defined as:

  $$\ddot{I}_{ii}=\begin{cases} 1, & \text{if } \boldsymbol{{x}}_{i}\in \boldsymbol{{X}}_{t} \\ o, & \text{otherwise}. \end{cases} $$

  Given (6), (8) and (10) and substituting them in (3), we can rewrite (3) as follows:

  $$ \begin{array}{@{}rcl@{}} \varphi(\boldsymbol{{P}}_{s},\boldsymbol{{P}}_{t})= tr(\boldsymbol{{P}}^{T}\boldsymbol{{K}}& (\boldsymbol{{M}}+\lambda \mathcal{L}-\beta \ddot{I})\boldsymbol{{K}}^{T}\boldsymbol{{P}})+ \\ \gamma\|\boldsymbol{{P}}\|_{2,1}&\\ s.t.,~~ \boldsymbol{{P}}^{T}\boldsymbol{{KHK}}^{T}\boldsymbol{{P}}&=\boldsymbol{{I}} \quad \text{and} \quad \lambda, \beta, \gamma > 0 \end{array} $$

  (11)

  where λ, β and γ are penalty parameters. Also, P^TKHK^TP = I is defined to avoid the trivial solutions in which $\textit {\textbf {H}}=\textit {\textbf {I}}_{n}-\frac {1}{n}\textit {\textbf {1}}_{n}$, 1_n is an n × n matrix that its elements are equal to 1 and $n=n_{s}+{n_{t}^{l}}+n_{t}$ where ${n_{t}^{l}}$ is the number of target samples for training.

3.2.3 Landmark selection

Since the number of labeled target data is rare to learn a target distance metric, we could utilize source samples in order to metric learning. However, some samples may have different distribution from target domain and thus may cause learning an inappropriate distance metric. To learn optimal distance metric, we can select more related source samples to domain adaptation, with the name landmarks, [7, 22, 39, 46, 47] via statistical analysis, which is a time consuming operation. Since landmarks are more correlated to geometrical structures, we suppose to select landmarks with graph optimization that extracts samples into vertices of graph and the similarity value of source samples is measured by its degree.

Considering a C class problem with X = X¹ ∪ X²... ∪ X^C, we construct graph G where each point of X form a vertex of graph. For each point of ${X_{t}^{i}}$ we find k-nearest neighbor of ${X_{s}^{i}}$ based on the cosine similarity after distribution matching in new feature space as follows:

$$ \mathcal{K}\mathcal{}=\bigcup_{i=1}^{C}knnsearch({\boldsymbol{P}}_{s}^{T}{\boldsymbol{K}}_{s}^{i}, \boldsymbol{P}_{t}^{T}{\boldsymbol{K}}_{t}^{i},k) $$

(12)

where $\mathcal {K}$ defines a vertex set of X_s samples that belongs to the k-nearest neighbor of X_t. Given $\mathcal {K}$, we could connect each sample of X_t to its k-nearest neighbor of X_s in $\mathcal {K}$. In this way, the degree of each vertex of source samples is updated. Those source samples in $\mathcal {K}$ with higher degree is selected as landmarks. We introduce weight vector w ∈ [0,1] where Σ_iw_i = 1 defines the weight of each source sample based on the degree of them in $\mathcal {K}$. At first for each sample, it considers the same weight and initializes w = 1/n_s. Then it updates w for each source sample via the degree of corresponding vertex $\mathcal {K}_{i}$ as follows where deg(.) is the degree of vertex:

$$ \textbf{\textit{w}}_{i}=\frac{deg(\mathcal{K}_{i})}{{\sum}_{i}deg(\mathcal{K}_{i})}. $$

(13)

At the end, the weight vector w is used to learn an optimal distance metric for target domain.

3.2.4 Loss function

To mitigate the classification problem, we adopt the proposed approach in [48] to define a loss function for using k-nearest neighbor classifier as follows:

$$ \ell(\textit{f}, \boldsymbol{A}, \boldsymbol{w})= \ell_{in}(\boldsymbol{A}, \boldsymbol{w})-\ell_{out}(\boldsymbol{A}, \boldsymbol{w}) $$

(14)

on which

$$ \begin{array}{@{}rcl@{}} \ell_{in}(\boldsymbol{{A}}, \boldsymbol{{w}})= \underset{y_{i}=y_{j}}{\sum}\boldsymbol{{w}}&(\boldsymbol{{x}}_{i})\boldsymbol{{w}} (\textbf{\textit{x}}_{j})\|\boldsymbol{{A}}(\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})\|^{2} and \\ \ell_{out}(\boldsymbol{{A}}, \boldsymbol{{w}})= \underset{y_{i}\neq y_{j}}{\sum}\boldsymbol{{w}}&(\textbf{\textit{x}}_{i})\boldsymbol{{w}} (\boldsymbol{{x}}_{j})\|\boldsymbol{{A}}(\boldsymbol{{x}}_{i}-\boldsymbol{{x}}_{j})\|^{2} \end{array} $$

where ℓ_in is the sum of intra-class weighted difference and ℓ_out is the sum of inter-class weighted difference. By substituting (2), (11) and (14) in (1), we obtain following objective function for classification problem:

$$ \begin{array}{@{}rcl@{}} \underset{\boldsymbol{{A}},\boldsymbol{{P}},{f}}{\min \mathcal{J}}&=& {tr}({{\boldsymbol{{A}}}^{T}}\boldsymbol{{A}})+ {tr}({{\boldsymbol{{P}}}^{T}}\boldsymbol{{K}} (\boldsymbol{{M}}+\lambda \mathcal{L}-\beta \ddot{I}){{\boldsymbol{{K}}}^{T}}\boldsymbol{{P}})\\ &&+ \gamma {{\left\| \boldsymbol{{P}} \right\|}_{2,1}}+ \\ && \eta {{\sum\limits_{i,j}{\boldsymbol{{w}}({{\boldsymbol{{x}}}_{i}}) \boldsymbol{{w}}({{\boldsymbol{{x}}}_{j}}) \left\| \boldsymbol{{A}}({{\boldsymbol{{x}}}_{i}}-{{\boldsymbol{{x}}}_{j}}) \right\|}}^{2}}{{\delta }_{ij}}\\ s.t.,&& \sum\limits_{i=1}^{N_{s}} \boldsymbol{{w}}(\boldsymbol{{x}}_{i})= N_{s},\quad \boldsymbol{{P}}^{T}\boldsymbol{{KHK}}^{T}\boldsymbol{{P}}=\boldsymbol{{I}}\\ and&& \boldsymbol{{w}}(\boldsymbol{{x}}_{i})>0 \end{array} $$

(15)

where δ_ij is the indicator function on which if y_i = y_j then δ_ij is equal to 1, otherwise is equal to -1. We characterize used instance pairs in the above equation (inter-class and intra-class instances) for computing loss function by C. With the increase of C value, which defines the number of instance pairs, the computational cost may also increases. To mitigate this problem, cross validation is used to obtain a tradeoff value for C. In the next section, we utilize (15) for optimization problem in an alternating manner.

4 Optimization problem

In this section, we optimize the objective function in (15). For the sake of simplicity, we convert an overall constrained optimization problem to an unconstrained one as follows:

$$ \begin{array}{@{}rcl@{}} \underset{\boldsymbol{{A}},\boldsymbol{{P}},f}{\min\mathcal{J}}\!&=&\! {tr}({{\boldsymbol{{A}}}^{T}}\boldsymbol{{A}})+ {tr}({{\boldsymbol{{P}}}^{T}}\boldsymbol{{K}}+ (\boldsymbol{{M}}+\lambda \mathcal{L}-\beta \ddot{I}){{\boldsymbol{{K}}}^{T}}P)\\ &&+ \gamma {{\left\| \boldsymbol{{P}} \right\|}_{2,1}} + \eta {{\underset{i,j}{\sum}{\boldsymbol{{w}}({{\boldsymbol{{x}}}_{i}})\boldsymbol{{w}}({{\boldsymbol{{x}}}_{j}}) \left\| A({{\boldsymbol{{x}}}_{i}} - {{\boldsymbol{{x}}}_{j}}) \right\|}}^{2}}{{\delta }_{ij}}\\ &&+ \rho \left( {{({{w}^{T}}e-{{N}_{s}})}^{2}}+ \sum\limits_{i=1}^{{{N}_{s}}}{{{(\max (0,-\textbf{\textit{w}}({{\textbf{\textit{x}}}_{i}})))}^{2}}} \right)\\ &&+ {tr}\left( (I-{{\boldsymbol{{P}}}^{T}}\boldsymbol{{KH}} {{\boldsymbol{{K}}}^{T}}\boldsymbol{{P}})\zeta \right) \end{array} $$

(16)

where ρ is a non-negative coefficient penalty, ζ is a Lagrange multiplier and $e\in \mathbb {R}^{(n_{s}+{n_{t}^{l}})\times 1}$ is computed based on e_i = 1 if i ≤ n_s and e_i = 0 if $n_{s} < i\le n_{s}+{n_{t}^{l}}$. We propose to learn A and P in an iterative optimization algorithm. Specifically, at iteration t, we first consider the matrix A_t to be fixed and update the matrix P_t based on the following rule:

$$ \boldsymbol{P}_{t+1}=\boldsymbol{P}_{t}-\gamma_{1}\frac{\partial \mathcal{J}}{\partial \boldsymbol{P}} $$

(17)

where γ₁ is the adaptive step-size. Moreover, the derivative of $\mathcal {J}$ with respect to P can be written as:

$$\frac{\partial \mathcal{J}}{\partial \boldsymbol{{P}}}= (\boldsymbol{{K}}(\boldsymbol{{M}}+\lambda \mathcal{L}-\beta \ddot{I})\boldsymbol{{K}}^{T}+ \gamma \boldsymbol{{G}})\boldsymbol{{P}}-\boldsymbol{{KHK}}^{T}\boldsymbol{{P}} $$

where G is the sub-gradient of ${{\left \| \textit {\textbf {P}} \right \|}_{2,1}}$ and also is a diagonal matrix where G_ii = 0 if Pⁱ = 0 else $\textit {\textbf {G}}_{ii}=\frac {1}{2\left \| \textit {\textbf {P}}^{i} \right \|}$ in which Pⁱ denotes the i^th row of P. After updating P_t to P_t+ 1, we alternatively update the value of A_t with the following rule:

$$ \boldsymbol{A}_{t+1}=\boldsymbol{A}_{t}-\gamma_{2}\frac{\partial \mathcal{J}}{\partial \boldsymbol{A}} $$

(18)

where γ₂ is the adaptive step-size. Moreover, the derivative of $\mathcal {J}$ with respect to A can be written as:

$$\frac{\partial \mathcal{J}}{\partial \boldsymbol{{A}}}= 2\eta \underset{i,j}{\sum} \boldsymbol{{w}}(\boldsymbol{{x}}_{i})\boldsymbol{{w}}(\boldsymbol{{x}}_{j}) \boldsymbol{{A}}\nu_{ij}{\nu}_{ij}^{T}\delta_{ij}+2\boldsymbol{{A}}$$

where ν_ij = x_i −x_j. Moreover, we alternatively update the value of P and A matrices and consequently the value of objective function in each iteration until its changes is smaller than determined threshold ε. The entire procedure of proposed MTL-GKE is summarized in Algorithm 1.

4.1 Computational complexity

In this section, the computational complexity of our proposed MTL-GKE is described. Since T, C and d denote the number of iterations, number of instance pairs and dimension of samples, respectively, the computation of kernel matrix K, MMD matrix M and Laplacian matrix ${\mathscr{L}}$ have $\mathcal {O}(n^{2})$ cost. The computational costs for updating the sub-gradient G and graph Laplacian ${\mathscr{L}}$ is $\mathcal {O}(Tn^{2})$; however, updating the projection matrix P costs $\mathcal {O}(Tdn^{2})$ and updating the source sample weights have $\mathcal {O}(Tn_{s}n_{t})$ cost. Moreover, the computational cost of updating Mahalanobis matrix A is $\mathcal {O}(T\textit {\textbf {C}}\textit {d}n^{2})$. As a result, the overall computation cost of MTL-GKE algorithm is $\mathcal {O}(T(\textit {\textbf {C}}\textit {d}n^{2}+n_{s}n_{t}))$.

5 Experiments

To represent the usefulness of our MTL-GKE, we examine our method on different image classification tasks on Office-Caltech256 [49], USPS [50] and MNIST [51] datasets. We first introduce the details of used datasets and provide parameter analysis and discussion in the following section and then the experimental results are described. For an unbiased comparison, all algorithms were implemented with same setup in MATLAB R2016 where no library is used in their implementation.

5.1 Data description

The Office-Caltech256 dataset that is used for cross domain object recognition, is a benchmark dataset with ten common classes that consists of four domains including Dslr (d), Webcam (w), Amazon (a) and Caltech256 (c). Amazon and Caltech256 domains consist of images, which obtained from office environment and Amazon.com, in turn. Also, Dslr and Webcam domains include images, which obtained from Dslr and Webcam cameras, respectively. Since the images of different domains were collected under various factors (position, angle view, resolution and location), all four domains have different distributions compared to each other. We construct 12 recognition tasks from datasets, where each of them is denoted by SD-TD in which SD defines source domain for training and TD represents target domain.

USPS and MNIST datasets are benchmark datasets including digit handwriting images from 10 categories in range of 0 to 9 of different distributions. The USPS dataset consists of 1,800 labeled images in size of 16 × 16, and the MNIST dataset consists of 2,000 labeled in size of 28 × 28. We construct two handwriting recognition tasks usps-mnist and mnist-usps. For usps-mnist task, 1,800 labeled images of USPS dataset are used as source domain (D_s),705 labeled images from MNIST are used as ${D_{t}^{l}}$ and 1,295 unlabeled image from MNIST dataset is used as test data ${D_{t}^{u}}$. For the mnist-usps task, 2,000 labeled samples are used as source domain, 637 labeled images from target domain are used for training and 1,371 unlabeled instances from target domain are used as test data. Since we introduce source and target domains with the same feature space, we resize all images to 16 × 16 scale.

5.2 Parameter tuning

In this section, we design some experiments on different datasets to obtain optimal value of parameters of proposed objective function. According to (16), we have three penalty parameters λ, β and γ, one penalty coefficient ρ, and one tradeoff parameter η. Additionally, in the classification setting, we own further parameters such as the number of instance pairs C and the number of nearest neighbors k that used in kNN classifier. Since, the proposed MTL-GKE uses the PCA dimensionality reduction, we conduct additional experiments on parameter d, which defines the reduced dimensions. Since in transfer learning, it is difficult to obtain the optimal parameters via cross validation, we perform parameter tuning empirically on each dataset and describe the best result of experiments.

5.2.1 Analysis of parameter k

Different number of nearest neighbor parameter k can affect the classification accuracy, which examined on Office-Caltech256 dataset where the results are shown in Fig. 1a. Given the figure, two tasks w-d and d-w receive high accuracy than other tasks. We examined the classification accuracy on different number of nearest neighbors from 1 to 30 and observe that, as the number of neighbors increased, the accuracy also decreased. Therefore, we intend to set parameter k equal to 1.

Fig. 1

Analysis of a number of nearest neighbors k, b number of instance pairs C, and c number of dimensions d in Office-Caltech256 dataset, and d number of dimensions d in USPS-MNIST dataset

5.2.2 Analysis of parameter C

The instance pairs are chosen randomly for optimization problem to conduct several experiments on the accuracy of different number of instance pairs in range of 50 to 1500 on Office-Caltech256 dataset as shown in Fig. 1b. According to experiments, with increase of C, the accuracy is also slightly increased. However, we are interested to set the parameter C to small values. Because, with large number of instance pairs, the computational cost will also increase. As a result in our experiments, we consider 50 instance pairs.

5.2.3 Analysis of parameter d

In our proposed method, on Office-Caltech256 and USPS-MNIST datasets, we use PCA for dimensionality reduction as preprocessing step. In this section, we investigate the impact of several number of reduced dimensions on classification accuracy in both Office-Caltech256 and USPS-MNIST datasets. The results of our experiments are shown in Fig. 1c and d. According to Fig. 1c, for Office-Caltech256 dataset, all tasks have increasing manner in accuracy related to the number of dimension from 1 to 30. However, for those numbers of dimensions greater than 30, the accuracy have no significant change. On the other hand, as shown in Fig. 1d, this is also the case for USPS-MNIST dataset in which the accuracy is slightly increased for the dimensions greater than 40. Since the greater number of dimensions causes higher computational cost, we set the number of reduced dimensions d = 40.

5.2.4 Analysis of parameters λ,β,γ and η

In this section, we present the effect of different values for λ, β and γ in range of [0.01, 1] and parameter η on accuracy of 12 tasks of Office-Caltech256 dataset in Fig. 2a and b, respectively. For λ, β and γ, the mean of 12 tasks is considered for comparison. As shown from figures, all four parameters are not sensitive and their changes do not make significant difference in classification accuracy. Since parameter β controls the target domain information, the higher values of it boosts the information preservation, while the adaptation degrades.

Fig. 2

Analysis of parameters a λ, β, γ and b η on Office-Caltech256 dataset

5.2.5 Analysis of algorithm convergence

In this section, we design experiments for analysis of different values of ρ from -3 to 3 on the Office-Caltech256 dataset where the results are shown in Fig. 3a. According to the figure, it is observable that the penalty coefficient ρ is not sensitive, while the larger values of ρ may increase the computational time. To analyze the convergence of algorithm, we design another experiment by several values of ρ from 1 to 10 on d-w task whose results are shown in Fig. 3b and c in which ${\Delta } \mathcal {J}=\mathcal {J}_{t+1}-\mathcal {J}_{t}$, ${\Delta } \textit {\textbf {w}}=\left \| \textit {\textbf {w}}_{t+1}-\textit {\textbf {w}}_{t}\right \|$ and t denotes the number of iterations. From the figures, we find that at the higher iteration, the value of ${\Delta } \mathcal {J}$ and Δw for each ρ are decreased, especially ${\Delta } \mathcal {J}$ and Δw are tend to zero. Since the parameter ρ is not very sensitive, it is better to have no large values, therefore, we set ρ = 1 or ρ = 2.

Fig. 3

Sensitivity analysis on parameter ρ and investigating the effect of ρ on the convergence rate. a Convergence rate of ${\Delta } \mathcal {J}$ on different values of ρ on d-w task, b convergence rate of Δw on different ρ on d-w task, c sensitivity analysis of parameter ρ on Office-Caltech256 dataset

As a result, the optimal values of obtained parameters from experiments are summarized in Table 1.

Table 1 The optimal values of parameters

5.3 Basics of comparison

In our experiments, we evaluate our proposed MTL-GKE with variety of methods for cross domain object recognition and cross domain digit recognition tasks. The baseline methods including principle component analysis (PCA) [52], transfer component analysis (TCA) [10], metric transfer learning methods consist of consistent distance metric learning (CDML) [53], metric transfer learning framework (MTLF) [4], information theoretic metric learning (ITML) [54], robust transfer metric learning (RTML) [27], semi-supervised maximum independence domain adaptation (SMIDA) [55], semi-supervised metric transfer learning framework (SSMT) [56], semi-supervised metric transfer learning with relative constraints (SSMTR) [57], domain adaptation using metric learning on manifolds (GCA) [58], and feature-based methods including geodesic flow kernel (GFK) [31], transfer independently together (TIT) [23], joint distribution adaptation (JDA) [18], marginalized stacked denoising autoencoders (mSDA) [59] and max-margin domain transforms (MMDT) [60].

5.4 Experiment results

In this section, we represent experimental results on different datasets to show the effectiveness of our MTL-GKE. In the experiments, at first we learn Mahalanobis distance metric, then construct a Laplacian graph via MTL-GKE, and finally use the distance defined in form of (1) in kNN classifier for classification. For the input test data x_i, we first transform it to the latent sub-space and compute Mahalanobis distance metric between x_i and each source and target samples in new space. The label of x_i is assigned with a senior vote of its k-nearest samples.

Experimental results on Office-Caltech256 and USPS-MNIST datasets are shown in Tables 2 and 3, respectively. For the Office-Caltech256 dataset, we perform 20 random permutation and compute the average of performances as well as the variation. From Table 2, we can observe that the classification accuracy of MTL-GKE is much better than the conventional metric learning algorithms i.e., PCA and ITML, which only use the source instances for training a classifier and make a prediction on different distributed target samples. Therefore, the learned metric on the source domain cannot work correctly on target data.

Table 2 Classification accuracy (%) of semi-supervised domain adaptation on Office-Caltech256 dataset using Surf features

Table 3 Classification accuracy (%) of semi-supervised domain adaptation on USPS-MNIST dataset

TCA is a feature-based method, which tries to seek a new representation with goal of feature matching, while JDA is a semi-supervised method that uses labeled target data in training classifier and utilizes a dimensionality reduction method for marginal and conditional distribution matching. Thus, in results of Tables 2 and 3, we can see that JDA outperforms TCA. In the meantime, we observe much better accuracy performance of MTL-GKE than TCA and JDA. This happens because unlike MTL-5GKE, JDA does not consider the impact of feature matching in classification accuracy and ignores the advantages of distance metric learning. Thus, the distribution matching performs under an inappropriate distance metric.

GFK attempts to mitigate the distribution gap between source and target domains via mapping samples to a low dimensional subspace in a Grassman manifold, which leads to lose some beneficial information of samples during map. However, the proposed MTL-GKE preserves the intrinsic information of samples during the projection and causes much better results in accuracy classification.

mSDA is a domain adaptation method, which adapts stacked denoising autoencoders by combining the source and target samples to learn a new representation for domain adaptation. However, it ignores the use of distance metric for class discrepancy. As a result, mSDA may not address the domain shift problem compared to MTL-GKE and thus we observe better results in experiments.

Compared to RTML, MTL-GKE receives better performance. It is because of that in RTML, the instance reweighting is ignored and model is not trained with more related source samples. While in MTL-GKE, the instance reweighting is performed due to the increase of classification accuracy by finding a more related samples. Thus, the model will be trained, accurately.

From Table 2, we also can find that MTL-GKE outperforms CDML, because in CDML, learning distance metric and sample reweighting performs in a pipelined framework. In contrast, in MTL-GKE, the instance reweighting and metric learning performs, simultaneously. Therefore, instance reweighting performs well under an appropriate distance metric.

SMIDA is a semi-supervised feature-based method for domain adaptation, which tries to find domain-invariant feature space. Since it ignores the important impact of distance metric learning and instance reweighting in minimizing the distribution difference, it shows low classification accuracy compared to our proposed MTL-GKE.

SSMT and SSMTR are semi-supervised metric learning frameworks that use KL divergence for instance reweighting. Since the KL divergence is a parametric method and reflects the amount of data lost, requires expensive distribution density calculation. Also, they do not take into consideration the effect of feature matching in reducing the distribution gap. Therefore, in comparing with SSMT and SSMTR, our MTL-GKE results are much better.

GCA is a domain adaptation method that reduces the statistical and geometrical differences between domains. However, unlike MTL-GKE, the effective role of instance reweighting and feature matching on distribution matching is ignored on GCA. As a result, the classification accuracy of MTL-GKE has significant improvement against GCA.

In comparison with TIT and MTLF, MTL-GKE has better performance in classification accuracy. This happens because of that in TIT, learning a distance metric is ignored and inter-class discrepancy is denied and it adversely affects the classification accuracy. Also, MTLF does not take the importance of feature matching in reducing of distribution divergence into consideration. Thus, the distribution gap is not minimized, explicitly.

In order to compare our proposed MTL-GKE withMMDT in Table 3, MTL-GKE performs better on both tasks. This is because of that, MMDT only seeks a new representation for feature space and ignores the negative impact of distribution gap between source and target domains on domain adaptation.

5.5 Time complexity

In this section, the computational cost of our proposed MTL-GKE in comparison with several compared methods has indicated in Table 4. Experiments are designed on usps-mnist task with 1800 source samples and 2000 test samples and each of which has 256 features. We observe that MTL-GKE has much better running time than TIT, JDA and TCA. However, MTLF and GFK have better running time than our proposed method.

Table 4 Time complexity of MTL-GKE on usps-mnist task

6 Conclusion

In this paper, we proposed MTL-GKE framework, which is a generalized model for domain adaptation task. MTL-GKE defines an objective function based on the Mahalanobis distance metric that makes it possible to more efficiently classify the data by maximizing the inter-class and minimizing the intra-class distances. Moreover, it utilizes two projection matrices to project the source and target samples into latent common sub-space, separately, to mitigate the distribution gap. We also proposed a novel instance reweighting approach to select more related instances for training. We conduct extensive experiments on Office-Caltech256 and USPS-MNIST datasets, and compared our experimental results with following machine learning and domain adaptation methods, PCA, TCA, JDA, GFK, CDML, ITML, mSDA, RTML, SMIDA, SSMT, SSMTR, GCA, TIT and MTLF to demonstrate our proposed MTL-GKE efficiency. The results shows the superiority of MTL-GKE against other compared baselines where it could be used for several cross domain problems with significant distribution gap. Hereafter, we aim to study multi-label classification, zero-shot transfer learning and utilize deep structure for learning.