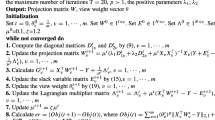Distributed learning for supervised multiview feature selection

Abstract

Multiview feature selection technique is specifically designed to reduce the dimensionality of multiview data and has received much attention. Most proposed multiview supervised feature selection methods suffer from the problem of efficiently handling the large-scale and high-dimensional data. To address this, this paper designs an efficient supervised multiview feature selection method for multiclass problems by combining the distributed optimization method in the Alternating Direction Method of Multipliers (ADMM). Specifically, the distributed strategy is reflected in two aspects. On the one hand, a sample-partition based distributed strategy is adopted, which calculates the loss term of each category individually. On the other hand, a view-partition based distributed strategy is used to explore the consistent and characteristic information of views. We adopt the individual regularization on each view and the common loss term which is obtained by fusing different views to jointly share the label matrix. Benefited from the distributed framework, the model can realize a distributed solution for the transformation matrix and reduce the complexity for multiview feature selection. Extensive experiments have demonstrated that the proposed method achieves a great improvement on training time, and the comparable or better performance compared to several state-of-the-art supervised feature selection algorithms.

1 Introduction

In practical application, the collected data are becoming increasingly high-dimensional and large-scale, which will bring the considerable challenges because the computational complexity is dramatically increased when dealing with the big data. Therefore, establishing the fast and effective algorithm becomes more and more important. One of the efficient solutions is to get a low-dimensional representation of the original data so as to enhance the generalization while reducing the probability of over-fitting. Among the dimensionality reduction techniques, feature selection [11, 39] has been proven to be an efficient method. It removes the irrelevant and redundant features, and finds out the optimal subset from the original dataset without altering the semantics of features. According to the availability of label, the feature selection algorithms can be divided into three categories: supervised feature selection algorithms [35, 43], semi-supervised feature selection algorithms [12, 33], and unsupervised feature selection algorithms [31, 42]. The supervised feature selection uses class labels to select the discriminative features. The unsupervised feature selection selects the relevant features by mining the underlying correlation information among the unlabeled samples. The semi-supervised feature selection is designed to handle the dataset with a few available labels and it can be seen as a compromise between the supervised and unsupervised feature selection.

In recent years, the structured sparsity-inducing feature selection (SSFS) methods have demonstrated the powerful performance for specific tasks, such as classification and clustering. SSFS selects the most discriminative features via joint structured sparsity. Lasso [24] is the representative SSFS method for the binary classification problem. Subsequently, many variants of lasso have been developed, such as fused lasso [25] and group lasso [37]. Compared to lasso which is expressed in vector form, many matrix-based SSFS methods are proposed for solving the multiclass problems. For instance, the L_2,1-norm regularization [16] was used to select features across all data points with joint sparsity. In [2], the L_2,0-norm was employed on feature selection and achieved the good performance. In [27], the G_2,1-norm regularization was proposed to exploit the importance of different views and perform feature selection across views. In [29], the G₁-norm regularization was developed to capture the group structures among the heterogeneous features and enforce sparsity at group level. A comprehensive summary of SSFS methods was exhibited in [8].

With the rapid development of data acquisition devices and feature extraction techniques, an object is often described by multiple modalities (views) or comes from multiple sources. For example, in image processing, an image has multiple heterogeneous features via different descriptors, such as HOG [5], LBP [18], SIFT [14], GIST [19] and so on. Compared with the single-view data exhibited in one homogeneous feature space, the multiview data have multiple representations which can provide much richer information about the data. In real life, the multiview data are often defined in a high-dimensional space, which may result in the curse of dimensionality, so the multiview feature selection is a vital research topic. In this paper, we focus on the supervised multiview SSFS methods. Xiao et al. [32] proposed a two-view feature selection method for cross-sensor iris recognition. Wang et al. [29] used the G₁-norm to integrate heterogeneous features beyond two views. There are many other supervised multiview SSFS algorithms [3, 34, 40, 41] that have also been proposed in recent years. They have successfully selected the representative features through exploring the correlation across views and mining the contributions of different views. However, it is noted that these methods usually combine features from multiple representations into a high-dimensional vector and then take this concatenation as the inputs directly, which is usually confronted with the complicated calculation and high computational cost in the process of matrix operations. Moreover, considering the explosion boost of data size, it is crucial to design a powerful model to learn problems with large scale data.

Alternating Direction Method of Multipliers (ADMM) [1], as an efficient algorithm with the superior convergence properties, is successful applied to the distributed optimization problems, such as consensus and sharing. Enlightened by this, we design an efficient supervised multiview feature selection method through the distributed learning strategy. Specifically, to reduce the computational cost of large scale data, we split the original dataset into multiple subsets according to category, and use the capped l₂-norm based loss function on each subset to deal with outliers efficiently. To fully exploit the characteristics and consistency of views, we minimize the individual view-based regularization and the common loss term which is obtained by combining all views together to share a label matrix. By incorporating the distributed strategy into multiview feature selection, the proposed method can not only capture the relationship among views, but also learn the transformation submatrices in a parallel manner, which can greatly reduce the computational complexity.

In summary, the main contributions of this paper are listed below:

• 1. A distributed learning strategy is incorporated into the multiview feature selection by adopting the sample-partition and view-partition. The sample-partition is beneficial to improve the computing power of the solution algorithm since the loss term is calculated in blocks.

• 2. The consistency and characteristics of multiple view representations are protected via the common loss term across views and individual regularization on each view.

• 3. Compared with the traditional supervised multiview feature selection methods which obtain the entire transformation matrix directly, we realize the distributed solution from different view subspace, which can provide a new choose to multiview feature selection.

The structural framework of this paper is as follows. In Section 2, we review the related work on multiview SSFS methods. In Section 3, we introduce the proposed model and the solution procedure in detail. The experimental setting up and results are exhibited in Section 4. Finally, we make a conclusion in Section 5.

2 Related work

The multiview SSFS feature selection algorithms emphasize the correlation of different views and bring a certain boost on feature selection performance. In this section, we review the recent work on the multiview SSFS methods, including supervised, semi-supervised and unsupervised ones.

2.1 Supervised methods

The supervised multiview SSFS methods use class labels to perform feature selection. Xiao et al. [32] proposed a two-view supervised feature selection method for cross-sensor iris recognition. Then, Wang et al. [29] introduced the G₁-norm regularization for handling datasets beyond two views. In [40], the G_2,1-norm and L_2,1-norm joint structured sparsity regularization terms were used to enforce the sparsity between features of different views. Cheng et al. [3] added a hypergraph based regularization to enhance the inherent association of data and combined a low-rank constraint with the L_2,1-norm to perform feature selection. Wang et al. [30] proposed a supervised multiview feature selection method based on the weighted hinge loss (WHMVFS) that can learn the corresponding weight for each view and implement sparsity across views. Yang et al. [34] proposed a multiview feature learning framework with a discriminative regression and learned the weights of different views adaptively. Zhang et al. [41] proposed a self-weighted supervised feature selection method with the L_2,1-norm regularization to solve an orthogonal linear discriminant analysis problem. Yang et al. [36] proposed a sparse lasso based mutltiview feature selection method for binary classification, which can capture the contribute of different samples and views. Lin et al. [13] proposed a multiview feature selection method by adopting a common penalty for all views and a structured sparsity-inducing norm for each view. Yang et al. [35] proposed a joint local-and-global multiview feature selection method, in which the local neighbor structure and global label-relevant analysis are combined to select the final features. You et al. [38] proposed Multiview Common Component Discriminant Analysis (MvCCDA) to handle view discrepancy, discriminability and nonlinearity in a joint manner. Specifically, it incorporated supervised information and local geometric information to learn a discriminant common subspace.

2.2 Semi-supervised methods

The semi-supervised multiview SSFS methods use a small proportion of labels to perform feature selection. Sindhwani et al. [22] proposed a co-regularization framework for multiview semi-supervised learning. They adopted the least square loss term over the labeled samples and the laplacian regularization over the unlabeled samples. Li et al. [12] constructed a view-based manifold regularization to design a semi-supervised multiview feature selection method. Xue et al. [33] proposed a semi-supervised multiview feature selection algorithm, and it can simultaneously capture individual information in each view and correlations among multiple views by learning a common component. Nie et al. [17] studied a multiview semi-supervised classification framework by modeling the importance of each view with a parameter-free manner. Considering the different roles of labeled and unlabeled samples, Tao et al. [26] added a score for each sample and designed a semi-supervised multiview classification framework with L_2,1-norm loss function for each view, and the final object function is formulated as the linear weighted combination of all loss functions. Shi et al. [21] designed a novel semi-supervised feature selection framework by utilizing the multiview Hessian regularization to combine the correlated and complementary information of multiview data.

2.3 Unsupervised methods

The unsupervised multiview SSFS algorithms usually construct the similar graph structure and latent subspace to preserve the intrinsic structure of multiview data. Wang et al. [31] proposed an adaptive multiview feature selection (AMFS) method by constructing the view-based Laplacian graphs to preserve the local geometric structure of multiview data. Hou et al. [9] proposed an unsupervised multiview feature selection method which can learn a common similarity matrix among all views to characterize the structures across different views, and the weights of views were also learned. Wang et al. [28] designed a multiview clustering and feature learning framework with the structured sparsity. Their model explored the unsupervised heterogeneous data fusion and clustering analysis by emphasizing structured sparsity across views. Feng et al. [7] proposed an adaptive unsupervised multiview feature selection (AUMFS) method by adding the view-based Laplacian graphs and L_2,1-norm regularization. Shao et al. [20] processed the multiview data chunk by chunk and proposed an unsupervised feature selection method via the nonnegative matrix factorization (NMF) and graph regularization. Tang et al. [23] embedded the multiview feature selection into an NMF based clustering framework and added weights for measuring the importance of different views.

It is worth noting that some unsupervised multiview SSFS models combine non-negative matrix factorization and clustering framework to conduct feature selection. With the above strategies, these models can learn the transformation submatrices from different view spaces simultaneously [20, 23]. However, for supervised multiview SSFS methods, since all views are combined together to determine the attribute of an object, they usually need to concatenate features in different representation spaces into a high-dimensional vector to calculate the loss term [3, 34, 40, 41]. Under these circumstances, the transformation matrix has to be calculated in an overall way, which will result in a heavy computation when handling high-dimensional data. So, it is challenging for the traditional supervised SSFS models to effectively deal with large scale data.

3 Proposed model

In this section, we first describe the objective function of the proposed method. Then the derivation procedure of solution is given in detail. The computational complexity of the designed algorithm is analyzed in the third part.

3.1 Objective function

In this paper, matrices and vectors are denoted by the boldface uppercase letters and boldface lowercase letters, respectively. Given a multiview dataset $\mathbf {X}\in \mathbb {R}^{n\times d}$ with C categories and V views, where n is the number of objects and d is the dimension of each object. Denote $\mathbf {X}_{i}=[{\mathbf {x}}_{i}^{1}; {\mathbf {x}}_{i}^{2}; ... ; {\mathbf {x}}_{i}^{n_{i}}]\in \mathbb {R}^{n_{i}\times d}(i=1,2,..,C)$ the i th category, where n_i is the number of the i th category, and ${\mathbf {x}}_{i}^{q}$ represents the q th sample of the i th category. For the i th class, let $\mathbf {X}_{iv}\in \mathbb {R}^{n_{i}\times d_{v}}(v=1,2,...,V)$ be the subset from the v th view, where d_v represents the dimension of the v th view. Here, we have $n={\sum }_{i=1}^{C} n_{i}$ and $d={\sum }_{v=1}^{V} d_{v}$. Let Y ∈{0,1}^n×C be the label matrix. The label matrix of the i th category is defined by $\mathbf {Y}_{i}=[{\mathbf {y}}_{i}^{1}; {\mathbf {y}}_{i}^{2}; ... ; {\mathbf {y}}_{i}^{n_{i}}]\in \mathbb {R}^{n_{i}\times C}$. The L_2,1-norm in this paper is represented as: $\|\mathbf {W}\|_{2,1}={\sum }_{p=1}^{m} \|\mathbf {w}^{p}\|_{2}$, where w^p means the p th row of W. In this paper, we attempt to learn a transformation matrix $\mathbf {W}\in \mathbb {R}^{d\times C}$ to help us select features.

We will introduce our model from the sample level and feature level. Firstly, according to the sample-partition based distributed strategy, we split X and Y by categories

$$ \mathbf{X}= \left[ \begin{array}{cccc} \mathbf{X}_{1}\\ \mathbf{X}_{2}\\ \vdots\\ \mathbf{X}_{C} \end{array} \right ] , \mathbf{Y}= \left[ \begin{array}{cccc} \mathbf{Y}_{1}\\ \mathbf{Y}_{2}\\ \vdots\\ \mathbf{Y}_{C} \end{array} \right ] $$

(1)

We attempt to calculate the loss function of each category separately and then combine them as a whole loss term. Specifically, with the training data X_i and the label matrix Y_i for the i th category, the traditional least squares loss function with l₂-norm for the i th block of data can be summarized as follows

$$ \mathcal{L}_{i}(\mathbf{W})= {\sum\limits_{q=1}^{n_{i}} \|{\mathbf{x}}_{i}^{q}\mathbf{W}+\mathbf{b}-{\mathbf{y}}_{i}^{q}\|_{2}^{2}} $$

(2)

where $b\in \mathbb {R}^{d}$ is the bias. We can absorb b into W when the constant value 1 is added as an additional dimension for each data ${\mathbf {x}}_{i}^{q}$. Then the loss term becomes

$$ \mathcal{L}_{i}(\mathbf{W})= {\sum\limits_{q=1}^{n_{i}} \|{\mathbf{x}}_{i}^{q}\mathbf{W}-{\mathbf{y}}_{i}^{q}\|_{2}^{2}} $$

(3)

To improve the robustness of the regression model, we adopt the capped l₂-norm based loss function [10]. However, different from [10] which applies the capped l₂-norm to the whole training data to calculate the loss function, the proposed model calculates the loss term on each category separately

$$ \mathcal{L}_{i}(\mathbf{W})= \sum\limits_{q=1}^{n_{i}} \underset{\mathbf{W}}{\min}\ \left( \|{\mathbf{x}}_{i}^{q}\mathbf{W}-{\mathbf{y}}_{i}^{q}\|_{2},\varepsilon \right),i=1,2,...C $$

(4)

where ε > 0 is the thresholding parameter to identify the latent outliers.

Denote a diagonal matrix F_i, and define the q th diagonal element of F_i as

$$ (\mathbf{F}_{i})_{q,q}=\frac{1}{2}\|{\mathbf{x}}_{i}^{q}\mathbf{W}-{\mathbf{y}}_{i}^{q}\|_{2}^{-1}\cdot I \left( \|{\mathbf{x}}_{i}^{q}\mathbf{W}-{\mathbf{y}}_{i}^{q}\|_{2}\leq\varepsilon \right) $$

(5)

where I(⋅) is an indicative function. It is equal to 1 if $\|{\mathbf {x}}_{i}^{q}\mathbf {W}-{\mathbf {y}}_{i}^{q}\|_{2}\leq \varepsilon$, and 0 otherwise. Then the (4) can be converted to

$$ \mathcal{L}_{i}(\mathbf{W})= \sum\limits_{q=1}^{n_{i}}\left( \mathbf{F}_{i}\right)_{q,q}\|{\mathbf{x}}_{i}^{q}\mathbf{W}-{\mathbf{y}}_{i}^{q}\|_{2}^{2} $$

(6)

which is equivalent to

$$ \mathcal{L}_{i}(\mathbf{W})= tr\left[\left( \mathbf{X}_{i}\mathbf{W}-\mathbf{Y}_{i}\right)^{T}\mathbf{F}_{i}\left( \mathbf{X}_{i}\mathbf{W}-\mathbf{Y}_{i}\right)\right] $$

(7)

Considering the loss of all C categories, we get the following loss term

$$ \underset{\mathbf{W}_{v},\ \mathbf{F}_{i}}{\min}\ \sum\limits_{i=1}^{C}tr\left[\left( \mathbf{X}_{i}\mathbf{W}-\mathbf{Y}_{i}\right)^{T}\mathbf{F}_{i}\left( \mathbf{X}_{i}\mathbf{W}-\mathbf{Y}_{i}\right)\right] $$

(8)

Secondly, a view-partition based distributed strategy is used for emphasizing the characteristics and consistency of views. We adopt the individual regularization on each view and the common loss term which is obtained by fusing different views to jointly share the label matrix. Specifically, we split X_i and transformation matrix W into V views

$$ \mathbf{X}= \left[ \begin{array}{cccc} \mathbf{X}_{1}^{1} &\mathbf{X}_{1}^{2} &{\cdots} \mathbf{X}_{1}^{V}\\ \mathbf{X}_{2}^{1} &\mathbf{X}_{2}^{2} &{\cdots} \mathbf{X}_{2}^{V}\\ {\vdots} & {\vdots} &{\ddots} \vdots\\ \mathbf{X}_{C}^{1} &\mathbf{X}_{C}^{2} &{\cdots} \mathbf{X}_{C}^{V} \end{array} \right ] , \mathbf{W}= \left[ \begin{array}{cccc} \mathbf{W}_{1}\\ \mathbf{W}_{2}\\ \vdots\\ \mathbf{W}_{V} \end{array} \right ] $$

(9)

Then, (8) can be rewritten as follows

$$ \underset{\mathbf{W}_{v},\ \mathbf{F}_{i}}{\min}\ \sum\limits_{i=1}^{C}tr \left[ \left( \sum\limits_{v=1}^{V}\mathbf{X}_{iv} \mathbf{W}_{v} - \mathbf{Y}_{i} \right)^{T}\mathbf{F}_{i} \left( \sum\limits_{v=1}^{V}\mathbf{X}_{iv} \mathbf{W}_{v} - \mathbf{Y}_{i} \right) \right] $$

(10)

With the individual L_2,1-norm regularization based on each view, our model is built as follows:

$$ \begin{array}{@{}rcl@{}} &&\underset{\mathbf{W}_{v},\ \mathbf{F}_{i}}{\min}\ \sum\limits_{i=1}^{C}tr \left[ \left( \sum\limits_{v=1}^{V}\mathbf{X}_{iv} \mathbf{W}_{v} -\mathbf{ Y}_{i} \right)^{ T}\mathbf{ F}_{i} \left( \sum\limits_{v=1}^{V}\mathbf{X}_{iv} \mathbf{W}_{v} - \mathbf{Y}_{i} \right) \right]\\ &&+\lambda\sum\limits_{v=1}^{V} \|\mathbf{W}_{v}\|_{2,1} \end{array} $$

(11)

where λ > 0 is the trade-off parameter for balancing the weight of loss term and regularization. In this model, we implement distributed feature learning from two aspects. We first adopt the sample-partition scheme to segment the loss term according to each category, providing the feasibility for the distributed solution. Then, the view-partition scheme with individual regularization and common loss term is incorporated into the model, which is conducive to explore the correlations of views.

3.2 Optimization and solution

The optimization problem (11) is convex with respect to one variable when the other variables are fixed. We will alternatively update W_v and F_i via the ADMM [1]. By introducing an auxiliary variable Z_iv = X_ivW_v, we can rewrite (11) in ADMM form

$$ \begin{array}{@{}rcl@{}} &&\underset{\mathbf{W}_{v},\mathbf{Z}_{iv},\mathbf{F}_{i}}{\min}\ \sum\limits_{i=1}^{C}tr \left[\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv} - \mathbf{Y}_{i}\right)^{T}\mathbf{F}_{i}\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)\right]\\&&~\qquad\qquad\qquad+\lambda\sum\limits_{v=1}^{V} \|\mathbf{W}_{v}\|_{2,1}\\ &&\quad s.t. \quad \mathbf{Z}_{iv}=\mathbf{X}_{iv}\mathbf{W}_{v} \end{array} $$

(12)

The augmented lagrangian of (12) is

$$ \begin{array}{@{}rcl@{}} &&\mathcal{L}\left (\mathbf{W}_{v},\mathbf{Z}_{iv},\mathbf{F}_{i},\mathbf{P}_{iv}\right)\\ &=& \sum\limits_{i=1}^{C}tr\left[\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)^{T}\mathbf{F}_{i}\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)\right]\\ &&+\lambda{\sum}_{v=1}^{V} \|\mathbf{W}_{v}\|_{2,1}+\sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}tr\left[{\mathbf{P}}_{iv}^{T}(\mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v})\right] \\ &&+\frac{\rho}{2} \sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}\|\mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v}\|_{F}^{2} \end{array} $$

(13)

where P_iv is the Lagrangian multiplier and ρ is a non-negative constant to penalize the equality constraints. Since

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}tr\left[ {\mathbf{P}}_{iv}^{T}\left( \mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v}\right)\right]\\ &&+\frac{\rho}{2}\sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}\|\mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v}\|_{F}^{2} \\ &=&\frac{\rho}{2}\sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}\left( \|\mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v}+\frac{1}{\rho}\mathbf{P}_{iv}\|_{F}^{2}-\|\frac{1}{\rho}\mathbf{P}_{iv}\|_{F}^{2}\right)\\ \end{array} $$

(14)

The (13) can be rewritten as

$$ \begin{array}{@{}rcl@{}} &&\mathcal{L}\left (\mathbf{W}_{v},\mathbf{Z}_{iv},\mathbf{F}_{i},\mathbf{P}_{iv}\right)\\&=& \sum\limits_{i=1}^{C}tr\left[\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)^{T}\mathbf{F}_{i}\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)\right]\\ &&+\lambda\sum\limits_{v=1}^{V} \|\mathbf{W}_{v}\|_{2,1}+\frac{\rho}{2}\sum\limits_{i=1}^{C} \sum\limits_{v=1}^{V}\\ && \left( \|\mathbf{Z}_{iv}-\mathbf{X}_{iv}\mathbf{W}_{v}+\frac{1}{\rho}\mathbf{P}_{iv}\|_{F}^{2}-\|\frac{1}{\rho}\mathbf{P}_{iv}\|_{F}^{2}\right) \end{array} $$

(15)

According to the distributed optimization learning via ADMM [1], the entire transformation matrix W can be obtained by learning V transformation submatrices W_v. For the v th subproblem, ADMM consists of the iterations

$$ \begin{array}{@{}rcl@{}} {\mathbf{W}_{v}}^{(k+1)}&:=&\underset{\mathbf{W}_{v}}{\arg\min} \left( \lambda\|\mathbf{W}_{v}\|_{2,1}+\frac{\rho}{2}\sum\limits_{i=1}^{C}\|{\mathbf{Z}_{iv}}^{(k)}\right.\\ &&\qquad\qquad \left. -\mathbf{X}_{iv}\mathbf{W}_{v}+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}\|_{F}^{2}\vphantom{\sum\limits_{i=1}^{C}}\right) \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} {\mathbf{Z}_{iv}}^{(k+1)}&:=& \underset{\mathbf{Z}_{iv}}{\arg\min} \left( tr\left[ \left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)^{T}\right.\right.\\ &&\qquad\qquad \left.\left. \times {\mathbf{F}_{i}}^{(k)} \left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)\right]\right.\\ &&\qquad\qquad \left. + \frac{\rho}{2}\sum\limits_{v=1}^{V} \|\mathbf{Z}_{iv}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}\right.\\ &&\qquad\qquad \left.+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}\|_{F}^{2}\vphantom{\left( \sum\limits_{v=1}^{V}\mathbf{Z}_{iv}-\mathbf{Y}_{i}\right)^{T}}\right) \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} \left (\mathbf{F}_{i}\right)_{q,q}^{(k+1)}&=&\frac{1}{2}\big\|\left( \sum\limits_{v=1}^{V} {\mathbf{Z}_{iv}}^{(k+1)}-\mathbf{Y}_{i}\right)_{q}\big\|_{2}^{-1}\\ &&\cdot I\left( \big\|\left( \sum\limits_{v=1}^{V} {\mathbf{Z}_{iv}}^{(k+1)}-\mathbf{Y}_{i}\right)_{q}\big\|_{2}\leq\varepsilon\right) \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} {\mathbf{P}_{iv}}^{(k+1)}&=&{\mathbf{P}_{iv}}^{(k)}+\rho\left( {\mathbf{Z}_{iv}}^{(k+1)}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}\right) \end{array} $$

(19)

where ${{\mathbf {W}_{v}}^{(k)}}, {{\mathbf {Z}_{iv}}^{(k)}}, {{\mathbf {F}_{i}}^{(k)}}, {{\mathbf {P}_{iv}}^{(k)}}$ are the values of the k th iteration, $\big \|\left ({\sum }_{v=1}^{V} {\mathbf {Z}_{iv}}^{(k+1)}-\mathbf {Y}_{i}\right )_{q}\big \|_{2}$ in (18) means the loss of the q th samples in i th class. The optimization problems (16)-(19) can be inverted into a concise form according to the following theorem.

Theorem 1

Equations (16)-(19) is equivalent to (20)-(23).

$$ \begin{array}{@{}rcl@{}} {\mathbf{W}_{v}}^{(k+1)} &:=& \underset{\mathbf{W}_{v}}{\arg \min} \left( \lambda\|\mathbf{W}_{v}\|_{2,1}+\frac{\rho}{2}\sum\limits_{i=1}^{C}\|\mathbf{X}_{iv}\mathbf{W}_{v}\right.\\ &&\qquad\qquad \left.-\left( \mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k)}+ \overline{\mathbf{Z}_{i}}^{(k)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k)}\right.\right.\\ &&\qquad\qquad \left.\left.+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right)\|_{F}^{2}\vphantom{\sum\limits_{i=1}^{C}}\right) \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \overline{\mathbf{Z}_{i}}^{(k+1)} &:=& \underset{\overline{\mathbf{Z}_{i}}}{\arg \min} \left( tr\left[\left( V\overline{\mathbf{Z}_{i}} - \mathbf{Y}_{i}\right)^{T}{\mathbf{F}_{i}}^{(k)}\left( V\overline{\mathbf{Z}_{i}} - \mathbf{Y}_{i}\right)\right]\right.\\ &&\qquad\quad~ \left. +\frac{\rho V}{2}\| \overline{\mathbf{Z}_{i}} - \overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)} + \frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\|_{F}^{2}\right) \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \left (\mathbf{F}_{i}\right)_{q,q}^{(k+1)} &=& \frac{1}{2}\|(V\overline{\mathbf{Z}_{i}}^{(k+1)}-\mathbf{Y}_{i})_{q}\|_{2}^{-1}\\ &&\cdot I\left( \| (V\overline{\mathbf{Z}_{i}}^{k+1}-\mathbf{Y}_{i})_{q}\|_{2}\leq\varepsilon\right) \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} \overline{\mathbf{P}_{i}}^{(k+1)} &=& \overline{\mathbf{P}_{i}}^{(k)}+\rho\left( \overline{\mathbf{Z}_{i}}^{(k+1)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}\right) \end{array} $$

(23)

where $\overline {\mathbf {Z}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V}\mathbf {Z}_{iv}$, $\overline {\mathbf {X}_{i}\mathbf {W}}=\frac {1}{V}{\sum }_{v=1}^{V} \mathbf {X}_{iv}\mathbf {W}_{v}$, and $\overline {\mathbf {P}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V} \mathbf {P}_{iv}$.

Proof

See the Appendix. □

It can be seen from the simplified problems that we only need to calculate a matrix $\overline {\mathbf {Z}_{i}}$ in the (21) instead of calculating Z_iv(v = 1,...,V ) in (17) for fixed i. The same strategy for computing the matrix $\overline {\mathbf {P}_{i}}$ rather than P_iv is used in (23).

According to the (20)-(23), the solution of W_v, $\overline {\mathbf {Z}_{i}}$, F_i and $\overline {\mathbf {P}_{i}}$ are presented as follows.

• 1) Updating W_v, where v = 1,2,...,V

  To update W_v, we fix all other variables. By setting the derivative of (20) w.r.t. W_v to zero, we have

  $$ \begin{array}{@{}rcl@{}} &&2\lambda \mathbf{D}_{v}\mathbf{W}_{v} + \rho\sum\limits_{i=1}^{C}\mathbf{X}_{iv}^{T}\left( \vphantom{\frac{1}{\rho}}\mathbf{X}_{iv}\mathbf{W}_{v} - \left( \mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k)} +\overline{\mathbf{Z}_{i}}^{(k)}\right.\right.\\ &&\qquad\qquad\qquad\qquad\quad \left.\left.-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k)}+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right)\right)=0\\ \end{array} $$

  (24)

  where D_v is a diagonal matrix with the h th diagonal element $(\mathbf {D}_{v})_{h,h}=\frac {1}{2\|\mathbf {w}_{v}^{h}\|_{2}}$, where $\mathbf {w}_{v}^{h}$ means the h row of W_v. Then, we have

  $$ \begin{array}{@{}rcl@{}} {\mathbf{W}_{v}}^{(k+1)} &=& \rho\left( 2\lambda \mathbf{D}_{v}+\rho \sum\limits_{i=1}^{C}\mathbf{X}_{iv}^{T}\mathbf{X}_{iv}\right)^{-1}\\ &&\times \left( \sum\limits_{i=1}^{C}\mathbf{X}_{iv}^{T}\left( \mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k)} +\overline{\mathbf{Z}_{i}}^{(k)} - \overline{\mathbf{X}_{i}\mathbf{W}}^{(k)}\right.\right.\\ &&\qquad \left.\left.+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right)\right) \end{array} $$

  (25)

• Updating $\overline {\mathbf {Z}_{i}}$, where i = 1,2,...,C

  2) By setting the derivative of (21) w.r.t. $\overline {\mathbf {Z}_{i}}$ to zero with current ${\mathbf {W}_{v}}^{(k+1)}, {\mathbf {F}_{i}}^{(k)}, \overline {\mathbf {P}_{i}}^{(k)}$, we have

  $$ 2V{\mathbf{F}_{i}}^{(k)}\left( V\overline{\mathbf{Z}_{i}} - \mathbf{Y}_{i}\right)+\rho V\left( \overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)} + \frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right) = 0 $$

  (26)

  Then, we have

  $$ \begin{array}{@{}rcl@{}} \overline{\mathbf{Z}_{i}}^{(k+1)}&=&\left( 2V{\mathbf{F}_{i}}^{(k)}+\rho \mathbf{I}_{i}\right)^{-1}\\ &&\times \left( 2{\mathbf{F}_{i}}^{(k)}\mathbf{Y}_{i}+\rho\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}-\overline{\mathbf{P}_{i}}^{(k)}\right) \end{array} $$

  (27)

  where $\mathbf {I}_{i}\in \mathbb {R}^{n_{i}\times n_{i}}$ is an identity matrix.

• 3) Updating F_i and $\overline {\mathbf {P}_{i}}$, where i = 1,2,...,C

  With ${\mathbf {W}_{v}}^{(k+1)}$ and $\overline {\mathbf {Z}_{i}}^{(k+1)}$, we calculate ${\mathbf {F}_{i}}^{(k+1)}$ and $\overline {\mathbf {P}_{i}}^{(k+1)}$ according to (22) and (23), respectively.

In summary, the complete procedure of our algorithm is shown in Algorithm 1. In each iteration, the transformation submatrices W_v(v = 1,...,V ) are calculated in parallel with the current $\overline {\mathbf {Z}_{i}}$ and $\overline {\mathbf {P}_{i}} (i=1,...C)$. We repeat this iteration procedure until it satisfies the convergence condition.

3.3 Complexity analysis

As is shown in Algorithm 1, we need to update four variables in each iteration, i.e. W_v, F_i, $\overline {\mathbf {Z}_{i}}$, $\overline {\mathbf {P}_{i}}$. In the process of calculating W_v, the complexity of matrix multiplication is $\mathcal {O}(d_{v}n(d_{v}+C))$ and the computational complexity of matrix inversion is $\mathcal {O}({d_{v}^{3}})$. The computational complexity of $\overline {\mathbf {X}_{i}\mathbf {W}}$ is n_idC, and the complexity for solving $\overline {\mathbf {Z}_{i}}$ is $\mathcal {O}({n_{i}^{3}}+{n_{i}^{2}}C+n_{i}dC)$. The complexity of F_i-update is $\mathcal {O}(n_{i}C)$. The complexity of updating $\overline {\mathbf {P}_{i}}$ is included in the $\overline {\mathbf {X}_{i}\mathbf {W}}$-update. So, the total complexity of each iteration is $\mathcal {O}\left ({\sum }_{v=1}^{V} ({d_{v}^{3}}+{d_{v}^{2}}nC)+2dnC+nC\right .$$\left .+{\sum }_{i=1}^{C} ({n_{i}^{3}}+{n_{i}^{2}}C)\right )$.

Instead of computing the entire matrix inversion with size of n × n or d × d in the traditional feature selection methods, the matrix inversion of the proposed algorithm is divided into blocks, with size of n_i × n_i or d_v × d_v. Similarly, the matrix multiplication is also calculated in blocks, such as X_ivW_v instead of XW. So, the distributed learning strategy can exceedingly cut down the computational cost on multiview feature selection.

4 Experiments

In this section, a series of experiments are conducted on public multiview datesets to compare the efficiency of the proposed method with one single-view supervised feature selection algorithm and five multiview supervised feature selection algorithms.

4.1 Datasets

Eight datasets are employed to validate the performances of competitors. The detailed descriptions about these datasets are as follows. And Table 1 shows the detailed information about the datasets used in experiments.

• Multiple Features (MF) [6]¹: This dataset consists of 2,000 handwritten numerals (‘0’–‘9’) with 10 classes. These digits are shown with six feature sets: 76-D Fourier coefficients of the character shapes, 216-D profile correlations, 64-D Karhunen-Love coefficients, 240-D pixel averages in 2 x 3 windows, 47-D Zernike moments and 6-D morphological features.

• Internet Advertisements Dataset (Ads)²: This dataset contains 3,279 (2,821 nonads and 458 ads) instances with five types of representations for each instance: 457-D features from url terms, 495-D features from origurl terms, 472-D features from ancurl terms, 111-D features from alt terms and 19-D features from caption terms.

• COIL₂₀ [15]³: This dataset contains 1,440 grayscale images for 20 objects. This paper extracts four different features via different feature descriptors, including 512-D GIST, 1764-D HOG, 1239-D LBP and 1000-D SIFT.

• Animals with Attributes⁴: This dataset consists of 30,475 images for 50 animals with six feature representations for each image: 2688-D Color Histogram features, 2000-D Local Self-Similarity features, 252-D Pyramid HOG features, 2000-D SIFT features, 2000-D SIFT features and 2000-D SURF features. In this paper, we select the first 20 classes in the alphabetical order (named Animal₂₀) as the training data.

• NUS-WIDE-OBJECT (NWO) [4]⁵: This dataset contains 30,000 objects for 31 classes with six types of low-level features, including 64-D color histogram, 144-D color correlogram, 73-D edge direction histogram, 128-D wavelet texture, 225-D block-wise color moments and 500-D bag of words based on SIFT descriptions. In this paper, we select the first 5 classes, 10 classes from NUS-WIDE-OBJECT training dataset in the alphabetical order (named NWO1 and NWO2) and adopt all samples (named NWO3) as the training data.

• NUS-WIDE (NW)⁵: This dataset contains 81 classes with five types of low-level features, including 64-D color histogram, 144-D color correlogram, 73-D edge direction histogram, 128-D wavelet texture and 225-D block-wise color moments. We have removed the unlabeled samples and three categories whose number exceeds 30000. The final NW dataset used in this experiments contains 104542 samples with 79 categories.

Table 1 Multiple view representations of different datasets

4.2 Experimental setup

To justify the superiority of the proposed method, we compare it with six state-of-the-art feature selection algorithms: DSML-FS [40], SSD-FS [41], HLR-FS [3], SCM [10], AWD [34] and SFS [13]. The detailed descriptions about these compared methods are as follows.

• 1. DSML-FS: It is a supervised multimodal feature selection method which adopts the L_2,1-norm and G_2,1-norm based joint structured sparsity regularization. There are two trade-off parameters λ₁ and λ₂ in this model.

• 2. SSD-FS: It is a supervised multiview self-weighted feature selection method established by introducing the sparsity-inducing regularization into a self-weighted orthogonal linear discriminant analysis. A trade-off parameter λ is set in this model.

• 3. HLR-FS: It is a supervised multiview feature selection method, and adopts the hypergraph based manifold regularization to enhance the inherent association of all points. There are two trade-off parameters λ₁ and λ₂ in this model.

• 4. SCM: It is a single-view supervised feature selection method which emphasizes the capped-l₂ norm loss and the L_2,p-norm regularizer minimization simultaneously. This model has two parameters λ and ε, where λ is the trade-off parameter and ε is the threshold parameter defined in the capped l₂-norm based loss term.

• 5. AWD: It is a supervised multiview feature selection method established by employing the discriminative regression and adapted-weighting coefficients on each view. A trade-off parameter λ is set in this model.

• 6. SFS: It is a supervised multiview feature selection method with the sharing category via the ADMM. A trade-off parameter λ is set in this model.

In the multi-view feature selection process, KNN and SVM classifiers are commonly used for the subsequent classification in feature selection. Thus, we adopt the KNN and SVM classifiers in the experiments. For SVM classifier, we apply the Gaussian kernel and linear kernel. The Gaussian kernel value in SVM classifier ranges {10^− 3,...,10¹}. To avoid the experimental deviation and overfitting problem, we embed an inner 5-fold cross validation into the outer 5-fold cross validation for searching the optimal classifier parameters. The whole dataset is first divided into five equal parts. One of them is used as the testing set and the remaining four sets are merged as the training set. Then, an inner 5-fold cross validation is employed on the training set to find the optimal parameters which are then used for the testing process. For all feature selection methods, the trade-off parameter λ, λ₁ and λ₂ are all searched in the range of {10^− 3,10^− 2,...,10²,10³}. The experiments are implemented in MATLAB 2016b with Intel(R) Core(TM) i7-8700, CPU 3.20 GHz 3.19 GHz and RAM 8 GB.

4.3 Experimental results and analysis

Firstly, we conduct experiments on five small scale datasets including Multiple Features, Ads, COIL₂₀, NWO1 and NWO2. Both KNN and SVM are adopted to test the performance of compared methods. For each dataset, the detailed classification accuracies⁶ in the different top-K feature cases are listed in Tables 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11, respectively. From the results of these tables, we can make some conclusions: (1) The accuracy is not positively related to the number of selected features, i.e. the classification accuracy does not always increase when the number of selected features increases. (2) The proposed method obtains the best results on more than half of the experiments in terms of KNN classifier. On the SVM classifier, our algorithm achieves the best results in almost half of the experiments.

Table 2 Classification accuracies of different feature selection methods on MF dataset (KNN)

Table 3 Classification accuracies of different feature selection methods on Ads dataset (KNN)

Table 4 Classification accuracies of different feature selection methods on COIL₂₀ dataset (KNN)

Table 5 Classification accuracies of different feature selection methods on NWO1 dataset (KNN)

Table 6 Classification accuracies of different feature selection methods on NWO2 dataset (KNN)

Table 7 Classification accuracies of different feature selection methods on MF dataset (SVM)

Table 8 F1 scores of different feature selection methods on Ads dataset (SVM)

Table 9 Classification accuracies of different feature selection methods on COIL₂₀ dataset (SVM)

Table 10 Classification accuracies of different feature selection methods on NWO1 dataset (SVM)

Table 11 Classification accuracies of different feature selection methods on NWO2 dataset (SVM)

In order to analyze the computational complexity of different algorithms, the training times for getting the transformation matrix W on five datasets are shown in Fig. 1. We can see that the proposed method and SFS exceed the other five algorithms on four datasets (MF, Ads, NWO1 and NWO2). Specifically, compared with DSML-FS and SCM, the proposed method takes less than a quarter of their training time. Since the proposed method includes the optimization of the outlier ratio parameter ε, it is slightly lower than SFS. However, in terms of the classification accuracy, the proposed method outperforms SFS.

Fig. 1

Comparisons of the training time for getting the transformation matrix W by DSML-FS, HLR-FS, SSD-FS, SCM, AWD, SFS and Ours on five datasets

Next, to verify the superiority of the proposed model when there are a large number of training samples or features, we further conduct experiments on Animal₂₀, NWO3 and NW datasets. Since the SVM classifier takes too long time on large-scale and high-dimensional datasets, we only use KNN classifier in this part. The detailed results including classification accuracy, optimal parameter combination and the training time are shown in Table 12 and Fig. 2. Particularly, the symbol “−” in Table 12 represents an algorithm running for more than 60 hours or exceeding the memory of the computer. For the HLR-FS algorithm, it needs to calculate the singular value decomposition (SVD) and matrix inversion, which requires high computational cost when dealing with the high-dimensional and large-scale datasets. The SSD-FS algorithm also has to compute the SVD based on the feature dimensionality, so it is hard to handle the high-dimensional datasets well. In the solution procedure of SCM algorithm, an n × n based matrix inversion needs to be calculated, which is easy to face memory overflow problems when handling the large-scale datasets. For DSML-FS and AWD algorithms, they need to calculate the matrix multiplication with size of n × n, which requires high computer memory when dealing with large scale dataset.

Table 12 Classification accuracies of the compared methods on Animal₂₀, NWO3 and NW datasets (KNN)

Fig. 2

Comparisons of the training time for getting the transformation matrix W by different feature selection methods on NWO3 and Animal₂₀ datasets

From the results in Table 12 and Fig. 2, we can get the following conclusions: (1) The proposed method and SFS require less training time. The HLR-FS, SSD-FS and SCM method run too much longer than the other methods on Animal₂₀ or NWO3 dataset. This suggests that these three methods have obvious inferiority when solving the high-dimensional or large-scale problems. On NW dataset, except the proposed method and SFS, the other methods can not obtain the classification accuracies because of the memory overflow. (2) The DSML-FS method obtains the best accuracies on Animal₂₀ and NWO3 datasets and our method ranks about 2% less than the best ones. However, in terms of time complexity, the training time of our method is 19 times faster than that of DSML-FS method on Animal₂₀ dataset and 295 times faster than that of DSML-FS method on NWO3 dataset, which demonstrates that the proposed method brings great superiority on reducing the computational cost. (3) Compared with SFS, the proposed method is weaker in the training time, but the accuracies on these big datasets are generally higher than those of SFS.

4.4 Friedman statistical analysis

Based on the experimental results in Tables 2-11, Friedman statistical hypothesis tests are adopted to determine whether the performances of these algorithms are different. Firstly, based on the Tables 2-6, we calculate the variable

$$ \tau_{\chi^{2}}=\frac{12N}{k(k+1)}\left( \sum\limits_{i=1}^{k} {r_{i}^{2}}-\frac{k(k+1)^{2}}{4}\right)=107.21 $$

(28)

where r_i represents the average rank of the i th method listed in Table 13, N = 35 is the number of cases and k = 7 is the number of methods. $\tau _{\chi ^{2}}$ obeys the χ² distribution with k − 1 degrees of freedom. The Friedman statistics variable is then calculated by

$$ \tau_{F}=\frac{(N-1)\tau_{\chi^{2}}}{N(k-1)-\tau_{\chi^{2}}}=50.1 $$

(29)

where τ_F obeys the F distribution with k − 1 and (k − 1)(N − 1) degrees of freedom. When the significance level α = 0.05, the critical value F_α(6,204) = 2.14 and it is less than τ_F = 50.1, which means the performances of these algorithms are significantly different. In order to further distinguish the performance difference among these algorithms, we compute the critical difference (CD) value by adopting Nemenyi test

$$ CD=2.949\sqrt{\frac{k(k+1)}{6N}}=1.523 $$

(30)

Since the differences between the proposed method and the compared methods are as follows

$$ \begin{array}{@{}rcl@{}} &&d(\text{DSML-FS}-\text{Ours})=1.143<1.523, \\ &&d(\text{HLR-FS}-\text{Ours})=2.143>1.523\\ &&d(\text{SSD-FS}-\text{Ours})=3.943>1.523, \\ &&d(\text{SCM}-\text{Ours})=1.172<1.523\\ &&d(\text{SFS}-\text{Ours})=3.7>1.523, \\ &&d(\text{AWD}-\text{Ours})=3.7>1.523 \end{array} $$

where d(i − j) means the difference between the algorithm i and j. We can then conclude that the proposed method outperforms the HLR-FS, SSD-FS, SFS and AWD algorithms because the differences are bigger than the critical difference. There is no significant difference between DSML-FS, SCM and the proposed method.

Table 13 The average rank of different feature selection methods

Secondly, based on the Tables 7-11, we calculate the variable

$$ \tau_{\chi^{2}}=\frac{12N}{k(k+1)}\left( \sum\limits_{i=1}^{k} {r_{i}^{2}}-\frac{k(k+1)^{2}}{4}\right)=98.963 $$

(31)

The Friedman statistics variable is then calculated by

$$ \tau_{F}=\frac{(N-1)\tau_{\chi^{2}}}{N(k-1)-\tau_{\chi^{2}}}=30.303 $$

(32)

The critical value F_0.05(6,204) = 2.14 is less than τ_F = 30.303, which means the performances of these algorithms are significantly different. With the $CD=2.949\sqrt {\frac {k(k+1)}{6N}}=1.523$, the differences between the proposed method and the compared methods are as follows

$$ \begin{array}{@{}rcl@{}} &&d(\text{DSML-F}S-\text{Ours})=0.057<1.523, \\ && d(\text{HLR-FS}-\text{Ours})=2.386>1.523\\ &&d(\text{SSD-FS}-\text{Ours})=3.357>1.523, \\ &&d(\text{SCM}-\text{Ours})=1.514<1.523\\ &&d(\text{SFS}-\text{Ours})=3.529>1.523, \\ &&d(\text{AWD}-\text{Ours})=2.757>1.523 \end{array} $$

We can then conclude that the proposed method outperforms the HLR-FS, SSD-FS, SFS and AWD algorithms because the differences are bigger than the critical difference. There is no significant difference between DSML-FS, SCM and the proposed method. The SVM based statistical analysis results are the same as that of KNN.

4.5 Verification experiment analysis

To verify how the capped l₂-norm based loss function effects the performance of experimental results, we further add some experiments on NWO1 and NWO2 datasets with KNN classifier to compare the performance between the capped l₂-norm and traditional l₂-norm. By replacing the capped l₂-norm with l₂-norm, the proposed model can be changed as follows.

$$ \underset{\mathbf{W}_{v}}{\min}\ \sum\limits_{i=1}^{C}\sum\limits_{v=1}^{V}\|\mathbf{X}_{iv} \mathbf{W}_{v}-\mathbf{Y}_{i}\|_{F}^{2} + \lambda\sum\limits_{v=1}^{V}\|\mathbf{W}_{v}\|_{2,1} $$

(33)

The KNN based classification accuracies of the (33) and ours are shown in Fig. 3. We can see that the classification accuracies of the capped l₂-norm based loss term get 2% higher than traditional l₂-norm on these two datasets, which validates that the proposed model has robustness to noise and is helpful to subsequent classification task.

Fig. 3

Classification accuracies of (33) and Ours on NWO1 and NWO2 datasets

4.6 Parameter analysis

In this part, the parameter sensitivity of the proposed model is analyzed. We research the influence of λ and the ratio of outliers on experimental results, respectively. The ratio of outliers determines the value of threshold ε. The value of another parameter is fixed when we investigate the effect of one parameter.

Firstly, we vary λ in the range {0.001,0.01,0.1,1,10, 100,1000} with fixed ratio of outliers. The classification accuracies by KNN with respect to λ on six datasets are shown in Fig. 4. We can see that the classification accuracies are not sensitive to the value of λ on MF and Ads datasets, but they have a certain degree of fluctuation on the other datasets. Particularly, the better results are usually achieved in the range {0.001,0.01,0.1}.

Fig. 4

Classification accuracies of the proposed method with respect to λ under different number of selected features, where λ is tuned from {0.001,0.01,0.1,1,10,100,1000}

Secondly, considering that there may be potential outliers in the datasets, we set the ratio of outliers to all data points as {0,0.01,0.05,0.1,0.2} and fix the value of λ to exploit how the accuracies change when removing different number of latent outliers. The classification accuracies by KNN with respect to the ratio of outliers on four datasets are shown in Fig. 5. We can observe that the proposed model is less sensitive with respect to the ratio of outliers on MF and Ads datasets but more sensitive to the ratio of outliers on NWO1 and NWO2 datasets, which may suggest that there exists some noises and outliers in these two datasets. From the results on NWO1 and NWO2 datasets, we can see that as the ratio of outliers increases, the accuracies first increase and then decrease in most cases. The reason may be that our model is removing outliers and noises when the ratio gradually rises. But when the ratio reaches a certain value, the accuracies start to decrease because too much data points are removed. In summary, the feature selection performance obtains a certain improvement when removing a proportion of potential outliers. The better results are usually obtained in the proportion of {0.01,0.05}.

Fig. 5

Classification accuracies of the proposed method with respect to the ratio of outliers under different number of selected features, where the ratio of outliers is tuned from {0,0.01,0.05,0.1,0.2}

4.7 Convergence analysis

To verify the convergence performance of Algorithm 1, we conduct some experiments on eight datasets. For each dataset, the parameters λ and ε are fixed as the optimal combination. Figure 6 shows how the convergence criterion term er in Algorithm 1 changes as the number of iteration increases. We can see that the value of er gradually reduces and then tends to zero, which means that the proposed method can satisfy the convergence condition within 15 iterations.

Fig. 6

Convergence curve of Algorithm 1

5 Conclusion

In this paper, an efficient multiview feature selection framework is designed via the distributed learning strategy. The proposed method adopts the sample-partition based distributed strategy to compute the loss term on each category and uses the view-partition based distributed strategy by minimizing the individual regularization of each view and common loss term across views. The capped l₂-norm based loss term instead of traditional l₂-norm is used to improve the robustness to outliers. Based on the distributed strategy, the proposed method has great superiority on reducing the computational complexity and fastening the running time of feature selection. The comparison experiments show the effectiveness of the proposed model in terms of the training time and classification accuracy.

In our model, the relationship of different views is taken into account via the distributed multiview learning. In the future work, we will try to introduce a set of weight parameters on different views to design a more fitting model for multiview learning.

Appendix

Theorem 2

Equations (16)-(19) is equivalent to (20)-(23).

Proof

• 1) For fixed i, the solution in (17) is obtained by updating V matrices $\mathbf {Z}_{iv}\in \mathbb {R}^{n_{i}\times C}(v=1,2...V)$ with totally n_iCV variables. Now, we will carry it out by solving the (21) with only n_iC variables.

  Let $\overline {\mathbf {Z}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V}\mathbf {Z}_{iv}$, the (17) can be rewritten as

  $$ \begin{array}{@{}rcl@{}} \underset{\overline{\mathbf{Z}_{i}},\mathbf{Z}_{iv}}\min &&tr\left[\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)^{T}{\mathbf{F}_{i}}^{(k)} \left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)\right]\\ &&\qquad+\frac{\rho}{2}\sum\limits_{v=1}^{V} \|\mathbf{Z}_{iv}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}\|_{F}^{2}\\ s.t. && \overline{\mathbf{Z}_{i}}=\frac{1}{V}\sum\limits_{v=1}^{V}\mathbf{Z}_{iv} \end{array} $$

  (34)

  Minimizing over Z_iv(v = 1, 2,...,V ) with $\overline {\mathbf {Z}_{i}}$ fixed has the solution

  $$ \mathbf{Z}_{iv}-\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}+\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}=0 $$

  (35)

  Let ${\overline {\mathbf {X}_{i}\mathbf {W}}}=\frac {1}{V}{\sum }_{v=1}^{V} \mathbf {X}_{iv}{\mathbf {W}_{v}}, {\overline {\mathbf {P}_{i}}}=\frac {1}{V}{\sum }_{v=1}^{V} {\mathbf {P}_{iv}}$. Then, we have

  $$ \overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}=0 $$

  (36)

  Combining (35) and (36), we have

  $$ \mathbf{Z}_{iv} = \mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)} - \frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)} + \overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)} $$

  (37)

  Substituting (37) into (34),we get the following equation.

  $$ \begin{array}{@{}rcl@{}} \underset{\overline{\mathbf{Z}_{i}}} \min && tr\left[\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)^{T}{\mathbf{F}_{i}}^{(k)}\left( V\overline{\mathbf{Z}_{i}}-\mathbf{Y}_{i}\right)\right]\\ &&+\frac{\rho V}{2}\|\overline{\mathbf{Z}_{i}}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}+\frac{1}{\rho} {\overline{\mathbf{P}_{i}}}^{(k)}\|_{F}^{2} \end{array} $$

  (38)

  Based on the above derivation, we can see that solving (17) is equivalent to solving (21).

• 2) Similarly, for fixed i, the P_iv-update in (19) can be carried out by solving the (23) with only n_iC variables. Replacing Z_iv in (37) with ${\mathbf {Z}_{iv}}^{(k+1)}$ obtains

  $$ \begin{array}{@{}rcl@{}} {\mathbf{Z}_{iv}}^{(k+1)}&=&\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k+1)}-\frac{1}{\rho}{\mathbf{P}_{iv}}^{(k)}+\overline{\mathbf{Z}_{i}}^{(k+1)}\\ &&-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)} +\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)} \end{array} $$

  (39)

  Substituting (39) into (19) gives

  $$ {\mathbf{P}_{iv}}^{(k+1)}=\rho\left( \overline{\mathbf{Z}_{i}}^{(k+1)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}\right)+\overline{\mathbf{P}_{i}}^{(k)} $$

  (40)

  (40) shows that the variables ${\mathbf {P}_{iv}}^{(k+1)}(v=1,2,...,V)$ are all equal for fixed i. So we can get ${\mathbf {P}_{iv}}^{(k+1)}=\frac {1}{V}{\sum }_{v=1}^{V} {\mathbf {P}_{iv}}^{(k+1)}=\overline {\mathbf {P}_{i}}^{(k+1)}$. Then, we have

  $$ \overline{\mathbf{P}_{i}}^{k+1}=\rho\left( \overline{\mathbf{Z}_{i}}^{(k+1)}-\overline{\mathbf{X}_{i}\mathbf{W}}^{(k+1)}\right)+\overline{\mathbf{P}_{i}}^{(k)} $$

  (41)

  Based on the above derivation, we can see that solving (19) is equivalent to solving (23).

• 3) By replacing Z_iv in (37) with ${\mathbf {Z}_{iv}}^{(k)}$ and substituting ${\mathbf {Z}_{iv}}^{(k)}$ into (16), we have

  $$ \begin{array}{@{}rcl@{}} {\mathbf{W}_{v}}^{(k+1)} &:=& \underset{\mathbf{W}_{v}}\arg \min \left( \lambda\|\mathbf{W}_{v}\|_{2,1} + \frac{\rho}{2}\sum\limits_{i=1}^{C}\|\mathbf{X}_{iv}\mathbf{W}_{v}\right.\\ &&\qquad\qquad \left. -\left( \vphantom{\frac{1}{\rho}}\mathbf{X}_{iv}{\mathbf{W}_{v}}^{(k)}+ \overline{\mathbf{Z}_{i}}^{(k)} - \overline{\mathbf{X}_{i}\mathbf{W}}^{(k)}\right.\right.\\ &&\qquad\qquad\left.\left. +\frac{1}{\rho}\overline{\mathbf{P}_{i}}^{(k)}\right)\|_{F}^{2}\vphantom{\sum\limits_{i=1}^{C}}\right) \end{array} $$

  (42)

  Based on the above derivation, we can see that solving (16) is equivalent to solving (20).

• 4) According to $\overline {\mathbf {Z}_{i}}=\frac {1}{V}{\sum }_{v=1}^{V}\mathbf {Z}_{iv}$, we can see that solving (18) is equivalent to solving (22).

□