1 Introduction

In real industrial applications, the system model is the key to the effective analysis and control. An ideal model should be able to describe the behavior of the system very adequately. When the system has only some knowledge, or no knowledge to use, it can use the results of system modeling to obtain the trajectory information of process variables from the input-output data collected from the actual measurement. Since most industrial process systems are nonlinear in nature, nonlinear system modeling has drawn considerable attention in process analysis [1], soft sensor [2, 3], controller design [4, 5] and other fields. The accuracy of the model has a critical influence on describing the dynamic behavior of nonlinear system. Thus, it is extremely urgent to establish an accurate model for the complex nonlinear industrial process system. However, due to the existence of structural and parameter uncertainties in nonlinear systems, it is overwhelmingly difficult to establish the model [6].

In recent decades, the traditional mathematical methods [7, 8] have been widely applied to design nonlinear systems modeling. However, when the nonlinear systems show strong nonlinearity, multivariable coupling, complex biochemical reactions and other characteristics, the above methods cannot get the considerable performance. With the continuous development of artificial intelligence, neural network(NN) algorithm has been widely used in nonlinear system modeling. Theoretically, feedforward neural network can approximate any continuous function defined on a compact set to a given accuracy. This universal approximation property makes NN very suitable for nonlinear system modeling, especially in the nonlinear systems difficult to be described mathematically [9,10,11]. Hence, the feedforward neural networks are used to establish the nonlinear systems model. For example, a nonlinear system based on the denoising autoencoders and neural network was proposed in [12]. The results demonstrated that this model can achieve good predictive performance. In [13], an empirical mode decomposition was applied to optimize the BPNN to model the complex nonlinear system. Attributed to this modeling, the good prediction effectiveness was been achieved. Xiao et al. [14] developed a nonlinear system modeling method based on the elastic BP neural network and grey Wolf optimizer. Then, based on this modeling, the control effectiveness can be ensured. However, the structure of the nonlinear system model need to be fixed in advance.

Since the structure of NN has a very important influence on the network performance of nonlinear system modeling, Therefore, many scholars focus on changing the topological structure of nonlinear system model. Some growing algorithms for the number of neurons have been proposed in [15, 17]. In [15], A fully connected cascade feedforward neural network algorithm based on fast cascade(FCNN) algorithm was proposed. Then, the hidden nodes of neural networks were grown by cascade algorithm. A nonlinear system modeling method of growing resource allocation RBF network was devised in [16]. Based on the novelty of input information, the hidden layer was constructed. Moreover, paper [17] developed a nonlinear system modeling method based on incremental modular deep neural network. Then, the weights of the training can be copied into other similar models to improve the recognition performance. However, the number of neurons increases without decreasing, which leads to redundancy of network structure. Hence, how to obtain a concise and efficient structure for nonlinear system modeling has also attracted widespread attention. In [18], a pruning method was used to model nonlinear systems. In this method, the hidden neurons were deleted in the convolutional NN. The results demonstrated that this method can be uesed to decrease both the computational of NN and the frequent access of memory. A nonlinear system modeling method based on pruning algorithm was designed in [19]. By pruning the weights of weak connections in the deep neural network, an efficient and sparse connection architecture can be obtained. Meanwhile, A nonlinear system modeling method based on the group sparse regularization algorithm was proposed to optimize the weight of deep belief network [20]. However, the above algorithm still has the following problems. Because most of the training time is spent on networks that are larger than the actual requirements, it needs to spend more computing costs. Therefore, paper [21] first applied the minimum resource neural network(MRNN) to the nonlinear system modeling. This method can not only add hidden layer neurons in the learning process, but also adjust the neural network topology by introducing the clustering strategy, Then, the MRNN can obtain an appropriate structure. However, the MRNN neglects the adjustment of parameters after structural adjustment, which leads to slow convergence speed of neural network learning algorithm. The literature [22] used peak intensity and root mean square error to improve the deep belief network and finally obtained a better nonlinear system model. Although the method has achieved good modeling results, there are a lot of model parameters that need to be adjusted and consume a lot of time.

Therefore, inspired by the foregoing, in this paper, an RBM-IBPNN is proposed for nonlinear systems modeling. First, Based on sensitivity analysis(SA) [23, 24] and mutual information(MI) theory, the topological structure of BPNN is adjusted. When the contribution rate of the hidden layer neurons is too small, the hidden layer neurons are deleted. When the contribution rate of the hidden layer neurons is too large, then the hidden layer neurons are split. At the same time, the MI is used to measure the correlation between neurons, when the MI of two hidden layer neurons meets the set standard, it indicates that these two neurons have similar functions and can be merged into one neuron. In the process of dynamic adjustment of neuron, the weights between layers are automatically adjusted to realize the dynamic adjustment of the structure of the neural network, Considering that the improved neural network in the process of structural adjustment, the training of the neural network adopts the gradient descent method, and its initial weights and threshold are given randomly, which easy to cause the convergence speed of the improved network to slow down and fall into the local minimum. The research shows that the appropriate initial weights and thresholds can effectively reduce the training time and avoid falling into local minimum [25, 26]. then based on the deep learning theory, the initial weights and thresholds of the IBPNN are trained by using the RBM [27,28,29]. and the weights and thresholds after training are used as initial weights and thresholds for the improved neural network. Thus, the prediction accuracy and convergence speed of the network are further improved. Finally, the proposed RBM-IBPNN is tested on nonlinear system identification, Lorenz chaotic time series prediction and the total phosphorus prediction problems.

The structure of this paper is as follows: Section II elaborates the method of neuron splitting and deleting based on SA and the method of neuron merging based on MI. Section III elaborates on the improved neural network weights and threshold initialization methods based on the RBM. Section IV is the experimental part, which elaborates the application of the proposed algorithm in the prediction of nonlinear system identification, Lorenz chaotic time series prediction and the total phosphorus prediction. Section V is the discussion part, which analyzes the advantages and disadvantages of the experimental design and algorithm. The final section is the conclusion and future work.

2 Design of improved BP neural network

In the training process of NN, the number of neurons of input layer and output layer can be determined in advance according to the task requirements. The setting of the neurons in the hidden layer is more complicated. If the structure is too large, it would be easy to cause over-learning. If the structure is too small, it would be unable to achieve considerable learning ability. Therefore, how to design an appropriate network structure is still an open problem. Therefore, to solve these issues, this section adopts the method of adding and pruning hidden layer neurons based on SA and MI [30,31,32], so as to achieve the purpose of automatic structural adjustment.

2.1 Neuron growing and pruning based on SA

2.1.1 Sensitivity analysis

SA is applied to measure the contribution of hidden layer output variables to network output, It is defined as the proportion of output components produced by specific input variables to total output. The sensitivity calculation formula is

$$ S_{\varepsilon}^{k} = \frac{{Va{r_{{w_{\varepsilon k}}y_{\varepsilon}^{(1)}}}[{Y^{k}}|{w_{\varepsilon k}}{y_{\varepsilon}} = {{\Theta}_{\varepsilon}}]}}{{Var({Y^{k}})}}, $$
(1)

where

$$ {Y^{k}} = f({w_{1k}}{y_{1}},{w_{2k}}{y_{2}} {\cdots} {w_{{n_{1}}k}}{y_{{n_{1}}}}), $$
(2)

where \(S_{\varepsilon }^{k}\) denotes the contribution rate of the εth input variable to the output of the kth model, Yk represents the response of the kth model, wεkyε represents the εth input variable for the kth model. ε = 1, 2, ... , n1, k = 1, 2, ... n2, \([{Y^{k}}|{w_{\varepsilon k}}{y_{\varepsilon }} = {{\Theta }_{\varepsilon }}]\) represents the part of the output value of the kth model generated by the εth hidden layer neuron, V ar(Yk) represents the variance of the kth network output variable, \({w_{1k}}{y_{1}},{w_{2k}}{y_{2}} {\cdots } {w_{n1k}}{y_{{n_{1}}}}\) represents the input variable value, reflecting the relationship between each hidden layer neuron and the kth output neuron. n1 is the number of neurons in the hidden layer, n2 is the number of models, \(y_{n_{1}}\) denotes the output of the n1th hidden layer neuron. wn1k denotes the weight between the n1th hidden layer neuron and the kth output neuron. According to the formula (1)–(2), the influence of input factors on output can be calculated. The higher the activity of input variables is, the greater the contribution rate will be.

2.1.2 Growing of hidden layer neurons

When the contribution rate of hidden layer neurons is large, it will cause violent fluctuations of network output. In order to avoid the existence of this situation, the neuron needs to be split into two moderately contributing neurons. Assuming that the contribution rate of neurons in the εth hidden layer is Sε. The criteria to be satisfied when it is split is

$$ {S_{\varepsilon}} > {\xi_{2}}, $$
(3)

where ξ2 is the threshold for by neuron split. When the εth neuron is split into new hidden layer neurons ∂ and δ, the weight adjustment rules of the newly added neurons are

$$ \left\{ \begin{array}{l} {w_{\Psi {\Theta} }} = {w_{\Psi\varepsilon}}\\ {w_{\Psi\vartheta }} = {w_{\Psi\varepsilon}}\\ {w_{\Theta k}} = (1 - \mu ){w_{\varepsilon k}},\\ {w_{\vartheta k}} = \mu {w_{\varepsilon k}} \end{array} \right. $$
(4)

where wΨΘ denotes the connection weight between the input layer neuron Ψ and the hidden layer neuron Θ, wΨε denotes the connection weight between the input layer neuron Ψ and the εth neuron in the hidden layer, wΨ𝜗 denotes the connection weight between the input layer neuron Ψ and the hidden layer neuron 𝜗, wΘk denotes the connection weight between the hidden layer neuron Θ and the output neuron k. w𝜗k denotes the connection weight between the hidden layer neuron 𝜗 and the output neuron k.

2.1.3 Pruning of hidden layer neurons

When the contribution rate of a hidden layer neuron is small, this neuron will be considered to be invalid, it can be deleted. Assuming that the contribution rate of neurons in the εth hidden layer is Sε, the criteria to be met when it is deleted is

$$ {S_{\varepsilon}} < {\xi_{3}}, $$
(5)

where ξ3 is the threshold value set for neuron deletion. After the εth neuron is pruned, the corresponding weight mutation is set to 0. In order to keep the output unchanged, it is necessary to compensate the neurons l with the most correlation of the pruned neurons.

$$ \left\{ \begin{array}{l} w_{\Psi \kappa }^{d}(t) = {w_{\Psi \kappa}}(t)\\ w_{\kappa k}^{d}(t) = {w_{\kappa k}}(t) + \frac{{{y_{\varepsilon}}}}{{{y_{\kappa}}}}{w_{\varepsilon k}}(t), \end{array} \right. $$
(6)

where \(w_{\Psi \kappa }^{d}\) denotes the connection weight of the Ψth neuron and the neuron κ of the input layer after the neuron is pruned. wΨκ denotes the connection weight of the Ψth neuron and neuron κ in the input layer before neuron pruning, \(w_{\kappa k}^{d}\) is the connection weight between the hidden layer neuron κ and the output neuron k after the neuron is pruned, wκk is the connection weight between the hidden layer neuron κ and the output neuron k before neuron pruning. And yε represents the output of the εth hidden layer neuron being pruned, yκ represents the output of neuron κ.

2.2 Neuron merging based on MI

2.2.1 Mutual information estimation

Assuming that any two hidden layer neurons output variables X and Y, the range of variable X is evenly divided into equal length KX segments by histogram method. The formula for KX is

$$ {K_{X}} = round\left\{ {\frac{\ell }{6} + \frac{2}{{3\ell }} + \frac{1}{3}} \right\}, $$
(7)
$$ \ell = \sqrt[3]{{8 + 324{\Omega} + 12\sqrt {36{\Omega} + 729{{\Omega}^{2}}} }}, $$
(8)

where ℓ is a constant that can be determined based on the number of samples, round represents the integer closest to the real variable, Ω denotes the number of samples. The entropy expression of variable X is

$$ H(X) = - \sum\limits_{k = 1}^{{K_{X}}} {{p_{k}}(x)} \log {p_{k}}(x), $$
(9)

where

$$ {p_{k}}(x) = \frac{{{n_{k}}}}{\Omega }, $$
(10)

It can be obtained from (9) and (10)

$$ H(X) = - \sum\limits_{k = 1}^{{K_{X}}} {\frac{{{n_{k}}}}{\Omega }} \log \frac{{{n_{k}}}}{\Omega } $$
(11)

where pk(x) denotes the probability that the sample falls into the kth segment, nk denotes the number of samples falling into the kth segment. Similarly, the joint entropy expression of variables Y, X and Y are

$$ H(Y) = - \sum\limits_{k = 1}^{{K_{Y}}} {\frac{{{n_{k}}}}{\Omega }} \log \frac{{{n_{k}}}}{\Omega }, $$
(12)
$$ H(X,Y) = - \sum\limits_{{k_{\Psi}} = 1}^{{K_{X}}} {\sum\limits_{{k_{\varepsilon}} = 1}^{{K_{Y}}}, {\frac{{{n_{{k_{\Psi}}{k_{\varepsilon}}}}}}{\Omega }} } \log \frac{{{n_{{k_{\Psi}}}}{n_{{k_{\varepsilon}}}}}}{\Omega } $$
(13)

Then the expression of MI between variables X and Y is

$$ I(X;Y) = M - \sum\limits_{{k_{\Psi}} = 1}^{{K_{X}}} {\frac{{{n_{{k_{\Psi}}}}}}{\Omega }} \log \frac{{{n_{{k_{\Psi}}}}}}{\Omega }- \sum\limits_{{k_{\varepsilon}} = 1}^{{K_{Y}}} {\log \frac{{{n_{{k_{\varepsilon}}}}}}{\Omega }\log }, \frac{{{n_{{k_{\varepsilon}}}}}}{\Omega } $$
(14)
$$ M = \sum\limits_{{k_{\Psi}} = 1}^{{K_{X}}} {\sum\limits_{{k_{\varepsilon}} = 1}^{{K_{Y}}} {\frac{{{n_{{k_{\Psi}}{k_{\varepsilon}}}}}}{\Omega }} } \log \frac{{{n_{{k_{\Psi}}{k_{\varepsilon}}}}}}{\Omega }, $$
(15)

where \({n_{{k_{\Psi }}}}\) and \({n_{{k_{\varepsilon }}}}\) denote the number of samples falling into the kΨ and kε segments, respectively, \( {n_{{k_{\Psi }}{k_{\varepsilon }}}}\) denotes the number of samples falling into the unit (kΨ,kε).

2.2.2 Merging of hidden layer neurons

In order to make each neuron have its own unique function, a method based on mutual information is proposed to evaluate the similarity between hidden layer neurons, and the neurons with higher similarity degree are merged into one neuron. The criterion of neuronal merger is shown in (16):

$$ I_{\varpi ,\phi } > {\zeta_{1}}, $$
(16)

where Iϖ,ϕ represents the mutual information between any two hidden layer neurons ϖ. ϕ, ζ1 is the threshold set for neuron merging.

$$ \left\{ \begin{array}{l} {w_{\Psi L}} = \alpha {w_{\Psi \varpi}} + \upbeta {w_{\Psi \phi}}\\ {w_{Lk}} = {w_{\varpi k}} + {w_{\phi k}},\\ {\tau_{L}} = \alpha{\tau_{\varpi}} + \upbeta {\tau_{\phi}} \end{array} \right. $$
(17)

where wΨϖ represents the weight between the Ψth input layer neuron and the hidden layer neuron ϖ, wΨϕ represents the weight between the Ψth input layer neuron and the hidden layer neuron ϕ, wΨL represents the weight between the Ψth input layer neuron and the newly generated neuron L of the hidden layer, wLk represents the weight between the newly generated neuron L of the hidden layer and the kth neuron of the output layer, wϖk represents the weight between the hidden layer neuron ϖ and the kth the output layer neuron, wϕk represents the weight between the hidden layer neuron ϕ and the kth output layer neuron, τL represents the bias of the new hidden layer neuron L, τϖ represents the bias of hidden layer neuron ϖ, τϕ represents the bias of hidden layer neuron ϕ, α and β are constant and the sum of them is 1.

3 Training of improved BP neural network based on restricted Boltzmann machine

3.1 Restricted Boltzmann machine

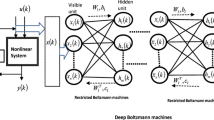
RBM is a kind of random NN model without self-feedback and symmetrical connection. There is no connection within the layer, and all connections between the layers. RBM has a two-layer structure, shown in Fig. 1.

Fig. 1
figure 1

RBM structure schematic diagram

Full size image

Where v denotes the visible layer, h denotes the hidden layer. Taking a layer RBM as an example, the training process is introduced. The visible layer of RBM contains r visible neurons, and the hidden layer contains s hidden neurons. The vectors v and h can denote the states of the visible and hidden neurons, respectively. Where vq represents the state of the qth visible neuron,hp represents the state of the pth hidden neuron. For any q, p, vq, hp, all satisfy the binary distribution. The energy of RBM is defined as

$$ E(v,h|\theta ) = \sum\limits_{q = 1}^{r} {{a_{q}}{v_{q}} - \sum\limits_{p = 1}^{s} {{b_{p}}{h_{p}}} } - \sum\limits_{q = 1}^{r} {\sum\limits_{p = 1}^{s} {{v_{q}}{w_{qp}}{h_{p}}} }, $$
(18)

where \(\theta = \left \{ {{w_{qp}},{a_{q}},{b_{p}}} \right \}\) represents the real parameter of RBM, wqp denotes the weight between the visible neuron q and the hidden neuron p, aq represents the bias of visible neuron q, bp represents the bias of hidden neuron p. The joint probability distribution of (v,h|θ) is

$$ P(v,h|\theta ) = \frac{{{e^{- E(v,h|\theta )}}}}{{Z(\theta )}}, Z(\theta ) = \sum\limits_{v,h} {{e^{- E(v,h|\theta )}}}, $$
(19)

where Z(θ) denotes partition function. According to the special structure of RBM, given the state of the visible neuron the state of the hidden neuron is conditionally independent of each other. Therefore, the probability of the pth hidden neuron is:

$$ p({h_{p}} = 1|v,\theta ) = \sigma \left( {b_{p}} + \sum\limits_{q} {{v_{q}}} {W_{qp}}\right) $$
(20)

where σ(x) denotes the sigmoid function. Given the state of the hidden neuron, the state of each visible unit is still conditionally independent of each other, that is, the activation probability of the qth visible neuron is

$$ P({v_{q}} = 1|h,\theta ) = \sigma \left( {a_{q}} + \sum\limits_{p} {{W_{qp}}{h_{p}}}\right), $$
(21)

Assuming that the training set contains T samples, the parameter θ is obtained by maximizing the logarithmic likelihood function of RBM on the training set. The key step is to calculate the partial derivative of \(\log P(v|\theta )\) with respect to θ, that is

$$ \begin{array}{@{}rcl@{}} \frac{{\partial \log P(v|\theta )}}{{\partial \theta }} &=& \sum\limits_{t = 1}^{T} { < \frac{{\partial (- E({v^{(t)}},h|\theta ))}}{{\partial \theta }}} { >_{P(h|{v^{(t)}},\theta )}} - \sum\limits_{t = 1}^{T}\\ &&{< \frac{{\partial (- E(v,h|\theta ))}}{{\partial \theta }}} { >_{P(v,h|\theta )}} \end{array} $$
(22)

where < ⋅>P denotes the mathematical expectation of the distribution P, \(\log P(h|{v^{(t)}},\theta )\) denotes the probability distribution of the hidden layer when the visible neuron is the known training sample v(t), P(v,h|θ) denotes the joint distribution of visible and hidden neurons.

Assuming that there is only one training sample, probability distribution \(\log P(h|{v^{(t)}},\theta )\) and joint distribution P(v,h|θ) are represented by “data” and “model”, respectively. Then the log-likelihood function connects the weight Wqp, and the partial derivatives of the visible layer neuron bias aq and the hidden layer neuron bias bp are

$$ \frac{{\partial \log P(v|\theta )}}{{\partial {W_{qp}}}} = < {v_{q}}{h_{p}}{ >_{data}} - < {v_{q}}{h_{p}}{ >_{model}}, $$
(23)
$$ \frac{{\partial \log P(v|h)}}{{\partial {b_{p}}}} = < {h_{p}}{ >_{data}} - < {h_{p}}{ >_{model}}, $$
(24)

where < ⋅>data is the expectation of observation data in the training set, < ⋅>model is the expectation on the distribution determined by the model.

RBM can optimize the whole model by contrasive divergence (CD) algorithm to achieve the local optimal state. This method is a layer by layer greedy training algorithm. It not only solves the problem of slow training speed, but also can find better initial values of model parameters.

3.2 Improved BP neural network weight and threshold initialization based on restricted Boltzmann machine

The basic implementation steps of the proposed algorithm are as follows

  1. 1)

    The SA value of each neuron in the hidden layer are calculated. Considering that the neurons in the hidden layer whose SA value is less than the threshold ξ3, Then this neuron will be regarded as invalid and redundant neurons, and it will be deleted.

  2. 2)

    Then the MI value between any two hidden layer neurons is calculated, The hidden layer neurons with too large MI value are determined. Two neurons whose MI value are greater than ζ1 are regarded as neurons with too much correlation, and they are merged into one neuron.

  3. 3)

    Then the neurons with excessive sensitivity are identified, and when the neuron SA value is greater than the set threshold ξ2, the neurons would be split.

  4. 4)

    Finally, the weight and threshold parameters of IBPNN are initialized by RBM.

3.3 Structure design of IBPNN based on restricted Boltzmann machine

The structure design of IBPNN based on RBM is shown in Fig. 2

Fig. 2
figure 2

Structural block diagram of EBPNN based on restricted boltzmann machine

Full size image

4 Experimental analysis

4.1 Nonlinear system identification

In this experiment, a benchmark problem is applied to test the prediction performance of the neural network, and its expression is described as follows

$$ \begin{array}{@{}rcl@{}} y(t + 1) &=& g(y(t),y(t - 1)) + u(t)\\ &=& \frac{{y(t)y(t - 1)[y(t) + 2.5]}}{{1 + {y^{2}}(t) + {y^{2}}(t - 1)}} + u(t), \end{array} $$
(25)

where 1 ≤ t ≤ 1000, y(0) = 0, y(1) = 0, \(u(t) = {\sin \limits } (2\pi t/25)\).

According to formula (25), 1000 time-discrete data samples are generated, of which the first 800 are applied to train the neural network proposed in this paper, the last 200 are employed to test the prediction effect of the network. The initial weight and threshold of each hidden layer node are generated by the restricted boltzmann machine training, The model can be described by

$$ \mathop y\limits^\wedge (t + 1) = \mathop f\limits^\wedge (y(t),y(t - 1),u(t)), $$
(26)

In the proposed RBM-IBPNN, there are a total of three inputs and one output, where y(t), y(t − 1), u(t) represents the input of the neural network, \(\mathop y\limits ^ \wedge (t + 1)\) represents the output of the neural network, the data is normalized before network training, and the expected error is 0.001. The maximum number of iterations is 10000. The threshold values of mutual information merging neurons, sensitivity division and pruning neurons are set to 3.25, 0.15 and 0.03 respectively. The number of iterations of RBM is 100, the learning rate is 1, The number of neurons in the initial hidden layer is 20 and 2.

Figure 3 shows the training effect of 800 samples trained by RBM-IBPNN in the training process. Based on the analysis of Fig. 3, we can conclude that the actual training output curve and the target curve have the same trend of change, thus realizing the good tracking of the target curve by the actual training output, which has a very good fitting effect. Figure 4 is the test effect diagram of RBM-IBPNN for testing 200 samples in the test process. It can be seen that the actual output curve fluctuates up and down with the predicted target curve, which achieves a good tracking of the predicted target curve and has a good fitting effect. Figure 5 shows the dynamic adjustment diagram of the hidden layer neurons with the initial hidden layer neuron of 20 in the training process of the RBM-IBPNN. When the number of hidden layer neurons reaches 8, the network structure will never change. Figure 6 is the dynamic adjustment chart of RBM-IBPNN in the training process. The initial number of hidden layer neurons is 2, During the training process, the number of neurons is constantly changing. When the number of neurons is 10, the structure no longer changes.

Fig. 3
figure 3

The training effect diagram of RBM-IBPNN

Full size image
Fig. 4
figure 4

The test effect diagram of RBM-IBPNN

Full size image
Fig. 5
figure 5

Dynamic adjustment diagram of structure with initial hidden layer neuron of 20

Full size image
Fig. 6
figure 6

Dynamic adjustment diagram of structure with initial hidden layer neuron of 2

Full size image

To test the performance of the proposed RBM-IBPNN, the predicting values are compared with those of SOA-SOFNN [33], DFNN [24], SOFNNGA [35], RBF-AFS, OLS. The performance comparison between RBM-IBPNN and other algorithms is shown in Table 1. Accroding to the Table 1, The results can indicate that although the running time of the proposed algorithm is slightly behind that of DFNN and SOA-SOFNN, the prediction accuracy of the proposed RBM-IBPNN is much higher than that of the two algorithms, Therefore, The proposed RBM-IBPNN has excellent prediction performance. Meanwhile, compared with the original BPNN, the proposed algorithm improves the prediction accuracy and convergence speed significantly, which proves that the proposed algorithm is scientific and effective.

Table 1 Performance comparison of different algorithms
Full size table

In order to illustrate the impact of threshold changes on the model performance, random changes are performed for the thresholds of mutual information, sensitivity splitting and sensitivity deleting. The impact on the change of hidden layer neurons is shown in Figs. 7, 8 and 9, The impact on the prediction performance is shown in the Table 2.

Fig. 7
figure 7

IBPNN hidden layer neuron variation diagram when sensitivity splitting threshold is 0.45

Full size image
Fig. 8
figure 8

IBPNN hidden layer neuron change diagram when the threshold of mutual information merge is 2

Full size image
Fig. 9
figure 9

IBPNN hidden layer neuron variation diagram when the sensitivity deletion threshold is 0.1

Full size image
Table 2 Comparison of prediction performance at different thresholds
Full size table

4.2 Lorenz chaotic time series prediction

Chaotic time series prediction is one of the benchmark problems for testing the effectiveness of neural network structures and methods, Lorenz effect is also called butterfly effect because its phase diagram resembles a butterfly. It means that weather is sensitive and dependent on initial conditions, so its long-term prediction is almost impossible. It’s equation is shown as

$$ \left\{ \begin{array}{l} \frac{{dx}}{{dt}} = \sigma ({y_{t}} - {x_{t}})\\ \frac{{dy}}{{dt}} = - {x_{t}}{z_{t}} + \gamma ({x_{t}} - {y_{t}}),\\ \frac{{dz}}{{dt}} = {x_{t}}{y_{t}} - \upbeta {z_{t}} \end{array} \right. $$
(27)

where x denotes the convection intensity, y denotes the horizontal temperature difference between the rising and sinking airflows, z is the vertical temperature difference. t denotes time. σ = 10,γ = 28, β = 8/3. In the experiment, a time series in the x dimension is generated, the training sample is 1500 sets of data, and the test sample is 1000 sets of data. In the network, the number of the initial hidden layer neurons is 30 and 6, and the expected error is 0.0001. the mutual information and sensitivity threshold settings are 3, 0.45 and 3, respectively, and the number of iterations of RBM is 100, the learning rate is set to 1.

Figure 10 shows the effect of RBM-IBPNN on 1500 samples during training. Accroding to the Fig. 10, we can see that the actual training output curve tracks the target curve very well and has a very good fitting effect. Figure 11 shows the RBM-IBPNN effect on the test set. It can be seen from Fig. 11 that the actual output curve achieves good tracking of the predicted target curve and has a good fitting effect. Figure 12 is a dynamic adjustment diagram of RBM-IBPNN with 6 initial hidden layer neurons in the training process, Fig. 13 is a dynamic adjustment diagram of RBM-IBPNN with 30 initial hidden layer neurons in the training process. As can be seen from Figs. 12 and 13, under the conditions of different initial structures, stability are finally achieved after a series of adjustments.

Fig. 10
figure 10

The training effect diagram of RBM-IBPNN

Full size image
Fig. 11
figure 11

The test effect diagram of RBM-IBPNN

Full size image
Fig. 12
figure 12

Dynamic adjustment diagram of structure with initial hidden layer neuron of 6

Full size image
Fig. 13
figure 13

Dynamic adjustment diagram of structure with initial hidden layer neuron of 30

Full size image

To test the performance of the proposed algorithm, the predicting values of the proposed RBM-IBPNN are compared with those of ESN [36], R-RTRL [36], RBFNN [37], DFNN [34], PSO-DBN [33], S-DBN [38], DRDNN [39]. The performance comparisons between the proposed algorithm and other algorithms are shown in Table 3. It can be seen that the proposed algorithm owns a higher prediction accuracy and convergence speed than the other algorithms. The results demonstrate that RBM-IBPNN is scientific and valid.

Table 3 Performance comparison of different algorithms
Full size table

4.3 The total phosphorus prediction

Many studies have shown that total phosphorus is the main cause of eutrophication in water bodies. Therefore, it is very important to strengthen the detection of total phosphorus concentration in wastewater effluent. However, the prediction of total phosphorus in wastewater treatment process has the characteristics of strong non-linearity and large time-varying, It is difficult to measure the total phosphorus concentration of the key variables. This study uses RBM-IBPNN to predict total phosphorus with the help of other key variables that can be easily measured. A total of 350 sets of wastewater water quality data from June to August 2018 are obtained from a small wastewater treatment plant in Beijing, 300 sets of data are randomly selected as training set, and the remaining 50 sets are selected as test set. The key measurable variables NH4-N, DO1, COD, SS, TN and ORP are used as inputs to the prediction model. The key measurable variables and their meanings are shown in Table 3. In the experiment, the number of the initial hidden layer neurons is 20 and 5, and the expected error is 0.0001. the mutual information and sensitivity threshold settings are 3, 0.45 and 3.25, respectively, and the number of iterations of RBM is 100, the learning rate is 2 (Table 4).

Table 4 Measurable variables and meaning
Full size table

Figure 14 shows the effect of RBM-IBPNN on 350 samples during training, accroding to the Fig. 14, we can conclude that the actual training output curve tracks the target curve very well and has a very good fitting effect. Figure 15 shows the RBM-IBPNN effect on the test set. It can be seen from Fig. 15 that the actual output curve can achieve good tracking of the predicted target curve and has a good fitting effect. Figure 16 is a dynamic adjustment diagram of RBM-IBPNN with 20 initial hidden layer neurons in the training process. Figure 17 is a dynamic adjustment diagram of RBM-IBPNN with 5 initial hidden layer neurons in the training process. As can be seen from Figs. 16 and 17, the number of neurons in the hidden layer is adjusted rapidly at the beginning and stabilized at the end, which shows the effectiveness of the structural adjustment algorithm.

Fig. 14
figure 14

The training effect diagram of RBM-IBPNN

Full size image
Fig. 15
figure 15

The test effect diagram of RBM-IBPNN

Full size image
Fig. 16
figure 16

Dynamic adjustment diagram of structure with initial hidden layer neuron of 20

Full size image
Fig. 17
figure 17

Dynamic adjustment diagram of structure with initial hidden layer neuron of 5

Full size image

To test the performance of the proposed algorithm, the predicting values of the proposed RBM-IBPNN are compared with those of DBN [40], ALRDBN [40], CDBN [41], SSDBN [17], S-DBN [38], RFNN [42], SCNN [43], EBP-SVDFNN [44], EBP-FNN [44]. The performance comparisons between the proposed algorithm and the existing algorithms are shown in Table 5. Accroding to the table, it can be seen that the proposed algorithm owns a higher accuracy and convergence speed than the other algorithms. The results demonstrate that RBM-IBPNN is scientific and effective.

Table 5 Performance comparison of different algorithms
Full size table

5 Discussion

The purpose of this study is to propose a fast and accurate improved neural network model for nonlinear systems. According to the evaluation results in three experiments, the following conclusions can be drawn.

5.1 New structure adjusting citerion

The structure adjustment of the IBPNN depends on the SA and MI of hidden neurons in the NN. Then, the RBM is employed to perform parameters initialization of training on the IBPNN. When the contribution rate of the hidden layer neurons is too small, the hidden layer neurons are deleted. When the contribution rate of the hidden layer neurons is too large, then the hidden layer neurons are split. At the same time, the MI is used to measure the correlation between neurons, when the MI of two hidden layer neurons meets the set standard, it indicates that these two neurons have similar functions. Therefore, the hidden neurons can be merged into one neuron. The dynamic adjustment of network structure can be achieved.

5.2 Higher prediction accuracy and faster convergence speed

The key problems faced by training algorithms are prediction accuracy and convergence speed. There are many reasons that affect prediction accuracy and convergence speed, such as algorithm architecture, structure learning method and parameter adjustment. Here we will discuss the effect of the structure learning method. It can be seen from Tables 1, 3 and 5. The proposed RBM-IBPNN has higher prediction accuracy and convergence speed. In the past, the network structure was preset, and the structure did not change from beginning to end. The structure was inevitably redundant. At the same time, the initial weights and thresholds of the network were given randomly and the training of the neural network was carried out by using the stochastic descent algorithm. The above reasons easily led to the redundancy of the neural network structure, slow convergence speed of training, low prediction accuracy and easy to fall into local optimum problems. Therefore, the NN structure adjustment method based on the SA value and the MI value automatically increases and deletes the neurons, reduces the redundancy of the structure. Then, the RBM is employed to perform parameters initialization of training on the IBPNN. As can be seen from Tables 1, 3 and 5, it’s easy to figure out that the convergence speed of the RBM-IBPNN is slower than those of SOFNNGA, DFNN and RBFNN. The reason is that the algorithm of parameter adjustment is based on supervised gradient descent algorithm. To ensure the convergence of the algorithm, the gradient method reduces the learning rate and the learning step, which results in the slow convergence speed.

5.3 Compact structure

Another important issue is the size of the final neural network. A smaller neural network can make the network structure more compact. The final structure depends on the adjustment of hidden layer neurons based on SA value and MI value, and the training of initial weight and threshold by the RBM. The proposed RBM-IBPNN algorithm obtains a more compact structure according to the new dynamic adjustment criterion. In addition, it can be known from the changes of initial hidden layer neurons to final neurons in Tables 1, 3 and 5 that the proposed algorithm achieves a relatively satisfactory compact neural network structure.

6 Conclusion and future work

This study proposes an RBM-IBPNN, which can automatically adjust its structure. Then, the proposed RBM-IBPNN is evaluated on nonlinear system identification, Lorenz chaotic time series prediction and the total phosphorus prediction problems. The expermental results demonstrate that the proposed RBM-IBPNN is better than other compared algorithms. The advantages of the algorithm are as follows.

  1. 1)

    The algorithm relies on the SA and MI of the neurons of the hidden neurons, as well as the RBM to meet the key design objectives. Its basic design idea is to adjust the structure based on SA and MI values between the hidden neurons, and RBM is used to train the initial weights and thresholds of the IBPNN. This design strategy can well adapt to the different situations that may occur at different times in the design process of BPNN.

  2. 2)

    The algorithm automatically adjusts the structure of the NN by SA value and MI value between the hidden neurons. When the contribution rate of the hidden layer neurons is too small, the hidden layer neurons are deleted. When the contribution rate of the hidden layer neurons is too large, then the hidden layer neurons are split. At the same time, the MI is used to measure the correlation between neurons, when the MI of two hidden layer neurons meets the set standard, it indicates that these two neurons have similar functions. Therefore, the hidden neurons can be merged into one neuron. According to the above design criteria, a compact neural network can be obtained. This design solves the problem of over-fitting and improves the prediction performance of the network. and then the initial weights and thresholds of the network are trained by using the RBM, thus solving the problem of slow convergence speed and easy to fall into local optimum.

Regardless of the structure of the original NN, the proposed algorithm can maintain good performance, and it can be applied to many practical applications, three of which have been described in this paper. In this paper, a large number of experiments are carried out to compare RBM-IBPNN with other algorithms. In the future, our main focus is to improve the RBM-IBPNN algorithm and greatly improve the convergence speed and to some extent improve the prediction accuracy of the network.