Reduced-order observer-based robust leader-following control of heterogeneous discrete-time multi-agent systems with system uncertainties

Abstract

In this paper, the leader-following control of heterogeneous discrete-time multi-agent systems (HD_MASs) in the presence of system uncertainties under directed topology is addressed. It aims to achieve reference tracking, disturbance rejection and robust control while the references and disturbances are generated by an autonomous exosystem. In practice, these agents are often different types of devices, thus they have different internal dynamics. Moreover, it is difficult to measure all states of each aircraft due to high cost or technical limitation. In this case, a novel leader-following output consensus problem is formulated and solved in this paper. Firstly, an appropriate linear transformation is proposed to divide the state information of each agent into measurable and unmeasurable parts. Then the reduced-order observer is designed only for unmeasurable parts. Based on the designed observer, the distributed feedback controller is proposed such that the outputs of all followers reach the same trajectory with the leader. In light of the internal model principle and discrete-time algebraic Riccati equation, the robust leader-following consensus of HD_MASs is achieved. Furthermore, this paper extends the results to continuous-time multi-agent systems. Finally, several simulation experiments are presented to verify the effectiveness of the theoretical results.

1 Introduction

In the last few years, the efficient hierarchical control of industrial plants has achieved remarkable benefits in reducing energy consumption, and improving operational efficiency. More concretely, the industrial plants are generally considered as the large-scale systems with high complexity, large delay, and strong uncertainty. Industrial processes can be divided into several subsystems with different properties, such as energy or information flows [1, 2]. When the measured and controlled plant variables increase, the cooperative control of industrial plants becomes more and more challenging. In order to solve this problem, many researchers regard industrial subsystems as agents, thus the industrial systems can be considered as multi-agent systems (MASs). It should be noted that the cooperative control of MASs is essentially different from the single-system control of existing control systems. It mainly communicates with neighbors through network topology and cooperates with each other to accomplish tasks that individual cannot accomplish. The cooperative control of MASs has attracted great attention and has been applied in many fileds, such as smart grid, vehicle systems, sensor networks, and mobile robots [3,4,5].

Generally speaking, the application object of multi-agent distributed cooperative control is autonomous systems, such as quad-rotor UAV [6]. At present, a large number of applications consider autonomous formation control for quad-rotor UAV [7, 8]. The typical problem of these applications is how to design a coordination controller. Previous studies have rarely considered how these UAVs fly in formation when their structures are different. Moreover, in practice, it is difficult to measure all states of each aircraft due to high cost or technical constraint. Take the state variable x = (s, v) as an example, the state s can be observed while the state v is unmeasurable. Furthermore, due to the parameter mismatch or model imprecision, the uncertainty is inevitable in aircraft model. Therefore, it is an urgent problem to design the distributed communication protocol and enable aircrafts to achieve consensus under the above circumstances. Motivated by this, this paper focuses on the distributed robust leader-following consensus problem of heterogeneous MASs with system uncertainties and unmeasurable states.

Many profound results about leader-following control of MASs based on different dynamic systems have been obtained [9,10,11,12,13,14,15,16,17,18,19,20]. For instance, the tracking problems have been studied for first-order systems [12], second-order systems [13], and the works in [14, 15] extended the dynamics of systems to general linear systems. It is noted that the aforementioned literatures assume that the dynamics of all agents are homogeneous. However, such assumption is too restrictive for many practical applications. When homogeneous dynamics fail to describe agent behaviors in many practical scenarios, consensus for network of agents with heterogeneous dynamics becomes more interesting. For example, the leader-following consensus problem of heterogeneous MASs was developed in [16] under static network topology. The cooperative robust output regulation for second-order discrete-time MASs was investigated in [17]. And the work in [18] addressed the leader-following consensus of heterogeneous MASs with different individual adaptation structures and input constraints.

It is worth noting that there is a key assumption in the aforementioned consensus techniques [13,14,15,16,17,18] that state variables are available for measurement. However, in many practical systems, many states are unmeasurable due to technological limitations. In this case, it is important to develop effective observers to measure the states accurately [19,20,21]. For example, the leader-following consensus problem of discrete-time MASs was investigated in [19] by the distributed observer-based consensus protocols. The authors of [20] discussed the state consensus problem of linear MASs under time-invariant directed communication topology via state observers. Moreover, Zhu et al. [21] studied the cooperative tracking control problem for MASs with unknown external disturbances by a novel observer-based cooperative tracking protocol. In most existing literatures on observer-based leader-following problem, the observers are usually designed to be full-order. In order to reduce the energy consumption, decrease calculation dimension and improve operational efficiency, it is necessary to design the reduced-order observers.

Motivated by the above-mentioned works, we make further endeavors to consider the distributed leader-following consensus problem of heterogeneous MASs with system uncertainties. The main contributions of the present work are three-fold. Firstly, this paper focuses on more general systems—heterogeneous MASs in the presence of unmeasurable states and uncertain dynamics. It relaxes the assumptions that all agents dynamics are homogenous [12,13,14,15] and all state variables are available [13,14,15,16,17,18]. Secondly, compared with a class of distributed tracking algorithms that are derived based on full-order observers [19,20,21], this paper designs the reduced-order observer to reduce the energy consumption and calculation dimension. Finally, in light of the internal model principle and discrete-time algebraic Riccati equation, the robust leader-following consensus of HD_MASs under directed topology is achieved. Furthermore, the results can be extended to continuous-time MASs.

This paper is organized as follows. Some basic notations of graph theory, system model and problem formulation are introduced in Section 2. Section 3 discusses the distributed leader-following consensus of HD_MASs. Section 4 extends the results to continuous-time MASs. Several numerical simulations are given to illustrate the effectiveness of theoretical results in Section 5. Finally, this paper is concluded in Section 6.

Notations

Throughout this paper, let Rⁿ, R^n×n and C^n×n denote the set of n-dimension vector space, n × n real matrix space and n × n complex matrix space, respectively. $\mathcal {C}$ represents the complex field and λ_i(A) stands for the i-th eigenvalue of the matrix A. Notation A^∗ represents the conjugate transpose of A, A ⊗ B denotes the Kronecker product of A and B, 0_m×n represents a zero matrix with m × n dimension and 1_n indicates (1,1,…,1)^T with dimension n. Moreover, $\mathbb {N}$ is the natural number set and $\mathbb {N}^{+}$ is the set of positive integers.

2 Preliminaries and problem formulation

2.1 Algebraic graph theory

Let digraph $\mathcal {G}=\{\mathcal {V},\mathcal {E}\}$ denote the relationships of information transmission among N agents and one leader. $\mathcal {V}$ = {v₀, v₁,…, v_N} represents the vertex set and $\mathcal {E} = \{e_{ij}=(v_{i},v_{j})\in \mathcal {V} \times \mathcal {V}\}$ denotes the edge set. Let $\mathcal {I}=\{1,2,\ldots ,N\}$ be a node index set, v₀ be the leader and v_i(i = 1,2,…, N) be the i-th agent, the neighborhood of the agent v_i is defined as $\mathcal {N}_{i}=\{v_{j}\in \mathcal {V}:(v_{i},v_{j})\in \mathcal {E}\}$. A directed path from agent v_i to agent v_j (v_i and v_j are two distinct agents) of the digraph $\mathcal {G}$ is a sequence of ordered edges of the form $(v_{i}, v_{i_{1}}), (v_{i_{1}}, v_{i_{2}}), \ldots , (v_{i_{m}}, v_{j})$. In addition, the digraph $\mathcal {G}$ contains a directed spanning tree if there exists at least one agent called root node such that the node has directed paths to all other nodes. The adjacency matrix of the digraph $\mathcal {G}$ is denoted as $\mathcal {A}=[a_{ij}]_{N\times N}$ ($a_{ij}\geq 0, \forall i, j\in \mathcal {I}$). If edge $e_{ij}=(v_{i},v_{j})\in \mathcal {E}$, then a_ij > 0, which means that the i-th agent can receive the information from the j-th agent directly. And if $(v_{i},v_{j})\notin \mathcal {E}$ for all $i, j\in \mathcal {I}$, then a_ij = 0. The degree matrix is defined as $\mathcal {D}=diag\{d_{1}, d_{2}, \ldots , d_{N}\}$ with d_i = deg_out(v_i), where deg_out(v_i) is the out-degree of agent v_i, defined as $deg_{out}(v_{i})={\sum }_{j=1}^{N}a_{ij}$. Correspondingly, the Laplacian matrix is defined as ${\mathcal{L}}=\mathcal {D}-\mathcal {A}$. Let ${\mathcal{H}}=\mathcal {A}_{0}+{\mathcal{L}}$, where $\mathcal {A}_{0}=diag\{a_{10}, a_{20}, \ldots , a_{N0}\}$, a_i0 > 0 if the i-th agent can receive information from leader, else a_i0 = 0.

Assumption 2.1

The digraph$\mathcal {G}$contains a directed spanning tree with one leader as its root node.

Lemma 2.1

[22] The Laplacian matrix${\mathcal{L}}$of$\mathcal {G}$has an eigenvalue zero with multiplicity 1 and corresponding eigenvector1_N, and all other non-zero eigenvalues have positive real parts, if and only if Assumption 2.1 is satisfied.

2.2 System model and problem formulation

In this paper, the i-th agent has following dynamic

$$ \begin{array}{lll} &x_{i}(k+1)=\bar{A}_{i}x_{i}(k)+\bar{B}_{i}u_{i}(k)+\bar{E}_{i}\omega(k),\\ &y_{i}(k)=C_{i}x_{i}(k), i=1,2,\ldots,N, \end{array} $$

(1)

where x_i(k) ∈ Rⁿ, y_i(k) ∈ R^p, u_i(k) ∈ R^q are the system state, measurable output and control input of the i-th agent, separately. The matrices $\bar {A}_{i}=A_{i}+{\varDelta } A_{i}, \bar {B}_{i}=B_{i}+{\varDelta } B_{i}, \bar {E}_{i}=E_{i}+{\varDelta } E_{i},$ where A_i, B_i, C_i and E_i are the nominal matrices and ΔA_i, ΔB_i and ΔE_i are the uncertain matrices. These uncertain matrices are considered as time-invariant, which are common and considered in [17, 23,24,25]. If these perturbed matrices are all zero matrices, the system (1) is called a nominal system. $\bar {E}_{i}\omega (k)$ is the external disturbance of the i-th agent. In general, an exosystem can be regarded as a leader system representing the reference input or external disturbance with the following form,

$$ \begin{array}{lll} &\omega(k+1)=A_{0}\omega(k),~~y_{r}(k)=F_{0}\omega(k), \end{array} $$

(2)

where ω(k) ∈ R^s is the state of the leader, and y_r(k) ∈ R^p is the reference output. The main purpose of this paper is to design the control protocol u_i(k) to make all followers reach the leader asymptotically, i.e.

$$ \begin{array}{@{}rcl@{}} \lim\limits_{k\rightarrow \infty}e_{i}(k)&=&\lim\limits_{k\rightarrow \infty}y_{i}(k)-y_{r}(k)\\ &=&\lim\limits_{k\rightarrow \infty}C_{i}x_{i}(k)-F_{0}\omega(k)= 0, \end{array} $$

(3)

for any i = 1,2,…, N. Here, e_i(k) denotes the tracking error between the measurement output and reference output of the i-th agent.

Remark 2.1

The tracking error e_i(k) is an index for describing (or verifying) whether the agent i tracks the leader, but not for controller feedback.

Definition 2.1

Given systems (1), (2), design an appropriate distributed feedback control law u_i(k) such that

1):

the system matrices of the nominal closed-loop system

$$ \begin{array}{lll} &x_{i}(k+1)=A_{i}x_{i}(k)+B_{i}u_{i}(k)+E_{i}\omega(k),\\ &y_{i}(k)=C_{i}x_{i}(k), i=1,2,\ldots,N, \end{array} $$

(4)

are Schur.

2):

there exists an open neighborhood W of Δ = 0 such that for any Δ ∈ W and for any initial states x_i(0), ω(0), the tracking errors converge to zero asymptotically, i.e. $\lim \limits _{k\rightarrow \infty }e_{i}(k)= 0$, i = 1,…, N,

then the robust leader-following output consensus problem is solved.

3 The leader-following consensus of HD_MASs

3.1 The leader-following consensus of nominal system

Assumption 3.1

The matrix pairs (A_i, B_i, C_i) are controllable and observable for i = 1,2,…, N, and the matrices C_ihave row full rank.

Assumption 3.2

The exosystem matrix A₀has no eigenvalues in the interior of the unit circle in the complex plane, i.e., |Reλ(A₀)|≥ 1.

Assumption 3.3

All systems satisfy the transmission zeros condition, i.e. ∀λ ∈ σ(G₁), $Rank \left ({\begin {array}{*{20}{c}} A_{i}-\lambda I_{n} & B_{i}\\ C_{i} & \mathbf {0} \end {array}} \right )=n+p,$ here σ(G₁) is the spectrum of G₁.

3.1.1 The design of reduced-order observer

Assume that each agent cannot receive the state information of itself or its neighbors directly, it is necessary to design the observer to estimate these unmeasurable states. A linear transformation is given at first

$$ x_{i}(k)=\mathcal{T}_{i} \bar{x}_{i}(k), i=1, 2,\ldots, N, $$

(5)

where $\mathcal {T}_{i}=(C_{i}^{+}, C_{i}^{\bot })$ is a reversible matrix, $C_{i}^{+}\in R^{n\times p}$ is the Penrose-Moore inverse of C_i, i.e. $C_{i}C_{i}^{+}=I_{p}$, and $C_{i}^{\bot }\in R^{n\times (n-p)}$ is an orthogonal basis of the kernel space of C_i, i.e. $C_{i}C_{i}^{\bot }=\mathbf {0}$. Submitting (5) into (4), one has

$$ \left\{ \begin{array}{lll} x_{mi}(k+1)=A_{i}^{11}x_{mi}(k)+A_{i}^{12}x_{ui}(k)+{B_{i}^{1}}u_{i}(k)+{E_{i}^{1}}\omega(k), \\ x_{ui}(k+1)=A_{i}^{21}x_{mi}(k)+A_{i}^{22}x_{ui}(k)+{B_{i}^{2}}u_{i}(k)+{E_{i}^{2}}\omega(k), \\ y_{i}(k)=x_{mi}(k), i=1, 2, \ldots, N, \end{array} \right. $$

(6)

where x_mi(k) ∈ R^p, x_ui(k) ∈ R^n−p are the measurable and unmeasurable states, respectively.

$\hat {A}_{i}=\mathcal {T}_{i}^{-1}A_{i}\mathcal {T}_{i}=\left ({\begin {array}{*{20}{c}} A_{i}^{11} & A_{i}^{12} \\ A_{i}^{21} & A_{i}^{22} \end {array}} \right ), \hat {B}_{i}=\mathcal {T}_{i}^{-1}B_{i}=\left ({\begin {array}{*{20}{c}} {B_{i}^{1}} \\ {B_{i}^{2}} \end {array}} \right ), \hat {C}_{i}=C_{i}\mathcal {T}_{i}=\left ({\begin {array}{*{20}{c}} I_{p} & \mathbf {0} \end {array}} \right )$, and $\hat {E}_{i}=\mathcal {T}_{i}^{-1}E_{i}=[{E_{i}^{1}}, {E_{i}^{2}}]'$. The reduced-order observer is designed as

$$ \begin{array}{@{}rcl@{}} \tilde{x}_{ui}(k+1)&=&A_{i}^{21}x_{mi}(k)+A_{i}^{22}\tilde{x}_{ui}(k)+{B_{i}^{2}}u_{i}(k)\\ &&+{E_{i}^{2}}w(k)+L_{i}A_{i}^{12}(x_{ui}(k)-\tilde{x}_{ui}(k)), \end{array} $$

(7)

where $\tilde {x}_{ui}(k)\in R^{n-p}$, and L_i is a constant matrix to be designed later.

Remark 3.1

In order to facilitate the design of distributed feedback controllers, we assume that all dimensions of the unmeasurable states of all agents are consistent. It is one of our future research topics to study the unmeasurable states with different dimensions.

The errors between the unmeasurable state x_ui(k) and observer state $\tilde {x}_{ui}(k)$ are defined as $x_{ui}^{*}(k+1)=x_{ui}(k+1)-\tilde {x}_{ui}(k+1)= (A_{i}^{22}-L_{i}A_{i}^{12})x_{ui}^{*}(k)$. To make the errors $x_{ui}^{*}(k)$ asymptotically converge to 0, the matrix pairs $(A_{i}^{22}, A_{i}^{12})$ need to be fully measurable, then the following lemma is given.

Lemma 3.1

For system dynamics (4) and (6), if Assumption 3.1 is satisfied, the matrix pairs$(\hat {A}_{i}, \hat {B}_{i})$are stabilizable, and$(A_{i}^{22}, A_{i}^{12})$are detectable.

Proof

See Appendix A. □

3.1.2 The design of distributed feedback controller

The output-coupled relationship between agent i and its neighbors is given

$$ \begin{array}{@{}rcl@{}} \delta_{i}(k)&=&\sum\limits_{j\in\mathcal{N}_{i}}a_{ij}(y_{i}(k)-y_{j}(k))\\ &&+a_{i0}(y_{i}(k)-y_{r}(k)), i=1, 2, \ldots,N, \end{array} $$

(8)

where a_ij and a_i0 are defined in Section 2.1. The formula (8) can be seen as the error feedback information between agent i and its neighbors.

Based on the defined reduced-order observer (7), the distributed feedback controller is given as

$$ \left\{ \begin{array}{ll} \xi_{i}(k)={\sum}_{j\in \mathcal{N}_{i}}a_{ij}(\tilde{x}_{ui}(k)-\tilde{x}_{uj}(k))+a_{i0}\tilde{x}_{ui}(k),\\ \eta_{i}(k+1)=G_{1}\eta_{i}(k)+G_{2}\theta_{i}\delta_{i}(k), \\ u_{i}(k)=K_{1i}\theta_{i}\xi_{i}(k)+K_{2i}\theta_{i}\delta_{i}(k)+K_{3i}\eta_{i}(k), i=1, 2, \ldots, N, \end{array} \right. $$

(9)

where $\eta _{i}(k)\in R^{s_{m}}$. $K_{1i}\in R^{q\times (n-p)}$, K_2i ∈ R^q×p and $K_{3i}\in R^{q\times s_{m}}$ are the gain matrices to be solved. 𝜃_i > 0 is a parameter to be designed later. The matrix pair (G₁, G₂) is said to incorporate a p-copy internal model of the matrix A₀, selected as G₁ = blockdiag(β₁, β₂,…, β_p), G₂ = blockdiag(σ₁, σ₂,…, σ_p), where β_i, σ_i, i = 1,2,…, p are constant square matrices and constant column vectors such that the matrix pairs (β_i, σ_i) are controllable and the minimal polynomial of A₀ divides the characteristic polynomial of β_i. Submitting (9) into (6) and (7), we can get the compact form

$$ \begin{array}{@{}rcl@{}} x_{m}(k+1) &=& (A_{11}+B_{1}K_{2}(\theta \mathcal{H}\otimes I_{p}))x_{m}(k)+A_{12}x_{u}(k)\\ &&+B_{1}K_{1}(\theta \mathcal{H}\otimes I_{n-p})\tilde{x}_{u}(k)+B_{1}K_{3}\eta(k)\\ &&+(E_{1}-B_{1}K_{2}(\theta \mathcal{A}_{0}\otimes F_{0}))(1_{N}\otimes I_{s})\omega(k),\\ x_{u}(k+1) &=& (A_{21}+B_{2}K_{2}(\theta \mathcal{H}\otimes I_{p}))x_{m}(k)+A_{22}x_{u}(k)\\ &&+B_{2}K_{1}(\theta \mathcal{H}\otimes I_{n-p})\tilde{x}_{u}(k) +B_{2}K_{3}\eta(k)\\ &&+(E_{2}-B_{2}K_{2}(\theta \mathcal{A}_{0}\otimes F_{0}))(1_{N}\otimes I_{s})\omega(k),\\ \tilde{x}_{u}(k+1) &=& (A_{21}+B_{2}K_{2}(\theta \mathcal{H}\otimes I_{p}))x_{m}(k)\\ &&+(A_{22}-LA_{12}+B_{2}K_{1}(\theta \mathcal{H}\otimes I_{n-p}))\tilde{x}_{u}(k)\\ &&+LA_{12}x_{u}(k)+B_{2}K_{3}\eta(k)+(E_{2}\\ &&-B_{2}K_{2}(\theta \mathcal{A}_{0}\otimes F_{0}))(1_{N}\otimes I_{s})\omega(k), \eta(k + 1)\\ &=&(\theta \mathcal{H}\otimes G_{2})x_{m}(k)+(I_{N}\otimes G_{1})\eta(k)\\ &&-(\theta \mathcal{A}_{0}\otimes G_{2}F_{0})(1_{N}\otimes I_{s})\omega(k), \end{array} $$

(10)

where $A_{1i}=block~diag(A_{1}^{1i}, A_{2}^{1i}, \ldots , A_{N}^{1i}), A_{2i}=block~diag(A_{1}^{2i}, A_{2}^{2i}, \ldots , A_{N}^{2i})$, K_j = blockdiag(K_j1, K_j2,…, K_jN), $\aleph _{i}=block~diag({\aleph _{1}^{i}}, {\aleph _{2}^{i}}, \ldots , {\aleph _{N}^{i}})$, Υ = blockdiag(Υ₁, Υ₂,…, Υ_N), with i = 1,2, j = 1,2,3, ℵ = {B, E}, Υ= {L, 𝜃}.

Let $\zeta (k)=({x_{m}^{T}}(k), {x_{u}^{T}}(k), \eta ^{T}(k), \tilde {x}_{u}^{T}(k))^{T}$, then the (10) is rewritten as

$$ \zeta(k+1)=A_{c}\zeta(k)+W_{c}\omega(k), $$

(11)

where $A_{c}=\left ({\begin {array}{*{20}{c}} A_{11}+B_{1}K_{2}(\theta {\mathcal{H}}\otimes I_{p})& A_{12} & B_{1}K_{3} &B_{1}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p})\\ A_{21}+B_{2}K_{2}(\theta {\mathcal{H}}\otimes I_{p}) & A_{22} & B_{2}K_{3} &B_{2}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p})\\ \theta {\mathcal{H}}\otimes G_{2}& \mathbf {0} & I_{N}\otimes G_{1} & \mathbf {0}\\ A_{21}+B_{2}K_{2}(\theta {\mathcal{H}}\otimes I_{p})& LA_{12}& B_{2}K_{3} & \varXi \end {array}} \right ), \varXi =A_{22}-LA_{12}+B_{2}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p}), W_{c}=\left ({\begin {array}{*{20}{c}} E_{1}-B_{1}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0})\\ E_{2}-B_{2}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0})\\ -(\theta \mathcal {A}_{0}\otimes G_{2}F_{0})\\ E_{2}-B_{2}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0}) \end {array}} \right )(1_{N}\otimes I_{s}).$

3.1.3 Main results

To get the main conclusions, the following basic lemmas are given.

Lemma 3.2

[26] If Assumptions 3.1 and 3.2 are satisfied, and the matrix pair (G₁, G₂) incorporates a p-copy internal model of the matrix A₀, then the matrix pairs$\left [\left ({\begin {array}{*{20}{c}} A_{i} & \mathbf {0}\\ G_{2}C_{i} & G_{1} \end {array}} \right )\left ({\begin {array}{*{20}{c}} B_{i}\\ \mathbf {0} \end {array}} \right )\right ], i=1, 2,\ldots , N$are stabilizable. Moreover, if the matrix equation XA₀ = G₁X + G₂Ωhas a solution X, thenΩ = 0.

For discrete-time system, if Assumption 3.1 is satisfied, for any $Q_{i}={Q_{i}^{T}}$, the algebraic Riccati equation ${A_{i}^{T}}P_{i}A_{i}-P_{i}-{A_{i}^{T}}P_{i}B_{i}({B_{i}^{T}}P_{i}B_{i})^{-1}{B_{i}^{T}}P_{i}A_{i}+Q_{i}=0$ has an unique solution $P_{i}={P_{i}^{T}}$, and the equation $A_{i}P_{i}{A_{i}^{T}}-P_{i}-A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}+Q_{i}=0$ also has an unique solution $P_{i}={P_{i}^{T}}$. Then the following lemma is obtained.

Lemma 3.3

If Assumption 3.1 is satisfied, the gain matrices K_iand L_iare defined as$K_{i}=-({B_{i}^{T}}P_{i}B_{i})^{-1}{B_{i}^{T}}P_{i}A_{i}$and$L_{i}=A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}$respectively, and$c_{i}\in \mathcal {C}$is distributed in the stable region${\varPhi }_{c_{i}}=\{c_{i}\in \mathcal {C}: |c_{i}-1|^{2}<\delta _{c_{i}}\},$where$\delta _{c_{i}}^{-1}=max_{k=1,2,\ldots , n}\lambda _{k}[Q_{c_{i}}^{-1}{A_{i}^{T}}P_{i}B_{i}({B_{i}^{T}}P_{i}B_{i})^{-1}{B_{i}^{T}}P_{i}A_{i}Q_{c_{i}}^{-1}], Q_{c_{i}}=Q_{c_{i}}^{-1}Q_{i}>0$, then the matrices A_i + c_iB_iK_iare Schur. If$s_{i}\in \mathcal {C}$is distributed in the stable region${\varPhi }_{s_{i}}=\{s_{i}\in \mathcal {C}: |s_{i}-1|^{2}<\delta _{s_{i}}\},$where$\delta _{s_{i}}^{-1}=max_{k=1,2,\ldots , n}\lambda _{k}[Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}], Q_{s_{i}}=Q_{s_{i}}^{-1}Q_{i}>0$, then the matrices A_i − s_iL_iC_iare Schur.

Proof

See Appendix B. □

In order to get the main conclusion of this paper, it is necessary to prove that the closed-loop system matrix A_c in (11) is Schur at first.

Theorem 3.1

Suppose that the digraph$\mathcal {G}$contains a directed spanning tree, and the eigenvalues of the matrix$\theta {\mathcal{H}}$in ascending order are λ₁ ≤ λ₂ ≤⋯ ≤ λ_N. The closed-loop system matrix A_cis Schur, if and only if the matrices$\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2},~ \mathbf {0}) & G_{1} \end {array}} \right ),$and$A_{i}^{22}-L_{i}A_{i}^{12}, i=1, 2, \ldots , N$are Schur.

Proof

See Appendix C. □

Theorem 3.2

If Assumptions 3.1-3.3 hold, $\lambda _{i}\in \mathcal {C}$is distributed in the stable domain${\varPhi }_{i}=\{\lambda _{i}\in \mathcal {C}:|\lambda _{i}-1|^{2}<\delta _{i}\},$where λ_i, i = 1,2,…, Nare the eigenvalues of the matrix$\theta {\mathcal{H}}$with λ₁ ≤ λ₂ ≤⋯ ≤ λ_N, and$\delta _{i}^{-1}=max_{j=1,2,\ldots ,n}\lambda _{j}[\mathcal {Q}_{c_{i}}^{-1}\mathcal {A}_{i}^{T}\mathcal {P}_{i}{\mathcal{B}}_{i}({\mathcal{B}}_{i}^{T}\mathcal {P}_{i}{\mathcal{B}}_{i})^{-1}{\mathcal{B}}_{i}^{T}\mathcal {P}_{i}\mathcal {A}_{i}\mathcal {Q}_{c_{i}}^{-1}], \mathcal {Q}_{c_{i}}=\mathcal {Q}_{c_{i}}^{-1}\mathcal {Q}_{i}>0$, where$\mathcal {P}_{i}$is the unique solution of the following Riccati equation

$$ \mathcal{A}_{i}^{T}\mathcal{P}_{i}\mathcal{A}_{i}-\mathcal{P}_{i}-\mathcal{A}_{i}^{T}\mathcal{P}_{i}\mathcal{B}_{i}(\mathcal{B}_{i}^{T}\mathcal{P}_{i}\mathcal{B}_{i})^{-1}\mathcal{B}_{i}^{T}\mathcal{P}_{i}\mathcal{A}_{i}+\mathcal{Q}_{i}=\mathbf{0}, i=1, 2, \ldots, N, $$

(12)

with$\mathcal {A}_{i}=\left ({\begin {array}{*{20}{c}} \hat {A}_{i} & \mathbf {0} \\ (G_{2},~ \mathbf {0}) & G_{1} \end {array}} \right ), {\mathcal{B}}_{i}=\left ({\begin {array}{*{20}{c}} \hat {B}_{i}\\ \mathbf {0} \end {array}} \right )$, then the system matrix A_cis Schur.

Proof

See Appendix D. □

3.2 The leader-following consensus of uncertain system

The internal model method can be used to solve the robust consensus problem. In this paper, the proposed distributed feedback controller (9) is also suitable for solving the robust leader-following consensus of HD_MASs (1). By the distributed feedback controller (9), the uncertain system (1) can be written as

$$ \zeta(k+1)=\bar{A}_{c}\zeta(k)+\bar{W}_{c}\omega(k), $$

(13)

where $\bar {A}_{c}=\left ({\begin {array}{*{20}{c}} \bar {A}_{11}+\bar {B}_{1}K_{2}(\theta {\mathcal{H}}\otimes I_{p})& \bar {A}_{12} & \bar {B}_{1}K_{3} &\bar {B}_{1}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p})\\ \bar {A}_{21}+\bar {B}_{2}K_{2}(\theta {\mathcal{H}}\otimes I_{p}) & \bar {A}_{22} & \bar {B}_{2}K_{3} &\bar {B}_{2}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p})\\ \theta {\mathcal{H}}\otimes G_{2}& \mathbf {0} & I_{N}\otimes G_{1} & \mathbf {0}\\ \bar {A}_{21}+\bar {B}_{2}K_{2}(\theta {\mathcal{H}}\otimes I_{p})& L\bar {A}_{12}& \bar {B}_{2}K_{3} & \bar {\varXi } \end {array}} \right ), \bar {\varXi }=\bar {A}_{22}-L\bar {A}_{12}+\bar {B}_{2}K_{1}(\theta {\mathcal{H}}\otimes I_{n-p}),$ and $\bar {W}_{c}=\left ({\begin {array}{*{20}{c}} \bar {E}_{1}-\bar {B}_{1}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0})\\ \bar {E}_{2}-\bar {B}_{2}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0})\\ -(\theta \mathcal {A}_{0}\otimes G_{2}F_{0})\\ \bar {E}_{2}-\bar {B}_{2}K_{2}(\theta \mathcal {A}_{0}\otimes F_{0}) \end {array}} \right )(1_{N}\otimes I_{s})$. Based on the above analysis, we give the main conclusion of this section.

Theorem 3.3

If Assumptions 3.1-3.3 hold, the digraph$\mathcal {G}$contains a directed spanning tree with v₀as its root, and$\lambda _{i}\in \mathcal {C}$satisfies the condition in Theorem 3.2, then the distributed feedback controller (9) solves the robust leader-following consensus of HD_MASs (1) and (2).

Proof

See Appendix E.□

A multi-step design procedure is given to construct the controller (9).

Algorithm 3.1

Suppose that Assumptions 3.1-3.3 hold, the distributed feedback controller (9) can be constructed as follows

• 1. Do linear transformation (5) on system dynamics (4).

• 2. For any $Q_{i}={Q_{i}^{T}}>0$, solve the algebraic Riccati equation (31) to get a positive matrix P_i, then the constant matrix $L_{i}=A_{i}^{22}P_{i}(A_{i}^{12})^{T}(A_{i}^{12}P_{i}(A_{i}^{12})^{T})^{-1}$ of the reduced-order observer (7) can be obtained.

• 3. Let $\theta _{i}=\frac {1}{a_{i0}+d_{i}}$, i = 1,2,…, N, where a_i0 and d_i are the diagonal elements of $\mathcal {A}_{0}$ and $\mathcal {D}$ respectively.

• 4. For any $\mathcal {Q}_{i}=\mathcal {Q}_{i}^{T}>0$, solve the algebraic Riccati equation (12) to get a positive matrix $\mathcal {P}_{i}$, then the gain matrix $\mathcal {K}_{i}=-({\mathcal{B}}_{i}^{T}\mathcal {P}_{i}{\mathcal{B}}_{i})^{-1}{\mathcal{B}}_{i}^{T}\mathcal {P}_{i}\mathcal {A}_{i}$ of the distributed feedback controller (9) can be obtained.

Remark 3.2

Algorithm 3.1 is the basic operation to solve the robust leader-follower consensus of HD_MASs (1) and (2). The parameter L_i and the gain matrix $\mathcal {K}_{i}$ can be obtained offline, thus, the time complexity of Algorithm 3.1 can be denoted as O(1). Besides, the basic operation needs to be executed n times, therefore, the time complexity of the proposed method is O(n). Using the same analysis method, we can get that the time complexities of [28, 29] are also O(n), however, full-order observers were designed in [28, 29], which cannot reduce the system dimensions and save resources consumption.

4 The leader-following consensus of HC_MASs

4.1 The leader-following consensus of nominal system

The nominal system dynamics of continuous-time MASs can be expressed as

$$ \begin{array}{lll} &\dot{x}_{i}(t)=A_{i}x_{i}(t)+B_{i}u_{i}(t)+E_{i}\omega(t),\\ &y_{i}(t)=C_{i}x_{i}(t), i=1,2,\ldots,N, \end{array} $$

(14)

and

$$ \begin{array}{lll} &\dot{\omega}(t)=A_{0}\omega(t),~~y_{r}(t)=F_{0}\omega(t), \end{array} $$

(15)

where all variables and matrices have the same meaning as (4).

Before moving on, some assumptions and lemmas are given.

Assumption 4.1

All eigenvalues of the exosystem matrix A₀ in (15) are distributed in the closed right-half complex plane.

Lemma 4.1

[23] For the stabilizable matrix pair (A_i, B_i), the algebraic Riccati equation${A_{i}^{T}}P_{i}+P_{i}A_{i}+I_{n}-P_{i}B_{i}{B_{i}^{T}}P_{i}=0$has an unique solution$P_{i}={P_{i}^{T}}>0$, and the matrix$A_{i}-(a+jb)B_{i}{B_{i}^{T}}P_{i}$is Hurwitz for a ≥ 1, b ∈ R.

Similar to (5), the linear transformation for continuous-time MASs is designed as

$$ x_{i}(t)=\mathcal{T}_{i} \bar{x}_{i}(t), i=1, 2,\ldots, N, $$

(16)

then the system (14) are transformed into

$$ \left\{ \begin{array}{lll} \dot{x}_{mi}(t)=A_{i}^{11}x_{mi}(t)+A_{i}^{12}x_{ui}(t)+{B_{i}^{1}}u_{i}(t)+{E_{i}^{1}}\omega(t), \\ \dot{x}_{ui}(t)=A_{i}^{21}x_{mi}(t)+A_{i}^{22}x_{ui}(t)+{B_{i}^{2}}u_{i}(t)+{E_{i}^{2}}\omega(t), \\ y_{i}(t)=x_{mi}(t), i=1, 2, \ldots, N. \end{array} \right. $$

(17)

The reduced-order observer is designed as

$$ \dot{\tilde{x}}_{ui}(t) = A_{i}^{21}x_{mi}(t)+A_{i}^{22}\tilde{x}_{ui}(t)+{B_{i}^{2}}u_{i}(t)+{E_{i}^{2}}w(t)+L_{i}A_{i}^{12}(x_{ui}(t)-\tilde{x}_{ui}(t)), $$

(18)

then the distributed feedback controller is designed as

$$ \left\{ \begin{array}{ll} \delta_{i}(t)={\sum}_{j\in\mathcal{N}_{i}}a_{ij}(y_{i}(t)-y_{j}(t))+a_{i0}(y_{i}(t)-y_{ri}(t)),\\ \xi_{i}(t)={\sum}_{j\in \mathcal{N}_{i}}a_{ij}(\tilde{x}_{ui}(t)-\tilde{x}_{uj}(t))+a_{i0}\tilde{x}_{ui}(t),\\ \dot{\eta}_{i}(t)=G_{1}\eta_{i}(t)+G_{2}\delta_{i}(t), \\ u_{i}(t)=K_{1i}\xi_{i}(t)+K_{2i}\delta_{i}(t)+K_{3i}\eta_{i}(t), i=1, 2, \ldots, N. \end{array} \right. $$

(19)

Submitting (19) into (17) and (18), one has

$$ \dot{\zeta}(t)=A_{c}\zeta(t)+W_{c}\omega(t), $$

(20)

where $A_{c}=\left ({\begin {array}{*{20}{c}} A_{11}+B_{1}K_{2}({\mathcal{H}}\otimes I_{p})& A_{12} & B_{1}K_{3} &B_{1}K_{1}({\mathcal{H}}\otimes I_{n-p})\\ A_{21}+B_{2}K_{2}({\mathcal{H}}\otimes I_{p}) & A_{22} & B_{2}K_{3} &B_{2}K_{1}({\mathcal{H}}\otimes I_{n-p})\\ {\mathcal{H}}\otimes G_{2}& \mathbf {0} & I_{N}\otimes G_{1} & \mathbf {0}\\ A_{21}+B_{2}K_{2}({\mathcal{H}}\otimes I_{p})& LA_{12}& B_{2}K_{3} & A_{22}-LA_{12}+B_{2}K_{1}({\mathcal{H}}\otimes I_{n-p}) \end {array}} \right )$, $W_{c}=\left ({\begin {array}{*{20}{c}} E_{1}-B_{1}K_{2}(\mathcal {A}_{0}\otimes F_{0})\\ E_{2}-B_{2}K_{2}(\mathcal {A}_{0}\otimes F_{0})\\ -(\mathcal {A}_{0}\otimes G_{2}F_{0})\\ E_{2}-B_{2}K_{2}(\mathcal {A}_{0}\otimes F_{0}) \end {array}} \right )(1_{N}\otimes I_{s})$.

Theorem 4.1

If Assumptions 3.1, 3.3, and 4.1 hold, then the nominal system matrix A_cis Hurwitz.

Proof

See Appendix F. □

4.2 The leader-following consensus of uncertain system

In this section, the i-th agent has the following dynamic

$$ \begin{array}{lll} &\dot{x}_{i}(t)=\bar{A}_{i}x_{i}(t)+\bar{B}_{i}u_{i}(t)+\bar{E}_{i}\omega(t),\\ &y_{i}(t)=C_{i}x_{i}(t), i=1,2,\ldots,N, \end{array} $$

(21)

and the exosystem has the same dynamic as (15).

Similar to Section 3.2, the proposed distributed controller (19) is also suitable for solving the robust leader-following consensus of HC_MASs (21). Then by the controller (19), the uncertain system (21) can be denoted as

$$ \dot{\bar{\zeta}}(t)=\bar{A}_{c}\bar{\zeta}(t)+\bar{W}_{c}\omega(t), $$

(22)

where $\bar {A}_{c}=\left ({\begin {array}{*{20}{c}} \bar {A}_{11}+\bar {B}_{1}K_{2}({\mathcal{H}}\otimes I_{p})& \bar {A}_{12} & \bar {B}_{1}K_{3} &\bar {B}_{1}K_{1}({\mathcal{H}}\otimes I_{n-p})\\ \bar {A}_{21}+\bar {B}_{2}K_{2}({\mathcal{H}}\otimes I_{p}) & \bar {A}_{22} & \bar {B}_{2}K_{3} &\bar {B}_{2}K_{1}({\mathcal{H}}\otimes I_{n-p})\\ {\mathcal{H}}\otimes G_{2}& \mathbf {0} & I_{N}\otimes G_{1} & \mathbf {0}\\ \bar {A}_{21}+\bar {B}_{2}K_{2}({\mathcal{H}}\otimes I_{p})& L\bar {A}_{12}& \bar {B}_{2}K_{3} & \bar {A}_{22}-L\bar {A}_{12}+\bar {B}_{2}K_{1}({\mathcal{H}}\otimes I_{n-p}) \end {array}} \right ),\\ \bar {W}_{c}=\left ({\begin {array}{*{20}{c}} \bar {E}_{1}-\bar {B}_{1}K_{2}(\mathcal {A}_{0}\otimes F_{0})\\ \bar {E}_{2}-\bar {B}_{2}K_{2}(\mathcal {A}_{0}\otimes F_{0})\\ -(\mathcal {A}_{0}\otimes G_{2}F_{0})\\ \bar {E}_{2}-\bar {B}_{2}K_{2}(\mathcal {A}_{0}\otimes F_{0}) \end {array}} \right )(1_{N}\otimes I_{s})$.

Based on the above analysis, we give the main conclusion of this section.

Theorem 4.2

If Assumptions 3.1, 3.3, and 4.1 hold, and the directed graph$\mathcal {G}$contains a directed spanning tree with v₀as its root, then the distributed feedback controller (19) solves the robust leader-following problem of HC_MASs (21) and (15).

Proof

The proof is similar to that of Theorem 3.3, so we omit it.□

A three-step design procedure is given to construct the distributed feedback control law (19).

Algorithm 4.1

Suppose that Assumptions 3.1, 3.3, and 4.1 hold, the distributed feedback controller (19) can be constructed as follows

• 1. Do linear transformation (16) on system dynamics (14).

• 2. For any $Q_{i}={Q_{i}^{T}}>0$, and $R_{i}={R_{i}^{T}}>0$, solve the continuous-time algebraic Riccati equation (37) to get a positive matrix P_i, then the constant matrix $L_{i}=P_{i}(A_{i}^{12})^{T}R_{i}^{-1}$ of the reduced-order observer (18) can be obtained.

• 3. The gain matrix $\mathcal {K}_{i}=-(min~Re(\lambda _{i}))^{-1}({\mathcal{B}}_{i})^{T}\mathcal {P}_{i}$ of the distributed controller (19) can be obtained by solving the algebraic Riccati equation (36).

Remark 4.1

The parallel-observer based leader-following problem was solved in [30], however, it assumed that the leader and followers have the same dynamics, while the dynamics of all agents are heterogeneous in this paper. Moreover, assume E_i = 0, A_i = A₀ = A, and C_i = F₀ = C, the leader-following problem in [30] can be solved by the controller in this paper.

Remark 4.2

According to Remark 3.2, the time complexity of Algorithm 4.1 can be obtained as O(1). Similarly, the basic operation needs to be executed n times, therefore, the time complexity of the proposed method is O(n). Through the analysis of the methods in [30, 31], we can get that the time complexities of [30, 31] are O(n²), and O(n) respectively. Therefore, the time complexity of this paper is lower than that of [30]. Although the time complexity of this paper is the same as that of [31], the full-order observer was designed in [31], which cannot reduce the system dimensions and save resources consumption.

5 Numerical examples

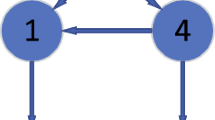
To verify the effectiveness of above results, the MASs consisting of four followers (nodes 1-4) and one leader (node 0) are considered in this paper. The communication topology $\mathcal {G}$, shown in Fig. 1, is applied to both discrete-time and continuous-time systems.

Fig. 1

The communication topology $\mathcal {G}$

5.1 The robust leader-following consensus of HD_MASs

The system matrices of HD_MASs are given as $A_{i}=\left ({\begin {array}{*{20}{c}} 1& 0 & 0 \\ 0& 0.1i & 1\\ 1& 0 & 0 \end {array}} \right ), B_{i}=\left ({\begin {array}{*{20}{c}} 0.5i \\ 0 \\ 0 \end {array}} \right ), \\C_{i}=\left ({\begin {array}{*{20}{c}} 0 & 1 & 0 \end {array}} \right ), E_{i}=\left ({\begin {array}{*{20}{c}} 0 & 0 & 1\\ 0 & -1 & 0\\ 0 & 0 & i \end {array}} \right ),$${\varDelta } A_{i}={\varDelta } E_{i}=\left ({\begin {array}{*{20}{c}} 0.01i& 0 & 1 \\ 0& 0.01 & 0\\ 0& 0 & 0 \end {array}} \right ), {\varDelta } B_{i}=\left ({\begin {array}{*{20}{c}} 0 \\ 0.1i \\ 0 \end {array}} \right ),$$A_{0}=\left ({\begin {array}{*{20}{c}} 1 & 1 & 0\\ 0 & -1 & 1\\ 0 & 0 & 2 \end {array}} \right )$ and F₀ = (1,0,0). Let $\mathcal {T}_{i}=(C_{i}^{+}, C_{i}^{\bot })=\left ({\begin {array}{*{20}{c}} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end {array}} \right )$, the reduced-order observer for x_ui(k), i = 1,2,3,4 is designed. By the discrete-time algebraic Riccati equation (12), the control gain can be obtained $\mathcal {K}_{1}=(-16.4809 ~ -5.6328 ~ -8.2545 ~ -32.3113 ~ -32.1842 ~ -97.6800), \mathcal {K}_{2}=(-8.5938 ~ -2.8898 ~ -4.2785 ~ -15.9721 ~ -15.9091 ~ -48.2864), \mathcal {K}_{3}=(-5.9872 ~ -1.9759 ~ -2.9627 ~ -10.5239 ~ -10.4823 ~ -31.8156), \mathcal {K}_{4}=(-4.7037 ~ -1.5194 ~ -2.3125 ~ -7.7996 ~ -7.7688 ~ -23.5793)$.

Hereto, the controller design has been completed. The estimation errors $x_{ui}^{*}(k)=x_{ui}(k)-\tilde {x}_{ui}(k), i=1, 2, 3, 4$ are depicted in Fig. 2. It is obvious that the system considered in this paper is three-order, but only two-order observer is used to estimate the unmeasurable state x_ui(k). Moreover, from Fig. 2, the estimation errors $x_{ui}^{*}(k)$ converge to zero when time goes to infinity, therefore, the reduced-order observer (7) can estimate the unmeasurable states reasonably. Besides, the tracking errors of four agents are shown in Fig. 3a. It demonstrates that the tracking errors converge to zero asymptotically, thus the robust leader-following consensus of HD_MASs of (1) and (2) is solved.

Fig. 2

Discrete-time: the estimation errors of the unmeasurable states x_ui(k) for (a) the first variable, (b) the second variable

Fig. 3

The tracking errors of four agents for (a) discrete-time, (b) continuous-time

5.2 The robust leader-following consensus of HC_MASs

The system matrices A_i, B_i, C_i, E_i, ΔA_i, ΔB_i, ΔE_i and F₀ are consistent with Section 5.1. Let $A_{0}=\left ({\begin {array}{*{20}{c}} 0 & 0 & 0\\ 1 & 0 & -1\\ 0 & 1 & 0 \end {array}} \right )$, $G_{1}=\left ({\begin {array}{*{20}{c}} 0 & 1 & 0\\ -1 & 0 & 1\\ 0 & 0 & 0 \end {array}} \right ),$ and $G_{2}=\left ({\begin {array}{*{20}{c}} 0 \\ 0\\ 1 \end {array}} \right ),$ the control gain of the controller (19) can be obtained $\mathcal {K}_{1}=(-7.9057 ~ -8.6573 ~ -9.8299$$~ 0.2039 ~ 1.3994 ~ -1.6181), \mathcal {K}_{2}=(-7.7235~ -5.1429 ~ -7.5816 ~ 0.7980 ~ 1.1676 ~ -2.2122), \mathcal {K}_{3}=(-7.8064 ~ -3.8889 ~ -6.7035 ~ 1.0214 ~ 0.9781 ~ -2.4356)$, and $~\mathcal {K}_{4}=(-8.0555 ~ -3.2442 ~ -6.2806 ~ 1.1292 ~ 0.8514 ~ -2.5434)$.

The trajectories of unmeasurable system states x_ui and estimated states $\tilde {x}_{ui}, i=1, 2, 3, 4$ are given in Fig. 4a, b, c and d respectively (where x_uik and $\tilde {x}_{uik}$ represent the k-th (k= 1,2) variable of the unmeasurable system states x_ui and estimated states $\tilde {x}_{ui}$, respectively. x_ui(0) and $\tilde {x}_{ui}(0)$ indicate the initial values, and x_ui(100) and $\tilde {x}_{ui}(100)$ indicate the termination values). We can see that the unmeasurable system states x_ui and estimated states $\tilde {x}_{ui}$ have similar trajectories. Besides, the estimation errors $x_{ui}^{*}(t)=x_{ui}(t)-\tilde {x}_{ui}(t)$ are depicted in Fig. 5. It can be seen that the estimation errors $x_{ui}^{*}(t)$ converge to zero when time goes to infinity. Therefore, the reduced-order observer (18) can estimate the unmeasurable system states reasonably. Besides, the tracking errors of four agents are given in Fig. 3b. It demonstrates that the tracking errors under the distributed feedback controller (19) converge to zero asymptotically, thus the robust leader-following consensus of HC_MASs of (21) and (15) is solved.

Fig. 4

a The trajectories of x_u1 and $\tilde {x}_{u1}$, b the trajectories of x_u2 and $\tilde {x}_{u2}$, c the trajectories of x_u3 and $\tilde {x}_{u3}$, and d the trajectories of x_u4 and $\tilde {x}_{u4}$

Fig. 5

Continuous-time: the estimation errors of the unmeasurable states x_ui(t) for (a) the first variable, (b) the second variable

5.3 Practical application

5.3.1 Background of the simulation

MuPAL-α, owned and operated by the Japan Aerospace Exploration Agency, is a multi-purpose research aircraft used for testing advanced guidance and control technologies and evaluating research on human factors. It is a Dornier Do228-202 aircraft equipped with a research Fly-By-Wire system. The MuPAL-α platform supports both HIL tests and actual flight tests for advanced Guidance, Navigation and Control technologies [32].

In what follows, we take the aircraft model (MuPAL-α) given in [24, 25, 33] as an application example to demonstrate the control effect of the designed controller. The control goal of each MuPAL-α is to track the given sideway velocity and roll angle. Here, each aircraft can be regarded as an agent of the MASs. The communication graph among four aircrafts and the exosystem is demonstrated in Fig. 1. As shown in Fig. 1, label 0 is the exosystem and labels 1-4 are four follower aircrafts. For aircrafts 1 and 2, they can directly receive the exosystem’s information, i.e. a₁₀ = a₂₀ = 1. Aircrafts 3 and 4 cannot receive the exosystem’s information directly, i.e. a₃₀ = a₄₀ = 0. They track the exosystem by transmitting information with their neighbors.

5.3.2 Aircraft model and simulation results

According to [24, 25, 33], the linearized lateral-directional motions around the equilibrium point can be described as (21), and its standard system dynamic is (14). The system state of the i-th (i= 1,2,3,4) aircraft is given by

$$ x_{i}=[v_{i}(m/s),p_{i}(rad/s),\phi_{i}(rad),y_{ri}(rad/s),T_{ai}(rad),T_{ri}(rad)]^{T}, $$

(23)

which denote sideway velocity, roll rate, roll angle, yaw rate, delay of the aileron deflection command, and delay of the rudder deflection command, respectively. The system input u_i of the i-th aircraft is given by

$$ u_{i}=[\delta_{a_{c}i}(rad),\delta_{r_{c}i}(rad)]^{T}, $$

(24)

which denote aileron deflection command, and rudder deflection command, respectively. And the system output of the i-th aircraft is given by

$$ y_{i}=[v_{i}(m/s),\phi_{i}(rad)]^{T}. $$

(25)

The exosystem can be modeled as (15), and the exosystem state is given by

$$ w = [r_{v}(m/s), r_{p}(rad/s), r_{\phi}(rad), d_{p}(rad/s), d_{\phi}(rad)]^{T}, $$

(26)

where r_v, r_p and r_ϕ denote reference signal generator; d_p and d_ϕ denote the sensor noise in the channel of roll angle. To verify the effectiveness of the controller designed in this paper, the system matrices in [24, 25] are applied in this paper, as follows: $\bar {A}_{i}=A+\hbar _{i}\bar {A}, ~~\bar {B}_{i}=B+\hbar _{i}\bar {B},~~ \hbar _{i}\in [-1,1]$, with

$A=\left ({\begin {array}{*{20}{c}} -0.1781 & 6.0791 & 9.7633 & -65.6230 & 0 & 2.8900\\ -0.0575 & -3.8100 & 0 & 1.3430 & -10.7500 &1.1870 \\ 0 & 1.0000 & 0 & 0.0944 & 0 & 0\\ 0.0253 & -0.0628 & 0 & -0.4750 & 0.3450 & -2.2200 \\ 0 &0& 0& 0& -11.1111 &0\\ 0 &0 &0 &0 &0 &-11.1111 \end {array}} \right ), \bar {A}= \left ({\begin {array}{*{20}{c}} 0.0185 & 0.2416 & 0.0021 & 1.0038 & 0 & 0\\ 0.0037 & 0 & 0 & 0.0150 & 0 &0.0010 \\ 0 & 0 & 0 & 0.0023 & 0 & 0\\ 0.0062 & 0.0050 & 0 & 0 & 0.0030 & 0 \\ 0 &0& 0& 0& 0 &0\\ 0 &0 &0 &0 &0 &0 \end {array}} \right ),\\ B=\left ({\begin {array}{*{20}{c}} 0 & -2.8900\\ 10.7500 & -1.1870 \\ 0 & 0 \\ -0.3450 & 2.2200\\ 22.2222 &0\\ 0 &22.2222 \end {array}} \right ), \bar {B}=\left ({\begin {array}{*{20}{c}} 0 & -2.8900\\ 0 & -1.1880 \\ 0 & 0 \\ 0.0030 & 0\\ 0 &0\\ 0 &0 \end {array}} \right )$, and the uncertain parameters $\hbar _{1}=0.5, \hbar _{2}=-0.9, \hbar _{3}=-0.3$ and $\hbar _{4}=0.7$, respectively. Moreover, the other system matrices are given as $C_{i}=\left ({\begin {array}{*{20}{c}} 1 & 0& 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 &0 \end {array}} \right ), \bar {E}_{i}=E_{i}=\left ({\begin {array}{*{20}{c}} 0 & 0& 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 &0 \\ 0 & 0 & 0 & 0 & 0 &0.0873 \\ 0 & 0 & 0 & 0 & 0 &0 \\ 0 & 0 & 0 & 0 & 0 &0 \\ 0 & 0 & 0 & 0 & 0 &0 \end {array}} \right ),$$A_{0}=\left ({\begin {array}{*{20}{c}} 0 & 0& 0 & 0 & 0 \\ 0 & 0 & -\frac {2}{9} & 0 & 0 \\ 0 & \frac {1}{2}& 0 & 0 & 0 \\ 0 & 0& 0 & 0 & 1 \\ 0 & 0& 0 & -1 & 0 \end {array}} \right ), \text {and}~ F_{0}=\left ({\begin {array}{*{20}{c}} -1 & 0& 0 & 0 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 &0 \end {array}} \right )$.

Remark 5.1

The system matrices $\bar {A}_{i}$ and $\bar {B}_{i}$ in the linearized lateral-directional motions dynamics (21) are uncertain. The uncertainty of these matrices may be caused by inaccurate modeling or measurement. $\bar {A}_{i}=A+\hbar _{i}\bar {A}$, $\bar {B}_{i}=B+\hbar _{i}\bar {B}$, where the matrices A and B are nominal matrices; the matrices $\hbar _{i}\bar {A}={\varDelta } A_{i}$ and $\hbar _{i}\bar {B}={\varDelta } B_{i}$ are uncertain matrices. These uncertain matrices are considered as time-invariant, which are common and considered in [17, 23,24,25]. Because the system matrices cannot be obtained completely, the uncertain part should be considered. If the precision model method is used to control the actual system, the control effect may be not ideal. Therefore, we need to consider the problem with uncertain parameters to improve certain robustness.

Given the system matrices, we take the following three steps to describe how our method is applied to the tracking problem of four networked aircrafts.

• Step 1: Due to high cost or technical constraint, it is difficult to measure all states of each aircraft. Thus the linear transformation (16) is constructed to divide the system states into measurable part and unmeasurable part. By the definition of $\mathcal {T}_{i}$, we can get $\mathcal {T}_{i}=(C_{i}^{+}, C_{i}^{\bot })=\left ({\begin {array}{*{20}{c}} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end {array}} \right )$. The linear transformation (16) can transform the standard system (14) into (17) with $A_{i}^{11}=\left ({\begin {array}{*{20}{c}} -0.1781 & 9.7633\\ 0 & 0 \end {array}} \right )$,

  $A_{i}^{12}=\left ({\begin {array}{*{20}{c}} 6.0791 &-65.6230 & 0 & 2.8900\\ 1.0000 & 0.0944 & 0 & 0 \end {array}} \right )$, $A_{i}^{21}=\left ({\begin {array}{*{20}{c}} -0.0575 & 0\\ 0.0253 & 0\\ 0 & 0\\ 0 & 0 \end {array}} \right )$, $A_{i}^{22}=\left ({\begin {array}{*{20}{c}} -3.8100 & 1.3430& -10.7500& 1.1870\\ -0.0628 & -0.4750 & 0.3450 & -2.2200\\ 0 & 0 & -11.1111 & 0\\ 0 & 0 & 0 & -11.1111 \end {array}} \right )$, ${B_{i}^{1}}=\left ({\begin {array}{*{20}{c}} 0 & -2.8900\\ 0 & 0 \end {array}} \right )$, ${B_{i}^{2}}=\left ({\begin {array}{*{20}{c}} 10.7500 & -1.1870\\ -0.3450 & 2.2200\\ 22.2222 & 0\\ 0 & 22.2222 \end {array}} \right )$, ${E_{i}^{1}}=\left ({\begin {array}{*{20}{c}} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0& 0.0873 \end {array}} \right )$, and ${E_{i}^{2}}=\mathbf {0}_{4\times 5}$.

• Step 2: From the Step 1, we get that the number of system states (27) is six, and the number of unmeasurable states is four. These unmeasurable states are roll rate, yaw rate, delay of the aileron deflection command, and delay of the rudder deflection command, respectively. Therefore, the reduced-order (four-order) observer (18) is used to estimate these unmeasurable states. By the continuous-time algebraic Riccati equation (34), the constant matrix $L_{i}=\left ({\begin {array}{*{20}{c}} 0.0728 & 0.2234\\ -0.9884 & 0.0211\\ -0.0444 & -0.0320\\ 0.1070 & 0.0029 \end {array}} \right )$ can be obtained.

• Step 3: By solving the algebraic Riccati equation (36), the gain matrix of the controller (19) can be obtained:

  $\mathcal {K}_{i}= \left [\begin {array}{cccccccc} 0.6839 & 7.8247 & 2.0287 & -7.5422 & -2.1099&1.1499 &0.3646 \\ -1.8577 & -1.4553 & -1.6187& 25.3290 & 1.3755&-4.1057& -0.9312 \end {array}\right .\\ \left .\begin {array}{ccccccccccc} 1.3015 & 2.5768 & 1.9369 &1.6903 & 0.9312 & 3.2317 & 9.0656 &5.2924& 8.4129\\ -3.3183 & -6.6294 & -4.9415 &-4.3986 & 0.3646 & 1.2661 & 3.5696& 2.0795 & 3.3251 \end {array}\right ]$.

The internal model of A₀ are selected as G₁ = diagblock(β, β), and G₂ = diagblock(γ, γ), with $\beta =\left ({\begin {array}{*{20}{c}} 0 & 1.0000 & 0 &0 &0\\ 0 & 0 & 1.0000 & 0 &0\\ 0 & 0 & 0 & 1.0000 &0\\ 0 & 0 & 0 & 0 &1.000\\ 0 & -0.1667 & 0 & -1.1667 &0 \end {array}} \right ), \text {and}~ \gamma =[0,0,0,0,1]^{\prime }$.

Assuming that there is sufficient safe distances among aircrafts and applying the designed controller (19) to the uncertain aircraft model (21), the simulation results are obtained, shown in Figs. 6 and 7. Let $x_{ui}^{*}(t)=x_{ui}(t)-\tilde {x}_{ui}(t)=(x_{ui1}^{*},x_{ui2}^{*},x_{ui3}^{*},x_{ui4}^{*})^{T}$, where $x_{ui1}^{*}, x_{ui2}^{*}, x_{ui3}^{*}$, and $x_{ui4}^{*}$ represent the estimation errors of roll rate, yaw rate, delay of the aileron deflection command, and delay of the rudder deflection command, separately. Figure 6 presents the above results (the estimation errors of the reduced-order observer), and it exhibits that all the estimation errors converge to zero rapidly. The time responses describing the measurement outputs y_i(t) = (v_i, ϕ_i)^T are shown in Fig. 7a. Moreover, let e_i(t) = (e_i1, e_i2)^T, where e_i1 and e_i2 represent the tracking errors of sideway velocity and roll angle, respectively. The tracking errors of four research aircrafts are given in Fig. 7b. It demonstrates that the tracking errors under the distributed feedback controller (19) converge to zero asymptotically, thus the controller proposed in this paper can be used for the tracking problem of networked aircrafts.

Fig. 6

The estimation errors of (a) roll rate, (b) yaw rate, (c) delay of the aileron deflection command, and (d) delay of the rudder deflection command

Fig. 7

a The measurement outputs, b the tracking errors of four research aircrafts

Remark 5.2

It is worth mentioning that the results in this paper refer to information synchronization rather than position synchronization. When the control objects are particle variables such as temperature, water level of four water tanks, multi-turbine speed regulation, etc., the control objective of these variables is to track the same signal. For application example, the output variables are sideway velocity, and roll angle. The control goal of each aircraft is to track the given sideway velocity and roll angle. After achieving the tracking target, their position coordinates can be different. In fact, the application example is based on the assumption that there is enough safe distance among aircrafts, i.e. there is no collision among the moving aircrafts. Under this assumption, the volumes of aircrafts can be neglected, thus these aircrafts can be regarded as particles. In this paper, the problem of multi-aircraft tracking is solved from the perspective of coordinated control. If we want to avoid collision, the safe distance needs to be considered, and its control objective becomes $\lim \limits _{k\rightarrow \infty }y_{i}(t)-h_{i}(t)-y_{r}(t)= 0$, rather than $\lim \limits _{k\rightarrow \infty }y_{i}(t)-y_{r}(t)= 0$. If h_i(t) ≡ 0, the time-varying formation tracking problem is reducible to the consensus tracking problem. If h_i(t) is a nonzero constant vector, it becomes the time-invariant formation tracking problem. How to solve the multi-aircraft safety problem needs to study formation control method [34, 35]. This issue is meaningful and is the direction of our future research.

5.4 Comparison experiment

In order to verify the merits of the proposed controller, the comparison method in [36] is used in this section. Moreover, the directed graph in [36] is used for comparison. The system matrices are given as follows $A_{1}=\left ({\begin {array}{*{20}{c}} 0 & 1 \\ 0 & 0 \end {array}} \right ), B_{1}=\left ({\begin {array}{*{20}{c}} 0 \\ 1 \end {array}} \right ), E_{1}=\left ({\begin {array}{*{20}{c}} 0 & 0 \\ 1 & -0.5 \end {array}} \right ), A_{2}=\left ({\begin {array}{*{20}{c}} 0 & 1 \\ -1 & 0 \end {array}} \right ), B_{2}=\left ({\begin {array}{*{20}{c}} 1 \\ 1 \end {array}} \right ), E_{2}=\left ({\begin {array}{*{20}{c}} -1 & 0.5 \\ -1 & 0.5 \end {array}} \right ), A_{3}=\left ({\begin {array}{*{20}{c}} 0 & -1 \\ 1 & 0 \end {array}} \right ), B_{3}=\left ({\begin {array}{*{20}{c}} 0 \\ 1 \end {array}} \right ), E_{3}=\left ({\begin {array}{*{20}{c}} 0 & 2 \\ -1 & 0 \end {array}} \right ), A_{4}=\left ({\begin {array}{*{20}{c}} 0 & -1 \\ 0 & 0 \end {array}} \right ), B_{4}=\left ({\begin {array}{*{20}{c}} 0 \\ 1 \end {array}} \right ), E_{4}=\left ({\begin {array}{*{20}{c}} 0 & 2 \\ -1 & 1 \end {array}} \right ), C_{i}=\left ({\begin {array}{*{20}{c}} 1 & 0 \end {array}} \right ), i=1,2,\ldots ,9, A5=A6=A7=A8=A9=A4, B5=B6=B7=B8=B9=B4, E5=E6=E7=E8=E9=E4$.

The exosystem matrices A₀ and F₀ are given as $A_{0}=\left ({\begin {array}{*{20}{c}} 0 & 1 \\ -1 & 0 \end {array}} \right ), F_{0}=\left ({\begin {array}{*{20}{c}} 1 & 0 \end {array}} \right )$.

The comparative experiment is conducted with the same initial states x₁(0) = [2,− 1]^T, x₂(0) = [− 2,1]^T, x₃(0) = [0,− 2]^T, x₄(0) = [0.5,− 2]^T, x₅(0) = [3,1]^T, x₆(0) = [− 1,− 1]^T, x₇(0) = [3,1]^T, x₈(0) = [2,− 1]^T, x₉(0) = [0.5,1.5]^T, ω(0) = [0,0]^T, and all the other initial states are chosen to be zero. After simple calculation, the solutions of the linear matrix equations (5) in [36] have obtained $X_{i}=\left ({\begin {array}{*{20}{c}} 1 & 0 \\ 0 & 1 \end {array}} \right ), i=1,\ldots , 9$, U₁ = [− 2,0.5], U₂ = [1,− 0.5], U₃ = [− 1,0], U₄ = [0,− 1], and U₅ = U₆ = U₇ = U₈ = U₉ = U₄. The distributed dynamic state feedback control law (7) in [36] is designed with gain matrices K₁₁ = [− 8,− 4], K₂₁ = [− 5.5,1.5], K₃₁ = [7,− 4], K₄₁ = [8,− 4], K₅₁ = K₆₁ = K₇₁ = K₈₁ = K₉₁ = K₄₁, K₁₂ = [6,4.5], K₂₂ = [6.5,− 2], K₃₂ = [− 8,4], K₄₂ = [− 8,3], K₅₂ = K₆₂ = K₇₂ = K₈₂ = K₉₂ = K₄₂, and $\hat {K}=[0.2821,0.0198]^{T}$. Moreover, the internal model of A₀ in this paper is selected as $G_{1}=\left ({\begin {array}{*{20}{c}} 0 & 1\\ -1 & 0 \end {array}} \right ), G_{2}=\left ({\begin {array}{*{20}{c}} 0 \\ 1 \end {array}} \right )$. And the distributed tracking protocol (19) is designed with control gains $\mathcal {K}_{1}=(K_{21}, K_{11}, K_{31})=(-2.6415 ~ -2.5066 ~ 1.2273 ~ -0.7027), \mathcal {K}_{2}=(K_{22}, K_{12}, K_{32})=(-1.9864 ~ -0.7180 ~ 0.2683 ~ -1.3885), \mathcal {K}_{3}=(K_{23}, K_{13}, K_{33})=(1.8343 ~ -2.1607 ~ -1.1023 ~ 0.8860), \mathcal {K}_{4}=(K_{24}, K_{14}, K_{34})=(2.6415 ~ -2.5066 ~ -1.2273 ~ 0.7027), \mathcal {K}_{5}=\mathcal {K}_{6}=\mathcal {K}_{7}=\mathcal {K}_{8}=\mathcal {K}_{9}=\mathcal {K}_{4}$.

From Fig. 8, we can get that the overshoot of tracking errors in this paper is [–2 6] while the overshoot in [36] is [–2 3]. Therefore, the overshoot in this paper is about 1.6 times of that in [36]. From the convergence speed, we can see that the convergence speed of this paper is about twice as fast as that of [36]. However, the improvement of convergence speed in this paper is at the cost of expanding overshoot, but the overshoot is within the acceptable. In the future, we will study how to design the controller to improve the convergence speed and reduce the overshoot. Moreover, the states of all agents are assumed to be measurable in [36]. However, in practice, it is difficult to measure all states due to high cost or technical constraint. For the case of unmeasurable states, the controller proposed in [36] is not applicable, while the controller proposed in this paper can solve this problem.

Fig. 8

The tracking errors of all agents of (a) [36], and (b) the proposed method

5.5 Result analysis

Section 5.1 considers the third-order system model, however, after linear transformation (5), the dimension of unmeasurable system states is 2. Therefore, only reduced-order observer is needed to observe these unmeasurable states. The reduced-order observer is designed by solving discrete-time algebraic Riccati equation (31). Figure 2 shows the estimation errors of the unmeasurable states. It can be seen that the estimation errors $x_{ui}^{*}(k)$ converge to zero within 10s, therefore, the designed reduced-order observer (7) can estimate the unmeasurable states very well. Then, the distributed feedback controller (9) is designed by solving the discrete-time algebraic Riccati equation (12). The tracking errors are depicted in Fig. 3a. We can see that the tracking errors converge to zero quickly, i.e. all followers can track the leader through the designed controller, which verifies the effectiveness of the proposed method. Therefore, the proposed controller (9) can solve the robust leader-following consensus problem of HD_MASs of (1) and (2).

Similarly, from the results in Figs. 4, 5, and 3b of Section 5.2, we can get that the estimation errors of the unmeasurable states and the tracking errors converge to zero asymptotically. Therefore, the proposed algorithm can be extended to the continuous-time systems. Moreover, from the actual operating motivation of the MuPAL-α model, we apply the proposed algorithm to this model. From Figs. 6 and 7 of Section 5.3, it can be obtained that the tracking errors of four research aircrafts converge to zero in a very short time, thus the designed algorithm can solve the tracking problem of networked aircrafts, which verifies the application value of the proposed method.

To further investigate the effectiveness of the proposed controller, the comparison method in [36] is used in Section 5.4. The comparison results are shown in Fig. 8. The results show that proposed method obtains the better performance. The reasons are as follows. Firstly, the proposed method adopts the reduced-order observer to reduce the dimension of the system, and it plays a significant role in improving the efficiency. Secondly, the proposed method considers internal model principle and output coupling relation among agents, which can capture more communication information than the chosen benchmark. Therefore, the proposed method can obtain superior performance than [36] in terms of convergence speed. As summarized from the experimental results, the proposed method is feasible and promising for dealing with the robust leader-following consensus problem.

6 Conclusion

In this paper, the leader-following consensus of HD_MASs with system uncertainties has been investigated. The state information of each agent is not detected by itself and its neighbors, therefore, an linear transformation is designed to divide the states into measurable and unmeasurable parts. Then the reduced-order observer is designed only for the unmeasurable states. And the distributed feedback controller is proposed such that all outputs of the followers reach the leader’s output. In light of the internal model principle and discrete-time algebraic Riccati equation, the leader-following problem is achieved. Moreover, this paper extends the results to continuous-time MASs. Finally, several numerical examples are provided to verify the effectiveness of the proposed method. Future research along this direction will address the leader-following consensus of MASs with time delay under switching topology based on event-triggered mechanism. Moreover, the issue of formation control with obstacle avoidance is the direction of our future research.

Appendices

Appendix A: Proof of Lemma 3.1

Since the matrix pairs (A_i, B_i) are stabilizable, (A_i, C_i) are detectable, for any $\lambda _{i}\in \mathcal {C}$, the matrix pairs (A_i − λ_iI_n, B) with n × (n + q) dimensions are full row rank, and the matrix pairs $\left ({\begin {array}{*{20}{c}} A_{i}-\lambda _{i} I_{n} \\ C_{i} \end {array}} \right )$ with (n + p) × n dimensions are full column rank. For any invertible matrix $\mathcal {T}_{i}$, one has $Rank~ \mathcal {T}_{i}^{-1}(A_{i}-\lambda _{i} I_{n}, B_{i})\mathcal {T}_{i}=Rank~ (\hat {A}_{i}-\lambda _{i} I_{n}, \hat {B}_{i}\mathcal {T}_{i})=n,$ i.e., there exist matrices K_i such that $\hat {A}_{i}+\hat {B}_{i}\mathcal {T}_{i}K_{i}$ are Schur. Then, there exist matrices $\bar {K}_{i}=\mathcal {T}_{i}K_{i}$ such that $\hat {A}_{i}+\hat {B}_{i}\bar {K}_{i}$ are Schur. For any invertible matrix $\mathcal {T}_{i}$, one also has $Rank~ \left ({\begin {array}{*{20}{c}} A_{i}-\lambda _{i} I_{n} \\ C_{i} \end {array}} \right )=Rank~ \left ({\begin {array}{*{20}{c}} \mathcal {T}_{i}^{-1} & \mathbf {0}\\ \mathbf {0} & I_{p} \end {array}} \right ) \left ({\begin {array}{*{20}{c}} A_{i}-\lambda _{i} I_{n} \\ C_{i} \end {array}} \right )\mathcal {T}_{i}$. Since $C_{i}\mathcal {T}_{i}=(I_{p}, \mathbf {0})$, we have $\left ({\begin {array}{*{20}{c}} \mathcal {T}_{i}^{-1} & \mathbf {0}\\ \mathbf {0} & I_{p} \end {array}} \right )\left ({\begin {array}{*{20}{c}} A_{i}-\lambda _{i} I_{n} \\ C_{i} \end {array}} \right )\mathcal {T}_{i}=\left ({\begin {array}{*{20}{c}} A_{i}^{11}-\lambda _{i} I_{p} & A_{i}^{12}\\ A_{i}^{21} & A_{i}^{22}-\lambda _{i} I_{n-p}\\ I_{p} & \mathbf {0} \end {array}} \right )$. Therefore, the matrices $\left ({\begin {array}{*{20}{c}} A_{i}^{12} \\ A_{i}^{22}-\lambda _{i} I_{n-p} \end {array}} \right )$are full column rank, i.e., the matrix pairs $(A_{i}^{22}, A_{i}^{12})$ are detectable, for any $\lambda _{i}\in \mathcal {C}$. The proof has been completed.

Appendix B: Proof of Lemma 3.3

Since the gain matrix L_i is defined as $L_{i}=A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}$, we have

$$ \begin{array}{@{}rcl@{}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad&(A_{i}-s_{i}L_{i}C_{i})P_{i}(A_{i}-s_{i}L_{i}C_{i})^{*}-P_{i} \\ &= & A_{i}P_{i}{A_{i}^{T}}-s_{i}^{*}A_{i}P_{i}{C_{i}^{T}}{L_{i}^{T}}-s_{i}L_{i}C_{i}P_{i}{A_{i}^{T}}+s_{i}s_{i}^{*}L_{i}C_{i}P_{i}{C_{i}^{T}}{L_{i}^{T}}-P_{i}\\ & = & A_{i}P_{i}{A_{i}^{T}}-s_{i}^{*}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}-s_{i}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad& +s_{i}s_{i}^{*}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}-P_{i}\\ & = &A_{i}P_{i}{A_{i}^{T}}-P_{i}-A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}+(1+s_{i}s_{i}^{*}-s_{i}^{*}-s_{i})A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}.\\ & = &-Q_{i}+(1+s_{i}s_{i}^{*}-s_{i}^{*}-s_{i})A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}. \end{array} $$

(27)

According to Lyapunov stability theory, $\forall P_{i}={P_{i}^{T}}>0$, the matrices A_i − s_iL_iC_i are stabilizable for $s_{i}\in \mathcal {C}$, if and only if (A_i − s_iL_iC_i)P_i(A_i − s_iL_iC_i)^∗− P_i < 0, i.e.

$$ -Q_{i}+(1+s_{i}s_{i}^{*}-s_{i}^{*}-s_{i})A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}<0. $$

(28)

Since $Q_{i}={Q_{i}^{T}}$, there exist matrices $Q_{si}=Q_{s_{i}}^{T}>0$ such that $Q_{s_{i}}=Q_{s_{i}}^{-1}Q_{i}$. Post-multiplying and pre-multiplying (28) by $Q_{s_{i}}^{-1}$, respectively, one has

$$ -I_{n}+|s_{i}-1|^{2}Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}<0, $$

(29)

where $1+s_{i}s_{i}^{*}-s_{i}^{*}-s_{i}=(1-s_{i})(1-s_{i})^{*}=|s_{i}-1|^{2}$. By the (29), we get

$$ -1+|s_{i}-1|^{2}\lambda_{k}[Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}]<0, $$

(30)

if the eigenvalues $\lambda _{k}[Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}]>0$ and satisfy $|s_{i}-1|^{2}<\frac {1}{max_{k=1,2,\ldots , n}\lambda _{k}[Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}]},$ the (30) holds. Moreover, if $\lambda _{k}[Q_{s_{i}}^{-1}A_{i}P_{i}{C_{i}^{T}}(C_{i}P_{i}{C_{i}^{T}})^{-1}C_{i}P_{i}{A_{i}^{T}}Q_{s_{i}}^{-1}]=0, k=1, 2,\ldots , n$, the (30) also holds for any $s_{i}\in \mathcal {C}$. Similarly, if $c_{i}\in \mathcal {C}$ is distributed in the stable domain ${\varPhi }_{c_{i}}=\{c_{i}\in \mathcal {C}: |c_{i}-1|^{2}<\delta _{c_{i}}\},$ where $\delta _{c_{i}}^{-1}=max_{k=1,2,\ldots , n}\lambda _{k}[Q_{c_{i}}^{-1}{A_{i}^{T}}P_{i}B_{i}({B_{i}^{T}}P_{i}B_{i})^{-1}{B_{i}^{T}}P_{i}A_{i}Q_{c_{i}}^{-1}], Q_{c_{i}}=Q_{c_{i}}^{-1}Q_{i}>0$, the matrices A_i + c_iB_iK_i are Schur. This completes the proof.

Appendix C: Proof of Theorem 3.1

If the digraph $\mathcal {G}$ contains a directed spanning tree, according to Lemma 2.1, all eigenvalues of the matrix $\theta {\mathcal{H}}$ have positive real parts. By the Jordan canonical form theorem, there is a nonsingular matrix T_s ∈ R^N×N satisfying $\theta {\mathcal{H}}=T_{s}JT_{s}^{-1}$, where $J=block~ diag(J_{N_{1}}(\lambda _{1}^{\prime }), \ldots , J_{N_{m}}(\lambda _{m}^{\prime })),N_{1}+\ldots +N_{m}=N, \lambda _{1}^{\prime }<\ldots <\lambda _{m}^{\prime }, \lambda _{1}=\cdots =\lambda _{N_{1}}=\lambda _{1}^{\prime }, \lambda _{N_{1}+1}=\lambda _{N_{1}+2}=\cdots =\lambda _{N_{1}+N_{2}}=\lambda _{2}^{\prime }, \ldots \lambda _{N_{1}+N_{2}+\cdots +N_{m-1}+1}=\lambda _{N_{1}+N_{2}+\cdots +N_{m-1}+2}=\cdots =\lambda _{N_{1}+N_{2}+\cdots +N_{m-1}+N_{m}}=\lambda _{m}^{\prime }, J_{N_{l}}(\lambda _{l}^{\prime })=\left ({\begin {array}{*{20}{c}} \lambda _{l}^{\prime } & 1 & & \\ &\lambda _{l}^{\prime }& {\ddots } & \\ & & {\ddots } & 1\\ & & & \lambda _{l}^{\prime } \end {array}} \right ), l=1,\ldots , m,$ Let $T_{1}=\left ({\begin {array}{*{20}{c}} I_{Np} & \mathbf {0} & \mathbf {0} & \mathbf {0} \\ \mathbf {0} & I_{N(n-p)}& \mathbf {0} & \mathbf {0}\\ \mathbf {0} & \mathbf {0} & \theta {\mathcal{H}}\otimes I_{s_{m}} & \mathbf {0}\\ \mathbf {0} & I_{N(n-p)} & \mathbf {0} & I_{N(n-p)} \end {array}} \right ),\\ T_{2}=\left ({\begin {array}{*{20}{c}} T_{s}\otimes I_{p} & \mathbf {0} & \mathbf {0} & \mathbf {0} \\ \mathbf {0} & T_{s}\otimes I_{n-p} & \mathbf {0} & \mathbf {0}\\ \mathbf {0} & \mathbf {0} & T_{s}\otimes I_{s_{m}} & \mathbf {0}\\ \mathbf {0} & \mathbf {0} & \mathbf {0} & T_{s}\otimes I_{n-p} \end {array}} \right ),$$\bar {A}_{c} =T_{2}^{-1}T_{1}^{-1}A_{c}T_{1}T_{2}= \left ({\begin {array}{*{20}{c}} \bar {A}_{c}^{11} & \bar {A}_{c}^{12}\\ \mathbf {0} & A_{22}-LA_{12} \end {array}} \right ),$ where

$\bar {A}_{c}^{11}=\left ({\begin {array}{*{20}{c}} A_{11}+B_{1}K_{2}(J\otimes I_{p}) & A_{12}+B_{1}K_{1}(J\otimes I_{n-p}) & B_{1}K_{3}(J\otimes I_{s_{m}}) \\ A_{21}+B_{2}K_{2}(J\otimes I_{p}) & A_{22}+B_{2}K_{1}(J\otimes I_{n-p})& B_{2}K_{3}(J\otimes I_{s_{m}}) \\ I_{N}\otimes G_{2} & \mathbf {0} & I_{N}\otimes G_{1} \end {array}} \right ), \bar {A}_{c}^{12}=\left ({\begin {array}{*{20}{c}} B_{1}K_{1}(J\otimes I_{n-p}) \\ B_{2}K_{1}(J\otimes I_{n-p})\\ \mathbf {0} \end {array}} \right )$. It is obvious that A_c is stabilizable if and only if $\bar {A}_{c}$ is stabilizable. According to Theorem 3 in [27], A_c is Schur if and only if $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2}, ~\mathbf {0}) & G_{1} \end {array}} \right )$ and $A_{i}^{22}-L_{i}A_{i}^{12}, i=1, 2, \ldots , N$ are Schur. This completes the proof.

Appendix D: Proof of Theorem 3.2

According to Theorem 3.1, A_c is stabilizable if and only if $A_{i}^{22}-L_{i}A_{i}^{12}$ and $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2}, ~\mathbf {0}) & G_{1} \end {array}} \right )$are Schur. It thus follows from Lemma 3.1 that $(A_{i}^{22}, A_{i}^{12})$ is completely detectable. The gain matrix $L_{i}=A_{i}^{22}P_{i}(A_{i}^{12})^{T}(A_{i}^{12}P_{i}(A_{i}^{12})^{T})^{-1}$ can be obtained by the following discrete-time algebraic Riccati equation

$$ \small A_{i}^{22}P_{i}(A_{i}^{22})^{T}-P_{i}-A_{i}^{22}P_{i}(A_{i}^{12})^{T}(A_{i}^{12}P_{i}(A_{i}^{12})^{T})^{-1}A_{i}^{12}P_{i}(A_{i}^{22})^{T}+Q_{i}=0. $$

(31)

Let $\mathcal {K}_{i}=(K_{2i}, K_{1i}, K_{3i})$, we have $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2},~ \mathbf {0}) & G_{1} \end {array}} \right )=\mathcal {A}_{i}+\lambda _{i}{\mathcal{B}}_{i}\mathcal {K}_{i}$. By Lemmas 3.1 and 3.2, the matrix pairs $(\mathcal {A}_{i}, {\mathcal{B}}_{i})$ are stabilizable. Then, according to Lemma 3.3, if λ_i is distributed in the stable domain Φ_i, $\mathcal {A}_{i}+\lambda _{i}{\mathcal{B}}_{i}\mathcal {K}_{i}$ is Schur, where $\mathcal {K}_{i}=-({\mathcal{B}}_{i}^{T}\mathcal {P}_{i}{\mathcal{B}}_{i})^{-1}{\mathcal{B}}_{i}^{T}\mathcal {P}_{i}\mathcal {A}_{i}$, and $\mathcal {P}_{i}$ can be solved by (12). Therefore, the system A_c is Schur. This completes the proof.

Appendix E: Proof of Theorem 3.3

According to the proof in Theorem 3.2, it is easy to find suitable feedback gain matrix such that the nominal form A_c of system matrix $\bar {A}_{c}$ is Schur. To solve the robust leader-following consensus problem by distributed feedback controller (9), the following Sylvester equation is considered

$$ \bar{X}_{c}A_{0}=\bar{A}_{c}\bar{X}_{c}+\bar{W}_{c}, $$

(32)

with $\bar {X}_{c}\in R^{N(2n-p+s_{m})\times s}$. For each sufficiently small Δ, $\bar {A}_{c}$ is stable. By the Assumption 3.2, (32) has an unique solution $\bar {X}_{c}$. Let $\bar {X}_{c}=(\bar {X}_{c1}^{T}, \bar {X}_{c2}^{T}, \bar {X}_{c3}^{T}, \bar {X}_{c4}^{T})^{T}$, where $\bar {X}_{c1}, \bar {X}_{c2}, \bar {X}_{c3}$ and $\bar {X}_{c4}$ have appropriate dimensions, we have

$$ \begin{array}{lll} \bar{X}_{c3}A_{0} &= (\theta \mathcal{H}\otimes G_{2})\bar{X}_{c1}+(I_{N}\otimes G_{1})\bar{X}_{c3}-(\theta \mathcal{A}_{0}\otimes G_{2}F_{0})(1_{N}\otimes I_{s})\\ &= (\theta \mathcal{H}\otimes G_{2})\bar{X}_{c1}+(I_{N}\otimes G_{1})\bar{X}_{c3}-(\theta \mathcal{H}\otimes G_{2}F_{0})(1_{N}\otimes I_{s})\\ &= (I_{N}\otimes G_{1})\bar{X}_{c3}+(I_{N}\otimes G_{2})[(\theta \mathcal{H}\otimes I_{p})\bar{X}_{c1}-(\theta \mathcal{H}\otimes F_{0})(1_{N} \otimes I_{s})]. \end{array} $$

(33)

Since (I_N ⊗ G₁, I_N ⊗ G₂) incorporates a pN-copy internal model of A₀, on the basis of Lemma 3.2, we obtain

$$ (\theta \mathcal{H}\otimes I_{p})\bar{X}_{c1}-(\theta \mathcal{H}\otimes F_{0})(1_{N} \otimes I_{s})=(\theta \mathcal{H}\otimes I_{p})[\bar{X}_{c1}-(I_{N}\otimes F_{0})(1_{N} \otimes I_{s})]=0. $$

(34)

Moreover, the matrix ${\mathcal{H}}$ is reversible, we have $\bar {X}_{c1}-(I_{N}\otimes F_{0})(1_{N} \otimes I_{s})=0$. Let $\hat {\zeta }(k)=\zeta (k)-\bar {X}_{c}\omega (k)$, and consider the following equation

$$ \small \hat{\zeta}(k+1)= \zeta(k+1)-\bar{X}_{c}\omega(k+1)= \bar{A}_{c}\zeta(k)+(\bar{W}_{c}-\bar{A}_{c}\bar{X}_{c}-\bar{W}_{c})\omega(k)= \bar{A}_{c}\hat{\zeta}(k). $$

(35)

Since $\bar {A}_{c}$ is Schur for each sufficiently small Δ, thus $\hat {\zeta }(k)\rightarrow 0 ~(k\rightarrow \infty )$, then $x_{m}(k)-\bar {X}_{c1}\omega (k)\rightarrow 0 ~(k\rightarrow \infty )$. The purpose of this paper is to solve the robust leader-follower consensus of HD_MASs (1) and (2), i.e. $e_{i}(k)=y_{i}(k)-y_{r}(k)\rightarrow 0, k\rightarrow \infty$. After the linear transformation (5), the error e_i(k) can be expressed as e_i(k) = x_mi(k) − y_r(k) = x_mi(k) − F₀ω(k). The global form of e_i(k) could be denoted as $e(k)=x_{m}(k)-(I_{N}\otimes F_{0})(1_{N}\otimes I_{s})\omega (k)=x_{m}(k)-\bar {X}_{c1}\omega (k)\rightarrow 0, k\rightarrow \infty$. Therefore, the robust leader-follower consensus of HD_MASs (1) and (2) under directed topology is solved.

Appendix F: Proof of Theorem 4.1

By Theorem 3.1, A_c is Hurwitz if and only if the matrices $A_{i}^{22}-L_{i}A_{i}^{12}$ and $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2}, ~\mathbf {0}) & G_{1} \end {array}} \right )$are Hurwitz, where λ_i(λ₁ ≤ λ₂ ≤⋯ ≤ λ_N), i = 1, 2,…, N are the eigenvalues of the matrix ${\mathcal{H}}$. Let $\mathcal {A}_{i}=\left ({\begin {array}{*{20}{c}} \hat {A}_{i} & \mathbf {0} \\ (G_{2},~ \mathbf {0}) & G_{1} \end {array}} \right ),$${\mathcal{B}}_{i}=\left ({\begin {array}{*{20}{c}} \hat {B}_{i}\\ \mathbf {0} \end {array}} \right ),$and $\mathcal {K}_{i}=(K_{2i}, K_{1i}, K_{3i})=-(min~Re(\lambda _{i}))^{-1}({\mathcal{B}}_{i})^{T}\mathcal {P}_{i}$, where $\mathcal {P}_{i}$ is the solution of the following Riccati equation

$$ \mathcal{A}_{i}^{T}\mathcal{P}_{i}+\mathcal{P}_{i}\mathcal{A}_{i}+I_{n+p}-\mathcal{P}_{i}\mathcal{B}_{i}\mathcal{B}_{i}^{T}\mathcal{P}_{i}=\mathbf{0}, $$

(36)

we have $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2},~ \mathbf {0}) & G_{1} \end {array}} \right )=\mathcal {A}_{i}+\lambda _{i}{\mathcal{B}}_{i}\mathcal {K}_{i}, i=1,2,\ldots , N$. By Lemma 3.2, the matrix pair $(\mathcal {A}_{i}, {\mathcal{B}}_{i}), i=1,2,\ldots , N$ is Hurwitz. By Lemma 4.1, $\mathcal {A}_{i}+\lambda _{i}{\mathcal{B}}_{i}\mathcal {K}_{i}$ is Hurwitz, i.e. the matrix $\left ({\begin {array}{*{20}{c}} \hat {A}_{i}+\lambda _{i}\hat {B}_{i}(K_{2i}, K_{1i}) &\lambda _{i}\hat {B}_{i}K_{3i}\\ (G_{2}, ~\mathbf {0}) & G_{1} \end {array}} \right )$is Hurwitz. Besides, on the basis of Lemma 3.1, the matrix $(A_{i}^{22}, A_{i}^{12})$ is completely detectable, and the gain matrix $L_{i}=P_{i}(A_{i}^{12})^{T}R_{i}^{-1}$ can be obtained by the following continuous-time algebraic Riccati equation

$$ A_{i}^{22}P_{i}+P_{i}(A_{i}^{22})^{T}+Q_{i}-P_{i}(A_{i}^{12})^{T}R_{i}^{-1}A_{i}^{12}P_{i}=0, $$

(37)

where $Q_{i}={Q_{i}^{T}}>0$ and $R_{i}={R_{i}^{T}}>0$ are arbitrary positive definite matrices. Based on the above analysis, the closed loop system A_c is Hurwitz. This completes the proof.