1 Introduction

Complex systems such as social networks, protein-protein networks, and airline networks can be modeled by a graph. The complex network or simply network refers to a real system; while, from a mathematical point of view it is considered as a graph [1]. Hence, in this paper, complex networks and graphs are used interchangeably. Formally, graph is an ordered pair G = (V, E), where V = {v1, v2, , vn} and E = {e1, e2, , en} refers to a set of vertexes and edges respectively. The vertexes in graphs refer to participants and edges indicate to relationships between the vertexes [2].

The graph is used to show data and their relations which are represented by vertexes and edges respectively. Once the complex network is modeled, the network can be analyzed. The network analysis is the process of mapping and measuring the connections and relationships that take place among agents, people, organizations, machines and etc. [2]. Various types of analysis such as frequent sub-graph mining, vertex centrality analysis, community detection and etc. can be performed on graphs [3]. However, this paper mainly focuses on community detection. In literature, a community also is introduced as a group, module, cluster, and component [4]. Although community detection is different from graph partitioning or graph clustering, sometimes they are used interchangeably. Clustering is the process of assigning data objects into a set of separate groups which is called a cluster. The objects of each cluster are more similar to each other than the objects of other ones [6]. In graph partitioning and clustering the number of communities should be known beforehand [7]. Although there is not a specific definition for communities, visually, the nodes of a community have dense connections; while, the nodes of different communities are connected loosely [5, 8]. Community detection is one of the fundamental parts in complex network analysis. Regardless of the nature of the complex network, the analysis of communities can reveal some useful covered information.

Exact algorithms for community detection is an NP-Hard problem [9] and can be used only for small graphs [10]. Hence, in recent years various heuristic algorithms were proposed for modularity optimization [5]. Community detection algorithms can be classified into agglomerative and divisive categories [5, 11]. In an agglomerative approach, each vertex is assigned to a community and in an iterative process they are merged and form a larger community. On the other hand, in the divisive approach, the graph is considered as a community and in an iterative process, it is broken down into some smaller communities [11]. In both approaches, the process can be represented by dendrogram that is a hierarchical tree.

The Girvan-Newman’s method (GN) is hierarchical, divisive and one of the popular algorithm for community detection which is widely used in recent years [13]. GN detects clusters of a graph using the concept of edge betweenness centrality that removes the most central edges progressively [14, 15]. This process will be continued, until it reaches to high modular communities. In this algorithm, the stop condition is defined by modularity functions [14]. In other words, modularity functions are used to evaluate the goodness of detected communities [15]. Although GN is a popular method for graph clustering, due to its computational complexity it can process medium-size graphs [5, 16]. Hence, in this paper, a new approach for the evaluation of edges centrality is proposed that helps community detection algorithm run faster. In addition, the detected communities by the proposed approach often have better qualities than the GN method. Therefore, the main contribution of the paper is summarized as follows:

  1. 1.

    Defines degree for edges.

  2. 2.

    Defines edge betweenness centrality based on edge’s degree.

  3. 3.

    Performs community detection based on the defined betweenness centrality.

  4. 4.

    In this paper, multiple edges can be removed in an iteration (Multiple edge elimination property). This important feature helps the algorithm run faster.

  5. 5.

    Results show that our proposed approach is extremely faster than plain GN algorithm.

  6. 6.

    Results prove that our proposed algorithm often detects better communities (high modular communities) than GN method.

In addition, we compare our proposed approach with meta-heuristic algorithms which are recently used for community detection. Results show that our proposed method has some important advantages which are summarized below:

  • Scalable: our proposed method can apply to medium and large scale graphs; while, meta-heuristic algorithms are suitable for small graphs.

  • Stable: our proposed method is stable and can create a unique response after different runs; while, meta-heuristic algorithms reach to different responses after different runs.

  • Reliable: our proposed method always detects logical and real communities; while, meta-heuristic algorithms might detect fake communities. The fake community is a new concept that we have introduced in this paper. In the fake communities, two irrelevant vertexes are put in the same community. This concept will be highlighted in the rest of the paper.

  • Efficient: our proposed method needs significantly less memory than the meta-heuristic algorithms.

  • Our proposed method is free from predefined knowledge such as the number of communities; while, this kind of information is vital for meta-heuristic algorithms to reach a suitable response.

  • Meta-Heuristic algorithms completely depend on parameter tuning such as population size, mutation and crossover rates to return a good response; while, our proposed algorithm is free from this kind of parameter tuning.

The aforementioned features will be highlighted in the rest of the paper. Moreover, our proposed method has some important features which are as below:

  1. 1.

    It is a divisive (Top-Down) and hierarchical method.

  2. 2.

    It is free from predefined knowledge such as the number of communities.

  3. 3.

    The proposed method can detect non-overlapped communities.

The structure of the paper as follows: related work is expressed in Section 2. Section 3, introduces Girvan and Newman’s algorithm which is used for community detection. The proposed approach for community detection will be highlighted in Section 4 and evaluation is done in Section 5. Finally, the last section concludes the paper.

2 Related work

In recent years various types of algorithms were introduced to detect communities. From one perspective, the community detection algorithms can be classified into agglomerative (bottom-up) and divisive (top-down) classes [11, 12]. Some algorithms such as GN [14], Kernighan-Lin [17], Radicchi [4] are based on the divisive approach. In addition, some algorithms such as Blondel’s method [18] use an agglomerative approach for community detection.

From another point of view, community detection algorithms can be categorized into two classes. One type of algorithms can detect overlapped communities; while, the second class can detect just non-overlapped communities [5, 12]. For instance, some methods such as GN, Kernighan-Lin, and Blondel discover non-overlapped communities and some algorithms such as CPM, RaRe, and IS detect overlapped communities [5]. In overlapped communities, vertexes can belong to more than one cluster.

In 1970, Kernighan and Lin introduced a simple partitioning algorithm (KL) to disjoint a graph into two parts [17]. In 1988, KL was extended to fragment a graph in any number of parts [5, 19]. KL is a partitioning algorithm and depends on predefined knowledge about the number of clusters [5]. Afterward, Girvan and Newman introduced a divisive and hierarchical algorithm for community detection (GN) [13]. GN is based on edge betweenness centrality. Girvan and Newman use the shortest path for the calculation of edge betweenness [15]. According to the shortest path centrality, an edge with a high betweenness value has a high centrality. In 2004, Radicchi introduced edge clustering coefficient, to evaluate edges’ centralities [4]. In contrast to edge betweenness based on shortest path, in the edge clustering coefficient, the small number indicates to a high edge centrality.

In modularity based methods [10, 13], a modularity function is considered as a fitness function which defines a stopping criterion for algorithms. Since community detection is an NP-Hard problem [10]; some approaches like heuristic and Meta-heuristic methods were proposed to detect communities quickly. For example, Louvain algorithm was proposed by Blondel in 2008, is a greedy, agglomerative and hierarchical technique [18]. In this method, at the starting step, each vertex is assigned to a separate cluster and then in an iterative process they might merge and form a larger vertex which called meta-vertex [10, 18]. This algorithm continues while the obtained network cannot be reduced more. In addition, many extensions were applied to the Louvain method. For instance, Rotta and Noak introduced multi-level refinement [20] and Lu et al. [21] implemented the Louvain algorithm in parallel. Moreover, [22] discovers latent links among social objects according to their behavioral interactions. Then communities are detected by the consideration of k-clique and k-nearest neighbor set concept.

Furthermore, recently, some other meta-heuristic algorithms were introduced to discover communities. For instance: Simulated Annealing (SA) which comprises local move and global move are used for community detection [23]. Also, SA was extended by Massen [24] to escape from local optima. In 2005, Duch and Arenas used Extremal Optimization (EO) for modularity optimization [25]. Moreover, some approaches such as [26,27,28], used Genetic Algorithm (GA), [29] used the memetic method, and [30] utilizes discrete biogeography (BBO) for community detection. In [31] a discrete modified firework algorithm was used to detect communities. In their proposed approach a new initialization and mutation strategy is used to improve the convergence speed of the algorithm. Furthermore, a multi-objective optimization such as MOGA-net [32], MOCD [33], and MOEA/D-net [34] and also MOPSO were used for graph clustering [35]. In multi-objective optimization, we have sets of measurable objectives, constraints, and adequate process to get information about comprises between all objectives [36]. For instance, in [37], multi-objective discrete bat algorithm is used to discover communities of a complex network. In their proposed method, snapshot cost (Modularity (Q)) and temporal cost (Normalized Mutual Information (NMI)) are used as objective functions. In addition, [38] used MOPSO for community detection in signed networks.

These papers introduce a divisive and hierarchical approach based on edge betweenness centrality. Centrality is used to evaluate the importance of edges. Hence, in this section, some current research on the calculation of edge and vertex centrality will be expressed. Some present studies on edge betweenness are as follows [5]:

  • Based on the shortest path: for a given edge such as (i, j), this measure is based on the number of shortest paths that goes through the considered edge [42].

  • Based on random walk: the centrality of an edge is computed according to the frequency of passages that go from a given edge during the running of the random walk algorithm [5].

  • Current-flow: finally, a graph is considered as a resistor network that edges have resistant units. The betweenness of an edge is the average current value that is carried by itself. This approach is called current-flow betweenness [39].

However, the calculation of edge betweenness based on the shortest path is faster than betweenness of using both random walk and current-flow [5]. In addition, some other similar metrics was proposed to calculate vertex centrality [40, 41].

  • Degree: degree centrality is the basic approach to calculate the centrality of nodes. According to this centrality, a vertex with a high degree involves in a vast number of interactions and is a central node.

  • Closeness centrality: according to the closeness centrality, the central node can communicate quickly with other vertexes in a graph.

  • Betweenness centrality: in betweenness centrality, a vertex is central, if it highly participates in the shortest paths between any pair of vertexes [42].

  • Random walk: in some cases, the computation of the shortest paths between vertexes might not possible; hence, another vertex betweenness was suggested that is based on the probability of visiting vertexes. The random walk can be used to calculate this centrality [43].

  • Eigenvector centrality: according to the eigenvector centrality, an important vertex is connected to important adjacent vertexes in a network [40].

  • Furthermore, some other centrality measures such as sub-graph centrality, flow betweenness centrality and information centrality were introduced to assess the importance of vertexes [40].

In recent years some other community detection algorithms were introduced that are based on the centrality assessment. For example [44] introduces leader based community detection that the selection of central nodes is done by eigenvector centrality. Their proposed method has two stages that are: 1) the leader’s discovery and 2) community detection through vertexes similarities.

3 Girvan and Newman’s algorithm (GN)

GN is the first method of the current age community detection algorithms in complex networks. This algorithm is a divisive and hierarchical approach that is based on shortest path betweenness [15, 45]. The divisive approaches start while putting the whole network in a cluster and then the split is performed recursively. The idea is that an edge that connecting two different communities has high edge betweenness centrality. GN has two important features which are: 1) using a divisive approach to remove iteratively the central edges from the network and 2) recalculation of the edge betweenness value after each iteration [15]. Thus GN has four main steps which are as follow [46]:

  1. 1.

    Calculate the betweenness of all existing edges in a graph.

  2. 2.

    Delete the most central edge. According to the shortest path betweenness, the most central edge has the highest centrality value.

  3. 3.

    Recalculate the betweenness of all remaining edges of the graph.

  4. 4.

    Steps 2 and 3 will be repeated while they help to detect better communities.

In the GN, the recalculation of edge betweenness (step 3) is the most important characteristic of the algorithm. If in this algorithm a standard divisive clustering based on edge betweenness was performed, then the edge betweenness for all edges could be calculated and removed in decreasing order. However, when the first edge in the graph is removed, the betweenness values for the remaining edges will not show the network as it is now. This can lead to undesirable behaviors. Hence, after each iteration, the value of betweenness for each edge should be recalculated and updated.

According to this method, the most central edges will be removed iteratively, but it does not indicate which split is better than the other ones. Therefore, in order to assess the goodness of the detected components, modularity functions are used [14]. In the rest of the paper, one of the famous modularity functions will be introduced.

Furthermore, edge betweenness based on shortest paths is the number of the shortest path between each pair of vertexes in a graph that involves the edge [5]. Hence, according to the edge betweenness centrality, an inter-community edge has a high importance. Although GN, is a popular algorithm for community detection, due to its computational complexity can be applied on graphs with around 10000 vertexes [5, 16]. By using breadth-First-Search (BFS) technique, the betweenness of edges in the unweighted graph can be computed in O(m2). After removing the central edge, this process should be repeated on the graph for at most m times (for every edge of the graph). Therefore, the GN needs O(m3) to process unweighted graphs. In addition, this algorithm can be extended easily to compute the betweenness of weighted graphs [15]. For weighted graphs and by using Dijkstra’s algorithm, the betweenness of all edges can be calculated in O(m2 + m2logm) and GN needs O(m3 + m3logm) time [5, 47].

Afterward, Newman uses the random walk instead of the shortest path to compute the edge’s betweenness. The former definition implicitly expresses that information just flows from those shortest paths; while, random walk betweenness lessens that assumption and defines the centrality as a frequency of passages that goes from a given edge [43]. However, the computation of betweenness based on the shortest path is faster than random walk [5]. Therefore, in this paper a new divisive approach is introduced which is extremely faster than the GN method and can detect communities with a high quality. The proposed method will be introduced in the next section.

4 The proposed method for community detection

The proposed method has some important features which are as follow:

  • It is a greedy, divisive, and hierarchical method.

  • The proposed algorithm does not depend on predefined knowledge such as the number of communities.

  • The elements of detected communities cannot belong to more than one community at the same time. It means the communities do not have intersection with each other.

In addition to the mentioned features of the proposed method, it has some notable characteristics that make it a fast and efficient method for community detection. These characteristics are listed below:

  • Defines a new metric for the calculation of edge’s centrality which is based on the edge’s degrees. The computation of edges’ degrees will be expressed in this section.

  • In order to do a fast community detection, multiple edges can be removed in each iteration. It means that if we have some edges with the highest centrality, all of them will be removed at the same iteration. This functionality is called multiple edge elimination property.

  • Finally, the detection of communities can be performed according to the edge’s degree centrality and multiple edge elimination property.

Therefore, the sudo code of the proposed algorithm for community detection is as follows:

figure c

Hence, the structure of this section is as follows:

  1. A)

    Calculation of edges degree

  2. B)

    Removing the most central edge(s)

4.1 Calculation of edge’s degree

There are two ways for the computation of edge’s betweenness centrality based on edge’s degree which are as follows:

  1. 1.

    Using edges direct neighbors.

  2. 2.

    Using the line graph (Also called dual graph).

4.1.1 Using edges direct neighbors

Using edges direct neighbors is the first way for the calculation of edges degree which will be introduced with a simple example.

Definition 1 (direct neighbors)

For a given graph (G), and an edge such as (u, v) ∈ E, the direct neighbors of supposed edge are the edges that have the following condition:

$$\begin{array}{@{}rcl@{}} D(E)&&=\{\forall (i,j) \in E |(i=u \wedge j\neq v) \vee (i\neq u \wedge j=v) \\&&\quad\vee (i=v \wedge j\neq u) \vee (i\neq v \wedge j=u) \}\end{array} $$

In definition (1), D(E) refers to a set of edges that have a direct relation with the given edge ((u, v)). Hence, the degree of edge (u, v) for both unweighted and weighted graphs can be calculated by the (1) and (2) respectively. In (2), w(u, v) denotes to the weight of edge (u, v). For example, Fig. 1 shows a simple example about the edges’ degrees.

$$ Deg(u,v) = |D(E)| $$
(1)
$$ Deg(u,v) = \sum\limits_{i,j}^{|D(E)|} w(u,v) $$
(2)
Fig. 1
figure 1

An example from edge’s degree

Full size image

4.1.2 Using the line graph

Using the line graph is another way to compute edges’ degree which will be introduced in this section.

Definition 2 (Line Graph – L(G))

for a graph G = (V, E), L(G) = (E, L) is its line graph that the nodes of L(G) are the edges of G. Two vertexes of L(G) are connected, if they have a common vertex in the original graph G. Line graph is also called dual graph, adjoint graph, derived graph, or edge-to-vertex dual [1]. Figure 2 shows an example of the line graph.

Fig. 2
figure 2

Example: Line graph (http://mathworld.wolfram.com/LineGraph.html)

Full size image

Although the vertex betweenness based on the shortest path in line graph differs from edge betweenness in its original graph [48], for the degree betweenness it is true. Hence, using the line graph is the other way to calculate the betweenness centrality based on edges’ degree.

4.2 Removing the most central edge(s)

After the detection of most central nodes, they can be removed in the next step. Removing the central nodes will be applied if this process increases the modularity. The modularity assessment is an action that aims to evaluate the goodness of detected communities. Many different modularity functions (also called quality function) such as performance and coverage have introduced to evaluate the detected groups of a graph [5]. In this paper, Girvan and Newman’s modularity function is used to evaluate the quality of detected communities [14]. For all edges of a graph, removing the most central nodes will be applied. After removing the edge(s) in each iteration, the quality of detected communities will be assessed by the quality function. The best response is kept which refers to the best detected community.

Although there is no universally accepted definition for communities, visually the members of a community have dense connections with each other and there are sparse interconnection edges between different communities. Hence, if n, nc, δint(C) and δext(C) refers to the total number of vertexes in a graph, the total number of vertexes in a cluster C, the internal density of cluster C, and the external density of cluster C respectively, then the internal density of cluster C, and the external density of cluster C is calculated by (3) and (4) respectively [5].

$$ \delta_{int}(C) = \frac{\# Internal Edges of C}{\frac{n_{c}(n_{c}-1)}{2}} $$
(3)
$$ \delta_{ext}(C) = \frac{\# External Edges of C}{n_{c}(n-n_{c})} $$
(4)

By the consideration of (3) and (4), the detected communities are modular, if δint(C) − δext(C) is high as much as possible. Hence, the increase of δint(C) − δext(C) is the main goal of all community detection algorithms.

In addition, in order to increase the speed of the proposed algorithm, in this paper removing more than one edge in one iteration is permitted (multiple edge elimination property). Figure 3 shows an example to highlight the proposed method.

Fig. 3
figure 3

Example: the proposed method for community detection

Full size image

5 Evaluation

Since our proposed algorithm aims to improve the speed of the GN algorithm, this section compares the quality, accuracy, and speed of the proposed algorithm with the plain GN.

  1. 1.

    Accuracy: this feature is used to assess the correctness of the proposed approach.

  2. 2.

    Quality: is used to calculate the quality of detected groups.

  3. 3.

    Speed: this feature elaborates that the proposed approach is faster than plain GN.

5.1 Accuracy

The accuracy of the proposed method is calculated by comparing its output and the expected results. Hence, after gathering the ground truth data, accuracy assessment can be applied. For the accuracy assessment, various measures such as Normalized Mutual Information (NMI), Purity, and Adjusted Rand Index (ARI) was introduced [49, 50]. In this paper, NMI and purity are used to show the accuracy of the proposed approach. Since this paper aims to extend the GN method, the accuracy of the proposed approach and GN are compared.

  • Normalized Mutual Information (NMI): this measure compares two clusters based on information theory (entropy). The (5) is used for NMI:

    $$ NMI(\pi^{a},\pi^{b}) = \frac{{\sum}_{h = 1}^{k^{(a)}}{\sum}_{l = 1}^{k^{(b)}}n_{h,l}log(\frac{n.n_{h,l}}{n_{h}^{(a)}.n_{l}^{(b)}})}{\sqrt{({\sum}_{h = 1}^{k^{(a)}}.n_{h}^{(a)}log(\frac{n_{h}^{(a)}}{n}))({\sum}_{l = 1}^{k^{(b)}}.n_{l}^{(b)}log(\frac{n_{l}^{(b)}}{n}))}} $$
    (5)

  • Purity: is the other measure to evaluate the correctness of clustering which is based on counting the number of correctly assigned objects. Purity is computed by (6):

    $$ Purity({\Omega},C) = \frac{1}{N}{\Sigma} max_{j}|\omega_{k} \cap c_{j}| $$
    (6)

Afterward, by the consideration of ground truth data, the accuracy of proposed algorithms can be assessed. In this paper, the accuracy assessment is done over Zachary’s karate club which is a dataset with 34 vertex and 78 edges. Since this paper wants to improve the GN method, the accuracy of the proposed approach is compared with the GN method. By the consideration of both NMI and Purity, Figs. 4 and 5 compare the accuracy of the proposed method with GN during their iterations.

Fig. 4
figure 4

Accuracy assessment of both proposed and GN methods with NMI

Full size image
Fig. 5
figure 5

Accuracy assessment of both proposed and GN methods with purity

Full size image

5.2 Quality and speed

For the evaluation of quality, various types of quality functions have been introduced in recent years. Quality functions are also known as modularity functions that aim to assess the goodness of detected communities. Girvan and Newman’s modularity function is one of the important ones which is as (7). In this paper, GN’s modularity function is used to evaluate the quality of detected communities [14].

$$ Q = \frac{1}{2m}{\Sigma}_{ij}(A_{ij}-\frac{d_{i}d_{j}}{2m}\sigma(C_{i},C_{j})) $$
(7)

In (7), m denotes the total number of edges in the graph, and i and j indicate to two separated nodes in a graph which di and dj show their degrees respectively. Aij indicates whether i and j are connected or not. If they are linked, the value of Aij will be set to 1; otherwise, it will be set to 0. If i and j are in an identical community then σ(Ci, Cj) will be set to 1 and otherwise, it will be set to 0. According to (7), Q will have a high value if the graph is modular.

Furthermore, speed is the most important feature of the proposed approach. From the mathematical point of view, our proposed approach has lower complexity than plain GN method. Although both methods are divisive and based on removing the most central nodes, our proposed method is extremely faster than the GN method. Moreover, the detected communities by the proposed method often have better quality than the detected ones by GN method. Hence, the complexity of the GN method is summarized as follow:

  1. 1.

    GN removes the central edges according to their betweenness centrality which is based on the shortest path. For unweighted graphs and by BFS, shortest path between all pair of nodes in a graph can be calculated in O(m2). For weighted graphs, all shortest path of a graph can be computed by Dijksra’s algorithm in O(m2 + m2logm).

  2. 2.

    After removing a central vertex, the calculation of the betweenness will continue for at most m times. Hence, the total complexity of the GN algorithm will be O(m3) and O(m3 + m3logn) for unweighted and weighted graphs respectively.

In this paper, an efficient approach for the calculation of edges betweenness was proposed that is based on edge degree centrality. Hence, the complexity of the proposed method is according follow:

  1. 1.

    For both weighted and unweighted graphs, the calculation of each edge’s degree can be done in O(m) and the calculation of all edges’ degree can be performed in O(m2).

  2. 2.

    Next, the most central edge should be detected and then deleted which is done in O(m).

  3. 3.

    Removing a central edge will change the degree of its neighbor edges. Hence, updating the just affected edges can be done in O(cm) which c is a constant number and denotes to the number of the deleted edge’s neighbors. So, the updating process needs O(m) time.

  4. 4.

    The deleting and updating will be repeated for at most m time. Therefore, the total complexity of the proposed method for both weighted and unweighted graphs can be performed in O(m2) which is highly faster than GN method.

Table 1, compares the quality and speed of both the proposed method and the GN algorithm. For this, five different networks with various sizes are considered and then the quality of detected communities and their running speed is evaluated. Results prove that our proposed method is remarkably faster than GN and often detects communities that have better quality than those that are detected by GN. The tests are performed on a computer with Intel Core i5 CPU and 4GB of RAM.

Table 1 Evaluation of Speed and quality of the proposed method for community detection
Full size table

In addition, Fig. 6 shows that our proposed method often detects communities that have better quality than the detected communities by GN method. Moreover, Fig. 7 proves that our proposed approach is enormously faster than GN method.

Fig. 6
figure 6

The quality comparison of both the proposed approach and the GN method

Full size image
Fig. 7
figure 7

The speed comparison of both proposed approach and GN method

Full size image

5.3 Further evaluation

In recent years, some other novel approaches such as meta-heuristic algorithms were used to detect communities. Meta-heuristic algorithms use both exploration and exploitation functions to solve NP-Hard problems [51]. These methods can find good enough solutions in a suitable time. Hence, in this section, our proposed method will also be compared with meta-heuristic algorithms which aim to detect communities.

Meta-heuristic algorithms often start with the population of answers, which aims to converge to a good solution. The majority of meta-heuristic algorithms are inspired from the natural phenomena such as swarm intelligence (e.g. PSO, ant colony, and bee) and evolutionary algorithms (such as genetic algorithms). We implemented some meta-heuristic approaches such as GA and PSO which are the most important and popular ones which are used to detect community. The implementation reveals some interesting results which are as follows:

  • Meta-heuristic algorithms are suitable just for small size graphs. It means that for small graphs (e.g. Around 300 edges and vertexes), they can detect better communities, but for medium or large graphs our proposed method is extremely faster than meta-heuristic algorithms.

  • Since the meta-heuristic algorithms are based on the population of possible answers, in comparison with our proposed method they need more memory resources. In meta-heuristic methods, each solution stores in an array with the length of vertex number that is repeated for more than the population size (population size + intermediate results).

  • The meta-heuristic algorithms are not stable. The non-stable algorithms reach to different answers in different runs. Therefore, in order to attain a good response, they should run multiple times which is not feasible especially for large scale graphs. The results of the meta-heuristic algorithms are completely based on the primary population and some parameters such as mutation and crossover rates in genetic algorithm and the velocity of particles, the effect of local best position and global best position in PSO.

  • In addition, the meta-heuristic algorithms rely on predefined knowledge such as the number of communities. Predefined knowledge is necessary for the initialization of population. Therefore, analyzers should be aware of the number of communities or have a good guess about them. Furthermore, analyzers can do preprocess on a complex network to make a suitable guess about the number of communities and perform good initialization. Our proposed method does not depend on predefined knowledge.

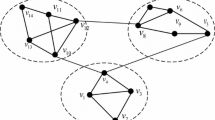
  • Furthermore, although in some small networks the meta-heuristic algorithms might detect better communities than the proposed method, they may be fake communities. The detected communities by our proposed method and the GN algorithm are reliable and cannot detect fake communities. Figure 8, represents an example of fake communities. The fake community is a new definition that we introduced in this paper and indicate to the vertexes that are considered in the same community; whilst, they don’t have any connection with each other at all.

    Fig. 8
    figure 8

    a Real communities b Fake communities

    Full size image

  • In our proposed method, the size of a problem will be reduced after removing the most central edges during the run of the algorithm, but in meta-heuristic algorithms the size of a problem will remain unchanged.

Table 2, compares and summarizes the features of the meta-heuristic algorithms with the proposed method and the plain GN method for the community detection.

Table 2 Comparing the meta-heuristic algorithms with our proposed method and GN algorithm
Full size table

For small graphs, meta-heuristic algorithms can find high modular communities, but they may be fake communities which were elaborated in Fig. 8. In addition, in medium and large scale graphs, meta-heuristic methods might crash. It means that they need more memory and the detected communities might have low modularity. Therefore, the meta-heuristic methods are not scalable for the community detection. In addition, since the detected communities may be fake, the result of this approach is not reliable. In recent years, various meta-heuristic algorithms were introduced. In this paper, the result of the best algorithm is selected and compared with the proposed and GN methods. According to our implementation, Genetic Algorithm (GA) dominates the other methods such as PSO. Therefore, the result of the GN algorithm is reflected for the evaluation of meta-heuristic algorithm. Table 3 highlights these claims in summary.

Table 3 Evaluation of meta-heuristic algorithms and the proposed method
Full size table

Table 3 prove that the meta-heuristic algorithms are significantly slower than the proposed method and they are suitable for the small networks. Moreover, although meta-heuristic methods can detect communities of a small network with high quality, sometimes they may detect fake communities. Hence, the proposed algorithm is extremely faster than the meta-heuristic methods and it can detect better and reliable communities in medium and large scale graphs. Moreover, the proposed approach does not suffer from the detection of fake communities. In addition, in Table 3 and for Euroroad, our proposed algorithm detects modular communities in just 13704.96 seconds; while the implemented meta-heuristic algorithm could not terminate after 24 hours. However, for Euroroad, the quality of detected communities after 24 hours was just 0.041 which was disappointing in contrast to the proposed method. Hence, we just put a question mark in the relevant cells of Euroroad and meta-heuristic algorithm.

In addition, Fig. 9, compares the speed of the proposed and the meta-heuristic algorithm. According to this figure, our proposed algorithm is notably quicker than the meta-heuristic algorithms and by the increase of the graphs sizes this important feature becomes more and more highlighted.

Fig. 9
figure 9

The speed comparison of the proposed method and meta-heuristic algorithms

Full size image

6 Conclusion

Nowadays, community detection is used widely in complex network analysis to discover similar groups of nodes that have a tight connection with each other. In recent years various methods were introduced to discover communities which Girvan and Newman’s method (GN) is one of them. GN is a divisive, greedy, and hierarchical method that is based on edge shortest path betweenness centrality. Although GN is a popular method, suffers from scalability and computation complexity. Therefore, in this paper, a novel divisive, greedy and hierarchical approach is introduced that detects communities remarkably faster than GN method. Moreover, the detected communities by our proposed method often have better quality than the GN algorithm. The proposed paper has two important contributions that are: 1) multiple edges can be deleted in each iteration and 2) edge betweenness centrality is calculated based on edges degree. These features help our proposed method run more efficient than GN method. Furthermore, in the evaluation section, the efficiency of the proposed approach is proved through the assessment of its accuracy, quality, and speed by comparing with GN method. Finally, our proposed method is compared with meta-heuristic algorithms which results prove that our proposed method is scalable, stable, reliable, efficient, and free from predefined knowledge and parameter tuning.