Keywords

1 Introduction

We know that real networks are not random and they usually exhibit inhomogeneity, indicating the coexistence of order and organization. The most famous character of the networks is the community structure. Community structure embodies the famous saying that “the birds of a feather flock together”. In society, individuals with similar interests are more likely to become friends [6, 16]. In the Web, web pages with related topics are often hyperlinked together [5]. In the protein interaction network, communities are composed of proteins with the same specific function for chemical reactions [3, 17]. In metabolic networks, communities may correspond to functional modules such as cycles and pathways [9]. In food webs, compartments can be viewed as communities [12, 19]. Hence, the community becomes the entry point of researches of networks structure and functionality. Community detection is a fundamental research issue and attracts much interest over the last decade.

Community detection is to recognize the inherent structure of networks, i.e., dividing a network into several communities which have high density of edges within communities and low density between them. Nowadays, the most often used method is the modularity optimization-based community detection approach. Precise formulations of this optimization problem are known to be computationally intractable.

Several algorithms have therefore been proposed to find reasonably good partitions efficiently. The first algorithm devised to maximize modularity was a greedy method proposed by Newman [4]. It is an agglomerative hierarchical clustering method, where groups of vertices are successively joined to form larger communities such that modularity increases after the merging. A different greedy approach has been introduced by Blondel [1], for the general case of weighted graphs, which is the best algorithm that can be used in large networks. We take the two methods for comparison on different kinds of sizes of networks.

Besides, we make use of the PageRank algorithm [10] which is applied widely in community kernel detection to evaluate the importance of nodes. PageRank is a link analysis algorithm and it assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of “measuring” its relative importance within the set. As the structure of the World Wide Web is very similar to the structure of network, in which we can regard the nodes as the web pages and the edges as the hyperlink.

Our new algorithm, which we refer to as a smart local moving algorithm, takes advantage of both local moving heuristic and PageRank algorithm. Furthermore, the experimental result verifies the superior performance in modularity and computational efficiency in compare with the lovian algorithm.

The remainder of this paper is organized as follows. In Sect. 2, we present our new algorithm. We analyze the result of community kernel detection and compare the performance of the lovian algorithm with the fastgreedy algorithm in Sect. 3. We first consider small and medium-sized networks, and then focus on large networks. We summarize the conclusions of our research in Sect. 4.

2 Algorithm

Before we introduce our algorithm, we should make a detailed introduction on two crucial concepts, namely PageRank and modularity.

2.1 PageRank

PageRank [10] is a probability distribution used to represent the likelihood that a person would randomly visit a particular webpage. The idea is to imagine a random web surfer visiting a page and randomly clicking links to visit other pages then randomly going to a new page and repeating the process. The original PageRank of page A can be expressed as:

$$ PR\left( A \right) = \frac{1 - d}{n} + d\mathop \sum \limits_{{a \in W_{b} }} \frac{PR(a)}{L(a)} $$
(1)

Where n is the total number of pages in the system and d is the dampening factor that has been tried and tested in numerous studies happens to be about 0.85. W b is the set of pages connected to page A, PR(A) is the PageRank(A) and L(a) is the number of outbound links on page A.

But the difference from the original PageRank in web page is that the network we study here is undirected. So, we have to change the formula to:

$$ PR\left( i \right) = \frac{1 - d}{N} + d\mathop \sum \limits_{j \ne i} PR(j)\frac{{w_{ij} }}{{\mathop \sum \nolimits_{k \in adj[i]} w_{ik} }} $$
(2)

Where N denotes the number of nodes, \( adj\left[ i \right] \) denotes the set of neighbors of i, and W ij denotes the weight of edge ij.

2.2 Modularity

The modularity function [4] of Newman and Girvan is based on the idea that a random graph is not expected to have a cluster structure, thus the possible existence of clusters is revealed by the comparison between the actual density of edges in a subgraph and the density one would expect in the subgraph if the vertices of the graph were attached regardless of community structure. So it is written as:

$$ Q = \frac{1}{2m}\sum\limits_{ij} {(A_{ij} - \frac{{k_{i} k_{j} }}{2m})} \delta (c_{i} ,c_{j} ) $$
(3)

Where \( c_{i} \) denotes the community to which node \( i \) has been assigned; A ij denotes whether there is an edge between nodes i and \( j\left ( {A_{ij} = { 1}} \right) \) or not \( \left( {A_{ij} = \, 0} \right);k_{i} = \sum_{j} A_{ij} \) denotes the degree of node \( i, \) and \( {\text{m }} = { 1}/ 2\sum_{ij} A_{ij} \) denotes the total number of edges in the network. The function \( \delta \left( {c_{i} ,c_{j} } \right) \) indicates whether nodes i and j belong to the same community, which equals 1 if \( c_{i} = \, c_{j} \) and 0 otherwise.

The gain in modularity \( \varDelta Q \) obtained by moving an isolated node i into a community C can be easily computed by

$$ \varDelta Q = [\frac{{\varSigma_{in} + k_{i,in} }}{2m} - (\frac{{\varSigma_{tot} + k_{i} }}{2m})^{2} ] - [\frac{{\varSigma_{in} }}{2m} - (\frac{{\varSigma_{tot} }}{2m})^{2} - (\frac{{k_{i} }}{2m})^{2} ] $$
(4)

Where \( \sum_{in} \) is the sum of the weights of the links inside C, \( \sum_{tot} \) is the sum of the weights of the links incident to nodes in C, and \( k_{i,in} \) is the sum of the weights of the links from \( i \) to nodes in C.

2.3 Algorithm Description

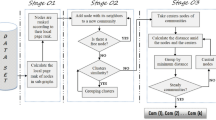
The main steps of the algorithm named LPR(Local PageRank) are shown in Algorithm 1:

Our algorithm consists of three phases that are repeated iteratively. Assume that we start with a weighted network of N nodes. Initially, we assign a different community to each node of the network, so each node in a network is assigned to its own singleton community.

Firstly, we calculate the PageRank value in which assigning initial PageRank value of each node with one, and recalculating each value according to the Eq. 6 until each PageRank value does not change any more. The PageRank value is not only used as the measurement to evaluate the importance of each node, but also used to determine the order in which nodes are chosen in the second phase.

In the second phase, we take out the node i in the reversed order according to the PageRank value calculated in first phase. Then, considering the neighbours j of node i, we evaluate the gain of modularity that would take place by removing i from its current community and by placing it in the community of j. If the maximal gain is positive, the node i is then placed in the community for which this gain, otherwise, node i stays in its original community. This process is applied repeatedly and sequentially for all nodes until a local maxima of the modularity is attained and the phase is then complete.

In the last phase of the algorithm, we rebuild a new network whose nodes are now the communities found during the second phase. To do so, the weights of the links between the new nodes are given by the sum of the weight of the links between nodes in the corresponding two communities. Links between nodes of the same community lead to self-loops for this community in the new network. After the last phase is completed, it is then possible to reapply the first two phases of the algorithm to the resulting weighted network and to iterate.

3 Experiments and Results

In this section, we study the performance of our LPR algorithm in contrast to the lovian algorithm and the fastgreedy algorithm. To quantitatively evaluate our algorithms, we take the modularity Q as the measurement and compare the computational time. Empirically, higher values of the Q function have been shown to correlate well with better graph clusterings [18]. In addition, we apply the LPR algorithm to the karate club network.

3.1 Data Set

We have selected ten small and medium-sized networks and three large networks commonly used in community detection, originating from a number of different domains. Although the real system is more complex, most directed networks can be transformed to undirected networks. Therefore all networks considered are undirected, shown in Tables 1 and 2.

Table 1. Number of nodes and edges of ten small and medium-sized networks.
Full size table
Table 2. Number of nodes and edges of three large networks
Full size table

3.2 Result Analyses

Result of Community Kernel Detection. In this section, we adopt the PageRank algorithm independently which is the first step in our algorithm to detect the community kernel in the karate club network. We show the original karate club network in Fig. 1 and the PageRank values in Fig. 2. We could get some information from Fig. 2 that the PageRank values of node 0 and node 33 are the greatest and obviously much higher than other’s which is consistent with the fact that at some point, a conflict between the club president (indicated by node 33) and the instructor (indicated by node 0) led to the fission of the club into two separate groups, supporting the instructor and the president respectively.

Fig. 1.
figure 1

The original network of karate club

Full size image
Fig. 2.
figure 2

The PageRank values of karate club

Full size image

Quantitative Performance. We can get modularity results when applying all algorithms to each network, shown in the Tables 3 and 4. It indicates that the modularity of our algorithm is always higher than the others two in all network data source. Especially comparing with the fastgreedy algorithm, our algorithm is obvious higher, but our algorithm gets slightly higher modularity when compared to lovian algorithm. However, as we can see from the Table 5, our algorithm has an advantage in computational time when applying in large networks, and especially in the com-LiveJournal network, our algorithm gets a 25 % reduction in comparison with the lovian algorithm.

Table 3. Results for 10 small and medium-sized networks.
Full size table
Table 4. Results for 3 large networks. For the com-LiveJournal network, the result of fastgreedy is not available because the computational complexity of those algorithm is too high to get a result in reasonabletime.
Full size table
Table 5. The time each algorithm takes in three large networks.
Full size table

Application Case Study. From our experiment, we know that the modularity of the karate club network is 0.4198, which is the best compared to the other algorithms’. We show the original karate club network in Fig. 1 and the division results in Fig. 3. The division result of our algorithm is the same as the famous lovian algorithm’s that splits the network into four parts.

Fig. 3.
figure 3

The application of our algorithm to the karate club network

Full size image

4 Conclusion

In this paper, we have introduced the LPR algorithm for modularity-based community detection. Our algorithm is intended primarily for community detection in large networks, and is combined with the PageRank algorithm to evaluate the importance of the nodes. Compared with five other algorithms, our algorithm gets a better result in the modularity and performs well in the division result of karate club network.

In future work, we would like to investigate the effect of other methods of community detection using the seed set expansion. Also, it is very interesting to detect community using the distributed computation method when dealing with super large networks.