1 Introduction

Social networking services such as Twitter, Facebook and WeChat provide convenient platforms where people can interact with each other without being limited by time and space. The people and their relationships built through these platforms constitute various social networks, through which a message can travel insanely wide and fast. The word-of-mouth manner of social networks is found of great value for viral marketing and social advertising. Compared to the traditional ways, viral marketing is based on the trust within individuals’ close social relationships like families, relatives, friends and co-workers. Research has shown that people tend to believe the information coming from their close social circles far more than that from general advertisement channels such as TV, newspapers and online ads[3]. A key and difficult point is to find the individuals who can spread information efficiently to more of their close circles. The problem of influence maximization is hence raised, which aims to discover a small group of people who can trigger the maximal number of the remaining to be involved in information spreading.

In recent years, this emerging research branch has obtained significant attention from both industry and academia [18]. The problem was first studied by Domingos and Richardson [7, 20] from an algorithmic perspective, and has attracted much research interest ever since. Especially in the recent decade, lots of algorithms have been proposed which generally can be divided into two categories: the methods based on explicit Monte-Carlo simulation results, such as Greedy [10] and CELF [12], and those based on a specific scoring system, like Degree and DegreeDiscount [4]. The former ones can usually get better performance with theoretical guarantee, while their high computational burden often makes them inapplicable to large-scale networks. The latter ones are efficient with respect to time, while they are sensitive to different networks and spreading models with unstable performance.

In this paper, we propose an influence maximization algorithm named Reversed Node Ranking (RNR), which finds influential seed nodes by exploiting the ranking information of a node to estimate its influence power. The advantages of utilizing the ranking are generally two-fold. First, the ranking of nodes contains global information compared with most scores which are designed based on local information. Second, the resolution of node ranking is much higher than the degree-based centralities, which means a lot of nodes share the same degree and meanwhile each node has its unique rank. Besides, we exploit the reversed node ranking as the weight for each node and present two different optimization strategies.

To evaluate the performance of our proposed RNR algorithm for influence maximization in social networks, we use both Independent Cascade model (the IC model) and Weighted Cascade model (the WC model) to measure the influence spread of seed nodes selected by our method and several other baselines including Degree, PageRank, DegreeDiscount, ProbDegree, LIR and Greedy. Compared with these baseline algorithms, our RNR algorithm always gives better performance, even superior to the Greedy algorithm under the IC model for some networks. Moreover, we present two optimization strategies to tackle the rich-club effect. As a by-product, we find that the IC model is more sensitive to the rich-club effect than the WC model.

The remainder of this paper is organized as follows. In Section 2, we present some core concepts concerning to the influence maximization problem and elaborate on the related literature. Section 3 describes our proposed method in details. Section 4 presents the experimental results under both the IC model and the WC model on real-world networks. Final conclusions will be given in Section 5.

2 Preliminaries and related works

2.1 Notations and preliminaries

Social network

A social network is denoted as G(V,E) where V and E are the sets of nodes and edges respectively. The number of nodes is usually denoted as either |V | or N, and the number of edges is usually denoted as either |E| or M.

Independent cascade model

Given a network G and a constant p which is the spreading probability during the whole spreading process, the IC model works as follows. If at time t, v is active and its neighbour u is inactive, v will try to infect u with the probability p. If this process is successful, u will be active at time t + 1. However, no matter it succeeds or not, v has only one chance to infect u. Besides, if u has more than one neighbour, the order of the neighbours that v will try to infect is arbitrary. The spreading process starts from the initial seed nodes until no new node can be activated.

Weighted cascade model

The WC model works just the same as the IC model, except for the spreading probability that is somehow different. In the IC model, the spreading probability that v can infect u (denoted by p(v,u)) is a constant, while the p(v,u) in the WC model is defined as 1/d(u) where d(u) represents the degree of node u.

Influence spread

Given a social network G, a set of seed nodes S and a spreading model, the influence spread σ(S) of the set S is the total number of both the seed nodes and the nodes that have ever been activated during the whole spreading process under the given spreading model.

Since the spreading is a stochastic process, the expected value of σ(S) is usually obtained by performing a considerably high number (typically 10,000) of Monte-Carlo simulations.

Influence maximization

Given a social network G and an integer k, the influence maximization problem needs to find k nodes (called seed nodes) such that the expected influence spread of these nodes is maximal.

Rich-club effect

The rich-club phenomenon is that the rich nodes (i.e. a small number of nodes with large numbers of links) tend to connect with each other [23]. For the influence maximization problem, nodes with a higher degree always have stronger influence power. Hence, if picked only according to the influence power, many of the seed nodes may connect with each other, which reduces the influence spread since there will be much overlap within their influence scope.

To evaluate an influence maximization algorithm, the influence spread σ(S) is usually computed with S denoting the node set containing k seed nodes output by the algorithm [1, 4, 5, 10, 16]. Besides, the stability and scalability of an algorithm is often checked by comparing its σ(S) with that of other algorithms under different spreading models, different network sizes and different k [4, 5, 10]. Obviously, a greater value of σ(S) indicates the higher quality of selected seed nodes and hence also better performance of the algorithm [1, 10].

2.2 Related works

The Monte-Carlo simulation is to simulate the spreading behaviour of each node throughout the network topology under a given spreading model in order to estimate the influence spread of a set of nodes. That is to say, the explicit influence spread of any given set can be evaluated if given enough time. Kempe et al. [10] first proved the influence maximization problem is NP hard. They also found the problem is submodular, based on which they presented the Greedy algorithm that can guarantee the influence spread to be within (1 − 1/e) of the optimal solution. However, when adding a new seed to the current set, the Greedy algorithm requires to find the node that brings the maximal gain to the influence spread of the current set. This process costs a huge amount of time since it needs to perform the Monte-Carlo simulation on all possible combinations of the current set and the remaining nodes. To overcome this drawback, Leskovec et al. [12] presented the CELF algorithm which is 700 times faster than the Greedy algorithm. They exploited the submodularity based on the simple idea that the marginal gain of a node in the current iteration cannot be better than that in the previous iterations. Moreover, Goyal et al. [9] presented the CELF++ algorithm which further optimizes the CELF algorithm but only brings limited improvements [1]. Generally, this category of algorithms performs quite well for influence spread in social networks as they always choose high-quality seed nodes. But they are still too time-consuming when compared to the algorithms based on the scoring system. This is because the submodularity of the influence maximization problem is not strictly guaranteed unless influence spread is evaluated through a large number of Monte Carlo simulations [5], which will lead to expensive computation.

The idea of the scoring system is to calculate a score for each node according to specific rules and pick the node with the highest score as the seed node iteratively. Some rules may require to refresh the scores when a seed node is picked out. A scoring system is usually designed based on classical indicators such as Degree, Betweenness [8], Closeness [2], and PageRank [17], etc. Among them, the Degree takes the degree (i.e. number of neighours) as the score for each node, and iteratively picks the node with the highest degree as the seed node. The DegreeDiscount algorithm [4], however, discounts a node’s score once a seed node is picked out. Its performance is much better than the Degree, but still inferior to that of the Greedy algorithm, mainly because its scoring system is essentially only based on the degree. Nguyen et al. [16] proposed the ProbDegree algorithm which considers the propagation probabilities of nodes in the network individually as well as the effects of a node’s neighbours. It scores a node according to not only its own degree but also the differences of its neighbours. Besides, after a seed node is picked out, the scores of its neighbours will be reset to zero to tackle the rich-club phenomenon [6, 23]. Analogously, Wang et al. [22] proposed the DegreePunishment algorithm which applies a punishing strategy to the neighbours of the selected seed nodes. The difference is that when discounting or punishing the neighbours, the DegreePunishment exploits the degree of the selected seed nodes. Liu et al. [13] proposed a fast and efficient algorithm named LIR. Its key idea is to find the nodes with locally maximal degree. First, the LIR filters out the nodes with an LI value bigger than zero. Then, each node is given a score equal to its own degree. Finally, seed nodes are selected according to their scores. These scoring-system based algorithms are much faster than those based on the Monte-Carlo simulation results. However, most of them have inferior performance to that of the Greedy algorithm. In fact, Greedy algorithm usually achieves better influence spread and is more stable on different networks or under different spreading models.

The Monte-Carlo simulation methods can obtain the actual marginal gain of influence spread for any node based on an arbitrary seed set. Therefore, they can guarantee their performance to be within (1 − 1/e) of the optimal solution. Theoretically, the same seed nodes will be obtained with these algorithms, but with different runtime which is still too much after several improvements. Comparatively, under a scoring system, all nodes will be scored according to certain rules. Thus the scoring-system based algorithms are much faster since they only need to score each node within one or several formulas. However, the influence maximization should be a global optimization problem while most scoring systems are based on the degree that only reflects local information. Besides, most scoring systems do not have a good discrimination ability when many nodes with the same degree sharing a same score for which however the topology is always different. Moreover, a lot of scoring systems are designed without taking into account the spreading model. They often equate the IC model and the WC model and use the same optimization strategy.

2.3 Illustration

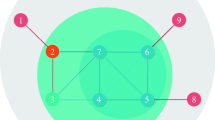
Take the network in Fig.1 as an example, where we show the limitations of some scoring-system based algorithms and also the advantage of our algorithm. We compute the scores of all the nodes with the Degree, the DegreeDiscount, the ProbDegree and our RNR algorithm. For comparison, we perform the Monte-Carlo simulation for 100,000 times to get the specific influence spread of each node. Detailed results are shown in Table 1.

Fig. 1
figure 1

A small network consisting of 8 nodes

Full size image
Table 1 Results of different algorithms on the small network in Fig. 1
Full size table

According to the influence value, the nodes should be ranked in the following order: N5, N1, N7, N6, N3, N2, N8, N4. It is clear that three nodes, namely N1, N5 and N7, share the same max degree of this network. Thus it will be hard to pick the first seed node with the Degree. Normally, the node with the smallest ID number is picked in this case. However, the influence power of these nodes with the same score are actually different and picking arbitrarily is obviously improper. The same problem also arises for the DegreeDiscount. The score computed by the DegreeDiscount (referred to as DD value in Table 1) has low resolution. The DegreeDiscount first picks N1 as the seed node (as N1 has a smaller Node ID compared to N5 and N7), which results in iterative discount on the DD value of N5. Thus the N5 has the lowest DD value at the end while it actually is the strongest spreader. Although the ProbDegree can pick the first seed node correctly, it still meets such a node selecting problem in the selection of the second seed node since the ProbD values of N1 and N7 are the same. Since RNR exploits the node ranking wich has high resolution, the RNR values of these nodes are different from each other, with an order as N5, N1, N7, N6, N3, N2, N8, N4. Besides, it is worth noting that the ranking acquired by the RNR algorithm is the same as the ground truth.

3 Reversed Node Ranking (RNR)

3.1 Innovation

The degree is a parameter that is often used in the scoring systems. A higher degree of a node often leads to stronger influence power, but they are not completely linearly dependent. Normally, a node with strong influence power will bring more benefits to its neighbours. Or reversely, a node will have stronger influence power if its neighbours are more influential. Therefore, we propose a ranking-based algorithm considering the following two aspects.

  • If the degree of a node is higher, the node should have stronger influence power.

  • If the neighbours of a node are more influential, the node should have stronger influence power.

As aforementioned, the resolution of ranking is much higher than that of the degree-based centralities, so the proposed algorithm utilizes the rank of the nodes to estimate their influence power.

3.2 Primary algorithm

Based on the above consideration, the algorithm is designed as follows.

Starting from a given ranking r, each node v will get its own rank according to the r. Noted that r maps from indices to nodes and rank maps from nodes to indices, i.e., for each positive integer i, r(i) indicates the node ranking the ith in the array and rank(i) represents the rank of node i. Thus, it is tenable that rank(r(i)) = i. Then, each node will be given a weight equal to its reversed rank as described in (1).

$$ reversed\_rank(v)=N + 1-rank(v) $$
(1)

Exploiting the reversed rank of each node as described in (1) brings three benefits. Firstly, it is easy to calculate with time complexity of O(N). Secondly, it accords with the fact that the node with a higher rank has stronger influence power. Thirdly, due to the high resolution of the ranking, each node has a unique weight.

Next, the algorithm calculates each node’s RNR value according to (2).

$$\begin{array}{@{}rcl@{}} RNR(v)&=&reversed\_rank(v)\\ &&+ \sum\limits_{u\in neigh(v)} reversed\_rank(u)*p(v,u) \end{array} $$
(2)

A node with a higher degree will have a higher RNR value as its RNR value will be accumulated by more reversed_rank(u). Also, the RNR value of a code will be higher if reversed_rank(u) of its neighbours is bigger. In other words, more neighbours or bigger reversed ranking of the neighbours will bring gains to the RNR value of the centred node.

After the RNR value is calculated for all the nodes, the algorithm will rank the nodes to get a new ranking according to their RNR values. Then, the RNR calculating process and the node sorting process will be repeated until the ranking is of no difference between two iterations. When the ranking reaches stable, the algorithm picks the node with the highest rank as a seed node and also deletes this node from the network. The whole process will be repeated until it finds k seed nodes in total.

The primary algorithm is summarized in Algorithm 1. The input includes the network G, the number of seed nodes k and an initial ranking r.

figure e

3.3 Advanced algorithms with optimization strategies

The primary algorithm provides the basic framework for selecting the seed nodes. However, the rich-club phenomenon that selected seed nodes may be adjacent to each other will make the influence scope highly overlapped among the seed nodes. To deal with this issue, we present two different optimization strategies.

  • Once a seed node is chosen, delete its neighbours from the network.

  • When calculating the RNR value of node v, reduce a neighbour’s contribution if the neighbour is adjacent to some seed nodes.

The algorithm with the first optimization strategy is named RNR_ND (Neighbour Delete). After a node is chosen as a seed node, the RNR_ND deletes both the node and its neighbours from the network. The whole process is formally depicted in Algorithm 2.

figure f

The algorithm with the second optimization strategy is named RNR_NW (Neighbour Weaken). Instead of directly deleting neighbours of the seed nodes from the network, the RNR_NW chooses to weaken the neighbours that are adjacent to the seed nodes when calculating the RNR value. The gain of the RNR value that a neighbour u would bring to the centred node should be reversed_rank(u) ∗ p(v,u). If the neighbour u is already adjacent to a certain number of seed nodes (denoted as neigh_seed(u)), the gain it brings to the centred node will be reduced since it may have already been activated by seed nodes with the probability of \(1-{\prod }_{w\in neigh\_seed(u)}(1-p(w,u))\). Thus, the expected gain it will bring to the centred node is \(reversed\_rank(u)*p(v,u)*{\prod }_{w\in neigh\_seed(u)}(1-p(w,u))\). The whole process of RNR_NW is formally depicted in Algorithm 3.

figure g

The optimization strategy of RNR_ND seems kind of so brute that there will be no connections between all the seed nodes. In contrast, the optimization strategy of RNR_NW is smoother as the nodes will be continuously weakened during the whole process. The two strategies are targeted at and thus suitable for different spreading models, which will be exhibited in the following experiments.

3.4 Impact of initial ranking

Both RNR_ND and RNR_NW need the input of a network G, the seed number k and an initial ranking r. G and k are affirmatory under a given circumstance while r can be variable. Thus, we are interested in the impact that different initial rankings will make. To be exact, we intend to check whether different initial rankings will affect the final results of the algorithms. We explore this problem by running both RNR_ND and RNR_NW with four initial rankings as follows.

  • Degree: The initial ranking is sorted in a descending order by degree.

  • PageRank: The initial ranking is sorted in a descending order by the PageRank value.

  • DegreeDiscount: The initial ranking is the result of the DegreeDicount algorithm.

  • Node ID: The initial ranking is the same as the node ID of the network.

We get the first 50 seed nodes with different initial rankings using RNR_ND and RNR_NW respectively. Besides, we use the Jaccard index to measure the similarity among the seed nodes obtained from the four different initial rankings. The experiments are conducted on the NetScience network [15].

As shown in Figs. 2 and 3, different initial rankings barely make any difference to the RNR algorithm. Starting from four different initial rankings, both RNR_ND and RNR_NW get the same 50 seed nodes eventually. The fluctuations of Figs. 2 and 3 are caused by the occasionally opposite selection order (mostly occurring with the initial ranking of Node ID) between two successive seed nodes. It is the reason why the Jaccard coefficient decreases a little bit and then goes back to 1 immediately.

Fig. 2
figure 2

Jaccard index between seed nodes with different initial rankings using RNR_ND

Full size image
Fig. 3
figure 3

Jaccard index between seed nodes with different initial rankings using RNR_NW

Full size image

Therefore, we use the ranking of degree for the algorithm as the degree is easier to calculate compared with PageRank and DegreeDiscount and more stable compared to Node ID.

3.5 Time complexity analysis

To pick a seed node, the Algorithm 2 needs to run loops until the ranking r is stable. Each loop containing the following four steps.

  • Lines 3-8, which requires O(N) to initialize the reversed_rank for each node.

  • Lines 9-11, which requires O(〈d〉N) to compute the RNR value for all nodes.

  • Lines 12, which requires O(NlogN) to sort the series.

  • Lines 13, which requires O(N) to compare whether two series are the same.

In summary, it requires O(N + 〈d〉N + NlogN) for each loop. If it takes at most q loops for the ranking r to get stable each time, the whole time complexity of Algorithm 2 is O(kq(N + 〈d〉N + NlogN)), which can be simplified to O(kq(M + NlogN)) where M is the number of edges in the network. The situation is roughly the same for Algorithm 3, which means the time complexity is O(kq(M + NlogN)) for both RNR_ND and RNR_NW.

4 Experiment

4.1 Dataset

In this paper, we conduct experiments on five different networks of the real world. (i) NetScience [15]: a coauthorship network of scientists working on network theory and experiment. (ii) Ca-GrQc [11]: a collaboration network of Arxiv General Relativity. (iii) Gnutella08 [11, 21]: a Gnutella peer to peer network from August 8, 2002. (iv) Ca-HepTh [11]: a collaboration network of Arxiv High Energy Physics Theory. (v) WordNet [14]: a lexical network of words. Detailed features of these networks are shown in Table 2.

Table 2 Detailed features of five real-world networks
Full size table

N and M are the numbers of nodes and edges of the network respectively. 〈d〉 and dmax denote the average degree and the max degree of the network. C is the clustering coefficient that measures the degree to which nodes in a graph tend to cluster together. pc is the spreading threshold of the network, which is determined as the position of the maximum of the susceptibility 〈s2〉/〈s〉2 (where 〈sn〉 is the nth moment of the outbreak size distribution computed for random initial single spreaders) [19].

4.2 Baseline algorithms

Experiments are performed with seven algorithms, six of which are used as comparisons to our RNR algorithm. The algorithms are listed below.

RNR

The algorithm proposed in this paper, which exploits the ranking information with high resolution for influence maximization. After several iterations, the RNR can obtain the ranking containing global information. Besides, two different optimization strategies (RNR_ND and RNR_NW) are designed to avoid the rich-club effect. The time complexity of the RNR is O(kq(M + NlogN)).

PageRank [17]

A node importance sorting algorithm based on the link relationships among nodes (referred to as PR in the following text). The PR evaluates each node with a score which also contains the global information, thus is used for comparison. The time complexity of the PageRank is O(q′M + kN) where q′ is the number of iterations for the algorithm to converge.

DegreeDiscount [4]

A classic algorithm based on the nodes’ degree (referred to as DD in the following text). After picking the node with the biggest degree, the DD will discount the degree of its neighbours, which can avoid the rich-club effect to a certain extent. The time complexity of the DegreeDiscount is O(kN + 〈d〉2), which is also claimed to be O(klogN + M) if using Fibonacci heap [4].

ProbDegree[16]

An algorithm taking into account the degree of both a node itself and its neighbours (referred to as ProbD in the following text). The ProbD scores a node with the sum of the node’s degree and its neighbours’ degree multiplied by the spreading probability. The time complexity of the ProbDegree is O(k〈d〉M).

LIR[13]

A simple and fast algorithm. To avoid the rich-club effect, the LIR directly picks the nodes with the locally biggest degree as the seed nodes. The time complexity of the LIR is O(M + kN′) where N′ represents the number of nodes with LI value being 0.

Greedy [10] (implemented with CELF optimization [12])

A classic greedy algorithm based on the explicit Monte-Carlo simulation. Theoretically, the Greedy can guarantee its influence spread to be within about 63% of the optimal solution with both stability and universality. Therefore, the Greedy is usually used as a benchmark to measure the performance of other algorithms. The time complexity of the CELF is O(kMNR) where R represents the times of repetitions needed for the Monte-Carlo simulations.

4.3 Experimental results

We implement the algorithms mentioned above on the five networks to acquire their seed nodes. However, We do not acquire the seed nodes of the Greedy under the WordNet network because it is too time-consuming. We also run the Monte-Carlo simulation for 10,000 times under both IC and WC model with their seed nodes. Detailed results are shown as follows.

4.3.1 Influence spread

We run the Monte-Carlo simulation with the number of seed nodes varying from 1 to 50. The results under the IC model are shown in Fig. 4 and the results under the WC model are shown in Fig. 5.

Fig. 4
figure 4

Influence spread of different algorithms under the IC model

Full size image
Fig. 5
figure 5

Influence spread of different algorithms under the WC model

Full size image

As shown in Fig. 4, the purple and red curves with circles represent the influence spread of RNR_ND and the RNR_NW respectively. Obviously, the influence spread of RNR_ND is generally bigger than the algorithms based on the scoring system and even exceeds the Greedy (curve in cyan) on Ca-GrQc network, Gnutella08 network and Ca-HepTh network. As the DD and the LIR essentially score a node based on its degree, they show similar performance with the Degree when k is small. Although the PR scores each node based on the global information, it still gives poor performance under the IC model. The is because, in the PR, each node shares its weight with its neighbours while the spreading probability is a constant in the IC model, thus nodes with a higher degree and a greater weight can not bring greater gains to their neighbours. Besides, it is worth noting that the performance of the RNR_ND is obviously better than the RNR_NW under the IC model. Once a node is chosen as a seed node, the gain of influence spread brought by picking its neighbours will be greatly reduced since the spreading probability is the same between nodes. The results show that the IC model is sensitive to the rich-club effect.

The case is somehow different under the WC model. As shown in Fig. 5, the Greedy and the RNR_NW are the two best-performing algorithms in influence spread except for the WordNet network under which the Degree performs best. The influence spread of RNR_NW and the Greedy is similar on NetScience network and Ca-HepTh network while the Greedy is slightly better than RNR_NW on Ca-GrQc network and Gnutella08 network w.r.t. the influence spread. However, since the spreading probability in the WC model accords with the weight assignment strategy of the PR, the performance of PR is significantly promoted. Moreover, opposite to the case under the IC model, the performance of RNR_NW is now much better than the RNR_ND, since under the WC model, the bigger the degree of a node is, the less likely it will be spread. When two nodes with a large degree are neighbours, the probability of their spreading to each other is small, thus the rich-club effect will also be weakened. Therefore, a node with a large degree can still bring a considerable gain if picked as a seed node even if its neighbours have already been picked. Compared with the IC mode, the WC model is not that sensitive to the rich-club effect.

It is revealed by the experiments that the IC model is more sensitive to the rich-club effect than the WC model. For the IC model, it is better to use the RNR_ND since it completely avoids the rich-club effect and ensures that seed nodes will never be neighbours. For the WC model, it is more appropriate to use the RNR_NW which just weakens the rich-club effect. Actually, the RNR_ND under the WC model will incorrectly delete some high degree nodes.

4.3.2 Spreading speed

Apart from the influence spread, we also consider the spreading speed of the algorithms, which can be revealed by the number of activated nodes at each time step during the whole process. All the algorithms are tested with 50 seed nodes.

As shown in Figs. 6 and 7, RNR_ND (purple curve with circles) and RNR_NW (red curve with circles) achieve high spreading speed respectively under the IC model and the WC model, which reflects the efficiency of the proposed RNR algorithm.

Fig. 6
figure 6

Spreading speed of different algorithms under the IC model

Full size image
Fig. 7
figure 7

Spreading speed of different algorithms under the WC model

Full size image

However, since the spreading probability is a constant for the IC model, some degree-based algorithms which tend to select the nodes with more neighbours may achieve a faster speed at the beginning. But their speed will soon slow down within just a few time steps. Besides, although the spreading speed of RNR_ND is not the most outstanding under the IC model, it is always better than or at least equal to that of Greedy which has the state-of-the-art performance. It is shown that RNR_ND is better considering the trade-off between influence spread and spreading speed.

The spreading speed is more stable under the WC model as Fig. 7 shows. It is obvious that RNR_NW is, by and large, better than other algorithms based on the scoring system throughout the timeline on the five networks. Because the influence spread of RNR_NW is a little inferior to that of Greedy, Greedy could always influence a bit more nodes in each time step. So that RNR_NW is a little worse than the Greedy in spreading speed.

4.3.3 Relations among seed nodes

To explore the difference between the IC model and the WC model, we investigate the relations among the seed nodes of different algorithms. We figure out the number of edges among the 50 seed nodes picked by these algorithms under two spreading models. The results are shown in Fig. 8.

Fig. 8
figure 8

The relations among the seed nodes picked by different algorithms under two models

Full size image

We do not show the results of the Degree in the figure since there are a large number of relations, which makes it hard to see clearly the figure. We also do not include the results of the ProbD and the RNR_ND since there is always no relation owing to their optimization strategies. Besides, We do not show the results under the WordNet network since the standard (seed nodes of the Greedy) is not available. The results of the PR and the LIR are the same between two spreading models because their scoring process has nothing to do with the spreading probability. Compared with the IC model, more relations appear for the DD under the WC model, for which the changing trend is the same with the Greedy. As the Greedy always finds the optimum for each step, the relations among the seed nodes under the WC model should be more than those under the IC model. This phenomenon agrees with our previous observation that the IC model is more sensitive to the rich-club effect than the WC model. Thus, there should be fewer relations under the IC model to avoid the rich-club effect. The seed nodes of RNR_ND have no relation among each other under the IC model and there are a small number of relations among the seed nodes of RNR_NW under the WC model. Moreover, the numbers of relations for RNR_NW and the Greedy under the WC model are relatively close. The different optimization strategies of RNR exactly correspond to the features of two different spreading models and thus give superior performance.

The experiments have shown that although the IC model and the WC model are both cascade models, the same strategy usually has different performance under the two models. Therefore, when designing the influence maximization algorithms, the IC model and the WC model should be treated differently and different optimization strategies should be considered according to the model’s features.

4.3.4 Comparison of time complexity

The time complexity of both our proposed algorithm and baseline algorithms are summarized in Table 3. It is shown that the Degree has the lowest time complexity but its performance is not satisfactory in terms of influence spread. The LIR is also lower in time complexity since it is very simple and finds the nodes with locally maximal degree, but it only brings limited improvement to the Degree. Since q and q′ which denote the number of iterations are usually constant, the Pagerank and the DegreeDiscount (without Fibonacci heap) are slightly better than the ProbDegree and the RNR w.r.t. runtime. However, the performance of the ProbDegree and the RNR is superior and more stable. Particularly, the RNR achieves comparable performance in both influence spread and spreading speed to that of the Greedy with much less time cost.

Table 3 Comparison of time complexity among different algorithms
Full size table

5 Conclusion

In this paper, we propose an algorithm with two different optimization strategies for the influence maximization, which is named Reversed Node Ranking (RNR). Compared to existing algorithms, the proposed RNR exploits the ranking information with high resolution to iteratively pick the seed nodes. Besides, the reversed rank is used as the weight for estimating the influence power. The reversed rank accords with the fact that the node with a higher rank has stronger influence power and is unique for each node. To avoid the rich-club effect, two different optimization strategies are presented. One ensures that there will be no connections between seed nodes, and the other reduces the gain that a neighbour brings to the centred node if it is adjacent to some seed nodes. Experiments are conducted under both the IC model and the WC model to examine and compare the influence spread among different algorithms. The results show that the proposed RNR algorithm is superior to most of the algorithms and even to the Greedy algorithm under the IC model. Furthermore, the RNR algorithm reveals that the IC model and the WC model need different optimization strategies due to their different levels of sensitivity towards the rich-club effect. We therefore suggest that different spreading models be treated differently and algorithms be designed in accord with the model’s features.

For future work, we will try to optimize our algorithm to reduce its time cost, especially in the sorting part which occupies most of the runtime. Moreover, we believe our proposed iterative global ranking framework is of generality for some scenarios in which global evaluations are requested, and it can also be adapted in some re-ranking applications. We will also try to exploit the gap between the Greedy algorithm and the optimal solution to find out how much room is left for improvement in this field.